A measure for describing and comparing post-reproductive lifespan as a population trait

Summary

1. While-classical life-history theory does not predict post-reproductive lifespan (PRLS), it has been detected in a great number of taxa, leading to the view that it is a broadly conserved trait, and attempts to reconcile theory with these observations. We suggest an alternative: the apparently wide distribution of significant PRLS is an artifact of insufficient methods.

2. PRLS is traditionally measured in units of time between each individual’s last parturition and death, after excluding those individuals for whom this interval is short. A mean of this measure is then calculated as a population value. We show this traditional population measure (which we denote PrT) to be inconsistently calculated, inherently biased, strongly correlated with overall longevity, uninformative on the importance of PRLS in a population’s life-history, unable to use the most-commonly available form of relevant data and without a realistic null hypothesis. Using data altered to ensure that the null hypothesis is true, we find a false positive rate of 0.47 for PrT.

3. We propose an alternative population measure, using life-table methods. Post-reproductive Representation (PrR) is the proportion of adult years lived which are post-reproductive. We briefly derive PrR and discuss its properties. We employ a demographic simulation, based on the null hypothesis of simultaneous and proportional decline in survivorship and fecundity, to produce a null distribution for PrR based on the age-specific rates of a population.

4. In an example analysis, using data on 84 populations of human and non-human primates, we demonstrate the ability of PrR to represent the effects of artificial protection from mortality and of humanness on PRLS. PrR is found to be higher for all human populations under a wide range of conditions than for any non-human primate in our sample. A strong effect of artificial protection is found, but humans under the most-adverse conditions still achieve PrR of >0.3.

5. PrT should not be used as a population measure, and should be used as an individual measure only with great caution. The use of PrR as an intuitive, statistically valid and intercomparable population life-history measure is encouraged.

Introduction

Post-reproductive lifespan (PRLS) is the phenomenon of individuals or cohorts surviving past the age at which they can no longer expect to produce offspring. Put another way, it is the demographic outcome of a delay in actuarial senescence (increase in mortality rate with age) compared to reproductive senescence (Hill and Hurtado 1991). The classical evolutionary theory of senescence and most-life-history optimization models do not predict PRLS, as survival does not improve fitness if the individual is no longer reproducing. However, post-reproductive individuals, and seemingly significant PRLS at the population level have been detected in a wide range of organisms, not only diverse human populations (Hawkes et al. 1998, Lahdenpera et al. 2004), but also several other primates (Fedigan et al. 2007), very many mammals (Cohen 2004), guppies (Reznick et al. 2006), aphids (Kidd and Tozer 1985), nematodes (Chen et al. 2007) and species as phylogenetically distant as yeast (Minois et al. 2005). These findings have lead to the view that PRLS is a phylogenetically conserved trait (Cohen 2004), and Austad (1997), questions the need for, "special pleading for a novel evolutionary explanation,” for women's PRLS. Despite this, research into human-specific explanations for the origin and function of PRLS is a thriving field (Lee 2008, Alvarez 2000, Cant and Johnstone 2008, Pavard et al. 2008, Gurven 2008, Tuljapurkar et al. 2007, Gillespie et al. 2010, Hawkes et al. 2009, Sear and Mace 2008). This apparent contradiction is generally explained by stating that human PRLS is importantly greater than, if not qualitatively different from, PRLS in other species.

Attempts have been made to reconcile the evolutionary theory of senescence with the finding of widespread significant PRLS (Cohen 2004, Peccei 2001). In this paper we argue that such efforts may be premature, as the methods we have been using to assess the significance of PRLS are inappropriate and statistically invalid when applied to populations. We propose an improvement, both to reduce Type I Error (falsely rejecting the null hypothesis), but also what has been called Type 0 Error: failing to ask the question (Michels and Rosner 1996). Data to test for PRLS are available for many taxa, but are often unexploited, being in a form unsuited to the current method.

PRLS is traditionally measured in units of time. We will refer to such measurement as Post-reproductive Time (PrT). We will argue here that PrT is an inherently flawed measure when applied to populations, useful only under very limited circumstances. We offer an alternative measure, which estimates the representation of post-reproductive individuals in a stable population, Post-reproductive Representation (PrR). We then compare the behavior of PrT and PrR using a large data-set on the demography of humans and other primates.

Methods old and new

The old method

PrT measures the distance between the end of fecundity and the end of life. Generally, its calculation proceeds as follows: First, all individuals not reaching a certain threshold are excluded. Most often this means only those individuals living some minimum time beyond last parturition or a population measure of reproductive cessation are considered. Second, the time between each included individual's last parturition and that individual's death is measured. Finally, a mean of these times is calculated to produce a population measure. While these measures have been made for a wide range of species (as described above) they have rarely been used to compare between populations and taxa. PrT suffers from six shortcomings, described below, which may explain this lack of comparative application.

1. PrT is inconsistently calculated

Many methods have been used to calculate PrT. Fedigan et al. (2007) present a table of PrT for 20 primate species, all in units of years, but calculated in six different ways. Some authors subtract a measure of time during which the individual could have reproduced, but did not; others don't consider an individual to be post-reproductive until she is well beyond the age at which her population ceases reproducing, or other variations (compiled in Cohen 2004). Fedigan et al. advocate a standardization of the measurement of PrT as individual age at death minus that individual's age at last birth based on the calculations of Caro et al. (1995). This would include standardization in significance testing based on interbirth interval, as discussed below.

2. PrT is a biased measure of PRLS

PrT is measured based only on the experience of those living well beyond reproductive cessation (Caro et al. 1995, Pavelka and Fedigan 1999, Cohen 2004). Other individuals are excluded from analysis to avoid classifying as post-reproductive those who simply die before they can give birth again. However, their exclusion introduces a serious bias. In order to be very confident that every individual in the sample is post-reproductive, we must abandon confidence that every post-reproductive individual is in the sample. Specifically, those individuals with short but legitimate PrT (the lower end of the distribution) will be excluded. Any mean so calculated is seriously inflated.

3. PrT fails to convey the relevance of PRLS

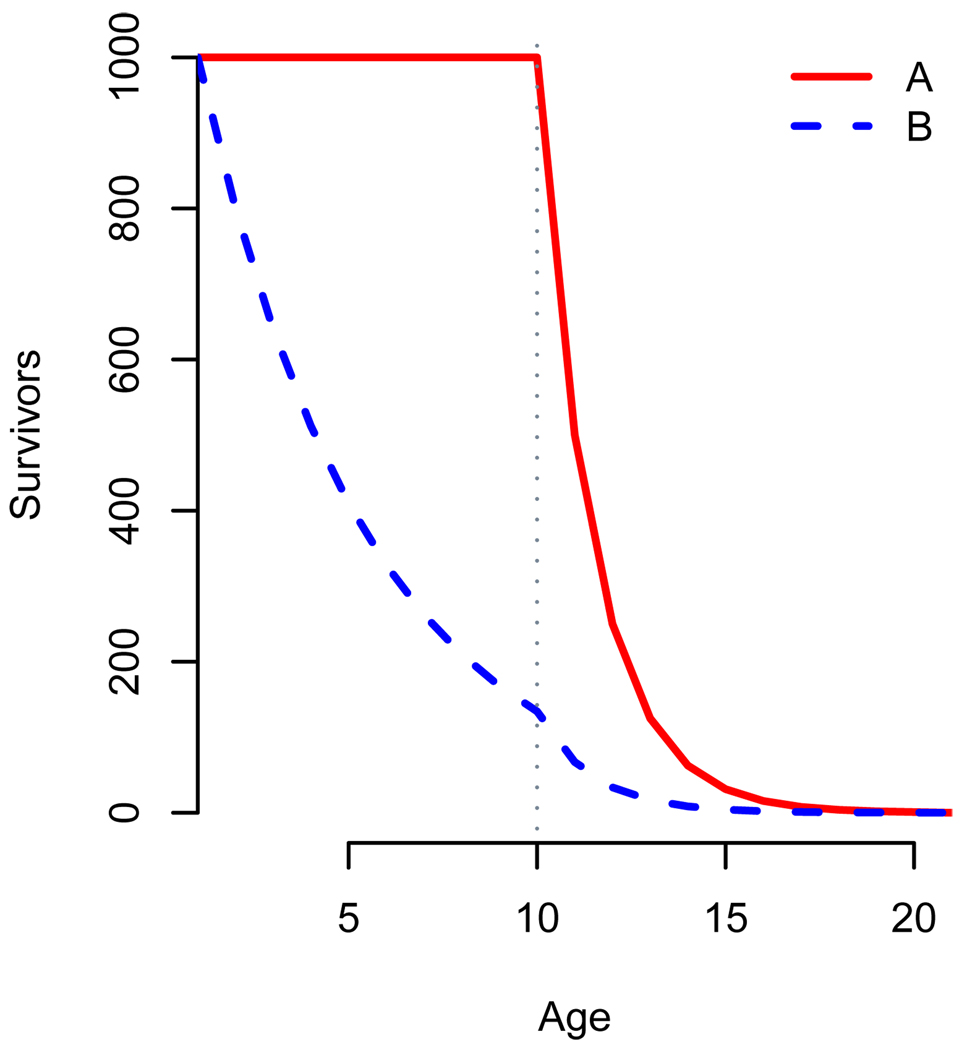
An associated effect is that PrT gives little guidance as to how important post-reproductive periods are in the life-history of populations, because it does not take into account how many individuals live to be post-reproductive. Fig. 1 gives a hypothetical example of two populations. In each case, reproductive lifespan is ten years, and PrT is one year, but fewer individuals in population B reach reproductive cessation. An individual in Population A would be far more likely to have post-reproductive kin, and to have a post-reproductive period of her own, than one in Population B. Some authors (Cohen 2004, Fedigan et al. 2007) address this problem by giving both PrT and an estimate of what proportion of individuals reach reproductive cessation. For comparisons between populations this information must be incorporated into a single parameter.

Figure 1.

Age-specific survival for populations with identical Post-reproductive Times are shown. Populations A (red line) and B (blue dashed line) both begin reproducing at age=0, reach reproductive cessation at age=10, and both experience 50% annual mortality in years 10 and above. Population A experiences no mortality prior to reproductive cessation, while Population B experiences 20% annual mortality. 16.6% of years lived by population A are post-reproductive, compared to 4.5% of years lived by B. However, PrT for each population is one year. For both these populations the ratio of PrT to fertile lifespan is 1/10.

4. PrT is strongly correlated with overall longevity

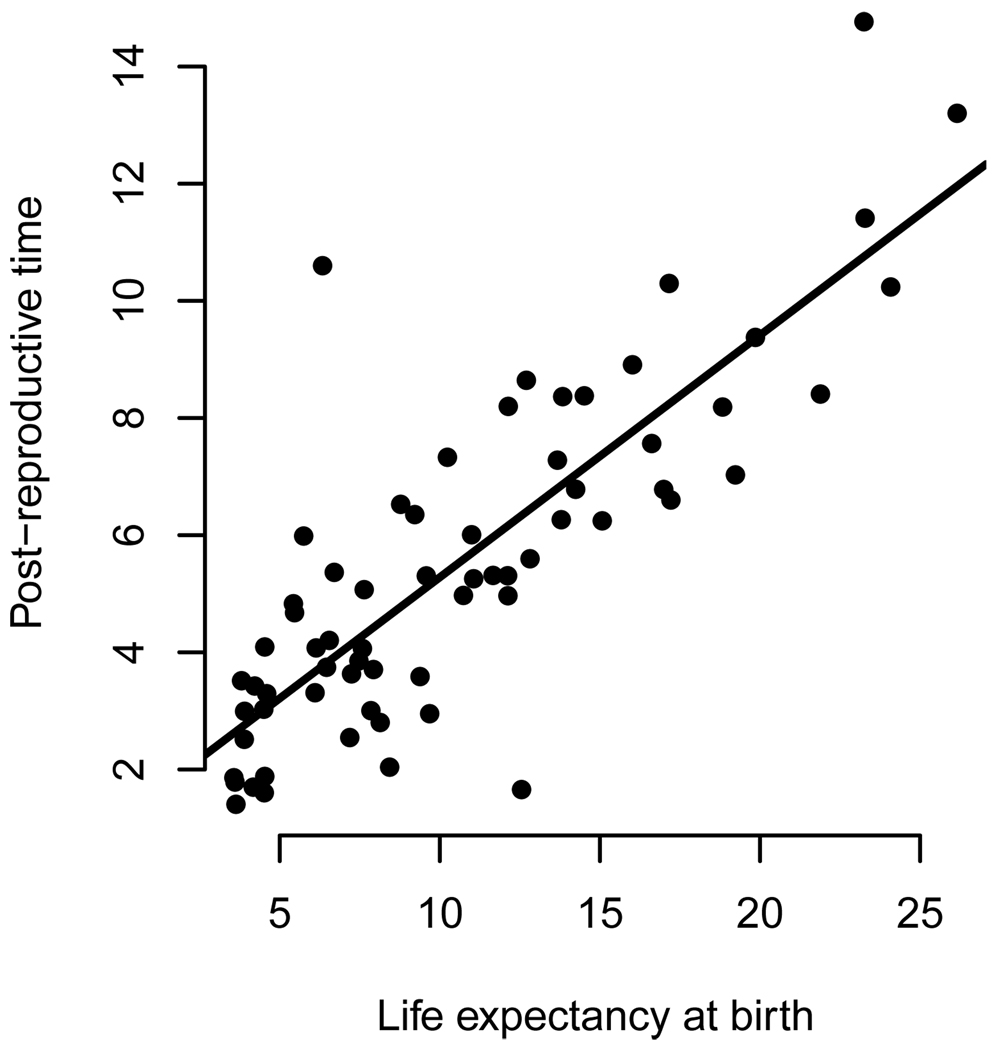
It is common to read statements such as, “humans are unique among primates in that women regularly outlive their reproductive period by decades,” (Kachel et al. 2010) or that among mammals, only humans and some whales “stop reproducing long before they die” (Johnstone and Cant 2010). These statements would be true regardless of the biological significance of PRLS in these species. Women are unique among primates in having life-expectancies of several decades, and few other mammals live as long as humans and whales do. Organisms generally (Kirkwood 1992) and mammals specifically (Carey and Judge 2000), live on widely varying time scales and PrT scales isometrically with lifespan. Fig. 2 plots PrT against life expectancy at birth (e₀) for 66 captive primate populations, revealing that two thirds of the variation in PrT is attributable to the overall time scale on which organisms live. While the PrT of humans and some whales (Foote 2008, McAuliffe and Whitehead 2005, Ward et al. 2009) is in fact disproportionately long compared to overall longevity, one cannot conclude this from PrT alone. Similarly, the short PrT of a mouse or rotifer should not dissuade us from looking for biological or statistical significance. Authors wishing to make quantitative comparisons between populations should have at their disposal a parameter which controls for the time-scale of life-histories.

Figure 2.

Post-reproductive time (PrT) scales with life expectancy at birth. A measure of PrT (e_M) plotted against life expectancy at birth (e₀) for 63 species of captive primates. Data are from the International Species Information System. The majority of information in these interspecies comparisons of PrT is attributable to the overall longevity of the organisms (Adjusted R-squared: 0.67), not to variation in the representation of post-reproductive individuals in the populations, indicating that PRLS is of limited value for comparisons between species with different overall longevities. The upper outlier in this graph is the Brown Wooly Monkey, Lagothrix lagotricha, a species known to be difficult to breed in captivity (Mooney and Lee 1999), and without exceptional PRLS as measured by PrR or ecological reason to expect unusual PRLS.

5. PrT cannot use available data

The standard calculation of PrT requires data on individual life histories. At what age did each individual have each of her parturitions and die? PrT cannot be calculated or reasonably estimated from age specific rates (population life-tables and fecundity-tables). Consider two populations with identical age-specific fecundity and mortality schedules. In the first population all individuals remain fertile up to the age M, but the fecundity rate declines because interbirth interval increases with age. This will lead to relatively short PrT. In the second population interbirth interval remains constant but many females stop reproducing prior to age M, achieving long post-reproductive times. These two populations will differ in PrT values in ways not communicated by their shared age-specific rates.

Age-specific rates are often available for populations where large samples of full individual life-histories have not been published (Biodemographic Database 2010). While the full sharing of underlying data is a desirable goal, it has often not been achieved, for reasons of confidentiality, priority, journal space or logistical simplicity. As such, comparisons using individual-based PrT must omit the large number of populations for which only age-specific rates are available.

In a less conventional approach, one can calculate PrT from age-specific rates, as survival past the age when the population is judged to reach reproductive cessation. To do so, one needs to decide how to measure when cohort survival ends (mean life-expectancy, maximum longevity or some other measure), as well as when cohort reproduction ends. There is no standard for these decisions. In Fig. 1, we have used e_M, (see Box 1) mean life-expectancy at an age which is a near endpoint of cohort fecundity. For human populations, maximum longevity and age 45 years has been used for these purposes (Blurton-Jones et al. 2002). This method can be employed successfully if the populations being compared reach reproductive cessation at the same age, the probability of surviving to that age is similar, and sample sizes are comparable. Under these conditions, this calculation will reveal only which population has greater PrT, not how many post-reproductive individuals one will find in the populations.

Box 1: Ages and Demographic Notation.

The demographic notation used here, based on standard life-table methods, are as follows:

• x represents exact age at the start of an age interval.

• L_x is the number of individual-years lived between ages x and x+1

• m_x is age-specific fecundity (as defined by biologists), the total number of offspring of both sexes born to all individuals between the ages of x and x+1 divided by L_x. Note that this is what demographers refer to as fertility (i.e., realized reproduction, strongly influenced by behavior) and is distinct from the demographic usage of fecundity (the physiological capacity to reproduce).

• l_x is the number of individuals surviving to exact age x (Life-tables are generally presented with an arbitrary initial cohort size, or radix. Where radix=1 l_x is the probability that a newborn survives to x).

• e_x is the mean remaining life expectancy at x.

• T_x =e_x*l_x is the total individual-years lived after x

The calculation of these parameters is described in detail in Preston et. al. (2001).

PrR is calculated based on these functions evaluated at two ages: Age B, the beginning of the reproductive lifespan, or of adulthood.

Operationally, we define B as the first time period of age at which 5% of life-time fecundity has been realized, on average, independent of mortality. That is:

$${\displaystyle \sum _{x=0}^B{m}_x\ge 0.05{\displaystyle \sum _{x=0}^{\infty }{m}_x\text{ for B an integer}.}}$$

Age M, the end of fecund lifespan. Operationally, we define M as the first time period of age at which 95% of life-time fecundity has been realized, on average, independent of mortality. That is:

$${\displaystyle \sum _{x=0}^M{m}_x\ge 0.95}{\displaystyle \sum _{x=0}^{\infty }{m}_x\text{ for M an integer}.}$$

Our calculations of M for human natural-fertility populations are similar to published estimates of mean maternal age at last parturition for natural-fertility populations (Bongaarts 1982). B and M each exclude 5% of the area under one tail of the fecundity curve. For that reason, and because they are cumulative measures, these parameters are resistant to demographic outliers (e.g., human females who have babies in their late fifties or later). They are useful in determining near-endpoints on the population level, not extreme individuals.

Age F is the last age of peak fecundity: F is the largest integer value of x satisfying the condition that m_F = max(m_x).

The use of age-specific rates excludes important information relating to individual stochastic events and life-history plasticity. An individual's reproductive history plays an important role in determining her mortality (Doblhammer 2000), and where the goal is to understand with-population variation, age-specific rates are uninformative. That said, age-specific mortality rates evolve based on the average reproductive output at each age. This implies that even if a woman does not reproduce after age 30, her evolved age-specific mortality risk at age 31 reflects primarily the fact that many of her ancestors did reproduce at later ages, not the fact that she has had her last child. A 31 year old woman may be individually post-reproductive, but her continued survival requires no explanation beyond that offered in the classical evolutionary theory of senescence (Charlesworth 2000, Hamilton 1966, Kirkwood and Shanley 2010). We therefore argue that population averages rather than individual variations around those averages are most-useful for understanding post-reproductive lifespan at the population level. Where individual level data are available, and the goal is to compare one individual's life-history to another's within the same population, PrT may be a sensible measure for some questions; its use in describing or comparing between populations should be avoided.

6. PrT lacks a robust null

If reproductive senescence exactly parallels falling survivorship, what will PrT be? It cannot be zero. Indeed, even Pacific salmon, a common example of lack of PRLS (Wachter et al. 1997), exhibit short but non-zero PrT (Carlson et al. 2007). Nor can PrT be negative, as fecundity generally cannot occur after death. Every population in which reproduction and death are not simultaneous has PrT > 0 (Kirkwood and Shanley 2010).

Biologists have approached this problem by testing whether PrT for individuals exceeds the mean plus two standard deviations of interbirth interval $\overline{\mathit{\text{IBI}}}+2\mathit{\text{SD}}(\mathit{\text{IBI}})$ (Caro et al. 1995). The thinking is that if an individual hasn’t reproduced for significantly longer than the mean of her interbirth intervals, she can confidently be labeled as post-reproductive. A similar approach is to ask whether the individual’s final, open birth interval is significantly greater than 95% of the distribution of her closed birth intervals (Reznick et al. 2006). However, because interbirth interval increases markedly with age (Bronikowski et al. 2002, Koyama et al. 1992), these approaches may greatly exaggerate the incidence of PRLS in populations in which older individuals have greatly increased birth spacing. Further, by selectively excluding those individuals whose PrT is small, and those with no second parturition, authors greatly increase the risk of false positives. Determining whether PRLS is extensive enough to carry biological or statistical significance requires a measure other than PrT.

The new method

We therefore seek a measure of PRLS which can be calculated consistently and without bias, using age-specific rates to compare between demographically diverse populations. This method should allow for statistical comparison to a null hypothesis. We propose PrR, Post-reproductive Representation, as such a measure. We will first describe the calculation of PrR and its characteristics, before discussing significance testing.

Deriving PrR

The simplest population measure of survival beyond reproductive cessation is e_M, remaining life expectancy of those individuals who have survived to age M. This parameter is a measure of PrT in that it is given as a length of time after reproductive cessation. By multiplying e_M*l_M=T_M we account for both how many individuals become post-reproductive, and for how long they survive post-reproductively. T_M represents the mean expectation of a new-born individual for life beyond age M. T_M is still of limited utility in comparing between populations with different scales of longevity or different levels of pre-reproductive (x<B) mortality.

These drawbacks can be overcome by taking the ratio of T_M to T_B. T_B gives the number of years an average newborn can expect to live as an adult, while T_M gives the number of years an average newborn can expect to live as a post-reproductive adult. We therefore calculate

$$\text{Pr}R=\raisebox{1ex}{$T_M$}\!\left/ \!\raisebox{-1ex}{$T_B$}\right.=\frac{l_M}{l_B}*\frac{e_M}{e_B}$$

PrR is particularly useful in comparisons between populations. As with a Charnovian invariant (Charnov 1993), it is unitless, and therefore independent of time scale, and the size of the organism. It is independent of infant and juvenile mortality but dependent upon survival through the reproductive and post-reproductive periods. It provides an intuitive measure of post-reproductive survival. In a stationary population (where rates and population size are constant), PrR tells us what proportion of the adults are post-reproductive. For example, if PrR for the females in a stationary human population is 0.66, 66% of women in that population are post-reproductive. Girls in a stable population (one in which rates remain constant through time, but population size may change), with PrR=0.66 can expect to spend an average of two thirds of their adult lives older than age M.

Using this demographic notation, a variety of measures (e.g., l_M/l_B, e_M/e_B) can be derived to suit particular questions regarding post-reproductive lifespan; the usage of demographic methods by biologist studying demographic traits is encouraged.

Significance testing

As with PrT, PrR generally cannot be zero or negative. However using demographic simulations and an explicit null hypothesis, a null distribution for PrR can be calculated for each population.

Our null hypothesis is that cohort mortality and cohort fecundity loss should occur in parallel once reproductive senescence sets in. More formally, $\frac{-\mathrm{\Delta }{l}_x}{l_x}=\frac{-\mathrm{\Delta }{m}_x}{m_x}$ _x, for x>F, the age of maximum fecundity.

A null distribution of PrR values can be generated using repeated demographic simulation. Annotated code for these simulations, written in the statistical programming language R (RCDT 2010), is given online in Appendix 3. Age specific rates consistent with the null hypothesis are estimated by altering the population’s l_x series after age F such that the proportional decline in l_x at each age is equal to the proportional decline in a smoothed m_x series (Fig. 3). Smoothing is necessary to ensure a monotonic decline; m_x can meander downward, but l_x can only decrease with age. Individuals are then simulated using the observed m_x series and the altered l_x series. 1000 populations, each with the same number of female individuals as the original data, are simulated in this way, generating 1000 estimates of PrR consistent with the null hypothesis. This is taken as the null distribution, and compared to the PrR calculated for the real population. The probability of obtaining a value at least as high as the real PrR if the null hypothesis is correct is equal to the number of simulated populations with higher values, divided by 1000. For example, a population PrR value which is lower than or equal to only 25 of the 1000 simulations would be significant at the 0.05 level for a two-tailed test. All P-values given below are based on this two-tailed test. PrR significantly above the null distribution implies that actuarial senescence is delayed as compared to reproductive senescence.

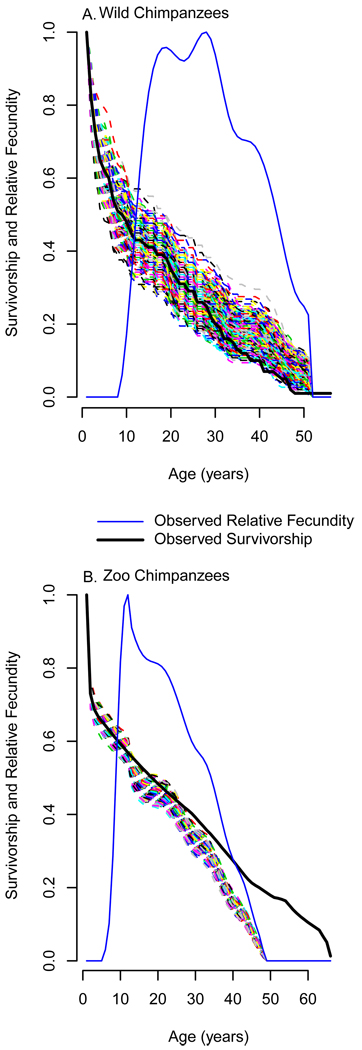
Figure 3.

A null hypothesis for Post-reproductive representation (PrR) is generated by altering the observed survivorship curve (solid black line), such that its decline after the age of maximum fecundity is proportional to the decline of age-specific fecundity (solid blue line). This new curve is employed to calculate yearly survival probabilities (p_x) for a population in which survivorship and fecundity decline in parallel. 1000 populations are simulated using these altered survival probabilities. PrR is calculated for each, generating the null distribution against which the observed value can be compared. We illustrate this process for two chimpanzee populations. Each dashed multicolored line is the survivorship curve (l_x) for a single simulated population. Wild chimpanzee (A) survivorship decline is at the low end of their null distribution. Zoo chimpanzees (B) live significantly longer than is expected based on their rate of reproductive senescence. The larger sample size in B leads to a tighter null distribution.

Application of the methods

To demonstrate the use of PrR and examine the properties of both PrR and PrT, we employ age-specific vital rates for the females of each of several human and non-human primate populations. We asked three questions of these data: what is the false positive rate when using standard methods to test the significance of PrT?; how do humans compare to non-human primates in PrR?; and what effect does artificial protection and improving environment have on PrR?

Data employed. Details on data sources and methods are given in online Appendix 1. For each population we entered into the dataset a yearly lx and mx series, and a sample size (equal to the number of individuals alive at age zero). Fifteen human populations were grouped according to level of development. These groups are: Hunter-Gatherer, Historical Sweden in 1751, and (using United Nations designations) Least Developed Countries, Less Developed Countries and More Developed Countries. In addition, we included in our analysis the plantation slaves of Trinidad (1813–1816). We include this population because, “the plight of the plantation slaves in Trinidad may be the most dismal known for any reliably reported population, save in time of natural disaster.” (John 1988, xv). Among other inhumane practices, slave-owners in this period often avoided caring for or housing elderly slaves by freeing them and expelling them from the plantations when they became too sick or old to care for themselves. If human PRLS is an artifact of benevolent conditions or social protection, this population, which experienced unnaturally harsh conditions, will lack it.

We employ data on 69 populations of non-human primates, 66 in zoos, one free-ranging provisioned population and two wild populations. Similarly to our human populations, these three groups of primate populations vary according to the degree of protection from mortality risk. Zoo populations, and to a lesser extent, semi-wild primates receive care and protection from e.g., predation, medical problems, malnutrition, and aggression from conspecifics.

Values for each population for each of the following parameters are given in online Appendix 2: Observed PrR and its level of significance, simulated (as described above) PrR, simulated PrT, and the null expectation for PrT.

All calculation were performed in R, using the annotated code available online as Appendix 3.

PrT's Type I error rate

The same simulations used to generate a null distribution for PrR allow us to examine the behavior of the measurement PrT when the same null hypothesis holds. Few significant values should be found, as we have ensured that the null hypothesis is correct. For each simulated population, we calculated PrT for each individual living past age M and giving birth more than once. The most-standard null hypothesis for PrT is that $\text{Pr}T<\overline{\mathit{\text{IBI}}}+2\mathit{\text{SD}}(\mathit{\text{IBI}})$ (mean plus two standard deviations of interbirth interval). For each individual, we therefore also calculated whether PrT fell above this limit. 81 of 83 populations included individuals who did. This is not surprising, as each sample included many more than 20 individuals, so some false positives are expected, however it is a reminder that a population should not be described as having meaningful PRLS simply because a subset of individuals greatly outlives their fecundity. More troubling, for 39 of 83 populations (47%) so examined, the mean individual PrT was greater than the mean individual’s $\overline{\mathit{\text{IBI}}}+2\mathit{\text{SD}}(\mathit{\text{IBI}})$.

Using a conservative form of this standard test, the null hypothesis can be confidently but falsely rejected in close to half of populations. No test with so high a Type I error rate can be considered valid, and any conclusions which have been reached based on this test must be reexamined. These false positives arise both because of the selective inclusion of long-lived individuals and because of the increase in inter-birth interval with age.

By comparison, for every population simulated under the null hypothesis, the ‘true’ value of PrR fell near the middle of the null distribution, and no false positives were detected. This is so because our simulations assume that the input demographic rates are the true values, accounting for demographic stochasticity and population size, but not uncertainty or bias in the measured demography. Methods for estimating the uncertainty in life-table data exist (e.g., Steinsaltz and Orzack 2011) but must be applied with care to each case, and are not implemented here. Accounting for this uncertainty would tend to make fewer populations seem to have significant PRLS.

Environment and PrR

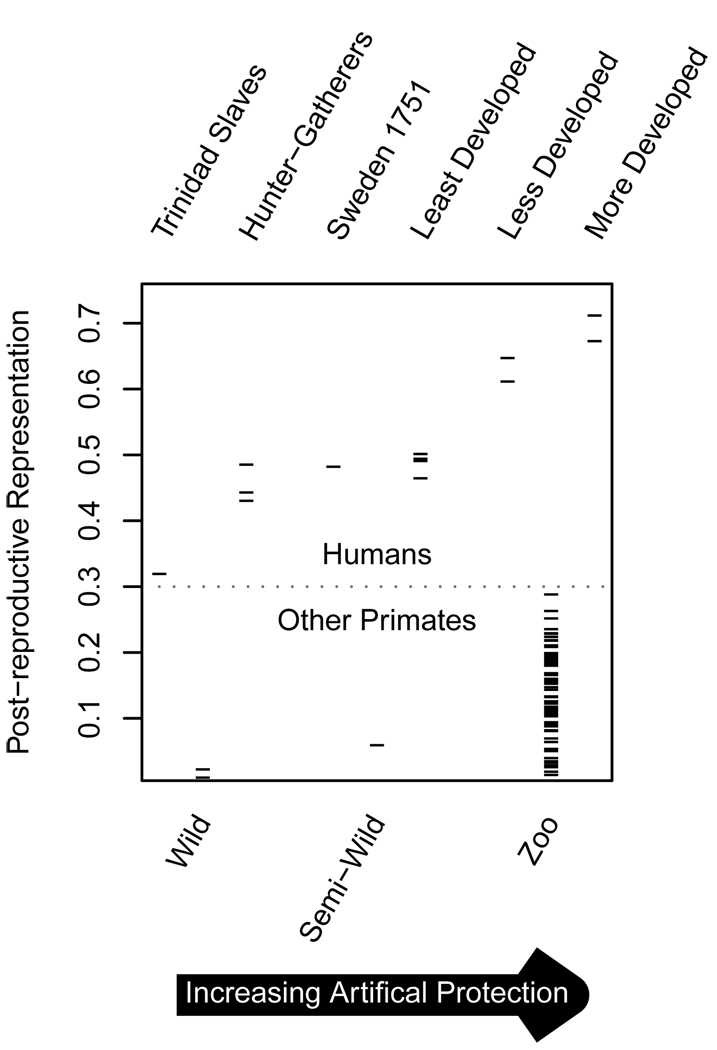
The effect of protected environments is evident (Fig. 4). In the two species of non-humans for which we have both wild and captive data, PrR increases more than tenfold in captivity (PrR=0.23 for captive chimpanzees, Pan troglodytes, but PrR=0.018 for wild chimpanzees. In baboons, Papio hamadryas, PrR=0.08 and PrR=0.005, for captive and wild populations respectively.) Humans at higher levels of socio-economic development, and primates experiencing higher levels of care experience greater PrR. This effect is due to both greater longevity and an earlier reproductive cessation under better conditions. PrR varies little between Hunter-Gatherers (PrR=0.42 to 0.48), Historical Sweden (PrR=0.48) and Least Developed Countries (PrR=0.46 to 0.49), perhaps indicating that a threshold level of development must be reached to expand PRLS. However, it is clear when comparing among UN member nations that PRLS expands rapidly as one examines increasingly developed nations (Less Developed Counties PrR=0.61 to 0.64, More Developed Countries PrR<0.68). Japan is the extreme case, with PrR= 0.76.

Figure 4.

Post-reproductive representation (T_M/T_B) for humans (top) and non-human primates (bottom) under varying circumstances. Primate populations are wild Pan troglodytes and Papio cyanocephalus, semi-wild Macaca fuscata and 66 zoo populations. While both humans and non-humans reveal increasing PrR in increasingly tailored habitats, all human populations experience greater PrR than any non-human population, and no primates but humans experience substantial PrR under natural conditions.

Humanity and PrR

At the other extreme for humans, the Trinidadian slaves experienced PrR=0.3, very low for a human population, but still higher than any non-humans. This suggest an interaction between the inhumanity of their conditions and the strong predisposition for PRLS in human biology. PrR for all human populations under a wide range of circumstances is greater than for any non-human primates in the wild or in captivity. These differences are particularly striking when comparing populations in their natural habitats. PrR values for hunter-gatherers range from 0.42 to 0.48, while PrR values for the wild primates in our sample are below 0.02. PrR is highly significant for all human populations; no simulation generated a PrR as high as that of any human population (i.e., all P-values are less than 0.001). In contrast, wild and semi-wild primates and 15 of 66 populations of captive non-human primates lack significant PrR (P>0.05).

Lessons from example analysis

Analyses based on PrT, with its extraordinary Type I Error rate, give the impression that significant PRLS is ubiquitous. However the wild primates in our sample experience actuarial senescence that is in no way delayed compared to their reproductive senescence. Those few individuals who greatly survive their last parturition are exceptional, not representative. While environment has a strong influence on PRLS, and most species of primates have at least the capacity to experience significant PrR, there is little evidence that it is realized in non-human primates in their natural environments. Humans are unusual primates in experiencing highly significant PrR>0.3 under all conditions for which reasonable data exist.

Discussion

Our understanding of post-reproductive lifespan as a population trait has been hindered by the use of an inappropriate measure. PrT arose as an attempt to extend individual-level measures of PRLS to the population level. However, as a population measure, it is inconsistently calculated, biased, primarily conveys differences in overall longevity, and cannot make use of demographic data in their most-frequently available form. It reveals little regarding how much time the average individual will spend in a post-reproductive state. The test which has been used to examine the significance of measures of PrT is highly prone to Type I errors, giving the false (and currently widespread) impression that significant PRLS is a trait found in most-organisms. We advocate the total abandonment of PrT as a population measure, and extreme care in its use as an individual measure. Any test of significance or comparative analysis using PrT values should now be reexamined.

PrR is a population level trait, and cannot meaningfully be applied to the individual. As such it is not directly acted on by selection, but rather is an outcome of selection at the individual level, and of the population’s current environment. It provides an intuitive and statistically valid measure which is comparable across populations, regardless of differences in pre-reproductive mortality or the time-scale on which the population lives. Further, it comes with a meaningful null hypothesis, allowing for straightforward examination of significance. A significant PrR in a population in its natural environment requires evolutionary explanation, as most evolutionary theory does not predict this. Significant PrR in an unnaturally safe environment may also be informative, showing that maximum age at death is not an inflexible genetically determined trait.

We have not in this paper addressed the problem of asking if the PrR of two species can statistically be shown to be significantly different. For example, are the range of PrR values calculated for humans (0.31 through 0.76) significantly different than that calculated for short-finned pilot whales Globicephala macrorhynchus (0.28, P<0.001), using the data of Kasuya and Marsh (1984), given the uncertainties inherent in the data, and the lack of replication? As PrR depends upon both species and environment, which population of humans may be considered to live in an environment comparable to that of wild, hunted, pilot whales? These problems (each population representing only a single non-independent data point and questionable comparability given environmental influences) are found throughout comparative biology. The introduction of PrR provides a measure suited to use with comparative methods, but does not alleviate the need for those methods when asking what ecological, social or environmental traits influence the evolution of PRLS.

Despite these difficulties, post-reproductive survival is a life-history puzzle well worth exploring with comparative methods. We need to identify those populations which do have biologically meaningful PRLS and understand how this trait evolved; having an appropriate measure is necessary for both of these steps. The data necessary to calculate PrR are now available for some hundreds of species. Work is actively proceeding to compile biodemographic data for easy comparative analysis between species (Biodemographic Database 2010). The intraspecific differences in PrR documented here suggest its usefulness in exploring how society and environment influence PRLS. The use of Post-reproductive Representation as a measure will allow rapid progress in our understanding of the evolution of post-reproductive lifespan.