Joint modeling of multiple longitudinal patient-reported outcomes and survival

Abstract

Researchers often include patient-reported outcomes (PROs) in Phase III clinical trials to demonstrate the value of treatment from the patient’s perspective. These data are collected as longitudinal repeated measures and are often censored by occurrence of a clinical event that defines a survival time. Hierarchical Bayesian models having latent individual-level trajectories provide a flexible approach to modeling such multiple outcome types simultaneously. We consider the case of many zeros in the longitudinal data motivating a mixture model, and demonstrate several approaches to modeling multiple longitudinal PROs with survival in a cancer clinical trial. These joint models may enhance Phase III analyses and better inform health care decision makers.

1 Introduction

Researchers design phase III oncology clinical trials to include serial assessment of treatment efficacy, including disease progression. Although overall survival is regarded as the primary treatment goal for most oncology trials, progression-free survival (PFS) is also used as a clinical trial endpoint. Corroborative support, often in the form of supporting patient-reported outcomes (PROs), may be required to demonstrate the benefit of an extended disease-free interval (Joly et al., 2007; Markman, 2009). Joint models of longitudinal PROs and PFS can be used to investigate the association between these two endpoints and to account for informative censoring of longitudinal outcomes upon disease progression (Ibrahim et al., 2010). Such censoring results in discontinuation of the treatment regimen and the regularly-scheduled PRO assessment that correspond with treatment visits.

Development of joint longitudinal-survival models in the literature has been prolific during the last 10–15 years (see Tsiatis and Davidian (2004) for a review). The most common approach is to suppose that a set of latent variables underlie both longitudinal and survival outcomes, inducing correlation between them (Henderson et al., 2000). That is, a joint model for longitudinal observation Y and survival observation T supposes that a latent u underlies both, [Y, T] = ∫ [Y, T|u]du, where it is often assumed that the u completely mediate the dependence so that [Y, T|u] = [Y |u][T|u]. Within this general mixed modeling framework, countless variations have been studied, drawing upon innovations developed in the longitudinal and survival modeling literatures. Work has expanded longitudinal submodels to accommodate multivariate continuous (Chi and Ibrahim, 2007; Lin et al., 2002), count (Dunson and Herring, 2005), and zero-inflated (Rizopoulos et al., 2008) outcomes. Notable extensions to the survival submodels may include incorporation of competing events (Elashoff et al., 2008), cure fractions (Yu et al., 2004; Chi and Ibrahim, 2006), or go beyond proportional hazards models (Tseng et al., 2005; Chen et al., 2004). Other authors have considered relaxing parametric assumptions by allowing flexible longitudinal trends (Brown et al., 2005) and nonparametric random effect distributions (Brown and Ibrahim, 2003; Wang and Taylor, 2001).

Several conceptual approaches to joint modeling may be distinguished. First, one may be interested primarily in the survival time and wish to use the longitudinal data only as time-varying covariate information. The justification for joint modeling is then as an errors-in-covariates problem, which was the motivation for early two-stage models (Tsiatis et al., 1995). Second, if primary interest is in the longitudinal data, then survival data are included to address informative censoring (Hu and Sale, 2003). The absence of longitudinal observations beyond the event time is a form of non-ignorable missingness, so that one must specify a joint distribution for the longitudinal and missingness (survival) processes. Longitudinal measures may also be considered as potential surrogate endpoints (Xu and Zeger, 2001a,b). Supposing treatment affects survival through the latent variables, we wish to learn about them by considering longitudinal data. Finally, we may be interested in the distinct effects of the treatment on each of the two outcome types. It is for this setting that we propose a fully Bayesian approach to multivariate joint models for multiple longitudinal measurements and survival outcomes.

At least one paper (Hanson et al., 2010) has thoroughly investigated whether there is any measurable advantage to joint modeling versus utilizing the observed longitudinal data directly as a time-varying covariate. These authors’ primary interest was in the survival outcome, and the time-varying covariate was measured essentially without error; the study concluded that using raw longitudinal data was superior. Notwithstanding this outcome, many other authors have shown efficiency and bias advantages to joint modeling (Faucett and Thomas, 1996; Faucett et al., 1998; Wulfsohn and Tsiatis, 1997).

Although the FDA has stated that demonstration of a clinically meaningful difference in PFS renders it an appropriate endpoint for oncology registration trials, the use of PFS as an acceptable endpoint remains highly contested (Tuma, 2009). In this context, patient-reported symptom assessments constitute an available and useful endpoint to demonstrate the patient benefit associated with an incremental PFS improvement (Markman, 2009). Unfortunately the inclusion of PRO assessments is seldom done with the rigor used to specify and analyze traditional endpoints of survival and tumor response (Joly et al., 2007). It is possible that this lack of robust PRO information in submission data packages has resulted in few examples where PRO assessment has influenced clinical decision making. We therefore present several approaches for the joint analysis of PRO and PFS data to demonstrate the value of new oncology therapies.

Our approaches were motivated by data from a phase III clinical trial of second-line therapy for malignant pleural mesothelioma (MPM), a rare and rapidly fatal form of lung cancer associated with asbestos exposure (Jassem et al., 2008). The study featured a repeatedly observed multi-item symptom-based PRO questionnaire. Models that simultaneously incorporate these multiple PRO items potentially increase efficiency by utilizing all available information and its correlation structure. The PROs were measured using a finite visual analogue scale that ranges from 0 (the absence of the measured construct) through 100 (the greatest possible severity).

We designed our joint modeling applications to address the bounded support of the measurement scale and the large number of zero longitudinal observations. The hierarchical parametric approach we advocate affords significant flexibility in the way correlation across time and PROs is captured through person-specific random effects. Accordingly, we are able to estimate the associations among PROs and between PROs and survival, the separate treatment effects on each questionnaire symptom, and the individual-level variation in latent disease process.

The remainder of this paper evolves as follows. Our oncology data set is introduced in Section 2. In Section 3 we develop our multivariate and univariate models in generality, emphasizing the breadth of our model class, and specify the “base” joint model that we fit to these data. Section 4 gives details of the model comparison metrics and computational methods employed to fit the models. Section 5 then presents model comparison summaries and detailed results for a few chosen models, along with graphical displays to help interpret the random effects. Finally, Section 6 concludes with a discussion of our findings, a description of the approach limitations, and a listing of future potential research avenues.

2 Motivating Mesothelioma Clinical Trial Data

To motivate the development of our models, we consider data from a clinical trial that enrolled 243 patients with locally advanced or metastatic MPM (Jassem et al., 2008). The primary goal was to compare pemetrexed plus best supportive care (Pem+BSC) to BSC alone. These patients had received only one prior chemotherapy regimen for advanced or metastatic disease, but prior treatment with pemetrexed was an exclusion criterion. Procedures included a baseline visit and every-21-day PRO assessments during the therapeutic phase, then follow-up until death or censoring. Each patient contributed between 1 and 14 (median 3) PRO observations and censoring was rare (7 %). Let us next consider the longitudinal and survival measures in more detail.

2.1 Longitudinal Measures

The PROs were measured using the well-established and validated Lung Cancer Symptom Scale (LCSS) (Hollen et al., 1995). This questionnaire assesses the impact of treatment on six lung-cancer-related symptoms (anorexia, fatigue, cough, dyspnea, pain, and hemoptysis) and three global measures (symptom distress caused by lung illness, interference with carrying out normal activities, and quality of life). Study participants rated their symptom experience for the 24 hours prior to data collection by placing a mark on a 100 mm visual analogue scale, with 0 indicating no symptoms and 100 indicating the worst possible symptoms. Baseline LCSS scores showed large numbers of zeros (for all items except Quality of Life), with proportions ranging from 5% (interference) to 21% (cough). For purposes of this paper, we have simplified our analyses by considering only symptoms directly attributed to pathology of the primary organ (the lung) but have excluded hemoptysis, which occurs only rarely in these patients (Hollen et al., 2006). Hence, we demonstrate our approaches by modeling only longitudinal LCSS cough and dyspnea (shortness of breath).

2.2 Survival Outcomes

In the original analysis of these data (Jassem et al., 2008), treatment was found to have a significant effect on PFS but not overall survival (OS). As stated in that study report, the OS treatment group comparison was confounded by the patients in BSC group switching to the active treatment arm regimen (BSC and pemetrexed) upon disease progression. According to the objectives of this research outlined in the introduction, we limited our analyses of time-to-event data to the PFS endpoint. Progression of disease was defined on the basis of the size of the primary tumor; the PFS variable is the time in months from randomization to progression or death from any cause. We established by visual inspection of the Kaplan-Meier curves and likelihood-based comparison of various parametric survival models that the Weibull distribution is reasonable for the PFS outcome. The only other covariate we considered, in addition to treatment group, was a binary indicator of previous response to the chemotherapy (responder vs. non-responder) that patients received prior to entering this second-line study.

3 Multivariate Joint Longitudinal-Survival Models

In the following section, we introduce a general latent variables framework for joint modeling, tailor this to PRO data by adding a longitudinal mixture model, and give details of several models fit to our mesothelioma clinical trial data.

3.1 General Approach

We begin with some notation. Let Y_i(s) = (Y_i1(s), …, Y_iK(s))^T be a vector of K distinct PROs for the i^th person at time s. Then let T_i be the event or censoring time for the i^th person, with δ_i an indicator of censoring (= 1 if progression or death was observed). We assume that a set of underlying latent trajectories U_i(s) = (U_i1(s), …, U_iK(s))^T influences both the longitudinal PRO and survival outcomes.

To construct parametric linear models for each outcome, let μ be the mean of the longitudinal distribution, where we assume all the longitudinal outcomes come from the same distributional family. Then let λ be some feature of the survival distribution (say, the hazard or odds) and let g₁ and g₂ be appropriate link functions so that we can build linear models for these two types of parameters. Each longitudinal PRO submodel depends on a p_1k-vector of parameters β_1k with corresponding vectors of covariates X_1ik(s). The survival submodel depends on a p₂-vector of parameters β₂ with covariate vector X_2i(s). Finally, let A be a function of the trajectories U_i(s) and a parameter vector α₂ (we reserve α₀ and α₁ for future use). Assembling these into a general joint mean response model,

$$\begin{array}{c}{g}_1({\mu }_{ik}(s))={\mathbf{X}}_{1ik}(s){\mathit{\beta }}_{ik}+U_{ik}(s)\\ \text{and}{g}_2({\lambda }_i(s))={\mathbf{X}}_{2i}(s){\mathit{\beta }}_2+A({\mathit{\alpha }}_2,{\mathbf{U}}_i(s)),\end{array}$$ (1)

where k = 1, …, K indexes the PROs. We assume that all the outcomes are conditionally independent given the person-specific trajectories, U_i(s). That is, the underlying disease trajectory induces all the interdependence among PROs, across times, and between PROs and survival. The connection between PROs and survival is clear from this expression, by virtue of U_i(s) appearing in both submodels. However, we must be a bit more explicit to clarify how we incorporate correlation across time (i.e., between Y_i(s) and Y_i(s′)) and among longitudinal measures (i.e., between Y_ik(s) and Y_ik′(s)).

To this end, we first simplify the model by supposing that a single underlying trajectory, U_i(s), influences all the outcomes. Then we let the trajectory depend on a small, finite set of person-specific random variables, u_i. In order to learn about the latent trajectory, we assume that it appears in each longitudinal submodel, scaled by a factor α_1k, so that U_ik(s) = α_1kU_i(s). For identifiability, we choose a single PRO to determine the scale of the trajectory, say k = 1 so that α₁₁ = 1 is fixed. Then we may link the K longitudinal submodels and the single survival submodel either via the value of the random trajectory U_i(s) or the vector of random variables u_i. The first case yields g₂(λ_i(s)) = X_2i(s)β₂ + α₂U_i(s), while the second case yields g₂(λ_i(s)) = X_2i(s)β₂ + α₂u_i. Note that the second is computationally simpler because it does not lead to time-varying covariates in the survival submodel.

We make a further distinction between these “shared effect” models, in which common parameters across submodels induces a limited form of association, and “correlated effect” models, in which separate parameters in each submodel come from a common distribution, inducing a more flexible form of association (Fitzmaurice et al., 2009). As an example of the latter, suppose that different trajectories underlie the evolving disease, U_ik(s) for k = 1, …, K PROs. Then let each of these be governed by a set of person-specific random variables u_ik, so ${\mathbf{u}}_i={({\mathbf{u}}_{i1}^T,\dots ,{\mathbf{u}}_{iK}^T)}^T$. Correlation among longitudinal outcomes may be induced by supposing that these come from some joint distribution, ${\mathbf{u}}_i\stackrel{\mathit{iid}}{\sim }{G}_u(\cdot \mid {\mathrm{\sum }}_u)$ where Σ_u parameterizes Cov(u_ik, u_ik′). Of course, one can also specify hybrid approaches using some combination of these two methods, linking via the value of the trajectories or the random variables, and using shared or correlated random effects.

3.2 Two-Part Longitudinal Model

An additional modeling complication is motivated by the data in Section 2, namely, a large number of observed zeros in the longitudinal data. A common approach to modeling “excessive” zeros is to mix a point mass at zero with a parametric distribution. In the case of count data, such two-part models combine a point mass at zero with a discrete distribution that may also generate zero values, yielding, for example, zero-inflated binomial (Branscum et al., 2004) or zero-inflated Poisson (Lachenbruch, 2002). In the case of continuous data, a “spike and slab” mixture combines a point mass at zero with a continuous distribution, for example a normal (Ghosh and Albert, 2009), lognormal (Zhang et al., 2006), or gamma (Yau et al., 2002).

We extend our Section 3.1 joint modeling framework to include two submodels for each longitudinal outcome, one for each mixture component. The point mass at zero is governed by mixing parameter (1 − ω), while the other mixture distribution is assumed to depend on μ, a mean parameter. Extending the notation of (1), we add a p_0k-vector of coefficients β_0k with corresponding design vector X_0ik(s) for ω_ik(s), using link g₀.

The next question is whether the two longitudinal submodels will be connected by shared or correlated random effects. For now, we assume the latter, so that there are two underlying trajectories per person per PRO, namely U_0i(s) = (U_0i1(s), …, U_0iK)^T and U_1i(s) = (U_1i1(s), …, U_1iK(s))^T. Then (1) is extended to

$$\begin{array}{l}{g}_0({\omega }_{ik}(s))={\mathbf{X}}_{0ik}(s){\mathit{\beta }}_{0k}+U_{0ik}(s),g_1({\mu }_{ik}(s))={\mathbf{X}}_{1ik}(s){\mathit{\beta }}_{1k}+U_{1ik}(s),\\ \text{and}{g}_2({\lambda }_i(s))={\mathbf{X}}_{2i}(s){\mathit{\beta }}_2+A({\mathit{\alpha }}_2,{\mathbf{U}}_{0i}(s),{\mathbf{U}}_{1i}(s)).\end{array}$$ (2)

Notice that we build the model for ω, which is the probability of not being in the point mass at zero, so that the effects on ω, μ, and λ will have the same clinical sign, i.e., larger is detrimental.

3.3 Model Implementation for Meso Data

In order to implement joint longitudinal-survival models for the mesothelioma data described in Section 2, we must specify distributional assumptions and link functions for the joint model (2). In the longitudinal submodels, we must address the bounded support of the PRO scores ∈ [0, 100]; a beta distribution values is a natural choice. In contrast to the cases in Section 3.2, zero is not in the support of the continuous distribution, so following the suggestion of a referee, we use the term “zero-augmented” to describe our two-part approach.

First, we transform the support to [0, 1) by dividing all the scores by 100 and subtracting a small amount from the few values equal to the upper bound. Next, we consider a reparameterization of the usual Beta(a, b) distribution using the mean μ and a dispersion parameter φ, via a = μφ and b = (1 − μ)φ. Thus we obtain a zero-augmented beta (ZAB) distribution for a random variable Y ∈ {0} ∪ (0, 1) having three parameters: ω for the probability of Y ∈ (0, 1), μ for the mean of Y ∈ (0, 1), and φ for the dispersion of Y ∈ (0, 1). We then build a logistic model for ω (presence of the PRO) and a beta regression model for μ (severity of the non-zero PRO). Both of these parameters are ∈ [0, 1], so we use logit link functions for both g₀ and g₁.

Turning to the survival submodel, we suppose that a parametric Weibull distribution describes the errors and build a proportional hazards model. The hazard for the i^th person at time s, h_i(s), is a product of baseline hazard function h₀(s) = γs^γ−1 and the parameter λ_i(s) > 0. Thus we use a log link function for g₂, and the usual method of taking the survival function at the censoring time as the likelihood contribution for censored observations.

Assembling all of these components, we obtain the following manifestation of (2):

$$\begin{array}{l}{Y}_{ik}(s)\sim \mathit{ZAB}({\omega }_{ik}(s),{\mu }_{ik}(s),{\phi }_k),\\ \text{logit}({\omega }_{ik}(s))={\mathbf{X}}_{0ik}(s){\mathit{\beta }}_{0k}+U_{0ik}(s),\\ \text{logit}({\mu }_{ik}(s))={\mathbf{X}}_{1ik}(s){\mathit{\beta }}_{1k}+U_{1ik}(s),\\ T_i\sim \text{Weibull}(\gamma ,{\lambda }_i),\\ \text{and}log({\lambda }_i(s))={\mathbf{X}}_{2i}{\mathit{\beta }}_2+A({\mathit{\alpha }}_2,{\mathbf{U}}_{0i}(s),{\mathbf{U}}_{1i}(s)).\end{array}$$ (3)

In the implementation of these models below, we assume the U_0i(s) and U_1i(s) depend on r-dimensional person-specific parameter vectors u_i and possibly parameter vectors α₀ and α₁, as described in Section 3.4 below. Then we assume a zero-centered multivariate normal distribution governs these, with r × r covariance matrix Σ_u.

We specify independent normal prior distributions centered at 0 with variance 100 for the main regression effects, ${\mathit{\beta }}_0={({\mathit{\beta }}_{01}^T,\dots ,{\mathit{\beta }}_{0K}^T)}^T,{\mathit{\beta }}_1={({\mathit{\beta }}_{11}^T,\dots ,{\mathit{\beta }}_{1K}^T)}^T$ β₂, and $\mathit{\alpha }={({\mathit{\alpha }}_0^T,{\mathit{\alpha }}_1^T,{\mathit{\alpha }}_2^T)}^T$. Using the conjugate inverse Wishart prior on Σ_u, we center it at I_r. Letting the degrees of freedom equal r ensures this prior is as vague as possible while still proper. The Weibull shape parameter is bounded, γ > 0, so we choose a gamma prior with mean 1 and variance 10. The beta precision parameters are similarly bounded, φ_k > 0, so we specify a gamma prior for each. These have mean φ̂_k and variance φ̂_k², where φ̂_k is an empirical estimate based on preliminary analysis. These priors represent a balance between minimal informativeness and the need to constrain the parameters to a reasonable range to achieve acceptable MCMC convergence.

In the application to our mesothelioma clinical trial data, let the fixed effect design matrices X_0i(s) = X_1i(s) = X_i(s) consist of four entries: an intercept, a linear time effect (day, standardized by its mean, 75, and standard deviation, 69), a binary indicator of response to prior treatment (rsp= 1 if responder, = 0 if non-responder), and an interaction term for treatment (trt= 1 if Pem+BSC, = 0 if BSC alone) with time. No treatment intercept is included because patients were randomized to treatment, and the treatment groups do not differ at baseline. The three entries we use in X_2i(s) = X_2i are simply an intercept, responder status indicator, and treatment group indicator.

3.4 Latent Trajectories and Hierarchical Structure

The remainder of this subsection specifies several reasonable forms for the latent components of these models, choosing between shared and correlated random effects, and choosing whether to link via the values of the random trajectories or the random variables. The clinical trial data we consider in Section 2 have few observations per person (median: 3), restricting us to fairly simple forms for the person-specific trajectories in these two longitudinal submodels. In particular, we take the very simple case of random intercepts in each model, so that U_0ik(s) = u_0ik and U_1ik(s) = u_1ik. This removes the time dependence of the random trajectories, so that linking via the value of the random trajectory and linking via the random variables is the same. It remains to specify the underlying structure of these latent variables.

Single Shared Intercept Model (MV1I)

An extremely simple case of a shared effects model contains a single random intercept, u_i, underlying all K PROs and the survival outcome. This intercept must be scaled appropriately for each submodel. We use coefficients α_0k and α_1k for each longitudinal presence and severity submodel, respectively, so that u_0ik = α_0ku_i and u_1ik = α_1ku_i. Then we fix α₀₁ = α₁₁ = 1 for identifiability, and in the survival submodel, let A(α₂, u_i) = α₂u_i. This model represents the simplest possible shared effects model, but may miss important variations within individuals across PROs.

Two Shared Intercepts Model (MV2I)

A slightly more flexible version of a shared effects model assumes that two random intercepts, u_i = (u_0i, u_1i)^T, underlie all K PROs. One influences the presence of all the PROs, and the other influences their severity. Again, these random intercepts must be scaled appropriately for the longitudinal submodels, so we use coefficients α_0k and α_1k for the presence and severity, respectively, so that u_0ik = α_0ku_0i and u_1ik = α_1ku_1i. Then fix α₀₁ = α₁₁ = 1 for identifiability and use A(α₂, u_0i, u_1i) = α₂(u_0i +u_1i) in the survival submodel. We observed that separate multipliers for the two intercepts substantially impaired model convergence. Summing is sensible because we expect and in fact, observe, that the two intercepts are positively correlated, that is, individual-level probability and severity of symptoms are related. This model allows the presence and severity of PROs to have different individual-level adjustments, but limits the structure of these adjustments across PROs.

K Intercepts Hybrid Model (MVKI)

Moving to a hybrid correlated/shared effects model, let each PRO have a different random intercept u_i = (u_i1, …, u_iK)^T, but suppose that this drives both the presence and severity longitudinal submodels. Assuming the intercept is on the scale of the severity submodel, we need a scaling parameter α_0k for its contribution to the presence submodel, so that u_0ik = α_0ku_ik and u_1ik = u_ik. Then in the survival submodel, we use $A({\alpha }_2,{\mathbf{u}}_i)={\alpha }_2({\sum }_{k=1}^k{u}_{ik})$. Similar to model UV2I above, summing is sensible because we observe that the intercepts across PRO items are positively correlated. This model allows individuals to have different underlying intercepts for each PRO, but requires that the individual PRO presence and severity effects be proportional to one another, according to α_0k.

2K Intercepts Hybrid Model (MV2KI)

Further expanding the flexibility, we might assume two random intercepts for each PRO, u_ik = (u_0ik, u_1ik)^T, then there is no need for scaling factors in the longitudinal submodels. In the survival submodel, we use $A({\alpha }_2,{\mathbf{u}}_i)={\sum }_{k=1}^K{\alpha }_{2k}(u_{0ik}+u_{1ik})$, though this may not be sensible in all settings, e.g., if the individual-level parameters for the two longitudinal submodels were negatively correlated, the meaning of α_2k would be obscure. This specification, which we term MV2KI, is the most flexible, allowing an individual’s latent level to vary across all PROs and between the presence and severity.

Random Effect Distribution

There are several ways of structuring the distribution of the random effects. For simplicity, we assume ${\mathbf{u}}_i\stackrel{\mathit{iid}}{\sim }N(\mathbf{0},{\mathrm{\sum }}_u)$, where the r × r covariance matrix Σ_u parameterizes covariance between the presence and severity longitudinal components. When r is small, a single multivariate normal distribution on the r-vector u_i is tractable. This is the approach we take in the mesothelioma example below, where r is never larger than 2K = 4. We fit an unstructured Σ_u matrix, and discuss alternative approaches for larger r, including means of structuring Σ_u, in Section 6.2 below.

Univariate Models

We are also interested in fitting a single PRO at a time, jointly with survival. This leads to interesting special cases of our models above, where we suppress the k notation for simplicity.

First consider a simplification having only a single random effect, u_i, on the scale of the severity submodel. We use multiplier α₀ and for the contribution to the probability submodel, so that u_0i = α₀u_i and u_1i = u_i. Then letting A(α₂, u_i) = α₂u_i in the survival submodel leads to a special case of MV1I, which we call UV1I (for univariate 1 intercept).

Next, let u_i = (u_0i, u_1i)^T be a 2-vector of random intercepts and suppose that these influence the presence and severity PROs separately. This leads to a special case of MV2I, which we call UV2I, where we choose a simple linear combination of the two intercepts in the survival model, α₂(u_0i + u_1i).

Table 1 present these multivariate and univariate joint models in simple notation that emphasizes the differences in the contribution of the individual-specific disease process. In Section 5, we fit these univariate models twice, with each of two PROs playing the role of Y_i(s) in turn. Then we compare the results to multivariate model fits that use the same two PROs simultaneously with survival.

Table 1.

Summary of joint models.

Name	individual trajectories		contributions to each submodel
	U0ik(s)	U1ik(s)	presence	severity	survival
UV1I	ui	ui	α0ui	α1ui	α2ui
UV2I	u0i	u1i	u0i	u1i	αa2(u0i + u1i)
MV1I	ui	ui	α0kui	α1kui	α2ui
MV2I	u0i	u1i	α0ku0i	α1ku1i	α2(u0i + u1i)
MVKI	uik	uik	α0uik	uik	${\alpha }_2({\sum }_{k=1}^K{u}_{ik})$
MV2KI	u0ik	u1ik	u0ik	u1ik	${\sum }_{k=1}^K{\alpha }_{2k}(u_{0ik}+u_{1ik})$

4 Technical Details

4.1 Likelihood Specification

Let the complete parameter vector for the fixed effects be Θ = (β₀, β₁, β₂, α, γ, φ, Σ_u), where φ = (φ₁, …, φ_K)^T. The latent trajectories U_0i(s) and U_1i(s) depend on individual-specific parameter vectors u_i, the elements of which may be PRO-specific random vectors, e.g., u_i = (u_i1, …, u_iK)^T as in MVKI, or be common across PROs, e.g., u_i = (u_0i, u_1i)^T as in MV2I. Collecting the u_i for all subjects, we obtain the complete latent parameter vector $\mathbf{U}={({\mathbf{u}}_1^T,\dots ,{\mathbf{u}}_N^T)}^T$. Then the following expression is proportional to the full joint posterior distribution,

$$p(\mathbf{\Theta },\mathbf{U}\mid \mathbf{Y},\mathbf{T},\mathbf{\Delta })\propto \{\prod _{i=1}^N\left[\prod _{k=1}^K\prod _{j=1}^{n_i}p(y_{\mathit{ikj}}\mid {\mathit{\beta }}_{0k},{\mathit{\beta }}_{1k},\mathit{\alpha },{\mathbf{u}}_i,{\phi }_k)\right]\times p{(t_i\mid {\mathit{\beta }}_2,{\mathbf{u}}_i,\mathit{\alpha },\gamma )}^{{\delta }_i}S{(t_i\mid {\mathit{\beta }}_2,{\mathbf{u}}_i,\mathit{\alpha },\gamma )}^{1-{\delta }_i}\}p(\mathbf{U}\mid {\mathrm{\sum }}_u)\pi (\mathbf{\Theta }),$$ (4)

where for the i^th person, the j^th observation of the k^th PRO is y_ikj at time s_ikj, t_i is the PFS/censoring time, and δ_i is the censoring indicator. Then Y, T, and Δ are the complete vectors of these observed quantities over all k = 1, …, K, i = 1, …, N, and j = 1, …, n_i. The prior π(Θ) is a product of the independent prior distributions on each element of Θ described in Section 3.3 above. The ZAB likelihood contribution for each PRO observation, p(y_ikj|β_0k, β_1k, α, u_i, φ_k), is

$$[1-{\omega }_{\mathit{ikj}}({\mathit{\beta }}_{0k},{\mathit{\alpha }}_0,{\mathbf{u}}_i)]I(y_{\mathit{ikj}}=0)+{\omega }_{\mathit{ikj}}({\mathit{\beta }}_{0k},{\mathit{\alpha }}_0,{\mathbf{u}}_i)\left[c_{\mathit{ikj}}{y_{\mathit{ikj}}}^{{\mu }_{\mathit{ikj}}({\mathit{\beta }}_{1k},{\mathit{\alpha }}_1,{\mathbf{u}}_i){\phi }_k-1}{(1-y_{\mathit{ikj}})}^{(1-{\mu }_{\mathit{ikj}}({\mathit{\beta }}_{1k},{\mathit{\alpha }}_1,{\mathbf{u}}_i)){\phi }_k-1}\right]I(y_{\mathit{ikj}}>0),$$ (5)

where the parameters are

$$\begin{array}{l}{c}_{\mathit{ikj}}=\frac{\mathrm{\Gamma }({\phi }_k)}{\mathrm{\Gamma }({\mu }_{\mathit{ikj}}({\mathit{\beta }}_{1k},{\mathit{\alpha }}_1,{\mathbf{u}}_i){\phi }_k)\mathrm{\Gamma }((1-{\mu }_{\mathit{ikj}}({\mathit{\beta }}_{1k},{\mathit{\alpha }}_1,{\mathbf{u}}_i)){\phi }_k)},\\ {\omega }_{\mathit{ikj}}({\mathit{\beta }}_{0k},{\mathit{\alpha }}_0,{\mathbf{u}}_i)={\text{logit}}^{-1}({\mathbf{X}}_{0\mathit{ikj}}{\mathit{\beta }}_{0k}+U_{0ik}(s_{\mathit{ikj}})),\text{and}\\ {\mu }_{\mathit{ikj}}({\mathit{\beta }}_{1k},{\mathit{\alpha }}_1,{\mathbf{u}}_i)={\text{logit}}^{-1}({\mathbf{X}}_{1\mathit{ikj}}{\mathit{\beta }}_{1k}+U_{1ik}(s_{\mathit{ikj}})),\end{array}$$

where we recall that U_0ik and U_1ik depend on u_i and perhaps also on α₀ and α₁, respectively.

The Weibull likelihood contribution for the i^th person is

$$\begin{array}{l}p(t_i\mid {\mathit{\beta }}_2,{\mathit{\alpha }}_2,{\mathbf{u}}_i,\gamma )=\gamma {\lambda }_i({\mathit{\beta }}_2,{\mathit{\alpha }}_2,{\mathbf{u}}_i)t_i^{\gamma -1}exp(-{\lambda }_i({\mathit{\beta }}_2,{\mathit{\alpha }}_2,{\mathbf{u}}_i)t_i^{\gamma })\\ \text{or}S(t_i\mid {\mathit{\beta }}_2,{\mathit{\alpha }}_2,{\mathbf{u}}_i,\gamma )=exp(-{\lambda }_i({\mathit{\beta }}_2,{\mathit{\alpha }}_2,{\mathbf{u}}_i)t_i^{\gamma }),\end{array}$$ (6)

according to whether the terminal event was observed or censored, respectively. The Weibull parameter is λ_i(β₂, α₂, u_i) = exp (X_2iβ₂ + A(α₂, u_i)).

4.2 Model Comparison

To compare among models with different random effect structures and A functions, we consider several measures of model fit and complexity. We compute both of these measures separately for the longitudinal and survival submodels of each joint model considered.

The Deviance Information Criterion (DIC) is a measure based on the deviance, D = −2 log(p(y|θ)) (Spiegelhalter et al., 2002). Model adequacy is captured by the posterior mean of the deviance, D̄(θ), where smaller values indicate better fit. Effective model complexity is captured by p_D = D̄(θ) − D(θ̄), the difference between the posterior mean of deviance and the deviance at the posterior means of the parameters. Then DIC = D̄(θ) + p_D penalizes model adequacy by the effective model complexity. Partitioning these statistics into longitudinal and survival components is straightforward via partitioning the likelihood; indeed this functionality is programmed into the WinBUGS software. The deviance for the longitudinal part is negative twice the log of (5), and for the survival part is negative twice the log of (6).

As several difficulties with DIC have been noted (van der Linde, 2005; Celeux et al., 2006; Gelman et al., 2004, Ch.4), we also consider predictive measures. Root mean squared prediction error (RMSPE) measures the model’s ability to predict outcomes not used in model fitting. We randomly select N⁽²⁾ = 23 subjects (i.e., 10% of the sample) and extract their longitudinal and survival outcomes to obtain a validation data set (y⁽²⁾, t⁽²⁾). We do not select from among those few subjects (7%) who had censored survival observations, since computing the usual prediction error on censored values is not sensible; assuming censoring occurs at random, this approach will not bias our results. We fit the model on the remaining training data, (y⁽¹⁾, t⁽¹⁾), and obtain posterior predictions for the held-out observations, (ŷ _i, t̂_i), for each i ∈ (y⁽²⁾, t⁽²⁾). Then we compute longitudinal root mean square prediction error ${\mathit{RMSPE}}_{\text{long}}={\left[1/N^{(2)}{\sum }_{i=1}^{N(2)}{(y_i-{\widehat{y}}_i)}^2\right]}^{1/2}$ for y_i ∈ y⁽²⁾, and similarly for the survival data substituting t_i for y_i in this expression to obtain RMSPE_surv.

Finally, we consider the log pseudo marginal likelihood (LPML). For the same validation data set, we compute the pseudo marginal likelihood of these predictions, where the marginalization is accomplished by averaging Monte Carlo samples from the posterior of the parameters. That is, for the longitudinal data, we estimate the conditional predictive ordinate (CPO) of each predicted observation by ${\mathit{CPO}}_{\text{long},i}=f(y_i\mid {\mathbf{y}}^{(1)})=\int f(y_i\mid \mathrm{\Omega })\pi (\mathrm{\Omega }\mid {\mathbf{y}}^{(1)})d\mathrm{\Omega }\approx 1/G{\sum }_{g=1}^{G}f(y_i\mid {\mathrm{\Omega }}^g)$ for y_i ∈ y⁽²⁾, where g indexes MCMC draws from the posterior of the complete parameter vector Ω = (Θ, U), and f(y_i|Ω) is computed using (5). Then we sum over the validation set to obtain ${\mathit{LMPL}}_{\text{long}}={\sum }_{i=1}^{N^{(2)}}log({\mathit{CPO}}_i)$, for which, being similar to a log likelihood, larger values indicate better fit. We repeat this procedure for the survival data, substituting t_i for y_i in these expressions and computing f (t_i|Ω) using (6) to obtain components CPO_surv,i and subsequently the sum LPML_surv.

4.3 Computing

We used the WinBUGS 1.4software (Lunn et al., 2000), freely available at www.mrc-bsu.cam.ac.uk/bugs, to fit these models. To implement our non-standard ZAB submodel, we run WinBUGS from within the BlackBox Component Builder 1.5 (Oberon Microsystems, Zurich) development environment using WinBUGS Development Interface (WBDev; Lunn (2003)). This allows the MCMC algorithms to access a ZAB distribution that we coded in component Pascal. For convenience and reproducibility, we do all of this via the R2WinBUGS (Sturtz et al., 2005) package for R. Convergence was monitored via the histories of each chain and their auto- and cross-correlations, density plots, and Brooks-Gelman-Rubin statistics (Gelman and Rubin, 1992; Brooks and Gelman, 1998). The results below reflect 2000 iterations of burn-in followed by 5000 production samples from each of three parallel chains.

5 Results

5.1 Model Choice

Model fit statistics for models described in Section 3.4 are summarized in Table 2 and Figure 1. The univariate models used one PRO (dyspnea or cough) with PFS, while the multivariate models fit these same two PRO items simultaneously with PFS.

Table 2.

DIC statistics for univariate and bivariate models fit to the mesothelioma data. The most favorable DIC statistics for each PRO (for UV) or the combination of both (for MV) are shown in bold type.

	Longitudinal			Survival
	D̄	pD	DIC	D̄	pD	DIC
UV1I Cough	797	179	977	1005	6	1011
UV1I Dyspnea	834	185	1019	998	6	1004
UV2I Cough	694	232	926	1001	8	1008
UV2I Dyspnea	781	215	995	981	13	994
MV1I Combined	840	191	1032	999	6	1006
MV2I Combined	571	276	847	991	10	1001
MVKI Combined	260	342	601	999	6	1005
MV2KI Combined	100	421	521	964	16	980

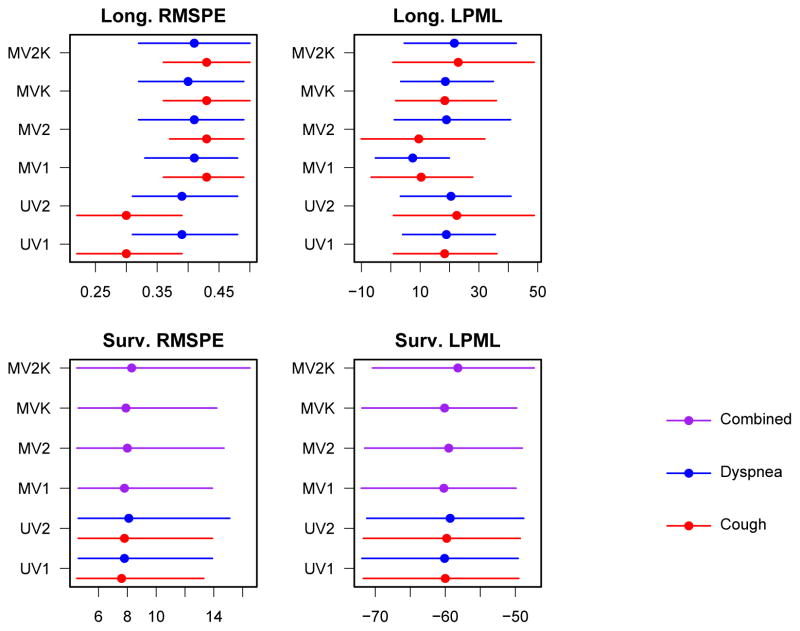
Figure 1.

Predictive model comparison statistics for models fit to mesothelioma data. Means and 95% posterior credible intervals are shown.

First, consider the differences between the univariate and multivariate approaches. DIC may not be compared fairly (summing the DIC for the cough and dyspnea univariate models would be “double counting” the contribution of survival data), but the prediction statistics may. The longitudinal RMSPE statistics seem to indicate a small advantage to considering the PROs separately. However, longitudinal LPML and both statistics in the survival component are very similar across UV and MV models.

Considering the difference in structure within univariate models, DIC favored the model with separate intercepts for presence and severity (UV2I). RMSPE values for UV1I and UV2I were essentially identical for both symptoms in the longitudinal and survival submodels, as was survival submodel LPML. Longitudinal submodel LPML showed a benefit to UV2I over UV1I for cough, but was tied for dyspnea.

Turning to the multivariate models, DIC and longitudinal LPML for cough strongly prefer MV2KI, while the rest of the predictive fit statistics fail to clearly distinguish a “winner.” Given these results, we advocate UV2I and MV2KI for these particular data.

5.2 Interpretation of Parameters

The β₀ parameters, shown in the top row of Figure 2, capture the effects of the covariates on the logit probability of a non-zero PRO score, with negative parameters representing improvement of PROs. In most models, these effects are not significantly different from zero, though the treatment effects trend toward negative values (i.e., improved symptoms) in all models, and reach significance for the effect of treatment by day on cough in the MV2KI model, and both PROs in the MV2I model.

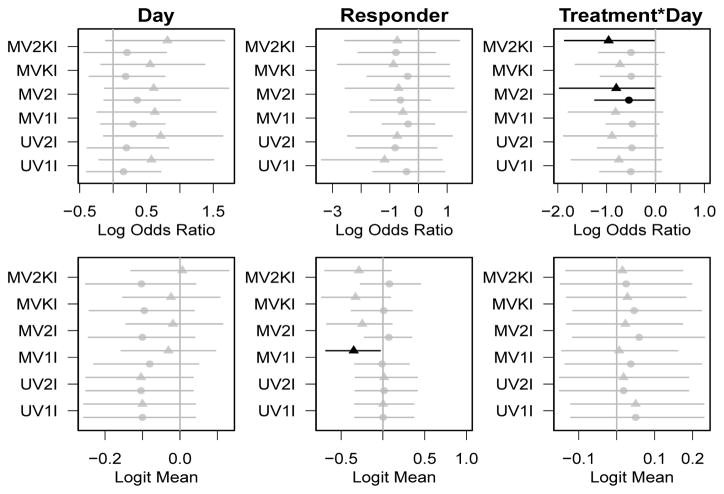
Figure 2.

Posterior means and 95% equal-tail credible intervals for parameters governing probability of non-zero PRO (β₀, top row) and mean of non-zero PRO (β₁, bottom row). Credible intervals that exclude the null value of 0 are shaded darker. Circles represent effects on cough, triangles for effects on dyspnea.

The β₁ parameters, shown in the bottom row of Figure 2, represent the effects of the covariates on the mean of the non-zero PRO scores. Thus, negative parameters represent improvement in non-zero PRO scores. Again, very few of the scores reach significance, though responders tend to have lower severity of cough in all of the multivariate models.

The β₂ parameters, plotted in Figure 3, represent the effects of the covariates on the log hazard of progression or death, so negative parameters represent decreased hazard, i.e., improved progression-free survival time. Only the univariate models showed trends for treatment benefits on survival, though the credible intervals narrowly include the null value of 0.

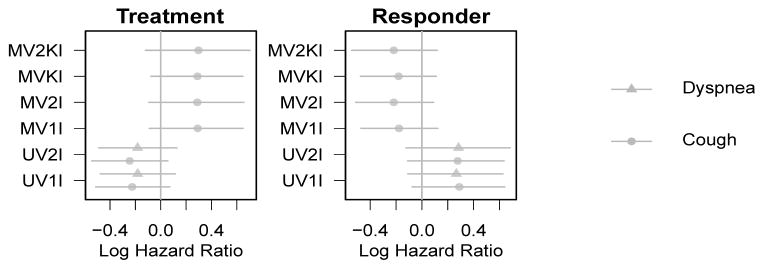
Figure 3.

Posterior means and 95% equal-tail credible intervals for parameters governing hazard of progression (β₂). Credible intervals that exclude the null value of 0 are shaded darker. Effects in models joint with cough are plotted as circles; models with dyspnea are triangles.

The matrix Σ_u contains off-diagonal entries that parameterize the relationships among person-specific parameters. For example, in the MV2KI model, the 4 × 4 Σ_u matrix governs the relationship between presence and severity intercepts for a single PRO (i.e., Cov(u_0ik, u_1ik)) and between intercepts for different PRO items (e.g., presence intercepts Cov(u_0ik, u_0ik′)). Strong positive correlations were observed within PRO items between presence and severity for an individual. The correlation coefficient was .61 (CI: .36 – .80) for the two cough intercepts and .70 (CI: .51 – .83) for the dyspnea intercepts. Similarly strong positive correlations were observed between PRO items, for example, the intercepts for presence of cough and dyspnea had correlation .78 (CI: .62 – .88), while the intercepts for severity of these two symptoms had correlation .62 (CI: .47 – .72). These relationships provide support for the consideration of multiple PRO items at once, despite the lack of marked efficiency gains in the main regression estimates (Figs. 2 and 3).

Recall that α₂ parameterizes the association between individual-level intercepts for the longitudinal outcomes and survival. The posterior credible intervals for these parameters exclude 0 and are positive in all cases except α₂₁ in MV2KI, where the interval did include the null value. These indicate that individual-level deviations from the norm in PROs behave consistently with the corresponding deviations in PFS, though perhaps not for cough. Broadly, the significantly positive α₂ parameters support the use of joint modeling of longitudinal and survival by indicating a significant connection between the two outcome types.

One interesting feature of our models (and one that is not available in standard models) is the pattern of individual intercepts that were significantly different from 0. While significantly non-zero u_1i values were evenly split between positive and negative, the significantly non-zero u_0i values were almost entirely negative (not shown). Further, the observed positive correlation was never reversed when u_0i was significantly negative; these individuals always had either non-significant or significantly negative u_1i.

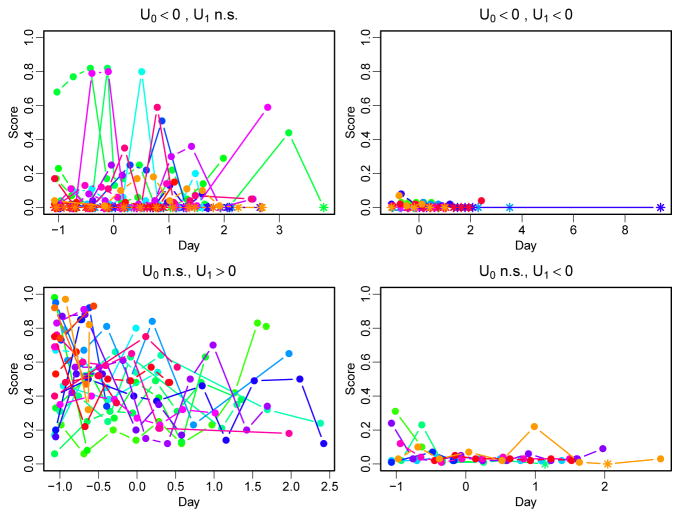
Examining the original data confirms that individuals with significantly negative u_0i had many observed zeros. Taking cough as a representative example, Figure 4 shows the observed cough scores over time in groups chosen on the basis of their estimated random effects. Zero values are plotted as stars and non-zeros as solid circles. Those with significantly negative u_0i estimates (top two panels) contain many zero values, while those with non-significant u_0i estimates (bottom two panels) contain no zero values. An absence of zeros, even with accompanying large LCSS scores, does not lead to significantly positive adjustments to the probability of non-zero scores (u_0i). In contrast, both positive and negative adjustments to the non-zero LCSS score means (u_1i) reach significance.

Figure 4.

Observed outcomes (zeros plotted as stars) according to individual probability of non-zero score (u_0i) and non-zero score mean (u_1i) in a model of cough and progression-free survival.

Further graphical investigation (not shown) suggests that in participants who never reported zero on the LCSS scores (suggesting a large, positive u_0i would be needed), missing data and poor PFS outcomes prevent the random intercept from reaching significance. Despite point estimates that are mostly positive, the credible intervals for u_0i are simply too wide to exclude zero. Further, poor progression-free survival is associated with the greatest probability of having a non-zero LCSS score. This suggests a possible explanation: missing data. Consider a participant with one of the largest u_0i estimates, who had only two observations for cough: values of 74 at day 5 and 93 at day 36. The participant then progressed/died at day 45, and our model produced a significantly positive estimate for u_1i [mean: 2.0, 95% CI: (1.1, 3.0)] and just barely non-significant estimate for u_0i [mean: 5.5, 95% CI: (−0.16, 11.9)]. Other patients with large u_0i estimates showed similar patterns.

6 Discussion

MPM has a high symptom burden, and symptom relief remains the main goal of MPM management (van Meerbeeck et al., 2010). Hence, clinical trials in MPM, and other advanced or metastatic disease with high patient-reported symptom levels, should be designed to include compelling and comprehensive assessment of patient well-being with serial collection of sufficient symptom-based PRO data. Effective use of these data will, however, require a broader standard of evidence than has been specified in the typical study protocols (Moinpour et al., 2007; Fredheim et al., 2007). Conventional randomized controlled trial analyses (e.g., the sample mean difference) fail to evaluate individual-level treatment benefit and its association with the survival outcomes. Our joint models of longitudinal repeated-measure PRO symptoms with PFS address this shortcoming.

Despite our use of rigorous joint modeling and inclusion of components to specifically accommodate the longitudinal measurement features of a bounded scale and excess zero floor effects, our data offered little support for our expectation that active treatment plus BSC would reduce symptom burden and that this reduction would be associated with increased PFS, compared with BSC alone. The lack of observed group treatment symptom differences in this second-line MPM study may be due to its relatively small sample size. The LCSS questionnaire is structured as a 24-hour recall instrument and the study administration schedule was approximately every 21 days. Hence, there is a large temporal gap between longitudinal measurements, and the single cycle assessments may not represent the true patient symptom experience or the association of symptom burden with PFS. At a minimum, consecutive daily assessments over a period of cycle days 1 through 7 would provide more reliable data upon which better statistical modeling could be predicated. To better evaluate the value of new oncology therapies, study protocols should be developed to include this enhanced data collection, possibly through the use of electronically reported PROs, along with analysis plans that include the joint modeling of longitudinal repeated-measure patient-reported symptom and survival data.

6.1 Limitations of our Analysis

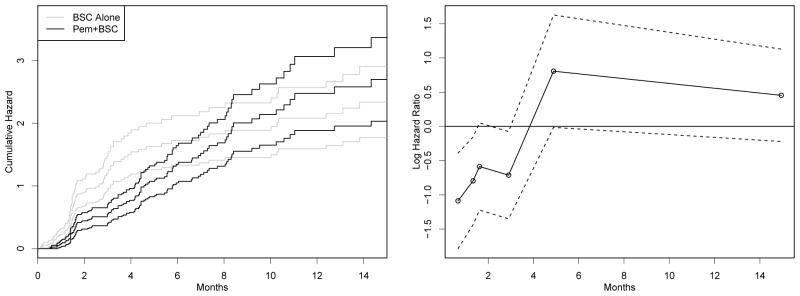
While we have outlined several attractive features of our multivariate joint model approach, several criticisms of our analysis can be made. One is a possible violation of the proportional hazards assumption in the Kaplan-Meier curves for the two treatment groups. The left panel of Figure 5 shows the cumulative hazards and 95% confidence intervals for each treatment group. While it is difficult visually to judge the proportionality in months 2 through 5, it is apparent that the curves converge at later times, when there are few events and the confidence intervals overlap completely.

Figure 5.

Estimated cumulative hazard functions and 95% confidence intervals for the treatment group, pemetrexed plus best supportive care (BSC), and BSC alone group (left panel). The right panel displays simple estimates (circles, plotted at time period midpoint) with 95% confidence intervals (dashed lines) of treatment effect on progression-free survival (PFS).

Naïve likelihood estimates of Cox regression parameters (i.e., log hazard ratio for treatment versus control, unadjusted for responder status or any other variable) are shown in the right panel of Figure 5. Time intervals were formed on the basis of having 40 events. The plot indicates that a piecewise exponential model for PFS (see e.g., Ibrahim et al. (2002, Example 4.3)) may be more appropriate, since the treatment effect appears to be changing over time. Such a model posits a baseline hazard λ_k within small intervals of time I_k = (s_k, s_k+1]. Then the individual hazard is a product of this baseline, a covariate effect θ_ik that could incorporate a time-varying treatment effect, and a frailty term u_i.

6.2 Future Work

Substantively, additional research should be conducted to confirm these findings through use of data from a larger, similarly-designed MPM study. One such study was originally reported by Vogelzang et al. (2003). These data come from a clinical trial of first-line therapy for MPM, where LCSS and survival were measured similar to the present study. With a larger patient population and more measurement times per individual, that study affords an opportunity to confirm the usefulness of our methods. We may also wish to consider a different cancer population with PROs measured by a different, yet valid and reliable, questionnaire.

Further expansions of the multivariate models are of interest. For larger dimension of K, we might simply consider ${\mathbf{u}}_{ik}\stackrel{\mathit{iid}}{\sim }N(\mathbf{0},{\mathrm{\sum }}_{uk})$, where u_ik are 2-vectors and Σ_uk parameterizes correlation between the two longitudinal submodels for a single PRO. However, this does not explicitly parameterize the relationship among PRO-specific latent effects. For further simplicity, we could let Σ_uk = Σ_u, k = 1, …, K to make the relationship between the presence and severity random effects the same across PROs.

Alternatively, we may think of adding additional levels to the model hierarchy to induce correlation among the random intercepts. For example, we might write u_0ik = v_1k + v₂₀ + ε_0ik and u_1ik = v_1k + v₂₁ + ε_1ik. This adds random effects v_1k, k = 1, …, K, for the type of LCSS score, and v_2ℓ, ℓ = 0, 1, for the type of intercept (presence or severity). We would then modify the design vectors X_0i(s) and X_1i(s) to remove the first (intercept) entries, in order to hierarchically center the random effects around β_0k1 and β_1k1. Structure within the 2K ×2K matrix Σ results from the correlation among random effects sharing index values of ℓ or k. Specifically, $\mathit{Cov}(U_{\ell ik},U_{{\ell }^{\prime }ik})={\sigma }_{v1}^2$ and $\mathit{Cov}(U_{\ell ik},U_{\ell {ik}^{\prime }})={\sigma }_{v2}^2$, but Cov(U_ℓik, U_ℓ′ik′) = 0 so that we model correlation for random intercepts of the same type (ℓ) or PRO (k), but not across these categories.

The general model (3) allows us to capture further heterogeneity among subjects by allowing individual- and PRO-specific random effects at each time point. Then we might impose structure on these time-varying random effects, such as autocorrelation according to U_0ik(t) ~ N U_0ik(t − 1), ${\sigma }_k^{2}exp(-{\rho }^{(k)}\mid {\text{day}}_i(t)-{\text{day}}_i(t-1)\mid ))$.

In addition, we may combine the two time-to-event variables (time-to-progression and time-to-death) into a multivariate survival model joint with either multivariate or univariate longitudinal outcomes. That is, we might expand (3) to include a multistate survival model (Huzurbazar, 2005) having three states: baseline disease, progressed disease, and death. We can build models for the effects of treatment and covariates on the allowed transitions among these states, accounting for the ordering inherent in these, namely, progression may occur before death, but not vice versa. We might also consider the use of a Cox proportional hazards model, which does not impose parametric constraints on the form of the baseline hazard function as in the Weibull. We hope to report on these and other development in a future manuscript.