Abstract
Determining the magnitude and location of neural sources within the brain that are responsible for generating magnetoencephalography (MEG) signals measured on the surface of the head is a challenging problem in functional neuroimaging. The number of potential sources within the brain exceeds by an order of magnitude the number of recording sites. As a consequence, the estimates for the magnitude and location of the neural sources will be ill-conditioned because of the underdetermined nature of the problem. One well-known technique designed to address this imbalance is the minimum norm estimator (MNE). This approach imposes an L2 regularization constraint that serves to stabilize and condition the source parameter estimates. However, these classes of regularizer are static in time and do not consider the temporal constraints inherent to the biophysics of the MEG experiment. In this paper we propose a dynamic state-space model that accounts for both spatial and temporal correlations within and across candidate intra-cortical sources. In our model, the observation model is derived from the steady-state solution to Maxwell's equations while the latent model representing neural dynamics is given by a random walk process. We show that the Kalman filter (KF) and the Kalman smoother [also known as the fixed-interval smoother (FIS)] may be used to solve the ensuing high-dimensional state-estimation problem. Using a well-known relationship between Bayesian estimation and Kalman filtering, we show that the MNE estimates carry a significant zero bias. Calculating these high-dimensional state estimates is a computationally challenging task that requires High Performance Computing (HPC) resources. To this end, we employ the NSF Teragrid Supercomputing Network to compute the source estimates. We demonstrate improvement in performance of the state-space algorithm relative to MNE in analyses of simulated and actual somatosensory MEG experiments. Our findings establish the benefits of high-dimensional state-space modeling as an effective means to solve the MEG source localization problem.
Keywords: Magnetoencephalography, source localization, Kalman filter, fixed interval smoother
1. Introduction
Electromagnetic source imaging is a neuroimaging technique that permits study of neural events on a millisecond timescale. This type of imaging reveals brain dynamics that cannot be seen with imaging modalities such as functional magnetic resonance imaging (fMRI) or positron emission tomography (PET) that capture brain activity on a much slower timescale. Two of the most important examples of electromagnetic imaging are electroencephalography (EEG) and magnetoencepholography imaging (MEG). These modalities acquire multiple time series recorded at locations exterior to the skull and are generated, respectively, by electric and magnetic fields of neuronal currents within the cortex of the brain [Hämäläinen et al. (1993), Nunez (1995)]. In these experiments subjects execute a task that putatively activates multiple brain areas. In the case of EEG recordings, the mode of acquisition involves affixing an array of electrodes to the surface of the scalp and measuring the potential differences relative to a reference node. In contrast, MEG records extremely weak magnetic fields emanating from the brain on the order of femtoTesla, that is, 10−15 Tesla [Nunez (1995)]. To put these quantities into context, the magnetic field of the earth is around 5 × 10−5 Tesla while that of a present-day magnetic resonance scanner used for medical diagnostic imaging ranges between 1.5 and 7 Tesla. Because the magnetic fields of the brain are extremely weak, a specially shielded room and highly sensitive array of detectors, called superconducting quantum interference devices (SQUIDs), are required to undertake the MEG recordings.
Generating images of the brain's cortical activity from MEG time-series recordings requires solving a high-dimensional ill-posed inverse problem. In the case of MEG imaging, the nonunique nature of the inverse problem arises because the number of potential three-dimensional brain sources (as a consequence of the biophysics of the problem) is infinite, while the measured two-dimensional SQUID array typically contain 306 magnetometer and gradiometer detectors.
The accuracy of the inverse solution depends critically on two main features of the problem, specifically, the precision of the forward model and the choice of inverse solution algorithm. The MEG forward model is designed to describe how activity propagates from sources in the cortex to the SQUID detectors. These forward models are normally constructed by combining information about head and brain geometry with the electromagnetic properties of the skull, dura and scalp to yield a numerical approximation to Maxwell's quasistatic equations; see, for example, Hämäläinen et al. (1993). Under this forward model the strength of the magnetic field recorded at a given SQUID detector near the surface of the head is approximately proportional to the reciprocal of its squared distance from a given cortical source. The second consideration we face relates to the choice of source localization algorithm. Solving this localization problem is one of the most technically challenging in MEG imaging research and has been an active area of methods development for both EEG and MEG over the past two decades. Historically, two of the most popular methods for solving the EEG/MEG inverse problem have been the dipole-based and (linear) distributed-source methods.
Dipole-based methods model the underlying neuronal sources as discrete current dipoles whose location, orientation and amplitude are unknown quantities to be estimated [Mosher, Lewis and Leahy (1992), Uutela, Hämäläinen and Salmelin (1998)]. Choosing the number of dipoles to include in the model is problematic. Eigenvalue decomposition methods have been developed to address this model selection issue [Mosher, Lewis and Leahy (1992)]. However, these approaches still require subjective interpretation when the eigenvalue distribution does not yield an obvious distinction between the signal and noise subspaces. In addition, finding the best-fitting parameters for the multidipole model requires nonlinear optimization. Since the measured fields depend nonlinearly on the dipole position parameters, typical minimization routines may not yield the globally optimal estimates for these parameters. Proposed solutions to this problem include the MUSIC (MUltiple SIgnal Classification) algorithm [Mosher and Leahy (1998)], global optimization algorithms and partly heuristic model constructions that use interactive software tools [Uutela, Hämäläinen and Salmelin (1998)]. However, none of these methods utilize the temporal sequence of the signals, that is, if the original data points are first permuted and an inverse permutation is applied to the source estimates, the results are the same as without permutation. Finally, in many important clinical and neuroscientific applications, such as epilepsy, sleep or general anesthesia, the dipole model is inappropriate, since the generating currents are most likely distributed across large areas on the cortex.
In the distributed source models, each location in the brain represents a possible site of a current source. Since the number of unknown sources vastly outnumbers the number of EEG or MEG data recordings, constraints are required to obtain a unique solution. The minimum-norm estimator (MNE) employs an L2-norm data “fidelity” term to quantify the relationship between the observed magnetic field recordings and the estimated source predictions and an L2-norm regularization or penalty term on the magnitude of those solutions. While the minimum-norm estimate (MNE) yields the solution with the smallest energy (sum of squares) across the solution space [Hämäläinen et al. (1993)], it tends to consistently favor low-amplitude solutions that are located close to the scalp surface. The relative contribution of the data term and source term can be controlled or tuned through a regularization parameter. In MNE, the data term is specifically the L2-norm of spatially whitened data while the source term is the L2-norm of the current amplitudes. A well-known variant of this approach is the LORETA (LOw-Resolution Electromagnetic Tomography Algorithm), where the L2-norm source term specified in MNE is replaced by a weighted norm that approximates the spatial Laplacian of the currents [Pascual-Marqui, Michel and Lehmann (1994)]. In the case of minimum-current estimates (MCE) [Uutela K. Hämäläinen and Somersalo (1999)], the source term is taken to be the L1-norm of the source current amplitudes. A consequence of this choice is that the estimates will be sparse as opposed to diffuse, leading to families of solutions that may closely resemble those uncovered through a dipolar analysis.
Beamformer approaches, originally inspired by problems in radar and sonar array signal processing [Krim and Viberg (1996)], seek to localize EEG/MEG activity by specifying a series of spatial filters, each tuned to maximize sensitivity to a particular spatial location within the brain [Van Veen et al. (1997)]. These methods assume, however, that EEG/MEG sources are spatially uncorrelated, and are limited by interference crosstalk from sources outside the focus of the beam-former spatial filter. A more recent related approach by Zumer et al. (2007) features a graphical model framework to characterize the probabilistic relationships among latent and observable temporal sources for averaged ERP data. Once a low-dimensional statistical data subspace is estimated, the algorithm computes full posterior distributions of the parameters and hyperparameters with the primary objective of alleviating temporal correlation between spatially distinct sources (source separation). In later work [Zumer et al. (2008)] this approach is extended somewhat to include explicit temporal modeling by drawing on estimated weightings from a predefined family of smooth basis functions. Wipf et al. (2010) explores an alternate procedure to empirical Bayesian source modeling that attempts to simultaneously capture and model correlated source-space dynamics in the presence of unknown dipole orientation and background interference.
Bayesian approaches to MEG source localization have included Phillips et al. (2005), Mattout et al. (2006) and Friston et al. (2008). Collectively, these techniques construct the source localization problem within an instantaneous empirical Bayes framework. These approaches specify a nested and hierarchical series of spatial linear models to be subsequently solved under a penalized Restricted Maximum Likelihood (ReML) procedure. The multiresolutional nature of this regime carries with it a measure of spatial adaptation for the estimated hyperparameters since the spatial clusters of activated dipoles are amalgamated across several (orthogonal) scales. At the same time the most likely set of spatial priors for each competing model is chosen using information selective model ranking procedures. The latter approach [Friston et al. (2008)] extends the use of ReML to engender a framework aiming to move from parametric spatial priors to larger sets of imputed sources with localized but not necessarily continuous support. The principle advantage of this extension is its intrinsic ability to capture source solutions ranging from sparse dipole models at one end of the localization spectrum to dense but smooth distributed configurations of spatial dipoles at the other.
State-space methods featuring latent temporal models have recently been proposed. For example, studies by Galka, Yamashita and Ozaki (2004) and Yamashita et al. (2004) have used a random-walk dynamical model with Laplacian spatial constraints to represent the dynamics of EEG source currents, employing the Kalman filter and recursive least-squares framework to perform source localization. Daunizeau and Friston (2007) used a state-space model to capture latent neuronal dynamics by placing a first-order autorgressive (AR) model within a full spatiotemporal variational Bayes procedure. Each ensemble of sources is characterized by establishing an effective region of influence in which the hidden neural state-dynamics are assumed constant. This leads to a temporal representation of each region in terms of a single average dynamic.
Ou, Hämäläinen and Golland (2009) have developed a mixed L1 L2-norm penalized model to estimate MEG/EEG sources. This methodology allows for spatially sparse solutions while ensuring physiologically plausible and numerically stable time course reconstructions through the use of basis functions. Since estimation of this kind of mixed-norm regularized problems represents a computational challenge, convex-cone optimization methods are implemented to efficiently compute the MEG/EEG source estimates. These procedures are shown to yield significant improvement over conventional MNE approaches in both simulated and actual MEG data.
In the majority of MEG stimulus response experiments, the objective is to estimate the activity in a given brain region based on multiple repetitions of the same stimulus. The time interval of the MEG recordings after the onset of the stimulus is usually around 1,000 msec. Consequently, the optimal estimate of the source activity at a given time point should be based on all the data recorded in this time window, as opposed to only the recordings within a small instantaneous subinterval as is the case in the MNE algorithm.
Thus, in the current work, we model the spatiotemporal structure of the MEG source localization problem as a full-rank state-space estimation procedure. In contrast to previous related approaches, for example, Galka, Yamashita and Ozaki (2004), Yamashita et al. (2004) and Ou, Hämäläinen and Golland (2009), we recover the underlying neural state dynamics across the entire solution space using all information available in the MEG measurements to compute a new source estimate at each location and time point. We do not restrict our state-covariance structure to operate either through reduced-rank approximations or through “small-volume” state-space models that operate within localized spatial neighborhoods [Galka, Yamashita and Ozaki (2004), Yamashita et al. (2004)]. The analysis computes activity at a particular source with activity at that source combined with (potentially all) neighboring sources in both preceding and subsequent time periods (spatiotemporal correlation). We find that solution of the resulting high-dimensional state-space model requires the application of high performance computing (HPC) resources.
We show that two solutions that are naturally suited to this type of dynamic inverse problem are the Kalman filter and the fixed-interval smoother [Kitagawa and Gersch (1996), Kay (1993)]. These algorithms are based on a series of mathematical relationships that employ principles from electromagnetic field theory to relate the observed MEG measurements to the underlying dynamics of the current source dipoles. In contrast to popular source localization methods such as MNE where the regularization constraints are formulated in terms of a fixed-error covariance matrix, the state-space estimators feature time-varying error covariances and propagate past (and future) information into the current update.
We describe how these algorithms may be used to perform this state estimation by conducting the computation on the NSF Teragrid Supercomputing Network. In Section 3 we detail the necessary supercomputing methods needed to implement the high-dimensional state-space estimation. We demonstrate the improvement in performance of the state-space algorithm relative to MNE in analyses of a simulated MEG experiment and actual somatosensory MEG experiment.
2. Theory
We assume that in an MEG experiment a stimulus is applied T times and at each time for a (short) window of time following the application of the stimulus MEG activity is measured simultaneously in S SQUID recording sites. Let Ys,r(k) denote the measurement at time k at location s on repetition r where k = 1, . . . , N, s = 1, . . . , S and r = 1, . . . , T. We take and we define Yk = Y(Y1(k), . . . , YS(k)) to be the S × 1 vector of measurements recorded at time k. We assume that there are P current sources in the brain and that the relation between the MEG recordings and the sources is defined by
| (2.1) |
where Jk = (Jk,1, . . . , Jk,P) is the 3P × 1 vector of source activities at time k, each Jk,i is a 3 × 1 vector, and H is the S × 3P lead field matrix, derived as described in Hämäläinen et al. (1993). This matrix is approximated in practice using the known conductivity profile of an MRI-derived T1 image to derive a one-layer head model using the boundary element method [Hämäläinen and Sarvas (1989)]. Furthermore, εk is a zero mean Gaussian noise with covariance matrix Σε. To build on an idea originally suggested in the EEG literature [Galka, Yamashita and Ozaki (2004), Yamashita et al. (2004)], we assume that the Jk behave like a stochastic first-order process with a potentially weighted neighborhood (six direct neighbors in the case below) constraint defined at voxel p by
| (2.2) |
where is some small neighborhood around voxel p and is a mask of (estimated) autoregressive weights, and vk is a 3P × 1 vector of Gaussian noise with mean zero and covariance matrix Σw. The linear structure in equation (2.2) means that we can generalize this structure into matrix format such that all sources in the brain (i.e., not only local relationships) are encompassed in the model. That is,
| (2.3) |
If F is an identity matrix, the state dynamics reduce to a random walk process. Equations (2.1) through (2.3) define the observation and latent time-series equations, respectively, for a state-space model formulation that can be used to provide a dynamic description of the MEG source localization problem.
2.1. Standard MEG inverse solution
The standard approach to the MEG source localization problem is to solve an L2 regularized least-squares problem at each time k. That is,
| (2.4) |
where denotes the Mahalanobis distance between the vectors y and x with error covariance matrix Q, μ is an offset parameter (prior mean) and C is the regularization covariance matrix [Hämäläinen and Ilmoniemi (1994)].
If we take μ = 0 and define the source covariance matrix as C = λR, where R is a diagonal, scaled matrix normally computed in advance, and if λ > 0, then at each time k an instantaneous MEG source estimate (the MNE solution) is given as
| (2.5) |
for k = 1, . . . , N. The MNE estimate is a local Bayes’ estimate because it uses in its computation only the data Yk at time k and the Gaussian prior distribution with mean μ = 0 and covariance matrix λR. Hence, the MNE estimation procedure imposes no temporal constraint on the sequence of solutions.
2.2. Kalman filter solution
Given the state-space formulation of the MEG observation process in equations (2.1) and (2.3), it follows that the optimal estimate of the current source at time k using the data Y1, . . . , YN up through time N is given by the Kalman filter [Kitagawa and Gersch (1996)]
| (2.6) |
| (2.7) |
| (2.8) |
| (2.9) |
which simplifies to
| (2.10) |
| (2.11) |
. for k = 1, . . . , N, given initial conditions J0 ~ N(0, W0|0), Σw = W0|0. At each time k the Kalman filter computes p(xk|Y1, . . . , Yk), which is the Gaussian distribution with mean Jk|k and covariance matrix Wk|k. In terms of the regularization criterion function in equation (2.4), the Kalman filter solution is equivalent to choosing at time k, μ = [I − KkH]F Jk−1|k−1 and C = Wk|k−1, where we have used the matrix inversion lemma to re-express the Kalman filter update in equation (2.9) in order that we can compare it directly with the MNE solution in equation (2.5). From this comparison we see that the Kalman solution improves upon the MNE solution in two important ways. First, in the Kalman solution, the offset parameter and the regularization matrix are different at each time k and are given, respectively, by μ and the one-step prediction error covariance matrix Wk|k−1. The MNE solution at each time k has a fixed prior mean μ = 0 and (temporally) fixed regularization matrix C = λR. Because of this choice of regularization constraint, equation (2.9) shows that the Kalman filter estimate at time k is a linear combination of Jk−1|k−1, the current source estimate at time k − 1, and Yk, the observations at time k. In contrast, the MNE solution at each time k is a linear combination of the observed data and a fixed prior mean of μ = 0. In this regard, the MNE estimate biases the solution at each time k toward 0. Taken together, these observations show that the stochastic continuity assumption in the Kalman state model results in a time-varying constraint upon the fluctuating source estimates.
2.3. Fixed-interval smoothing algorithm solution
Because the MEG time series are often fixed length recordings, we can go beyond the estimate Jk|k provided by the Kalman update and compute the posterior density p(xk|Y1, . . . , YN) at time k given all the data in the experiment. To do so, we combine the Kalman filter with the fixed-interval smoothing algorithm (FIS) [Kitagawa and Gersch (1996), Kay (1993)], that may be computed as follows:
| (2.12) |
| (2.13) |
| (2.14) |
for k = N −1, . . . , 1 and initial conditions JN|N and WN|N computed from the last step of the Kalman filter N. It is well known that p(xk|Y1, . . . , YN) is a Gaussian distribution with mean Jk|N and covariance matrix Wk|N [Kitagawa and Gersch (1996), Kay (1993)].
2.4. Practical considerations
Implementation of the Kalman filter first requires making estimates of both the initial state, the state covariance matrix Σw and the error covariance matrix Σε. We estimated the noise covariance matrix Σε from measurements taken in the scanner in the absence of a subject. We next estimated the initial state as the MNE solution and the state covariance matrix by first computing the MNE source estimates , subsequently deriving Σw from the sample covariance matrix using a differenced sequence of these static estimates.
3. Supercomputer implementation
Historically the Kalman filter has found widespread use in several high-dimensional modeling domains, including weather forecasting [Farrell and Ioannou (2001)] and oceanography [Fukumori et al. (1993), Fukumori and Malanotte-Rizzoli (1995)]. Kalman filters and fixed-interval smoothers are advantageous in these scenarios as, under assumptions of linearity and normality, they are (near) optimal estimators. In addition, their desirable properties hold across a wide variety of time-varying linear (and nonlinear) models. However, in its standard form the Kalman filter is computationally prohibitive for these classes of problems. In the example applications listed above, the numerical calculations are often carried out on systems of state dimension N ~ O(107) with state covariance matrices of size N2 ~ O(1014) [Farrell and Ioannou (2001)]. Computationally, the most intense aspects of the Kalman algorithm stem from the prediction update in the covariance matrices that require costly linear algebraic updates at each time step. Since the dynamical error structure of these systems is often well understood, many numerical solutions to these kinds of paradigms, for example, Farrell and Ioannou (2001) and Fukumori and Malanotte-Rizzoli (1995), employ a range of model-reduction techniques in their formulations to achieve computational tractability.
In the case of the MEG and EEG inverse problem, the solution space is ~ O(103 − 104), leading to error covariances of dimension P2 ~ O(106–108). Thus, the computational problem is not quite so intensive as in the forecasting applications, meaning that we can feasibly employ full-rank state-estimation methods to compute their solution on an HPC system. When performing Kalman filtering, the computations dominating each time step involve three high-dimensional full-rank matrix multiplications, leading to a total approximate computational cost of 3P3 (excluding auxiliary lower dimensional linear operations). When taking into account ancillary variables, the amount of memory required is at least 24+ gigabytes for each update operation. In addition, the FIS requires one additional such multiplication at each time step followed by a full-rank P × P matrix inversion (2P3). Also, FIS requires approximately three gigabytes of storage space per time point in order to save the prediction and update covariances (in 32-bit storage format) estimated during the forward pass of the Kalman filter. The scale of these computations renders them infeasible on nearly any state-of-the-art standalone computing resource. To address this limitation, we parallellized the Kalman and FIS filtering computations such that the data-intensive parts of the algorithm were distributed across multiple nodes of a High Performance Computing system [Blackford et al. (1997)]. For this purpose we utilized the NSF Teragrid resource at the TACC (Texas Advanced Computing Center). This resource comprised a 1024-processor Cray/Dell Xeon-based Linux cluster with a total of 6.4 Teraflops computing capacity.
4. Results
4.1. Simulated MEG experiment
We designed a set of simulation studies to compare the performance of the dynamic localization methods against MNE. Prior to constructing the dynamic simulation, we first computed the spatial conductance profile across the head and specified the spatial resolution of the discretized solution space (source locations). To restrict this source space to the cortical surface, we employed anatomical MRI data obtained from a single subject with a high-resolution T1-weighted 3D sequence (TR/TE/flip = 2,530 ms/3.49 ms/7°, partition thickness = 1.33 mm, matrix = 256 × 256 × 128, field of view = 21 cm×21 cm) in a 3-T MRI scanner (Siemens Medical Solutions, Erlangen, Germany). The geometry of the gray–white matter surface was subsequently computed using an automatic segmentation algorithm to yield a triangulated model with approximately 340,000 vertices [Dale, Fischl and Sereno (1999)]. Finally, we utilized the topology of a recursively subdivided icosahedron with approximately 5 mm spacing between the source nodes to give a cortical sampling of approximately 104 locations across both hemispheres.
Using MNE, we chose as the region of interest a section of the left hemisphere over the primary somatosensory and motor cortices. We computed a single layer homogeneous forward model or lead field matrix H over all the sampled voxels in the left and right hemispheres. The region of interest contained 125 active voxels from the more than 10,000 gray matter voxels that could be potential sources for an observed magnetic field under this parcellation. For this simulation, therefore, the number of active sources was Pactive = 125, and the number of measurement channels was S = 306. We next constructed H with dimension 306 × 5,120 (left-hemisphere), corresponding to a spatial sampling of 5 mm. Note that we chose to estimate only the dominant normal MEG component at each vertex (i.e., z-direction) as opposed to estimating the triplet of x, y and z contributions from which both magnitude and directional information could be resolved. In each of the chosen 125 voxels in the source space, we generated an “activation” signal consisting of a mixture of 10 and 20 Hz frequencies modulated by a 0.4 Hz envelope to simulate typical signal patterns commonly observed in the motor and somatosensory cortices; see, for example, Lounasmaa et al. (1995). Next we added Gaussian noise to all P = 5,120 vertices to generate an image-wide signal-to-noise ratio (SNR) that ranged between 0.1 and 2 (in line with typical SNRs encountered in MEG studies). Specifically, we defined SNR as
| (4.1) |
When computing the source reconstructions we set the observation covariance matrix as the empty room covariance, that is, that which is generated from background noise measurements taken from the system while the subject is absent from the scanner. We computed three inverse solutions: the MNE solution, the KF solution, and the FIS solution. In this simulation study, we recovered the source estimate for each method and for each value of SNR using three different choices of tuning parameter (λ = 0.5, 1, 3). The time-course length was 120 time points and with an assumed sampling rate of 600 Hz, equated to a data segment of about 200 msec.
To examine the benefits of the dynamic state-space procedures in relation to the MNE source localization algorithm, we computed the Kalman and Fixed-Interval Smoothing filters, generating estimates of the source locations and amplitudes within the entire cortex. When applied to the 200 ms window of MEG data, this analysis averaged about one hour for each simulated record when distributed across 16 of the CRAY-DELL cores. For each choice of SNR (through a sweep of 20 SNRs choices equispaced between 0.1 and 2), the FIS algorithm took around two hours on 24 CRAY-DELL computational nodes, leading to a total CPU time of around 1,280 hours for the whole simulation. Storage of the prediction and update covariances for each SNR required approximately 110 gigabytes of disk space, resulting in a total of 2 Terabytes of storage for each of the three choices of tuning parameter (λ), that is, 6 Terabytes in total.
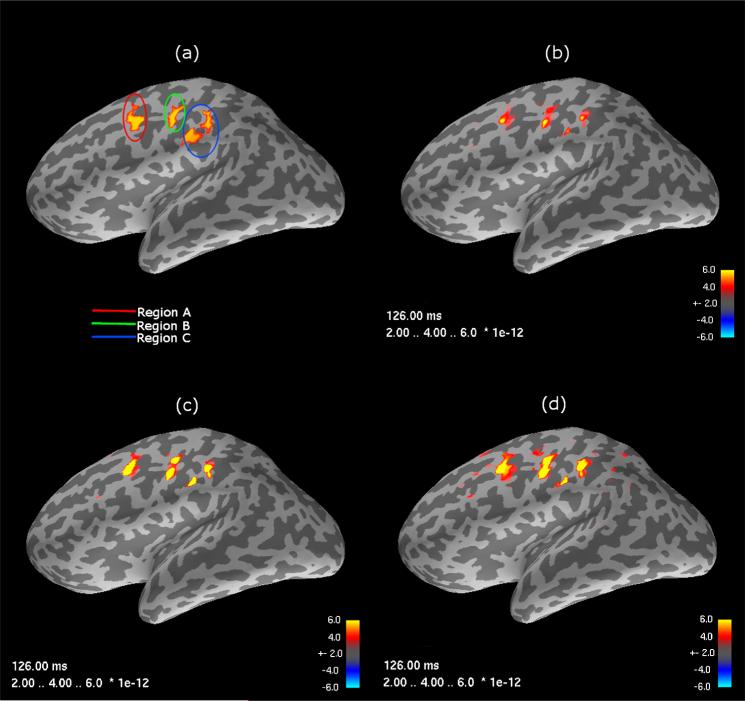
Figure 1 illustrates the spatial extent of the simulated signal (a) taken as a snapshot at the peak of the damped sinusoidal signal. Yellow to red color map values indicate progressively smaller current sources (J ) representing ground truth, panel (a), or the reconstructed estimates (b)–(d). Figure 1 panels (b)–(d) show the estimates as computed with (b) the minimum norm estimate, (c) the Kalman filter and (d) the Fixed Interval Smoother. For each method, the SNR as defined by equation (4.1) and the tuning parameter governing the strength of the estimate smoothness were set to SNR = λ = 1.
Fig. 1.
Activation maps in three regions, A, B and C at the peak response time of 126 ms for: (a) True signal; and source estimates computed by (b) MNE; (c) the Kalman filter; and (d) the Fixed Interval Smoother. These images were computed using a regularization parameter (λ = 1).
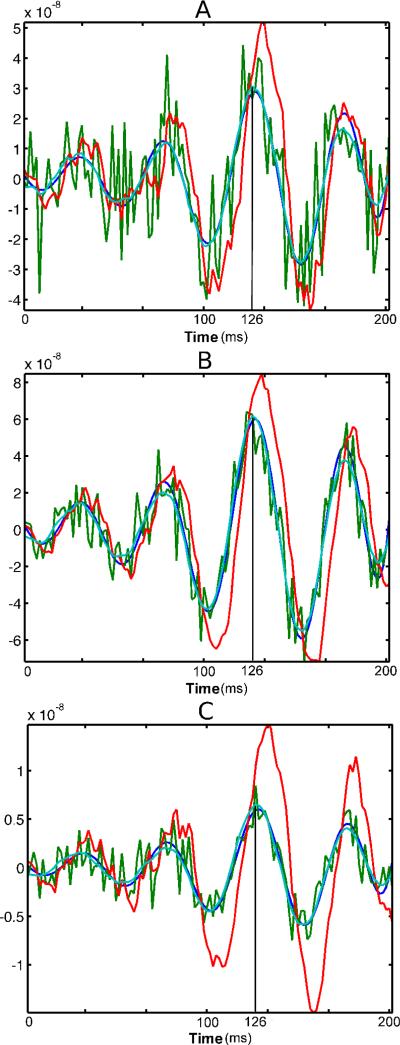
Figure 2 depicts temporal reconstructions for the three methods with the choice of SNR = λ = 1. For each region A, B or C, the time series at the voxel corresponding to the peak MNE response was plotted and overlaid onto the “ground-truth” simulated signal. The state-space reconstructions show considerably less variability than the static MNE time course, however, the KF approach displays elevated bias as compared to the FIS method. Furthermore, the KF method contains a temporal shift in relation to the simulated signal that is not apparent in MNE and FIS. These fundamental differences in the temporal behavior of the three methods are consistent in space, across SNR, and are invariant to choice of λ.
Fig. 2.
Time course of source estimates from the simulated MEG experiment for the maximally responding voxel relative to the MNE solution, where each panel (from top to bottom) corresponds directly to each of the three regions, A, B and C denoted in Figure 1(a). Green denotes the MNE solution, red the KF, dark blue is the FIS solution, while cyan represents the true signal.
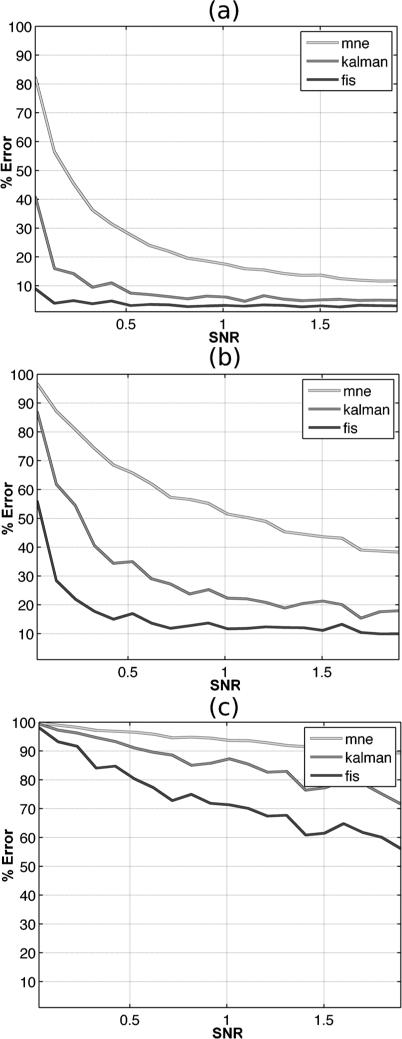
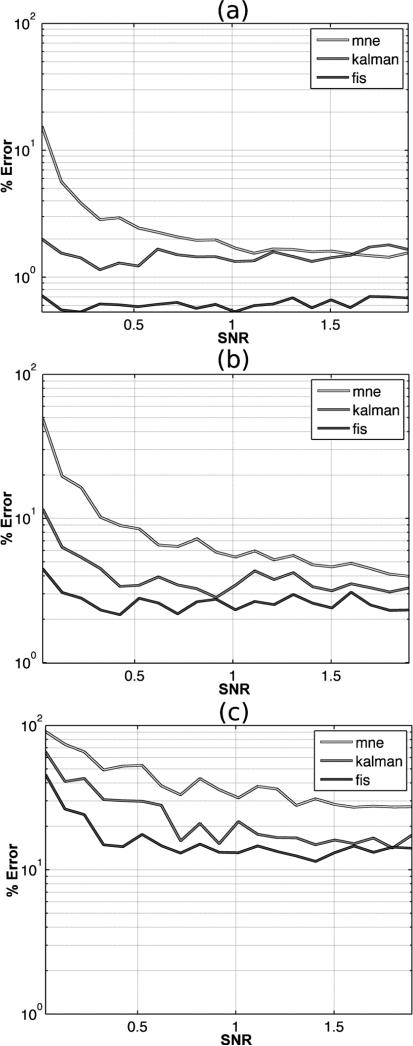
Figures 3 and 4 illustrate the behavior of MSE (Mean-Squared Error) as a function of SNR for the three choices of tuning parameter: panel (a) λ = 0.5, panel (b) λ = 1, and panel (c) λ = 3 between the true signal and the estimated signal for each estimation method. In Figure 3 MSE is calculated at all vertices in the reconstructed cortical surface and averaged spatially for each choice of SNR. The fixed-interval smoother shows the lowest MSE which indicates that the estimated source curves are closer to the ground truth simulations compared to the alternative methods. By contrast, the MNE approximations show the least favorable recovery of the simulated sources. In Figure 4 we computed the MSE at each vertex for each source reconstruction method in the same manner but calculated the average MSE only within the three activated regions. These plots, therefore, examine the behavior of the source reconstructions by zooming into areas that contain signal, thus decoupling the model fits to areas of true signal from those vertices containing background noise. The three methods show similar behavior as in Figure 3 in the activated regions, with the fixed-interval smoother again showing superior performance to the other two methods. As a consequence of the relative MSE errors exhibiting significantly smaller values in these signal-rich regions, we display their effects on a log linear scale to better delineate the salient differences between methods.
Fig. 3.
Average percentage relative change in MSE computed as a function of SNR from the simulated MEG experiment for all voxels on the cortical surface for each localization method: MNE (light gray), Kalman filter (dark gray), and Fixed Interval Smoother (charcoal). (a) λ = 0.5, (b) λ = 1, (c) = λ = 3.
Fig. 4.
Average percentage relative change in MSE computed as a function of SNR in the simulated MEG experiment across all active sources for each localization method: MNE (light gray), Kalman filter (dark gray), and Fixed Interval Smoother (charcoal). (a) λ = 0.5, (b) λ = (c), λ = 3.
5. Somatosensory MEG experiment
To illustrate the state-space and MNE methods on an actual MEG experiment, we estimated the sources of the alpha (8–13 Hz) and mu (10 Hz and 20 Hz) spontaneous brain activity using anatomically-constrained whole-head MEG. Synchronous cortical rhythmic activity of large populations of neurons is associated with distinct brain states and has been the subject of extensive investigation using unit electrophysiology, as well as EEG, MEG and fMRI techniques [Lounasmaa et al. (1995), Salmelin and Hari (1994)]. The alpha rhythm is recorded over the posterior parts of the brain, being strongest when the subject has closed eyes and reduced when the subject has open eyes. Sources of alpha rhythm have been identified with MEG and EEG to lie in the parietooccipital sulcus and calcarine fissure [Freeman, Ahlfors and Menon (2009)]. The mu rhythm represents activity close to 10 and 20 Hz in the somatomotor cortex, and is known to reflect resting states characterized by lack of movement and somatosensory input. The 20 Hz component tends to be localized in the motor cortex, anterior to location of the 10 Hz component [Lounasmaa et al. (1995)], being specifically suppressed or elevated at topographic locations representing moving or resting individual limbs, respectively. By comparison, the 10 Hz component arises in the somatosensory cortex, and is thought to reflect the absence of sensory input from the upper limbs [Liljeström et al. (2005), Salmelin et al. (2005)].
Following approval by the Massachusetts General Hospital Human Research Committee, the MEG signals were acquired in a healthy male subject in a magnetically and electrically shielded room at the Martinos Center for Biomedical Imaging at the Massachusetts General Hospital. MEG signals were recorded from the entire head using a 306-channel dc-SQUID Neuromag Vectorview system (Elekta Neuromag, Elekta Oy, Helsinki, Finland) while the subject sat with his head inside the helmet-shaped dewar containing the sensors. The magnetic fields were recorded simultaneously at 102 locations, each with 2 planar gradiometers and 1 magnetometer at a sampling rate of 600 Hz, minimally filtered to (0.1–200 Hz). The positions of the electrodes in addition to fiduciary points, such as the nose, nasion and preauricular points, were digitized using the 3Space Isotrak II System for subsequent precise co-registration with MRI images. The position of the head with respect to the helium-cooled dewar containing the measurement SQUIDS was determined by digitizing the positions of four coils that were attached to the head. These four coils are subsequently employed by the MEG sensors to assist in co-registration.
Ongoing magnetic activity was thus recorded under the following three conditions: (1) at rest with eyes closed; (2) at rest with eyes open; and (3) during sustained finger movement with eyes open. As described in previous studies, examination of raw data revealed strong alpha activity when the subject had eyes closed, and dampened or no alpha rhythm when the subject had eyes open (i.e., at rest or during sustained finger movement conditions). The mu activity was strongest at rest (i.e., with eyes open or closed) and suppressed during sustained fingers movement condition. 2 s long periods of raw data with either large amplitude alpha waves (e.g., during eyes-closed conditions) or large amplitude mu waves (e.g., during hand/finger resting conditions) were used as the input signal for MEG source localization. In addition, the empty MEG room noise was recorded just before the start of the experiment and subsequently used as measurement noise in the estimation of the alpha and mu activity generators.
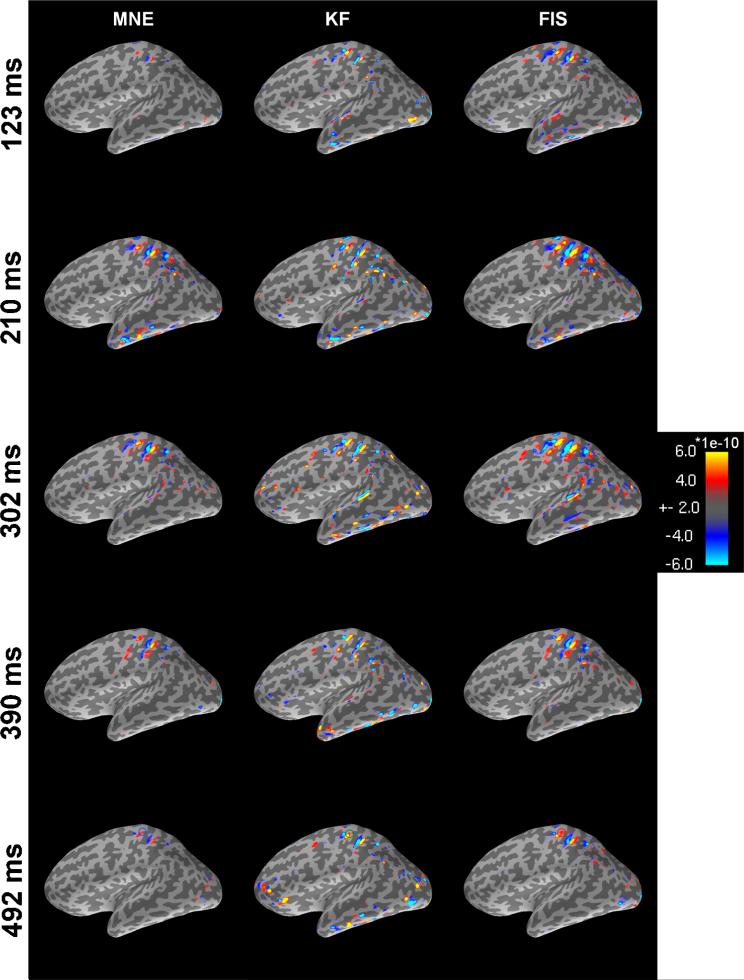
Figure 5 depicts the net estimated current distributions characterized in each panel by the length of each current triplet. In the inverse calculations, the orientation of the estimated currents was fixed such that they lay perpendicular to the cortical mesh. Each panel reveals the relative effect of the state-space approaches as compared to those gained from the static MNE technique as the dynamics of the mu-rhythm time course unfold (Figure 6). In all cases, we can observe regions in the central sulcus showing strong activation, but the FIS and KF solutions show stronger activations than those obtained through the MNE method. Moreover, Figure 6 shows that the reconstructed time courses of the KF and FIS solutions are much less variable than those of the MNE solution.
Fig. 5.
Source activation maps showing instantaneous reconstructions for the sensorimotor task. Each column shows the temporal evolution at the five peak modes of the mu-rhythm for each of the three methods: Minimal Norm Estimator (MNE); Kalman filter (KF); and Fixed Interval Smoother (FIS). The red and blue color maps correspond to inward and outward current flow, respectively. This reconstruction was carried out using a regularization parameter value of λ = 1.
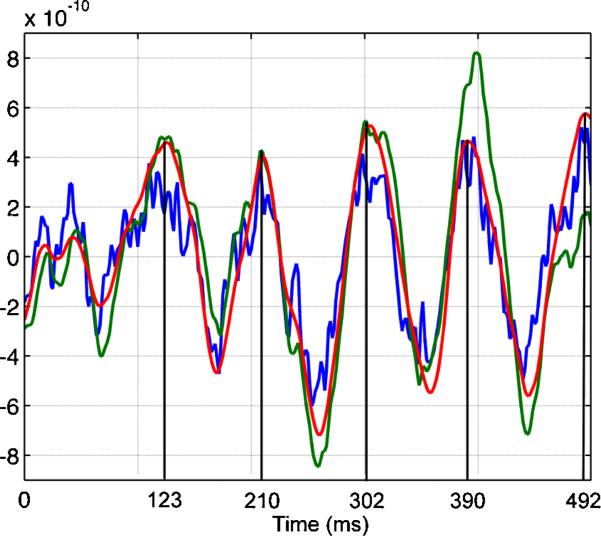
Fig. 6.
Representative time course reconstructions extracted from locations in the somatosensory cortex at 492 ms in Figure 5: MNE (blue), Kalman filter (green) and Fixed Interval Smoother (red).
In summary, analysis of the somatosensory experiment showed approximate agreement between MNE and the state-space models. As in the simulated MEG experiment, we note that the magnitudes of the estimate sources were greater for the state-space models (Figure 5). The temporal dynamics of the FIS agreed more closely with the MNE than with the KF (Figure 5). Not surprisingly, because the state-space models imposed a temporal constraint, their estimates were smoother than the MNE estimates (Figure 6). Also, as in the simulated MEG experiment, the KF estimates of the source amplitudes were larger than those computed by either MNE or the FIS.
6. Discussion
We have developed and implemented a state-space model solution to the MEG inverse problem. We examined its performance relative to the MNE algorithm on simulated and actual MEG experimental data. A simple analytic analysis showed that the state-space approach offers two important improvements over MNE. Namely, the KF/FIS estimate equation (2.9) uses a dynamic L2-norm regularization mean equation (2.6) and covariance matrix equation (2.7) update at each step, whereas the MNE estimate equation (2.5) uses a static L2-norm regularization zero mean and static covariance matrix to compute its instantaneous estimate. Making the prior mean zero at each update biases every solution toward zero. This makes it difficult to identify sources that are nonzero but weak (low amplitude). In contrast, the KF/FIS estimate is more likely to identify a weak source because if the source estimate at the previous time point, that is, 1 msec before, was similarly weak, it would be combined with the current observation to identify what would most likely be an attenuated source at the current time point. Second, the KF source estimates use all of the observations from the start of the experiment to the current time, then the FIS equation (2.13) uses the KF source estimates to compute new estimates based on all of the experimental observations. In contrast, the MNE source estimate uses only the observations recorded at the current time. Given that the MEG updates are computed every millisecond, the solutions at adjacent time periods are likely to be strongly correlated. Our state-space approach imposes a dynamic L2-norm regularization constraint to use this temporal information, whereas MNE imposes the same static L2-norm regularization constraint at each time point and thus does not consider the temporal structure. Our simulation studies demonstrated that the KF and FIS estimates are more accurate in terms of MSE (Figures 3 and 4) compared with MNE. Although the spatial maps of the state-space and MNE had comparable spatial extent, the KF and FIS estimates captured more accurately the magnitude of the activations (Figure 1). This accounts for the lower MSE for the FIS and the KF relative to MNE despite small numbers of erroneous activations in the case of the state-space models outside the areas of actual activations (Figure 1). In addition, the two state-space solutions were considerably smoother and in closer agreement with the simulated signal than the MNE solution. The KF which computes its estimates based exclusively on data up to the current time had a temporal lag with respect to the true signal (Figure 2). That is, the locations of the signal peaks and troughs were offset with respect to their true temporal locations. In addition, the KF estimates overestimated the true signal amplitude (Figure 2). The backward pass of the FIS corrected both of these problems, yielding a closer agreement with the true signal and a lower MSE (Figure 2). Although in the analysis of the actual MEG experiment MNE and the state-space models source estimates were in approximate agreement (Figure 5), the magnitudes of the FIS estimates were more consistent with those of the KF estimates, whereas the temporal dynamics of the FIS estimates followed more closely those of the MNE estimates (Figure 5). The KF estimates of the source amplitudes were larger than those computed by the either MNE or the FIS (Figure 6). Although our findings establish the feasibility of using high-dimensional state-space models for solving the MEG inverse problem, they also suggest several extensions. In our analysis we computed the KF and FIS estimates by testing different values of the regularization parameter. This parameter can be estimated in an empirical Bayesian [Lamus et al. (2007)] or a fully Bayesian framework. The spatial component of the model can be improved by using the structure of the particular experimental design to proposed specific forms of the F state-transition matrix. There are a broad range of techniques that have been used to accelerate computations in high-dimensional state-space models. The forward model can be extended to include subcortical sources. The MEG and EEG recordings are usually recorded simultaneously. Our state-space paradigm can be applied to the problem of estimating the sources from these two sources. These extensions will be the topics of future reports.
Footnotes
Supported in part by the National Science Foundation through TeraGrid resources provided by the Texas Advanced Computing Center (TACC). This work was also supported by NIH Grants NIBIB R01 EB0522 (E.N.B.), DP2-OD006454 (P.L.P.), K25-NS05780 (P.L.P.), DP1-OD003646 (E.N.B.), NCRR P41-RR14075, R01-EB006385 (E.N.B., P.L.P., M.S.H.) at Massachusetts General Hospital.
C. J. Long GlaxosmithKline Clinical Imaging Center Hammersmith Hospital London W12 0NN UK cjlong1@gmail.com
S. Temereanca Athinoula A. Martinos Center for Biomedical Imaging Massachusetts General Hospital Harvard Medical School Charlestown, Massachusetts USA
M. S. Hämäläinen Athinoula A. Martinos Center for Biomedical Imaging Massachusetts General Hospital Harvard Medical School Charlestown, Massachusetts USA and Harvard/Mit Division of Health Sciences & Technology Massachusetts Institute of Technology Cambridge, Massachusetts USA
P. L. Purdon Athinoula A. Martinos Center for Biomedical Imaging Massachusetts General Hospital Harvard Medical School Charlestown, Massachusetts USA
N. U. Desai Department of Electrical Engineering & Computer Science Massachusetts Institute of Technology Cambridge, Massachusetts USA
E. N. Brown Department of Brain and Cognitive Sciences Massachusetts Institute of Technology Cambridge, Massachusetts USA and Department of Anesthesia & Critical Care Massachusetts General Hospital Boston, Massachusetts USA and Harvard/Mit Division of Health Sciences & Technology Massachusetts Institute of Technology Cambridge, Massachusetts USA enbrown1@mit.edu
REFERENCES
- Blackford LS, Choi J, Cleary A, D'Azevedo E, Demmel J, Dhillon I, Dongarra J, Hammarling S, Henry G, Petitet A, Stanley K, Walker D, Whaley RC. ScaLAPACK Users’ Guide. SIAM; Philadelphia, PA: 1997. [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. NeuroImage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Daunizeau J, Friston KJ. A mesostate-space model for EEG and MEG. NeuroImage. 2007;38:67–81. doi: 10.1016/j.neuroimage.2007.06.034. [DOI] [PubMed] [Google Scholar]
- Farrell BF, Ioannou PJ. State estimation using a reduced order Kalman filter. J. Atmospheric Sci. 2001;58:3666–3680. [Google Scholar]
- Freeman W, Ahlfors S, Menon V. Combining fMRI with EEG and MEG in order to relate patterns of brain activity to cognition. Int. J. Psychophysiol. 2009;73:43–52. doi: 10.1016/j.ijpsycho.2008.12.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Daunizeau J, Kiebel S, Phillips C, Trujillo-Barreto N, Henson R, Flandin G, Mattout J. Multiple sparse priors for the M/EEG inverse problem. NeuroImage. 2008;39:1104–1120. doi: 10.1016/j.neuroimage.2007.09.048. [DOI] [PubMed] [Google Scholar]
- Fukumori I, Malanotte-Rizzoli P. An approximate Kalman filter for ocean data assimilation: An example with an idealized Gulf stream model. J. Geophys. Res. 1995;100:6777–6793. [Google Scholar]
- Fukumori I, Benvensite J, Wunsch C, Haid-vogel BD. Assimilation of sea surface topography into an ocean circulation model using a steady-state smoother. J. Phys. Oceanogr. 1993;23:2162–2181. [Google Scholar]
- Galka A, Yamashita O, Ozaki T, et al. A solution to the dynamical inverse problem of EEG generation using spatiotemporal Kalman filtering. NeuroImage. 2004;23:435–453. doi: 10.1016/j.neuroimage.2004.02.022. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Ilmoniemi RJ. Interpreting magnetic fields of the brain: Minimum norm estimates. Med. Biol. Eng. Comput. 1994;32:35–42. doi: 10.1007/BF02512476. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Sarvas J. Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE Trans. Biomed. Eng. 1989;36:165–171. doi: 10.1109/10.16463. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography—Theory, instrumentation, and application to noninvasive studies of the working human brain. Rev. Modern Phys. 1993;65:413–497. [Google Scholar]
- Kay S. Fundamentals of Statistical Signal Processing, Vol. I—Estimation Theory. Prentice Hall; Upper Saddle River, NJ: 1993. [Google Scholar]
- Kitagawa G, Gersch W. Smoothness Priors Analysis of Time Series. Lecture Notes in Statistics. Vol. 116. Springer; New York: 1996. p. MR1441074. [Google Scholar]
- Krim H, Viberg M. Two decades of array signal processing research: The parametric approach. IEEE Signal Processing Magazine. 1996;13:67–94. [Google Scholar]
- Lamus C, Long CJ, Hamalainen MS, Brown EN, Purdon PL. Parameter estimation and dynamic source localization for the magnetoencephalography (MEG) inverse problem.. IEEE International Symposium on Biomedical Imaging; Washington, DC. April 12–15, 2007; 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liljeström M, Kujala J, Jensen O, Salmelin R. Neuromagnetic localization of rhythmic activity in the human brain: A comparison of three methods. NeuroImage. 2005;25:734–745. doi: 10.1016/j.neuroimage.2004.11.034. [DOI] [PubMed] [Google Scholar]
- Lounasmaa O, Hämäläinen M, Hari R, Salmelin R. Information processing in the human brain: Magnetoencephalographic approach. Proc. Natl. Acad. Sci. USA. 1995;93:8809–8815. doi: 10.1073/pnas.93.17.8809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattout J, Phillips C, Penny WD, Rugg MD, Friston KJ. MEG source localization under multiple constraints: An extended Bayesian framework. NeuroImage. 2006;30:753–768. doi: 10.1016/j.neuroimage.2005.10.037. [DOI] [PubMed] [Google Scholar]
- Mosher JC, Leahy RM. Recursive MUSIC: A framework for EEG and MEG source localization. IEEE Trans. Biomed. Eng. 1998;45:1342–1354. doi: 10.1109/10.725331. [DOI] [PubMed] [Google Scholar]
- Mosher JC, Lewis PS, Leahy RM. Multiple dipole modeling and localization from spatio-temporal MEG data. IEEE Trans. Biomed. Eng. 1992;39:541–557. doi: 10.1109/10.141192. [DOI] [PubMed] [Google Scholar]
- Nunez PL. Neocortical Dynamics and Human EEG Rhythms. Oxford Univ. Press; New York: 1995. [Google Scholar]
- Ou W, Hämäläinen MS, Golland P. A distributed spatio-temporal EEG/MEG inverse solver. NeuroImage. 2009;44:932–946. doi: 10.1016/j.neuroimage.2008.05.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual-Marqui RD, Michel CM, Lehmann D. Low resolution electromagnetic tomography: A new method for localizing electrical activity in the brain. Int. J. Psychophysiol. 1994;18:49–65. doi: 10.1016/0167-8760(84)90014-x. [DOI] [PubMed] [Google Scholar]
- Phillips C, Mattout J, Rugg MD, Maquet P, Friston KJ. An empirical Bayesian solution to the source reconstruction problem in EEG. NeuroImage. 2005;24:997–1011. doi: 10.1016/j.neuroimage.2004.10.030. [DOI] [PubMed] [Google Scholar]
- Salmelin R, Hari R. Characterization of spontaneous MEG rhythms in healthy adults. Electroencephalogr. Clin. Neurophysiol. 1994;91:237–248. doi: 10.1016/0013-4694(94)90187-2. [DOI] [PubMed] [Google Scholar]
- Salmelin R, Forss N, Knuutila J, Hari R. Bilateral activation of the human somatomotor cortex by distal hand movements. Electroenceph. Clin. Neurophysiol. 2005;95:444–452. doi: 10.1016/0013-4694(95)00193-x. [DOI] [PubMed] [Google Scholar]
- Uutela K, Hämäläinen M, Salmelin R. Global optimization in the localization of neuromagnetic sources. IEEE Trans. Biomed. Eng. 1998;45:716–723. doi: 10.1109/10.678606. [DOI] [PubMed] [Google Scholar]
- Uutela K, Hämäläinen M, Somersalo S. Visualization of magnetoencephalographic data using minimum current estimates. NeuroImage. 1999;10:173–180. doi: 10.1006/nimg.1999.0454. [DOI] [PubMed] [Google Scholar]
- Van Veen BD, van Dronglen W, Yuchtman M, Suzuki A. Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. IEEE Trans. Biomed. Eng. 1997;44:867–880. doi: 10.1109/10.623056. [DOI] [PubMed] [Google Scholar]
- Wipf DP, Owen JP, Attias HT, Sekihara K, Nagarajan SS. Robust Bayesian estimation of the location, orientation, and time course of multiple correlated neural sources using MEG. NeuroImage. 2010;49:641–655. doi: 10.1016/j.neuroimage.2009.06.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamashita O, Galka A, Ozaki T, Biscay R, Valdes-Sosa P. Recursive penalized least squares solution for dynamical inverse problems of EEG generation. Hum. Brain Mapp. 2004;21:221–235. doi: 10.1002/hbm.20000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zumer JM, Attias HT, Sekihara K, Nagarajan SS. A probabilistic algorithm form integrating source localization and noise suppression for MEG and EEG data. NeuroImage. 2007;37:102–115. doi: 10.1016/j.neuroimage.2007.04.054. [DOI] [PubMed] [Google Scholar]
- Zumer JM, Attias HT, Sekihara K, Nagarajan SS. Probabilistic algorithms for MEG/EEG source reconstruction using temporal basis functions learned from data. NeuroImage. 2008;41:924–940. doi: 10.1016/j.neuroimage.2008.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]