Abstract
When people transport handheld objects, they change the grip force with the object movement. Circular movement patterns were tested within three planes at two different rates (1.0, 1.5 Hz), and two diameters (20, 40 cm). Subjects performed the task reasonably well, matching frequencies and dynamic ranges of accelerations within expectations. A mathematical model was designed to predict the applied normal forces from kinematic data. The model is based on two hypotheses: (a) the grip force changes during movements along complex trajectories can be represented as the sum of effects of two basic commands associated with the parallel and orthogonal manipulation, respectively; (b) different central commands are sent to the thumb and virtual finger (Vf- four fingers combined). The model predicted the actual normal forces with a total variance accounted for of better than 98%. The effects of the two components of acceleration—along the normal axis and the resultant acceleration within the shear plane—on the digit normal forces are additive.
Keywords: Grasping, manipulation, motor control, modeling
INTRODUCTION
In a static case of holding an object equilibrium dictates the net forces to be equal to zero. In particular, to hold a vertically oriented object with the prismatic grasp—thumb opposes the four fingers like in holding a bottle of water—the normal forces (Fn) of the thumb (Th) and the virtual finger (Vf—an imagined digit with the mechanical action equal to that of the four fingers combined, Arbib et al, 1985) must cancel out each other, i.e. these force should be equal in magnitude.
The above mentioned two equal and opposite normal forces of the Th and Vf are collectively referred to as the grip force. In static tasks of holding an object the notion of grip force is intuitively simple; everybody understands how to grasp the object stronger or weaker. However, during object manipulation, for instance during horizontal object transport, the normal forces of the Th and Vf are not equal anymore. They do not cancel out each other, and the notion of the grip force is becoming less evident. It should be defined in strict mechanical terms.
Mechanically, the forces applied by the digits on a hand-held object can be described in terms of two force sets (Kerr and Roth 1986; Yoshikawa and Nagai 1991), the manipulation forces and the internal forces. The manipulation force is the resultant force that may cause the movement of the object. The internal force is the set of forces applied by the digits that does not affect the equilibrium state of the object (Murray et al. 1994). The components of the internal force sets cancel out each other. In the present paper, the grip force is understood as an internal force, the set of the Th and Vf normal forces which cancel out each other (for a more detailed discussion see Gao et al. 2005; Zatsiorsky, Latash 2008). The grip force magnitude equals the minimal of the Th and Vf normal forces. For instance, if one of the forces equals −15 N and the other force is 10 N, the grip force (magnitude) is 10 N and the manipulation force (the resultant force) is −5 N. The goal of this study is to investigate and describe (model) the dependence of the grip force on movement kinematics during object manipulation.
The internal and manipulation forces are mathematically independent and can be controlled separately. Such a decoupled control is realized in robotic manipulators (e.g. Zuo and Qian 2000). People do not use this option: they change the internal forces, in particular the grip force, during object manipulation (reviewed in Zatsiorsky and Latash 2008). The grip force changes during object manipulation are influenced by movement mechanics but not completely necessitated by them: performers can grasp an object stronger or weaker at any phase of the movement.
Multifinger prehension during object manipulation has been studied previously in single motion paths of the object in hand (vertical, horizontal, diagonal) (Gao et al. 2005; Smith and Soechting 2005). The study by Gao et al. (2005) tested two movement scenarios of parallel manipulation tasks and orthogonal tasks. The tasks were categorized based on the alignment of the handle orientation and movement direction. For a prismatic grasp, where finger forces can be represented by two components, tangential and normal, the parallel manipulation is a movement in the tangential force direction while the term orthogonal manipulations designates movement in the direction of the normal force components.
In the parallel tasks, e.g. when a vertically oriented handle is being moved vertically, the grasp and manipulation forces are coupled: the normal forces increase in parallel with the load force [static weight + (mass × acceleration)] (Johansson and Westling 1984; Zatsiorsky et al. 2005). This tendency is evident even when forces already exceed the threshold force: minimum force required to prevent the object from slipping (Flanagan and Wing 1995). In the orthogonal tasks, e.g. when a vertically orientated handle is being moved horizontally in the direction of the normal forces, the magnitude of the normal force of the thumb changes 180° out of phase with respect to the Vf force changes (Kinoshita et al. 1996; Gao et al. 2005). During such movements, the normal forces of the Th and Vf are not equal in magnitude anymore and hence, as explained above, the grip force equals the minimal of these two values.
Note that during horizontal orthogonal transport of an object the grip force coordination is opposite to the object lifting: during lifting the maximal grip force is at the point of maximal acceleration while the maximal grip force for horizontal transport is observed at the instant of maximal velocity and hence the zero object acceleration (Gao et al. 2005; Smith and Soechting 2005). The origin of this effect is unclear as this could be due to purely passive digit mechanics and/or active control.
Another approach to describing the applied finger forces is in terms of force ‘fractions’, i.e. separate mechanical contributions to the digit tip forces. In a study by Zatsiorsky et al. (2005) the subjects oscillated a vertically oriented handle in the vertical direction (parallel manipulation). The three fractions were described: static, stato-dynamic, and dynamic. The static fraction reflects grip force related to holding a load statically. The stato-dynamic fraction reflects a steady change in the grip force when the same load is moved cyclically. The dynamic fraction is due to acceleration related adjustments of the grip force during oscillation cycles. These three fractions reflect the additive property of how the grip force is achieved as the fractions each reacted differently to changes in the system (handle mass and movement frequency).
When humans manipulate handheld objects through 2D space (e.g. picking up an object from one spot on a table and placing it down at another), trajectories tends to follow curved movement patterns. Such a movement path is a combination of at least two sub-movements, lifting/lowering vertically and transporting horizontally. How this combination of movements affect the control of prehension forces has not been fully studied.
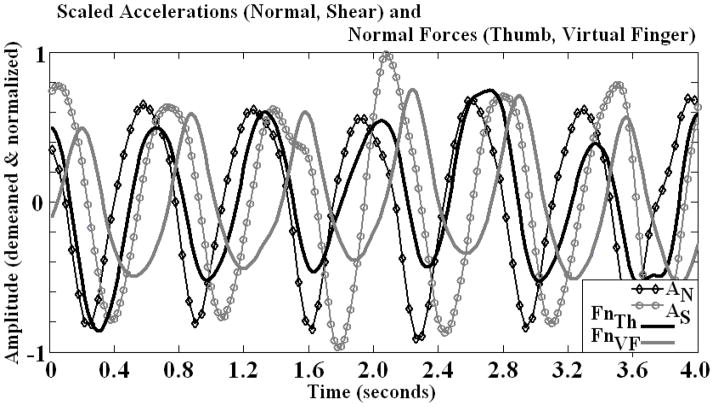
Preliminary testing of finger forces applied to an object when manipulating its position in 3-D space concluded in a couple of observation. Forces of the digits acting along the X-axis (parallel to the contact surface and orthogonal to gravity, see Figure 1) all tend to be applied in the same direction as each other, and are in phase with the object’s acceleration along that direction. Forces of the digits acting along the Y-axis (parallel to the contact surface and gravity) all tend to be applied in the same direction and are in phase with the acceleration of the object along that direction. However, the normal force (Fn) of the digits (Z-axis, normal with respect to the contact surface) behavior is not as simple as that in the other two directions. When looking at the phase shifts between the Th and Vf forces, it was observed that the Th and Vf forces were not in phase with each other, nor were either of the two normal forces in phase with any of the accelerations along the Z-axis, Y-axis, or X-axis (Figure 2).
Figure 1. Handle Design.
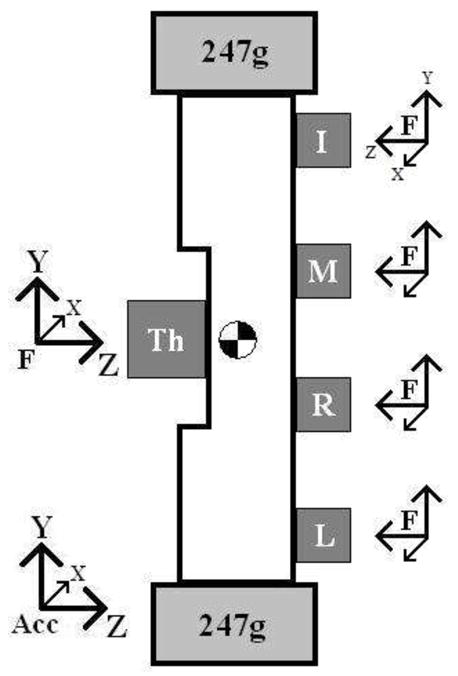
Handle design consists of four Nano-17 sensors for the fingers and a Nano-25 for the thumb. Not seen in the figure is the sensor cluster, located on the backside of the handle about the handle center of mass
Figure 2. Phases of Accelerations and Normal Forces.
Normalized accelerations (aN: Normal, Z-axis, aS: Shear, XY-plane) and normal forces (FnTh, FnVf) during a counter-clockwise circular movement in the sagittal plane (YZ plane). A representative example, frequency 1.5 Hz, circle diameter 20 cm. Note: aS lags aN, FnVf lags FnTh, and no two are in phase
The purpose of this study was twofold:
To quantify the force patterns of normal forces, in particular grip forces, during the prehension control of holding onto an object while performing circular motions. Our interests were in seeing whether and how the normal forces are coupled with manipulation in more than one direction at a time. We wanted to test 2-D movement combinations to investigate how each component of the movement affects the production of the resultant normal forces.
To develop and test a mathematical model for predicting the normal forces, in particular the grip force, from movement kinematics. The model is based on two hypotheses: (a) The grasping behavior during movements along complex trajectories can be represented as the sum of effects of two basic commands associated with the parallel and orthogonal manipulation, respectively. (b) The above-mentioned commands are different for the Th and Vf forces.
METHODS
Subjects
Nine male subjects participated in this experiment. The group data (mean ± SD) consisted of: age 28.7±6.7 years, height 178.6±5.8 cm, weight 85.0±9.4 kg, hand length from the proximal palmar crease to the tip of the middle finger 18.5±1.2 cm, width at the level of metacarpal heads 8.8±3.8 cm. All subjects were right-handed according to their hand use in writing and eating. None of them reported to have any neurological or upper extremity pathology. None of the subjects were involved in any professional activity, such as professional violin or piano playing or professional typing, which may affect their hand dexterity. Each subject provided informed consent according to The Pennsylvania State University Institutional Review Board.
Data Collection
The task involved holding onto an instrumented handle (Figure 1) that measured applied forces, linear accelerations, and rotational orientation. The coordinate frames of each system are also depicted in Figure 1. Four Nano-17 and one Nano-25 force/torque transducers (ATI Industrial Automation, Apex, NC, USA) for the four fingers and the thumb, respectively, were implemented to record the forces and moments (6 DoF) of each digit. These sensors were connected to individual Net-F/T cards (ATI) which were connected to a wireless router and transmitted to a laptop computer. Data from the sensors were sampled at 1000 Hz and then processed and calibrated into forces and moments at the Net-F/T cards. Each sensor was covered with 320 grit sand paper so that the fingertip-surface interface had a coefficient of static friction of 0.94 ± 0.11 (Cole and Johansson 1993; Savescu et al. 2008).
Handle linear acceleration (3 DoF) and orientation (3 DoF) were recorded from a 3DM-GX2 (Microstrain Inc., Williston, VT, USA) sensor cluster (weight 50 g) consisting of tri-axial sensors: linear accelerometer, gyroscope, and magnetometer. Information from the sensor cluster was wirelessly broadcasted to a USB Base Station (Microstrain) connected to the laptop computer. Data were initially processed and calibrated in the sensor cluster and were sampled at the laptop computer at 100 Hz. Both data streams, ATI and Microstrain, were collected on a single laptop computer using a custom written LabVIEW program (National Instruments, Austin, TX, USA). The program handled data stream initializations, synchronization, and terminations. Post processing was handled with custom written code in Matlab (Mathworks INC., Natick, MA, USA).
Protocol
The data collection protocol consisted of three sets of circular motions. For each of the motion paths, subjects were given a similar set of base instructions:
Hold onto the handle with tips of all five digits on their respective sensor using normal level of effort.
Hold and maintain the handle with an upright orientation.
Perform a circular motion within a plane spanned by two directional axes (Frontal: XY, Horizontal: XZ, Sagittal: YZ).
Minimize any motion orthogonal to the desired plane of movement.
Follow a metronome for a prescribed tempo of movement (1.0 or 1.5 Hz).
Use distance markers for reference of prescribed circular diameter (20 or 40 cm).
The tested motion paths were within the (1) Frontal, (2) Horizontal, and (3) Sagittal planes. For the motion in the frontal and sagittal planes, subjects performed a vertically oriented circular motion (up/down) while holding the handle in their right hand out in front of their bodies with their palm facing left. The horizontal plane motion consisted of a circle (left/right & forward/backward) performed in front of the subject with their palm facing left. All motions were performed in counterclockwise directions: frontal and horizontal planes as seen from the subject, the sagittal plane as seen from the subject’s right. The maximal values of diameters were presented to the subjects by a grid of strings defining the circular width and height. The subjects moved the handle parallel to the string grid without making contact. Trial conditions (movement plane, diameter, frequency) were presented in block random order: blocks of movement planes were in random order, while within each block the diameter and frequency were fully randomized. Three successful trials were recorded from each test condition before progressing to the next combination of conditions.
Before testing, the subjects were instructed on how to perform the three motion tasks and on the requirements of a successful data collection (less than 15° of handle tilt, less than 0.5 G off-axis acceleration, where G is acceleration due to gravity). The LabVIEW data collection program provided real-time feedback with a 2-D plot displaying the tilt of the handle and a time plot of the acceleration along the off-axis. A simplified handle with the 3DM-GX2 sensor cluster was used to allow for practice sessions until the subject felt that they were confident in performing the motion paths. After the practice sessions, the subject was fitted with a belt and suspender pack system that housed all the external sensor equipment. A cable bundle ran from the right shoulder down the arm of the subject to the instrumented handle. The cable bundle was secured to the subject’s upper and forearm with cloth ties. There was sufficient cable slack from the subject’s forearm to the handle to allow for the subject to set the handle down on a pedestal and relax their arm. Initial measurements were made to record the grip forces applied under static conditions. Each subject performed six baseline trials holding the handle upright and still while applying normal effort for three repetitions and also three trials while applying a minimal effort.
Each test run started with the handle sitting on the starting pedestal without the subject touching the handle so that the sensors could be zeroed. Once the data collection started, the subjects would grip the handle and situate themselves to start their motion path. Once the subject was observed to be in tempo and performing the circular motion, an event marker was triggered and data collection continued till completion of the data collection period. The data collection period was set to 30 seconds, which allowed for the initial start-up, adjustment period, and actual trial data. After trimming off the initial segment of data, as well as one second from the end of the trial, the average trial yielded 13 seconds of data (13 cycles at 1 Hz, 19.5 cycles at 1.5 Hz).
All data that were collected and processed were double checked for accuracy by checking whether Newton’s Second Law of Motion was upheld. Specifically, it was checked that the sum of all digit forces were matched to the mass × accelerations along each the X, Y, and Z axis. The measured deviations of net force from those computed from acceleration were on average 0.08±0.54 N (X), 0.15±0.38 N (Y), and 0.12±0.54 N (Z).
Data Processing
The data from each 30-second collected file were reduced in length to within the window marked by the event trigger signifying where the subject was performing the proper task movement. Additionally, each file was visually inspected, and trimmed, for any anomalies that were marked on the test record sheet or seen during post processing. These anomalies include the trials where a subject stuttered in movement when adjusting their movement tempo or due to finger slips. These “blips” in the data stream were well beyond two standard deviations from their natural fluctuations and only occurred in a limited number of cases. Forces and moments (6-DoF) were collected from all five digits. For the purpose of this current study, the data were reduced to a Thumb – Virtual Finger (Th – Vf) level of analysis, where the Vf force/moment is the sum of forces and moments produced by the four fingers (index, middle, ring, little).
Model
The model used for this study was designed to understand the elements that contribute to the normal forces (Fn) generated by the Th and Vf. The model—presented below in equations (1) through (5)—computes the forces based on the recorded movement kinematics and the known mass of the handle. Note that the model is not purely mechanical; it does not represent the dynamic equations of motion. The model includes the coefficients k and C that are under neural control.
Based on the previous studies on the parallel and orthogonal single axis movements (Gao et al. 2005) we surmised that the Fn of the Th and Vf reflect additive effects of:
the Fn reaction to movements within the shear plane, the local XY plane of the force sensor (the parallel object manipulation)—in equation (1) this effect is represented by the term FM.SP;
the Fn changes due to (orthogonal) movements along the normal (Z) axis of the force sensor—in equation (1) this contribution is represented by the term FM.SP;
base grasping forces (FBG) estimated as the average forces for holding onto the object (Equation 1). The base grasping force is similar to the sum of the static and stato-dynamic force fractions as described by Zatsiorsky et al. (2005). It is a constant term of equations (1)–(3).
Note the opposite signs of the contributions of FM.NA (equation 1) as it carries over into the formation of equations 2 and 3 (Fn of the Th and Vf).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Terms used in the above equations: Fn: normal force, FM.SP: forces due to movement in the local XY plane of the force sensor (shear), FM.NA: forces due to movement along the local normal (Z) axis of the force sensor, FBG: base grasping force, Th: thumb, Vf: virtual finger, k: coefficient for the shear element, m: mass of handle, aS: resultant acceleration within the shear plane, C: coefficient of Th–Vf effort sharing along normal axis, aN: acceleration along normal axis, (aX aY aZ): acceleration along the respective local axis, (ao): amplitude of acceleration, ω: frequency, t: time, G: gravity. The instant values of the grip force set (not presented explicitly in the above equations) equal the minimal absolute magnitude of the Th and Vf normal forces. Because the Th and Vf forces are in opposite directions, they in part cancel out each other. The forces that cancel each other out do not affect the object motion and hence by definition are the internal forces.
Separation of equation 1 into the equations for the Th and Vf (Equations 2 and 3) is based on the results of previous research on single-directional movements (Gao et al. 2005) in which different patterns of grasping force adjustment to the object movement in dissimilar directions have been reported. For movements along the local Y-axis, the FnTh and FnVf were observed to adjust in phase with each other (for the review see Zatsiorsky, Latash 2008). The fluctuations in the Fn are accountable in terms of adjustments for the friction forces required to manipulate the object. In the previous studies movements along the X-axis were not tested, but based on the evident mechanical considerations one may expect that acceleration in this direction would also add a normal force component associated with friction forces similar to the Y-axis. The suggested model accounts for all friction force requirements by using the resultant in the shear plane (XY) of the sensor, FM.SP is proportional to m×aS, where aS is the net acceleration in the shear plane, and is adjusted by the coefficient of proportionality k. (Equation 4).
For movements along the local Z-axis, the magnitudes of FnTh and FnVf were reported to be 180° out of phase (Gao et al. 2005), hence the different signs for the FnTh and FnVf. In this case, the net (manipulation) force of the Th and Vf is equal to the m × aN. The preceding multiplier (0.5±C) was applied for adjusting the ratio of Th and Vf in contribution to the force changes that accompany the movement along the Z-axis. The value of C can range from −0.5 (for normal force produced only by the Th) to 0.5 (for normal force produced only by the Vf), where a C value of zero would signify the equal (and opposite) magnitude contribution of both the Th and the Vf to the resultant force along the Z-axis.
The third contributing element to the Fn is a base grasping force (FBG) that is assumed to be constant throughout the cyclic movements. This element is similar to the summed effects of the static fraction and stato-dynamic fractions (Zatsiorsky et al. 2005). Unlike the dynamic fraction (similar to FM.SP and FM.NA in this study) which oscillates with the movement oscillations, the static and stato-dynamic fractions represent a nearly steady force that the dynamic fraction oscillates about. The static fraction represents the grasping force used to hold onto the handle and maintain equilibrium. The stato-dynamic fraction is an increase in the grasping force to shift it higher and allow for the range of force oscillation due to the dynamic fraction.
When an object is moved along a circular path, the two components of acceleration are of equal magnitude, equal frequency, and 90° out of phase (e.g. Equation 5, YZ-plane). In the example given, there is also the additional factor of gravity (G) along the global Y-axis. This 9.81 m/s2 offset is a contributing factor in determining aS.
The values of the parameters of k, C, and FBG, were estimated from matching the acceleration data to the actual force data for each collected trial. Validity of the model was tested by comparison of the actual recorded normal forces of the Th and Vf and the predicted values from the model (based on the recorded acceleration). The parameter used to measure the fit of the model was the variance accounted for (VAF, Equation 6).
| (6) |
Statistics
Measured variables were analyzed with a 3-way repeated measures ANOVA with factors DIRECTION [Frontal, Horizontal, Sagittal], DIAMETER [20, 40 cm], and FREQUENCY [1.0, 1.5 Hz]. Each task was performed three times. Measures for each trial were averaged across all cycles in that trial and then the results of the three repetitions of each task were averaged together. Subject data were pooled together and factors were tested with a ‘within subjects’ analysis. All statistics were performed in Statistica (StatSoft, Tulsa, OK, USA) using an α-level of 0.05. Mauchly’s sphericity tests were performed to verify the validity of using repeated measures ANOVA. No data deviation from the sphericity was found.
RESULTS
The results of this study are broken into the three main parts: (a) the performance of the tasks, (b) the force changes in the tasks, and (c) the correspondence between the actual force changes and the changes predicted from the model (model validation). To characterize the performance, i.e. to decide on how well the subjects performed the tasks, we analyzed the object accelerations. For the model validation, we were mainly interested in the general fit of the predicted forces to the actual ones as well as in the contribution of the three above mentioned elements into the predicted digit forces.
(a) Performance of the Task
The prescribed movement frequencies were reproduced by the subjects reasonably well, with the lower frequency measuring (mean±SD) 1.090±0.130 Hz (X), 1.098±0.114 Hz (Y), and 1.094±0.121 Hz (Z), respectively, and the higher frequency measuring 1.482±0.150 Hz (X), 1.498±0.157 Hz (Y), and 1.499±0.171 Hz (Z), respectively.
It is known from classical mechanics, that during linear periodic motions the maximum value of acceleration is amax = ω2x0 where ω is the frequency of oscillation, and x0 is the amplitude of the oscillation. Hence we expected an increase of the dynamic range of the accelerations (average difference between peaks and valleys of the acceleration oscillations, which is twice of the acceleration amplitude) with changes in circle DIAMETER (49.93% increase between 20 cm and 40 cm, p<0.001) and FREQUENCY (94.07% increase between 1.0 Hz and 1.5 Hz, p<0.001), as well as the additive effect of these two factors (as it should be expected from basic mechanics).
To describe how well a circular motion path was followed within the plane of desired movement, the ratios of the dynamic range of accelerations along the coordinate axes and their phase angle were used. A ratio of 1.0 with a phase angle of 90° would signify a perfect circular pattern. The ratio was calculated using the dynamic range values of the accelerations of the desired movement (Y and Z axis for the sagittal plane movement), dividing the smaller value by the larger one. The overall acceleration ratio within the desired plane was 0.971±0.154, with an overall phase angle between the two acceleration profiles of 93.75±19.03°, showing that on average a circular movement path was followed within 3% error and was not significantly affected by the different tasks (DIRECTION, DIAMETER, or FREQUENCY; p>0.130).
The ratio of off-plane acceleration to that in the desired plane (calculated as the off-axis dynamics range of acceleration divided by the average dynamic range of acceleration along the other two axes; 0 being the ideal performance) was on average 0.375±0.174. Off-plane accelerations were found to be significantly affected by DIRECTION (F2.16=17.46, p<0.001) as well as by the interactions DIRECTION × DIAMETER (F1,8=4.54, p<0.03) and DIRECTION × FREQUENCY (F1,8=22.27, p<0.001). Off-plane acceleration ratio was the smallest for the movements in the sagittal plane (0.207±0.043) versus that of the two other planes 0.467±0.110 (frontal) and 0.452±0.188 (horizontal). In terms of angular tilt of the movement outside the prescribed plane, the average observed tilts about the X and Y axes were −1.54±3.22° and −2.08±1.90° respectively, and the range of maximum observed tilts averaged ±12.06° about the X axis and ±7.90° about the Y axis (all forces and accelerations were recorded in the local coordinate system of the handle).
On the whole we concluded that the subjects performed required tasks reasonably well. They performed the movements close to the two prescribed frequencies and circular diameters along the circular trajectories, as it was required, however — in some cases — with substantial deviations from the prescribed plane.
(b) Forces Matching the Task
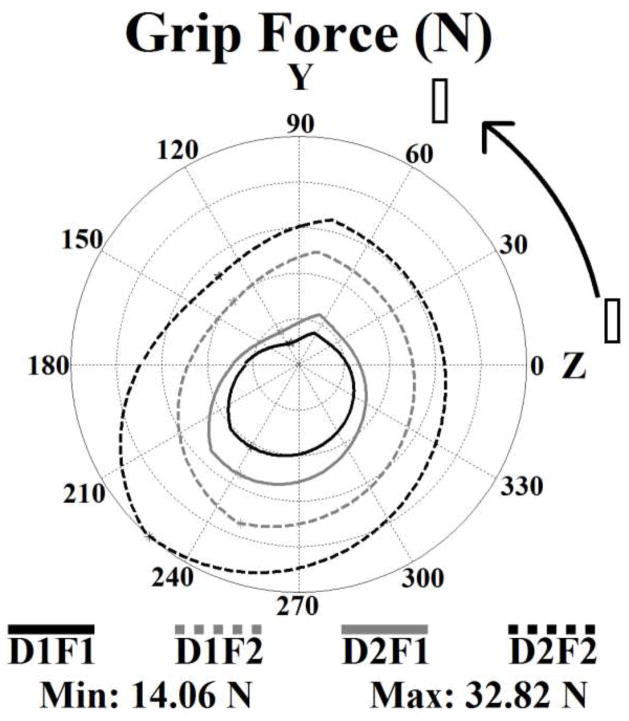
When plotted along a time axis, the forces and acceleration behave in a sine wave fashion (similar to those shown above in Figure 2). The radial plots presented below provide a better visual reference to the force values at different handle locations along the circular trajectory. In particular, Figure 3 illustrates the changes in the grip force at the different frequencies and diameters for the sagittal plane of movement while example forces (Th, Vf, Grip) in each of the planes are presented in Figure 4. The figures are scaled according to the smallest and largest value being plotted setting the range. The stated min force value for each plot is the center point of the plot while the max value is the outer most ring. This allows for visualization of the shapes while avoiding the loss of detail due to scaling with large data magnitudes and small deviation. The effect of the different polar plot scales can be noticed by the detail in the grip force (solid line) in Figure 4 sagittal plane with a noticeable dent near 140° and points near 90° and 240° while the lines in Figure 3 are also grip forces and appear rounder in shape.
Figure 3. Grip Force: Diameter and Frequency Changes.
Grip forces averaged to one cycle for a single subject (#4) in the sagittal plane movements. D1F1(black): 20cm 1.0Hz, D1F2(grey-dashed): 20cm 1.5Hz, D2F1(grey): 40cm 1.0Hz, D2F2(black-dashed): 40cm, 1.5Hz. The graph is scaled from min (center) 14.06N to max 32.82 N.
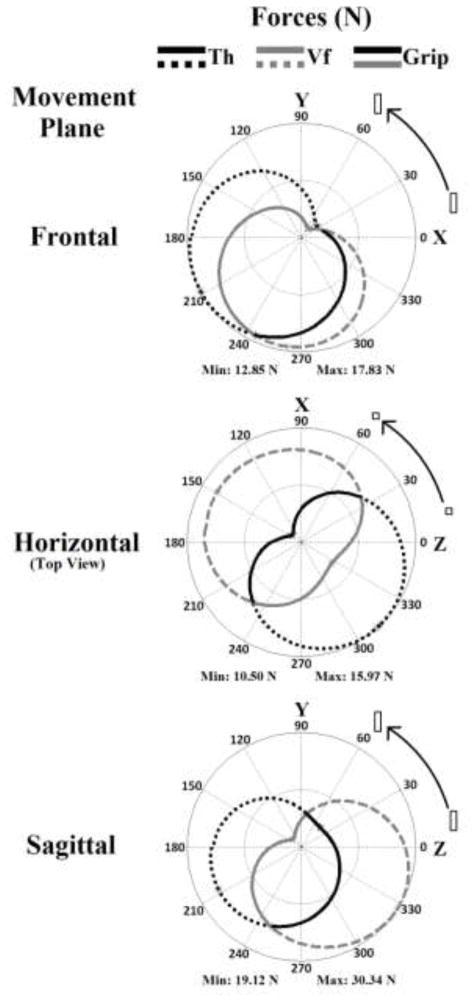
Figure 4. Normal Forces & Acceleration: Different Planes of Movement.
Normal forces of the Th, Vf, and grip force during one average cycle. Example shown is for an average value for one complete cycle (360°) for a single subject (#4) for 20 cm, 1.5 Hz task. For the frontal and sagittal figures, 90° represents the vertical top, while in the horizontal figure the vertical top represents the point furthest from the subject. For the forces, the color of the dotted line represents the source of the force (Th: black-dotted, Vf: grey-dashed) while the solid portion represents the grip force. Each force plot is scaled from the min (center) to max (outer circle). For instance, for the movement in the sagittal plane, the center of the graph corresponds to the value of 19.12 N and the outer ring to 30.34 N. Note that for a half of a cycle the grip force—which is an internal normal force—equals the Th normal force and for another half it equals the Vf normal force. The difference in grip force detail (visible ‘dent’ at 140°) when compared to the grey-dashed line of Figure 3 is due to the different scales.
All maximum and minimum values for the forces and accelerations were significantly affected by increases in DIAMETER and FREQUENCY (p<0.005), as it should be expected from basic mechanics. In the case of the forces, whose values are always positive, both minimal and maximal values increased. For the accelerations, all maximum values increased, while the minimal values decreased (for aX and aZ, this was an increase in negative acceleration magnitude).
In contrast, the locations (position around circular movement, degrees) of the minimal and maximal forces and acceleration were mostly unaffected by changes in movement diameter or frequency. However, there was a significant effect (p<0.05) of DIAMETER increase on the location of minimum of Vf (frontal plane, F1,8=7.17) and aS (horizontal plane, F1,8=14.23) which changed from 229° to 224° and from 205° to 230°, respectively. Also, increases in FREQUENCY significantly affected (p<0.05) the locations of maximum FnTh (overall, 113° to 93°, F1,8=6.06), grip force (XZ plane, 117° to 97°, F1,8=8.01), and aS (overall, 146° to 142°, F1,8=6.51).
The plane of movement has the most noticeable effect on the force plots (Figure 4). For the frontal plane, the Th and Vf forces are closer to each other than in other planes. The horizontal plane is noted for the near mirror image of the Th and Vf forces. The resultant grip force becomes ‘peanut’ shaped with two local minimums (at the minimums of the Th and Vf forces) and two local maximums at the point of intersection between the Th and Vf. The sagittal plane of movement represents a mix of the previous two, between the near overlap and the 180° mirror. The mean Th and Vf normal force values both increased significantly (p<0.001) with increases in DIAMETER and FREQUENCY (Table 1).
Table 1.
Mean Normal Forces of the Thumb and Virtual Finger (mean±SD)
| Diameter/Frequency | D1 | D2 | F1 | F2 |
|---|---|---|---|---|
| Thumb | 16.6±5.0 N | 20.6±6.1 N | 15.9±4.7 N | 21.3±5.8 N |
| Virtual Finger | 17.9±5.5 N | 22.8±7.0 N | 17.2±5.3 N | 23.6±6.5 N |
The dynamic ranges of the Th and Vf normal forces were significantly (p<0.001) affected by both DIAMETER and FREQUENCY, as well as their INTERACTION. Of interest are the post-hoc results of the interactions, where the task of the smaller diameter at the faster frequency was not statistically different from the task of the larger diameter at the slower frequency.
The grip force (internal force = min of two forces, FnTh and FnVf) was examined for the mean value across the trial and the dynamic range of oscillation, as grip force may not be predicted from basic mechanics. The mean value of grip force depended significantly on DIAMETER and FREQUENCY (F1,8=83.5 & 52.2, p <0.001). The increase in movement diameter or frequency resulted in larger mean grip forces from 16.06±4.95 N to 19.87±5.94 N for changes in movement diameter and from 15.42±4.67 N to 20.52±5.67 N for changes in movement frequency. The mean grip force did not depend significantly on DIRECTION (F2,16=2.99, p=0.079), however the p-value is near significance. The dynamic range of the grip force was significantly affected by each studied factor (DIRECTION F2,16=24.8, DIAMETER F1,8=47.0, FREQUENCY F1,8=39.0; p <0.001) as well as by DIRECTION × DIAMETER (F1,8=6.94, p<0.01) and DIAMETER × FREQUENCY interactions (F1,8=11.98, p <0.01).
The average dynamic ranges of the grip force for different planes of movement were 5.05±1.47 N (frontal), 3.11±0.98 N (horizontal), and 7.60±0.83 N (sagittal). Post-hoc comparisons demonstrated that the DIRECTION main effects were significant (p <0.02) for all pairs. For increases in DIAMETER and FEEQUENCY there were grip force dynamic range increases by on average 56.5% (for all three tested movement planes, from 4.10 to 6.41 N ) and 43.7% (4.31 to 6.20 N), respectively. The post-hoc analysis for the interaction of DIAMETER × FREQUENCY showed that all intra-paired differences — except the large diameter at the slow frequency trials versus the small diameter at the fast frequency trials — were significant.
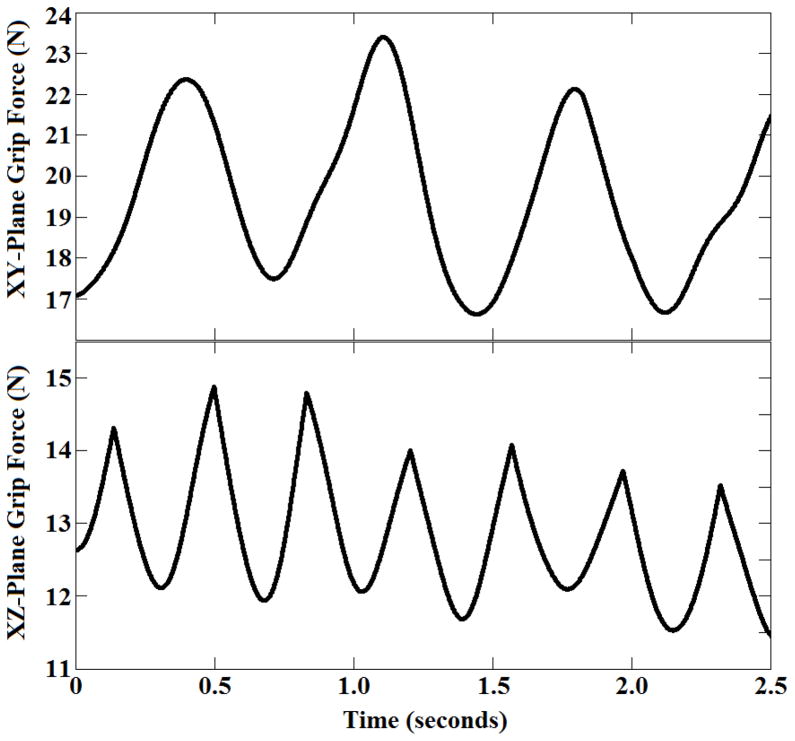
The grip force pattern was not always a simple sine wave like the FnTh and FnVf were. Looking back at Figure 4, the grip force pattern is cyclic but is also irregular in shape. Looking ahead at Figure 5, the time domain plot shows that cusps and corners occur when the Th and Vf forces intersect. While the object accelerations as well as the Th and Vf normal forces oscillate in a sine-like manner the grip force changes differently. In the frontal plane, the grip force appears sine-like (Figure 5, top graph). In the sagittal plane (Figure 6), a second dip in the grip force curve appears. In the horizontal plane (Figure 5, bottom graph) the second dip has expanded, giving the appearance of doubling the task frequency. The pattern of the grip force changes is more complex and cannot be reduced to harmonic oscillations with one frequency component. The detailed frequency analysis of the grip force variations is not presented here. We leave it for future research.
Figure 5. Grip Force of the Frontal and Horizontal ‘planes’ Movements.
Grip force during the frontal plane (XY) and horizontal plane (XZ) movements. Tasks were both 20 cm diameter at 1.5 Hz. The grip force in the frontal plane is changing in a sine-like fashion, while in the horizontal plane the pattern is different; in particular the frequency is doubled
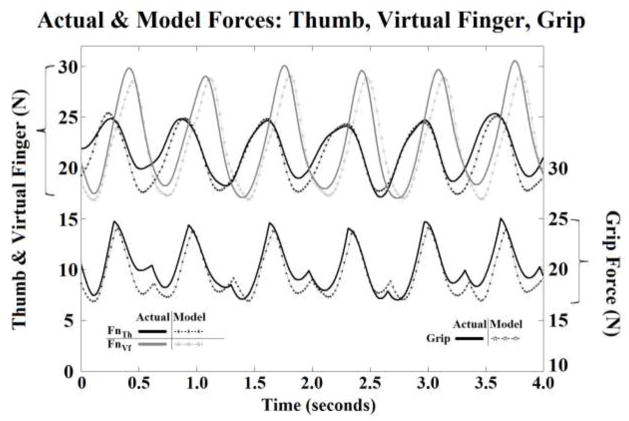
Figure 6. Actual vs Model: Thumb, Virtual Finger, and Grip.
Comparison between actual normal forces (Th, Vf, Grip) and modeled values for a sagittal plane (YZ) movement. Shown example data set: 10 cm, 1.5 Hz counter-clockwise movement, k=0.300, C=−0.176, FBG=19.8N, VAF=99.5%. The grip force is plotted on the same relative scale but shifted down for viewing convenience as otherwise it would overlap on the normal force plots
(c) Mathematical Model: Its Validation and Parameters
Model Validation
On the whole, the data predicted by the model matched the actual Fn data with a VAF of 98.48±0.749%. Such factors as DIRECTION (F2,16=2.11, p=0.154), DIAMETER (F1,8=0.53, p=0.486), and FREQUENCY (F1,8=1.43, p=0.267) did not affect the model’s accuracy. For the FnTh, the VAF was 99.19±0.415% and for FnVf it was 99.29±0.339%, both of which were not affected by any changes in the test conditions (p>0.150) (Figure 6). Subject and cycle-to-cycle variability was ever present (as can be seen in the data presented in Figure 6). This can be due to non-identical performance of the cycles (e.g. different off-plane accelerations, different tilt of the handle, different patterns of the angular accelerations, irregular movement speeds). Such differences, if they exist, do not undermine the model performance: the digit forces were predicted based on the actual movement kinematics recorded in the individual movement cycles.
Model Parameters
The three model parameters had overall averages of k=0.443±0.267, C=−0.0144±0.239, and FBG=15.42±6.58. The coefficient of the shear element (k) was found to be affected by DIAMETER (F1,8=14.27, p<0.006) and FREQUENCY (F1,8=16.49, p<0.004). With the increase in circle diameter, k increased from 0.408±0.240 to 0.478±0289, while an increase in movement frequency resulted in a decrease in k from 0.505±0.291 to 0.382±0.226. DIRECTION (F2,16=11.44, p<0.001) and DIRECTION×DIAMETER (F2,16=11.65, p <0.001) interaction also affected the k parameter. Post-hoc analysis of DIRECTION revealed that movements in the horizontal plane (k=0.256) had a significantly lower k value than in the frontal (0.469) and sagittal (0.605) planes. When the Y-axis, which is along the direction of gravity, was not involved in the circular movement, the shear component coefficient was at its lowest. The interaction of DIRECTION×DIAMETER was primarily a result of the effect of different directions, where the movement diameter effect was significant only within the frontal plane.
The coefficient of the Z-axis element (C) accounts for the difference of involvement of the Th and Vf in producing the net manipulation force responsible for the movement along the Z-axis. This parameter was significantly affected only by DIRECTION (F2,16=4.73, p <0.0243) with post-hoc results showing that the coefficient for the horizontal plane (C=−0.137) was less than for the frontal plane (C=0.091).
The base grasping force, FBG, was found to be significantly affected by both DIAMETER (F1,8=62.81, p <0.001) and FREQUENCY (F1,8=76.26, p <0.001). In both cases, FBG increased by 26.2% from 13.63±5.84 N to 17.20±6.85 N when the circle diameter increased and by 54.6% from 12.11±5.59 N to 18.72±5.83 N when the movement frequency increased.
Model Elements
The model’s three elements (FM.SP, FM.NA, FBG) each contribute to the total dynamic range and mean force generated by the Th and Vf (Table 4). The mean grasp forces (FBG being the primarily contributor) were greater than the values recorded from the static trials where the forces under normal efforts were 14.6±4.25 N and under minimal efforts 6.65±1.11 N. This increase of the mean force levels during object manipulations above the static trials has been reported previously (under the name of stato-dynamic fraction, (Zatsiorsky et al. 2005). The total dynamic range is equivalent to twice the dynamic fraction (Zatsiorsky et al. 2005), and is the sum of the effects from both FM.SP and FM.NA (they are typically not in phase with each other).
DISCUSSION
On the whole the data indicate that the normal force changes during the circular arm movements depend on and can be predicted from kinematics. The developed model was able to describe the patterns of applied forces, i.e. the two hypotheses on which the model is based (see the Introduction) are confirmed. The discussion addresses: (1) the effects of changes in the movement kinematics on the digit forces, and (2) the suggested model and the possible mechanisms of control of the grasping forces in manipulation tasks.
(1) The effects of movement kinematics on the forces
(1a) Changes in digit forces
The increasing of the prescribed circle diameter and movement frequency yielded concomitant increases in the acceleration and normal forces, as it should be expected. Effects of both main factors (DIAMETER, FREQUENCY) were significant. The two diameters (10 cm, 20 cm) and two frequencies (1.0 Hz, 1.5 Hz) were chosen with the expectation that their individual effects would be similar and additive. As seen in Figure 3, this pattern was present in several measured parameters.
The three motion path orientations were chosen not only for simplicity of testing circular motions in orthogonal planes, but also for their expected effects. Movements in the frontal plane focused on the shear plane and would result similar to that of parallel manipulations. The horizontal plane tasks emphasize the effects of the normal axis movements as the constant 1 G along the Y-axis would result in a diminished amplitude of oscillation of the shear plane resultant. Finally, the sagittal plane movements would show the results of combining of all three model elements together and would exhibit the additive effects of the movements in the shear plane and along the normal axis. As follows from the results presented above, see Table 1 and Figure 4, these expectations were realized.
(1b) The grip force changes
As follows from Figures 3 and 4, the grip force changes in the cycles were not symmetric with respect to the coordinate axes. While for movements in the frontal and sagittal planes, the asymmetry with respect to the horizontal X and Z axes is explained mainly by the effects of gravity, there is also a tendency for the loops to be inclined to the right. This inclination is due to larger values of the thumb normal forces with respect to the Vf force (e.g. Figure 4: XZ) in the 270–360° quadrant and the larger values of the Vf normal force in 90–180 ° quadrant. On the whole, the average values of the Th forces were slightly larger than the average values of the Vf forces (see Table 1). Such a force asymmetry is evidently due to non-equal accelerations in the rightward vs. leftward and upward vs. downward directions: we controlled the movement frequency but not the uniformity of the angular velocity. Additionally, a handle tilt can vary during a cycle, directing a component of gravity towards one side of the handle creating an imbalance in the normal forces of the Th and Vf.
There were evident differences in the grip forces between the subjects. The large values of the standard deviations presented above are indicative of that. It was already mentioned the increase in diameter or frequency resulted in mean grip force changes from 16.06±4.95 N to 19.87±5.94 N for the diameter and 15.42±4.67 N to 20.52±5.67 N for frequency, respectively. The magnitudes of the coefficient of variation, i.e. the ratio of the standard deviation to the mean, in these examples are around 0.3, which is indicative of substantial differences between the subjects.
(2) The model and its interpretation
As it was mentioned above the model is based on two hypotheses: (a) the effects of efferent commands associated with the three model elements—base grasping force (FBG), movements in the shear plane (FM.SP) and along the normal axis (FM.NA)— are additive; (b) the commands associated with the orthogonal manipulation are different for the Th and Vf forces. The observed good correspondence between the model predictions and the actual results support the hypotheses. While the parameters of the models (k, C, FBG) are found through curve fitting, once they are set the model predicts the time history of the force changes quite well. The changes in the parameters are then dependent on the task conditions.
(2a) Effects of the movement kinematics on the model parameters
The changes in circular diameter or movement frequency did not affect the C parameter of the model which modifies the sharing of the reciprocal control of the grasp, only the k and FBG parameters that affect the parallel control of the grasp were affected. The increase in circular diameter resulted in increased for both parameters, while the movement frequency change resulted in opposite trends between the parameters. It was found that with the increase in movement frequency, the system adopts a more static strategy (increase in FBG) while reducing adaptive oscillations (reduced k from 0.505±0.291 to 0.382±0.226).
The plane of motion affected the model parameters. While FBG was directionally independent, both k and C were significantly different when motion was in the horizontal plane, as compared with other planes. At this horizontal plane, the value of k was at its lowest while C was on average slightly, but not significantly, below zero.
(2b) The additivity problem
One of the advantages of using multi-finger prehension as an object of motor control research is the opportunity to broadly vary the task conditions. In several studies the researchers explored the effects of simultaneously varying: the supported load and resisted torque (Zatsiorsky et al. 2003a; Zatsiorsky et al. 2002a, b); handle geometry, e.g. the handle width, the thumb position, and the finger spreading(Li et al. 1998; Shim et al. 2004; Zatsiorsky et al. 2003b, 2006); handle orientation (Pataky et al. 2004b, a); friction and torque (Aoki et al. 2007; Aoki et al. 2006); and static torque and inertial forces (Gao et al. 2005, 2006, 2007; Zatsiorsky et al. 2005).
It was found that the combined effect of varying two factors was essentially the sum of the individual effects. For the individual fingers, redistribution of the normal forces occurred such that the agonist fingers—the fingers that resist external torque—increased the force in phase with the acceleration while the forces of the antagonist fingers—those that assist the external torque—especially, the fingers with the large moment arms, the index and little fingers, stayed unchanged (Gao et al. 2006). The observed effects agreed with the principle of superposition according to which some complex actions, e.g. prehension, can be decomposed into elemental actions controlled independently (Zatsiorsky and Latash 2004). It was surmised that additivity of the command effects, as well as the principle of superposition, are general phenomena of motor coordination which are manifested in many motor tasks.
Ruegg and Bongioanni (1989) reported nearly linear input-output properties of motoneuronal pools in tasks that involved a superposition of steady-state and ballistic contractions. Studies of neuronal populations in different areas of the brain have also supported applicability of the principle of superposition (Kowalski et al. 1996; Glezer and Gauzelman 1997). In the area of motor control, the idea of the principle of superposition has been developed by proponents of the equilibrium-point (EP) hypothesis (Feldman 1986, 1966). According to the EP-hypothesis, voluntary actions are controlled with variables that define spatial coordinates of muscle activation thresholds (reviewed in Feldman and Levin 1995). Feldman suggested that control of a joint could be described with two variables, a co-activation command (c) and a reciprocal command (r). Effects of these two control variables affect activation of individual muscles according to the principle of superposition. Experimental support for this principle has been obtained in studies of fact arm movements (Pigeon et al. 2000; Adamovich and Feldman 1984) and postural control (Slijper and Latash 2000).
This study further explores the additive effects in movement coordination using with this purpose the dynamic manipulation of the handheld handle and the studied model elements—base force, tangential and orthogonal object accelerations—as the input factors (gravity was accounted in the model as the part of the tangential acceleration effect.) The additive properties of the command effects were again confirmed.
(2c) On the control of grasping forces
Object grasping and manipulation rely heavily on the ability of the nervous system to anticipate the consequences of ongoing movements. In particular, before lifting a vertically oriented object, an action that is an example of the parallel manipulation, performers adjust the grasping force to the expected load, friction, and the speed of lifting (Flanagan et al. 1993; Flanagan and Tresilian 1994; Flanagan and Wing 1993, 1995; Flanagan et al. 1995; Gysin et al. 2003; Johansson and Westling 1984; Kinoshita et al. 1996). While it is broadly assumed that such a behavior is explained by the so-called internal models we are prone to agree with the recently made statement that “Whether these computational principles are actually implemented or just metaphors for what the human nervous system does remains uncertain” (p. 482, Grafton, 2010).
An opposite (to the internal model concept) point of view—the so-called referent configuration hypothesis—was suggested by Feldman (Feldman and Levin 2009; Feldman and Levin 1995) and developed recently for grasping (Pilon et al. 2007; Latash et al. 2010). The basic idea is that the central controller sets a referent body (digit) configuration; muscle activations and digit movements are driven by the difference between the actual and referent values of muscle length. The results of this study with respect to the control of FBG and FM.SP can be interpreted within this framework which is rooted in physics and physiology (see recent reviews by Feldman 2010 and Latash 2010). They can be viewed as consequences of feed-forward adjustments of the referent digit configuration.
The problem of agreement between the current theories of grasping control and the suggested model arises at the level of the normal digit forces associated with the orthogonal movements, i.e. at the level of FM.NA model elements (Equation 1). The employed approach does not assume an immediate control of the grasping force. At rest and during the parallel manipulation, the magnitudes of the Th and Vf forces are equal (these equal and opposite forces are the grasping force) while during the orthogonal manipulation the Th and Vf forces are different in magnitude. The model takes into account this fact and assumes that the commands associated with the normal force production are different for the Th and Vf. The grip force value in this case (i.e. the minimal of the above forces, an internal force) is an indirect consequence of several factors, in particular the object acceleration in the direction of normal digit force and passive mechanical properties of the digits and digit joints.
The force control model used in this study is analogous to the kinematic model on the control of reaching out for an object by Smeets and Brenner (2001). Such an action is often considered to consist of two components: transporting the hand to the object’s position, and scaling the grip to the object’s size (Jeannerod et al. 1998; Jeannerod et al. 1995; Jeannerod 1984). The grip scaling in kinematics is analogous to the grip force scaling in statics. Opposite to this point of view, according to Smeets and Brenner grasping consists of controlling individual digits, not the transport and grip components. The opening of the hand emerges from the trajectories of the digits. It is compatible with the separate control of the Th and Vf normal forces suggested in the present study.
The portion of the force pattern FM.NA derived from the movements along the normal axis was modeled to account for two effects. The model accounted for the 180° out of phase effect seen in single axis movements as well as for potential imbalances between the Th and Vf and hence for the grip force. The model parameter C describes the difference between the Th and Vf forces in the movement cycles. The facts presented above (Table 2) suggest that the C value does not depend on the movement frequency or the circular diameter.
Table 2.
Model parameters k, C, FBG per movement plane, with respect to changes in movement diameter and frequency. (mean±SD)
| k | D1-F1 | D1-F2 | D2-F1 | D2-F2 |
|---|---|---|---|---|
| Frontal | 0.434±0.249 | 0.343±0.154 | 0.574±0.355 | 0.524±0.229 |
| Horizontal | 0.322±0.172 | 0.192±0.125 | 0.308±0.229 | 0.205±0.091 |
| Sagittal | 0.682±0.241 | 0.479±0.186 | 0.710±0.241 | 0.548±0.249 |
| C | ||||
| Frontal | 0.076±0.339 | 0.046±0.280 | 0.150±0.377 | 0.092±0.271 |
| Horizontal | −0.154±0.147 | −0.101±0.159 | −0.182±0.165 | −0.112±0.134 |
| Sagittal | 0.006±0.222 | −0.020±0.150 | 0.016±0.202 | 0.010±0.145 |
| FBG | ||||
| Frontal | 10.74±6.10 | 16.86±6.64 | 13.13±7.94 | 20.12±6.09 |
| Horizontal | 10.48±3.43 | 16.14±4.24 | 13.99±3.35 | 20.39±4.61 |
| Sagittal | 10.47±4.44 | 17.07±5.60 | 13.84±6.91 | 21.75±6.56 |
One thing this study is unable to directly address is whether or not the element FM.NA is actively controlled, is a result of passive joint stiffness, or a combination of the two. A simple mechanical gripper can create the out of phase response (Gao et al. 2005). However, the contribution of the active control is also possible.
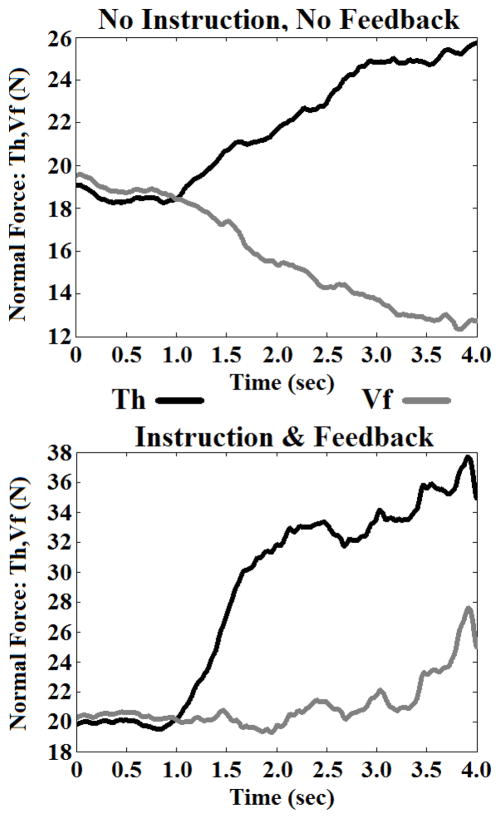
To get some preliminary insight on the possible contribution of the active control to the FM.NA we performed a supplemental experiment. The instrumented handle was mounted in a vertical, static position by attaching the base of the handle to the top of a fixed surface (Figure 1, replacing the bottom mass with a table). A single subject, separate of the subjects from the main experiment, provided informed consent and performed the tasks. The subject was instructed to grasp the handle and exert a comfortable grip force (20 N) while visual feedback on the force value was provided. Then, the subject was asked to perform a pushing effort with the thumb in the direction of the Vf. Two different task conditions were performed: (A) no instruction on the grip force with the feedback removed, and (B) under the instruction to keep the grip force constant with the grip force feedback is provided. The results are presented in Figure 7. A similar experiment with matched results was performed with the Vf pushing in the thumb direction, where the results were a mirror image of those in Figure 7. Note that in the described experiment the handle did not move and, hence, all the observed effects are solely due to the motor control mechanisms. From the presented data it follows that the subject exhibited a natural ‘tendency’ to decrease the grip force during lateral pushing efforts (condition A; Figure 7 top; Vf, grey line decreasing). However, the subject was also able to keep the force at more or less the same level when instructed to and informed on the task performance (condition B, Figure 7 bottom). The ‘natural tendency’ to decrease the grip force is indicative of a relaxation of the digits (either Th or Vf) resisting the pushing effort. The addition of instruction and feedback allows for the inhibition of the ‘natural coordination’, but required substantial conscious effort. We can then conclude, for the continuous, uniform circular movements of the main study, that motor control mechanisms set a base grip force (FBG) and then together with passive mechanical factors account for the fluctuation of the grip force including its decrease below the FBG levels.
Figure 7. Normal Forces in Trials with a Static Handle.
Thumb (black) and Vf (gray) normal forces in static trials of grasping the handle and then exerting a lateral pushing force towards the Vf side. The top graph is for a trial with no additional instruction or feedback. As the thumb force is increased, the Vf force—and hence also the grip force—is seen to decrease. The bottom graph includes the instruction of maintain a set grip force (with feedback) while increasing the thumb force. In both graphs, the grip force is the minimum of Th or Vf forces at any point in time
Limitations of the study and future research
Limitations of the current study are evident. Future testing can be done employing more complex non-circular patterns, e.g. ovals, ‘figure eights’, 3-D patterns. Additional testing can be performed on a non-upright handle as well as accounting for a varying handle orientation. The FBG parameter was assumed to be constant through a single trial. This may not be the case, as subtle adjustments can be made during a trail. The analysis for this study was only performed at the Th-Vf level looking at primarily the Fn. Future analysis and coming data can also look at the individual finger level of control as well as that of the torques generated.
Table 3.
Contributions of model elements to the mean and dynamic range of normal forces (N) averaged across all conditions. (mean±SD)
| FM.SP | FM.NA | FBG | Total | ||
|---|---|---|---|---|---|
| Th | Mean | 3.986±2.312 | −0.533±0.5476 | 15.42±6.58 | 18.569±5.898 |
| Dynamic Range | 4.423±3.876 | 4.484±3.227 | 5.409±2.994 | ||
| Vf | Mean | 3.986±2.312 | 0.573±0.629 | 15.42±6.58 | 20.389±6.694 |
| Dynamic Range | 4.423±3.876 | 5.128±3.719 | 7.364±3.678 |
Acknowledgments
This work was in part supported by National Institutes of Health grants AG-018751, NS-035032, and AR-048563.
This project was assisted by the design efforts of ATI-Industrial Automations (Apex, NC, USA) which allowed for the reduced equipment bulk and wireless capabilities of the force data system. This work was supported in part by National Institute of Health grants AG-018751, NS-035032, AR-04856.
Contributor Information
Gregory P. Slota, Email: GSlota@psu.edu, Pennsylvania State University, 39 Recreation Building, University Park, PA 16802, USA, +1-(814)-863-8554, Fax:+1-(814)-863-4755
Mark L. Latash, Email: mll11@psu.edu, Pennsylvania State University, 268N Recreation Building, University Park, PA 16802, USA, +1-(814)-863-5374, Fax:+1-(814)-865-1275
Vladimir M. Zatsiorsky, Email: vxz1@psu.edu, Pennsylvania State University, 39 Recreation Building, University Park, PA 16802, USA, +1-(814)-865-3446, Fax:+1-(814)-863-4755
References
- Adamovich SV, Feldman AG. A model of central regulation of movement parameters. Biofizika. 1984;29 (2):306–309. [PubMed] [Google Scholar]
- Aoki T, Latash ML, Zatsiorsky VM. Adjustments to local friction in multifinger prehension. J Mot Behav. 2007;39 (4):276–290. doi: 10.3200/JMBR.39.4.276-290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aoki T, Niu X, Latash ML, Zatsiorsky VM. Effects of friction at the digit-object interface on the digit forces in multi-finger prehension. Exp Brain Res. 2006;172 (4):425–438. doi: 10.1007/s00221-006-0350-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole KJ, Johansson RS. Friction at the digit-object interface scales the sensorimotor transformation for grip responses to pulling loads. Exp Brain Res. 1993;95 (3):523–532. doi: 10.1007/BF00227146. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of nervous system with control of movement or maintenance of a steady posture.2. Controllable parameters of muscles. Biophys-Ussr. 1966;11 (3):565–578. [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (lambda model) for motor control. J Mot Behav. 1986;18 (1):17–54. doi: 10.1080/00222895.1986.10735369. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. The origin and use of positional frames of reference in motor control. Behav Brain Sci. 1995;18 (4):723–744. [Google Scholar]
- Feldman AG, Levin MF. The equilibrium-point hypothesis--past, present and future. Adv Exp Med Biol. 2009;629 (7):699–726. doi: 10.1007/978-0-387-77064-2_38. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Tresilian J, Wing AM. Coupling of grip force and load force during arm movements with grasped objects. Neurosci Lett. 1993;152 (1–2):53–56. doi: 10.1016/0304-3940(93)90481-y. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Tresilian JR. Grip-load force coupling: a general control strategy for transporting objects. J Exp Psychol Hum Percept Perform. 1994;20 (5):944–957. doi: 10.1037//0096-1523.20.5.944. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Wing AM. Modulation of grip force with load force during point-to-point arm movements. Exp Brain Res. 1993;95 (1):131–143. doi: 10.1007/BF00229662. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Wing AM. The stability of precision grip forces during cyclic arm movements with a hand-held load. Exp Brain Res. 1995;105 (3):455–464. doi: 10.1007/BF00233045. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Wing AM, Allison S, Spenceley A. Effects of surface texture on weight perception when lifting objects with a precision grip. Percept Psychophys. 1995;57 (3):282–290. doi: 10.3758/bf03213054. [DOI] [PubMed] [Google Scholar]
- Gao F, Latash ML, Zatsiorsky VM. Internal forces during object manipulation. Exp Brain Res. 2005;165 (1):69–83. doi: 10.1007/s00221-005-2282-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao F, Latash ML, Zatsiorsky VM. Maintaining rotational equilibrium during object manipulation: linear behavior of a highly non-linear system. Exp Brain Res. 2006;169 (4):519–531. doi: 10.1007/s00221-005-0166-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao F, Latash ML, Zatsiorsky VM. Similar motion of a hand-held object may trigger nonsimilar grip force adjustments. J Hand Ther. 2007;20 (4):300–307. doi: 10.1197/j.jht.2007.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glezer VD, Gauzelman VE. Linear and nonlinear properties of simple cells of the striate cortex of the cat: two types of nonlinearity. Exp Brain Res. 1997;117 (2):281–291. doi: 10.1007/s002210050223. [DOI] [PubMed] [Google Scholar]
- Grafton ST. The cognitive neuroscience of prehension: recent developments. Exp Brain Res. 2010;204 (4):475–491. doi: 10.1007/s00221-010-2315-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gysin P, Kaminski TR, Gordon AM. Coordination of fingertip forces in object transport during locomotion. Exp Brain Res. 2003;149 (3):371–379. doi: 10.1007/s00221-003-1380-1. [DOI] [PubMed] [Google Scholar]
- Jeannerod M. The timing of natural prehension movements. J Mot Behav. 1984;16 (3):235–254. doi: 10.1080/00222895.1984.10735319. [DOI] [PubMed] [Google Scholar]
- Jeannerod M, Arbib MA, Rizzolatti G, Sakata H. Grasping objects: the cortical mechanisms of visuomotor transformation. Trends Neurosci. 1995;18 (7):314–320. [PubMed] [Google Scholar]
- Jeannerod M, Paulignan Y, Weiss P. Grasping an object: one movement, several components. Novartis Found Symp. 1998;218:5–16. doi: 10.1002/9780470515563.ch2. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Westling G. Roles of glabrous skin receptors and sensorimotor memory in automatic-control of precision grip when lifting rougher or more slippery objects. Experimental Brain Research. 1984;56 (3):550–564. doi: 10.1007/BF00237997. [DOI] [PubMed] [Google Scholar]
- Kerr J, Roth B. Analysis of multifingered hands. Int J Robot Res. 1986;4 (4):3–17. [Google Scholar]
- Kinoshita H, Kawai S, Ikuta K, Teraoka T. Individual finger forces acting on a grasped object during shaking actions. Ergonomics. 1996;39 (2):243–256. doi: 10.1080/00140139608964455. [DOI] [PubMed] [Google Scholar]
- Kowalski N, Depireux DA, Shamma SA. Analysis of dynamic spectra in ferret primary auditory cortex. II. Prediction of unit responses to arbitrary dynamic spectra. J Neurophysiol. 1996;76 (5):3524–3534. doi: 10.1152/jn.1996.76.5.3524. [DOI] [PubMed] [Google Scholar]
- Latash ML. Motor synergies and the equilibrium-point hypothesis. Motor Control. 2010;14 (3):294–322. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Friedman J, Kim SW, Feldman AG, Zatsiorsky VM. Prehension synergies and control with referent hand configurations. Exp Brain Res. 2010;202 (1):213–229. doi: 10.1007/s00221-009-2128-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li ZM, Latash ML, Zatsiorsky VM. Force sharing among fingers as a model of the redundancy problem. Exp Brain Res. 1998;119 (3):276–286. doi: 10.1007/s002210050343. [DOI] [PubMed] [Google Scholar]
- Murray RM, Li Z, Sastry S. A mathematical introduction to robotic manipulation. CRC Press; Boca Raton: 1994. [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Prehension synergies during nonvertical grasping, I: Experimental observations. Biol Cybern. 2004a;91 (3):148–158. doi: 10.1007/s00422-004-0505-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Prehension synergies during nonvertical grasping, II: Modeling and optimization. Biol Cybern. 2004b;91 (4):231–242. doi: 10.1007/s00422-004-0506-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pigeon P, Yahia LH, Mitnitski AB, Feldman AG. Superposition of independent units of coordination during pointing movements involving the trunk with and without visual feedback. Exp Brain Res. 2000;131 (3):336–349. doi: 10.1007/s002219900267. [DOI] [PubMed] [Google Scholar]
- Pilon JF, De Serres SJ, Feldman AG. Threshold position control of arm movement with anticipatory increase in grip force. Exp Brain Res. 2007;181 (1):49–67. doi: 10.1007/s00221-007-0901-8. [DOI] [PubMed] [Google Scholar]
- Ruegg DG, Bongioanni F. Superposition of ballistic on steady contractions in man. Exp Brain Res. 1989;77 (2):412–420. doi: 10.1007/BF00274999. [DOI] [PubMed] [Google Scholar]
- Savescu AV, Latash ML, Zatsiorsky VM. A technique to determine friction at the fingertips. J Appl Biomech. 2008;24 (1):43–50. doi: 10.1123/jab.24.1.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim JK, Latash ML, Zatsiorsky VM. Finger coordination during moment production on a mechanically fixed object. Exp Brain Res. 2004;157 (4):457–467. doi: 10.1007/s00221-004-1859-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slijper H, Latash M. The effects of instability and additional hand support on anticipatory postural adjustments in leg, trunk, and arm muscles during standing. Exp Brain Res. 2000;135 (1):81–93. doi: 10.1007/s002210000492. [DOI] [PubMed] [Google Scholar]
- Smeets JB, Brenner E. Independent movements of the digits in grasping. Exp Brain Res. 2001;139 (1):92–100. doi: 10.1007/s002210100748. [DOI] [PubMed] [Google Scholar]
- Smith MA, Soechting JF. Modulation of grasping forces during object transport. J Neurophysiol. 2005;93 (1):137–145. doi: 10.1152/jn.00775.2004. [DOI] [PubMed] [Google Scholar]
- Yoshikawa T, Nagai K. Manipulating and grasping forces in manipulation by multifingered robot hands. IEEE T Robotic Autom. 1991;7 (1):67–77. [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Finger force vectors in multi-finger prehension. J Biomech. 2003a;36 (11):1745–1749. doi: 10.1016/s0021-9290(03)00062-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Prehension synergies: effects of object geometry and prescribed torques. Exp Brain Res. 2003b;148 (1):77–87. doi: 10.1007/s00221-002-1278-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Motor control goes beyond physics: differential effects of gravity and inertia on finger forces during manipulation of hand-held objects. Exp Brain Res. 2005;162 (3):300–308. doi: 10.1007/s00221-004-2152-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Prehension stability: experiments with expanding and contracting handle. J Neurophysiol. 2006;95 (4):2513–2529. doi: 10.1152/jn.00839.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gregory RW, Latash ML. Force and torque production in static multifinger prehension: biomechanics and control. I. Biomechanics. Biol Cybern. 2002a;87 (1):50–57. doi: 10.1007/s00422-002-0321-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gregory RW, Latash ML. Force and torque production in static multifinger prehension: biomechanics and control. II. Control. Biol Cybern. 2002b;87 (1):40–49. doi: 10.1007/s00422-002-0320-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Latash ML. Prehension synergies. Exerc Sport Sci Rev. 2004;32 (2):75–80. doi: 10.1097/00003677-200404000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Latash ML. Multifinger prehension: an overview. J Mot Behav. 2008;40 (5):446–476. doi: 10.3200/JMBR.40.5.446-476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo BR, Qian WH. A general dynamic force distribution algorithm for multifingered grasping. IEEE T Syst Man Cy B. 2000;30 (1):185–192. doi: 10.1109/3477.826959. [DOI] [PubMed] [Google Scholar]