Abstract
Somatically acquired DNA rearrangements are characteristic of many cancers. The use of these mutations as diagnostic markers is challenging, because tumor cells are frequently admixed with normal cells, particularly in early stage tumor samples, and thus the samples contain a high background of normal DNA. Detection is further confounded by the fact that the rearrangement boundaries are not conserved across individuals, and might vary over hundreds of kilobases. Here, we present an algorithm for designing polymerase chain reaction (PCR) primers and oligonucleotide probes to assay for these variant rearrangements. Specifically, the primers and probes tile the entire genomic region surrounding a rearrangement, so as to amplify the mutant DNA over a wide range of possible breakpoints and robustly assay for the amplified signal on an array. Our solution involves the design of a complex combinatorial optimization problem, and also includes a novel alternating multiplexing strategy that makes efficient detection possible. Simulations show that we can achieve near-optimal detection in many different cases, even when the regions are highly non-symmetric. Additionally, we prove that the suggested multiplexing strategy is optimal in breakpoint detection. We applied our technique to create a custom design to assay for genomic lesions in several cancer cell-lines associated with a disruption in the CDKN2A locus. The CDKN2A deletion has highly variable boundaries across many cancers. We successfully detect the breakpoint in all cell-lines, even when the region has undergone multiple rearrangements. These results point to the development of a successful protocol for early diagnosis and monitoring of cancer. For online Supplementary Material, see www.liebertonline.com.
Key words: biology, cancer genomics, DNA arrays, genomic rearrangements, genomics, sequence analysis, viruses
1. Introduction
Cancers are characterized by somatically acquired DNA mutations. While these include point mutations, they often involve rearrangements of large genomic regions (Campbell et al., 2008). Recurrent events such as “gene-fusion” were originally characterized in leukemias, and uncommon solid tumors. This changed with the discovery of recurrent gene fusions in prostate cancers (Mitelman et al., 2007). This has motivated multiple sequencing surveys on primary tumors and tumor cell lines using high-throughput paired-end mapping (PEM) and conventional BAC end sequence profiling (ESP) (Raphael et al., 2008; Campbell et al., 2008; Ruan et al., 2007). In parallel, computational techniques have been developed to analyze PEM/ESP data to detect gene disruptions and gene fusions that impact tumor development (Bashir et al., 2008). These technological advancements will be key to developing new treatments and diagnostic tests. Nevertheless, there are substantial barriers to developing diagnostic tests based on identification of a characteristic somatic rearrangement.
Primarily, the aforementioned studies require relatively pure DNA samples. In the early stage of tumor development, the DNA samples contain a high background of normal DNA (below 1:100, tumor/normal). This makes a sequence based approach impractical; the depth of sequence coverage required to reliably detect a rearrangement would be enormous. Polymerase chain reaction (PCR) is used to amplify targeted genomic regions. Previous studies have focused on optimizing primer multiplexing strategies to target multiple genomic regions simultaneously (Beigel et al., 2001; Lipson, 2002). PCR can similarly be used to amplify a rearranged region, if the rearrangement boundaries are known. However, many rearrangements have highly variable boundaries across patients, often hundreds of kb in size, which means that naive PCR approaches would require a custom assay for each patient. Precisely to address these issues of heterogeneity and detection of variable genomic lesions in a high background of normal DNA, some of us designed a novel multiplex PCR-based assay, primer approximation multiplex PCR (PAMP) (Liu and Carson, 2007). We have shown success in optimizing primer designs that can detect variable genomic lesions in a highly heterogeneous background of normal DNA (Bashir et al., 2007). The basic approach is outlined here for deletions, but is applicable to any rearrangement.
1.1. PAMP overview
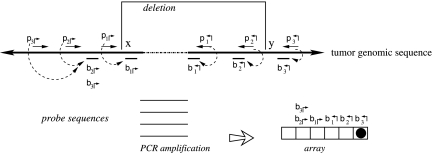
The genomic region of interest is tiled by forward (denoted by p↱) and reverse (p↰) primers (Fig. 1). All of the primers are incorporated into a multiplex tube (or tubes), along with the query DNA. The primers are spaced so that deletion at any boundary will bring a primer pair close enough to be amplified. In Figure 1, the deletion at (x, y) brings p1↱ and p↰3 close together. The amplified product is hybridized to a set of probes denoted by locations 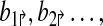 and detected on an array. Successful hybridization confirms the deletion event, and also resolves the deletion boundary to within 1kb.
and detected on an array. Successful hybridization confirms the deletion event, and also resolves the deletion boundary to within 1kb.
FIG. 1.
Schematic of PAMP detection failure. The breakpoint, (x, y), results in an amplified product, but is not detected on the left side.
In spite of its apparent simplicity, successful deployment of PAMP requires the solving of a challenging combinatorial optimization problem relating to the design of primers. Intuitively, the goal is to maximize the detection of any possible deletion while minimizing the number of multiplex reactions such that no primer-primer interactions occur within a reaction. The optimization is critical, as each missed deletion is a potentially undetected tumor in an individual. Likewise, we cannot overstate the need for computation, as the design can involve the selection of thousands of primers from tens of thousands of candidate primers, and even a single primer-primer interaction within a multiplex reaction nullifies all signals (Bashir et al., 2007).
1.2. Primer design for PAMP
Formally, a primer-design is described by a set of forward and reverse primers
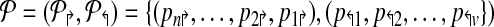 |
The genomic locations of the primers are denoted by
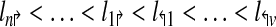 |
Consider a design, 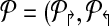 . Define a breakpoint as a pair of genomic coordinates (x, y) that come together because of a mutation. Breakpoint (x, y) is amplifiable by a primer pair (pi↱, p↰j) if
. Define a breakpoint as a pair of genomic coordinates (x, y) that come together because of a mutation. Breakpoint (x, y) is amplifiable by a primer pair (pi↱, p↰j) if 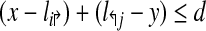 , where d, (≈2000) is a known parameter constrained by limitations of PCR. For each breakpoint (x, y), denote its coverage-cost,
, where d, (≈2000) is a known parameter constrained by limitations of PCR. For each breakpoint (x, y), denote its coverage-cost, 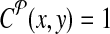 if it is not amplifiable by a pair in
if it is not amplifiable by a pair in 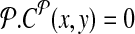 otherwise. This allows us to define two-sided cost of tiling a genomic region by primers as
otherwise. This allows us to define two-sided cost of tiling a genomic region by primers as . The critical constraint in selecting primers is dimerization: no pair of primers in a single multiplex reaction must hybridize to each other. One way to solve the dimerization problem is simply to put each pair of primers in their own multiplex tube. With 500 forward, and 500 reverse primers in a typical design, this is not tenable. We consider the following:
. The critical constraint in selecting primers is dimerization: no pair of primers in a single multiplex reaction must hybridize to each other. One way to solve the dimerization problem is simply to put each pair of primers in their own multiplex tube. With 500 forward, and 500 reverse primers in a typical design, this is not tenable. We consider the following:
1.3. The PAMP design problem
Input: Positive integer m, and a forward and reverse candidate region, with a collection of corresponding forward and reverse primers.
Output: A primer design over m multiplex tubes, so that no primer pair dimerizes in a multiplex reaction, and the coverage cost is minimized  .
.
We will add additional constraints to this formulation in the next section. We previously addressed this problem using a heuristic approach with a simplified coverage function which performed naive multiplexing (Bashir et al., 2007), hereafter termed Pamp-1D. Pamp-1D optimizes a one-sided variant of cost by penalizing each pair of adjacent primers if they were greater than half of the amplifiable distance. The advantage is computational expediency, as the change in coverage due to primer addition/deletion is easily computed. Even though Pamp-1D was able to handle a larger number (tens of thousands) of input primers and converge in a reasonable amount of time (minutes to hours), its coverage function underestimated true breakpoint coverage. Especially for non-symmetric regions, the designs are greatly improved by allowing longer primer gaps on the larger side, and vice-versa. The two-sided problem is very difficult to optimize; previous approaches were impractical for most data-sets only handling <100 input primers (Dasgupta et al., 2008). In our application, even simple input sets would entail thousands of potential primers.
Finally, initial experimental data showed fundamental flaws in these approaches. The initial formulation makes the reasonable, but incorrect assumption that an amplified PCR product can be readily detected by a corresponding probe. Second, it does not carefully account for other interactions, such as “mispriming,” which may also lead to false negatives.
In this article, we seek to redress these shortcomings with Pamp-2D. First, we describe the flaw in the Pamp-1D design and solve it using a novel alternating multiplexing scheme. We follow this by describing a generic framework for optimal alternating multiplexed primer design. The actual optimization is performed using simulated annealing. Next, we describe a data-structure to speed-up the simulated annealing iteration. Simulations on multiple genomic region demonstrate the efficacy and efficiency of the proposed approach. To test the overall methodology, we assayed events in 3 cell-lines, CEM, A549, and MOLT4. We show that, in each case, we can detect the lesion of interest, even in regions with multiple rearrangements.
2. Methods: A Multiplexed Approach to Pamp Design
2.1. Amplification ≠ detection
We begin by noting that amplification of a deleted genomic region is not synonymous with detection of the region. Figure 1 shows an example of this. Each primer is associated with a proximal downstream probe on the array, in order to detect the amplified product. Note the probe and the primer locations cannot match, because residual primers in the solution will hybridize to the array, giving a false signal. This leads to an “orphan” region between the primer and the probe. As an example, the point x in Figure 1 lies in between primer p1↱ and its probe b1↱. When the region (x, y) is deleted, p1↱ and p↰3 come together, and are amplified. However, the amplified region does not contain sequence complementary to any probe on the left hand side. Consequently, there is no signal corresponding to the left breakpoint.
The solution to this detection problem lies in recognizing that had the product (p2↱,p↰3) been amplified, the left breakpoint would be detected by hybridization to probe b2↱. However, even when (p2↱, p↰3) is close enough to be amplified, it is out-competed by (p1↱, p↰3) and will not amplify.
One possible solution is to add p1↱ and p2↱ in different multiplex tubes. Multiple multiplex reactions is a practical necessity in most cases, as it is challenging to amplify products with a larger number primers in a single tube (Fan et al., 2006). Indeed, the experimental design for PAMP, as first proposed by Liu and Carson (2007), consists of selecting groups of adjacent primers upstream and downstream of a putative breakpoint, in which each set is one half the desired multiplex size. Nevertheless, increased multiplexing increases the complexity and cost of the experiment, and must be controlled. We address these issues through a novel alternating multiplexing strategy.
2.1.1. Alternating multiplexing for primer design
Consider a primer design 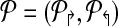 . Each forward primer pi↱ is associated with a downstream probe located at bi↱ (li↱ < bi↱). We abuse notation slightly by using bi↱ to denote both the probe, and its location. Also bi↱ ≤ b(i–1)↱ for all i, with equality indicating that pi↱ and p(i–1)↱ share the same probe. In this notation, probes bi↱ and bj↱ are adjacent (on the genome) if there exists i ≥ k > j such that
. Each forward primer pi↱ is associated with a downstream probe located at bi↱ (li↱ < bi↱). We abuse notation slightly by using bi↱ to denote both the probe, and its location. Also bi↱ ≤ b(i–1)↱ for all i, with equality indicating that pi↱ and p(i–1)↱ share the same probe. In this notation, probes bi↱ and bj↱ are adjacent (on the genome) if there exists i ≥ k > j such that
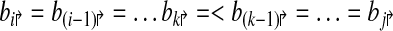 |
As an example, probes b3↱ and b1↱ are adjacent in Figure 1, as also b2↱ and b1↱, but not b3↱ and b2↱. Analogous definitions apply for reverse primers. The probes are located at 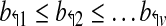 where b↰i < l↰i, for all i.
where b↰i < l↰i, for all i.
Definition 1.
Breakpoint (x, y) is left-detectable (respectively, right-detectable) by a primer-design 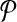 if it is amplifiable by some primer pair (pi↱, p↰j), and li↱ < bi↱, (respectively, l↰j > b↰j > y).
if it is amplifiable by some primer pair (pi↱, p↰j), and li↱ < bi↱, (respectively, l↰j > b↰j > y).
The set of left-detectable and right-detectable breakpoints is denoted by
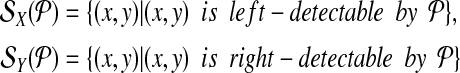 |
As a breakpoint might not be detected even when it is detectable, we define
Definition 2.
Breakpoint (x, y) is left-detected (respectively, right-detected) by  if it is left-detectable (respectively, right detectable), and the following are satisfied: (a) no pair of primers p,
if it is left-detectable (respectively, right detectable), and the following are satisfied: (a) no pair of primers p,  dimerize (non-dimerization); and (b) (x, y) is not amplified by any
dimerize (non-dimerization); and (b) (x, y) is not amplified by any  with l↰i < x < bt↱, or l↰j > y > b↰j (non-detection).
with l↰i < x < bt↱, or l↰j > y > b↰j (non-detection).
When 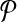 is used in a single reaction, we denote the set of left-detected (respectively, right-detected) breakpoints as
is used in a single reaction, we denote the set of left-detected (respectively, right-detected) breakpoints as 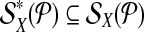 (respectively,
(respectively, 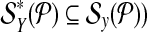 . By partitioning
. By partitioning  into multiple multiplexing tubes it may be possible to obtain better coverage. Simply, one could run each forward and reverse primer in its own multiplex reaction so that
into multiple multiplexing tubes it may be possible to obtain better coverage. Simply, one could run each forward and reverse primer in its own multiplex reaction so that
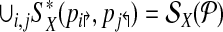 |
The idea behind alternate multiplexing is simple: Primers p2rsh;i,p↱j (correspondingly, plsh;i, plsh;j) can be added to the same multiplex set only if their downstream probes bi↱ and bj↱ (correspondingly, b↰i, b↰j) are not adjacent. A similar rule applies for reverse primers. Formally, first order the all unique probes by their genomic position (independently for the left and right sides), and then number them in increasing order. Partition 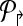 into
into 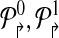 , where
, where 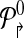 contains all primers whose probe is “even” numbered, and the sets
contains all primers whose probe is “even” numbered, and the sets 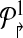 contains all primers whose probe is “odd” numbered. Similarly, define
contains all primers whose probe is “odd” numbered. Similarly, define 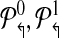 . The multiplexing reactions are given by choosing each of the 4 forward reverse partitions. In Figure 1, this scheme would place p2↱, p3↱ in different multiplex sets. Before we show that alternating multiplexing optimizes detection, we define a technical term. A design of forward (likewise, reverse) primers is non-trivial if there exists at least one pair of primers pi↱,pj↱ with 0 < li↱ – lj↱ < d, and bi↱ ≠ b↱. The definition is introduced for technical reasons only, as any useful design must be non-trivial.
. The multiplexing reactions are given by choosing each of the 4 forward reverse partitions. In Figure 1, this scheme would place p2↱, p3↱ in different multiplex sets. Before we show that alternating multiplexing optimizes detection, we define a technical term. A design of forward (likewise, reverse) primers is non-trivial if there exists at least one pair of primers pi↱,pj↱ with 0 < li↱ – lj↱ < d, and bi↱ ≠ b↱. The definition is introduced for technical reasons only, as any useful design must be non-trivial.
Theorem 1.
Let 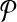 be a design with no dimerizing pairs. Then, alternating multiplexing allows us to detect all detectable breakpoints. In other words
be a design with no dimerizing pairs. Then, alternating multiplexing allows us to detect all detectable breakpoints. In other words
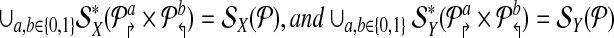 |
Further, if 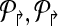 are non-trivial then the multiplexing is the minimal necessary to achieve detectability.
are non-trivial then the multiplexing is the minimal necessary to achieve detectability.
Proof
See Appendix. ▪
Note that Theorem 1 works only for non-dimerizing sets. In earlier work, we have shown that the achievable coverage diminishes with larger sets of primers because of dimerizations. To connect dimerization, detection, and multiplexing, we start by defining a primer-dimer-adjacency graph G, whose nodes are defined by the set of primers. A primer-pair is edge-connected if either of the following is true: (a) the primers dimerize, or (b) they are adjacent and in the same orientation. Theorem 2 is based on the property that a coloring of this graph partitions primers into non-dimerizing, alternatingly multiplexed sets.
Theorem 2.
Let each forward (reverse) primer in 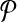 be edge connected with at most Δ↱ (Δ↰) other forward (reverse) primers Further, there is no dimerization between a forward-reverse pair. Then, there exists a design with no more than Δ↱ · Δ↰ multiplex reactions for which all breakpoints in
be edge connected with at most Δ↱ (Δ↰) other forward (reverse) primers Further, there is no dimerization between a forward-reverse pair. Then, there exists a design with no more than Δ↱ · Δ↰ multiplex reactions for which all breakpoints in 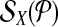 (respectively,
(respectively, 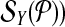 are left-detected (respectively, right detected).
are left-detected (respectively, right detected).
Proof
Proof is based on the theorem of Brooks (1941). See Appendix. ▪
Theorems 1 and 2 guide an overall iterative strategy that provides for the best coverage, given a bound on the number of multiplex reactions. Assume for now that we have a procedure OptCoverage (G, Δ↱, Δ↰) that takes G and numbers Δ↱, Δ↰ as input, and returns an optimized design, (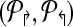 ). Specifically, it returns the sub-graph induced by (
). Specifically, it returns the sub-graph induced by (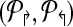 ) in which (a) each forward (respectively, reverse) primer is edge-connected to ≤ Δ↱ (≤Δlsh;) forward (reverse) primers; and (b) no forward-reverse primers are edge-connected. We can use Theorems 1 and 2 to obtain the same coverage using ≤ Δ↱ · Δ↰ multiplexing. The following section will describe the OptCoverage procedure. The overall algorithm is motivated by the fact Theorem 2 only provides a weak upper bound of Δ↱Δ↰ on the available multiplexing. If the actual number of multiplex reactions is smaller than available, we adjust and iterate.
) in which (a) each forward (respectively, reverse) primer is edge-connected to ≤ Δ↱ (≤Δlsh;) forward (reverse) primers; and (b) no forward-reverse primers are edge-connected. We can use Theorems 1 and 2 to obtain the same coverage using ≤ Δ↱ · Δ↰ multiplexing. The following section will describe the OptCoverage procedure. The overall algorithm is motivated by the fact Theorem 2 only provides a weak upper bound of Δ↱Δ↰ on the available multiplexing. If the actual number of multiplex reactions is smaller than available, we adjust and iterate.
Algorithm.
|
Procedure PrimerDesign(m, G, L↱, L↰) |
| (* L↱, L↰ represent lengths of the two regions *) |
1. Let 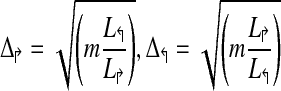 (* Initial estimate *) (* Initial estimate *) |
2. 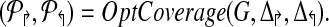 ) ) |
(* Return sub-graph induced by (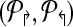 ) with Delta;↱ (Δ↰) edges per forward (reverse) primer and optimal coverage. *) ) with Delta;↱ (Δ↰) edges per forward (reverse) primer and optimal coverage. *) |
3. Compute Δc = MaxAdjacency(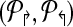 ) ) |
4. Use Welsh and Powell algorithm [Welsh and Powell, 1967] to color 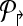 (and (and 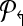 ). Return m↱ (and, m↰) colors. ). Return m↱ (and, m↰) colors. |
| 5. If |m – m↱ · m↰| is large, adjust Δ↱, Δ↰; Go to Step 2. |
Figure 3c shows that a large gap often exists between Δ↱Δ↰ and true multiplexing levels, especially as Δ↱Δ↰ gets large. In the following section, we describe the use of simulated annealing to optimize the design of primers.
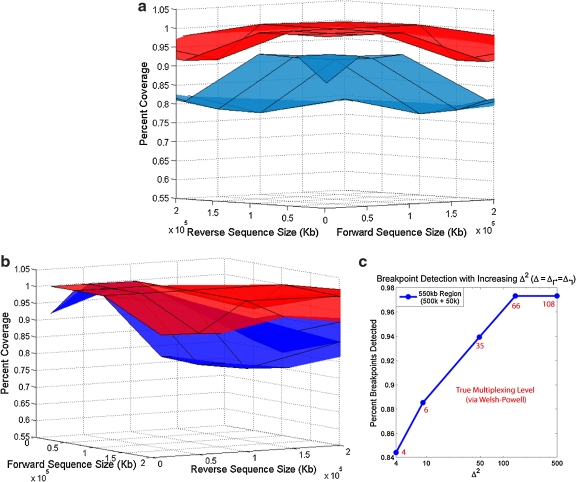
FIG. 3.
Performance of Pamp-2D. (a) The surface plot shows that a significant benefit in detectable coverage is seen when comparing Pamp-1D (blue) to Pamp-2D (red). (b) Applying the alternating strategy to Pamp-1D significantly improves its coverage. However Pamp-2D consistently obtains better coverage (especially in non-symmetric regions). (c) As allowed multiplexing, Δ2, in the final primer set increases, the resulting coverage increases. Red values represent the “true” number of multiplex reactions at each data point (as predicted via Welsh-Powell algorithm).
2.2. Simulated annealing for optimization
The computational goal is to choose a design 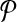 that minimizes coverage-cost
that minimizes coverage-cost 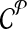 . The optimal design is chosen from candidate solutions
. The optimal design is chosen from candidate solutions 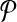 in which each forward primer (reverse primer) is edge-connected with at most Δ↱ (Δ↱) other primers. We use an established simulated annealing approach to perform the optimization (Kirkpatrick et al., 1983).
in which each forward primer (reverse primer) is edge-connected with at most Δ↱ (Δ↱) other primers. We use an established simulated annealing approach to perform the optimization (Kirkpatrick et al., 1983).
For any candidate solution 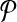 , define its neighborhood as the set of candidate solutions that are obtained by adding or removing a primer from
, define its neighborhood as the set of candidate solutions that are obtained by adding or removing a primer from 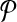 . In other words,
. In other words, 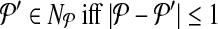 . Let
. Let 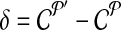 denote the change in coverage cost in moving from
denote the change in coverage cost in moving from 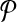 to
to 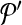 . Following the s.a. paradigm, we move to
. Following the s.a. paradigm, we move to 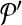 if δ < 0. If δ ≥ 0, we choose to move to
if δ < 0. If δ ≥ 0, we choose to move to 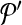 with probability
with probability 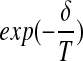 , in order to escape local minima. While the basic paradigm has been explored in our earlier work, and elsewhere, we extend this here by addressing two key issues: (1) incorporation of probe distances/interactions into the optimization and (2) rapid calculation of the 2D coverage-cost.
, in order to escape local minima. While the basic paradigm has been explored in our earlier work, and elsewhere, we extend this here by addressing two key issues: (1) incorporation of probe distances/interactions into the optimization and (2) rapid calculation of the 2D coverage-cost.
2.2.1. Incorporating probes
We address the first problem by noting the direct relationship between primers and probes. Specifically, we do not need to separately iterate over primers and probes; anytime a primer is added we attempt to add its proximal downstream probe. This probe is added unless it is already present in the set (in which case no additional probe is added) or it causes a mispriming signal (in which case the next most proximal probe is examined). As the first condition is trivial, we focus our attention on the second.
There have previously been rigorous attempts at identifying such mispriming pairs in a computational framework (Lipson, 2002). The mispriming problem in PAMP is somewhat unique; it is only problematic when it leads to a “false positive” signal. These signals occur when a primer pair anneals to another region of the genome and the amplified sequenced hybridizes to a probe on the array. This allows us to create a novel formulation for the probe/mispriming problem. Define a collection of probe-misprime-triads Tm on 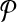 as follows:
as follows: 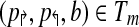 if and only if primers p↱ and p↰ misprime to genomic sequence s and probe b anneals to s. Checking this could be costly if many such mispriming triads exist. In practice, enforcing this criteria has no measurable effect on time complexity as most probes and primer-pairs are unique and |Tm| is small. This effect is, in fact, minimized prior to simulated annealing optimization by preferentially selecting probes in the input set which do not create probe-misprime-triads.
if and only if primers p↱ and p↰ misprime to genomic sequence s and probe b anneals to s. Checking this could be costly if many such mispriming triads exist. In practice, enforcing this criteria has no measurable effect on time complexity as most probes and primer-pairs are unique and |Tm| is small. This effect is, in fact, minimized prior to simulated annealing optimization by preferentially selecting probes in the input set which do not create probe-misprime-triads.
2.2.2. Updating coverage
For exposition, we focus on coverage (detection will naturally follow). Recall that a breakpoint (x,y) is covered if there exists some pair of primers (pi↱, p↰j) such that (x − li↱) + (l↰j − y) ≤ d. All such breakpoints, (x, y), can be considered as points in a two-dimensional space.
Consider a step in the simulated annealing when primer pi↱ is being added, and we need to compute the change in cost (Fig. 2a). We only need consider breakpoints (x,y), where li < x ≤ li+1. To check if (x,y) was previously covered, we only need to examine the most proximal upstream primer. This suggests a naive algorithm that scales with the length of the opposing region, L, and the amplifiable range of a PCR product, d, yielding a time complexity of O(Ld).
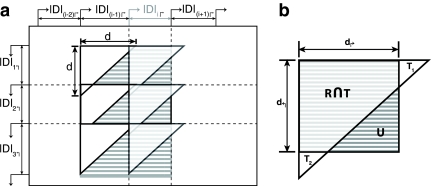
FIG. 2.
Schematic of uncovered breakpoint computation. (a) Diagram of a small primer set in which there are initially 4 forward and 4 reverse primers. An additional forward primer (lightly shaded) is added at position i, which reduces the uncovered space. The difference in uncovered space between p(i −1)↱ to pi↱ is seen as the difference in total shaded area compared to darkly shaded area. (b) Uncovered space for the added primer at a specific reverse pair location, given by the dotted lines in (a). Uncovered breakpoints are the coordinates contained in the rectangle not contained in the triangle. The total number of such breakpoints is given by, |U| = |R − R ∩ T| = |R|− (|T| − |T1|,−|T2|).
To make the computation more efficient, we partition the space into forward intervals Di↱ = (li, l1 + 1), and reverse intervals, using adjacent pairs of forward and reverse primers In Figure 2a, these intervals correspond to regions on the x and y axes, respectively. In adding primer pi↱, coverage is changed only in the forward interval Di↱. The algorithm proceeds by examining rectangles Rij = Di↱ × Dj↰, one for each reverse interval Dj↰. Denote the set of uncovered breakpoints in an arbitrary rectangle, R, as U (ignoring subscripts i and j), as in Figure 2b. Let T denote the total space covered by the corresponding primer pair. Observe that
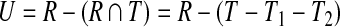 |
where T1,T2 represents portions of T not in R (Note that T1 and T2 can be equal to ∅). Let d↱ = min (|D↱|, d), and d↰ = min (|D↰|, d). Then,
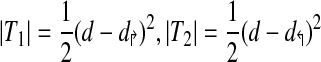 |
This leads to a simple equation for calculating the amount of uncovered space |U|, as
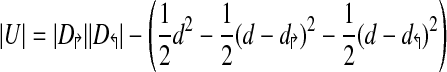 |
This update reduces the time complexity several orders of magnitude to O(n), where n is the total number of opposing primers.
Even so, the update remains expensive to compute, and must be improved further. In adding forward primer pi↱, the set of values d↰j do not change. If for some d↰j, di↱ + d↰j < d, then Di↱ × D↰j is entirely covered. To exploit this, we store all d↱j in a Max-Heap↰, and all di↱ in Max-Heap↱. When considering a forward primer, we scan Max-Heap↰ using a BFS to get all d↰j for which d↰j > = d − di↱, for a total of O(k) steps. If we add the forward primer, we need to make O(1) updates to Max-Heap↱. Total time is O(k) + O(lg n) per iteration. In most cases, there is either very little uncovered space or the uncovered space is relegated to a few specific regions (Fig. 4), implying k << n. When optimizing for coverage and detection, we need to maintain two additional heaps with primer-probe distances, with a slightly more complex algorithm. However, the update time remains the same.
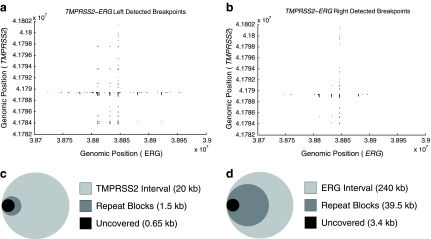
FIG. 4.
Left and right detectability. The shaded regions in (a) and (b) represent all undetected breakpoints (x,y) from the joining of TMPRSS2 and ERG. (a) Left detected breakpoints resulting from fusion of the TMPRSS2-ERG region. (b.) Right detected breakpoints. In both cases, the fraction of undetectable breakpoints is less than 5% of all possible breakpoints. (c, d) Venn diagrams (to scale) showing the overlap of missed regions with highly conserved repeats. The outermost circle represents the entire length of the corresponding axis. The “Repeat Block” shaded area corresponds to the sum of lengths for all repeat regions that are over 75% conserved, continuous (or with <100 bp between conserved repeats), and >500bp in length. “Uncovered” corresponds to any positions in TMPRSS2 (c) and ERG (d) that may be undetected—i.e., y coordinates that appear in shaded regions in (a) and x coordinates in (b), respectively. In both diagrams, “Uncovered” is completely contained within “Repeat Blocks.”
3. Results
We simulated data-sets from two genomic regions that have been implicated in cancers. A homozygous deletion in the CDKN2A region (9p21) is an important genetic marker for multiple cancers. The lesion has been observed in multiple cell-lines and primary tumor samples, including glioblastomas, leukemias, and lung, pancreatic and breast cancers (Rocco and Sidransky, 2001). However, the boundaries of the deletion are known to vary over a large region. Recently, the deletion was assayed and confirmed in 25/54(46%) of adolescent ALL patients (Sasaki et al., 2003). These results are based on array-CGH, which would not detect small deletions, or be useful for early diagnosis when the tumor cells are rare compared to wild-type ones. The observed deletions varied in size from 25kb all the way to the loss of an entire arm (52Mb), with a variety of intermediate sized deletions. The overlap among all specimens was 12.5kb. Thus the CDKN2A region is a prototypical case for PAMP. The second example comes from recently mapped deletions in the TMPRSS2 region (21q22.3), that fuse the 5′ UTR of the TMPRSS2 gene with ETS transcription factors (ERG, ETV1, or ETV4), resulting in over-expression of these genes, and progression of prostate cancer (Tomlins et al., 2005; Wang et al., 2006). The two regions are also good test cases in that the CDKN2A fusing regions are symmetric, while the TMPRSS2 is non-symmetric, and not as amenable to a one-sided cost function.
3.1. Simulations
The detectability achieved varies considerably according to the genomic regions in question. Therefore, we bench-marked the overall performance of Pamp-2D across a spectrum of sequences sizes (10, 50, 100, 200kb) for both the forward and reverse primer regions. For each pair of sizes, 10 corresponding pairs of genomic regions were randomly selected, making 160 unique input sets. Pamp-1D, and Pamp-2D were were run on each of these sets. Figure 3a shows that Pamp-2D is superior to Pamp-1D over all input sample sizes. Much of the improvement is in detection due to the use of alternating multiplexing. However, the performance remains superior to Pamp-1D even when alternating multiplexing is incorporated in Pamp-1D, particularly in non-symmetric regions (Fig. 3b, raw results available in online Supplementary Material at www.liebertonline.com).
The performance of all methods degrades for large regions (≥ 500kb) due to increased dimerizations. To improve detection for these large regions, increased multiplexing is important. Figure 3c shows the improvement observed in transition to an increasing number of multiplexing sets (represented by Δ↱ · Δ↰) for a non-symmetric 500×50kb region. Saturation occurs prior to reaching complete coverage, partially because in some regions it is simply not feasible to add in primers and probes. In this region, we also performed a specific optimization for 50 multiplex sets using the aforementioned PrimerDesign procedure. A symmetric strategy (Δ↱ = 7, Δ↰ = 7) provides only 94% coverage (Fig. 3c). The non-symmetric initial solution (Δ↱ = 22, Δ↰ = 2) provided 97% coverage with a “true” multiplexing level m = 38. Iterating with adjusted values, we achieved 98% coverage with m = 50 (Δ↱ = 11, Δ↰ = 6). A significantly more complex multiplexing strategy could help further improve of coverage and will be explored in future research.
3.2. Left versus right breakpoint detection
Figure 4 shows the results of our design on the TMPRSS2-ERG region (240kb × 20kb), with the obvious conclusion that less than 5% of the breakpoints remain undetected on either side (overall coverage 98%). Interestingly, the figure also differentiates between coverage (amplification), which is symmetric, and detection, which is not. To explain, note that more breakpoints are not detected on the left (ERG) side compared to the right (TMPRSS2). This is largely due to the presence of several large, highly conserved, LINE elements, in ERG introns (corresponding to vertical bands of uncovered breakpoints in Fig. 4a). While it was possible to design primers in these regions, it was nearly impossible to design unique probes. The primers allowed breakpoints to be amplified and right-detected (by TMPRSS2 probes), but not left-detected. In some repetitive regions, it was difficult to even design unique primers. When the sequence is not amplified, neither the left, nor the right end-point is detected, observable as shaded regions at the same breakpoints in Figure 4a, b. Figure 4c, d shows the total length of uncovered sequenced on each axis (1 dimensional) contained within highly-conserved “Repeat Blocks.” We see that as a fraction of the total sequence length, these regions are quite small. In the case of ERG, only a small fraction of total “Repeat Block” space is uncovered. A similar coverage was obtained for CDKN2A region (data not shown).
3.3. Experimental confirmation of CDKN2A
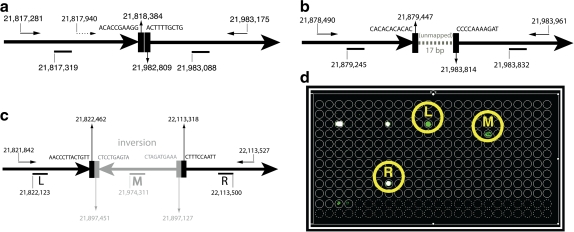
We had previously reported a design for the CDKN2A region, optimized using the single-sided scoring function. The design spanned 600kb, incorporating 600 primers (Bashir et al., 2007). Our Pamp-1D design successfully verified the deletion breakpoint in the Detroit 562 cell-line, but could not detect the lesion in 3 other cell-lines (Molt-4, CEM, and A549). Here, we report positive results on the 3 cell lines using a novel design that includes alternating multiplexing (see Appendix for modifications to experimental design). Note that two of three (CEM and MOLT4) resulted in experimental failure using Pamp-1D designs. In each case, the tests confirmed breakpoint boundaries previously described in the literature (Liu and Carson, 2007; Kitagawa et al., 2002; Sasaki et al., 2003]. See Figure 5 for an overview of the results. Confirmatory sequencing validated the breakpoint boundaries (Fig. 5a–c). Full sequencing results of the amplified primer products can be found in the online supplement.
FIG. 5.
Detecting rearrangements in cell-lines with complex rearrangements. Sequencing results confirming the breakpoint locations in CEM (a), MOLT4 (b), and A549 (c) cell-lines. The presence of multiple forward primers in CEM requires the use of alternating multiplexing. (d) Array results for the A549 cell line. Note that the array not only captures the left and right breakpoints, but also an inserted inversion. The remainder of the spots correspond to nonspecific background signals (corresponding to repeat locations) present across runs.
Note that in the absence of alternating multiplexing, the forward primer at 21,817,940 precludes left-detection of the CEM breakpoint (Fig. 5a). Interestingly, The A549 cell-line has a discontinuous 290kb CDKN2A deletion within which there is an internal 325 bp inversion. The array design successfully captured both left and right breakpoints as well as an internal event (Fig. 5d), indicating that the technique can be successful in detecting breakpoint boundaries even in complex regions with multiple rearrangements.
3.4. Running time
The update operation is critical to the success of Pamp-2D. A naive computation of coverage for an 200× 10kb region requires >0.05 CPU-min per iterations.1 In contrast, our optimized computation runs in <1.5× 10−7 CPU-min per iteration (including both coverage computation and updates). Both tests were run on a 3.4Ghz Pentium 4 with 1 GB RAM. Even so, the designs involve a very complex optimization. The simulations required a total of ∼7000 CPU Hours (ranging from as little as 2 minutes on average for 10×10kb regions to 26 hours for 500×500kb regions).
4. Discussion
Our results provide solid evidence of the feasibility of this approach for early diagnosis of cancer. The alternating primer scheme ensures that all breakpoints that can possibly be detected are detected. This scheme, in the non-dimerizing case, represents the minimal number of multiplexing reactions possible to achieve this optimal breakpoint coverage. We provide the number of multiplexing reactions as a parameter to be chosen by the experimentalist. This allows a trade-off between coverage and experimental cost/complexity. Other important trade-offs can factor into the decision making process. If one simply seeks to determine the presence of a rearrangement, then detection on either side is acceptable. In some cases, it is important to have positional information for both the left and and right breakpoint coordinate. For example, the amplifying primer pair could be used individually in follow-up tests for the individual (thereby, saving cost and making a more reliable assay). Also, the predicted breakpoint can be validated via sequencing or being run on a gel. In both cases, simply amplifying the event is insufficient.
A key point of debate is the choice of relatively older technologies (PCR and hybridization), given the rapid development of new parallel sequencing technologies. To explain our choice, note that there are two facets to our strategy: (a) PCR allows for the amplification of weak signals from the cancer sequence; and (b) oligonucleotide arrays allow for a cost-effective and reliable detection. On the face of it, high-throughput sequencing approaches appear to be a good alternative, as per base, such approaches are cost-effective. However, without amplification one would be primarily sequencing background DNA, not the cancerous signal. An enormous depth of coverage (and therefore cost) would be necessary to ensure detection of a weak cancerous signal. Additionally, once a mutation is detected in the individual, re-sequencing is a costly follow-up, while PAMP returns a custom pair of primers specific to that lesion event.
Second, hybridization yields an unambiguous detection of the PCR amplification. Sequencing could be used in lieu of hybridization to detect PCR-amplified mutants, but this is more challenging than it appears. There is always the possibility of amplifying background DNA (returning to the mispriming problem) or sequencing non-amplified DNA (especially if no true lesion exists). These would not hybridize to the probe, but would confound sequence based analyses and the reconstruction of the breakpoint. Such problems are magnified by artifacts inherent to multiplexing which could lead to several non-specific amplifications in addition to the targeted breakpoint. Moreover, there is a fixed cost (several thousand dollars) for running a single sample, which makes for an expensive early diagnostic, or even regular follow-up exam, to see cancer progression or remission in a single individual, whereas custom arrays are fairly cost-effective.
A significant remaining challenge is that our coverage drops off for larger regions (≥500kb). The primary reason for this is an inherent requirement in our design that each forward primer must be multiplexed with every reverse primer, and therefore cannot dimerize with it. With increased sizes, each forward primer is constrained to not dimerize with many reverse primers, which severely reduces the number of primers, and coverage. One way around this is to use a flexible multiplexing scheme. Subsets of forward primers can be permitted to dimerize with subsets of reverse primers as long as they are never in the same multiplex reaction. While this works in principle, optimizing such designs would require a substantial increase in the total number of primers (as multiple primers spanning the same genomic region would be necessary), the number of multiplexing sets, and the overall experimental complexity. As these approaches move to a more industrial or automated setting, it will become increasingly important to solve these more complex optimization problems.
5. Appendix
5.1. Experimental methods
The microarray procedure followed that of Liu and Carson (2007) with the following modification. Briefly, the 5′-ends of each designed primers have the sequence of primer B (GTTTCCCAGTCACGATC) for the subsequent step of PCR labeling with a single primer B as described previously (Wang et al., 2003; Lu et al., 2008).
5.2. Proofs
Theorem 1 makes 2 assertions, which we will prove independently.
- 1. Let
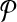 be a design with no dimerizing pairs. Using alternating multiplexing, we detect all detectable breakpoints.
be a design with no dimerizing pairs. Using alternating multiplexing, we detect all detectable breakpoints.
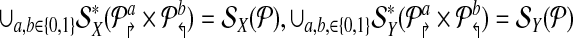
2. Further, if
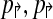 are non-trivial then alternating multiplex yields the minimum number (4) of multiplex reactions necessary to achieve detectability.
are non-trivial then alternating multiplex yields the minimum number (4) of multiplex reactions necessary to achieve detectability.
Proof 1 (by contradiction)
Consider 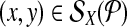 that is not left-detected by the strategy. All other cases are symmetric. By definition of detectability, there exists a proximal (’good’) amplifiable primer pair pi↱, pj↰, with left probe bi↱, such that li↱ < bi↱ < x. The primer is not left-detected only if there exists a (“bad”) primer pk↱ with bi↱ < lk↱ < x < bk↱, which amplifies (x, y) but does not left-detect. Among all good and bad left primers for x, choose the pair (pi↱, pk↱) with the most proximal probes on either side of x. By definition, pi↱, pk↱ are adjacent, and cannot be in the same multiplex reaction, a contradiction.
that is not left-detected by the strategy. All other cases are symmetric. By definition of detectability, there exists a proximal (’good’) amplifiable primer pair pi↱, pj↰, with left probe bi↱, such that li↱ < bi↱ < x. The primer is not left-detected only if there exists a (“bad”) primer pk↱ with bi↱ < lk↱ < x < bk↱, which amplifies (x, y) but does not left-detect. Among all good and bad left primers for x, choose the pair (pi↱, pk↱) with the most proximal probes on either side of x. By definition, pi↱, pk↱ are adjacent, and cannot be in the same multiplex reaction, a contradiction.
2: In a non-trivial forward design 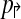 , there exists pair of primers pi↱, pk↱ with 0 < li↱ − lk↱ < d, and bi↱ ≠ bk↱. As primers and probes do not overlap in sequence, we can find a point x with lj↱ < x < bj↱. Consider an arbitrary reverse primer pj↱ and choose y so that bj↰ < y < lj↰. Consider a breakpoint (x,y). When (pi↱, pk↱) are in the same multiplex tube, pi↱, pj↰ gets preferentially amplified, but not left-detected. For left-detection, (pi↱, pk↱) must be in separate multiplex-tubes. An analogous argument can be used for non-trivial design
, there exists pair of primers pi↱, pk↱ with 0 < li↱ − lk↱ < d, and bi↱ ≠ bk↱. As primers and probes do not overlap in sequence, we can find a point x with lj↱ < x < bj↱. Consider an arbitrary reverse primer pj↱ and choose y so that bj↰ < y < lj↰. Consider a breakpoint (x,y). When (pi↱, pk↱) are in the same multiplex tube, pi↱, pj↰ gets preferentially amplified, but not left-detected. For left-detection, (pi↱, pk↱) must be in separate multiplex-tubes. An analogous argument can be used for non-trivial design 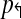 . As the set of forward and reverse primers is partitioned into at least two tubes each, a total of 4 reactions is needed to cover every pair. ▪
. As the set of forward and reverse primers is partitioned into at least two tubes each, a total of 4 reactions is needed to cover every pair. ▪
Proof (Theorem 2)
Brooks' theorem states that a graph can be colored using Δ colors provided Δ ≥ 3, and it is not a complete graph. Consider the primer-dimer-adjacency graph G. By definition, no forward (reverse) vertex has degree greater than Δ↱ (Δ↰). We will impose the constraint that the first and last primer cannot dimerize. Note that this constraint can always be imposed on the primer set by the addition of dummy nodes at the beginning and end, which are adjacent to some primers (and edge-connected), but do not dimerize with any primer. This formulation is outlined in our original optimization (Bashir et al., 2007). Therefore, the graph cannot be either an odd-cycle, or a complete graph, and Brooks' theorem applies. In practice, the graphs are very sparse and we apply the Welsh-Powell algorithm to obtain good colorings. ▪
5.3. Supplementary material
For online Supplementary Material, see www.liebertonline.com.
Footnotes
This represents the largest region for which it was possible to complete even a short test run.
Acknowledgments
V.B. and A.B. were supported by the National Institutes of Health (NIH; grant 5R01HG004962).
This work was also supported in part by NIH grant CA119335 to the UCSD NanoTumor Center of Excellence for Cancer Nanotechnology and CA113634. Computational analysis was supported in part by the UCSD FWGrid Project, NSF Research Infrastructure (grant EIA-0303622). B.J.R. was supported by a Career Award at the Scientific Interface from the Burroughs Wellcome Fund and by funding from the ADVANCE Program at Brown University (under NSF grant 0548311).
Disclosure Statement
No competing financial interests exist.
References
- Bashir A. Liu Y. Raphael B., et al. Optimization of primer design for the detection of variable genomic lesions in cancer. Bioinformatics. 2007;23:2807. doi: 10.1093/bioinformatics/btm390. [DOI] [PubMed] [Google Scholar]
- Bashir A. Volik S. Collins C., et al. Evaluation of paired-end sequencing strategies for detection of genome rearrangements in cancer. PLoS Comput. Biol. 2008;4:4. doi: 10.1371/journal.pcbi.1000051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beigel R. Alon N. Apaydin S., et al. An optimal multiplex PCR protocol for closing gaps in whole genomes. Proc. RECOMB 2001. 2001.
- Brooks R. On colouring the nodes of a network. Proc. Cambridge Phil. Soc. 1941;37:194–197. [Google Scholar]
- Campbell P. Stephens P. Pleasance E., et al. Identification of somatically acquired rearrangements in cancer using genome-wide massively parallel paired-end sequencing. Nat. Genet. 2008;40:722. doi: 10.1038/ng.128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dasgupta B. Jun J. Mandoiu I. Primer selection methods for detection of genomic inversions and deletions via PAMP. Proc. 6th Asia-Pacif. Bioinform. Conf. 2008.
- Fan J. Chee M. Gunderson K., et al. Highly parallel genomic assays. Nat. Rev. Genet. 2006;7:632. doi: 10.1038/nrg1901. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick S. Gelatt C.D. Vecchi M.P. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Kitagawa Y. Inoue K. Sasaki S., et al. Prevalent involvement of illegitimate V (D) J recombination in chromosome 9p21 deletions in lymphoid leukemia. J. Biol. Chem. 2002;277:46289–46297. doi: 10.1074/jbc.M208353200. [DOI] [PubMed] [Google Scholar]
- Lipson D. Technion–Israel Institute of Technology. 2002. Optimization problems in design of oligonucleotides for hybridization-based methods [Master's thesis] [Google Scholar]
- Liu Y. Carson D. A novel approach for determining cancer genomic breakpoints in the presence of normal DNA. PLoS ONE. 2007;2:e380. doi: 10.1371/journal.pone.0000380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Q. Nunez E. Lin C., et al. A sensitive array-based assay for identifying multiple TMPRSS2: ERG fusion gene variants. Nucleic Acids Res. 2008. [DOI] [PMC free article] [PubMed]
- Mitelman F. Johansson B. Mertens F. The impact of translocations and gene fusions on cancer causation. Nat. Rev. Cancer. 2007;7:233–245. doi: 10.1038/nrc2091. [DOI] [PubMed] [Google Scholar]
- Raphael B. Volik S. Yu P., et al. A sequence-based survey of the complex structural organization of tumor genomes. Genome Biol. 2008;9:3. doi: 10.1186/gb-2008-9-3-r59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocco J. Sidransky D. p16 (MTS-1 /CDKN2/INK4a) in cancer progression. Exp. Cell Res. 2001;264:42–55. doi: 10.1006/excr.2000.5149. [DOI] [PubMed] [Google Scholar]
- Ruan Y. Ooi H. Choo S., et al. Fusion transcripts and transcribed retrotransposed loci discovered through comprehensive transcriptome analysis using Paired-End diTags (PETs) Genome Res. 2007;17:828–838. doi: 10.1101/gr.6018607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasaki S. Kitagawa Y. Sekido Y., et al. Molecular processes of chromosome 9p21 deletions in human cancers. Oncogene. 2003;22:3792–3798. doi: 10.1038/sj.onc.1206589. [DOI] [PubMed] [Google Scholar]
- Tomlins S. Rhodes D. Perner S., et al. Recurrent fusion of TMPRSS2 and ETS transcription factor genes in prostate cancer. Science. 2005;310:644–648. doi: 10.1126/science.1117679. [DOI] [PubMed] [Google Scholar]
- Wang D. Urisman A. Liu Y., et al. Viral discovery and sequence recovery using DNA microarrays. PLoS Biol. 2003;1:E2. doi: 10.1371/journal.pbio.0000002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J. Cai Y. Ren C., et al. Expression of variant TMPRSS2/ERG fusion messenger RNAs is associated with aggressive prostate cancer. Cancer Res. 2006;66:8347–8351. doi: 10.1158/0008-5472.CAN-06-1966. [DOI] [PubMed] [Google Scholar]
- Welsh D. Powell M. An upper bound for the chromatic number of a graph and its application to timetabling problems. Comput. J. 1967;10:85–86. [Google Scholar]