HYDROGEN-BOND ENERGETICS DRIVE HELIX FORMATION IN MEMBRANE INTERFACES

Abstract

The free energy cost ΔG of partitioning many unfolded peptides into membrane interfaces is unfavorable due to the cost of partitioning backbone peptide bonds. The partitioning cost is dramatically reduced if the peptide bonds participate in hydrogen bonds. The reduced cost underlies secondary structure formation by amphiphilic peptides partitioned into membrane interfaces through a process referred to as partitioning-folding coupling. This coupling is characterized by the free energy reduction per residue, ΔG_res that drives folding. There is some debate about the correct value of ΔG_res and its dependence on the hydrophobic moment (μ_H) of amphiphilic α-helical peptides. We show how to compute ΔG_res correctly. Using published data for two families of peptides with different hydrophobic moments and charges, we find that ΔG_res does not depend upon μ_H. The best estimate of ΔG_res is −0.37±0.02 kcal mol⁻¹.

1. INTRODUCTION

In the absence of secondary structure formation, the free energy cost ΔG of partitioning unfolded peptides into membrane interfaces is unfavorable due to the cost of partitioning backbone peptide bonds. But if the peptide bonds participate in hydrogen bonds, the cost of partitioning is dramatically reduced [1, 2]. This reduction underlies secondary structure formation by hydrophobic and amphiphilic peptides partitioned into membrane interfaces. This process, partitioning-folding coupling, can be characterized by the free energy reduction per residue, ΔG_res, that drives folding. There is some debate about the correct value of ΔG_res; values of −0.14 to −0.28 kcal mol⁻¹ have been reported by Seelig and coworkers [3–5], −0.25 kcal mol⁻¹ by Li et al. [6], −0.4 kcal mol⁻¹ by Ladokhin and White [2], and −0.5 kcal mol⁻¹ by Wimley et al. [1]. Collectively, these modest values can dramatically improve the partitioning free energies (ΔΔG) of peptides, because ΔΔG ≈ NΔG_res where N is the number of residues that adopt regular secondary structure. For example, if N = 10, the portioning free energy of a peptide would be improved by 2.5 to 5 kcal mol⁻¹. The hydrophobic moment (μ_H) of amphiphilic α-helical peptides is also important in partitioning-folding coupling, because the helicities of peptides on the membrane and in solution increase with μ_H [7]. This raises the question, addressed here, of the connection between μ_H and ΔG_res.

Fernández-Vidal et al. [7] carried out a systematic study of the effect of μ_H on the partitioning and folding of a family of 17-residue peptides that differed in sequence but not in amino acid composition (Ac-A₈Q₃L₄-GW-NH₂). The sequences of the family members of the ‘AQL’ peptides were chosen to cover a 10-fold range of hydrophobic moments (μ_H varied from 0.55 to 5.54). Because all of the sequences have the same total hydrophobicity, variations in ΔG must arise solely from differences in ΔG_res. The analysis presented by Fernández-Vidal et al. [7] suggested that the magnitude of ΔG_res increased linearly with μ_H from −0.1 to −0.3 kcal mol⁻¹ as μ_H increased from 0.55 to 5.54. We revisit this analysis in this paper and show that in fact ΔG_res is independent of μ_H. The corrected value of ΔG_res combined with new results from measurements on the partitioning-folding of transportan 10 (TP10) cell-penetrating peptides [8] support the conclusion that the best “typical” value of ΔG_res for practical estimations is about −0.4 kcal mol⁻¹ [2].

2. THERMODYNAMIC ANALYSIS OF PARTITIONING-FOLDING COUPLING

The thermodynamic cycle for computing free energy changes is shown in Figure 1. State A is the fully unfolded peptide in water, B is the fully unfolded peptide in the membrane interface, C is the peptide in water, and D is the folded peptide in the membrane interface. State C is actually an ensemble of folded and unfolded conformations. State D may also represent an ensemble of folded and unfolded peptides, but few data are available that bear on this issue. The folded conformation in the interface is not generally fully helical. By folded, we mean peptide states with the average helicities determined experimentally.

Figure 1.

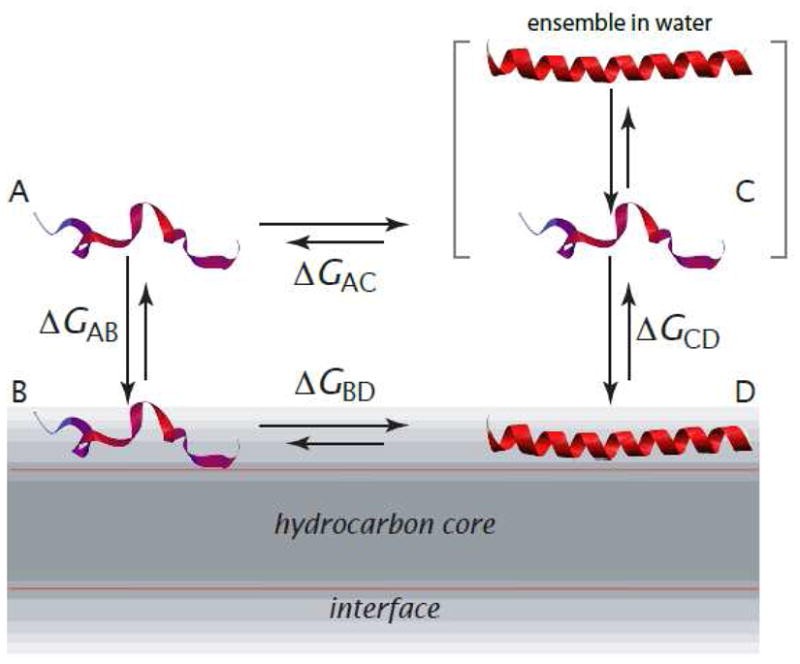
Thermodynamic cycle for partitioning-folding of an α-helical peptide in the membrane interface (modified from [7]). State A is the fully unfolded peptide in water; B is the fully unfolded peptide in the interface; C is the actual state of peptide in water, which is an ensemble of folded and unfolded conformations; and state D is the peptide in a α-helical conformation partitioned into the membrane interface. The conformation is not necessarily, and usually isn’t, fully α-helical. States A and B are virtual states that cannot be observed experimentally due to their low occupancy. The free-energy difference, ΔG_AB, is computed using the experiment-based algorithm of Hristova and White [10]. The other free-energy differences are determined experimentally (Figure 2).

State A is a hypothetical state, because peptides in aqueous solution usually have some, even if small, amounts helical structure. We choose state A as the reference state, because it is the simplest and most convenient option. Imagine that we place the unfolded peptide in water, but somehow do not allow it to fold. This is the reference state, on the top left corner of the thermodynamic cycle. Then imagine that we remove this fictitious constraint, allowing the peptide to fold, which allows an equilibrium between unfolded and folded conformations to be established. The establishment of this equilibrium necessarily follows a reduction of free energy until the minimum is reached.

Given that A is experimentally inaccessible, why is it a convenient reference state? Although A is a hypothetical state, ΔG_AB can be calculated from the Wimley-White interfacial hydrophobicity scale [9] using the algorithm of Hristova and White [10], which has been validated using indolicidin [11–15] mutants that do not adopt regular secondary structure [15]. Because C and D are the actual states in solution and on the membrane, ΔG_CD is obtained from experimental measurements of interfacial partitioning. The possibility that an ensemble may also exist on the membrane surface is discussed later. The Gibbs free energy of the peptide in solution, relative to the unfolded reference state A, ΔG_AC, can be determined experimentally by circular dichroism (CD) spectroscopy (see Fernández-Vidal et al. [7] for helicity values). The free energy for folding on the membrane, ΔG_BD is obtained by closing the thermodynamic cycle.

The calculation of ΔG_AC is the most subtle part of the analysis, but is made simpler under the two-state approximation [16], which was not used by Fernández-Vidal et al. [7]. An equilibrium constant K_α is defined between the folded (α) and unfolded (u) conformations in solution by K_α = f_α/(1 − f_α), where f_α is the fraction of helical and f_u = (1 − f_α) is the fraction of unfolded peptide. The Gibbs free energy difference between the folded and unfolded conformations is given by ΔG_α = −RTlnK_α. However, ΔG_α ≠ ΔG_AC , because state C is not the folded conformation, but an ensemble. (Fernández-Vidal et al. [7] mistakenly assumed ΔG_AC = ΔG_α.)

The two-state approximation assumes that the ensemble of states that exist in aqueous solution (state C) consists only of the fully folded and the fully unfolded peptide conformations in equilibrium with each other. The Gibbs free energy of the fully-helical peptide in solution can be obtained from f_α, which is the fraction of helical peptide determined experimentally by CD spectroscopy, for example. Fernández-Vidal et al. [7] demonstrated that an isodichroic point exists in solution when the helical content is increased by addition of trifluoroethanol. This observation supports the correctness of the two-state approximation in water. The essential concept behind the calculation of ΔG_AC under the two-state approximation is that state C is a mixture of folded and unfolded conformations. To calculate ΔG_AC, one writes the partition function for the peptide in water under the two-state approximation as the sum of the statistical weights (or relative probabilities) of all accessible states [16, 17]. With the unfolded state in water as the reference, the partition function can be written as Q = (1 + K_α), where the statistical weight of the unfolded conformation is 1, and the statistical weight of the helical conformation (relative to the unfolded state) is the equilibrium constant Kα. The Gibbs free energy change of going from the unfolded state to the mixture of helical and unfolded conformations at equilibrium is thus ΔG_AC = −RTln(1 + K_α). This makes sense, because the accessibility of a new state (the helical conformation in this case) can never increase the free energy of the ensemble, but only decrease it. Thus, the Gibbs energy of the actual ensemble of peptide conformations in aqueous solution is lower than the Gibbs energy of the unfolded state alone.

The Gibbs energy of membrane partitioning of the peptide, represented by ΔG_CD, can be obtained experimentally as a long a suitable difference in an observable property exists between the peptide states in solution and on the membrane. Several standard equilibrium techniques include equilibrium dialysis, calorimetry, fluorescence, and CD [18]. In addition, the dissociation constant can be obtained from the on- and off-rate constants determined by stopped-flow fluorescence, for example, as the ratio K_D = k_off/k_on [8, 19].

In principle, the free energy of folding in the membrane interface (ΔG_BD) should follow the same rules as folding in solution (ΔG_AC), which implies that state D should be considered as an ensemble. However, the assumption is generally made that state D consists of peptides having a single well defined helicity, i.e., the helicity measured on the membrane represents the mean value of a relatively narrow distribution. Is this assumption correct? To distinguish between an ensemble of conformations and a single conformation experimentally, one would have to perform an unfolding/folding experiment for peptides in the interface just as was done for peptides in the aqueous phase. As far as we can establish, such an experiment has never been done for any peptide. Furthermore, it is not clear that an on-membrane titration experiment is even feasible. We therefore assume for the present that the measured helicity of the peptide in the interface represents the mean of a very narrow distribution.

3. ANALYSIS AND INTERPRETATION OF EXPERIMENTAL DATA

The most extensive data available to calculate the different branches of the thermodynamic cycle for partitioning into palmitoyloleoylphosphocholine (POPC) bilayers are those on the AQL peptide variants of Fernández-Vidal et al. [7]. Analysis of these data shows that folding to a helix on the membrane (ΔG_BD) and in solution (ΔG_AC) increases linearly with the hydrophobic moment (Fig.2A,C). This suggests that the propensity to form a helix is determined in part by the hydrophobic moment of the full helix. Furthermore, binding of the AQL peptides to the membrane (ΔG_CD) also increases linearly with the hydrophobic moment (Fig. 2B).

Figure 2.

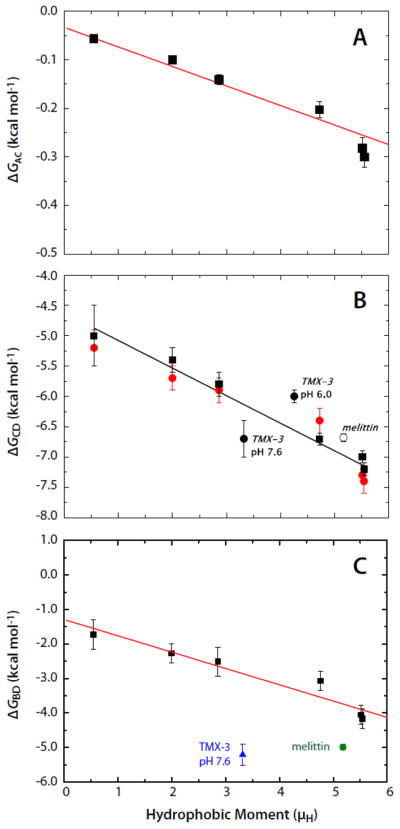
The Gibbs free-energy differences for the AQL family of peptides as a function of hydrophobic moment (μ_H) determined from the data of Fernández-Vidal et al. [7]. Panels A, B, and C show, respectively, the μ_H-dependence of ΔG_AC, ΔG_CD, and ΔG_BD. The free energy differences are defined in Figure 1. Included in the panels B and C are free energy values for 26-residue melittin [20] and the 31-residue designed peptide TMX-3 at pH 7.6 [21]. The lipid bilayers used were POPC LUV (solid squares) in panels A and C. In panel B, in addition to data for partitioning into POPC LUV (solid squares) data are also presented for partitioning into 1:1 POPC:POPG LUV (solid red circles). The data of panel B, replotted from [7], show that partitioning of the neutral AQL peptides is not affected by the presence of charged (anionic) lipids. Also included in panel B are data for melittin (open circle) and TMX-3 at pH 7.6 and pH 6.0 (solid circles). The data of panel C are calculated from experimental data in panels A and B and the theoretical estimate for ΔG_AB illustrated in Figure 1.

We are now in a position to answer the question of whether this binding enhancement is a direct result of the hydrophobic moment of the helix or of the formation of polypeptide backbone hydrogen bonds in the membrane interface. From the data of Figure 2, we first find that the total free energy decrease upon folding on the membrane is ΔG_BD = ΔG_AC + ΔG_CD − ΔG_AB. The free energy reduction per helical residue is thus obtained from ΔG_res = ΔG_BD/Nf_α, where N is the number of residues and f_α is the fractional helicity on the membrane. The AQL peptides have N = 17 residues. The results, plotted in Figure 3, show that ΔG_res is independent of μ_H and equal to −0.328±0.013 (SEM) kcal mol⁻¹. A similar analysis can be carried out for the TP10 peptide family whose helicities and free energies of partitioning into POPC, determined by McKeown et al. [8], yield a value of −0.434±0.014 kcal mol⁻¹. Unlike the AQL peptides, the TP10 peptides have charged residues, which may explain the slightly higher values for TP10. Values of ΔG_res for the TP10 family are included in Figure 3 along with values for 26-residue melittin and the 31-residue designed peptide TMX-3 whose partitioning free energies and helicities have determined by Ladokhin and colleagues [20–22]. The weighted average of ΔG_res for the AQL and TP10 peptides is −0.37±0.02 kcal mol⁻¹. If melittin and TMX-3 are also included, the weighted average for ΔG_res is −0.35±0.02 kcal mol⁻¹. The data, overall, are consistent with G_res being independent of μ_H. The value for ΔG_res of −0.41±0.06 determined by Ladokhin and White using diastereomeric melittin [2] agrees with these weighted averages within experimental error. As first noted by Wimley et al. [1], partitioning-folding coupling is driven by the reduction in the free energy ΔG_hb that accompanies hydrogen bonding of peptide bonds. From the data analysis presented here, ΔG_hb can be taken as ΔG_res.

Figure 3.

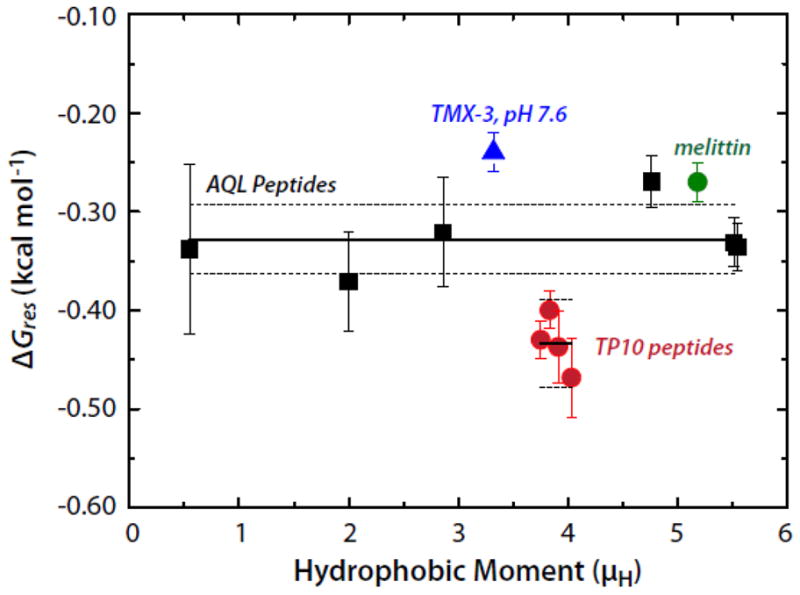
The per-residue free energies of folding (ΔG_res) of several peptides in the POPC membrane interface plotted as a function of the hydrophobic moment (μ_H). The Gibbs free energy of helix formation in the membrane interface as a function of hydrophobic moment for the AQL (solid black squares) and TP10 (solid red circles) families of peptides. Data for melittin and TMX-3 are shown as well (solid green circle and solid blue triangle, respectively). The solid and dotted lines superimposed on the AQL and TP10 data points represent the means and the standard errors of the means (SEMs), respectively. The mean ± SEM for AQL is −0.328±0.013 kcal mol⁻¹; the values for the TP10 peptides are -0.434±0.014 kcal mol⁻¹. The weighted mean of the AQL and TP10 data is −0.37±0.02 kcal mol⁻¹. The values of ΔG_res for the TP10 peptides were computed using the free energies and helicities reported by McKeown et al. [8].

4. DISCUSSION

If the solution state of the peptides were assumed folded instead of the real state of the peptide in solution, which is an equilibrium ensemble of folded and unfolded peptides, a significant error results in the calculation of ΔG_BD. Failure to recognize that ΔG_AC is very different (much smaller in absolute value) from ΔGα, the free energy difference between folded and unfolded states in solution, led Fernández-Vidal et al. [7] to a calculation of the ΔG_res that appeared to indicate a direct contribution of the hydrophobic moment to the free energy of folding in the membrane interface in addition to its contribution due to enhance helicity, which we now see is not correct.

If the peptide is assumed to be completely unfolded in solution, as has been done previously [8, 19, 23], only a small error is incurred. For example, if the peptide is 10% helical in aqueous buffer (K_α = 0.11), but is assumed completely unfolded, the correct ΔG_AC = −RTln(1 + K_α) = −0.06 kcal mol⁻¹ at room temperature; the assumption that it is fully unfolded would amount to setting ΔG_AC = 0. If a peptide is 50% helical in water (K_α = 1)—which is rare for these types of peptides—then the correct value of ΔG_AC would be −0.4 kcal mol⁻¹. If the peptide is assumed to be completely unfolded in solution, and the thermodynamic cycle of Figure 1 is completed using an experimental measurement of G_CD, this procedure results in the underestimation of the absolute value of ΔG_BD (which is negative) by 0.06 to 0.4 kcal mol⁻¹ for peptides that are actually 10 to 50% helical, respectively, in aqueous buffer. This is a very small error, well within the range of the uncertainty in the experimental values of the Gibbs energy of folding (ΔG_CD).

According to the Wimley-White interfacial hydrophobicity scale [9, 10, 24], partitioning of an unfolded amphipathic peptide to the surface of a zwitterionic lipid bilayer, specifically POPC, is very weak. Low partitioning agrees entirely with the experiments on amphipathic peptides of Fernández-Vidal et al. [7] and studies of diastereomeric melittin [2], which cannot readily fold into a helix. As far as we can establish, except in the cases of small peptides with very atypical compositions, such as tryptophan-rich peptides (indolicidin [13–15], for example), no significant binding of unfolded peptides to membranes has been measured in the absence of Coulombic interactions. Essentially, the favorable Gibbs free energy of transfer from water to the membrane interface due to the hydrophobic effect is overridden by the unfavorable contributions of the polar residues and backbone amide groups. Therefore, peptides only bind significantly to the membrane if binding is coupled with folding to a helix (or other hydrogen-bonded structures) that reduces the cost of partitioning backbone amide groups.

From the analysis of the data for the AQL peptides, it is clear that ΔG_res does not directly depend the hydrophobic moment μ_H. Therefore, μ_H must exert its influence on the Gibbs free energy of by increasing the probability of helix formation in solution and in the interface, as observed by Fernández-Vidal et al. [7]. Mean values of ΔG_res obtained from two very different sets of peptides, the AQL and TP10 families, differ by only 0.1 kcal mol⁻¹ per helical residue. The weighted average of the two data sets two sets, −0.37±0.02 kcal mol⁻¹, is probably the best current estimate that we can provide for the Gibbs free energy contribution to binding resulting from the formation of a peptide hydrogen bonds in the membrane interface. This value falls well within the experimental uncertainty of the value of −0.4 kcal mol⁻¹ originally suggested by Ladokhin and White [2], which is the default value used in Membrane Protein Explorer (MPEx) [25]. The agreement with the present analysis is probably because the Ladokhin and White experiment [2] was based on a differential measurement of the helicities of L-melittin and D₄L-melittin, which has the inherent advantage of canceling out minor (often unknown) effects.

Although ΔG_res ≈ −0.4 kcal mol⁻¹ by itself is a modest number, one must remember that it is the collective effect of H-bond formation that ultimately drives folding and partitioning. This is illustrated by the increase in helicity of L-melittin compared to D₄L-melittin; L-melittin has 12 additional α-helical residues, which translates into an improvement in partitioning free energy of 4.8 kcal mol⁻¹ [2].

That there is some variability of ΔG_res between peptide families is not surprising, because different peptides probably lie somewhat differently in the interface, and therefore sense slightly different environments. Peptides of one family may sink deeper in the interface than those of another, for example. The nature of the hydrophobic effect in the complex interface [26–28] may be responsible for differences. Schow et al. [29] have discussed this issue and concluded that in the phospholipid bilayer interface the state of the water in that complex environment likely determines the apparent solvation parameter for partitioning, which is only about 50% of the value for partitioning non-polar solutes between water and non-polar bulk phases [24].

Highlights.

• Partitioning of unfolded peptides to the membrane interface is generally unfavorable

• Helix formation reduces the partitioning free energy by ΔG_res per residue

• ΔG_res is independent of the hydrophobic moment of amphipathic α-helical peptides

• ΔG_res is ascribed to formation of backbone hydrogen bonds

• The best estimate Delta;G_res is −0.37±0.02 (SEM) kcal mol⁻¹