Predicting Extreme pKa Shifts in Staphylococcal Nuclease Mutants with Constant pH Molecular Dynamics

Abstract

Accurate computational methods of determining protein and nucleic acid pKa values are vital to understanding pH-dependent processes in biological systems. In this paper we use the recently developed method constant pH molecular dynamics (CPHMD) to explore the calculation of highly-perturbed pKa values in variants of staphylococcal nuclease (SNase). Simulations were performed using the replica exchange (REX) protocol for improved conformational sampling with eight temperature windows, and yielded converged proton populations in a total sampling time of 4 ns. Our REX-CPHMD simulations resulted in calculated pKa values with an average unsigned error (AUE) of 0.75 pK units for the acidic residues in Δ+PHS, a hyperstable variant of SNase. For highly pKa-perturbed SNase mutants with known crystal structures, our calculations yielded an AUE of 1.5 pK units and for those mutants based on modeled structures an AUE of 1.4 pK units was found. Although a systematic underestimate of pK shifts was observed in most of the cases for the highly perturbed pK mutants, correlations between conformational rearrangement and plasticity associated with the mutation and error in pKa prediction was not evident in the data. This study further extends the scope of electrostatic environments explored using the REX-CPHMD methodology and suggests it is a reliable tool for rapidly characterizing ionizable amino acids within proteins even when modeled structures are employed.

Introduction

Stability and function of many proteins and nucleic acids are dependent on the charge of titratable residues. Changes in the protonation state of these residues have the potential to trigger significant configurational variation. Some examples include the proton-gradient in mitochondria, which enables the rotary motion of ATP synthetase for virtually all known metabolizing life forms.^1,2 Additionally, the catalytic mechanisms of numerous enzymes are driven by locally perturbed protonation equilibria at the active site.³ Furthermore, amyloidogenic protein aggregation into oligomers is a pH driven process, demonstrating the role of ionization states in protein function.^4,5 In order to study these biological mechanisms, it is crucial to understand how they are dependent on the ionization states of their amino acid residues.

Understanding these phenomena requires a system that describes the complex coupling between structure, chemical composition and proton affinities as a function of proton concentration (pH). Residue specific pKa values provide a framework from which to begin to provide quantitative relationships among the above noted properties. However, the pKa of a particular site and its tendency to ionize or accept a proton is highly responsive to the surrounding solvent environment as well as to charge-dipole and charge-charge interactions.^6–8 These in turn alter the specific tendency for that residue to change its ionization state, i.e., its pKa. For extreme cases, such as aspartic acid-96 in bacteriorhodopsin, the measured perturbation is at least 8.0 pK units greater than that of the isolated amino acid in pure water.³ This creates a need for measuring the relative amino acid pKa perturbations in a folded protein. Determining these experimentally, however, is nontrivial, though possible through a range of techniques.⁹

Experimentally investigating pKa values involves titrating a species over a wide range of pH.⁹ Most biologically functional proteins, however, are natively folded only within a very narrow pH range. Outside of these native conditions they often adopt non-native, denatured, or unfolded conformations. Since the pKa values of an ionizable residue is highly dependent on its interactions with solvent and surrounding protein tertiary structures, titrating a protein to pH values outside of this range may not provide pKa values relevant to its natively folded configuration.⁷ To aid in both the calculation and interpretation of such experiments, theoretical tools have been developed to make pKa predictions based on knowledge of the native protein structure. For many proteins, a reliable method of experimentally determining residue-specific pKa values is either too cost prohibitive, or infeasible. Before such experimental methods become viable, computational tools are the only means available for studying their pKa values.^7,8

The theoretical framework and computational methods to predict pKa shifts in large molecules can be divided into three basic approaches: finite difference Poisson-Boltzmann based continuum electrostatics methods, empirical methods, and molecular dynamics coupled with explicit free energy estimates using explicit solvent or implicit solvent (generalized Born continuum electrostatics) methods. Empirical methods, such as PROPKA,^10,11 are based upon empirical algorithms that relate structural metrics to pKa perturbation. Provided with sufficient relevant experimental data and an accurate structure of a protein, this method has been shown to yield predictions within 1 pKa unit root-mean-squared deviation (RMSD) from experimental observation. This level of agreement with experimental pKa values shows that the corresponding link between structural metrics and pKa shifts is an important tool in understanding the electrostatic environments of proteins. Empirical methods, however, cannot be used to determine pKa values without both extensive experimental data and a high-resolution protein structure.¹¹ Poisson-Boltzmann equation based methods, such as MCCE^12,13 and MEAD^14,15 calculate the macroscopic electrostatic effects of ion-ion and ion-dipolar interactions, such as between a titrating site and polar solvent molecules given the dielectric response of the protein interior. Provided with a high-resolution crystal structure, they offer predictions within 1 pKa unit root-mean-square deviation (RMSD) for residues with relatively high solvent exposure. Since the accuracy of this method is directly related to solvent interactions, it often leads to inaccurate predictions when the target titrating residue has little macroscopic solvent interaction, or if the target site’s pKa is significantly altered by conformation.¹⁶ In order to explore poorly understood protein systems, relatively more brute-force methods using molecular dynamics (MD) with simulated titration may be necessary.

MD simulations can derive information from virtually any protein system as long as atomic interactions can be parameterized into a consistent force field and explicit coordinates can be defined.^7,8 This provides the potential for MD based methods to estimate residue pKa values of lower-resolution or even partially solved structures. Calculating pKa then relies upon parameterizing the solvent model. The effective Born radii of individual residues may be calculated from the shape of the protein’s solvent exposure, and from that information ionization energies may be calculated. In comparative tests, MD based methods consistently provide more accurate pKa estimates over a wider variety of protein residues and environments than other computational methods.^7,8

There are two dominant approaches available for the inclusion of titrating sites in MD based pKa calculation methods: discrete and continuous. Discrete methods titrate residues using Monte Carlo (MC) sampling, which allow protons to be added and deleted from amino acids.¹⁷ However, recurring instantaneous switches of protonation states by adding or deleting the protons result in discontinuities of energy and force calculations. Additionally, only one proton addition or deletion move is made during a MC step, which contributes to slower convergence for systems with many ionizable groups.¹⁷ Nevertheless, discrete protonation state methods coupled with molecular dynamics have proven to be useful in exploring pKa values of proteins.¹⁸

Continuous methods by definition allow a gradual change in the “titration” coordinates during the MD simulation. This permits continuous energy and force calculations, yields greater sampling rates, and enables the titration of multiple sites simultaneously. The accuracy and efficiency of continuous dynamical methods make them a useful methodology for studying many proteins.^7,8,19

In this paper we utilize a recently developed continuous method called Constant pH Molecular Dynamics (CPHMD).^6,20 It is a component of the CHARMM simulation and modeling package²¹ and employs a variant of the λ dynamics methodology in CHARMM^22,23 and the generalized Born with simple switching (GBSW) implicit solvent model to mimic the effects of the solvent environment^24,25 with continuous atomic trajectories.²⁶ The dynamics of the titration coordinates for ionizable residues is characterized by as many as two continuous coordinates for each ionizable amino acid in the form (λ, x). The variable λ corresponds to the protonation state of the residue and x controls of the interconversion between tautomeric states.⁶ For single site titrations, such as the atom NZ in lysine, x is unnecessary since there are no tautomerers. Residues with multiple protonation sites such as aspartic acid are defined with three states, (λ=1) for the deprotonated, (λ=0, x=1) for the OD1-protonated state, and (λ=0, x=0) for the OD2-protonated state. By simulating protonation in this manner, pKa predictions are made with both rapid convergence and accurate predictions to within 1.0 pK units.^6,7,20

CPHMD has been successfully employed in the prediction of the pKa values of amino acids both in small peptides and in proteins. Recently Khandogin and colleagues demonstrated CPHMD’s accuracy on turkey ovomucoid third domain and bovine pancreatic ribonuclease A, by predicting experimental pKa values within 0.6 to 1.0 pK units, respectively.⁶ Although their simulations verified CPHMD’s ability to provide accurate pKa estimates of ionizable side chains, almost all protein residues included in this study had relatively small pKa perturbations of several pK units or less. Considering the earlier example of aspartic acid-96 in bacteriorhodopsin, a perturbation of several units represents a narrow range of possible pKa values for protein residues. In pursuit of computational methods to address these highly perturbed electrostatic environments, the methods must be able to calculate the pKa of titrating amino acids regardless of the size of the perturbation. Therefore, it is necessary to test CPHMD in predicting highly perturbed pKa values for biologically relevant systems. Staphylococcal Nuclease (SNase) represents an ideal example of such a system, because it has both decades of folding and structural research and a variety of hyperstable mutants, including many with highly perturbed pKa values.^27–30

SNase is a relatively small protein consisting of a single polypeptide chain of 149 amino acids with no disulfide bonds. Its simple structure, prevalence in nature, and lack of chaperon-assisted folding to achieve its native fold have made it a model system for studying protein folding, point mutations, and the role of amino acids in protein function. Using site-directed mutagenesis, the various roles of residues in SNase’s stability and folding pathway have been discovered, leading to a thorough understanding of the protein.^30–33 Putting theory into practice, this information was used to develop a hyperstable variant of SNase, known as Δ+PHS. This variant has five point mutations (G50F, V51N, P117G, H124L, and S128A) and a truncation (residues 44–49).³⁰ It is extraordinary in its ability to remain in its native conformation both over a broad range of pH and temperature, and when subjected to additional point mutations.^27,30 This resilience enables all its ionizing residues to be titrated experimentally, even with the introduction of hydrophilic residues into the protein’s hydrophobic core.^27,30

In previous work by Garcia-Moreno et al., the conformational role of aspartic and glutamic acids in Δ+PHS were studied in detail.³⁰ All such residues were titrated for pKa calculations by measuring the pH dependence of the chemical shifts of Cγ or Cδ with two-dimensional HBHC(CBCG)CO experiments.³⁰ These results are summarized in Table 1 under “experimental pKa”. Additionally, 27 point-mutation variants of Δ+PHS (2 aspartic acids and 25 glutamic acids) were successfully created. Each variant was titrated to measure the pKa at the mutation site by analyzing the pH correlation with changes in Gibbs free energy of unfolding (ΔΔG°_H2O) with GdnHCl as a denaturant. These results are given in Tables 2 and 3 under “experimental pKa”.²⁷ These experiments provide a comprehensive quantification of the changes of internal energy within Δ+PHS in relation to introducing a hydrophilic residue into the hydrophobic core of the protein. The shielding effect of the surrounding hydrophobic amino acids greatly reduces solvent interactions with the glutamic and aspartic acid mutations, and consequently perturbs their pKa values by as much as 5 pK units. The measured perturbation in pKa values for these systems provides an experimental basis for testing and comparing the accuracy of CPHMD simulations in the calculation of highly perturbed pKa values of these acidic side chains.

Table 1.

Observed versus calculated pKa values in ∆+PHS. pKa values for residues beyond 141 were not reported here, because their coordinates are not solved in most of the crystal structures used during this study. This includes the 3BDC structure used to calculate the data for this table.

Residue	Experimental pKa32	Calculated pKa	Error (CPHMD)	Error (Null Model)
Asp-19	2.2	3.8	1.6	1.7
Asp-21	6.5	5.4	−1.1	−2.7
Asp-40	3.9	2.0	−1.8	0.0
Asp-77	<2.2	0.8	COR	<−1.7
Asp-83	<2.2	3.8	COR	<−1.7
Asp-95	2.2	3.4	1.3	1.7
Glu-10	2.8	3.3	0.5	1.3
Glu-43	4.3	3.8	−0.6	−0.2
Glu-52	3.9	4.9	1.0	0.2
Glu-57	3.5	4.4	0.9	0.6
Glu-67	3.8	3.6	−0.1	0.3
Glu-73	3.3	2.4	−0.9	0.8
Glu-75	3.3	4.9	1.6	0.8
Glu-101	3.8	3.5	0.3	0.3
Glu-122	3.9	4.7	0.8	0.2
Glu-129	3.8	4.4	0.7	0.4
Glu-135	3.8	4.4	0.7	0.3

Table 2.

Observed versus calculated pKa values for buried charge mutants of ∆+PHS with crystallographically determined structures. RMSD are in Angstroms.

PDB	Mutation	Experimental pKa27	Calculate d pKa	Error (CPHMD)	Error (Null Model)	RMSD (Å)
3H6M	V104E	9.4	7.6	−1.8	−5.3	1.3491
1TR5	I92E	9.0	6.8	−2.2	−4.9	1.3903
1TQO	I92E	9.0	7.3	−1.7	−4.9	1.4413
3EVQ	L25E	7.5	8.4	0.9	−3.4	1.2621
3ERO	I72E	7.3	6.8	−0.5	−3.2	1.1948
3D4D	Y91E	7.1	5.5	−1.6	−3.0	1.3142

Table 3.

Observed versus calculated pKa values for buried charge mutants of ∆+PHS where mutations were modeled.

Mutation	Experimental pKa27	Calculated pKa	Error (CPHMD)	Error (Null Model)	RMSD (Å)
L125E	9.1	6.8	−2.3	−5.0	1.2716
L103E	8.9	7.4	−1.6	−4.8	1.3857
L36E	8.7	7.1	−1.6	−4.6	1.2542
V66E	8.5	6.4	−2.1	−4.4	1.2862
V99E	8.4	7.2	−1.2	−4.3	1.2762
V39E	8.2	4.6	−3.7	−4.1	1.4638
A109E	7.9	4.4	−3.5	−3.8	1.3753
V74E	7.8	8.4	0.6	−3.7	1.2469
A58E	7.7	5.2	−2.5	−3.6	1.3959
T62E	7.7	6.9	−0.8	−3.6	1.2945
N100E	7.6	5.8	−1.8	−3.5	1.3650
F34E	7.3	7.3	0.0	−3.2	1.1966
V23E	7.1	7.0	−0.1	−3.0	1.2704
A132E	7.0	6.5	−0.5	−2.9	1.3416
L38E	6.8	6.3	−0.5	−2.7	1.1974
T41E	6.8	6.5	−0.3	−2.7	1.3341
A90E	6.4	6.7	0.3	−2.3	1.4063
L37E	5.2	6.2	1.0	−1.1	1.1912
G20E	4.5	5.5	1.0	−0.4	1.3533
N118E	4.5	2.5	−2.0	−0.4	1.2462

The calculations we present below provide a significant test of the robustness of CPHMD predictions of pKa. We consider four sets of calculations for glutamic acid (GLU) and aspartic acid (ASP) residues in Δ+PHS: (1) predicting the pKa values for each GLU and ASP in the Δ+PHS structure, (2) the value of each point mutation for proteins with solved crystal structures, (3) those of each point mutation without crystallographically determined structures, and (4) and calculating the pKa values of specific residues in systems similar to Δ+PHS. The first set of calculations confirms that our computational methods can accurately predict the pKa values for this protein. The second and third studies explore the accuracy of pKa calculations for proteins of less understood systems. The last set of calculations investigates the use of similar crystal structures to study a target system. For mutants without solved structures, structures of the mutant proteins were built in CHARMM by mutating the Δ+PHS structure. The computational results are compared with NMR titrations to establish the overall quality and capability of CPHMD pKa predictions over a range of perturbed pKa systems. It should be noted that this protocol was not a blind study. The calculations within this paper were carried out over the course of two years, which both preceded and followed the release of the measured pKa values of SNase and Δ+PHS. This study represents an ongoing effort to assess the accuracy of the REX-CPHMD process during its development.

Methods

REX-CPHMD Protocol

Replica Exchange (REX), or parallel tempering, is a method of increasing barrier crossing rates by simulating an ensemble of proteins distributed through temperature space.³⁴ During a REX simulation a single protein structure is replicated and simulated in parallel over an exponentially spaced temperature range. After a defined time (replica cycle), the replicas are allowed to exchange atomic configurations with adjacent temperature windows based on the Metropolis criterion.³⁴ This technique has shown success in modeling protein folding and peptide dynamics³⁴ and has been incorporated into numerous simulation environments.^7,35,36 As it concerns our study, it was used to enhance sampling of the protein conformational space around the vicinity of the native fold as well as the conformations of the tautomeric states of the titrating amino acids during CPHMD.

CPHMD is a methodology developed by Brooks and coworkers that assigns titration coordinates to ionizable hydrogen atoms, (λ, x), which are propagated simultaneously with atomic coordinates.^6,20 These coordinates control a smooth turning on or off of van der Waals and electrostatic interactions of hydrogen atoms in these groups, which enables a direct coupling between conformation and protonation states.²⁰

In the REX-CPHMD protocol, λ and x coordinates are recorded at the end of each replica cycle for all titrating residues as defined in equation 1.

$$\begin{array}{c}{N}^{\mathit{\text{unprot}}}=\sum N(\mathrm{\lambda }>0.9;x<0.1\vee x>0.9)\hfill \\ N^{\mathit{\text{prot}}}=\sum N(\mathrm{\lambda }<0.1;x<0.1\vee x>0.9)\hfill \end{array}$$ (1)

As such, x defines the dominant tautomer during the cycle (x < 0.1; x > 0.9) and λ indicates whether that tautomer is protonated (λ < 0.1) or deprotonated (λ > 0.9). The non-physical regions of λ and x space that are not representative of protonated or deprotonated configurations enable a continuous transition between protonation states. Barriers are added to the energy functions for these coordinates to diminish the time spent in such states. ^6,20 After completing all REX cycles, analysis was performed using the CPHMD tools within the MMTSB Tool Set (rexanalysis.pl) to collect all titration coordinates into the values N^prot and N^unprot.³⁵ With enough replica exchanges, the population of states converges to the probability of state (S) as defined in equation 2.

$$S^{\mathit{\text{unprot}}}=\frac{{\mathrm{\rho }}^{\mathit{\text{unprot}}}}{{\mathrm{\rho }}^{\mathit{\text{unprot}}}+{\mathrm{\rho }}^{\mathit{\text{prot}}}}\approx \frac{N^{\mathit{\text{unprot}}}}{N^{\mathit{\text{unprot}}}+N^{\mathit{\text{prot}}}}$$ (2)

S^unprot is the probability of a residue being unprotonated. ρ^unprot and ρ^prot are the probabilities associated with the unprotonated and protonated states. S^unprot is related to pKa in the Henderson-Hasselbalch (HH) equation given in equation 3.

$$S^{\mathit{\text{unprot}}}=\frac{1}{1+{10}^{n({\mathit{\text{pK}}}_a-\mathit{\text{pH}})}}$$ (3)

In this equation, the Hill coefficient (n) and the pKa can be fit given a set of S and pH values. In this study, 10 to 15 (pH, S) points per titrating residue were found to give the optimal trade-off between accuracy and computational time. For residues titrating multiple protonation sites, such as aspartic and glutamic acids, pKa values for each site are calculated separately. These pKa values are combined into a total pKa via equation 4.

$${\mathit{\text{pK}}}_a={\text{log}}_{10}({10}^{\mathit{\text{pK}}1}{10}^{\mathit{\text{pK}}2})$$ (4)

Modeling Salt effects

As has been shown in earlier calculations, the accurate recapitulation of experimentally measured pKa values depends on modeling both the aspects of the solvent environment and the influence of ionic strength correctly.⁷ To model solvent in our REX-CPHMD calculations we use the optimized GBSW model³⁷ together with the simple Debye-Hückel correction introduced into GB models by Case et al.^38,39

Simulation Protocol

All REX-CPHMD simulations were run using the aarex.pl tool as part of the MMTSB Tool Set,³⁵ which performs replica exchange simulations using the PHMD^6,20 and GBSW²⁴ modules within the CHARMM program environment.²¹ Simulations were performed using the CHARMM22 all-atom force field for proteins⁴⁰ with CMAP^37,41 and optimized GB input radii.³⁷ This protocol was intended to follow closely to that performed by Khandogin and Brooks, and thus unprotonated fractions (S) of residues were calculated for pH values between pH=2 and pH=9 in all cases.⁷ For residues with highly perturbed pKa values, this range was extended by several pH units.

During each simulation, the protein was replicated in 8–16 temperature windows spanning from 298 K to 400 K. This range of temperatures was chosen so that the exchange ratio was approximately 35 to 45%.⁷ All replicas were run simultaneously through exchange cycles: each cycle consisted of 500 dynamic steps (a total of 1 ps) followed by an exchange attempt. During an exchange attempt, adjacent temperature windows were allowed to exchange replica structures based on the Metropolis criterion.³⁴ The total sampling time of each protein was 4 ns. Debye-Hückel screening²⁴ of charge-charge interaction was used to represent the 150 mM salt concentration in the solvent.⁷ All simulations included a Nosé-Hoover thermostat to maintain the desired temperature for each window.²⁶ For the GB calculations, a smoothing length of 0.6 Å at the dielectric boundary with 24 radial integration points up to 20 Å and 38 angular integration points were used. The nonpolar solvation energy was computed using the surface tension coefficient of 0.03 kcal mol⁻¹ Å⁻².⁴² The SHAKE algorithm allows a 2 fs time step when applied to hydrogen bonds, and a 22 Å distance cut off was applied to truncate the non-bonded in non-bonded energy evaluations.

Structures of Δ+PHS were processed according to their availability, which led to a division into two groups for this study: those with solved protein structures, and those without. All solved structures, including Δ+PHS and many of its mutants, are listed in Table 2 as their corresponding PDB codes. These structures were downloaded from the Protein Databank www.pdb.org.⁴³ For those without solved structures, the Δ+PHS structure was computationally mutated as explained in the following section.

Each PDB file was processed to remove all non amino acid residues and to convert the PDB file into a CHARMM supported format with convpdb.pl from the MMTSB toolset.³⁵ During this step the ligand thymidine-3’,5’-diphosphate was removed to make the crystal structures match those used during the NMR analyses performed by Isom et al.²⁷ Structures were minimized for 500 steps with steepest descents and harmonic restraints (10 x mass) on heavy atoms. All titrating residues were patched appropriately so that CPHMD could recognize them correctly. The glutamic acid and aspartic acid patches represent doubly-protonated residues with the hydrogen atoms bound to the ionizing oxygens.

Mutation Protocol

For Δ+PHS mutants without a PDB structure, coordinates were generated computationally from the Δ+PHS PDB structure (3BDC) using mutate.pl from the MMTSB toolset.³⁵ This protocol eliminates an amino acid at a user-specified location, and replaces it with the desired mutation. The structures were minimized using steepest descents for 500 steps with harmonic restraints (10 x mass) on all heavy atoms using minCHARMM.pl. Several mutants had significant atom clashes after running mutate.pl. These structures underwent 100 steps of steepest descents all-atom minimization using minCHARMM.pl to resolve the structural conflicts, followed the 500 step energy minimization with harmonic restraints on heavy atoms.

As a measure of confidence in the method, the average structure was calculated from each simulation trajectory and then compared to its original PDB of Δ+PHS by a backbone-based RMSD analysis of structural alignment. These values are given in Tables 2 and 3. The low values suggest that the mutations are accommodated without requiring significant reorganization of the protein.

Results

Δ+PHS

The pKa values of all 17 carboxylic acids in Δ+PHS were determined from 3BDC, as shown in Table 1. There is reasonable agreement between the observed and calculatedcalculated pKa values, with an AUE of 0.99 pK units. Fifty-nine percent (59%) of the residues had an error of less than 1 pK unit. This suggests that our protocol is able to determine pKa values of diprotic residues for this protein, even if they are in a greatly perturbed state. These findings are consistent with previous studies using CPHMD in that an AUE of 1 pK unit or less was achieved for proteins containing ionizable side chains in the core.⁷

Figure 1 shows that the titrated residues in our calculations sample a variety of solvent-exposed environments. Glutamic acid residues (GLU) at α-helical locations (57, 67, 101, 122, 129, 135) showed an average error of 0.5 pKa units, those in β-sheets (10, 73, 75) showed an error of 1.0 unit, and those in flexible side-chains (43, 52) showed an error of 0.8 units. Aspartic acid residues (ASP) (19, 21, 40, 77, 83, 95) were all on flexible side-chains, and showed an AUE of 1.5 units.

Figure 1. Locations of ionizable residues in Δ+PHS.

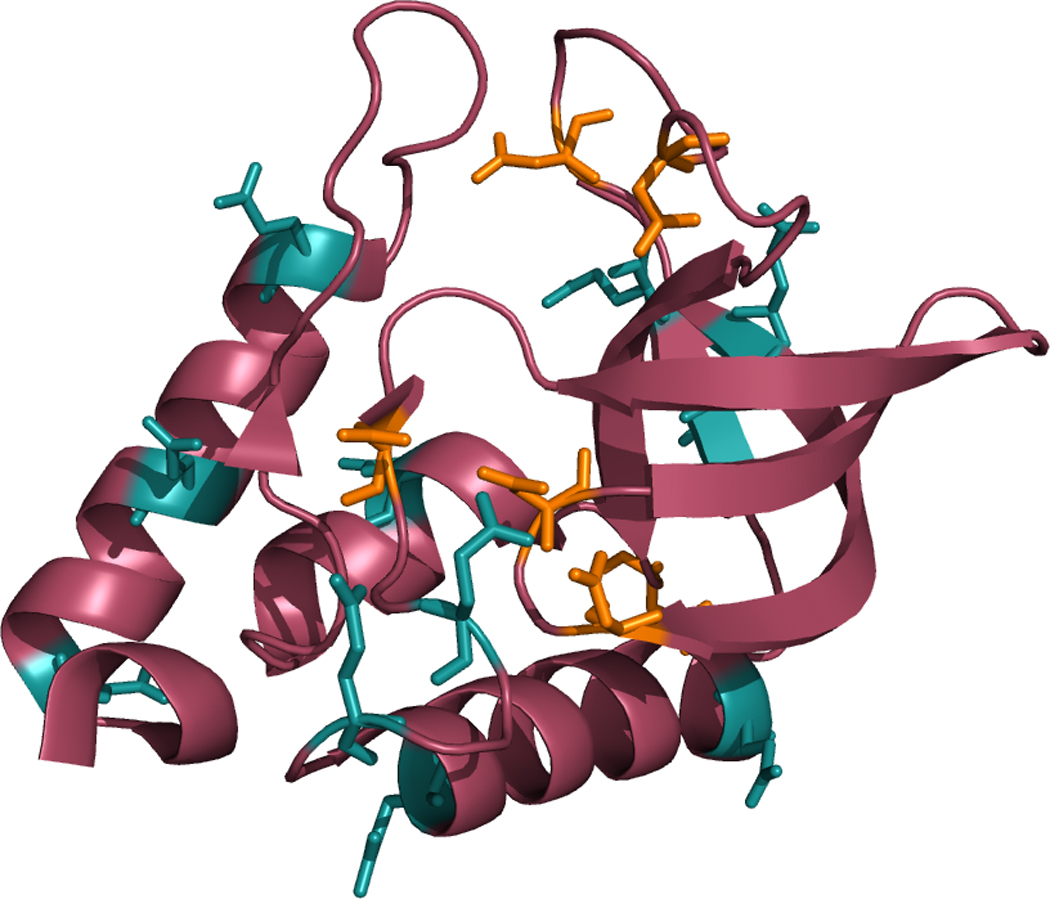
Δ+PHS staphylococcal nuclease is shown here with all ionizing residues highlighted. Glutamic acid is cyan, and aspartic acid is orange.

Of the titrating residues, 7 had errors in calculated pKa values that were greater than 1 pK unit from experimental values, 6 of these were ASP. Surprisingly, 4 of these 6 residues (Asp 19, Asp 21, Asp 40, and Asp 95) were in unstructured regions relatively far from the center of the protein. Previous research suggested that when a titrating residue has a large surface area exposed to solvent its ionization state is well defined by the GBSW model, resulting in a better pKa prediction.⁷ This phenomenon will be explored further in the Discussion section.

Δ+PHS mutants with known structure

Of the 27 Δ+PHS mutants studied in this work, five (5) had solved coordinates. Figure 2 illustrates their similarity by overlapping their secondary structural representations. The RMSD between any two proteins was less than 0.35 Å. Their six (6) corresponding PDB codes and calculated pKa values are shown in Table 2. We list only the pKa values of residues reported by the NMR titration experiments (see supplementary data for a complete list of computed pKa values). There is good agreement between the observed and calculated ionization equilibria, with an AUE of 1.5 pK units.

Figure 2. Apparent tertiary structure similarity between various solved crystal structures used in this study.

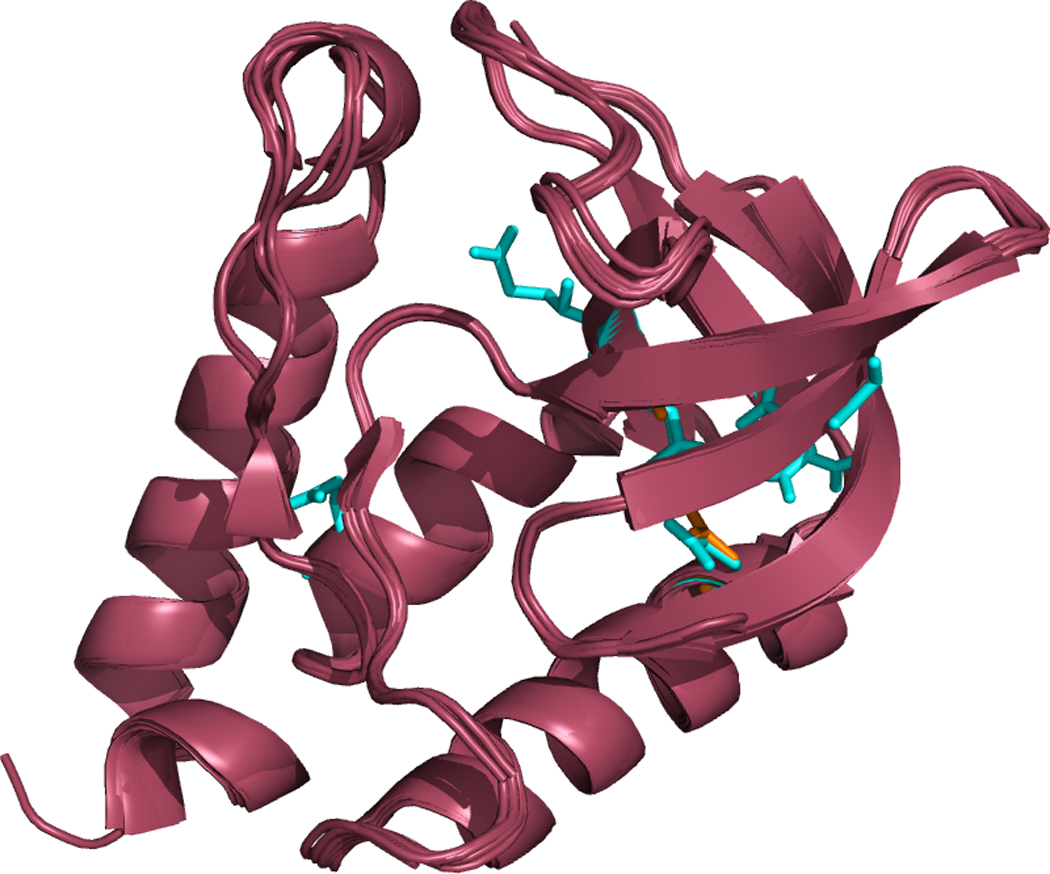
Δ+PHS staphylococcal nuclease, its 6 solved PDB structures, and three structural homologues are all shown overlaid with one another. The mutated residues are shown in red. All mutants had an RMSD of less than 0.35 Å, indicating that even with the introduction of hydrophilic residues into the protein’s interior, the structure of Δ+PHS is not significantly distorted.

The stability of proteins was monitored during the simulation by the RMSD between the initial and average structures of each simulation. The RMSD of all simulations averaged to 1.3 Å (specific values are shown in Table 3). This indicates that the conformational changes and fluctuations that occurred during the simulations are relatively small, even when the proteins were subjugated to a wide range of pH conditions. This also indicates that such fluctuations are greater than the structural differences between different mutants.

Δ+PHS compared to I92E mutants

The mutant glutamic acid pKa values for two I92E structures were predicted (1TR5 and 1TQO), which provides some insight into the sensitivity of CPHMD to conformational differences in the starting structures of the proteins. The two structures had an RMSD of 0.85 Å from each other, and an RMSD of 1.10 Å when compared to Δ+PHS. This suggests that in the case of Δ+PHS, conformational rearrangements near the point of mutation are comparable to differences in multiple ground state configurations. These rearrangements can be explained as the energy cost of allowing Glu 92 access to solvent.

When comparing the ionization of all titrating residues between Δ+PHS and its I92E mutants, most aspartic and glutamic acid residues titrated to values less than 1 pK unit from each other, as seen in Table 4. This falls within 1 pKa unit of error, as seen in previous research.⁷ Residues outside of this margin include all residues on flexible regions of the protein, such as all ASP residues. These residues sample a wide range of fluctuations in the environment, which may require a longer time to converge to a correct pKa estimate. There was a consistent trend that corresponding residues yielded similar pKa predictions, which suggests that the conformational changes induced by point mutations do not destroy the overall accuracy of the calculation for other ionizing residues. This opens the possibility that when predicting pKa values, a solved structure may not be necessary; if an approximation of the secondary and tertiary structures can be found, pKa values might still be predicted using REX-CPHMD. The remaining calculations in this study are designed to explore this possibility.

Table 4.

Comparison of ∆+PHS pKa values (all titrating residues) to its I92E mutant residues.

Residue	Experimental pKa32	Calculated pKa (3BDC)	Calculated pKa (1TR5)	Calculated pKa (1TQO)	Averaged Error from Experimental
Asp-19	2.2	3.8	1.6	3.6	1.2
Asp-21	6.5	5.4	5.6	5.6	1.0
Asp-40	3.9	2.0	2.5	2.5	1.5
Asp-77	<2.2	0.8	1.3	0.5	COR
Asp-83	<2.2	3.8	4.3	3.6	>1.7
Asp-95	2.2	3.4	3.4	3.8	1.4
Asp-143	3.9	--	--	3.7	--
Glu-10	2.8	3.3	4.6	3.9	1.1
Glu-43	4.3	3.8	3.4	3.6	0.7
Glu-52	3.9	4.9	4.8	5.1	1.0
Glu-57	3.5	4.4	4.5	4.6	1.0
Glu-67	3.8	3.6	3.9	3.8	0.1
Glu-73	3.3	2.4	3.2	3.2	0.4
Glu-75	3.3	4.9	4.7	4.5	1.4
Glu-92	--	--	6.8	7.3	--
Glu-101	3.8	3.5	3.4	3.3	0.4
Glu-122	3.9	4.7	5.2	4.9	1.0
Glu-129	3.8	4.4	4.1	4.2	0.5
Glu-135	3.8	4.4	4.5	4.6	0.8
Glu-142	4.5	--	--	4.4	--

Δ+PHS mutants with modeled structure

Eighteen (18) of the reported pKa values from previous analyses did not have a corresponding solved structure in the PDB. Assuming that the solved structure of Δ+PHS is an adequate approximation of the system, models for these proteins were created by computationally mutating the Δ+PHS PDB file 3BDC. For these mutants the results from our pKa calculations appear in Table 3. Changes in the amino acid sequence of Δ+PHS, and our modeling of them, could affect the quality of the calculated pKa values. However, these changes are apparently small enough to allow accurate predictions of the pKa values for the mutated proteins to within an AUE of 1.4 pKa units. This indicates that even in the absence of a crystallographically determined starting structure, the CPHMD methodology can yield accurate predictions of pKa shifts with an AUE similar to those calculated from solved crystal structures. A caveat here, is that this technique requires a near-match of crystal structure in order to model the chemistry of the target system.

Calculation of a single residue

During this study, all residues were titrated simultaneously for every structure. This ensured that all cooperative protonation interactions between nearby titrating residues were considered. When the pKa of only a single titrating residue is desired, however, it may be more efficient to titrate only the target residue. This was tested by calculating the pKa value of the glutamic acid residue of the I92E (1TR5) mutant by allowing only the mutant residue to titrate. The calculation produced a value of 6.4 pK units, compared to 6.8 pK units when all ionizable residues were allowed to titrate. Since titrating residues don’t significantly alter the ionization equilibria of distant parts of the system, these results suggests that the differences in accuracy by simulating the titration of one residue may be small enough to allow accurate pKa prediction. The caveat for performing only a single-site titration during a REX-CPHMD simulation is that it ignores any cooperative protonation chemistry and the subsequent dynamics influenced by it. This simplification can greatly reduce the computational cost of modeling pKa changes in large systems with many titrating residues by reducing time to reach convergence.

Calculation from similar PDB structures

In many cases atomic coordinates are not available for a particular protein from crystallographic or NMR studies. This portion of the study investigates the accuracy of pKa predictions when using a PDB with a similar tertiary structure to the target one to determine pKa values. Three mutants of Δ+PHS were matched with three PDB files that had nearly-identical conformations to Δ+PHS: 1U9R, 2OXP, and 2OEO. These pairings, including their experimental pKa values, appear in Table 5. To illustrate their similarity with Δ+PHS, all of these structures appear in Figure 2 overlaid with the other structures homologous to Δ+PHS.

Table 5.

Calculated and experimental pKa values of ∆+PHS mutants modeled from non-exact matches of amino acid sequences.

PDB	Mutation	Experimental pKa	Calculated pKa	Error (CPHMD)	Error (Null Model)	RMSD (Å)
1U9R	V66E27	8.9	8.2	−0.7	−4.8	1.1162
2OXP	V66D47	8.8	7.5	−1.3	−4.7	1.0719
2OEO	I92D48	7.5	7.5	0.0	−3.4	1.4566

The results from the pKa calculations were surprisingly accurate, especially considering that 2OEO (similar to Δ+PHS I92E), provided the most accurate result despite lacking five ionizable lysines from the Δ+PHS/I92D structure used in the experimental calculations. Since these residues only titrate at dissimilar pH values than GLU, it is unlikely these changes to the sequence had substantial effects on the target ASP-92 mutation. These results suggest that REX-CPHMD can provide accurate pKa calculations from a similar structure even in the absence of an exact match of amino acid sequences. These also suggest that approximating the tertiary conformation of a protein may be sufficient to predict its pKa values accurately.

V39E and A109E mutants

The two simulations that yielded the poorest outcome for calculated f pKa values, V39E and A109E, were examined for structural exceptions that may have caused their unusually high deviation. In both cases the mutant residue was on an unstructured region of the protein, and both residues flipped their orientations outward in the averaged structures from their respective simulations. The conformational change then exposed the GLU residues to more solvent than had they remained in the interior of the protein, thereby lowering their calculated pKa values. This change is evident in both structures’ having relatively large RMSD values between the average structure and the initial structure. This conformational change may be due to the understabilization of local salt bridges that would otherwise pull the residues into the interior of the protein or have arisen from model preparation and equilibration protocols. The averaged structure of the V39E mutant appears to have a stable GLU39 – LYS110 salt bridge that exposes the V39E mutation to more solvent (leading to a reduced pKa). During the calculation, however, the GLU39 – ARG35 salt bridge may be the dominant orientation of the mutant site, which would draw the GLU into the interior of the protein (leading to an elevated pKa). The A109E mutant showed an average structure with a solvent-exposed LYS108 – GLU109 salt bridge. This bridge may have been overstabilized relative to the ARG105 – GLU109 salt bridge that would draw the mutant residue into the core of the protein. These residues could be exceptions to the current update of the GBSW force field.³⁷

Comparison with similar work

During the course of this study, a publication with many similar results to this paper was published by Wallace et al.⁴⁴ These results are listed in Table SI1. Although they calculated pKa values both in CHARMM and using an identical GBSW force field, their calculations yielded a somewhat lower AUE of 1.1 pK units. This difference appears to have arisen from the linear fitting of the HH equation to single pH points. This technique involves calculating and averaging pKa values from several (or one as in their case) points where S^unprot is nearly 0.5, and assuming that the Hill coefficient (n) is equal to unity. To test this, a single S^unprot fraction from this study was used to calculate each pKa value available. The results gave an AUE identical to that from the Wallace et al. paper (1.1 pK units), and an average unsigned difference from the HH fit of less than 0.3 pK units per residue. When the pH values were chosen closest to this study’s calculated pKa values, the calculations yielded an identical AUE as the HH-equation curve fitting method (1.3 pK units), and an average unsigned difference from the HH fit of less than 0.3 pK units per residue. This indicates that more accurate pKa values may be calculated with fewer points than fitting a complete HH equation curve, when the appropriate single pH value has been determined. The caveat of this method is it may require manually choosing the data points used to solve the linear fit and is clearly not applicable when multiple sites are of interest.

Discussion

Making use of the replica-exchange enhanced sampling protocol and the improved parameterization of the GBSW implicit solvent model, we determined the pKa shifts of a large number of SNase buried charge mutants. Our study provides accurate calculations of the ionization properties of buried charge groups in proteins, and supports our REX-CPHMD method as a useful tool for studying pKa shifts.⁴⁵ Additionally, the titrating groups in the mutants of this study have among the most-perturbed carboxylic acid pKa values observed.²⁷ Being able to predict such titration shifts accurately suggests that CPHMD simulations and the GBSW implicit water model provide a robust methodology for exploring electrostatic environments of protein interiors.

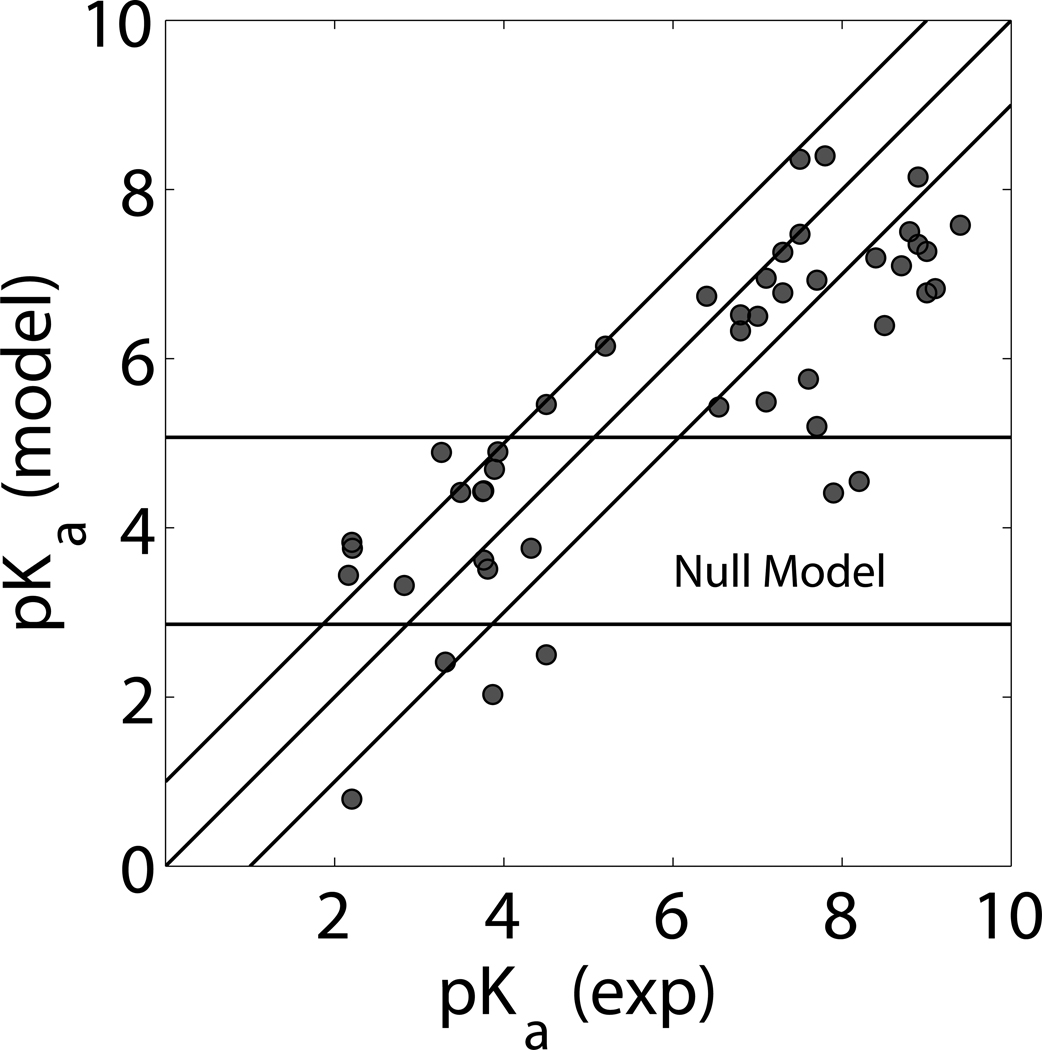
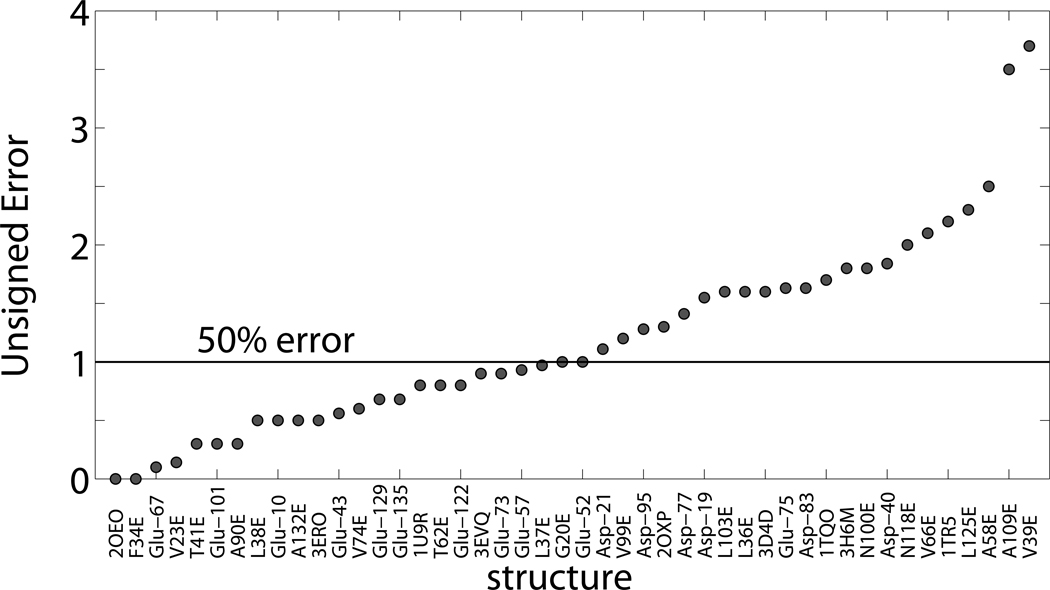
When taking the perspective of a null model, where all GLU and ASP are assumed to have fixed pKa values of 4.07 and 3.86, respectively,⁴⁶ the AUE of predicting pKa values is similar to CPHMD when observing amino acids with a small perturbation. Results in Table 1 show that the null model had an AUE of 0.85 pK units, while CPHMD had an AUE of 0.99 units. The null model fails when large perturbations are being observed. The low-pKa bias for ASP residues in Δ+PHS, for instance, was consistently modeled better with CPHMD by several tenths of a pK unit. As Figure 3 illustrates, when the perturbation of the amino acid is more than one unit, CPHMD calculations are significantly better. When considering all pKa predictions within this experiment, the analogous result from the null model prediction has a mean AUE of 3.54 pK units, as compared to the AUE of 1.31 units with CPHMD. A relative confidence level of CPHMD is shown in Figure 4 by listing the complete comparative statistics of this study. All calculated residues that had corresponding experimental data are listed by order of increasing error. 48% had an error below 1 pK unit. This margin contains 58% of Δ+PHS residues, 44% predictions from PDB files, and 50% of predictions from modeled structures.

Figure 3. Calculated vs Experimental pKa.

All pKa values that had a corresponding experimental pKa value are presented in this graph. This includes all values from Tables 1, 2, 3, and 5. Calculated pKa values that had no corresponding experimental value are presented in the supplementary information. A perfect prediction would presumably place all points along a 45° incline from the origin. The ideal range of ±1 pK unit error from this diagonal has been highlighted. The null model region is the horizontal range of ±1 pK unit error from unperturbed ASP and GLU pKa values of 3.86 and 4.07 respectively. As shown, CPHMD excels in discovering and mapping large perturbations in pKa.

Figure 4. pKa values of GLU and ASP residues in 29 internal positions in staphylococcal nuclease.

This is a list of mutations in order of increasing unsigned difference of experimental determination of apparent pKa value, and its calculated value using CPHMD. Approximately half (48%) of the calculated values had a difference of less than 1 pK unit.

We note that although pKa is defined by protein structure, no strong correlations were found between the error of the pKa prediction and large-scale structural phenomena within the scope of this study. These include conformational changes caused by the relaxation of the protein (supporting information: Figure SI 1), changes in residue volume from the mutation (supporting information: Figure SI 2), and proximity to the bound ligand thymidine-3’,5’-diphosphate present in the PDB structure (supporting information: Figure SI 3). The R² values of these trends were 0.29, 0.002, and 0.001 respectively. This indicates that the methodology may not be significantly improved by accommodating such conformational trends or exceptions. This provides insight into the robustness of CPHMD: our method repeatedly yields accurate predictions of pKa values almost irrespective to such phenomena.

The one trend consistent enough throughout this study was the under-prediction of pKa values, as seen in Figure 3. When calculating residue pKa values of Δ+PHS mutants, twenty-three of twenty-nine values were underpredicted. This suggests that CPHMD may systematically overstabilize the ionized form of the residues studied, and indicates avenues of refinement in the updated GBSW-specific force field created in previous work.³⁷ In order to refine the protocol significantly, adjustments may need to be made to the force field and titrating residue patches to increase the perceived perturbation of residue pKa values.

While refinements should be made to improve the accuracy of the CPHMD protocol, this study provides a modest benchmark of its capability to predict highly perturbed pKa values of buried charge residues in proteins. This promises to aid the evaluation and characterization of ionization in protein interiors, which could give valuable insight into the mechanism of pH-based biological activity.