Disentangling Prenatal and Postnatal Maternal Genetic Effects Reveals Persistent Prenatal Effects on Offspring Growth in Mice

Abstract

Mothers are often the most important determinant of traits expressed by their offspring. These “maternal effects” (MEs) are especially crucial in early development, but can also persist into adulthood. They have been shown to play a role in a diversity of evolutionary and ecological processes, especially when genetically based. Although the importance of MEs is becoming widely appreciated, we know little about their underlying genetic basis. We address the dearth of genetic data by providing a simple approach, using combined genotype information from parents and offspring, to identify “maternal genetic effects” (MGEs) contributing to natural variation in complex traits. Combined with experimental cross-fostering, our approach also allows for the separation of pre- and postnatal MGEs, providing rare insights into prenatal effects. Applying this approach to an experimental mouse population, we identified 13 ME loci affecting body weight, most of which (12/13) exhibited prenatal effects, and nearly half (6/13) exhibiting postnatal effects. MGEs contributed more to variation in body weight than the direct effects of the offsprings’ own genotypes until mice reached adulthood, but continued to represent a major component of variation through adulthood. Prenatal effects always contributed more variation than postnatal effects, especially for those effects that persisted into adulthood. These results suggest that MGEs may be an important component of genetic architecture that is generally overlooked in studies focused on direct mapping from genotype to phenotype. Our approach can be used in both experimental and natural populations, providing a widely practicable means of expanding our understanding of MGEs.

MATERNAL effects occur when the genotypes or phenotypes of mothers have some causal influence on traits expressed by their offspring (Wolf and Wade 2009). These effects can generally be viewed as resulting from the influence of the maternally provided environment (e.g., uterine environment, features of eggs, or seed composition, etc.) on offspring development, where some feature of the environment experienced by the offspring is generated by the mother through her behavior or expression of physiological traits. This is in contrast to maternal inheritance, such as mtDNA or cpDNA, where factors are inherited from the mother but act causally directly in the offspring (Cheverud and Wolf 2009; Wolf and Wade 2009). Because of the important role of the maternally provided environment in many species, maternal effects are often a major determinant of phenotypes and fitness in natural and experimental populations (Mousseau and Fox 1998; Maestripieri and Mateo 2009). They have been shown to occur across a diversity of species, including flies, plants, mammals, birds, and fish (Mousseau and Fox 1998), that differ widely in the modes through which mothers affect their offspring. In humans, they have been shown to play a particularly important role in health and the development of adult metabolic diseases (Wells 2007).

When maternal effects are genetic in origin, they are known as maternal genetic effects (see Cheverud and Wolf 2009). Maternal genetic effects are a type of indirect genetic effect in which the genotype of one individual affects the phenotype of another individual (Moore et al. 1997; Wolf et al. 1998). They contrast with direct genetic effects, where the genotypes of individuals directly influence their own phenotypes. Both direct and indirect (maternal) genetic effects can be important components of genetic architecture [i.e., our description of the genotype-to-phenotype map (Zeng et al. 1999)] and, therefore, both need to be considered to fully understand how genotypes map to phenotypes in populations (Mutic and Wolf 2007). The inclusion of maternal genetic effects is important because they can profoundly alter evolutionary dynamics, leading to phenomena such as evolutionary time lags, evolutionary momentum, and maladaptive responses to selection (Kirkpatrick and Lande 1989). They can also be a “hidden” source of variation available for evolutionary change (e.g., Badyaev et al. 2002; Wilson et al. 2005). Maternal genetic effects may play a role in a diversity of evolutionary processes such as sexual selection (Wolf et al. 1999), population differentiation (Wolf 2001; Badyaev et al. 2002), speciation (Wade 1998), range expansion (Duckworth 2009), and kin selection (Cheverud 1984).

In most studies of genetic architecture, such as backcross or F₂ intercross designs, maternal genetic effects are experimentally controlled (e.g., genetically identical F₁ parents of an F₂ experimental population) or otherwise omitted. Consequently, information on the contribution of maternal genetic effects is generally absent from our picture of genetic architecture. Experiments where maternal genetic effects have been included, such as in the mapping of maternal effects in small chromosomal blocks in subcongenic mice by Casellas et al. (2009) and the mapping of litter means in cross-fostered mice by Wolf et al. (2002), have suggested that maternal effects may be an important part of genetic architecture, but they have provided limited general insights (see below).

Empirical analysis of maternal genetic effects has been challenging because relatedness makes the maternal and offspring genotypes correlated, making it difficult to accurately assign effects to the maternal vs. offspring genomes. A common way around this confounding has been the use of experimental cross-fostering, where offspring are fostered to unrelated mothers (White et al. 1968; Legates 1972). Cross-fostering has allowed for the successful empirical dissection of maternal effects, but only if the cross-fostering is done prior to the time that the maternal effects arise. Although there have been many studies of maternal effects in systems where cross-fostering is relatively simple (e.g., where individuals can be moved between nests), as in birds (see Price 1998) or mammals (e.g. Wolf et al. 2002), there have been relatively few studies of maternal effects arising prenatally using embryo transfers in eggs (e.g., Ho et al. 2011) or uteri of mammals (e.g., Rhees et al. 1999).

Maternal effects are especially pronounced in mammals, where they arise through two distinct and potentially independent pathways. Early in development the uterine environment has a major effect on offspring development, through mechanisms such as nutrient transfer (Jones et al. 2007) and hormone transmission (Dloniak et al. 2006) across the placenta. The postnatal environment, on the other hand, is structured by the joint influence of milk quality and maternal behaviors, such as nest building and maintenance (Bult and Lynch 1997), offspring grooming, and time spent nursing (Ward 1980; Brown et al. 1999). The quality of milk varies in its composition, including fats, carbohydrates, and protein (Jenness 1979), and in biologically active proteins that can have growth and immunological effects (Lönnerdal 2003). To fully describe maternal effects in mammals, therefore, we must take into account both pre- and postnatal influences with their distinct physiological origins.

Here we present a framework for detecting maternal-effect quantitative trait loci (meQTL), using a linear mixed-model approach. This framework is likely to yield important insights into the genetic architecture of complex traits for two reasons. First, it can be used to detect maternal genetic effects and differentiate them from direct genetic effects even without experimental cross-fostering, thereby allowing for the identification of maternal effects in natural populations consisting of intact families. Second, when cross-fostering is done at birth, this framework can be used to separate pre- and postnatal maternal effects. We apply this framework to the analysis of maternal effects in an experimental population of mice and use a simulation approach to demonstrate that the model accurately assigns effects to their causal origin.

Methods

Experimental population

Our focal population is composed of the F₂ and F₃ generations from an intercross between the Large (LG/J) and Small (SM/J) inbred mouse strains (Cheverud et al. 1996; Kramer et al. 1998; Vaughn et al. 1999). These strains were independently derived through artificial selection for either large or small body weight at 60 days of age (Goodale 1938; MacArthur 1944; Chai 1956) and have been inbred for >120 generations, making them essentially devoid of within-strain genetic variation. This population is an excellent candidate for the analysis of maternal effects because previous analyses (Kramer et al. 1998; Jarvis et al. 2005) have suggested that maternal effects are a major source of variation for many traits. A variance partitioning analysis using comparisons of cross-fostered and nonfostered pups (Kramer et al. 1998) in the F₃ generation of this intercross showed that postnatal maternal effects are a major determinant of body weight for the first 4 weeks of life (accounting for 21–30% of the variance in preweaning weights). Although it identified the presence of maternal effects, this variance partitioning study was unable to identify the degree to which maternal effects are genetically based and could not quantify prenatal maternal effects. An experiment using reciprocal crosses between a tester strain (C57BL/6J) and a set of recombinant inbred lines derived from the same LG/J and SM/J strains suggested that maternal genotype has substantial effects on growth and on a set of adult obesity- and diabetes-related traits (Jarvis et al. 2005). That study found that pre- and postnatal maternal genetic effects together explained as much as ∼33% of the variation in body weight early in life (week 2) and continued to explain a significant component of variance (10–15%) through adulthood in body size and related traits. However, that study was unable to (a) differentiate between maternal genetic effects and other effects that appear in a cross-direction–specific manner, such as genomic imprinting effects, (b) determine the genomic basis of the maternal effects, or (c) differentiate between pre- and postnatal effects.

To generate the intercross population, 10 SM/J males were mated to 10 LG/J females, producing 52 F₁ individuals. These animals were randomly mated to produce 510 F₂ animals, a subset of which represents the parents in our study. These F₂ animals were randomly mated to produce 1632 F₃ individuals in 200 full-sibling families, although offspring from only 195 of these families (N = 1552) were phenotyped and genotyped. The average litter size in these families was 8.49 (SD = 2.5) at birth and 8.12 (SD = 2.4) at weaning, meaning that mortality averaged ∼0.35 pups per litter. In 157 of the 195 families there was no mortality (representing the rearing environment of 79% of the F₃ pups) and in 22 others there was a single death (representing 90% of all pups). Half litters were reciprocally cross-fostered at random between pairs of females that gave birth on the same day. Cross-fostered pups were permanently distinguished from resident pups by their toe-mark pattern. In this study we limit our focus to those mice that were cross-fostered: 611 F₃ individuals from 168 families. Litter sizes and mortality rates in this focal population are very close to those of the entire F₃ population (which includes both cross- and non–cross-fostered pups), indicating that cross-fostering did not result in increased mortality. Furthermore, a comparable level of mortality (average of 0.5 pups per litter) was seen in the intact litters where there was no cross-fostering manipulation. Pups were weaned at 21 days of age and randomly housed with 3 or 4 other same-sex individuals.

Phenotypes

Animals were weighed weekly from 1 to 10 weeks of age, using a digital scale with an accuracy of 0.1 g. To understand the influence of maternal effects on preweaning growth, we included growth traits calculated as the difference in weight from week 1 to 3 (preweaning growth), as well as the separate phases of growth from week 1 to 2 and week 2 to 3. All weight traits and growth traits were normally distributed (testing using either sex-adjusted values or those in the separate sexes). Patterns of growth in the LG/J and SM/J strains are shown in Hager et al. (2009). Mean body weights in males, females, and the whole population (with standard errors) are provided in Supporting Information, Figure S1. (See also File S1.)

Prior to fitting the genetic models (see below) variation associated with sex, the effects of litter size at birth, and weaning and cohort were removed in a linear model as described by Kramer et al. (1998). Analyses were also done using the raw phenotypic data with these terms (sex, litter size at birth, litter size at weaning, and cohort) included as either fixed or random effects and the results are essentially identical to those based on these corrected trait values. Therefore, we present results based on these “corrected” phenotypes to maintain consistency with previous analyses in this same population (e.g., Vaughn et al. 1999; Hager et al. 2008a, 2009; Wolf et al. 2008).

To examine the sources of variation in these weight traits through time, we fitted a mixed model using restricted maximum likelihood in the Mixed Procedure of SAS (SAS version 9.1; SAS Institute, Cary, NC), with dam and nurse included as random effects. The dam variance component estimate includes all genetic and environmental variation shared by siblings (e.g., direct genetic effects and prenatal maternal effects). The nurse variance component includes postnatal maternal effects and other shared postnatal environmental effects (e.g., common cage effects). These estimates are not direct measures of pre- or postnatal maternal-effect variation and obtaining such estimates requires a more complex design. Furthermore, note that the dam variance is not an estimate of broad sense heritability since it would need to be doubled, but doubling the dam variance would double the maternal-effect variance (Roff 1997) and grossly inflate the heritability estimate (Kramer et al. 1998).

Genotypes

Details of the genotyping are provided by Wolf et al. (2008) and are only briefly outlined here. All F₂ and F₃ individuals were genotyped at 353 autosomal loci, using the Illumina Golden-Gate assay, with an average map distance between markers in the F₂ generation of 4 cM. A list of the markers with their physical and map positions is given in Table S1.

The genotype data from parents and offspring were used to reconstruct chromosomal haplotypes. Haplotype reconstruction was done using the “integer linear programming” (ILP) algorithm in the program PedPhase (Li and Jiang 2003a,b). Haplotype reconstruction yielded a set of unordered haplotypes for the F₂ animals and a set of ordered haplotypes (i.e., ordered by parent-of-origin of alleles, such that the reciprocal heterozygotes can be distinguished) for the F₃ animals. The use of ordered genotypes allows for the inclusion of genomic imprinting effects in the analysis of genetic architecture (see Wolf et al. 2008).

QTL analysis

To fit a linear model at each locus we assigned a set of index values to the genotypes. In the F₂ generation the three unordered genotypes (LL, LS, and SS, with the “L” allele coming from LG/J and the “S” allele coming from SM/J) were assigned additive (X_a) and dominance (X_d) genotypic index values, where the values of X_a are LL = +1, LS, SL = 0, SS = –1 and those of X_d are LS, SL = 1, LL, SS = 0 (Cheverud et al. 2008; Wolf et al. 2008). In the F₃ generation, the four ordered genotypes (LL, LS, SL, and SS individuals) were used to assign additive (X_a) and dominance (X_d) genotypic index values as above as well as imprinting (parent-of-origin) genotypic index values (X_i) following Wolf et al. (2008), where the values of X_i are LL, SS = 0, LS = +1, SL = –1 (with the first allele specified coming from the father and the second from the mother). To distinguish the genotypes of the F₃ individuals from their F₂ mother and nurse, we include “M” and “N” subscripts for the mother and nurse, respectively, in the index values and associated genetic-effect terms (see below).

These genotypic index values were used in a linear mixed model, with the F₃ phenotypes as the dependent variables, to simultaneously fit the direct effects of the F₃ genotypes on their own phenotypes, the prenatal maternal effects of the F₂ mothers on their own offspring (hereafter the “dam” effect, but subscripted M for “mother” to avoid confusion with dominance), and the postnatal maternal effects of the F₂ nurses on their foster pups (hereafter the “nurse” effect). Although these are referred to as dam and nurse effects in the presentation of the analysis, we discuss them as prenatal and postnatal effects for clarity when presenting and discussing results. The model includes the fixed effects of the direct, dam, and nurse genotypic index values at each marker locus to produce regression coefficients corresponding to the direct additive (a), direct dominance (d), direct imprinting (i), dam additive (a_M), dam dominance (d_M), nurse additive (a_N), and nurse dominance (d_N) effects,

$$\begin{array}{c}{P}_{jkl(xyz)}=a{X}_{\text{a}(x)}+d{X}_{\text{d}(x)}+i{X}_{\text{i}(x)}\\ +a_{\text{M}}{X}_{\text{aM}(y)}+d_{\text{M}}{X}_{\text{dM}(y)}\\ +a_{\text{N}}{X}_{\text{aN}(z)}+d_{\text{N}}{X}_{\text{dN}(z)}\\ +{\text{dam}}_k+{\text{nurse}}_l+r_j,\end{array}$$ (1)

where P_jkl(xyz) is the phenotypic value of individual j with genotype x that has a mother (dam) k with genotype y and a nurse l with genotype z and r_j is the residual from the model for individual j. The first three lines correspond to the fixed effects of the offspring genotype (line 1), dam genotype (line 2), and nurse genotype (line 3) at the focal locus, respectively (i.e., they are the genotypes of the three individuals, but all at the locus being tested). The last line gives the random effects of the dam and nurse not associated with the genotypes at the locus in question. These random effects account for common environmental effects (e.g., common cage effects) and genetic effects at other loci (i.e., other polygenic effects). These random effects are shared by sets of siblings or littermates, and so they inflate the apparent significance of genetic effects and reduce power when they are not accounted for because individuals with correlated genotypes have correlated phenotypes (Lynch and Walsh 1998; Wolf et al. 2008). Note that litter sizes at birth and weaning, which were not included in the linear model because variation associated with them was removed prior to model fitting (see above), could potentially be influenced by the dam or nurse genotype in a cross-fostering pair. Therefore, it is possible that genetic effects on litter size at birth or weaning could be the causal origin of maternal effects on offspring phenotypes. However, when we allowed for this possibility in analyses by using trait values that were not corrected for litter size differences and including litter size as a random effect, we found no evidence that litter size effects produced maternal genetic effects on any of the traits we examined. This is not surprising given that a variance component analysis of litter size in this population finds only a very small, nonstatistically significant heritability, and searches for main-effect litter size QTL in this population identified only two marginally significant loci with minor effects (Peripato et al. 2004).

The estimated direct additive effects correspond to the classic definition of additive genotypic values (Falconer and Mackay 1996) as half the difference between the average phenotypes of the two homozygotes. In the case of dam and nurse additive effects, these differences are between the average phenotypes of the pups associated with those genetic classes of dams or nurses. Likewise, the dominance effect matches the classic definition of dominance as the deviation of the average heterozygote from the midpoint between the average phenotypes of the two homozygotes. The imprinting genotypic value is half the difference between the average phenotypes of the reciprocal heterozygotes (Wolf et al. 2008).

For each trait, the mixed model was fitted at each marker location using maximum likelihood as implemented in the Mixed Procedure in SAS (SAS version 9.1; SAS Institute). To increase the speed of the model fitting and allow for flexible hypothesis testing, the genome scan was accomplished by including the individuals’, dams’, and nurses’ genotypes as class variables (with four, three, and three classes, respectively). We devised a pair of contrasts to test the overall dam effect (2 d.f., corresponding to a_M and d_M) and nurse effect (2 d.f., corresponding to a_N and d_N). Denominator degrees of freedom for the model were determined using the Satterthwaite approximation (see Littell et al. 2006). This approach determines the effective degrees freedom using the variance structure of the model, which reflects the litter structure (i.e., it essentially determines the effective sample size for each effect) (Ames and Webster 1991; Keselman et al. 1999; Faes et al. 2009). Probabilities from these contrasts, and from the tests of individual model terms, were converted to logarithmic probability ratios [LPR = –log₁₀(probability)] to provide a measure of significance analogous to LOD scores. Proportions of variance explained by the QTL (R²) were estimated by calculating the variance component contributed by each effect (see Equation 2 in File S2) divided by the total phenotypic variance. Only significant effects were included in this calculation to avoid inflation generated by the large number of genetic terms in the model.

To simplify the search for QTL locations on our set of weekly weight measures we used a multivariate implementation of the model in Equation 1, which allowed for the identification of QTL affecting correlated sets of traits (see Hager et al. 2009). For the multivariate model, the weight measurements were divided into three sets: (1) preweaning weights (corresponding to weeks 1–3), (2) the period of rapid postweaning growth prior to “adulthood” (corresponding to weeks 4–6), and (3) “adult” weights (corresponding to weeks 7–10). Weight measurements within each growth period were modeled as a multivariate repeated weight trait (see Fry 2004) with the correlation between weekly weights modeled using the Heterogeneous Toeplitz autoregressive structure (TOEPH option in the SAS Mixed Procedure, see below) (Kincaid 2005), which approximates the phenotypic correlation structure (Kramer et al. 1998). The model was fitted using the Mixed Procedure in SAS (SAS version 9.1; SAS Institute), with “weight” as the dependent variable and individual designated as the repeated subject. This treats the weekly weight measurements as repeated measures of the same weight phenotype through a set of time intervals. Because weights change through time, the model also included week as a fixed effect to account for the change in weight across weeks within a growth period. Denominator degrees of freedom were determined using the Kenward–Roger approximation, which is similar to the Sattherthwaite method used in the univariate models, but is preferred for repeated measures designs (Kenward and Roger 1997; Schaalje et al. 2001).

QTL were first located using the LPR values from these multivariate models, with the highest LPR score on any chromosome that exceeded an appropriate threshold value (see below) taken to be evidence of a QTL on that chromosome. Confidence intervals were defined as a drop of one LPR, which is approximately equal to the commonly used one-LOD drop (Lynch and Walsh 1998), using the multivariate trait set that was most strongly affected by the locus. Maternal-effect QTL are designated as meQTLX.Y, where X is the chromosome number and Y is the locus number on that chromosome (to distinguish between multiple QTL on a chromosome).

When multiple (in all cases, two) QTL peaks were found on the same chromosome, we ran models containing all pairwise combinations of markers on the same chromosome. This scan was then used to establish whether there was support for two independent locations. We used a likelihood-ratio test to confirm support for the fit of the multiple-QTL model over a single-QTL model on the basis of the location of the highest LPR on the chromosome. Because the direct, prenatal, and postnatal maternal effects are potentially genetically distinct, we used an approach where we allowed each term to move independently of the other terms. The difference in the −2 log-likelihood values of the two models (multiple-QTL model minus single-QTL model) is approximately chi-square distributed with the number of degrees of freedom corresponding to the number of terms that changed position or the number of additional terms between the two models. A chromosome was determined to have multiple QTL when the multiple-QTL model had a significantly better fit than the single-QTL model.

Simulation

To examine the general properties of the model and to derive significance thresholds, we simulated the production of the F₂ and F₃ generations, maintaining the actual pedigree information for all individuals. For brevity we present details of the simulation procedure in File S2 and provide only a brief outline of the simulation methods and general results herein.

By simulating the intercross using the actual pedigree information, the pattern of genotypic variation and the genetic relationship between individuals within and between generations matches that of the real genotypes, but any causal association between genotype and phenotype is absent by design. From the simulation we derived a set of 20,000 independent (uncorrelated) marker loci. Using these simulated marker data we first examined the null model with no QTL effects to define significance thresholds. We then simulated QTL effects to examine the power and performance of the linear mixed model.

The simulation under the null model demonstrated that the significance tests of direct effects conform to those predicted. For tests involving maternal-effect terms, the distribution of probabilities is correct when using the denominator degrees of freedom determined by the Satterthwaite approximation (Littell et al. 2006), which accounts for the structure in the population (Faes et al. 2009). The effective numbers of denominator degrees of freedom for the dam and nurse tests are approximately equal to the numbers of dams or nurses in the population corrected for the number of terms in the model. The use of adjusted degrees of freedom for tests of the maternal-effect terms is important because the raw degrees of freedom, based on the overall number of F₃ individuals, produce biased thresholds. This is because the maternal-effect terms are pseudoreplicated by design, with each mother producing and each nurse raising, on average, about four pups that were included in the analysis (meaning each maternal genotype appears in the linear equation about four times). This pseudoreplication is easily removed by simply adjusting the denominator degrees of freedom of the model to reflect the level of pseudoreplication. This is what is accomplished by the Satterthwaite method, but a simpler approach could be implemented by manually adjusting the degrees of freedom to reflect the number of dams or nurses in the analysis. For the maternal-effect significance tests, the number of denominator degrees of freedom would be based on the number of dams or nurses (there are 171 of both).

We simulated QTL by modifying the real phenotypic value for an individual on the basis of the simulated genotype of the individual (Wolf et al. 2008). Using these simulated QTL we tested whether the model was able to detect these effects and whether it correctly identified the origin of the effect. The latter is summarized as the power of the tests (see below). Direct, dam, and nurse additive and dominance effects of QTL were simulated to account for 1, 2, 5, and 10% of the total phenotypic variance (V_p). We found that the mixed model accurately assigned the origin of the effects and that the presence of one type of effect (direct or maternal) had no influence on the significance test for other effects. For example, when simulating the occurrence of an additive dam effect accounting for 2% of the variance, we found that the significance values for all other terms in the model were unchanged from those under the null model. The overall results are summarized in the power analyses presented in Table S3. We found that there is lower power to detect maternal-effect loci compared to direct-effect loci because of the difference in effective sample size. For example, we have 75% power to detect an additive direct effect accounting for 2% of the variance using a chromosomewise threshold and 26.5% power to detect a comparable additive postnatal maternal effect. The difference in power declines as the effect size increases because power is measured as a percentage. For example, we have essentially 100% power to detect an additive effect accounting for 5% of the variance and 75% power to detect an additive postnatal maternal effect of this size. Overall, there is considerable power to detect all types of effects, especially those that account for >2% of the phenotypic variance, with all power values >20% for maternal-effects tests. Furthermore, the power to detect maternal effects is in line with the values expected for direct effects given the difference in effective sample size (Hu and Xu 2008). The power analysis results suggest that there is slightly more power to detect prenatal effects showing dominance than additive effects (e.g., 60% power to detect an additive effect that accounts for 5% of the variance and 72% power to detect a comparable dominance effect). There also appears to be more power to detect postnatal effects compared to prenatal effects but the power to detect postnatal effects is the same whether it is a dominance or an additive effect. Both of these results are obtained because there is no correlation between nurse and offspring genotypes while dam and offspring genotypes are correlated. For example, there is 75% power to detect an additive nurse effect and 74% power to detect a dominance nurse effect but 60% power to detect an additive maternal effect accounting for 5% of the variance.

Significance thresholds

The thresholds for direct and maternal effects were determined on the basis of the number of tests in a Bonferroni correction for familywise error, using the Šidák equation, 1 – 0.95^1/n, where n is the number of tests in the “family” of tests. To determine the number of independent tests we used the method of Li and Ji (2005; see also Cheverud 2001) to estimate the effective number of independent tests (markers) on each chromosome and over all chromosomes (i.e., genomewise). Because more recombination events have accumulated in the F₃ generation compared to the F₂, the number of independent tests is lower for the maternal-effect tests compared to the direct-effect tests. We used the effective number of markers (M_eff) to generate genomewise and chromosomewise thresholds in the Šidák equation. Chromosomewise thresholds are used because they have been shown to increase the discovery of true positives while avoiding a significant incidence of false positives (Chen and Storey 2006). Because mice have 19 autosomes, we would expect only about one false positive test using the chromosomewise thresholds per trait. This is an acceptable error rate given that we generally find several QTL for our focal traits, indicating that most identified QTL are likely to be true positives, with the possibility that the set includes a single false positive. Significance thresholds are given in Table S2. Once a maternal-effect QTL was identified, we used the single-test (pointwise) thresholds (i.e., a LPR significance threshold of 1.3) to determine which individual effects were significant at that locus.

Results

The dam and nurse variances generated by the variance partitioning analysis are shown in Figure S2, where dam is the same as family in this analysis, rather than corresponding solely to prenatal maternal effects. It can be clearly seen that nurse effects peak at week 2, where they account for ∼35% of the variance, and rapidly decline to <5% by week 6. In contrast, the dam variance starts high (∼32% at week 1), slowly increases to a peak of ∼45% at week 6, and then declines slightly to asymptote at just over 40% of the variance.

The QTL mapping analysis identified 13 loci showing maternal effects. Most of these loci (12 of 13) show prenatal (uterine) effects (Table 1), with 6 of 13 showing postnatal maternal effects (Table 2). Five loci show evidence of both a pre- and a postnatal effect (meQTL2.1, meQTL2.2, meQTL7.1, meQTL11.1, and meQTL17.1). Nearly all loci (12 of 13) also show some evidence of direct effects (Table 3), although all but 3 of these loci (meQTL6.1, meQTL7.1, and meQTL11.1) show relatively minor effects that are limited to a few weight or growth measures. Two QTL were identified on chromosome 2 that show different patterns of effect: meQTL2.1 shows an early dominance prenatal maternal effect and an additive postnatal maternal effect later in life, while meQTL2.2 shows a small additive prenatal maternal effect on growth and an additive postnatal maternal effect on early weights. Table S4 provides parameter estimates for each of these effects and the significance value of each of the significant effects.

Table 1. Prenatal maternal effects of meQTL.

	meQTL	1.1	2.1	2.2	6.1	7.1	9.1	11.1	12.1	15.1	16.1	17.1	18.1	R2
cM		0.9	37.5	53.8	74.9	57.0	47.6	52.0	36.9	18.1	18.0	15.8	1.8
Mb		11.0	62.6	112.1	147.3	122.7	87.2	90.6	83.7	44.6	31.9	32.8	10.1
C.I. (Mb)		3.2–37.8	39.6–75.9	82.2–118.0	140.5–147.3	117.6–134.5	73.1–105.3	84.8–96.6	77.2–94.8	32.2–69.5	25.4–44.4	28.5–46.6	3.7–16.4
Traits	Early		+dM		+aM–dM	–aM		+dM		+aM	+dMa		–aM–dM
	Mid	+aM			+aM–dM			+dM	+aM	+aM +dM	+dM	+dM
	Late	+aMa			+aM		+dM	+dM	+aM		+dM		–aM
	Week 1	+aM	+dM		+aM–dM	–aM	–aM	+dM		+aM	+dM		–aM	29.5
	Week 2	+aM	+dM		–dM	–aM		+dM		+dM	+dM		–dM	20.6
Weaning	Week 3	+aM	+dM		+aM–dM	–aM		+dM	+aM	+aM+dM	+dM	+dM	–dM	33.6
	Week 4	+aM	+dM		+aM–dM	–aM		+dM	+aM	+aM+dM	+dM	+dM	–dM	35.4
	Week 5	+aM			+aM–dM			+dM	+aM	+aM	+dM	+dM	–aM	23.8
	Week 6	+aMa			+aM		+dM	+dM	+aM		+dM		–aM	22.8
	Week 7	+aMa			+aM		+dM	+dM	+aM		+dM		–aM	22.6
	Week 8	+aMa			+aM		+dM	+dM	+aM		+dM			17.2
	Week 9	+aMa			+aM		+dM	+dM			+dM			15.3
	Week 10	+aMa			+aM		+dM	+dM			+dM			17.3
	Grow 1–2						–aM							3.8
	Grow 2–3		+dM	+aM	–dM	–aM			+aM	+aM	+dM	+dM		23.8
	Grow 1–3				–dM	–aM			+aM	+dM	+dM		–dM	14.9

For each of the 11 meQTL that map to the dam genotypes (indicating prenatal effects), we present the map position [in centimorgans (cM) and in megabases (Mb)] with confidence interval (in Mb) and the temporal pattern of effect. Early, mid, and late indicate the significance of the multivariate test. The effects on each of the weekly weight measurements and the three preweaning growth phases are given by the type (additive, a_M, or dominance, d_M) and sign of effect (i.e., positive or negative). Entries in boldface type are significant using the chromosome-level significance test. Numerical values of all effects and significance tests are given in Table S4. The proportions of variance accounted for by the set of QTL (R²) for each trait are also included.

^aSignificant using the genome-wide threshold.

Table 2. Postnatal maternal effects of meQTL.

	meQTL	2.1	2.2	7.1	11.1	17.1	19.1	R2
cM		37.5	53.8	57.0	52.0	15.8	49.7
Mb		62.6	112.1	122.7	90.6	32.8	53.8
C.I. (Mb)		39.6–75.9	82.2–118.0	117.6–134.5	84.8–96.6	28.5–46.6	47.3–58.6
Traits	Early		+aNa	+dN		–aN	+aN
	Mid	+aN		+dN	+dN	–aN	+aN–dN
	Late					–aN	+aN–dN
	Week 1		+aN	+dNa	–aN	–aN		12.6
	Week 2		+aN	+dN	+dN	–aN	–dN	12.9
Weaning	Week 3		+aN+dN	+dN		–aN	+aN	16.2
	Week 4	+aN		+dN	+dN	–aN	+aN–dN	16.6
	Week 5	+aN		+dN	+dN	–aN	+aN–dN	12.7
	Week 6	+aN			+dN	–aN	+aN–dN	10.6
	Week 7	+aN				–aN	+aN–dN	8.8
	Week 8	+aN				–aN	+aN–dN	8.7
	Week 9	+aN			+dN	–aN	–dN	8.3
	Week 10	+aN			+dN	–aN	–dN	7.6
	Grow 1–2						–dN	3.6
	Grow 2–3		+aN+dN	+dN			+aN	11.9
	Grow 1–3		+aN				+aN–dN	10.0

For each of the five meQTL that map to the nurse genotypes (indicating postnatal effects) we present the map position [in centimorgans (cM) and in megabases (Mb)] with the confidence interval (in Mb) and the temporal pattern of effect. Early, mid, and late indicate the significance of the multivariate test. The effects on each of the weekly weight measurements and the three preweaning growth phases are given by the type (additive, a_N, or dominance, d_N) and sign of effect (i.e., positive or negative). Entries in boldface type are significant using the chromosome-level significance test. Numerical values of all effects and significance tests are given in Table S4. The proportions of variance accounted for by the set of QTL (R²) for each trait are also included.

^aSignificant using the genome-wide threshold.

Table 3. Direct effects of meQTL.

	meQTL	1.1	2.1	2.2	6.1	7.1	9.1	11.1	12.1	15.1	16.1	18.1	19.1	R2
cM		0.9	37.5	53.8	74.9	57.0	47.6	52.0	36.9	18.1	18.0	1.8	49.7
Mb		11.0	62.6	112.1	147.3	122.7	87.2	90.6	83.7	44.6	31.9	10.1	53.8
CI (Mb)		3.2–37.8	39.6–75.9	82.2–118.0	140.5–147.3	117.6–134.5	73.1–105.3	84.8–96.6	77.2–94.8	32.2–69.5	25.4–44.4	3.7–28.1	47.3–58.6
Traits	Early				+a +i	+a +d					+a	–i
	Mid				+aa	+a		+a
	Late				+aa+i	+a		+aa
	Week 1				+i	+d						–i		1.6
	Week 2					+a								1.2
Weaning	Week 3				+a +i	+d				+d	+a			3.0
	Week 4				+aa			+a						4.5
	Week 5				+aa	+a		+a						8.6
	Week 6				+aa	+a	+i	+aa			+a			11.0
	Week 7	+i		+a	+aa+i	+a	+i	+a						11.6
	Week 8	+i	+a	+a	+aa+i	+a		+a						10.4
	Week 9			+a	+aa	+a		+a						7.3
	Week 10	+i	+a	+a	+a	+a								8.0
	Grow 1–2					–i		+d		+a			–i	5.3
	Grow 2–3				+a +i	+d								2.3
	Grow 1–3					–i			+i	+a +d				2.9

For each of the eight meQTL that map to the offspring genotypes (indicating a direct effect) we present the map position [in centimorgans (cM) and in megabases (Mb)] with the confidence interval (in Mb) and the temporal pattern of effect. Early, mid, and late indicate the significance of the multivariate test. The effects on each of the weekly weight measurements and the three preweaning growth phases are given by the type (additive, a; dominance, d; or imprinting, i) and sign of effect (i.e., positive or negative). Entries in boldface type are significant using the chromosome-level significance test. Numerical values of all effects and significance tests are given in Table S4. The proportions of variance accounted for by the set of QTL (R²) for each trait are also included.

^aSignificant using the genome-wide threshold.

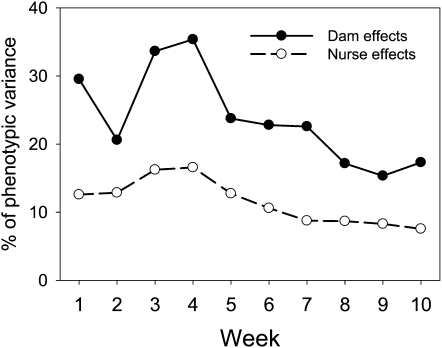
Overall, maternal effects (pre- and postnatal together) account for the most variance in body weight at weeks 3 and 4, with the proportion declining rapidly from week 4 to 5, after which it declines slowly (Figure 1). This contrasts with the pattern of direct effects (see Figure 1), where the proportion of variance explained by direct effects increases steadily from week 1 to week 6, at which time it plateaus.

Figure 1.

Relative contribution of maternal and direct effects to variation in body weight from week 1 to week 10 of age. Values are given as a percentage of phenotypic variance. Direct effects data are from Table 2 in Hager et al. (2009).

For most prenatal maternal-effect loci, the temporal patterns are highly variable, with some loci having stronger effects early in life (e.g., meQTL2.1 and meQTL15.1), while others have stronger effects later in life (e.g., meQTL1.1). The overall trend of effects, as reflected in the proportion of variance explained by the loci, shows that the variance explained by prenatal (dam) effects is highest for weeks 3 and 4 weights (R² = 33.6% and 36.4%, respectively) and remains >20% through week 7. Interestingly, prenatal maternal effects continue to explain a large proportion of variation in body weight into adulthood (after week 7), where the proportion asymptotes to values between ∼15 and 17% of the variance (see Table 1 and Figure 2).

Figure 2.

Relative contribution of prenatal (dam) and postnatal (nurse) effects on body weight from week 1 to week 10 of age. Values are given as a percentage of phenotypic variance.

For two of the six postnatal maternal-effect loci the effects are largely restricted to preweaning or just after weaning, and effects generally decline after weaning (Table 2). This can be seen in the proportion of variance explained, which peaks around weaning (R² = 16.2% at week 3 and 16.6% at week 4) and declines to low levels by week 10 (R² = 7.5%). Postnatal maternal effects explain a lower proportion of phenotypic variation than prenatal effects for all ages (Figure 2).

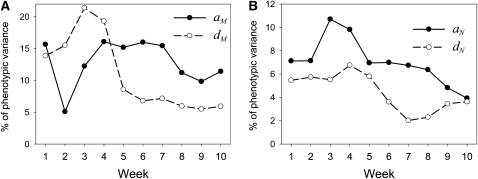
Dominance prenatal maternal effects generally contribute more variation to body weight through week 4 than do additive prenatal maternal effects, while the reverse is true of later body weights (Figure 3a). As a result, by week 6 dominance prenatal effects are relatively minor while additive prenatal effects continue to explain a large proportion of phenotypic variation. The expected net effect of these additive prenatal maternal effects to the difference between the SM/J and LG/J lines (i.e., twice the sum of additive effects) is positive for all weights after weaning, with prenatal maternal effects contributing as much as a 1.8 standard deviation difference in weight between the homozygotes at week 10 (see Table S4 and Figure S3). For postnatal maternal effects, additive effects are generally more important than dominance effects (Figure 3b), with the proportion of variation explained by additive effects peaking at weaning (week 3) and then declining. The expected net contribution of additive postnatal maternal effects to the difference between the SM/J and LG/J lines is positive (but small) for all weeks, peaking at weaning (see Table S4 and Figure S3).

Figure 3.

Relative contribution of additive and dominance maternal effects to variation in body weight from week 1 to week 10 of age. Values are given as a percentage of phenotypic variance. (A) Additive (a_M) and dominance (d_M) dam (prenatal) effects through time. (B) Additive (a_N) and dominance (d_N) nurse (postnatal) effects through time.

Discussion

Maternal effects in mammals are well described from a variance components perspective in both captive (Rutledge et al. 1972; Wilson and Reale 2006) and natural populations (Wilson et al. 2005; Mcadam 2009; Wilson and Festa-Bianchet 2009). These studies have shown that they are often one of the largest components of variation for traits expressed early in life, with effects generally eroding after weaning (see Wilson and Festa-Bianchet 2009 for a review of persistence), but often persisting at a low level into adulthood (e.g., Riska et al. 1984, 1985; Cowley et al. 1989; Jarvis et al. 2005; Casellas et al. 2009). It is important to keep in mind that most of our understanding of maternal effects has come from studies that used approaches that cannot differentiate between genetic- and environmentally based maternal effects (but exceptions exist; e.g., Wilson et al. 2005), so there is a particular dearth of information on the genetic basis of maternal effects. Maternal effects are especially well documented in mice (Legates 1972; Rutledge et al. 1972; Cheverud et al. 1983; Riska et al. 1984, 1985), although most studies are limited to estimations of postnatal effects identified using experimental cross-fostering after birth (but see Brumby 1960, Cowley et al. 1989, Atchley et al. 1991, and Rhees et al. 1999 for exceptions). Postnatal effects have also been shown to be an important component of phenotypic variation in the population of mice used in this study (Kramer et al. 1998), and experimental crosses suggest that prenatal effects are also important (Jarvis et al. 2005).

Although it is clear from the large number of variance partitioning studies that maternal effects are important in mammals, there have been very few studies of the genomic basis of maternal effects. Most noteworthy is the study by Casellas et al. (2009), who mapped maternal effects of two small genomic regions (accounting for ∼5% of the genome) on adult traits in a subcongenic population of mice. They identified loci in both genomic regions that had apparent maternal effects on adult body size and obesity traits but did not differentiate between pre- and postnatal influences and did not account for genomic imprinting effects, which could have led to the appearance of these apparent maternal effects (Hager et al. 2008b). Their study strongly suggests a major role for maternal-effect loci, with persistent effects on adult traits, originating from just a small portion of the genome. There are also limited examples of the genomic basis of maternal effects from the livestock literature, which have generally examined parturition-related traits that are associated with maternal effects. For example, Olsen et al. (2009) mapped direct and maternal effects on birthing-related traits (stillbirth and dystocia) by using information from a massive pedigree (with nearly a million records). They used the sons and daughters of sires in the pedigree to assess the contribution of the sires’ genotypes to direct effects (through the sons) and maternal effects (through the daughters). The analysis identified three loci with apparent maternal effects on dystocia, although it is unclear whether such birthing traits are maternal or offspring traits and, therefore, whether these are maternal or direct effects. Similarly, Sahana et al. (2011) examined direct and maternal effects on calving traits (ease of birth, stillbirth, and birthweight), using a very large set of “progeny-tested bulls”. Unlike Olsen et al. (2009), however, Sahana et al. (2011) found several maternal-effect loci, with a large fraction having both direct and maternal effects. These studies are similar to others from the livestock literature, where effects on birthing traits are examined and, therefore, are limited to prenatal effects. Here we have built upon this previous work by using an experimental population that provides a genome-wide view of maternal effects, and by using experimental cross-fostering, we are able to develop a novel approach that differentiates prenatal from postnatal effects.

Our analysis identified a total of 13 meQTL affecting body weight and weight gain. Most of these loci (12/13) have prenatal effects (Table 1), with nearly half (6/13) having postnatal effects (Table 2). Five loci showed both pre- and postnatal effects, suggesting that the genetic architecture of postnatal effects may be tied to that of prenatal effects, which is perhaps surprising given that they are likely to arise from very different origins (e.g., uterine environment vs. nest environment). Overall, these maternal genetic effects account for more variance than direct genetic effects for weight through the first 5 weeks of age (on the basis of direct-effects data from Hager et al. 2009), being nearly equal at 6 weeks, after which direct genetic effects account for more variance in the remaining weeks (Figure 1). Most loci showed evidence of some direct effect in addition to a maternal effect, although the evidence for the direct effect was often weak in that effects were often small and temporally limited. The co-occurrence of direct and maternal effects is perhaps not surprising given that maternal effects may be associated with maternal body size, either because maternal body size causes the maternal effect or because the two have a shared causal origin (e.g., both are influenced by growth factors or insulin-related traits). It is also not surprising given that quantitative genetic studies have generally found genetic correlations between direct and maternal effects (Cheverud 1984).

One of the most striking patterns in our results is the presence of significant maternal effects that persist well after weaning, including those from eight meQTL that influenced weight all the way through week 10. Interestingly, most of these persistent maternal effects (five of eight) are prenatal in origin. This pattern is also reflected in the fact that prenatal maternal effects account for a larger proportion of phenotypic variance in body weight at all ages (Figure 2). While postnatal effects peak in importance around weaning and then gradually fade, accounting for only ∼8% of the phenotypic variance by week 10, prenatal effects peak in importance at around weaning but continue to account for 15–17% of the phenotypic variance in adult weight. Because there is more power to detect postnatal compared to prenatal maternal effects (Table S3), the finding of more prenatal maternal effects than postnatal effects cannot be attributed to a simple difference in power and is in direct opposition to the difference in power. Although it may appear surprising that prenatal effects are more persistent than postnatal effects, these results are consistent with those reported by Jarvis et al. (2005) for adult obesity and diabetes-related traits in the LGXSM recombinant inbred strains (Hrbek et al. 2006).

We identified maternal-effect QTL on both of the chromosomes (2 and 7) examined in the study by Casellas et al. (2009) (see above), although the locations of the chromosome 7 QTL are relatively far apart. The chromosome 2 QTL are in overlapping regions, but the locus identified by Casellas et al. (2009) has effects on late adult traits, while meQTL2.2 has effects limited to earlier life, although it is important to note that Casselas et al. did not examine newborn or juvenile weights. Interestingly, a previous analysis of QTL affecting litter size in this same population (Peripato et al. 2004) identified a locus on chromosome 12 that maps within the physical confidence interval for meQTL12.1. However, the maternal effect of this locus is much stronger when the variance in weight contributed by litter size at birth is removed and the effect is no longer significant when this variation is included in the phenotypes tested. This strongly suggests that the meQTL at this location is unrelated to litter size and indeed provides strong evidence to the contrary.

Perhaps most interesting among the prenatal maternal-effect QTL are meQTL1.1 and meQTL9.1, which show little preweaning effect but their effect increases in importance through time. For example, by week 6, meQTL1.1 accounts for >5% of the phenotypic variance and by week 10 it accounts for 7.8% of the variance. This is a substantially larger proportion of the variance in week 10 body weight than is explained by any single direct-effect locus on these same traits in this population (Hager et al. 2009). The pattern seen for meQTL1.1 suggests that prenatal maternal effects may alter the developmental program in a way that is manifested later in life, perhaps through some sort of “priming” effect (Barker 1998). This sort of early developmental origin of adult phenotypes has been a major topic in human health and disease (Gluckman et al. 2010), but may be a general phenomenon wherein prenatal maternal effects contribute a potentially important component of adult phenotypic variation. Thus, it may be a general pattern that prenatal effects are more persistent, or more important later in life, because early developmental events may fundamentally alter physiological processes (Gluckman and Hanson 2004; Myatt 2006; Barker et al. 2010; Gillman 2010). Such variation is missed in most quantitative genetic studies focused on direct effects and even in studies that estimate maternal effects by experimental cross-fostering. This is because cross-fostering is necessarily done at birth, and thus this design cannot account for prenatal effects.

Because many prenatal maternal-effect loci contribute to variation in adult body weight, they may have accounted for some of the evolutionary divergence of the LG/J and SM/J inbred mouse strains. Interestingly, prenatal maternal effects appear to have contributed much more to the divergence of the two lines in adult body weight than postnatal maternal effects (see Figure S3), as measured by the difference between the LL and SS homozygotes (i.e., twice the additive effect), with the net effect of all prenatal maternal effects contributing to over one standard deviation difference in body weight between LL and SS homozygotes by week 4. For example, meQTL1.1 has a large additive effect (more than one-third of a standard deviation) on the adult body weight traits that were a target of the original selection (which was body weight at 60 days of age). Thus this locus may have been a target of the original directional selection regime in one population or the other. In contrast, meQTL7.1 has an additive direct effect, but not a maternal effect, on week 9 body weight (our trait closest to the original age of selection), where the allele derived from the Large strain increases weight compared to the allele from the Small strain (see Table 3). As a result, it is possible that the negative maternal effect of meQTL7.1 on preweaning body weight may be a correlated response to selection for differences in later life body weight.

Of course, the maternal-effect loci we have identified must also directly affect variation in some maternal traits that themselves influence offspring trait variation, even if we have not identified these maternal traits in our analysis. That is, we expect maternal-effect loci to necessarily have direct effects on maternal traits and indirect effects on offspring traits, with these two pleiotropic effects functionally linked through the influence of the maternal traits on offspring traits (Kirkpatrick and Lande 1989). Although this pleiotropic link between maternal and offspring traits must exist at some level (i.e., maternal effects must ultimately be caused by some feature of the mothers), we know very little about the connection from maternal loci to offspring trait variation through a set of known maternal traits. Maternal traits like milk quality characteristics, which may be largely responsible for maternal effects on offspring growth traits in livestock species (Meyer et al. 1994), have been successfully mapped in various livestock species (e.g., Gutierrez-Gil et al. 2009; Jiang et al. 2010), making such loci candidates for maternal effects on offspring developmental traits. However, searches for candidate genes associated with obvious maternal traits, such as lactation, nursing, or nesting traits, in the intervals around the maternal-effect loci we identified did not yield any specific candidate genes, which is perhaps not surprising since these traits have few identified candidates in the genome (Blake et al. 2011). One intriguing candidate gene for a prenatal effect is the placental growth factor gene, which is located at almost the exact genomic location as meQTL12.1. This gene has been suggested to play a role in birthing-related traits in cattle (Seidenspinner et al. 2011) and in preeclampsia in humans (Akolekar et al. 2008) and is known to affect adipose tissue development (Lijnen et al. 2006) and contribute to hyperinsulinemia in mice (Hemmeryckx et al. 2008).

Overall, we have demonstrated that, by using combined genotype information from parents and offspring, one can statistically disentangle direct and maternal genetic effects. When individuals have been cross-fostered, these maternal genetic effects can be decomposed into those attributable to the genotype of the mother, representing prenatal maternal effects if cross-fostering is done at birth, and those attributable to the nurse, representing postnatal maternal effects. Because maternal effects, and presumably their genetic component, contribute more variation to traits expressed early in life than do direct genetic effects, they are a crucial, but rarely assessed, component of genetic architecture. As a result, our understanding of traits expressed early in life is biased and incomplete. Our approach allows maternal genetic effects to be included in studies of the genetic architecture of traits in both experimental populations, where cross-fostering is used to manipulate maternal–offspring interactions, and natural populations not subjected to experimental intervention. In the latter case, one would use our approach, but variation in offspring traits would be mapped only to the maternal (dam) genome (so there is no separate nurse effect). This approach could be directly integrated into the methods developed for mapping loci in natural populations (Slate et al. 2010). Consequently, the approach we have outlined here provides a means through which we can begin to understand the importance of maternal effects in the genetic architecture of complex traits.