Pervasive Recombination and Sympatric Genome Diversification Driven by Frequency-Dependent Selection in Borrelia burgdorferi, the Lyme Disease Bacterium

Abstract

How genomic diversity within bacterial populations originates and is maintained in the presence of frequent recombination is a central problem in understanding bacterial evolution. Natural populations of Borrelia burgdorferi, the bacterial agent of Lyme disease, consist of diverse genomic groups co-infecting single individual vertebrate hosts and tick vectors. To understand mechanisms of sympatric genome differentiation in B. burgdorferi, we sequenced and compared 23 genomes representing major genomic groups in North America and Europe. Linkage analysis of >13,500 single-nucleotide polymorphisms revealed pervasive horizontal DNA exchanges. Although three times more frequent than point mutation, recombination is localized and weakly affects genome-wide linkage disequilibrium. We show by computer simulations that, while enhancing population fitness, recombination constrains neutral and adaptive divergence among sympatric genomes through periodic selective sweeps. In contrast, simulations of frequency-dependent selection with recombination produced the observed pattern of a large number of sympatric genomic groups associated with major sequence variations at the selected locus. We conclude that negative frequency-dependent selection targeting a small number of surface-antigen loci (ospC in particular) sufficiently explains the maintenance of sympatric genome diversity in B. burgdorferi without adaptive divergence. We suggest that pervasive recombination makes it less likely for local B. burgdorferi genomic groups to achieve host specialization. B. burgdorferi genomic groups in the northeastern United States are thus best viewed as constituting a single bacterial species, whose generalist nature is a key to its rapid spread and human virulence.

GENETIC discontinuity, the basis of biodiversity, is ubiquitous in prokaryotes as well as in eukaryotes. Most bacterial populations display a highly clonal genetic structure, in which the observable number of multilocus genotypes is far fewer than the number expected under the assumption of free recombination (Maynard Smith et al. 1993). Bacterial clonality was originally thought of as a result of a lack or rarity of recombination among asexually reproducing and independently evolving clones (Ochman and Selander 1984). Since then, molecular surveys of natural bacterial populations using protein electrophoresis, multilocus sequencing typing (MLST), and whole-genome sequencing revealed that horizontal genetic exchange is in fact often more frequent than point mutations in bacteria, including species known as strongly clonal (Maynard Smith et al. 1993; Feil and Spratt 2001; Didelot and Maiden 2010; Retchless and Lawrence 2010). A paradox thereby arises as to how distinct clonal groups may rise and be maintained in local bacterial populations in the absence of intrinsic gene-flow barriers akin to reproductive isolation between eukaryotic species. A widely held hypothesis is adaptive specialization, in which distinct genotypes coexisting within local bacterial populations are thought to represent ecologically differentiated subpopulations or “ecotypes” (Cohan 2002; Koeppel et al. 2008). In the ecotype model, though, natural selection needs to be persistent and strong enough to overcome the homogenizing effects of genetic exchange (Doolittle and Papke 2006; Fraser et al. 2007; Lawrence and Retchless 2010). Frequency-dependent selection (FDS) is a form of balancing selection capable of maintaining genetic diversity at an antigenic locus in a pathogen without the assumption of differentially adapted alleles (Levin 1988; Takahata and Nei 1990; Wiener 1996). To date, however, genome-wide consequences of FDS are largely unknown and FDS as a possible common cause of sympatric genome diversity in bacteria has not received nearly as much attention as the ecotype model.

Here we use comparative population genomics and computer simulation to understand the origin and maintenance of high local genomic diversity in natural populations of Borrelia burgdorferi sensu lato (“B. burgdorferi s.l.” hereafter), a bacterial species complex that includes Lyme disease agents. In many ways B. burgdorferi s.l. represents an ideal system for studying the processes of bacterial divergence in nature. First, B. burgdorferi s.l. shows a strong biogeographic structure as a result of being an obligate and tick-borne parasite of vertebrate hosts (Kurtenbach et al. 2006; Hoen et al. 2009). Local B. burgdorferi s.l. populations, especially those in the northeastern and midwestern United States, appear to have single recent origins so that possibilities such as constant migration maintaining local genetic diversities could be excluded (Qiu et al. 2008; Brisson et al. 2010). Second, local B. burgdorferi s.l. populations are highly diverse, consisting of a large number of distinct genomic groups coexisting in a strictly sympatric fashion, often co-infecting a single individual vertebrate host or tick vector (Wang et al. 1999b; Qiu et al. 2002; Brisson and Dykhuizen 2004; Bunikis et al. 2004). Third, the population structure of B. burgdorferi s.l. is representative of bacterial species in that it is neither strictly clonal nor freely recombining (Qiu et al. 2004; Travinsky et al. 2010).

The selective mechanisms underlying the origin and maintenance of local genomic diversity in B. burgdorferi s.l. remain unclear. Initial surveys of genetic diversity at loci under strong immune-escape selection revealed evenly distributed allele frequencies consistent with frequency-dependent selection (Qiu et al. 1997, 2002). An alternative, although not necessarily mutually exclusive, hypothesis is that distinct clonal groups are maintained by host specialization (Brisson and Dykhuizen 2004, 2006). Here, we compare newly and previously sequenced genomes to investigate how sympatric genome diversification in B. burgdorferi s.l. might have originated and be maintained under the joint influences of recombination and natural selection. We first estimated recombination rates on the core, most conserved parts of the B. burgdorferi s.l. genome, which revealed pervasive localized recombination throughout the genome. We then tested the compatibility of this observation with various forms of natural selection using computer simulations, which showed that frequency-dependent selection acting on a few antigenic loci is capable of maintaining distinct genomic groups in local B. burgdorferi s.l. populations despite frequent and pervasive recombination. In contrast, frequent recombination makes it less likely that these genomic groups are maintained by host specialization.

Materials and Methods

Strain source, genome sequencing, and ortholog identification

We compared 23 completed and draft B. burgdorferi s.l. genomes and focused on the comparison of 14 conspecific genomes of the genospecies B. burgdorferi sensu stricto (B. burgdorferi s.s.) (Table 1) (Fraser et al. 1997; Casjens et al. 2000, 2011a, 2011b; Glockner et al. 2004, 2006; Schutzer et al. 2011). Ten of the B. burgdorferi s.s. genomes were from sympatric isolates from the northeastern United States (Table 1). The new genomes were sequenced by the following procedures. Briefly, genomic DNA was obtained from 10 ml of low-passage, log-phase cultures as described previously (Qiu et al. 2008). Genomes were sequenced to an estimated eightfold coverage by the random shotgun method followed by the Sanger DNA sequencing method, as described in Nelson et al. (2004). For plasmid closure, one small insert plasmid library (2–3 kb) and one medium insert plasmid library (7–8 kb) were constructed for each strain and sequenced to approximately fivefold and threefold coverages, respectively. The sequences from each strain were assembled using a combination of the TIGR Assembler (Sutton et al. 1995) and the Celera Assembler (Myers et al. 2000).

Table 1. Strain and genome sources.

Strain	Genospecies	ospC type	Geographic origin	Biological sourcea	Project accessionb	Genome report
B31	B. burgdorferi s.s.	A	New York	I. scapularis	PRJNA3	Fraser et al. (1997)
64b	B. burgdorferi s.s.	B1	New York	Human	PRJNA28633	Schutzer et al. (2011)
ZS7	B. burgdorferi s.s.	B2	Germany	I. ricinus	PRJNA19839	Schutzer et al. (2011)
JD1	B. burgdorferi s.s.	C	Massachusetts	I. scapularis	PRJNA29359	Schutzer et al. (2011)
CA-11.2A	B. burgdorferi s.s.	D	California	I. pacificus	PRJNA28629	Schutzer et al. (2011)
N40	B. burgdorferi s.s.	E	New York	I. scapularis	PRJNA29357	Schutzer et al. (2011)
72a	B. burgdorferi s.s.	G	New York	Human	PRJNA21003	Schutzer et al. (2011)
156a	B. burgdorferi s.s.	H	New York, US	Human	PRJNA19835	Schutzer et al. (2011)
WI91-23	B. burgdorferi s.s.	I	Wisconsin, US	Bird	PRJNA28627	Schutzer et al. (2011)
118a	B. burgdorferi s.s.	J	New York	Human	PRJNA21001	Schutzer et al. (2011)
297	B. burgdorferi s.s.	K	Connecticut	Human	PRJNA29361	Schutzer et al. (2011)
29805	B. burgdorferi s.s.	M	Connecticut	I. scapularis	PRJNA28621	Schutzer et al. (2011)
Bol26	B. burgdorferi s.s.	S	Italy	I. ricinus	PRJNA19837	Schutzer et al. (2011)
94a	B. burgdorferi s.s.	U	New York	Human	PRJNA20999	Schutzer et al. (2011)
SV1	B. finlandensis		Finland	I. ricinus	PRJNA28631	Casjens et al. (2011a)
DN127	B. bissettii		California	I. pacificus	PRJNA29363	S. E. Schutzer et al., (unpublished results)
PKo	B. afzelii		Germany	Human	PRJNA17057	Glockner et al. (2006)
ACA-1	B. afzelii		Sweden	Human	PRJNA19841	Casjens et al. (2011b)
PBi	B. bavariensis		Germany	Human	PRJNA12554	Glockner et al. (2004)
PBr	B. garinii		Denmark	Human	PRJNA28625	Casjens et al. (2011b)
Far04	B. garinii		Denmark	Bird	PRJNA29573	Casjens et al. (2011b)
VS116	B. valaisiana		Switzerland	I. ricinus	PRJNA19843	S. E. Schutzer et al., (unpublished results)
A14S	B. spielmani		The Netherlands	I. ricinus	PRJNA28635	S. E. Schutzer et al., (unpublished results)

^aI. scapularis, I. pacificus, and I. ricinus, Ixodes (tick) vectors; Human, tissues from Lyme disease patients; Bird, bird blood.

^bNCBI BioProject accession (www.ncbi.nlm.nih.gov/bioproject).

Replicon identities of contigs were determined by comparisons with the completed genomes (B31, JD1, N40, and 297), using NUCMER (Delcher et al. 2002). ORFs on each contig were identified by using GLIMMER (Delcher et al. 1999). Orthologous ORFs were identified by clustering them into homologous protein families using all-against-all BLASTp (Altschul et al. 1997) followed by MCL (Enright et al. 2002). Orthologs were distinguished from paralogs on the basis of gene order, using customized synteny maps. Protein sequence alignments were constructed using ClustalW (Larkin et al. 2007). Codon alignments were derived from protein alignments using customized PERL scripts based on BioPerl (Stajich et al. 2002). Whole-plasmid sequence alignments were obtained by using ClustalW-MPI (Li 2003).

Linkage analysis

We identified SNPs segregating among conspecific B. burgdorferi s.s. strains using LDhat (version 2.1) and used LDhat again to estimate recombination rates between all pairs of SNP sites (McVean et al. 2002). In LDhat the recombination rate is estimated on the basis of the “four-gamete test” of recombination (Hudson and Kaplan 1985). SNP pairs showing scores of >2.0 or <2.0 in a likelihood test (implemented in LDhat) have significantly high and low recombination rates relative to the average rate of all SNP pairs, respectively. Results of linkage analysis were formatted by using customized PERL scripts and plotted using the software packages Circos (Krzywinski et al. 2009) and R (http://r-project.org).

Phylogenetic reconstruction

We used a strongly linked portion (bbb01–bbb14) of the cp26 plasmid to infer phylogenetic relationships among B. burgdorferi s.s. clonal groups. We obtained a concatenated alignment of 14 genes from 15 strains (14 B. burgdorferi s.s. and SV1 used as an outgroup). We used two methods of phylogenetic reconstruction, including a Bayesian method using MrBayes (v2.1) (Huelsenbeck and Ronquist 2001) and a maximum-likelihood method with 100 bootstrapped alignments using DNAML in PHYLIP (Felsenstein 1989). Branch support was measured with posterior probabilities obtained from MrBayes and bootstrap values from PHYLIP. Phylogenies and gene trees were plotted and annotated using the R package APE (Paradis et al. 2004) and FigTree (http://tree.bio.ed.ac.uk/software/figtree/).

Estimating recombination rates using sister genomes

Sequence differences between two recently diverged phylogenetic sister strains are more likely than those between distantly related genomes to be due to single—rather than multiple—events of point mutations or recombination. As such, direct comparison of sister-group genomes reveals relative rates of recombination to point mutation (Guttman and Dykhuizen 1994). For each SNP segregating between a pair of sister genomes, it is identified as a point mutation if it is unique across all aligned sequences and as recombination if it occurs in non–sister-group genomes as well (i.e., a homoplasy). In estimating the number of gene-conversion events, consecutive SNPs sharing the same phylogenetic pattern were combined into a single count.

Codon-based simulations of bacterial genome evolution

Codon-based fitness functions:

We simulated a population with a constant size of N = 500 haploid genomes. Each genome consisted of four disjoint 500-codon genes. When a gene evolved neutrally, fitness of each codon (w) remained at 1 regardless of synonymous or nonsynonymous substitutions. When a gene was under purifying selection (mimicking a housekeeping locus), each nonsynonymous substitution (relative to the founding amino acid state) resulted in a codon with its fitness reduced by a fraction: w = 1 − s_pur. When a gene was under negative frequency-dependent selection, fitness of a codon was a linearly decreasing function of the population frequency of its amino acid state: 1 − s_fdsx_i, where x_i is the population frequency of amino acid state i and s_fds is the selection coefficient (Takahata and Nei 1990; Neuhauser 1999). When a gene was under directional selection, each nonsynonymous substitution resulted in a codon with a fitness w = 1 while fitness of codons with the founding amino acid state was reduced: w = 1 − s_dir. Fitness of an individual was the multiplicative product of the fitness of its composite codons: W = ∏w.

Evolutionary algorithms:

To closely represent the B. burgdorferi s.l. genome, the codon composition and substitutions were simulated on the basis of the codon usage table (Nakamura et al. 2000) and a 4:1 transition-to-transversion ratio (W. G. Qiu, unpublished results, based on maximum-likelihood analysis of B. burgdorferi s.l. orthologs). In the beginning of each generation, a total number of U mutations (Poisson distributed) were added to each individual at randomly chosen codon positions. A chosen codon was replaced by one of the nine possible codons that differ from the parental codon by one base (stop codons excluded). We then introduced a total number of R gene-conversion events (Poisson distributed) into each individual, using the Didelot and Falush algorithm with a tract length of δ = 30 codons (exponentially distributed) (Didelot and Falush 2007). Briefly, the loci were assumed to be sufficiently far apart so that each gene-conversion event affected only a single gene. For each recipient genome, a donor genome was randomly chosen from the population. A gene-conversion event spans the first codon of a gene with the probability of δ/(bδ + L − b), where δ is the mean of exponentially distributed tract lengths of a gene-conversion event, b is the number of genes, and L is the total length of genes. Gene conversion starts within a gene block with the probability of 1/(bδ + L − b).

Genetic drift and natural selection were applied in a single step following algorithms by Hudson and Kaplan (1995) and Takahata and Nei (1990). Specifically, an individual was randomly chosen from the parental pool and a random number 1 ≥ P ≥ 0 was generated. If fitness of an individual W ≥ p, this individual was accepted as a parent for the next-generation population. Otherwise it was rejected and the next individual was chosen with replacement. The above process continued until the constant population size N was reached. To improve computational efficiency and reduce rounding errors, fitness of each individual was calculated using logarithms and normalized to between 0.5 and 1, using a linear extrapolation $W_{\text{norm}}=\{1+(W-W_{\text{min}})/(W_{\text{max}}-W_{\text{min}})\}/2$, where W_norm is the normalized fitness, and W_min and W_max are, respectively, the minimum and maximum fitness values in a population.

Program validation:

At regular intervals during simulation, a sample of n individuals was drawn and assayed for nucleotide diversity (π). We kept a record of reproductive (but not recombination) ancestors of each individual during the simulation so that gene genealogy of sampled individuals could be reconstructed. To validate the simulation program, we first simulated genome evolution under strictly neutral conditions by setting all selection coefficients to zero and compared the π-values of the sampled alleles with the neutral expectation π₀ = 2Nμ. We ran neutral evolution under three gene-conversion rates, R = 0, R = U, and R = 5U, and named these models NEU1, NEU2, and NEU3, respectively. Second, we simulated genome evolution under the influence of purifying selection at one locus and at the same three levels of gene conversion. We named these simulations background-selection models (BKG1, BKG2, and BKG3). The expected nucleotide diversity at a neutral locus linked to a locus under background selection is reduced relative to π₀. We compared the π-values of the neutral locus under the BKG simulation models with an analytical expectation of background selection: ${\pi }_{\text{bkg}}={\pi }_0\exp \{-U/(s+R)\}$ (Hudson and Kaplan 1995). Third, we simulated genome evolution with adaptive mutations at one locus and named these simulations directional-selection models (DIR1, DIR2, and DIR3). Fourth, we simulated genome evolution with negative frequency-dependent selection at one locus and named the simulations FDS1, FDS2, and FDS3 models. We compared nucleotide diversity and coalescence trees resulting from DIR and FDS models with expected patterns such as those from Takahata and Nei (1990) and Neuhauser (1999).

Testing frequency-dependent selection vs. directional selection:

After validating the simulation program by running it under each of the neutral (NEU) and selection models (BKG, DIR, and FDS) alone, we simulated B. burgdorferi s.l. genome evolution under mixed, more realistic models. To test maintenance of sympatric clonal groups by frequency-dependent selection, we applied negative frequency-dependent selection at one locus and purifying selection at other loci (FDS and BKG models, Figure 1A). To test genome divergence driven by directional selection, we created two subpopulations and applied directional selection at one locus and purifying selection at other loci (DIR and BKG models, Figure 1B). The two subpopulations underwent natural selection and genetic drift separately (mimicking independent adaptive evolution within different host species) but they were allowed to recombine (simulating co-infection of a single host).

Figure 1.

Simulation algorithms. (A) Frequency-dependent selection. A population of identical genomes consisting of disjoint genes (each with 500 codons) was created at the start of simulation. The genomes evolved under a uniform mutation rate, a uniform gene-conversion rate, genetic drift, frequency-dependent selection at one locus (in red), purifying selection at another locus (in blue), and neutral sequence variations at a third locus (in green). (B) Adaptive divergence. Two subpopulations underwent independent directional selection and genetic drift, but were allowed to recombine freely at the start of each generation. One locus was under directional selection (in red), another under purifying selection (in blue), and a third under neutral evolution (in green).

Parameters of the simulation are summarized in Table 2. Simulation programs were written in PERL and are available upon request. A simulation with a genome size of 2000 codons and N = 500 individuals evolving for 5000 generations took ∼12 hr on a microcomputer with a 3.3-GHz CPU.

Table 2. Simulation parameters.

Symbol	Description and settings
N	Population size (N = 500), held constant.
G	Total number of generations (G = 5000)
μ, U	Per-site and per-genome rates of mutations (μ = 10−6, U = 0.06), Poisson distributed and uniform across the genome
R	Per-genome rate of recombination (R = 0, R = U, R = 5U), Poisson distributed and uniform across the genome
L	Gene length (L = 500 codons)
B	Number of genes (b = 4)
δ	Tract lengths of gene conversion (δ = 30 codons), exponentially distributed
spur, sdir, sfds	Selection coefficients of purifying (spur = 0.1), directional (sdir = 0.01), and frequency-dependent (sfds= 0.01) selection
n, f	Sample size (n = 30 individuals), taken at every f = 50 generations
w, W	Fitness of a codon and an individual haploid genome
π, K	Average pairwise nucleotide differences within and between populations

Results

Genomic and ortholog alignments

We compared the core, mostly syntenic parts of the B. burgdorferi s.l. genome, consisting of the main chromosome, the linear plasmid lp54, and the circular plasmid cp26. These three replicons comprise ∼65% of the total ∼1.5 million bases of a B. burgdorferi s.l. genome (Casjens et al. 2000). The main chromosomes and the cp26 and lp54 plasmids are for the most part syntenic among the genomes, with the exception of two large-scale genome variations including the variable right end of the main chromosome and the PFam54 gene cluster on the lp54 plasmid (Huang et al. 2004; Wywial et al. 2009). We obtained a total of 73,451-bases-long genomic alignments of the cp26 plasmids and lp54 plasmids (the PFam54 gene cluster excluded) and 837 alignments of orthologous ORF families with a combined alignment length of 989,679 nucleotides (Table 3).

Table 3. Genomic and ORF alignments.

	Genomic alignments			Orthologous ORF alignments
	Length (bases)	No. SNPsa	% SNP density	No. ortholog families	Total alignment length (bases)	No. SNPs	% SNP density
cp26	26,591	1,267	4.76	26	26,451	826	3.12
lp54b	46,860	870	1.86	61	53,383	661	1.24
Main chromosome	NAc	NA	NA	750	909,845	12,311	1.35
Total	73,451	2,137	2.90	837	989,679	13,798	1.39

^aTwo-state sites only.

^bPFam54 gene array excluded for lack of synteny.

^cNot available.

Pervasive localized recombination

Figure 2 shows the recombination rates between pairs of SNPs based on the genomic alignment of cp26 plasmids from 14 B. burgdorferi s.s. strains. SNPs showing high recombination rates (red lines) were all located within 500 bases to each other. The ospC (encoding outer surface protein C) locus and its surrounding regions showed the highest levels of sequence polymorphism and localized recombination. Linkage disequilibrium (LD) grew stronger as the distance from ospC increased and the region directly opposite to ospC, including genes bbb01–bbb14, was the most strongly linked (Figure 2). Nevertheless, localized recombination rates were high throughout the cp26 plasmid (Figure 2). In contrast, SNPs situated ≥500 bases from each other had low recombination rates and high LD (blue lines) (Figure 2). The lp54 plasmid and the main chromosome showed similarly pervasive localized recombination and global clonality, with a recombination and sequence-diversity hotspot at dbpA (encoding decorin-binding protein A) on lp54 and a high-polymorphism hotspot at lmp1 (encoding surface-located membrane protein 1) on the main chromosome (Supporting Information, Figure S1 and Figure S2).

Figure 2.

Recombination rates and nucleotide polymorphisms on cp26. All values were based on a genomic alignment of cp26 plasmids from 14 B. burgdorferi s.s. genomes. Four data tracks are shown, representing (starting from the outside) the circular plasmid cp26 (black, B31 coordinates), ORFs (orange and yellow, indicating opposite coding directions), average nucleotide diversity (green, 120-base window size and 3-base window step; lower and upper gray lines indicating 0.15 and 0.3 differences per site, respectively), and recombination rates between pairs of SNPs. A red line links two SNPs with a high recombination rate and a blue line links two SNPs with a low recombination rate relative to the average rate (McVean et al. 2002).

Phylogeny of B. burgdorferi s.s. genomic groups

Using the concatenated bbb01–bbb14 sequences, we obtained an intraspecific phylogeny of B. burgdorferi s.s. genomic groups (Figure 3). This tree improves upon previously published phylogenies of the B. burgdorferi s.s. genomic groups by gaining significant statistical support for most of the branches (Bunikis et al. 2004; Margos et al. 2008; Qiu et al. 2008; Barbour and Travinsky 2010). This and other intraspecific phylogenies of B. burgdorferi s.l. isolates share the characteristics of nearly one-to-one association between the genomic lineages and the major ospC alleles, with rare exceptions of the same ospC allele appearing polyphyletically due to recombination (Qiu et al. 2008; Barbour and Travinsky 2010). Using a bootstrap cutoff value of 75%, we identified three pairs of strongly supported sister-group genomes, consisting of two North American pairs (118a-72a and 156a-297) and one European pair (Bol26-ZS7). These sister groups are strongly supported by a maximum-likelihood phylogeny inferred using all SNPs on the main chromosome, lp54, and cp26 (E. F. Mongodin, unpublished results).

Figure 3.

Plasmid-based phylogeny and ospC diversity. (A) Phylogeny of B. burgdorferi s.s. strains, rooted with the B. finlandensis strain SV1. The tree is based on the concatenated coding sequences including and between bbb01 and bbb14 on cp26, a region with strong linkage disequilibrium (Figure 2). Branch support values were obtained by using MrBayes (Ronquist and Huelsenbeck 2003) and DNAML with SEQBOOT (Felsenstein 1989). (B) A neighbor-joining tree of ospC nucleotide sequences from all 23 genomes. Fourteen B. burgdorferi s.s. strains were highlighted. The other 9 strains represent the following genospecies: B. fifinlandensis (by SV1), B. bissettii (DN127), B. afzelii (PKo and ACA-1), B. bavariensis (PBi), B. garinii (PBr and Far04), B. spielmanii (A14S), and B. valaisian (VS116).

Rates and tract lengths of gene conversion

The method of distinguishing SNPs caused by mutation and those caused by recombination based on sister-group comparisons is illustrated in Figure S3. Sequence comparisons between pairs of sister-group genomes revealed an ∼3:1 ratio of recombination to point-mutation rates (Table 4). Inclusion of proper and a large number of outgroup genomes as references is critical. For example, our sample of 14 B. burgdorferi s.s. genomes contains only two European strains, ZS7 and Bol26. As a result, most of the SNPs segregating between ZS7 and Bol26 appeared to be mutations and the ratio of recombination to mutation was <1 (Table 4). When we expanded the outgroup genomes to include nine European strains, most of the SNPs were found in these sympatric albeit non-B. burgdorferi s.s. strains, resulting in a recombination-to-mutation ratio similar to those estimated using the two North American sister-genome pairs (Table 4).

Table 4. Relative rates of recombination to mutation based on sister-group genomes.

Sister genomes	Outgroup genomes	Replicons	SNP density (%)	Muta	Recb	Rec/mut
118a-72a	American and European	cp26c	0.081	7	7	1.0
		lp54	0.306	16	82	5.1
		Main chr	0.139	203	564	2.78
156a-297	American and European	cp26c	0.233	13	25	1.92
		lp54	0.323	24	66	2.75
		Main chr	NAd	NAd	NAd	NAd
ZS7-Bol26	No European strains	cp26c	0.043	8	0	0
		lp54	0.145	30	16	0.53
		Main chr	0.088	544	73	0.134
ZS7-Bol26	With European strains	cp26c	0.034	2	4	2.0
		lp54	0.144	13	38	2.92
		Main chr	0.090	139	461	3.31
Average (SD) (ZS7-Bol26/no European strains results excluded)						2.72 (1.20)

chr, chromosome.

^aNumber of point mutations between sister genomes. These SNPs are unique.

^bNumber of SNPs between sister genomes due to recombination. These SNPs occur in outgroup genomes as well (i.e., homoplasies). Consecutive SNPs sharing the same phylogenetic pattern were counted as a single gene-conversion event.

^cOn cp26, the guaA, ospC, and bbb22 genes were excluded because of uncertainties in counting overlapping gene-conversion events.

^dData not available because the main chromosome of 297 is not sequenced.

The ZS7-Bol26 comparison was also informative on the tract length of gene conversion. Bol26 has a horizontally transferred ospC allele based on a multilocus sequence phylogeny (Qiu et al. 2008). It was unknown at the time whether the recombination event involved the ospC locus alone, its neighboring genes, or the entire cp26 plasmid. We first obtained gene trees using ortholog alignments on the cp26 plasmids, which indicated that phylogenetic inconsistencies involving Bol26 were limited to three loci including bbb18 (guaA, coding for GMP synthase), bbb19 (ospC), and bbb22 (function unknown). Instead of being grouped with its conspecific sister group ZS7, the closest known relative of Bol26, bbb22 from Bol26 is grouped with that from the B. afzelii strain PKo. A genomic alignment of the bbb17–bbb22 region showed nearly identical sequences between Bol26 and PKo in a region spanning the entire bbb22 locus (Figure S4). On the basis of shifts of phylogenetic relatedness along the plasmid alignment, we were able to identify both breakpoints of this cross-genospecies gene-conversion event and estimated its tract length to be between 1862 to 1903 bases long (Figure S4). There were at least two additional gene-conversion events at or near ospC, which introduced into Bol26 an ospC S-type allele from a conspecific donor (Qiu et al. 2008) and a guaA allele from an unknown donor. We therefore determined that at least three separate events of gene conversion have caused phylogenetically inconsistent guaA, ospC, and bbb22 alleles in Bol26, each originating from a different donor cell and affecting approximately a single gene.

Simulation results

We used computer simulations to test which of two forms of positive natural selection—adaptive divergence or frequency-dependent selection—is more compatible with the observed patterns of genetic linkage and polymorphisms. Specifically, we tested the ability of a selective mechanism to produce the following characteristics of the B. burgorferi s.s. population structure: (1) localized reduction in linkage disequilibrium within a genome-wide clonal frame, (2) a high recombination rate and a high level of sequence polymorphism at the locus under positive natural selection, and (3) a strong association between genomic lineages and large sequence variations at the positively selected locus.

Program validation:

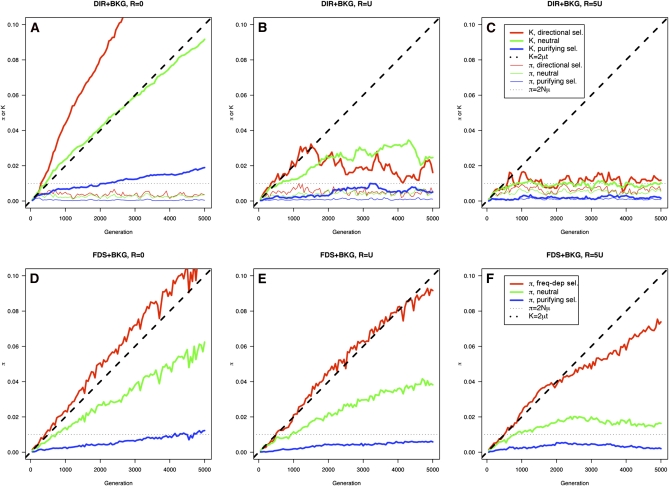
Simulations of genome evolution under single models produced results close to theoretical expectations. First, gene genealogies of the final simulated samples fit theoretical expectations. For example, the total coalescence time of the final sample was the shortest under the directional selection (DIR) model, longer under the background selection (BKG) model, even longer under the neutral evolution (NEU) model, and the longest under the frequency-dependent selection (FDS) model (Figure 4). Second, the equilibrium values of nucleotide diversities of simulated populations reached theoretically predicted levels of π₀ = 2Nµ under neutral models and $\pi ={\pi }_0\exp \{-U/(s+R)\}$ in models of background selection (Figure S5). Simulation under models of directional selection (DIR1–3) resulted in low genomic polymorphisms as expected from recurrent selective sweeps (Figure S6, top row). In the negative frequency-dependent selection (FDS1–3) models, sequence diversity increased quickly at the target locus (Figure S6, bottom row). Sequence diversity at linked neutral loci increased at slower rates and became increasingly independent as recombination rate increased, also as expected.

Figure 4.

Simulation validation: coalescence trees. Gene genealogies of the final samples of 30 individuals after simulated evolution of 5000 generations are shown. The scale bar indicates 500 generations. Genomes evolved without recombination and under (A) neutral evolution (NEU), (B) background selection (BKG), (C) directional selection (DIR), and (D) frequency-dependent selection (FDS).

Adaptive divergence:

In the absence of recombination (DIR and BKG1), the nucleotide divergence (K) between the two subpopulations at the neutral locus increased at the expected rate K = 2μt (an additional validation of the simulation program), while levels of divergence were higher at the positively selected locus and lower at the negatively selected locus (Figure 5A). In the presence of recombination, sequence divergence at all loci failed to increase with time and quickly settled to levels similar to that of within-subpopulation polymorphisms (Figure 5, B and C). The linkage analysis among SNPs identified by mixing the two subpopulations showed localized reduction in LD and strong LD among distant SNPs (Figure 6A). There was no increase of effective recombination rates or levels of sequence polymorphism at the positively selected locus relative to the neutral loci (Figure 6A).

Figure 5.

Simulation results: sequence diversity. We simulated evolution of a bacterial genome consisting of four protein-coding genes and plotted nucleotide divergence between two subpopulations (K) and polymorphisms within populations (π) every 100 generations. One locus (red lines) was under either directional selection or frequency-dependency selection. A second locus was under purifying selection (blue lines) and the last two loci (green lines) were under neutral evolution. In simulations of adaptive divergence (A–C, DIR and BKG models), two subpopulations diverged from an ancestral population and underwent independent directional selection and genetic drift. But the two subpopulations were allowed to recombine at each generation. A single population was tracked in simulations of frequency-dependent selection (D–F, FDS and BKG models). Three levels of gene conversion (R = 0,U, and 5U) were simulated. Shared parameters included a constant population size of N = 500 individuals, a haploid genome of L = 2000 codons, an average mutation rate of U = 0.06 nucleotide substitutions per genome per generation, and an average gene-conversion tract length of δ = 30 codons.

Figure 6.

Simulation results: recombination rates. See Figure 2 legend for descriptions of data tracks. (A) Recombination rates calculated on the basis of a sample of 50 individuals from two subpopulations evolving under the adaptive divergence model (DIR and BKG, R = 5U). One locus (DIR) was under directional selection, another locus (PUR) under purifying selection, and the last two loci (NEU) under neutral evolution. (B) Recombination rates calculated on the basis of a sample of 30 individuals from a population evolving under the frequency-dependent selection model (FDS and BKG, R = 5U). One locus (FDS) was under frequency-dependent selection, another locus (PUR) under purifying selection, and the last two loci (NEU) under neutral evolution. In both simulations, the genome was linear (not circular as depicted) and loci were sufficiently apart so that a single gene-conversion event affected only one locus.

Frequency-dependent selection:

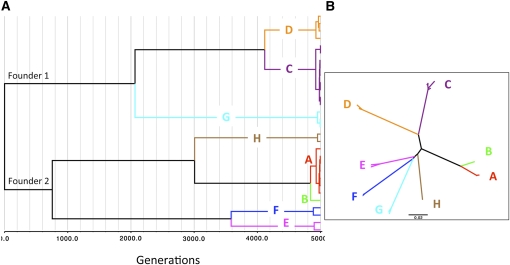
In the absence of recombination, within-population sequence diversity at all loci increased linearly over time (Figure 5D). With higher recombination rates, loci evolved more independently and sequence diversity eventually stabilized (or was expected to stabilize) (Figure 5, E and F). Although recombination slowed the rise of sequence diversity at the locus under positive selection, it had the beneficial effect of reducing deleterious polymorphisms at the locus under purifying selection (blue lines in Figure 5, D–F). As in the adaptive-divergence model, a pattern of global high LD and localized LD reduction was reproduced, with much smaller distances between the highly recombining SNPs than between those resulting from the adaptive-divergence model (Figure 6B). Also differing from the adaptive-divergence model, the locus under frequency-dependent selection displayed much higher effective recombination rates than the neutral locus (Figure 6B). Closely mirroring the pattern of genetic diversity at ospC, with a recombination rate of R = U the positively selected locus showed a star-like tree with strong sequence clustering and a one-to-one association of the major-group alleles with the genome lineages (Figure 7).

Figure 7.

Simulation results: genome genealogy. Thirty individuals were sampled from a simulated population (N = 500) after evolving for 5000 generations. The genome evolved under the influence of frequency-dependent selection at one locus and purifying selection at a second locus and with a gene-conversion rate equal to the mutation rate (R = U, FDS and BKG). (A) Genealogy of 30 individual genomes. (B) Neighbor-joining tree of nucleotide sequences at the positively selected locus. The simulation produced the following patterns observed in B. burgdorferi s.s. (Figure 3): two founder lineages persisting in the final sample, genomic sequences forming distinct clusters (labeled “A–H”, especially those at the positively selected locus), and an association of genomic groups with major sequence variations at the positively selected locus.

The simulation results could be summarized as follows: (1) Both the adaptive-divergence and the frequency-dependent selection models produced a similar pattern of genome-wide clonality with localized reduction of LD (Figure 6); (2) the high effective recombination rates and levels of sequence polymorphism at the selected loci (e.g., ospC) are more consistent with the frequency-dependent selection model than with the adaptive-divergence model (Figures 2 and 6); and (3) the frequency-dependent selection model produced the observed patterns of a star-like gene tree at the positively selected locus and a one-to-one association of major-group alleles at this locus with major genome lineages (compare Figures 3 and 7).

Discussion

Despite a highly clonal population structure, B. burgdorferi s.l. recombines more frequently than it mutates and its recombination takes the form of horizontal gene transfers of generally short DNA pieces (Dykhuizen and Baranton 2001; Qiu et al. 2004). By using genome sequences of a large number of sympatric genomic groups, the present study obtained genome-wide, robust estimates on the rate, tract length, and patterns of recombination in B. burgdorferi s.s. Our characterization of the genome-wide linkage structure in B. burgdorferi s.s. is based on estimating recombination rates and tract lengths by analyzing linkage between SNP pairs and by comparing sister-group genomes. LDhat has been widely used for estimating recombination rates in bacteria, using multilocus and genome sequences (Wirth et al. 2007; Touchon et al. 2009). We are aware of some potential biases in the sister-group method. For instance, identification of homoplasy is sensitive to the choice and number of outgroups. A small number of outgroup genomes leads to an underestimation of the recombination to mutation ratio because of a decreased chance of identifying donor sequences. Using distantly related genomes as sister-group or outgroup genomes, on the other hand, may lead to an overestimation of recombination rates due to recurrent mutations. In addition, it is possible that homoplastic SNPs are caused by recurrent “hotspot” mutations due to positive natural selection rather than recombination (Chattopadhyay et al. 2009). However, we found no evidence supporting this possibility in our samples. For instance, the hotspot-mutation hypothesis predicts a higher proportion of nonsynonymous SNPs at homoplastic sites than that at phylogenetically consistent sites. In comparing ORF sequences on the lp54 and cp26 plasmids between a pair of sister groups (156a-297), we found no evidence for accelerated nonsynonymous changes at homoplastic sites (Figure S3B). Alternative methods exist for estimating rates and tract lengths of gene conversion, including GenCo (Gay et al. 2007), ClonalFrame (Didelot and Falush 2007), and ClonalOrigin (Didelot et al. 2010). While these methods can be more powerful with the use of explicit models of gene conversion, their computation time is long and Bayesian estimates failed to converge for our data sets. In addition, effects of natural selection were not explicitly modeled in these coalescence-based simulations. In practice, direct estimates of recombination rates and phylogeny (using, e.g., LDHat and PHYLIP as in the present study) are comparable to those from model-based analysis (Didelot and Falush 2007; Didelot et al. 2010).

We further tested selective mechanisms responsible for the observed patterns of linkage and polymorphisms in the B. burgdorferi s.s. genome by using computer simulations. A technical novelty of the present study, in comparison with previous sequence-based forward-evolution simulations (Fraser et al. 2007, 2009), is that with the use of codon-based algorithms, we were able to simulate major forms of natural selection operating on a bacterial genome, including purifying selection, adaptive divergence, and frequency-dependent selection.

Patterns of recombination in B. burgdorferi s.l.

Four conclusions could be drawn on the nature of recombination in B. burgdorferi s.l. First, localized recombination is pervasive across the B. burgdorferi s.l. genome. While a few surface-protein loci appear to be recombination hotspots, this appearance is perhaps more indicative of natural selection than of a propensity for recombination (Vos 2009). Nucleotide polymorphisms are retained at surface-antigen loci like ospC by positive natural selection (Wang et al. 1999a; Barbour and Travinsky 2010). More directly, we found at least three independent gene-conversion events at the guaA-ospC-bbb22 loci in a single B. burgdorferi s.s. genome (Figure S4). In other words, bacterial loci under positive natural selection may have high effective, but not actual, gene-conversion rates (Vos 2009). Second, recombination maintains a majority of sequence polymorphisms within B. burgdorferi s.l. populations. About three-quarters of sequence diversity in B. burgdorferi s.l. is due to the reassortment of preexisting sequence variations through localized recombination and only one-quarter is due to de novo point mutations. This estimate is remarkably similar regardless of the strains and replicons used for comparison (Table 4). It is also nearly identical to our earlier estimates based on comparisons of isolates belonging to the same genomic groups (Qiu et al. 2004). Third, there is a considerable amount of cross-species genetic exchange among sympatric genomes. Although the European isolates ZS7 and Bol26 are conspecific with other B. burgdorferi s.s. strains from North America, there is a deficiency of shared SNPs among the two geographically separated populations (Table 4, “No EU strains”). In contrast, SNPs segregating between ZS7 and Bol26 are mostly shared with those in the non-B. burgdorferi s.s. yet sympatric European strains, suggesting a high rate of cross-species recombination (Table 4, “With EU strains”). Fourth, although LDHat analysis suggests that the tract lengths of gene conversion events in B. burgdorferi s.s. are small (<500 bases), the actual tract lengths of individual gene-conversion events may be considerably longer because multiple events could have occurred at a single locus (e.g., at ospC). In what seems to be a single event of gene conversion, a DNA fragment of a minimum length of ∼1900 bases from a close relative of the B. afzelii strain PKo was incorporated into the homologous locus of the B. burgdorferi s.s. strain Bol26 (Figure S4). This observed tract length is close to the experimentally estimated tract length of between 950 and 1850 bases in Helicobacter pylori (Lin et al. 2009). To summarize, we conclude that recombination in B. burgdorferi s.l. is pervasive across its genome, is localized with short tract lengths (<2000 bp), occurs approximately three times more frequently than mutations, and occurs frequently among sympatric genospecies.

Maintenance of genome clusters by frequency-dependent selection

Pervasive and frequent recombination suggests that natural selection plays a large role in the maintenance of distinct clonal groups coexisting within natural bacterial populations, but the exact forms of natural selection may vary from species to species (Doolittle and Papke 2006; Fraser et al. 2009). A widely held view is that sympatric bacterial genomic groups represent ecotypes, each one adapting to its microhabitat (Majewski and Cohan 1999; Cohan 2002; Koeppel et al. 2008). In the case of B. burgdorferi s.s., it has been proposed that genomic groups with distinct ospC alleles differ in their host preferences (Brisson and Dykhuizen 2004, 2006). The ecotype model has been challenged by computer simulations, which showed that neutrally evolving genomes would merge into a single cluster when the recombination rate is above three times the mutation rate (Fraser et al. 2007). Our simulation went further by showing that in the absence of a recombination barrier, nascent adaptive or neutral sequence divergence among the genome lineages is ephemeral and highly vulnerable to homogenization by periodic selective sweeps. For instance, sequence divergence between two independently adapted subpopulations virtually disappeared with a recombination rate as low as the mutation rate (Figure 5B). With an estimated recombination rate three times that of the mutation rate and with a limited number of competent host species in a given locality, it is unlikely that partitioning of host species is the primary mechanism maintaining the stable coexistence of ∼20 distinct B. burgdorferi s.s. genomic groups in the northeastern United States. Nor is it likely the maintenance of the high sequence diversity at positively selected loci such as ospC, dbpA, and lmp1. To sustain independent adaptive evolution of bacterial genomic groups, it is necessary that recombination rates decline precipitously with increasing sequence distances (Fraser et al. 2007; Lawrence and Retchless 2010).

In contrast, it is well known that negative frequency-dependent selection is capable of maintaining a high allelic diversity at surface-antigen loci of bacterial and viral pathogens as well as at the antigen-receptor (e.g., MHC) loci of vertebrates (Levin 1988; Takahata and Nei 1990; Wiener 1996). The adequacy of negative frequency-dependent selection for maintaining sympatric genetic diversity in an asexual species without niche partitioning has recently been demonstrated empirically (Weeks and Hoffmann 2008). Our results suggest that in a bacterial population where the recombination rate is of the same magnitude as the mutation rate, the diversifying and balancing effects of FDS at individual loci extend genome-wide. The population-genomic effects of FDS are perhaps best understood from the shape of genome genealogy. Mirroring the gene genealogy at the selected locus, the genealogy of genomes evolving under FDS is strongly balanced and characterized by long internal and short external branches (Figure 7). Such a genome genealogy has the following consequences. First, as a direct consequence of this balanced genome genealogy allele frequencies at all genomic loci tend to be evenly distributed (Figure 4). Indeed, allele frequency distributions in natural populations of B. burgdorferi s.s. are more even than expected from neutral evolution (Qiu et al. 1997, 2002; Rannala et al. 2000). Second, a genome genealogy with long internal and short terminal branches results in a clustering of genomic sequences into distinct groups, with large sequence differences between the groups and sequence homogeneity within the groups (Figure 7). It is indeed without exception that isolates within B. burgdorferi s.s. populations form a large number of distinct sequence clusters regardless of the genetic marker used (Wang et al. 1999b; Margos et al. 2008; Qiu et al. 2008; Travinsky et al. 2010). Third, such genome-sequence clusters are associated with major alleles at the locus targeted by FDS (Figure 7). In the core, conserved parts of the B. burgdorferi s.s. genome consisting of the main chromosome and the lp54 and cp26 plasmids, ospC displays the strongest association of major alleles with genomic lineages (with rare exceptions caused by horizontal transfers of ospC alleles, e.g., in Bol26) (Figure 3). This pattern suggests that FDS operating at ospC is a dominant selective mechanism maintaining the sympatric genome diversity in B. burgdorferi. Fourth, due to the prolonged persistence of founder lineages in a population, the level of sequence polymorphisms within populations could be as high as the level of sequence divergence between populations (e.g., between the A and C alleles in Figure 7). In the B. burgdorferi s.l. genome, a number of surface-protein loci display levels of polymorphisms within genospecies close to the levels of sequence divergence between the genospecies [e.g., ospC (Figure 3), dbpA (Figure S1), and lmp1 (Figure S2)].

While specific molecular functions of OspC are not yet clear, it is known that ospC is required for host infection and is among the most differentially expressed genes during host invasion (Brooks et al. 2003; Grimm et al. 2004; Liang et al. 2004; Tilly et al. 2006; Antonara et al. 2010). Considering that ospC is a serotype determinant of B. burgdorferi s.l., negative FDS operating at ospC is highly plausible. Presumably, cells with rare amino acid types in OspC would encounter weaker adaptive immune responses from the host population than cells with common OspC alleles (Wang et al. 1999b; Barbour and Travinsky 2010).

Implications for B. burgdorferi s.l. speciation and comparisons with other models of bacterial evolution

The ecotype model:

Implicit in the frequency-dependent selection model is that sympatric B. burgdorferi s.s. genomic groups in the northeastern United States represent variations within a single, generalist species rather than individually adapted ecotypes. Here we used the word “species” to refer to a shared population pipeline of natural selection and genetic drift among individual genomes as specified in our computational model (Figure 1A) (Hey 2006). On the basis of the FDS model, we predict that it is unlikely that sympatric B. burgdorferi s.s. genomic groups would diverge without bound and eventually become host-specialized species. Rather, the overall genetic diversity of individual B. burgdorferi s.s. populations is expected to reach a steady state as the diversifying effect of FDS being balanced out by the homogenizing effects of genetic drift, recombination, and purifying selection (Figures 5, E and F). On the basis of the assumption that all B. burgdorferi s.s. genomic groups share a uniform evolutionary process (e.g., by sharing the same transmission cycle consisting of a single tick species as the vector and the same set of vertebrate species as hosts), we think it appropriate to consider the B. burgdorferi s.s. groups in the northeastern United States as constituting a single ecotype or a single ecological species. Evidence supporting B. burgdorferi s.s. as a single, generalist species includes, first, that the host range of a number of B. burgdorferi s.s. genomic groups in the northeastern United States spans three or more mammalian orders (Hanincova et al. 2006). Second, consistent with the FDS model and less compatible with the host-specialization model, a number of recently dispersed B. burgdorferi s.s. genomic groups flourish in two separate transmission cycles (Europe and North America), which differ in tick-vector species and presumably in host-species composition as well (Qiu et al. 2008). Third, the severe human virulence of B. burgdorferi s.s. is itself evidence for it being a generalist parasite of mammalian hosts, since despite the fact that humans are not its natural reservoir hosts, B. burgdorferi s.s. is capable of invading and infecting the human tissues. Although B. burgdorferi s.s. strains appear to vary in human virulence (Dykhuizen et al. 2008; Wormser et al. 2008), it has been argued that associations between human pathogenecity and genomic groups are weak and all groups have the potential to cause invasive infections in humans (Alghaferi et al. 2005; Jones et al. 2006).

It follows from the FDS model that geographic isolation may be a prerequisite for host specialization and speciation in B. burgdorferi s.l. Biogeographic patterns of B. burgdorferi s.l. support this prediction. Globally most B. burgdorferi s.l. genospecies have distinct geographic distributions (Kurtenbach et al. 2006). Exceptional coexistence of multiple genospecies in a single geographic region (e.g., B. burgdorferi s.s., B. afzelii, and B. garinii in Europe) may be results of secondary contact of previously isolated populations. Although being members of a single genospecies, the European and North American B. burgdorferi s.s. populations have diverged and share only a few genomic groups due to recent trans-Atlantic migrations (Margos et al. 2008; Qiu et al. 2008). In the United States, the northeastern and midwestern B. burgdorferi s.s. populations have differentiated significantly (Qiu et al. 2008; Hoen et al. 2009; Brisson et al. 2010). Population divergence in B. burgdorferi s.l. as a biogeographic process is harder to understand under the niche-partitioning model. The ecotype and niche-partitioning models would predict that sympatric speciation is common in B. burgdorferi s.l. and that there is a strong association of host-species composition with the composition of B. burgdorferi s.l. genomic groups. As far as we know these predictions are either not supported by empirical observations or yet to be tested.

Contrary to the proposal by Brisson and Dykhuizen (2004), the FDS models are likely to be more parsimonious than ecotype models for explaining the maintenance of bacterial genome diversity. For instance, while we used a single mutation rate, recombination rate, and selection coefficient in the present FDS simulations, Majewski and Cohan (1999) used two mutation rates, three recombination rates, and two selection parameters for simulating the stable coexistence of two ecotypes. Nevertheless, our computational analysis is preliminary and not a full test of the ecotype model. For instance, we did not test the possibility of each genomic group adapting to multiple host species with slight fitness differences. In addition, the ecotype model and the frequency-dependent selection model may operate simultaneously in a population.

The “epidemic” model:

The “epidemic” model explains the maintenance of sympatric genomic groups with frequent recombination by the rapid growth of high-fitness clones within populations of pathogenic bacteria (Maynard Smith et al. 1993; Smith et al. 2000; Feil 2004). We reject the epidemic model as a major mechanism for the maintenance of B. burgdorferi s.s. genomic groups on the basis of the following considerations. First, the epidemic model predicts a rapid turnover of dominant clonal groups rather than a stable coexistence of genomic groups over time and space as observed in B. burgdorferi s.s. populations. Second, the epidemic model assumes the existence of a diverse, low-frequency reservoir of genomic groups, which serves as the source of new genotypes through recombination among the “background genomes”. Extensive surveys of B. burgdorferi s.s. populations in the United States and elsewhere in the past decades find no evidence for a shadow population with unknown genomic groups in any locality. In contrast, the FDS model has no need to assume a background population that is more diverse than what could be sampled. Third, the epidemic model requires that recombination is more frequent among the background genomes than among the high-fitness clones. In comparison, the FDS model does not require that recombination rates differ between genomic groups. Nevertheless, clonal expansion could still play a role in the maintenance of genomic groups in B. burgdorferi s.l. So far we have tested the FDS model only under a constant population size, which is unrealistic since the size of natural B. burgdorferi s.l. populations is likely to fluctuate. We expect that population growth combined with FDS would further boost genomic diversities in bacteria, a hypothesis that could be tested by further simulations.

The “species-less” model:

As an obligate parasite B. burgdorferi s.l. may not be representative of other, free-living bacteria. It is unclear whether and to what extent FDS plays a role in the maintenance of sympatric genomic diversity in other bacterial pathogens. However, comparisons of whole genomes of bacterial strains revealed that, similar to ospC in B. burgdorferi s.l., as few as one to two loci in the whole bacterial genome display highly elevated effective recombination rates and high sequence variability (Vos 2009; Didelot and Maiden 2010). Also similar to ospC, most such loci code for surface structures directly involved in interactions with the host, such as the rlr operon coding for a pilus in Streptococcus pneumonia (Lefebure and Stanhope 2007), the rfb operon coding for the O-antigen and the fim locus coding for an adhesion in Escherichia coli (Touchon et al. 2009), and the ompA locus coding for an outer-surface protein in Chlamydia trachomatis (Gomes et al. 2007). A further and key similarity to ospC is that many of these genes (e.g., rfb in E. coli) also appear to be lineage-defining genes associated with genomic groups in a bacterial pathogen (Lawrence and Retchless 2010). These similarities suggest that maintenance of sympatric genomic diversity by FDS may be a general evolutionary mechanism operating in free-living bacterial pathogens as well. Curiously, with a few exceptions (e.g., Touchon et al. 2009), most authors regard genomic groups of these bacterial pathogens as adapted to host or predator species and have not considered diversifying selection such as FDS as a possible contributing factor (Vos 2009; Lawrence and Retchless 2010). Such models are thus essentially ecotype models and thereby suffer from the same difficulties in explaining how positively selected loci are protected from selective sweeps in a population with frequent recombination. Although FDS may be considered a form of diversifying and balancing selection, it differs from balancing selection caused by ecological adaptation in not assuming specialized adaptations of individual alleles. As such, the FDS model is a selective, but nonadaptive model. In fact, FDS is maladaptive by elevating the deleterious mutation load at housekeeping loci when the recombination rate is low (blue lines in Figure 5D, E, and F).

To conclude, we showed that the high sympatric genomic diversity in natural B. burgdorferi s.l. populations (such as those in the northeastern United States) could sufficiently and parsimoniously be accounted for by negative frequency-dependent selection targeting a small number of surface-antigen loci and ospC in particular. Since recombination in B. burgdorferi s.l. is localized and not overly frequent, the diversifying and balancing effects of FDS extend genome-wide and the clustering of genomic sequences ensues. Meanwhile, recombination is pervasive and effective enough to reduce the load of deleterious mutations and to prevent neutral and adaptive divergence (e.g., host specialization) among the sympatric genomic groups. FDS may be a common selective mechanism maintaining sympatric genomic diversity in free-living bacterial pathogens as well, with the implication that, as in eukaryotes, speciation in bacteria is as much a biogeographic process as an ecological or adaptive process (Papke and Ward 2004). Although computationally slow and inefficient relative to coalescence simulations, our codon-based forward-simulation approach proves to be effective for testing hypotheses on bacterial genome evolution owing to more straightforward ways of simulating recombination and diverse forms of natural selection operating in molecular sequences.