Modulation of outer medullary NaCl transport and oxygenation by nitric oxide and superoxide

Abstract

We expanded our region-based model of water and solute exchanges in the rat outer medulla to incorporate the transport of nitric oxide (NO) and superoxide (O₂⁻) and to examine the impact of NO-O₂⁻ interactions on medullary thick ascending limb (mTAL) NaCl reabsorption and oxygen (O₂) consumption, under both physiological and pathological conditions. Our results suggest that NaCl transport and the concentrating capacity of the outer medulla are substantially modulated by basal levels of NO and O₂⁻. Moreover, the effect of each solute on NaCl reabsorption cannot be considered in isolation, given the feedback loops resulting from three-way interactions between O₂, NO, and O₂⁻. Notwithstanding vasoactive effects, our model predicts that in the absence of O₂⁻-mediated stimulation of NaCl active transport, the outer medullary concentrating capacity (evaluated as the collecting duct fluid osmolality at the outer-inner medullary junction) would be ∼40% lower. Conversely, without NO-induced inhibition of NaCl active transport, the outer medullary concentrating capacity would increase by ∼70%, but only if that anaerobic metabolism can provide up to half the maximal energy requirements of the outer medulla. The model suggests that in addition to scavenging NO, O₂⁻ modulates NO levels indirectly via its stimulation of mTAL metabolism, leading to reduction of O₂ as a substrate for NO. When O₂⁻ levels are raised 10-fold, as in hypertensive animals, mTAL NaCl reabsorption is significantly enhanced, even as the inefficient use of O₂ exacerbates hypoxia in the outer medulla. Conversely, an increase in tubular and vascular flows is predicted to substantially reduce mTAL NaCl reabsorption. In conclusion, our model suggests that the complex interactions between NO, O₂⁻, and O₂ significantly impact the O₂ balance and NaCl reabsorption in the outer medulla.

nitric oxide (NO) and superoxide (O₂⁻) exert opposite effects in the renal medulla, and changes in the balance between the two significantly impact renal function. Whereas NO inhibits tubular NaCl reabsorption and enhances medullary blood flow by dilating blood vessels, O₂⁻ stimulates NaCl reabsorption across the medullary thick ascending limb (mTAL) and acts to reduce medullary blood flow by mechanisms that remain to be fully elucidated (13).

Under normal conditions, O₂⁻ levels in the body are kept low due to O₂⁻ scavenging by NO and superoxide dismutase (SOD). As suggested by several studies (reviewed in Ref. 36), an imbalance between NO and O₂⁻ in the kidney significantly alters renal hemodynamics and excretory function and may contribute to the development of salt-sensitive hypertension.

An imbalance between NO and O₂⁻ may also affect medullary oxygenation. Renal hypoxia is exacerbated during hypertension, and tempol reduces renal tissue hypoxia in spontaneously hypertensive rats (32, 58). Oxidative stress and subsequent reduced NO bioavailability may result in an excessive use of O₂ to maintain the sodium balance (i.e., a decrease in T_Na/Qo₂, the ratio of transported sodium to oxygen consumption) during hypertension (58).

The objective of the current theoretical study was to investigate how shifts in the balance between NO and O₂⁻ affect medullary sodium reabsorption and oxygen availability. We developed a mathematical model of NO and O₂⁻ transport in the rat outer medulla to examine the impact of NO-O₂⁻ interactions on mTAL sodium transport and O₂ consumption, under both physiological and pathological conditions.

MODEL DESCRIPTION

Our representation of the rat outer medulla is that of the region-based approach developed by Layton and Layton (31). The model represents the loops of Henle, the collecting duct (CD) system, the vasa recta, and red blood cells (RBCs). The descending limbs, ascending limbs, and CDs are represented by rigid tubules that are oriented along the corticomedullary axis, which extends from x = 0 at the corticomedullary boundary to x = L at the outer-inner medullary (OM-IM) boundary (Fig. 1A). The model separates blood flow in vasa recta into two compartments, plasma and RBCs, divided by RBC membranes. The vascular plasma and RBC compartments are also represented by rigid tubules along the corticomedullary axis. Besides tubules and vasa recta, the model considers two other sets of compartments: one consists of the RBCs within the capillaries (which we refer to as “capillary RBCs”). Capillary flow is assumed to be perpendicular to the medullary axis; thus the capillary RBC compartment is represented by rigid tubules, extending radially (i.e., perpendicular to the medullary axis) across each medullary level. We assume that the highly fenestrated nature of the capillaries results in rapid equilibration of their plasma content with local interstitium. The other set of compartments represents the combination of interstitial spaces, interstitial cells, and capillary plasma flow, and is simply referred to as the “interstitium.”

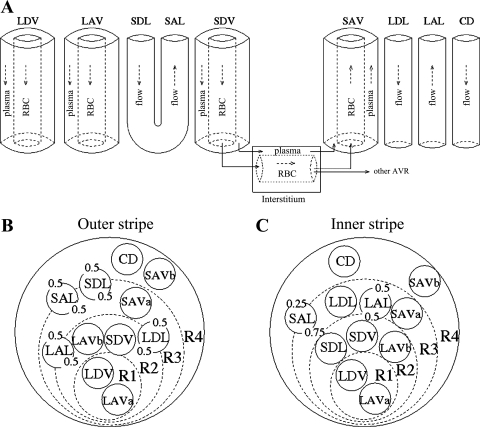
Fig. 1.

Schematic representation of tubules and vasa recta in the rat outer medulla (OM). Four concentric regions (R1–R4) are distinguished; the innermost (R1) contains the central vascular bundle. Note that R1–R4 have coincident centers; the display here is intended to minimize the figure area. A: tubules and vessels along the corticomedullary axis. B: cross section of the outer stripe. C: cross section of the inner stripe. LDV, long descending vas rectum; SDV, short descending vas rectum; LAVa and LVAb, 2 populations of LDV; SAVa and SAVb, 2 populations of SDV; LDL, long descending limb of Henle's loop; SDL, short descending limb; LAL, long ascending limb; SAL, short ascending limb; CD: collecting duct. The decimal numbers represent the relative weight of interaction between a type of vessel or tubule and a given region (i.e., the parameter κ_i,R in Eqs. 9–10).

The interstitium is divided into four concentric regions, which are used to represent the highly specific structural organization of the rat OM (Fig. 1, B and C): an innermost region containing the central vascular bundle (R1), where all the long descending vasa recta (i.e., DVR that reach into the inner medulla) and a third of the long ascending vasa recta (i.e., AVR that reach into the inner medulla) are sequestered; a peripheral region of the vascular bundle (R2), where the short DVR (i.e., DVR that turn within the OM) and the remaining long AVR reside; a region neighboring the vascular bundle (R3), which contains most medullary thick ascending limbs (mTALs), both long and short, and some short AVR; and the region most distant from the vascular bundle (R4), where CDs and the remaining short AVR are located. Descending limbs that reach into the inner medulla are located in R2 and R3 in the outer stripe (OS) and move toward the CDs in the inner stripe (IS). Conversely, the short descending limbs (i.e., those that turn within the OM) straddle R3 and R4 in the OS and move toward the bundle periphery (R2) in the IS.

The model yields tubular and vascular fluid flows as well as the concentration of eight species, i.e., Na⁺, urea, O₂, deoxy-hemoglobin (Hb), oxy-hemoglobin (HbO₂), nitrosyl-heme (HbNO), NO, and O₂⁻, in each type of tubule and vessel, and in the interstitium. These variables are determined based on conservation equations and appropriate boundary conditions. Detailed equations for fluid flows and the concentrations of the first five species (Na⁺, urea, O₂, Hb, HbO₂) can be found in our previous studies (7, 8). This section focuses on the new features of our model: the transport of NO and O₂⁻, as well as their effect on O₂ metabolism and Na⁺ reabsorption across mTALs.

Conservation Equations

Tubules.

Steady-state conservation equations are used to predict the volumetric flow rate (F_{i, V}) and the concentration of solute k (C_{i, k}) in a tubule of type i

$$\frac{\partial {\mathrm{F}}_{i,\mathrm{V}}\left(x\right)}{\partial x}=J_{i,\mathrm{V}}\left(x\right)$$ (1)

$$\frac{\partial \left[{\mathrm{F}}_{i,\mathrm{V}}\left(x\right){\mathrm{C}}_{i,k}\left(x\right)\right]}{\partial x}=J_{i,k}\left(x\right)+\theta A_i^{\text{epi}}\left(x\right)\left[G_{i,k}^{\text{epi}}\left(x\right)-{\Omega }_{i,k}^{\text{epi}}\left(x\right)\right]-A_i^{\text{lum}}\left(x\right){\Omega }_{i,k}^{\text{lum}}\left(x\right)$$ (2)

where x is the position along the OM, ranging from 0 at the corticomedullary junction to L at the OM-IM boundary; J_{i, V} and J_{i, k} denote the transmural flux of water and solute k into tubule i; A_i^lum and A_i^epi, respectively, designate the cross-sectional area of the lumen of i (i.e., based on its inner diameter) and that of the surrounding epithelium. Ω_{i, k}^lumand Ω_{i, k}^epi are the volumetric consumption rate of solute k in the lumen of tubule i and that of the surrounding epithelium, and G_{i, k}^epi is the epithelial volumetric generation rate of k. Since the model does not explicitly account for tubular and vascular walls, which are represented instead as single barriers, we assume that a fixed fraction θ of the net amount of solute k that is generated in epithelia or endothelia diffuses toward the lumen, and the remainder (1 − θ) diffuses toward the interstitium. For NO and O₂⁻, the fraction θ is taken as one-half everywhere.

Vasa recta.

As previously noted, plasma and RBCs are treated as two separate compartments. F_{i, V}^pl and F_{i, V}^rbc denote the plasma and RBC water flow rate in vessel i, respectively, so that the total water flow rate in vessel i is F_{i, V} = F_i,V^pl + F_i,V^rbc. Similarly, C_{i, k}^pl and C_{i, k}^rbc denote the respective plasma and RBC concentration of solute k in vessel i. Water conservation in the plasma and RBC compartments of blood vessel i can be expressed as

$$\frac{\partial {\mathrm{F}}_{i,\mathrm{V}}^{\text{pl}}\left(x\right)}{\partial x}=J_{i,\mathrm{V}}^{\text{pl}}\left(x\right)$$ (3)

$$\frac{\partial {\mathrm{F}}_{i,\mathrm{V}}^{\text{rbc}}\left(x\right)}{\partial x}=J_{i,\mathrm{V}}^{\text{rbc}}\left(x\right)$$ (4)

where J_{i, V}^pl is the net transmural flux of water into plasma (i.e., from the interstitium and RBCs) and J_{i, V}^rbc that into RBCs. Note that J_{i, V}^pl = J_{i, V}^int − J_{i, V}^rbc, where J_{i, V}^int designates the transmural flux from interstitium to plasma.

Similarly, solute conservation in the plasma and RBC compartments of blood vessel i is expressed as

$$\frac{\partial \left[{\mathrm{F}}_{i,\mathrm{V}}^{\text{pl}}\left(x\right){\mathrm{C}}_{i,k}^{\text{pl}}\left(x\right)\right]}{\partial x}=J_{i,k}^{\text{pl}}\left(x\right)+\theta A_i^{\text{endo}}\left(x\right)\left[G_{i,k}^{\text{endo}}\left(x\right)-{\Omega }_{i,k}^{\text{endo}}\left(x\right)\right]-A_i^{\text{pl}}\left(x\right){\Omega }_{i,k}^{\text{pl}}\left(x\right)$$ (5)

$$\frac{\partial \left[{\mathrm{F}}_{i,\mathrm{V}}^{\text{rbc}}\left(x\right){\mathrm{C}}_{i,k}^{\text{rbc}}\left(x\right)\right]}{\partial x}=J_{i,k}^{\text{rbc}}\left(x\right)-A_i^{\text{rbc}}\left(x\right){\Omega }_{i,k}^{\text{rbc}}\left(x\right)$$ (6)

where J_{i, k}^pl and J_{i, k}^rbc are the net transmural flux of solute k entering plasma and RBCs; Ω_{i, k}^rbc, Ω_{i, k}^pl, and Ω_{i, k}^endo, respectively, denote the volumetric consumption rate of solute k in RBCs, plasma, and surrounding endothelium, and G_{i, k}^endo is the endothelial volumetric generation rate of k. A_i^rbc, A_i^pl, and A_i^endo, respectively, designate the cross-sectional area of the RBC compartment, the plasma compartment, and the surrounding endothelium. The cross-sectional area of the RBC compartment is calculated as

$$A_i^{\text{rbc}}=A_i\left(\frac{{\mathrm{F}}_{i,\mathrm{V}}^{\text{rbc}}}{{\mathrm{F}}_{i,\mathrm{V}}^{\text{rbc}}+{\mathrm{F}}_{i,\mathrm{V}}^{\text{pl}}}\right)$$ (7)

Interstitium.

Water conservation equations in the interstitium of each region yield water flows into ascending vasa recta and can be found in our previous study (8). The conservation equation for solute k in region R yields the interstitial concentration of k, and is written as

$$\begin{array}{l}2\pi {\mathrm{r}}_{\text{R}}{\displaystyle \sum _{\text{R}\prime }}{P}_{\text{R,R}\prime ,k}\left({\text{C}}_{\text{R}\prime ,k}-{\text{C}}_{\text{R,}k}\right)+{\displaystyle \underset{i=\text{SDL,LDL,SAL,LAL,CD,LDV,LAV}}{\sum n_i{J}_{i,\text{R},k}}}\\ +n_{\text{SDV}}{\overline{J}}_{\text{SDV,R},k}+n_{\text{SAV}}{\overline{J}}_{\text{SAV,R},k}+n_{\text{SDV}}\left(-\text{d}{\omega }_{\text{SDV}}/\text{d}x\right)\\ \times \left[{\alpha }_{\text{SDV,R}}\left({\text{C}}_{\text{SDV,}k}{F}_{\text{SDV,V}}^{\text{pl}}\right)+{\overline{J}}_{\text{cRBC,R},k}\right]+{\text{C}}_{\text{R}\prime \text{,}k}{Q}_{\text{R}\prime \text{,R}}\\ -{\text{C}}_{\text{R,}k}\left(Q_{\text{AVR}}+Q_{\text{R,R}\prime }\right)+\left(1-\theta \right){\displaystyle \underset{i=\text{all\hspace{0.17em}tubules}}{\sum n_i{\text{A}}_i^{\text{epi}}}\left[G_{i,k}^{\text{epi}}-{\Omega }_{i,k}^{\text{epi}}\right]}\\ +\left(1-\theta \right){\displaystyle \underset{i=\text{all\hspace{0.17em}vessels}}{\sum n_i{A}_i^{\text{endo}}}\left[G_{i,k}^{\text{endo}}-{\Omega }_{i,k}^{\text{endo}}\right]}\\ +A_{\text{R}}^{\text{cap\hspace{0.17em}endo}}\left[G_{\text{R,}k}^{\text{cap\hspace{0.17em}endo}}-{\Omega }_{\text{R,}k}^{\text{cap\hspace{0.17em}endo}}\right]-A_{\text{R}}^{\text{int}}{\Omega }_{\text{R,}k}^{\text{int}}=0\end{array}$$ (8)

where P_{R, R′, k} is the permeability of the boundary between regions R and R′ to solute k, n_i denotes the number of tubules or vessels of type i, ω_SDV represents the fraction of short descending vasa recta (SDV) reaching to a given medullary level, Q_{R, R′} is the capillary flow from region R to R′, Q_AVR is the total fluid accumulation carried away by AVR, and A_R^int is the area occupied by interstitial cells in region R.

The first term in Eq. 8 represents the diffusion of solute into region R from adjacent regions R′. The second term is the sum of solute fluxes from tubules and long vasa recta into R. The third and fourth terms denote the composite solute fluxes at level x from all SDV and short ascending vasa recta (SAV), respectively, that are present in region R and that reach to medullary level y > x. The first term in the first pair of square brackets represents the solute flux from SDV terminating at level y = x into region R. The next term in that first pair of square brackets is the solute flux from capillary RBCs into R. The term C_{R′, k}Q_{R′, R} − C_{R, k}(Q_AVR + Q_{R, R′}) represents the net amount of solute that is carried by flow at the local concentration into AVR or into an adjoining region R′. The next two terms involving (1 − θ) represent the fraction of net solute produced by tubular epithelial and vascular endothelial cells that is released into the interstitium (see Eqs. 2 and 5). The next-to-last term denotes the net amount of solute k produced by capillary endothelium in region R (see below), and the last term denotes the consumption rate of solute k by interstitial cells in region R.

Transmural Fluxes

Tubules.

The transmural fluxes of water and solute k into tubule i are calculated as

$$J_{i,\mathrm{V}}=2\pi r_i{d}_i{\displaystyle \sum _{\text{region R}}}{\kappa }_{i,\mathrm{R}}\left[{\displaystyle \sum _{\text{solute}k}}{\sigma }_k{\varphi }_k\left({\text{C}}_{i,k}-{\mathrm{C}}_{\mathrm{R},k}\right)\right]$$ (9)

$$J_{i,k}=2\pi r_i{\displaystyle \underset{\text{region R}}{\sum {\kappa }_{i,\mathrm{R}}}}\left[P_{i,k}\left({\mathrm{C}}_{\mathrm{R},k}-{\mathrm{C}}_{i,k}\right)-{\mathrm{\Psi }}_{i,k}^{\text{active}}\right]$$ (10)

where r_i is the inner radius of the tubule, d_i is the product of the partial molar volume of water and the osmotic water permeability of i, σ_k is the reflection coefficient for solute k (taken to be 1 for all solutes), ϕ_k is the osmotic coefficient for solute k, and C_{R, k} is the concentration of solute k in region R. P_{i, k} denotes the permeability of i to solute k, and Ψ_{i, k}^active the rate of active transport of solute k. As illustrated in Fig. 1, in some cases, fractions of a tubule or vas rectum i are distributed between two concentric regions, and κ_{i, R} is the fraction of i that is in contact with region R. The spatial dependence of the variables in the flux equations has been omitted for simplicity.

Vasa recta.

The flux of water flowing from the interstitium into DVR plasma is given by

$$J_{i,\mathrm{V}}^{\text{int}\hspace{0.17em}}=2\pi r_i{d}_i{\displaystyle \sum _{\text{region R}}}\left[{\kappa }_{i,\mathrm{R}}{\displaystyle \sum _k}{\sigma }_k{\varphi }_k\left({\mathrm{C}}_{i,k}^{\text{pl}}-{\mathrm{C}}_{\mathrm{R},k}\right)\right]$$ (11)

The flux of water from plasma into RBCs is expressed as

$$J_{i,\mathrm{V}}^{\text{rbc}}=2\pi r_i^{\text{rbc}}{d}_i^{\text{rbc}}\left[\frac{1}{N{k}_{\mathrm{B}}T}\left(\Delta {\pi }_h-\Delta {\pi }_p\right)+{\displaystyle \sum _k}{\sigma }_k{\varphi }_k\left({\mathrm{C}}_{i,k}^{\text{rbc}}-{\mathrm{C}}_{i,k}^{\text{Pl}}\right)\right]$$ (12)

where Δπ_h and Δπ_p are the oncotic pressures due to hemoglobin in RBCs, and to albumin and other proteins in plasma; N is Avogadro's number, k_B the Boltzmann constant, and T is the absolute temperature (the product N k_BT equals 19.3 mmHg/mM).

The transmural flux of solute k flowing from the interstitium into DVR plasma, and that from plasma to RBCs, are given by

$$J_{i,k}^{\text{int}}=2\pi r_i{\displaystyle \underset{\text{region R}}{\sum {\kappa }_{i,\mathrm{R}}{P}_{i,k}}}\left({\mathrm{C}}_{\mathrm{R,}k}-{\mathrm{C}}_{i,k}^{\text{pl}}\right)$$ (13)

$$J_{i,k}^{\text{rbc}}=2\pi r_i^{\text{rbc}}{P}_{i,k}^{\text{rbc}}\left({\mathrm{C}}_{i,k}^{\text{pl}}-{\mathrm{C}}_{i,k}^{\text{rbc}}\right)$$ (14)

Note that J_{i, k}^pl = J_{i, k}^int − J_{i, k}^rbc.

NO Generation and Consumption

NO is generated in the vascular endothelium and tubular epithelium, and its synthesis rate depends on O₂ availability. The O₂ dependence of G_{i, NO} is modeled using a Michaelis-Menten relationship

$$\begin{gathered} G_{i,\text{NO}}^{\text{cell}}\left(x\right) \\ =G_{i,\text{NO}}^{\text{max}}\left[\frac{{\mathrm{C}}_{i,\mathrm{O}2}\left(x\right)}{K_{\mathrm{O}2}^{\text{NO}}+{\mathrm{C}}_{i,\mathrm{O}2}\left(x\right)}\right]\text{cell}=\text{endothelium, epithelium} \end{gathered}$$ (15)

where the Michaelis-Menten constant K_O2^NO (taken as 38 mmHg, based on Ref. 60) is the oxygen concentration at half the maximal rate of NO production in cell layer i, itself denoted by G_{i, NO}^max. The vasa recta-to-tubule G_NO^max ratios derive from published measurements (61), and the maximal rate of NO synthesis in vasa recta is chosen to yield interstitial NO concentrations of ∼100 nM, as determined experimentally (64).

As in our previous models of NO transport, the NO consumption reactions considered here are the auto-oxidation of NO (rate V₁), the scavenging of NO by superoxide (rate V₂), the irreversible reaction of NO with HbO₂ to form methemoglobin (rate V₃), and the reversible reaction of NO with Hb to form HbNO (rate V₄)

$${\mathrm{V}}_{i,1}=k_{\mathrm{O}2}{\left({\mathrm{C}}_{i,\text{NO}}\right)}^2{\mathrm{C}}_{i,\mathrm{O}2}\hspace{0.17em}\; \hspace{0.17em}i=\text{all compartments}$$ (16)

$${\mathrm{V}}_{i,2}=k_{\text{NO-Sup}}{\mathrm{C}}_{i,\text{NO}}{\mathrm{C}}_{i,\text{O}2-}\hspace{0.17em}\; \hspace{0.17em}i=\text{all compartments}$$ (17)

$$V_{i,3}=k_{\text{oxy}}{\mathrm{C}}_{i,\text{NO}}^{\text{rbc}}{\mathrm{C}}_{i,\text{HbO}2}^{\text{rbc}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=\text{vasa recta only}$$ (18)

$$V_{i,4}=k_{\text{deoxy}}{\mathrm{C}}_{i,\text{NO}}^{\text{rbc}}{\mathrm{C}}_{i,\text{Hb}}^{\text{rbc}}-k_{\text{rev}}{\mathrm{C}}_{i,\text{HbNO}}^{\text{rbc}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=\text{vasa recta only}$$ (19)

The reaction between NO and soluble guanylate cyclase is much slower than these four reactions and is therefore neglected. The total volumetric consumption rate of NO in compartment i is then equal to

$${\Omega }_{i,\text{NO}}={\mathrm{V}}_{i,1}+{\mathrm{V}}_{i,2}+{\mathrm{V}}_{i,3}+{\mathrm{V}}_{i,4}$$ (20)

As described above, our model does not explicitly represent endothelial and epithelial cell barriers. As shown in Eqs. 2 and 5, we account for NO synthesis (or consumption) in these cellular layers via “source” (or “sink”) fluxes into the vascular or tubular lumen and into the interstitium. Given that solute concentrations in endothelia and epithelia are not explicitly determined, the fraction of NO consumption in these layers that is attributed to plasma or tubular lumen (Eqs. 2 and 5) is calculated based on plasma or luminal concentrations, whereas the fraction that is attributed to the interstitium (Eq. 8) is calculated based on interstitial concentrations.

Hypoxia-Induced NO Release

Even though oxygen is a precursor in the synthesis of NO, hypoxia has been shown to raise medullary NO levels in anesthetized rats (22). Several mechanisms have been proposed to explain how hypoxia may induce NO release. Stamler and colleagues (50) have postulated that S-nitrosohemoglobin (SNOHb) constitutes a pool of available NO, which can be transferred to the vessel wall upon deoxygenation. According to another hypothesis, RBC nitrite is reduced by deoxy-hemoglobin to form NO, and low Po₂ stimulates NO release via this route (14). Some of the key steps in these processes remain to be fully elucidated. In a previous model (16), we used the approach developed by Chen et al. (9, 10) to model the SNOHb and RBC nitrite pathways, which suggested that neither significantly affects medullary NO concentrations. Thus, in the current model, we account for hypoxia-induced stimulation of NO release in the OM in a simple manner: we assume that as O₂ availability decreases, the RBC permeability to NO (P_NO^rbc) also decreases, thereby preserving more NO in kidney tissue. Specifically, P_NO^rbc is taken to vary linearly with Po₂

$$P_{\text{NO}}^{\text{rbc}}=P_{\text{NO}}^{\text{rbc,basal}}\left(\frac{1}{2}+\frac{1}{2}\left(\frac{{\text{Po}}_2-P_a}{P_b-P_a}\right)\right)$$ (21)

where the basal RBC permeability to NO (P_NO^{rbc, basal}) is taken as 0.1 cm/s (16). The parameters of Eq. 21 are chosen so that our previous model of NO transport (16) predicts a 14% increase in medullary NO levels (at the mid-IS in R3–R4) when medullary Po₂ decreases from P_b = 28 mmHg to P_a = 12 mmHg, as observed experimentally when indomethacin is administered to anesthetized rats (23).

O₂⁻ Generation and Consumption

The rate of epithelial and endothelial O₂⁻ synthesis also depends on O₂ availability. As we previously described (16), the effects of medullary hypoxia on O₂⁻ synthesis remain poorly understood. Given that some studies suggest that low Po₂ stimulates O₂⁻ production (34), whereas others report an inhibitory effect (12), we consider two different hypotheses. Case A assumes that low Po₂ inhibits O₂⁻ synthesis, and the oxygen dependence of the O₂⁻ generation rate is then modeled using a Michaelis-Menten relationship

$$G_{i,\mathrm{O}2-}\left(x\right)=G_{i,\mathrm{O}2-}^{\text{basal}}\left[\frac{{\mathrm{C}}_{i,\mathrm{O}2}\left(x\right)}{K_{\mathrm{O}2}^{\mathrm{O}2-}+{\mathrm{C}}_{i,\mathrm{O}2}\left(x\right)}\right]$$ (22a)

where Gi, O2−basal is fixed, and KO2O2− is taken as 15.4 mmHg (12). Case B assumes that low Po2 increases O2− production by 50% relative to well-oxygenated conditions (34), so that the rate of O2− synthesis under basal conditions is given by

$$G_{i,\mathrm{O}2-}\left(x\right)=1.5·G_{i,\mathrm{O}2-}^{\text{basal}}$$ (22b)

The GO2−basal ratios between vasa recta and the different types of tubules are based upon experimental measurements (34), and the basal rate of O2− synthesis in vasa recta is chosen so that predicted values of interstitial O2− are on the order of 1 nM, as discussed below.

The O₂⁻ consumption reactions considered here are the scavenging reactions with NO and with superoxide dismutase (SOD). The rate V₅ of the latter reaction is calculated as

$${\mathrm{V}}_{i,5}=k_{\text{SOD}}{\mathrm{C}}_{i,\mathrm{O}2-}{\mathrm{C}}_{i,\text{SOD}}\text{in all compartments}$$ (23)

The total volumetric consumption rate of O₂⁻ in compartment i is given by

$${\Omega }_{i,\mathrm{O}2-}={\mathrm{V}}_{i,2}+{\mathrm{V}}_{i,5}$$ (24)

As with NO, the fraction of O₂⁻ consumed in endothelial or epithelial cells that is attributed to plasma or tubular lumen (Eqs. 2 and 5) is calculated based on plasma or luminal concentrations, whereas the fraction attributed to the interstitium (Eq. 8) is calculated based on interstitial concentrations.

To the best of our knowledge, absolute concentrations of O₂⁻ in the medulla have not been reported. We therefore use measurements of its downstream product H₂O₂, the medullary interstitial concentration of which is ∼100 nM (55), to estimate medullary O₂⁻ levels. We assume that at steady state, the volumetric generation rate of H₂O₂ is approximately counterbalanced by its consumption rate by catalase (neglecting diffusion to/from other compartments and other reactions), that is

$$0=\frac{\mathrm{d}\left[{\mathrm{H}}_2{\mathrm{O}}_2\right]}{\mathrm{d}t}\approx k_{\text{SOD},\mathrm{O}2-}\left[\text{SOD}\right]\left[{\mathrm{O}}_2^{-}\right]-k_{\text{cat}}\left[\text{CAT}\right]\left[{\mathrm{H}}_2{\mathrm{O}}_2\right]$$ (25)

The catalase content of the rat liver was estimated as 13 nmol/g wet wt liver (49), that is, ∼13 μM. Based upon a kidney-to-liver catalase activity ratio of 0.4 (56), we estimate the renal concentration of catalase to be on the order of 5 μM. Assuming that 1) the intracellular concentration of SOD is 10 μM (18), 2) k_cat equals 3.4 × 10⁷ M⁻¹·s⁻¹ (42), and 3) k_{SOD, O2⁻} equals 1.6 × 10⁹ M⁻¹·s⁻¹ (3), Eq. 25 suggests that interstitial O₂⁻ concentrations are ∼1 nM.

Capillary Endothelial Sources of NO and O₂⁻

Recall that the model represents capillaries that traverse radially across the OM cross sections. Since there are very little quantitative data on the medullary capillary network, we assume that capillary plasma is well mixed with the local interstitium. The capillaries thus essentially carry red blood cells. To account for NO and O₂⁻ synthesis by the capillary endothelium, we assume that the latter releases NO and O₂⁻ directly into the interstitium (which includes capillary plasma). The maximal volumetric generation rate of NO and O₂⁻, as well as the endothelial thickness, are taken to be the same in vasa recta and in capillaries. We also assume that the capillary luminal diameter is 8 μm. Thus the total cross-sectional area of capillary endothelium in a given region R at a given level x along the OM is given by

$$A_{\mathrm{R}}^{\text{cap endo}}\left(x\right)=n_{\text{cap}}·\left(-\mathrm{d}{\omega }_{\text{SDV}}/\mathrm{d}x\right)·\pi ·\left[{\left(r_{\text{cap}}+{\delta }_{\text{endo}}\right)}^2-{\left(r_{\text{cap}}\right)}^2\right]·\left(r_{\mathrm{R}}-r_{\mathrm{R}-1}\right)$$ (26)

where n_cap is the number of capillaries per bundle, (−dω_SDV/dx) is the rate at which SDV break up into capillaries (see Eq. 43 below), r_cap is the capillary radius, and (r_R − r_{R − 1}) is the distance between the perimeters of regions R and R − 1.

HbNO Generation and Consumption

HbNO is the product of the reversible reaction between Hb and NO (Eq. 19), and it is sequestered in RBCs. The RBC concentration of HbNO in vessel i is calculated using Eq. 6, with

$${\Omega }_{i,\text{HbNO}}^{\text{rbc}}=-{\mathrm{V}}_{\mathrm{i},4}$$ (27)

Active and Basal O₂ Consumption

We distinguish between “active” O₂ consumption (that is, O₂ consumption for active Na⁺ transport), and “basal” O₂ consumption (that is, for the basal metabolism of interstitial, endothelial, and epithelial cells). In mTALs, sodium is actively reabsorbed at the basolateral membrane by Na⁺-K⁺-ATPase pumps; given the pump stoichiometry, the number of Na⁺ moles actively reabsorbed per mole of O₂ consumed is taken to be 18 under maximal efficiency. We assume that below a critical Po₂ value (denoted P_c), anaerobic metabolism provides a fraction of the energy needed to actively reabsorb Na⁺. The volumetric rate of active O₂ consumption in mTAL epithelia (Ω_{mTAL, O2}^active) is calculated as

$${\Omega }_{\text{mTAL},\text{O2}}^{\text{active}}\left(x\right)=\frac{2\pi r_{\text{mTAL}}\left(x\right){\mathrm{\Psi }}_{\text{mTAL},\text{Na}}^{\text{active}}\left(x\right)\Theta \left(P_{\text{mTAL},\mathrm{O}2}\right)}{18A_{\text{mTAL}}^{\text{epi}}\left(x\right)}$$ (28)

where Ψ_{mTAL, Na}^active denotes the mTAL active Na⁺ transport rate, and Θ(P_{mTAL, O2}) is the fraction of that transport rate that is supported by aerobic respiration, given by

$$\Theta \left(P_{\text{mTAL},\mathrm{O}2}\right)=\{\begin{array}{ll}1\hfill & P_{\text{mTAL},O2}\ge P_c\hfill \\ \frac{P_{\text{mTAL},\mathrm{O}2}/P_c}{a+\left(1-a\right)\left(P_{\text{mTAL},\mathrm{O}2}/P_c\right)}\hfill & P_{\text{mTAL},O2}<P_c\hfill \end{array}$$ (29)

The meaning of the parameter a is discussed below.

The volumetric rate of basal O₂ consumption in the epithelium of tubule i, or the endothelium of vessel i, is calculated as

$${\Omega }_{i,\mathrm{O}2}^{\text{basal}}\left(x\right)=\frac{{\Omega }_{\text{max}\hspace{0.17em},\mathrm{O}2}^{\text{basal}}{\mathrm{C}}_{i,\mathrm{O}2}\left(x\right)}{K_{\mathrm{M},i}^{\mathrm{O}2}\left(x\right)+{\mathrm{C}}_{i,\mathrm{O}2}\left(x\right)}$$ (30)

The maximal volumetric rate of O₂ consumption (Ω_{max, O2}^basal) is assumed to be the same in each compartment and is taken as 10 μM/s (8). To account for the inhibitory effects of NO on mitochondrial utilization, the Michaelis-Menten constant (K_{M, i}^O2) is taken to vary according to the local NO concentration, i.e.

$$K_{\mathrm{M},i}^{\mathrm{O}2}\left(x\right)=K_{\mathrm{M},\text{no NO}}^{\mathrm{O}2}\left[1+{\mathrm{C}}_{i,\text{NO}}\left(x\right)/{\mathrm{C}}_{\text{NO}}^{\text{inhib}}\right]$$ (31)

where K_{M,no NO}^O2 is the Michaelis-Menten constant in the absence of NO, and C_NO^inhib is the NO concentration that doubles K_{M, i}^O2; they are respectively taken as 1 mmHg and 27 nM (3).

Active Na⁺ Reabsorption Across mTAL

The mTAL active Na⁺ transport rate is generally characterized assuming sodium-dependent Michaelis-Menten kinetics

$${\Psi }_{\text{mTAL},\text{Na}}^{\text{active}}\left(x\right)=\frac{V_{\max \hspace{0.17em},\text{Na}}\left(x\right){\mathrm{C}}_{\text{mTAL},\text{Na}}\left(x\right)}{K_{M,\text{Na}}+C_{\text{mTAL},\text{Na}}\left(x\right)}$$ (32)

where V_{max, Na} (in mol Na⁺·m⁻²·s⁻¹) is the maximal rate of Na⁺ transport, and K_{M, Na} is the Michaelis-Menten constant. The metabolic requirements for this active process are high, and Na⁺ transport may become partly limited by insufficient O₂ availability below the critical Po₂ value. In addition, Na⁺ reabsorption across mTALs is inhibited by NO and stimulated by O₂⁻. As a simplified approach, the effects of oxygen availability, as well as those of NO and O₂⁻, on Ψ_{mTAL, Na}^active are incorporated separately as follows

$$V_{\text{max}\hspace{0.17em},\text{Na}}=V_{\text{max},\text{Na}}^{\mathrm{o}}·f\left({\mathrm{C}}_{\text{mTAL},\mathrm{O}2}\right)·g\left({\mathrm{C}}_{\text{mTAL},\text{NO}}\right)·h\left({\mathrm{C}}_{\text{mTAL},\mathrm{O}2-}\right)$$ (33)

where V_{max, Na}^o is a constant. We assume that below P_c, which is taken as 5 mmHg (7), anaerobic metabolism supplies a portion of the energy needed to actively transport Na⁺ across mTALs. More specifically, we assume that in the complete absence of O₂, anaerobic metabolism produces enough ATP to sustain an active Na⁺ transport rate that is a fraction a (where 0 ≤ a ≤ 1) of the maximum rate when O₂ supply is abundant. With this hypothesis

$$f\left({\mathrm{C}}_{\text{mTAL},\mathrm{O}2}\right)=\{\begin{array}{ll}1\hfill & {\mathrm{P}}_{\text{mTAL},O2}\ge {\mathrm{P}}_{\mathrm{c}}\hfill \\ a+\left(1-a\right){\mathrm{C}}_{\text{mTAL},\mathrm{O}2}/\left({\alpha }_{\mathrm{O}2}{\mathrm{P}}_{\mathrm{c}}\right)\hfill & {\mathrm{P}}_{\text{mTAL},\mathrm{O}2}<{\mathrm{P}}_{\mathrm{c}}\hfill \end{array}$$ (34)

where α_O2 is the O₂ solubility coefficient, taken as 1.34 μM/mmHg. In the base case, a = 0.5. A value of 0 means that there is no anaerobic metabolism, and a value of 1 means that anaerobic metabolism can fully sustain the maximal mTAL Na⁺ active transport rate in the absence of O₂.

Quantitative data regarding the effects of NO and O₂⁻ on NaCl transport across mTALs are very limited. The experiments demonstrating that NO inhibits, and O₂⁻ stimulates, NaCl reabsorption were performed in vitro, where some factors (such as the levels of interacting species) were not controlled. By necessity, the way in which we account for these effects is greatly simplified, and the corresponding parameters are ascribed values that are widely uncertain. To account for the inhibitory effect of NO on Ψ_{mTAL, Na}^active, we assume that V_{max, Na} decreases with increasing NO concentration according to

$$g\left({\mathrm{C}}_{\text{mTAL},\text{NO}}\right)=1-\frac{{\mathrm{C}}_{\text{mTAL},\text{NO}}}{\beta {+\mathrm{C}}_{\text{mTAL},\text{NO}}}$$ (35)

Ortiz et al. (48) reported that 10 μM spermine NONOate (or SPM, an NO donor) inhibits mTAL Cl⁻ reabsorption by 46%. At a concentration of 10 μM, SPM is expected to result in a bath concentration of 50–60 nM NO (51). Using these data, the constant β is estimated as 46.9 nM.

It has been shown that endogenously produced O2− stimulates mTAL NaCl transport independently of NO. In the absence of l-arginine, the O2− scavenger tempol (50 μM) was found to decrease mTAL Cl− reabsorption by ∼30% after 20-min incubation (46). Since the first-order rate constant for the dismutation of O2− by tempol is 6.5 × 104 M−1·s−1 (29), the concentration of O2− after a 20-min equilibration with tempol should be vanishingly small, and we assume that reducing the mTAL concentration of O2− from a reference value (CmTAL, O2−o) to zero decreases NaCl active transport by 30%. Specifically, we assume that Vmax, Na increases with increasing O2− concentration according to

$$h\left({\mathrm{C}}_{\text{mTAL},\mathrm{O}2-}\right)=0.7+0.6\left(\frac{{\mathrm{C}}_{\text{mTAL},\mathrm{O}2-}}{{\mathrm{C}}_{\text{mTAL},\mathrm{O}2-}+{\mathrm{C}}_{\text{mTAL},O2-}^{\mathrm{o}}}\right)$$ (36)

The reference values (CmTAL, O2−o) are chosen so that h ∼ 1 in the basal configuration. Based upon preliminary simulations, CmTAL, O2−o is taken as 20 pM in case A and 350 pM in case B. The constant VmTAL, Nao was previously estimated as 25.9 nmol/(cm2·s) in the inner stripe, and 10.5 in the outer stripe, in a model that did not account for NO and O2− effects (31). To obtain a two- to threefold increase in the osmolality of the CD fluid between the corticomedullary junction and the boundary between the outer and inner medulla, those VmTAL, Nao values are multiplied by 2.2.

Permeability to NO and O₂⁻

Aquaporin-1 (AQP1) water channels have been shown to transport NO (21). As previously described (16), we use the empirical correlation obtained by Herrera et al. (21) to estimate the permeability of tubule or vessel i (P_{i, NO}) to NO, given the basal RBC permeability to NO (P_NO^{rbc, basal})

$$P_{i,\text{NO}}=P_{\text{NO}}^{\text{rbc},\text{basal}}\left(\frac{0.64{\mathrm{P}}_{\mathrm{i}}+20.23}{0.64{\mathrm{P}}_f^{\text{rbc}}+20.23}\right)$$ (37)

where P_{i, f} is the water permeability of tubule or vessel i. In the vessels and tubules that do not express AQP1 (i.e., AVR, ascending limbs, and CDs) P_{i, f} is taken as zero in Eq. 37.

Even though the lipid bilayers are almost impermeable to O₂⁻ (19), chloride channels have been shown to mediate O₂⁻ transport in endothelial cell plasma membranes (43). In the absence of more specific data, we assumed that the permeability of OM tubules and vessels to O₂⁻ is 5 × 10⁻⁴ cm/s.

The effective permeability to solute k (k = NO, O₂⁻) of the boundary separating regions R and R′ is estimated as

$$P_k^{{\mathrm{R},\mathrm{R}}^{\prime }}=\frac{A_{\mathrm{F},\mathrm{R},\mathrm{R}\prime }{D}_k}{\gamma \tau d_{\mathrm{R},\mathrm{R}\prime }}\hspace{0.17em}\hspace{0.17em}k=\text{NO},{\mathrm{O}}_2{{\displaystyle }}^{-}$$ (38)

where A_{F, R, R′} is the fraction of the R-R′ interface available for interstitial diffusion, D_k is the diffusivity of solute k in dilute solution, and d_{R, R′} is the distance between the midpoints of regions R and R′. The parameter γ is a diffusion resistance which accounts for the hindering effects of macromolecules and cells in the interstitium. We assume that γ equals 5 for both NO and O₂⁻, based upon measured membrane-to-dilute solution NO diffusivity ratios (15). The factor τ represents the effect of tortuosity on the diffusion path length around tubules and vessels and is taken as π/2 (31). The diffusivity of NO and O₂⁻ in dilute solution is taken as 3,300 and 2,800 μm²/s, respectively (6, 38).

Boundary Conditions

The boundary conditions for the flows of water, Na⁺, urea, O₂, Hb, and HbO₂ were described previously (8). The concentrations of NO and O₂⁻ are specified at the corticomedullary junction in descending vessels and tubules (Table 1). They must also be prescribed in long ascending limbs (LAL) and long ascending vasa recta (LAV) at the boundary between the inner and outer medulla (i.e., at x = L). To do so, we assume that NO and O₂⁻ molar flow rates at x = L are equal in long ascending and descending limbs, and in long ascending and descending vasa recta. Thus the concentration of solute k (k = NO and O₂⁻) in LAL fluid and LAV plasma at x = L is obtained by solving the following equations.

Table 1.

Vessel and tubule dimensions

Vessel or Tubule	Inner Diameter, μm	Endothelial/Epithelial Layer Thickness, μm	Permeability to Water, μm/s
Long and short descending vasa recta	11	1.0	1,257
Long and short ascending vasa recta	28 → 10	1.0	*
Long descending limbs	80 in OS	1.1	3,570 in OS
	21 → 16 in IS		2,295 in IS
Short descending limbs	21 → 16	1.1	3,570 in OS
			3,257 in IS
Long ascending limbs	20	8.0	0
Short ascending limbs	21 → 10	8.0	0
Collecting ducts	31 → 22	9.0	463

Diameters and water permeabilities are taken from Ref. 31, thicknesses from Ref. 8. IS, inner stripe. The arrow indicates that the parameter value decreases linearly along the x-axis (from x = 0 to x = L, unless indicated otherwise). The large diameter of the long descending limbs in the outer stripe (OS) represents the tortuosity of the proximal straight tubules.

^*Ascending vasa recta (AVR) water permeability is not given because AVR water fluxes are computed based on fluid accumulation into a region.

Long ascending limbs.

$$n_{\text{LAL}}{\mathrm{F}}_{\text{LAL},\text{V}}\left(L\right){\mathrm{C}}_{\text{LAL},k}\left(L\right)=n_{\text{LDL}}{\mathrm{F}}_{\text{LDL},\mathrm{V}}\left(L\right){\mathrm{C}}_{\text{LDL},k}\left(L\right)$$ (39)

Long vasa recta.

$${\displaystyle \sum _{j=a,b}}{n}_{\text{LAV}j}{\mathrm{F}}_{\text{LAV}j,\mathrm{V}}^{\text{pl}}\left(L\right){\mathrm{C}}_{\text{LAV}j,k}^{\text{pl}}\left(L\right)=n_{\text{LDV}}{\mathrm{F}}_{\text{LDV},\mathrm{V}}^{\text{pl}}\left(L\right){\mathrm{C}}_{\text{LDV},k}^{\text{pl}}\left(L\right)$$ (40a)

$${\mathrm{C}}_{\text{LAV}a,k}^{\text{pl}}\left(L\right)={\mathrm{C}}_{\text{LAV}b,k}^{\text{pl}}\left(L\right)$$ (40b)

We also assume that the RBC-to-plasma concentration ratio for solute k (k = NO and O₂⁻) is the same in long ascending and descending vasa recta at x = L

$${\mathrm{C}}_{\text{LAV}j,k}^{\text{rbc}}\left(L\right)={\mathrm{C}}_{\text{LAV}j,k}^{\text{pl}}\left(L\right)\frac{{\mathrm{C}}_{\text{LDV},k}^{\text{rbc}}\left(L\right)}{{\mathrm{C}}_{\text{LDV},k}^{\text{pl}}\left(L\right)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j=a,b$$ (41)

The RBC concentration of HbNO is specified as 1 μM in descending vasa recta at the corticomedullary junction. This estimate is in the midrange of reported values (24, 30). At the boundary between the outer and inner medulla, the molar flow rate of HbNO leaving LDV is taken to be equal to that entering LAV

$$\begin{gathered} {\displaystyle \sum _{j=a,b}}{n}_{\text{LAV}j}{\mathrm{F}}_{\text{LAV}j,\mathrm{V}}^{\text{rbc}}\left(L\right){\mathrm{C}}_{\text{LAV}j,\text{HbNO}}^{\text{rbc}}\left(L\right) \\ =n_{\text{LDV}}{\mathrm{F}}_{\text{LDV},\mathrm{V}}^{\text{rbc}}\left(L\right){\mathrm{C}}_{\text{LDV},\text{HbNO}}^{\text{rbc}}\left(L\right) \end{gathered}$$ (42a)

$${\text{C}}_{\text{LAV}a,\text{HbNO}}^{rbc}\left(L\right)={\mathrm{C}}_{\text{LAV}b,\text{HbNO}}^{rbc}\left(L\right)$$ (42b)

Parameter Values

The dimensions of tubules and vessels are given in Table 1, those of interstitial regions in Table 2. Shown in Table 3 are NO and O₂⁻ generation rates, permeabilities, and inlet boundary conditions. Kinetic parameters are listed in Table 4. The fraction of short vasa recta present at level x is given by

$${\omega }_{\text{SDV}}\left(x\right)=\{\begin{array}{ll}1-0.1x/L\hfill & 0\le x\le L_{\text{OS}}\hfill \\ \left(1-0.1L_{\text{OS}}/L\right)\left(1-\frac{x-L_{\text{OS}}}{L-L_{\text{OS}}}\right)\hfill & L_{\text{OS}}\le x\le L\hfill \end{array}$$ (43)

where L_OS is the outer-stripe length (0.6 mm), and L is the total OM length (2.0 mm).

Table 2.

Region parameters

	R1	R2	R3	R4
Region radii, μm	36.7–42.4	225–121	348–191	388–226
Interstitial areas, ×10−6 cm2	2.41–2.26	87.8–16.2	126–137	53.2–91.6
Fractional area available for diffusion, AF, R, R+l	0.0560–0.0398	0.0560–0.120	0.0560–0.199
Area of capillary endothelial compartment, ×10−6 cm2	0.0424–0.666	0.435–2.47	0.284–2.20	0.0924–1.10

The first value corresponds to the corticomedullary junction, the second to the mid-IS. Except for capillary endothelial areas, which are given by Eq. 26, the data are taken from Ref. 31.

Table 3.

NO and O₂⁻ transport parameters

	Descending Vasa Recta	Ascending Vasa Recta	Descending Limbs	Ascending Limbs	Collecting Ducts
Maximal epithelial/endothelial NO generation rate, Gi,NOmax, μM·s−1	76.6	72.2*	12.3	0.985	0.415
Epithelial/endothelial O2− generation rate, Gi,O2−basal, μM·s−1	21.0	19.8*	15.2	3.2	1.8
NO permeability†, cm/s	0.496	0.0122	0.896 → 1.387‡	0.0122	0.0122
O2− permeability†, cm/s	0.0005	0.0005	0.0005	0.0005	0.0005
NO concentration at inlet, nM	RBC: 0.1	N.A.	100	NA	100
	Plasma: 100
O2− concentration at inlet, nM	RBC: 0.1	N.A.	0.02	NA	0.02
	Plasma: 0.1

NO, nitric oxide; O₂⁻, superoxide; NA, not applicable.

^*The AVR rate is obtained by multiplying the DVR rate by (1 − f_fen), where f_fen is the fraction of the AVR surface that is fenestrated (taken as 0.057, based on Ref. 35).

^†Permeability values correspond to the vascular or tubular wall. The red blood cell (RBC) permeability to NO is taken as 0.1 cm/s in the base case.

^‡Depending on the descending limb portion (note that the NO permeability scales with water permeability).

Table 4.

Reaction kinetic parameters

Parameter Definition	Parameter Value
NO-O2 reaction rate constant kO2, M−2·s−1	6.3 × 106
NO-O2− reaction rate constant kNO-Sup, M−1·s−1	6.7 × 109
NO-HbO2 reaction rate constant koxy, M−1·s−1	2.5 × 107
NO-Hb reaction rate constants kdeoxy, M−1·s−1 and krev, s−1	2.5 × 107 and 10−4
O2−-SOD reaction rate constant kSOD, M−1·s−1	1.6 × 109
SOD concentration, μM	5

HbO₂, oxyhemoglobin.

Numerical Methods

The steady-state differential equations are discretized to form a system of nonlinear algebraic equations. A spatial discretization of 200 grid points along the medullary axis and 50 grid points in the radial direction is used. The system of coupled, nonlinear conservation equations is solved using MINPACK, a numerical package implemented in FORTRAN for solving nonlinear equations with a modification of Powell's hybrid algorithm, in an iterative approach described in a previous study (8).

RESULTS

Base-Case Description

In baseline simulations, the RBC permeability to NO is kept constant, and the O₂⁻ generation rate is taken to vary in parallel with Po₂ (case A). In other words, the base case does not incorporate hypoxia-induced increases in NO release and in O₂⁻ generation. These effects are examined further below.

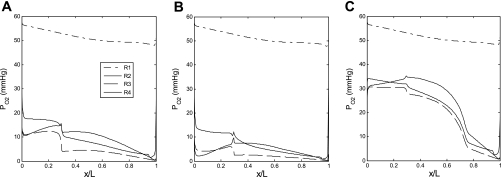
Po₂ profiles are similar to those described in our recent studies (7). Briefly, our model predicts that the OM architecture results in significant Po₂ gradients both in the axial and the radial directions (Fig. 2A). The segregation of long DVR at the center of the vascular bundles (in region R1) preserves enough O₂ for delivery to the inner medulla (IM), while the high metabolic requirements of mTALs in the peripheral regions (R2–R4) significantly deplete O₂ therein.

Fig. 2.

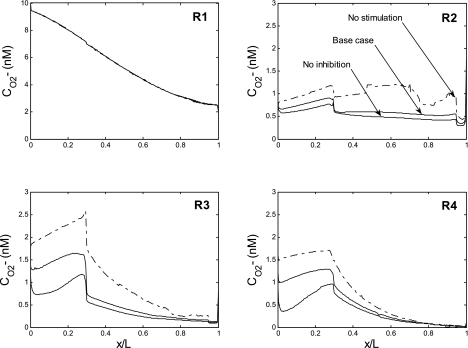
Oxygen tension (Po₂) profiles in the interstitium of the 4 regions (R1–R4) in the base case (A), assuming that nitric oxide (NO) does not inhibit medullary thick ascending limb (mTAL) NaCl reabsorption (B), and assuming that O₂⁻ does not stimulate mTAL NaCl reabsorption (C). x/L denotes the ratio of the axial coordinate to total length of outer medulla. In all cases, the red blood cell (RBC) permeability to NO (P_NO^rbc) is kept constant, and the O₂⁻ generation rate (G_O2⁻) is taken to vary in parallel with Po₂.

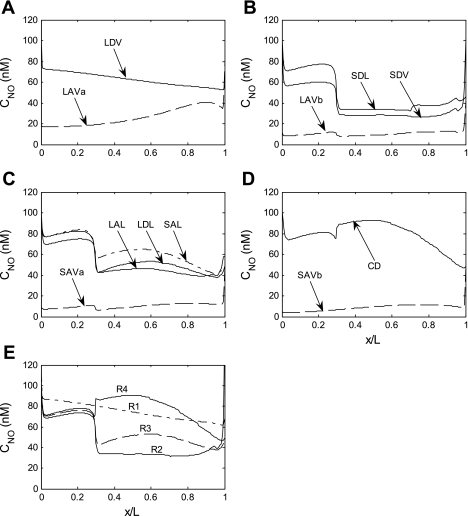
NO concentration (C_NO) profiles are shown in Fig. 3. As described in our previous model of transport in cross sections of the rat OM (16), the large radial Po₂ gradients in turn generate substantial radial NO and O₂⁻ concentration gradients, since the synthesis of both solutes is O₂ dependent. Vasa recta endothelial cells are by far the largest source of NO, but RBCs constitute a sink for NO because hemoglobin scavenges NO at a very rapid rate (∼100 times faster than O₂⁻ does), and the RBC permeability to NO is relatively high. Thus, without the rate-limiting effects of O₂ on NO generation, C_NO would be lowest in the vascular bundle core, that is, the region with the highest density of RBCs. When those rate-limiting effects are taken into account, C_NO is predicted be significantly higher in R1 (the region with the highest Po₂) than in R2 and R3 (the regions with the poorest O₂ availability) in the inner stripe (Fig. 3E).

Fig. 3.

Base case NO concentration (C_NO) in tubules, vasa recta, and interstitia. A–D: regions R1, R2, R3, and R4, respectively; tubules are assigned to the region with which they are in contact for 50% or more of their inner stripe length. E: C_NO profiles in the interstitium of the 4 regions.

In the outer stripe (OS) of the OM, several classes of tubules straddle two peripheral regions (see Fig. 1B), leading to significant mixing between R2, R3, and R4. Thus interstitial C_NO is very similar in those three regions. It is slightly higher in R4, a region with relatively high Po₂ levels and few vessels (i.e., few NO sinks). In the inner stripe (IS), the external regions are more segregated, leading to sharper C_NO differences between regions.

The sharp rise in interstitial C_NO in R4 at the OS-IS junction is caused by tubule migration. As illustrated in Fig. 1, the short descending limbs are near CDs in the OS (i.e., they straddle R3 and R4), but move to the immediate periphery of the vascular bundle (i.e., to R2) in the IS. These short (and thin) descending limbs generate less NO than the other tubular and vascular structures in R4. Thus, in the OS, NO diffuses from the R4 interstitium into their lumen, and when this flux abruptly ceases at the OS-IS junction, interstitial C_NO increases sharply in R4. If the position of these short descending limbs were to be maintained constant in the OM, there would be no such sharp increase (results not shown). In the deep IS, R4 Po₂ drops significantly, and so does the interstitial C_NO in R4.

In R2 and R3, by contrast, interstitial C_NO drops suddenly at the OS-IS junction. Indeed, due to an increase in the maximal rate of Na⁺ active transport across mTALs at the junction, Po₂ levels fall significantly in R2 and R3 (see Fig. 2A), thereby greatly reducing NO generation in those regions. In addition, long descending limbs are taken to be very large in the OS (to account for the tortuosity of proximal tubules), and thus constitute a significant source of NO therein; their diameter decreases sharply at the OS-IS junction, which further reduces NO generation in R2–R3. Even though Po₂ is higher in R2 (where there are fewer mTALs), interstitial C_NO is higher in R3 than in R2 mainly because of the short ascending limbs: the latter tubules straddle R3 and R4 and receive a substantial amount of NO from R4, which then diffuses from the short ascending limb lumen in the R3 interstitium. Note that along the corticomedullary axis, and within each stripe, C_NO generally rises and falls with Po₂.

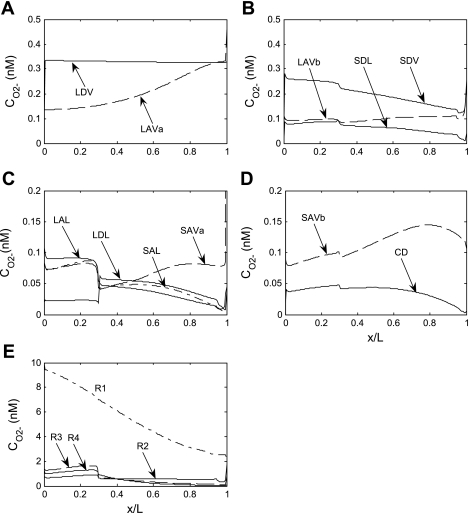
Superoxide concentration (C_O2⁻) profiles are illustrated in Fig. 4. There is as yet no evidence that AQP1 is permeable to O₂⁻, and vascular and tubular permeabilities to O₂⁻ are taken to be significantly lower than those to NO. Thus transmembrane C_O2⁻ gradients are predicted to be significant, and in a given region, C_O2⁻ is significantly higher in the interstitium than in tubular lumen or plasma. In the base case, the O₂⁻ generation rate is assumed to decrease with decreasing Po₂, and close examination of the curves reveals that interstitial C_O2⁻ profiles closely track Po₂ profiles. Note that C_O2⁻ is more elevated in R1 than in the peripheral regions not only because Po₂ is higher in the vascular bundle core but also because the model postulates that there is much less water accumulation, and therefore less dilution, therein. The sharp decrease in interstitial C_O2⁻ at the OS-IS junction in the interbundle region stems from the sudden diminution in the long descending limb diameter in R2 and R3, as well as the migration of short descending limbs out of R4 (Fig. 4).

Fig. 4.

Base case O₂⁻ concentration (C_O2−) in tubules, vasa recta, and interstitia. A–D: regions R1, R2, R3, and R4, respectively. E: C_O2⁻ profiles in the interstitium of the 4 regions. Note the different y-axis scales.

One measure of the concentrating capacity of the OM is the osmolality of the tubular fluid in the CD at the OM-IM junction (denoted osm_CD^L hereafter). Under basal conditions, the latter equals 787 mosmol/kgH₂O (Table 5).

Table 5.

Effects of NO and O₂⁻ on the concentrating capacity of the OM

	osmCDL, mosmol/kgH2O
	Case A	Case B	Case C
Base case	787	878	729
Without the NO/O2− reaction	770	714	708
Without NO-mediated inhibition of mTAL active transport	1,333	1,398	1,328
Without O2−-mediated stimulation of mTAL active transport	493	584	453

osm_CD^L, osmolality of the collecting duct (CD) tubular fluid at the boundary between the outer (OM) and inner medulla; case A, O₂⁻ synthesis is taken to decrease with decreasing Po₂ (Eq. 22a), and the RBC permeability to NO (P_NO^rbc) is taken to remain constant; case B, O₂⁻ synthesis is taken to increase with decreasing Po₂ (Eq. 22b), and P_NO^rbc is taken to remain constant; case C, O₂⁻ synthesis is taken to decrease with decreasing Po₂ (Eq. 22a), and P_NO^rbc is taken to vary with Po₂ (Eq. 21); mTAL, medullary thick ascending limb.

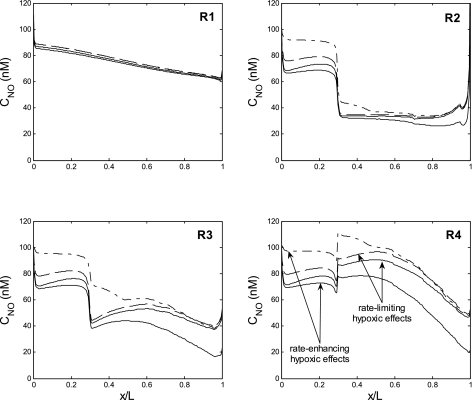
Effects of Hypoxia

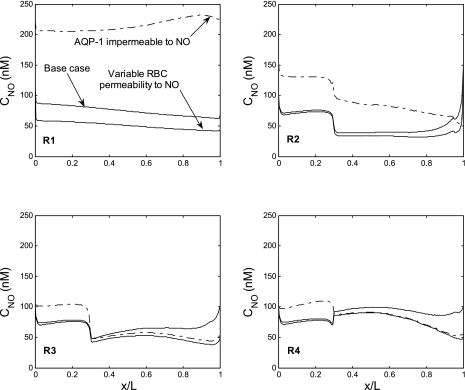
As described above, the mechanisms by which hypoxia modulates medullary NO and O₂⁻ levels remain uncertain. To incorporate the effects of hypoxia on C_NO in a simple manner, we assumed that the RBC permeability to NO (P_NO^rbc), and thus the strength of the RBC sink, decrease with decreasing Po₂ (Eq. 21). With this hypothesis, interstitial C_NO is predicted to rise significantly relative to the base case in the peripheral, O₂-starved regions (R2–R4), and to decrease in the central, O₂-rich region (R1), as displayed in Fig. 5. Higher NO levels in mTALs result in greater inhibition of Na⁺ transport, and thus a diminished concentrating capacity; osm_CD^L, is predicted to be 729 mosmol/kgH₂O in this case.

Fig. 5.

C_NO profiles in the interstitium of the 4 concentric regions (R1–R4). In the base case (solid curves), P_NO^rbc remains constant, and aquaporin-1 (AQP1) is permeable to NO. In the second case (dotted curves), P_NO^rbc is taken to increase with decreasing Po₂. In the third case (dash-dotted curves), AQP1 is taken to be impermeable to NO.

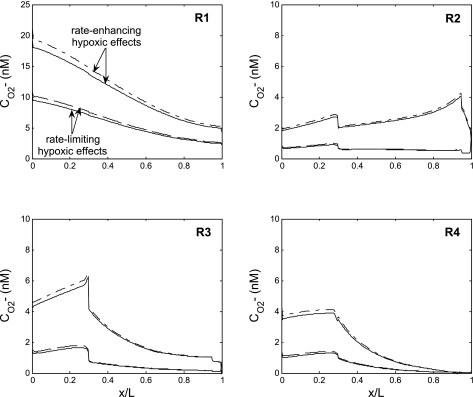
As to the effects of hypoxia on O₂⁻, if we assume that a low Po₂ enhances rather than limits O₂⁻ generation (as described by Eq. 22b), the predicted C_O2⁻ is then two to three times higher than in the base case (Fig. 6). Since the volumetric generation rate of O₂⁻ is highest in vasa recta and descending limbs, interstitial C_O2⁻ varies in proportion to the fractional area occupied by vasa recta and descending limbs within each region, as previously described (16). In the OS, this fractional area is highest in R1 and lowest in R2, and so is C_O2⁻. In the deep IS, the relative area occupied by vasa recta and descending limbs decreases monotonically from R1 to R4, and so does interstitial C_O2⁻. The CD fluid osmolality at the OM-IM junction is predicted to be 878 mosmol/kgH₂O in this case.

Fig. 6.

C_O2⁻ profiles in the interstitium of the 4 concentric regions (R1–R4), assuming a fixed P_NO^rbc. The solid and dashed curves, respectively, depict C_O2⁻ with and without O₂⁻ scavenging by NO, assuming that the O₂⁻ generation rate (G_O2⁻) decreases with decreasing Po₂. The dotted and dash-dotted curves, respectively, depict C_O2⁻ with and without O₂⁻ scavenging by NO, assuming that G_O2⁻ is enhanced rather than limited by low medullary Po₂. C_O2⁻ increases moderately in the absence of the NO-O₂⁻ reaction because SOD is the main O₂⁻ scavenger.

Direct NO-O₂⁻ Interactions

To assess the impact of direct NO-O₂⁻ interactions, we then set the NO-O₂⁻ reaction rate to zero. Simulations were performed for three cases: G_O2⁻ and P_NO^rbc were taken to be fixed or to vary with Po₂. In all three scenarios, predicted O₂⁻ concentrations rose by 10% at most (Fig. 6), because the rate of O₂⁻ consumption by SOD is significantly faster than that by NO.

The extent to which C_NO is modulated by the NO-O₂⁻ reaction depends on O₂⁻ levels, as displayed in Fig. 7. If G_O2⁻ and C_O2⁻ are low to start with (as in the base case), eliminating the NO-O₂⁻ reaction raises C_NO by 2–10 nM, and osm_CD^L drops slightly, from 787 to 770 mosmol/kgH₂O (Table 5). If C_O2⁻ is two to three times higher (as when G_O2⁻ is enhanced by low medullary Po₂), eliminating the NO-O₂⁻ reaction raises C_NO by up to 30 nM in R3–R4, i.e., those regions where the major NO scavenger, hemoglobin, is the least predominant. In that case, osm_CD^L is predicted to decrease by 20%, from 878 to 714 mosmol/kgH₂O (Table 5).

Fig. 7.

C_NO profiles in the interstitium of the 4 regions, assuming a fixed P_NO^rbc. The solid and dashed curves, respectively, depict C_NO with and without NO consumption by O₂⁻, assuming that G_O2⁻ decreases with decreasing Po₂. In the absence of the NO-O₂⁻ reaction, C_NO increases by <10 mM relative to the base case. The dotted and dash-dotted curves, respectively, depict C_NO with and without NO consumption by O₂⁻, assuming that G_O2⁻ is elevated under hypoxic conditions. Under that assumption, O₂⁻ scavenging of NO is predicted to significantly impact NO levels in the peripheral regions. (Note that the dashed and dash-dotted lines cannot be distinguished in R1.)

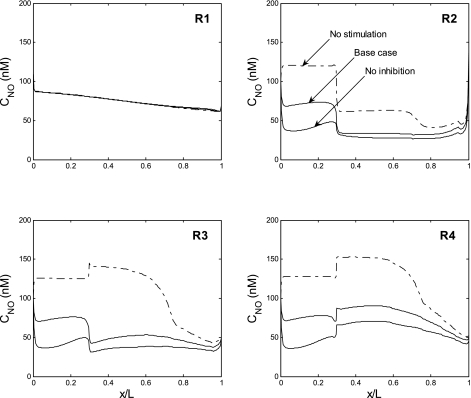
NO-Mediated Inhibition of mTAL Sodium Reabsorption

To determine the extent to which NO-induced inhibition of mTAL NaCl reabsorption affects the concentrating capacity of the OM and its oxygenation, we performed simulations in which NO effects on NaCl transport were abolished. That is, we set g(C_{mTAL, NO}) = 1 in Eq. 33. In the absence of NO-mediated inhibition, the rates of NaCl reabsorption and O₂ consumption are predicted to both rise markedly relative to the base case. In R2 and R3, Po₂ drops below the critical pressure throughout most of the IS (Fig. 2B). The rate of NaCl active transport can nevertheless increase substantially because of anaerobic metabolism. The model predicts that the concentrating capacity of the OM rises by 70%, that is, osm_CD^L increases from 787 to 1,333 mosmol/kgH₂O (Table 5). In the vascular bundle core (R1), Po₂ remains relatively unchanged and oxygen delivery to the IM is preserved.

Since NO generation decreases with decreasing Po₂, C_NO is then significantly lower in R2–R4, relative to the base case (Fig. 8). Under these conditions, C_NO remains higher in R1 than in R2–R4 along the entire medullary axis.

Fig. 8.

C_NO profiles in the interstitium of the 4 regions, in the base case (solid curves), assuming that NO does not inhibit mTAL NaCl reabsorption (dotted curves), and assuming that O₂⁻ does not stimulate mTAL NaCl reabsorption (dash-dotted curves). Profiles were obtained assuming that P_NO^rbc is constant and that G_O2⁻ varies in parallel with Po₂.

Similar trends are obtained if we assume that the RBC permeability to NO decreases with decreasing Po₂, as described by Eq. 21. Eliminating NO-mediated inhibition of mTAL transport raises osm_CD^L by 80% in that case (Table 5). Even though the Po₂ drop in R2–R4 reduces RBC removal of NO therein, the concomitant decrease in NO generation predominates and C_NO is also predicted to decrease in the peripheral regions under this assumption (results not shown).

Given that NO scavenges O₂⁻, an isolated reduction in C_NO should raise C_O2⁻. However, assuming that O₂⁻ generation decreases with decreasing Po₂, the reduction in O₂⁻ consumption is accompanied by a greater reduction in O₂⁻ production, and C_O2⁻ is predicted to decrease in R2–R4 when NO-mediated inhibition of mTAL transport is eliminated (Fig. 9). The decrease is more pronounced in the OS (20–50%) than in the IS (10–20%) because Po₂ drops more sharply in the upper OM. Conversely, if we were to assume fixed O₂⁻ generation rates, C_O2⁻ would increase by ∼5% in the peripheral regions in the absence of NO effects on NaCl reabsorption, given the concomitant reduction in the O₂⁻ consumption rate (results not shown).

Fig. 9.

C_O2⁻ profiles in the interstitium of the 4 regions, in the base case (solid curves), assuming that NO does not inhibit mTAL NaCl reabsorption (dotted curves), and assuming that O₂⁻ does not stimulate mTAL NaCl reabsorption (dash-dotted curves). Profiles were obtained assuming that P_NO^rbc is constant and that G_O2⁻ varies in parallel with Po₂.

O₂⁻-Mediated Activation of mTAL Sodium Reabsorption

As opposed to NO, O₂⁻ stimulates NaCl reabsorption across the mTAL. In the next set of simulations, we removed these O₂⁻-induced effects to assess their importance. That is, we set h(C_{mTAL, NO}) = 0.70 in Eq. 33.

In the absence of O₂⁻-mediated stimulation of active transport, the rate of O₂ consumption diminishes, interbundle Po₂ levels increase, and so does NO production in R2–R4. Thus NO-induced inhibition of mTAL active transport rises in turn, thereby increasing Po₂ levels further and exerting a positive feedback loop. Nevertheless, the limited O₂ supply to the interbundle region halts the Po₂ and NO increase therein. Given this positive feedback loop, the concentrating capacity of the OM is predicted to be significantly lower relative to the base case: osm_CD^L is then equal to 493 (vs. 787) mosmol/kgH₂O (Table 5).

Without O₂⁻-mediated stimulation of NaCl reabsorption, Po₂ is predicted to hover above 20 mmHg in all regions all the way down to the mid-IS (Fig. 2C). With or without hypoxia-mediated effects on NO release, interstitial C_NO is then predicted to remain higher in R3–R4 than in R1 throughout most of the medulla (Fig. 8). Indeed, as noted above, without the rate-limiting effects of O₂ on NO generation rates, C_NO is predicted to be the lowest in the vascular bundle core, where the relative density of Hb-carrying blood vessels is the highest.

When O₂⁻ effects on NaCl transport are eliminated, the Po₂ elevation translates into an increase in O₂⁻ generation, assuming that O₂⁻ generation increases in parallel with Po₂, so that interstitial C_O2⁻ rises by ∼50% in R2–R4 (Fig. 9). However, if O₂⁻ generation is taken to be fixed, the increase in O₂⁻ consumption due to higher NO levels causes C_O2⁻ to drop by ∼5% in the interbundle region (results not shown).

Contribution of Anaerobic Metabolism

In all the preceding simulations, we assumed that glycolysis provides a substantial fraction of the energy needed to actively reabsorb NaCl across mTALs when Po₂ drops below the critical pressure. How would our predictions differ in the absence of anaerobic metabolism (i.e., if the parameter a in Eqs. 28 and 29 were equal to 0 instead of 0.5)? The active transport rate would then be considerably limited by the hypoxic conditions that prevail in the renal medulla, and all else being equal, the concentrating capacity of the OM would greatly diminish.

Specifically, assuming that a = 0, osm_CD^L drops to 621 mosmol/kgH₂O under basal conditions (vs. 787 with a = 0.5). Abolishing NO-mediated inhibition of mTAL transport has a small impact on NaCl reabsorption, because the supply of O₂ in the interbundle region is not sufficient to support significantly greater metabolic needs by itself. Thus, with a = 0, osm_CD^L only increases by 5% (to 655 mosmol/kgH₂O) when NO-mediated inhibition of mTAL transport is eliminated. In contrast, in the absence of O₂⁻-mediated stimulation of NaCl reabsorption, Po₂ reaches comparable levels with and without anaerobic metabolism, NO and O₂⁻ concentration profiles are similar, and so is osm_CD^L (464 mosmol/kgH₂O if a = 0, vs. 493 if a = 0.5).

AQP1-Mediated NO Transport

The base case assumes that AQP1 transports NO, as observed experimentally (21). Nonetheless, there is some controversy as to whether AQP1 is indeed permeable to small gases such as CO₂, NH₃, and NO (57). We performed simulations in which AQP1 was taken to be impermeable to NO: the NO permeability of the vessels and tubules that express AQP1 in the OM, namely, DVR and descending limbs, was set to 0.0122 cm/s, equal to that of other vessels and tubules (Table 3). As displayed in Fig. 5, in the absence of NO transport via AQP1, interstitial NO concentrations are predicted to increase significantly relative to the base case. Elevations are most pronounced in the core (R1) and immediate periphery (R2) of the vascular bundle, where all DVR, which represent the largest volumetric source of NO, are located. Interstitial C_NO increases because as the resistance to NO diffusion from endothelium to plasma increases, a smaller fraction of NO makes its way into RBCs, and more NO is preserved elsewhere. The subsequent decrease in mTAL NaCl reabsorption reduces osm_CD^L from 787 to 736 mosmol/kgH₂O (Table 6).

Table 6.

Effects of luminal flow and O₂⁻ synthesis on the concentrating capacity of the OM

	osmCDL, mosmol/kgH2O
Base Case	787
Without anaerobic metabolism	621
Without anaerobic metabolism and no mediated inhibition of mTAL active transport	655
Without anaerobic metabolism and no mediated stimulation of mTAL active transport	464
Without facilitated NO transport via AQP1	736
With a 20% increase in inlet water flows	648
With a 20% increase in inlet water flows and in GNO	575
With a 20% increase in inlet water flows, in GNO and in GO2−	591
With a 10-fold increase in GO2−	1,073
With a 10-fold increase in GO2− and a 25% decrease in GNO	1,175
With a 10-fold increase in GO2−and a 50% decrease in GNO	1,297
With a 10-fold increase in GO2−and a 50% decrease in TNa/Qo2	935
With a 10-fold increase in GO2−, a 50% decrease in TNa/Qo2, and a 25% decrease in GNO	1,020
With a 10-fold increase in GO2−, a 50% decrease in TNa/Qo2, and a 50% decrease in GNO	1,124

AQP1, aquaporin-1; G_NO and G_O2⁻ are the volumetric rates of NO and O₂⁻ synthesis, respectively; T_Na/Qo₂, ratio of transported sodium to oxygen consumption. In all these simulations, G_O2⁻ is taken to decrease with decreasing Po₂, and P_NO^rbc is fixed.

Flow-Induced Endothelial Nitric Oxide Synthase Activation

Studies have shown that increased luminal flow activates endothelial nitric oxide synthase (eNOS) and enhances NO production in DVR and TALs (47, 62). Luminal flow also stimulates O₂⁻ production in TALs (26). Flow-induced effects on O₂⁻ are partly inhibited by NO via a nonscavenging mechanism, as discussed below. To determine whether eNOS and NADPH oxidase activation by luminal flow plays an important role in the regulation of OM Na⁺ reabsorption, we performed simulations in which inlet volume flows (i.e., in DVR, descending limbs, and CD at x = 0) and maximal NO and O₂⁻ synthesis rates were simultaneously increased by 20%. Vasa recta express both eNOS and neuronal NOS (nNOS) (40), but in the absence of specific data on the distribution of these enzymes, we raised NO (and O₂⁻) volumetric generation rates by 20% everywhere.

We first examined the isolated effects of increasing inlet volume flows on the OM concentrating mechanism. An increase in medullary perfusion augments O₂ availability and thereby stimulates NaCl reabsorption, but this effect is more than counterbalanced by two opposite forces: a Po₂-induced increase in NO synthesis, which acts to inhibit NaCl active transport, and higher loads, which mean that larger fluid flows must be concentrated. Thus the OM concentrating capacity is predicted to decrease relative to the base case. As shown in Table 6, an isolated 20% increase in inlet volume flows is calculated to lower osm_CD^L by 18%, from 787 to 648 mosmol/kgH₂O.

When inlet volume flows and maximal NO synthesis rates (i.e., Gi, NOmax in Eq. 15) are both increased by 20%, CNO rises further, and osmCDL is predicted to drop even more, to 575 mosmol/kgH2O (Table 6). When inlet volume flows, NO synthesis rates, and O2− synthesis rates (i.e., Gi, O2−basal in Eq. 22a) are all increased by 20%, O2− exerts greater compensating effects on mTAL transport, and osmCDL climbs slightly, to 591 mosmol/kgH2O (Table 6). Together, these results suggest that an increase in tubular and vascular flows substantially reduces the OM axial osmolality gradient.

Hypertensive Conditions

Medullary infusions of the SOD inhibitor DETC have been shown to induce hypertension in rats: DETC induced an eightfold increase in interstitial C_O2⁻, with a subsequent 40% decrease in medullary blood flow and a nearly 20-mmHg increase in blood pressure (37). To dissect some of the underlying mechanisms, we raised maximal O₂⁻ generation rates in the OM by a factor of 10. As expected, the higher levels of O₂⁻ stimulate NaCl reabsorption and O₂ consumption, thereby reducing Po₂ and C_NO. In the interbundle region, Po₂ is predicted to drop by ∼5–10 mmHg at the mid-OS and ∼2 mmHg at the mid-IS.

Per se, a 10-fold increase in O₂⁻ concentration raises osm_CD^L by ∼300 mosmol/kgH₂O, i.e., by 35% (Table 6). The increase is limited because 1) the effects of O₂⁻ on NaCl reabsorption across the mTAL are described using a saturable expression (Eq. 33) and 2) NO still exerts significant inhibitory effects on this NaCl transport pathway.

The 35% increase in osm_CD^L is predicted assuming that the number of Na⁺ moles actively reabsorbed per mole of O₂ consumed (i.e., the mTAL T_Na/Qo₂ ratio) remains fixed at 18. There is some evidence, however, that NO and/or reactive oxygen species (ROS) modulate the amount of O₂ consumed per Na⁺ ion transported, as discussed below. However, the explicit impact of NO and ROS on T_Na/Qo₂ in the mTAL has not been measured, to the best of our knowledge. If we assume that this ratio is halved (based on data from spontaneously hypertensive rats in Ref. 59) when O₂⁻ concentrations increase 10-fold, our model then predicts a smaller (20%) increase in osm_CD^L (Table 6).

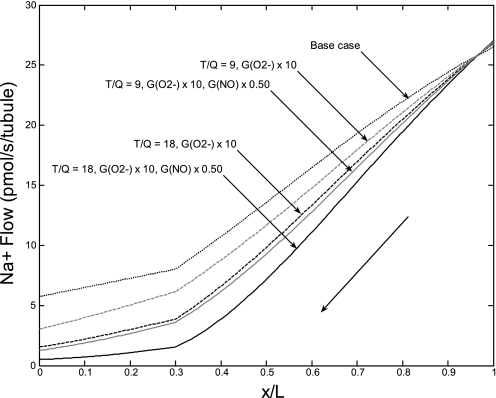
Some models of hypertension, such as the Dahl salt-sensitive rat, are also characterized by a decrease in NO production (39). In the absence of specific data, we simulated graded reductions (25 and 50%) in NO synthesis in parallel with the 10-fold increase in O₂⁻ levels. As expected, the greater the reduction in G_NO, the faster NaCl transport across mTALs, and the higher the concentrating capacity of the OM (Table 6). The impact of the G_O2⁻ increase, G_NO decrease, and T_Na/Qo₂ variations on NaCl reabsorption along the long ascending limb (LAL) is illustrated in Fig. 10. The Na⁺ flow at the LAL inlet (at x = L) is very similar in all cases, ∼27 pmol/s (per tubule). In the base case, it decreases to 5.8 pmol/s at the corticomedullary junction (x = 0). If the O₂⁻ synthesis rate is multiplied by 10 and Na⁺ reabsorption thereby stimulated, it decreases much more rapidly. If T_Na/Qo₂ remains equal to 18, the LAL Na⁺ flow decreases to 1.6 and 0.5 pmol/s at x = 0, assuming no change and a 50% decrease in G_NO, respectively. If T_Na/Qo₂ drops to 9, it decreases slightly less, to 3.0 and 1.3 pmol/s, respectively.

Fig. 10.

Na⁺ flow (in pmol·s⁻¹·tubule⁻¹) along the LAL. The thick arrow indicates the direction of the flow, from the OM-inner medullary (IM) boundary (x/L = 1) to the corticomedullary junction (x/L = 0). The black dotted line represents the base case. In all other cases, G_O2⁻ is multiplied 10-fold to mimic hypertensive conditions. The ratio of transported sodium to oxygen consumption (T_Na/Qo₂) is taken as 18 (black curves) or 9 (grey curves), and the NO synthesis rate (G_NO) is either maintained constant (dashed lines) or halved (solid lines). NaCl reabsorption is maximal when the Na⁺ flow at x = 0 is the lowest.

DISCUSSION

Feedback Mechanisms

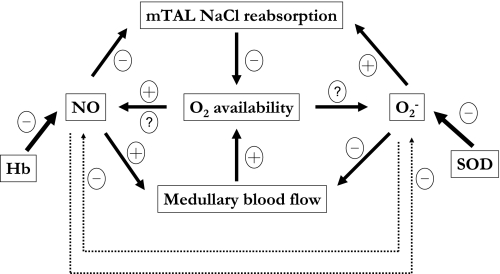
Our results suggest that NaCl reabsorption across mTALs and the concentrating capacity of the OM are substantially modulated by NO and O₂⁻. Moreover, the effect of each solute on NaCl transport in the OM cannot be considered in isolation, given the feedback loops resulting from the reciprocal interactions between O₂, NO, and O₂⁻, which are summarized in Fig. 11.

Fig. 11.

Feedback mechanisms involving NO, O₂⁻, and O₂. NO synthesis is O₂ dependent, but RBC trapping of NO may also decrease under hypoxic conditions, via uncertain mechanisms. NO is scavenged very rapidly by hemoglobin (Hb), and to a smaller extent by O₂⁻. The relationship between O₂⁻ synthesis and Po₂ remains unclear. Superoxide dismutase (SOD) consumes O₂⁻ at a faster rate than NO does. As a vasodilator, NO enhances medullary perfusion and O₂ supply, whereas O₂⁻ exerts opposite effects. NO inhibits NaCl reabsorption by the thick ascending limb and therefore O₂ consumption, whereas O₂⁻ stimulates both. Not shown on the diagram are the many other paracrine agents (such as endothelins and prostaglandins) that also act on vascular contraction and tubular NaCl reabsorption in the renal medulla.

The net production rate of NO and O₂⁻ is oxygen dependent. Reciprocally, NO and O₂⁻ affect oxygen availability in two ways: by modulating active transport across mTAL cells and therefore O₂ consumption, and by regulating vessel contraction and therefore O₂ supply. Our current model does not take into consideration vessel diameter changes, i.e., vasoactive effects are not accounted for in this study. In the absence of such vasoactive effects, our model predicts that O₂⁻-mediated stimulation of NaCl reabsorption raises the OM concentrating capacity (evaluated as the tubular fluid osmolality in collecting ducts at the OM-IM boundary) by >50% under basal conditions. Note that the numerical values in this study are necessarily approximations, given the significant uncertainty associated with several key parameters (see above). Conversely, NO-induced inhibition of NaCl reabsorption is predicted to decrease the OM concentrating capacity by >50% (Table 5). Our prediction that active transport of NaCl would substantially increase in the absence of NO is predicated on the hypothesis that anaerobic metabolism can supply a significant fraction of the energetic requirements of mTALs. Without glycolysis, NaCl transport would only increase by 5% in the absence of NO (Table 6), because there isn't enough O₂ in the interbundle region to support per se significantly greater metabolic needs.

If NO didn't inhibit NaCl active transport across mTALs, faster transport rates and therefore enhanced O₂ consumption would reduce Po₂, which in turn would lower NO production. The resulting decrease in C_NO should then lead to vasoconstriction, which would further reduce Po₂ by limiting O₂ supply. However, several mechanisms would then put a break on this positive feedback loop. Hypoxic-induced NO release should partly counteract the reduction in NOS-mediated NO synthesis, as discussed above. Moreover, the medullary microcirculation is controlled by many signaling molecules. In particular, adenosine and prostaglandins, like NO, act both as saliuretic agents and as paracrine vasodilators; such agents would most likely exert mitigating effects so as to preserve medullary perfusion and raise medullary Po₂. Similarly, activation of K_ATP channels due to reduction of intracellular ATP might hyperpolarize vasa recta pericytes to favor vasodilatation (5).

Conversely, without O₂⁻-mediated stimulation of sodium reabsorption and O₂ consumption, elevation of Po₂ would favor a rise in C_NO and vasodilation, tending to enhance O₂ supply. In this case, however, active transport by the mTAL would also tend to increase, since it is partly limited by O₂ availability under basal conditions. Thus a rise in mTAL O₂ consumption would be favored, tending to offset the increase in O₂ supply. Finally, it seems plausible that other paracrine agents such as endothelins or vasoconstrictor prostaglandins might be released to limit such NO-dependent vasodilation. Given the complex nature of events that balance O₂ supply and consumption, we formulated the current model to facilitate prediction of the net effect of such interactions.

Impact of NO on O₂⁻ Bioavailability

Our model predicts that NO scavenging reduces O₂⁻ levels by ∼10% in the renal medulla. As recently observed by Hong and Garvin (25), flow-induced enhancement of O₂⁻ production in the TAL is reduced in the presence of NO, but this effect cannot be attributed to scavenging only. Approximately 70% of the inhibitory effect of NO on net O₂⁻ production appears to be mediated via the cGMP/PKG pathway (25). These novel findings suggest that NO and O₂⁻ may interact in more complex ways than previously thought. It is not presently known under which conditions, and precisely how, the cGMP/PKG pathway leads to inhibition of net O₂⁻ production. In the absence of data, we did not incorporate this pathway in our model.

Impact of O₂⁻ on NO Bioavailability

The impact of basal O₂⁻ levels on NO bioavailability in the OM remains to be fully ascertained, in part because there have been until now no direct measurements of medullary O₂⁻ levels. In a recent mathematical model of NO-O₂⁻ interactions in OM cross sections (17), we showed that if O₂⁻ is present in subnanomolar concentrations, it affects NO to a small extent only. In the current study, we assumed that O₂⁻ is present at higher levels (1–10 nM), based on measured H₂O₂ concentrations. Thus C_NO increased significantly when the NO-O₂⁻ reaction rate was set to zero (Fig. 7). Moreover, when the effects of O₂⁻ on mTAL reabsorption were abolished, C_NO increased even more in the interbundle region (Fig. 8). In other words, the present model indicates that O₂⁻ modulates NO levels both directly and indirectly: O₂⁻ may indirectly reduce NO generation via its stimulation of mTAL metabolic requirements, leading to reduction of O₂ as a substrate for NO formation in the OM. It is likely, however, that hypoxia-induced NO release acts to compensate for the decrease in NO synthesis. Our current model suggests that hypoxia-mediated effects would not suffice to fully counteract the G_NO decrease, but complete elucidation of the mechanisms by which hypoxia raises NO levels is needed to draw definitive conclusions.

Experimental observations regarding the effects of basal O₂⁻ on NO bioavailability are conflicting. Cowley and colleagues (11) observed that renal medullary interstitial infusion of the SOD mimetic tempol in anesthetized rats raised medullary blood flow and sodium excretion; these effects were partly counteracted by the dismutation of superoxide into H₂O₂, but were not affected by pretreatment with a NOS inhibitor (63). These results, combined with the observation that tempol by itself does not affect the basal tone of microperfused descending vasa recta (4), suggest that basal O₂⁻ has little direct impact on medullary NO levels. In contrast, several ex vivo studies have found that tempol enhances the release and diffusion of NO from mTALs (41, 45). However, these studies were performed in the absence of RBCs (i.e., of hemoglobin), and with a disrupted vascular endothelium (which, particularly when stimulated by shear, constitutes the main source of NO in vivo); under such conditions, O₂⁻ would have had a disproportionate impact on NO levels.

In contrast, studies consistently indicate that O₂⁻ significantly reduces NO bioavailability under oxidative stress conditions. In spontaneously hypertensive rats, or in rats infused with ANG II, tempol markedly affects arterial blood pressure, renal blood flow, glomerular filtration rate, and/or sodium excretion (28, 44, 54). Pretreatment with N^G-nitro-l-arginine methyl ester (l-NAME) eliminates the antihypertensive effects of tempol (53), implying that, in these hypertensive animals, O₂⁻ is present at sufficient levels to significantly scavenge NO.

Hypertensive Conditions

Our model predicts that shifting the NO-O₂⁻ balance in favor of superoxide substantially enhances NaCl reabsorption across mTALs (Fig. 10) and further depletes oxygen in the OM, as experiments have suggested. Our simulations suggest that a 10-fold increase in the rate of O₂⁻ synthesis raises the concentrating capacity of the OM by ∼35%, and reduces Po₂ in the peripheral regions by 5–10 mmHg in the OS and 1–3 mmHg in the IS, assuming that the mTAL T_Na/Qo₂ ratio remains constant. In fact, the number of Na⁺ moles reabsorbed per mole of O₂ consumed is reported to be lower in hypertensive subjects (59). As discussed by Welch (58), possible explanations for the lower T_Na/Qo₂ involve 1) oxidative stress-mediated changes in the Na⁺ reabsorption profile, such that more Na⁺ is reabsorbed downstream of the proximal tubule, at a higher energy cost; 2) back-leak of Na⁺ in the tubular lumen; and 3) reduced efficiency of mitochondria in producing ATP in the presence of lower NO concentrations; note that NO modulates the respiration rate by inhibiting cytochrome oxidase in competition with O₂ (2). The extent to which oxidative stress reduces T_Na/Qo₂ specifically in the mTAL remains to be ascertained. A twofold reduction would partly counteract the stimulating effects of O₂⁻ on NaCl reabsorption across the mTAL (Fig. 10), but would further reduce Po₂ by a few millimeters mercury outside the vascular bundle. These results suggest that the inefficient use of O₂ in hypertensive models slows down active transport while exacerbating hypoxia in the OM.

Tubular and Vascular Flow Increases

We examined the net effect of increased flow on NaCl transport in the OM, given that luminal flow stimulates O₂⁻ production, via PKC-mediated activation of NADPH oxidase (26), but also induces NOS activation in DVR and TALs. Shear stress enhances the intrinsic activity of NOS at least partly by stimulating its translocation to the membrane (47). We previously showed that per se, increases in vascular and tubular flows lower the OM concentrating capacity: despite greater O₂ availability, the higher loads make it harder to concentrate the tubular fluid (7). Our earlier study, which did not include the transport of NO and O₂⁻, predicted that a 25% increase in volume flows lowers osm_CD^L by 10%. The current model suggests that increasing volume flows may in fact reduce the osmolality gradient even more, because NO-mediated inhibition of mTAL transport intensifies. The flow-induced increase in O₂⁻ synthesis, if comparable to that in NO synthesis, is not sufficient to offset these effects. Hence, in the absence of other counteracting mechanisms, a 20% increase in flow rates that is accompanied by a 20% increase in the production of NO and O₂⁻ is predicted to lower osm_CD^L by ∼25% (Table 6).

Model Validation, Comparison, and Limitations

There are very few experimental data with which our model predictions can be compared and validated. Predicted NO concentrations in the OM fall within the range of measured values, which extend from 60–100 nM (27, 64) to 800 nM (52), but there have been no direct measurements of O₂⁻ levels in the OM, to the best of our knowledge. We compared the predicted and measured reduction in Po₂ induced by the NOS inhibitor l-NAME. Li et al. (33) used BOLD MRI to detect changes in renal medullary oxygenation. In Wistar-Kyoto rats, the parameter R2* (which is inversely proportional to Po₂) increased by ∼40% following administration of l-NAME. Similarly, we found that abolishing NO generation reduced interstitial Po₂ in the interbundle region by 30–50%, depending on position (results not shown).

The current model differs from our previous model of NO and O₂⁻ transport in the OM (16, 17) in several important respects. The latter was restricted to medullary cross sections, focused on the transport of three solutes only (NO, O₂⁻, and ONOO⁻), and assumed fixed Po₂ profiles. In particular, it did not consider the effects of NO and O₂⁻ on sodium reabsorption and O₂ consumption in the OM, and therefore failed to capture important reciprocal interactions. In addition, basal O₂⁻ concentrations were previously taken to be subnanomolar, based on measured O₂⁻ synthesis rates in aortic endothelial cells. In this study, basal O₂⁻ concentrations are taken to be ∼10 times higher, based on experimental determinations of medullary H₂O₂.

Some of the significant limitations of our study were discussed above. In the absence of quantitative data, several model parameters are necessarily uncertain, particularly those related to NO- and O₂⁻-mediated effects on NaCl reabsorption in the mTAL. In addition, our steady-state model does not account for vasomotion and hormone-induced changes in vessel diameter. Finally, we did not examine the effects of ONOO⁻ (the product of the NO-O₂⁻ reaction) and H₂O₂ (the product of the SOD-O₂⁻ reaction) on medullary function. ONOO⁻ is thought to exert potent cytotoxic effects at high concentrations and to induce vascular relaxation at lower (nM) concentrations, but the role of ONOO⁻ in regulating kidney function remains to be investigated (36). Similarly, the far-reaching vascular effects of H₂O₂ have yet to be fully characterized in vivo (1).

In vivo, solute reabsorption and medullary blood flow are controlled by many endocrine and paracrine factors. This study aimed to yield a better understanding of the interactions between NO and O₂⁻ and their combined effects on tubular and vascular function in the OM. Given the complex nature of events that balance O₂ supply and consumption and modulate NaCl transport, we formulated the current model to facilitate prediction of the net effect of such interactions.

GRANTS

This work was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant DK053775 to A. Edwards.