Linked opening angle and histological and mechanical aspects of the proximal pulmonary arteries of healthy and pulmonary hypertensive rats and calves

Abstract

Understanding how arterial remodeling changes the mechanical behavior of pulmonary arteries (PAs) is important to the evaluation of pulmonary vascular function. Early and current efforts have focused on the arteries' histological changes, their mechanical properties under in vitro mechanical testing, and their zero-stress and no-load states. However, the linkage between the histology and mechanical behavior is still not well understood. To explore this linkage, we investigated the geometry, residual stretch, and histology of proximal PAs in both adult rat and neonatal calf hypoxic models of pulmonary hypertension (PH), compared their changes due to chronic hypoxia across species, and proposed a two-layer mechanical model of artery to relate the opening angle to the stiffness ratio of the PA outer to inner layer. We found that the proximal PA remodeling in calves was quite different from that in rats. In rats, the arterial wall thickness, inner diameter, and outer layer thickness fraction all increased dramatically in PH and the opening angle decreased significantly, whereas in calves, only the arterial wall thickness increased in PH. The proposed model predicted that the stiffness ratio of the calf proximal PAs changed very little from control to hypertensive group, while the decrease of opening angle in rat proximal PAs in response to chronic hypoxia was approximately linear to the increase of the stiffness ratio. We conclude that the arterial remodeling in rat and calf proximal PAs is different and the change of opening angle can be linked to the change of the arterial histological structure and mechanics.

pulmonary hypertension (PH), defined as a chronic, resting mean pulmonary artery pressure (mPAP) > 25 mmHg, yields increases in right ventricular (RV) afterload and is associated with distal arterial remodeling and eventual RV failure. Clinical and basic science studies of the disease have begun to focus on the proximal pulmonary arteries (PAs), as these vessels also display significant vascular remodeling in PH (11, 16–20, 29). Such remodeling is believed to impair proximal pulmonary vascular function, and in turn, detrimentally affect RV afterload. Therefore, understanding the arterial remodeling and the resulting changes in proximal PA functional behavior could be useful for both clinical diagnosis of PH and development of new therapies.

Several chronically hypoxic animal models have been used to study PH, including the mouse, rat, and calf. These animal model studies have shown that significant histological changes occur in the proximal PAs. Remodeling of the proximal PAs in these animals results in the accumulation of smooth muscle cells (SMCs), elastin, and collagen, but the fractional change of each component varies in different studies on different species. For example, a study on the mouse right PA (RPA) found that the area fraction of elastin in response to 10 days or 15 days of hypoxia did not change significantly, but that of collagen and SMCs significantly increased and decreased, respectively, compared with the control condition (19). In the rat model, Huang et al. (16) found that both the intima-medial and adventitial layers thickened but the thickness of the adventitial layer exceeded that of the intima-medial layer after more than 4 days of hypoxia. A recent study by our group on neonatal calves found significant decreases in the elastin area fraction of all the proximal PAs—main, left, and right PAs (MPA, LPA, and RPA, respectively)—after 2 wk of hypoxia (20).

As a result of arterial remodeling, the arterial geometry and mechanical properties may also change. All the aforementioned studies on mice, rats, and calves found significant increases in proximal PA thickness in response to chronic hypoxia (16, 19, 20). The opening angle (OA) of the artery at zero-stress state, which characterizes the residual stretches in the artery (7), was also found to significantly decrease in the MPA and LPA of rats after more than 4 days of hypoxia (9, 16). This is in contrast to our recent study that did not find a significant difference in calf MPA OA between control and hypertensive groups (30). With respect to mechanical changes due to remodeling, Lammers et al. (20) found significant increases in the circumferential elastic moduli and stiffness of pure elastin scaffolds and fresh intact tissue samples taken from calf MPAs, LPAs, and RPAs after 2 wk of hypoxia. Kobs et al. (19) also found significant increases in the effective elastic moduli of mouse LPAs after 10- and 15-day hypoxic exposure periods. Huang et al. (16) found increases in both the circumferential and longitudinal Young's moduli and the cross modulus of rat LPAs with only 24 h of exposure to a 10% O₂ condition, although such increases were not significant. Drexler et al. (6) also found the proximal PAs of rats stiffened in response to 3 wk of hypoxia.

These previous studies have clearly shown that the histological and mechanical effects of arterial remodeling on the proximal PAs are species dependent. A recent study by Lammers et al. (21) has shown that the neonatal calf model is more relevant to the study of pediatric PH compared with the adult rat model, in that the collagen engagement stretch does not change significantly in calf and human proximal PAs; however, decreases in collagen engagement stretch were found in the rat proximal PAs from control to hypertensive groups. Another recent study by Kobs et al. (19) has found that the in vitro elastic modulus of mouse LPAs is moderately correlated to their collagen thickness as well as their sum of collagen and elastin thickness. These studies began to demonstrate that the histological and mechanical aspects of arterial remodeling are related. However, the opening angle (OA), a simple and useful parameter that can characterize the arterial zero-stress state and reveal intrinsic histological changes (9, 16), has not been considered. In view of the importance of understanding the histological and mechanical changes occurring in the arteries and their associated change in OA, we wish to understand the linkage between the opening angles of proximal PAs and their histological and mechanical aspects. We hypothesize that the change in OA of the proximal PAs due to chronic hypoxia is an indication of the combined influence of changes in the outer layer (collagen-rich) thickness fraction and its modulus. The goals of this study were 1) to investigate the geometry and residual stretches (especially OA) of the rat and calf proximal PAs under the no-load state and the PA outer layer thickness fractions which is the ratio of the outer layer thickness to the whole arterial tissue thickness; 2) to compare these quantities' changes due to chronic hypoxia between calf and rat; and 3) to propose and employ a mechanical model to explore the relationship between OA and the changes of the thickness fraction and elastic modulus of the outer layer.

MATERIALS AND METHODS

Animal models.

All experimental studies were performed after approval by institutional animal care and use committees. Twenty-four newborn Holstein calves with ages between 1 and 3 days and weights between 35 and 50 kg were used with the hypoxic experiment procedure as described in previous studies (27, 32). Eleven of the calves were put into a large hypobaric chamber at an atmospheric pressure of 430 mmHg (4,570 m equivalent air pressure) for 2 wk to develop pulmonary hypertension (PH). The others remained at local ambient pressure (elevation 1,500 m; 640 mmHg at Fort Collins, CO) for 2 wk before testing. Both calf groups were held in the chamber at ambient pressure for at least 1 h before testing to minimize residual hypoxic vasoconstriction and then tested at ambient pressure. The instantaneous pressure within the middle section of main PA (MPA) at ambient pressure condition was measured with standard fluid-filled catheters (Transpac IV, Abbott Critical Care Systems, Abbott Park, IL). Six control adult bovine MPA tissues were obtained from Denver slaughterhouse (Denver, CO) for in vitro uniaxial tests.

Twenty-five Sprague-Dawley rats with ages of 10 wk ± 3 days and weights of 440 ± 26 g were used with the hypoxic experiment procedure as described in a previous study (6). Thirteen of the rats were put into a hypobaric chamber at an atmospheric pressure of 380 mmHg (5,486 m equivalent air pressure) for 3 wk to develop PH. The rest remained at local ambient pressure (elevation 1,610 m; 630 mmHg at Denver, CO) for 3 wk before testing. Both rat groups were held at ambient pressure for at least 1 h before testing to minimize residual hypoxic vasoconstriction and then tested at ambient pressure. The instantaneous pressure within the middle section of MPA was measured with a custom fluid-filled catheter setup consisting of a section of PE-10 tubing coupled to a standard clinical pressure transducer (Transpac IV, Abbott Critical Care Systems, Abbott Park, IL).

In vitro artery geometry measurement.

Proximal PA (MPA and RPA) rings were obtained from all animal groups within 5 h of the animal being euthanized. The rings were generally harvested at the straight (longitudinal) section of the pulmonary arterial tube away from curved sections. Each ring was immediately soaked in calcium- and magnesium-free NaCl-PBS buffer (0.01 mol/l, ionic strength 0.15, pH 7.4) at room temperature and photographed to obtain a scaled digital image on the cross-sectional area through a Canon camera (EOS Digital Rebel XTi, Canon, Tokyo, Japan) with Canon Macro Lens (Canon Macro Lens EF 100mm 1:2.8 USM). Each ring was then cut once along the radial direction to obtain the stress-free state and photographed again on the cross-sectional area after 2 min to allow for possible viscoelastic relaxation. No changes were observed in the cross-sectional shape of the sectors (or the opened rings) after the rings had been cut for 2 min.

Ring and sector edge lengths were determined from tracing their images in a custom-written MATLAB image-processing code (MATLAB, The Mathworks, Natick, MA). In general, the arterial ring has a clearer edge definition on the inner wall than on the outer wall; thus the inner wall length was always traced. For the sector, the edge definitions were clearer and both the lengths of inner and outer walls were traced. The OA of the sector was obtained directly from the image of the opened sector with the so-called three-point measurement, in which the angle between two lines connecting the middle point of the inner wall to its two tips is computed (8–10, 23). The thicknesses of the artery at six different circumferential locations of the ring or sector were measured and averaged as the thickness of the ring or sector. Due to low pixel resolution of the rat PA images, the circumferential lengths of inner and outer walls of the rat PA sectors were not traced and only OAs were obtained from the rat PA sectors.

In vitro uniaxial test.

Rectangular strips of fresh tissues from six control adult bovine MPAs in the circumferential direction were prepared for uniaxial tensile testing in a universal material testing system (MTS insight II, MTS Systems, Eden Prairie, MN). Strip width, thickness, and gauge length were measured using digital caliper. The tests were then conducted in calcium- and magnesium-free NaCl-PBS buffer (0.01 mol/l, ionic strength 0.15, pH 7.4) at 36°C through the use of an environmental chamber. The specimens underwent 10 loading and unloading cyclic uniaxial tensile tests with a constant strain rate of 10% length/s, and the force-stretch data were taken from the loading portion of the 10th cycle. After the test on the whole strip, the outer layer or the collagen-rich layer of the tissue was cut off with a very sharp blade. The outer layer was identified by its spongelike appearance and was readily removed from all samples. The remaining tissue (consisting of only the inner layer) was tested again in the MTS with the same procedure as the intact tissue.

Histology.

Biopsies of cross-sectional PA tissue strips were fixed in 10% buffered formalin, embedded in paraffin wax, and stained with Verhoeff's Van Gieson (VVG). For neonatal calf PAs, the bright-field photomicrographs of the stained tissues were taken with a SPOT RT-900 digital camera (Diagnostic Instruments, Sterling Heights, MI) mounted on a Nikon TE-200 microscope (Nikon Instruments, Melville, NY; 4× magnification). For rat and adult bovine PAs, the bright-field photomicrographs of the stained tissues were captured with a Zeiss Axiocam camera (Oberkochen, Germany) mounted on a Zeiss Axiovert S100 microscope (Oberkochen, Germany; 20× and 10× magnifications for rat and adult bovine, respectively).

Calculations.

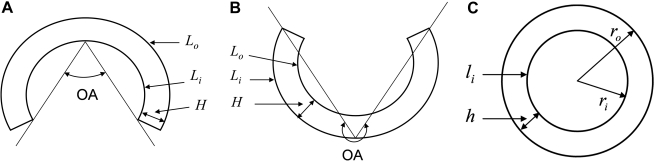
Figure 1 illustrates the opened sector at stress-free state with two possible configurations and the closed ring at no-load state. As the ring was cut radially, it opened up and could even turn inside out for some arteries as shown in Fig. 1B. Since the opening configuration of the artery in general is not a perfect shape of circular sector, obtaining an OA from a three-point measurement (denoted as OA₁) may yield large errors in the estimation of residual stretch (22). Alternately, a second method can be adopted to calculate OA by using the geometry data of the opened sector (denoted as OA₂). Under this method, we assumed a perfect circular sector having the same lengths of inner and outer walls and thickness as were measured from real arterial sector, and calculated OA of the imagined perfect circular sector. Using the geometry of the circular sector (5, 12, 24), the OA of the imagined perfect circular sector can be expressed as

$$\begin{array}{c}{\text{OA}}_2=\pi -\left(L_o-L_i\right)/2H,if{L}_o>L_i,\\ {\text{OA}}_2=\pi -\left(L_i-L_o\right)/2H,if{L}_o>L_i,\end{array}$$ (1)

where L_i, L_o, and H are the lengths of inner and outer walls and the thickness of the sector, respectively.

Fig. 1.

The cross-sectional representations of arteries at stress-free state with opening angle (OA) < 180° (A), at stress-free state with OA > 180° (B), and at no-load state (C). L_i, L_o, and H are the lengths of inner and outer walls and the thickness of the sector, respectively. For other symbol definitions, see Calculations.

The artery may be considered as incompressible (3, 4). As the opened sector deforms to a closed ring at the no-load state (no inner pressure and no axial traction, Fig. 1C), the incompressible condition leads to (5, 12)

$$\begin{array}{c}{\lambda }_z\pi \left(r^2-r_i^2\right)=\left(L^2-L_i^2\right)/4\left(\pi -\text{OA}\right),if{L}_o>L_i;\\ {\lambda }_z\pi \left(r^2-r_i^2\right)=\left(L_i^2-L^2\right)/4\left(\text{OA}-\pi \right),if{L}_o>L_i,\end{array}$$ (2)

where r is the radius of an arbitrary point in the ring, L is the corresponding circumferential length inside the sector, and λ_z is the longitudinal stretch of the ring. The circumferential stretch at this arbitrary point of the ring is then defined as

$${\lambda }_{\theta }\left(r\right)=2\pi r/L.$$ (3)

For the ring in its no-load state, the inner diameter of the ring is calculated from the measured length of inner wall (l_i): ID = 2r_i = l_i/π. The longitudinal stretches calculated from Eq. 2 using all the measured geometry data of the ring and sector were very close to unity for all the arteries. Within the measurement error, it is appropriate to assume the longitudinal stretch to be unity (5, 12). The stretch thus calculated by Eq. 3 is called the residual circumferential stretch of the artery at the no-load state. Applying Eq. 3 to the inner and outer walls, the residual circumferential stretches at the inner and outer walls [(λ_θⁱ)_R and, (λ_θ^o)_R, respectively] can be calculated directly from the measured dimensions of the sector and ring:

$${\left({\lambda }_{\theta }^i\right)}_{\text{R}}=l_i/L_i,{\left({\lambda }_{\theta }^o\right)}_{\text{R}}=\left(l_i+2\pi h\right)/L_o,$$ (4)

where h is the measured thickness of the closed ring.

We note that the above calculations were applied to calf PAs with available geometry data and the OA used in Eq. 2 is from Eq. 1, i.e., OA₂. For rat PAs, however, there is no measured length of the inner or outer wall of each arterial sector. To circumvent this difficulty, we assume the neutral surface is located at 0.4 of the wall thickness from the inner wall of the closed ring (10, 12). At this neutral surface, the residual stretch is unity, i.e., at r = r_i + 0.4h in Eq. 2, and the corresponding circumferential length of the sector (L) is equal to 2π(r_i + 0.4h). Then the inner length of the sector (L_i) can be calculated from Eq. 2. With r = r_i + h and knowing L_i, the outer length of the sector (L_o) can be obtained by Eq. 2. It is noted that the OAs in these calculations for rat PAs are the OAs obtained directly from the three-point measurement (OA₁).

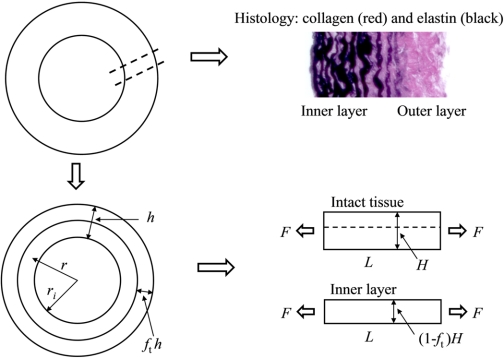
To relate OA to the mechanical and histological aspects of the collagen component in the artery, we proposed a histologically based two-layer artery model as shown in Fig. 2. The outer layer of the artery represents the collagen-rich or adventitial layer with less or no elastin and is expected to have smaller elastic modulus before collagen engagement than the inner layer, which is an elastin-rich layer. In the uniaxial tests of intact PA tissues and pure elastin tissues, the stress-strain relation in the small strain region before collagen engagement is approximately linear (19, 20). Therefore, it is assumed that the stress-stretch relation for the intact two-layer tissue and both the outer and inner layers can be expressed as

$$\sigma =E\left({\lambda }^2-1\right)/2,$$ (5)

where E is the elastic modulus, λ is the stretch ratio, and (λ² − 1)/2 is the Green-Lagrange strain. Based on the laminate composite theory (1), the effective modulus (Ē) of the intact two-layer tissue can be expressed as

$$\overline{E}=E_{\text{in}}\left(1-f_t\right)+f_m{E}_{in}{f}_t,$$ (6)

where the subscript “in” denotes for the inner layer, E_in is the elastic modulus of the inner layer, f_t is the thickness fraction of the outer layer (i.e., h_out/h, where subscript “out” denotes for outer layer), and f_m is the modulus ratio of the outer to inner layer (i.e., E_out/E_in). Although the outer layer thickness fraction (f_t) can be slightly different between the closed ring and opened ring, any difference was neglected here and only the f_t measured from histological image of the opened ring was used in the calculation. In general, the outer layer is collagen rich and appears mainly red in the VVG-stained histological image and the inner layer is elastin rich and appears mainly black, and so the boundary between the two layers is determined by the color of the image; and the outer layer thickness fraction, f_t, is then estimated at six different locations with the average value reported for each PA tissue by measuring the thicknesses of both the outer layer and the whole tissue.

Fig. 2.

A representative histological image of PA (top right), a 2-layer representation of an arterial ring (bottom left), and the schematic plot for the uniaxial tests on the intact tissue and inner layer (bottom right). For symbol definitions, see Calculations.

Due to the lack of the in vitro testing on the inner or outer layer of the neonatal calf PAs, we used the in vitro measurement on the adult bovine MPAs for the model validation. Since the residual stretch of the artery is within the range of ∼0.8 to ∼1.15 (5, 12), we obtain the elastic moduli Ē and E_in from the intact and inner layer samples, respectively, at the stretch ratio of 1.15 from in vitro uniaxial tests. With the thicknesses measured for the intact and inner layer strips, the thickness fraction, f_t, can be obtained and the modulus ratio, f_m, can be calculated from Eq. 6.

In conventional solid mechanics, the stiffness of a bar is defined as k = EHW/L (31), where H, W, and L are the thickness, width, and length of the bar, respectively. Thus the stiffnesses of the outer and inner layers are expressed as k_out = f_mE_inf_tHW/L and k_in = E_in(1 − f_t)HW/L, respectively. We define the stiffness ratio (SR) of the outer to inner layer as

$$\text{SR}=k_{out}/K_{in}=f_m{f}_t/\left(1-f_t\right).$$ (7)

For a ring with two layers at the no-load state as shown in the bottom left of Fig. 2, the equilibrium condition requires that the sum of the circumferential forces or residual circumferential stresses due to the residual circumferential stretches along the cross-section area of the ring is zero, i.e., ∫_ri^r_i+hσdA. With the residual stresses of the two layers expressed by Eq. 5 and dA = dr·w (w is the axial length of the ring), the equilibrium equation can be rewritten as

$${\displaystyle {\int }_{r_i}^{r_i+h}\sigma \text{d}A}={\displaystyle {\int }_{r_i}^{r_i\left(1-f_t\right)h}\left[{\lambda }^2\left(r\right)-1\right]\text{d}r}+{\displaystyle {\int }_{r_i+\left(1-f_t\right)h}^{r_i+h}{f}_m\left[{\lambda }^2\left(r\right)-1\right]\text{d}r=0,}$$ (8)

where λ(r) is the residual stretch at radius r of the ring which was obtained from Eqs. 2 and 3. Given the arterial ring thickness and the residual stretch distribution, the relationship between f_t and f_m can be determined by Eq. 8. SR can then be calculated from Eq. 7. Because we do not have all the required data (residual stretch and outer layer thickness fraction) of each PA for the model calculation, we used the mean values of each group to estimate the relationship between f_t and f_m and SR for that group.

The above model calculation provides one estimated value of SR for each group. If both the estimated SR and the measured mean OA change significantly from control to hypertensive group for one type of animal PA (MPA or RPA), there may be a relationship between SR and OA for that type of animal PA. To investigate this relationship for the calf, linear step changes (decrease or increase) are assigned to the mean values of f_t, inner diameter (ID), OA, thickness and residual stretches of the PA from control to hypertensive groups, and SRs are then calculated during all the step changes; for the rat, all the procedures are the same as the calf except that the neutral surface is kept at 0.4 of the wall thickness from the inner wall due to the unmeasured residual stretches for all rat PAs.

Statistics.

All the data are presented as means ± SD unless specified otherwise. Bland-Altman analysis (2) was used to assess the agreement between the two measurements of OA from the three-point measurement (OA₁) and from the geometry data (OA₂) by using Eq. 1. The two-tailed two-sample t-test assuming normality in the data with variances determined from an F-test was used to compare the pressure, geometry dimensions, residual stretches of PAs, and thickness fraction of outer layer between control and hypertensive groups. Equivalence tests (13) were performed to compare these quantities between control and hypertensive groups assuming the equivalence interval equal to 10% of the average value of the control group. All the statistical analyses were performed with MATLAB software (MATLAB, The Mathworks, Natick, MA).

RESULTS

Overall.

Table 1 summarizes the mean pulmonary arterial pressure (mPAP), artery morphology, OA, and residual circumferential stretches at the inner and outer walls of arteries for both control and hypertensive groups for calf MPA, calf RPA, rat MPA, and rat RPA. mPAP increased significantly for both rat and calf as a result of chronic hypoxia. For the calf MPA, the changes in ID, OA, and residual stretches from control to hypertensive group are not statistically significant and the IDs and the residual stretches at both inner and outer walls of the two groups are statistically equivalent. However, both the arterial wall thickness and the thickness to ID ratio have significant increases from control to hypertensive group. For the calf RPA, the changes in all these parameters from control to hypertensive group are not statistically significant, and the residual stretches at both inner and outer walls of the two groups are statistically equivalent. Nonetheless, there is an increasing trend for both arterial wall thickness and thickness-to-ID ratio in response to chronic hypoxia. For the rat MPAs and RPAs, however, there is more dramatic arterial remodeling as a result of chronic hypoxia than the calf PAs. The IDs, thickness, and thickness-to-ID ratios all increase significantly and OAs decrease significantly in response to chronic hypoxia in both rat MPAs and RPAs.

Table 1.

Comparison of mean pulmonary arterial pressure (mPAP), arterial morphology, and residual circumferential stretches at the inner and outer walls between control and hypertensive groups for calf MPA, calf RPA, rat MPA, and rat RPA

>	Control	Hypertensive	P Value	Equivalent?
Calf MPA
n	13	11
mPAP, mmHg	23.6 ± 9.3	59.9 ± 22.2	<0.001	No
ID, mm	19.4 ± 2.1	19.9 ± 1.4	0.505	Yes
h, mm	3.4 ± 0.3	4.0 ± 0.4	<0.001	No
h/ID	0.18 ± 0.03	0.20 ± 0.02	0.035	No
OA2,°	127 ± 38	130 ± 23	0.957	No
OA1,°	124 ± 38	130 ± 27	0.966	No
(λθi)R	0.91 ± 0.06	0.90 ± 0.02	0.820	Yes
(λθo)R	1.13 ± 0.06	1.15 ± 0.05	0.315	Yes
Calf RPA
n	10	6
ID, mm	12.1 ± 1.5	11.0 ± 1.2	0.139	No
h, mm	1.6 ± 0.3	1.6 ± 0.3	0.660	No
h/ID	0.13 ± 0.02	0.15 ± 0.02	0.074	No
OA2,°	142 ± 48	117 ± 20	0.250	No
OA1,°	137 ± 56	112 ± 21	0.225	No
(λθi)R	0.93 ± 0.04	0.94 ± 0.04	0.851	Yes
(λθo)R	1.12 ± 0.05	1.11 ± 0.02	0.458	Yes
Rat MPA
n	9	13
mPAP, mmHg	21.4 ± 6.9	43.3 ± 10.3	<0.001	No
ID, mm	2.2 ± 0.2	2.7 ± 0.2	<0.001	No
h, mm	0.13 ± 0.02	0.20 ± 0.02	<0.001	No
h/ID	0.06 ± 0.02	0.08 ± 0.01	0.030	No
OA2,°	265 ± 68	122 ± 14	<0.001	No
(λθi)R	0.93	0.96	N/A	N/A
(λθo)R	1.11	1.06	N/A	N/A
Rat RPA
n	7	10
ID, mm	1.6 ± 0.3	2.0 ± 0.1	<0.001	No
h, mm	0.10 ± 0.01	0.17 ± 0.02	<0.001	No
h/ID	0.07 ± 0.01	0.09 ± 0.01	0.004	No
OA2,°	125 ± 83	35 ± 30	0.007	No
(λθi)R	0.97	0.99	N/A	N/A
(λθo)R	1.05	1.02	N/A	N/A

Values are means ± SD; n, no. of arteries; mPAP, mean pulmonary arterial pressure measured at the ambient pressure condition (n = 9 and 11 for calf control and hypertensive groups, respectively; n = 9 and 7 for rat control and hypertensive groups, respectively); MPA, main pulmonary artery; RPA, right pulmonary artery; ID and h, inner diameter and thickness of artery ring at no-load state, respectively; OA, opening angle; OA₁ is obtained from the 3-point measurement and OA₂ from the geometry data (using Eq. 1); (λ_θⁱ)_R and (λ_θ^o)_R, residual circumferential stretches at inner and outer walls, respectively. For the rat, residual circumferential stretches are estimated from the mean geometry data as mentioned in the previous section and only one value at each of the inner and outer walls of artery of each group is provided, rendering statistical comparison impossible. N/A, not applicable. Statistically significant quantities are shown in boldface.

OA measurements.

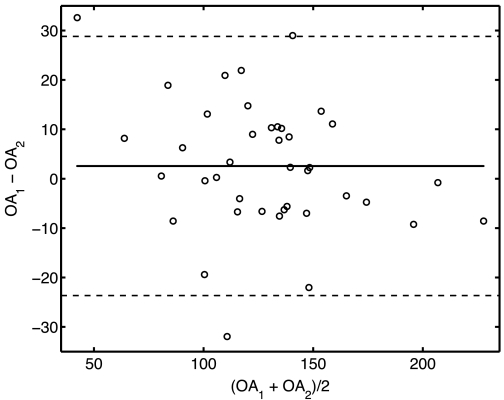
Figure 3 shows the Bland-Altman plot for the OAs obtained from the three-point measurement (OA₁) and from the geometry data using Eq. 1 (OA₂) for all 40 calf MPAs and RPAs. The three-point measurement for OA has a bias (or average difference) of 2.6° with the limits of agreement at two SDsof the difference at 26° compared with the other method, and there are only two outliers.

Fig. 3.

Bland-Altman agreement analysis between the 2 measurements of OA from the 3-point measurement (OA₁) and from the geometry data (using Eq. 1; OA₂) for 40 calf main pulmonary arteries (MPAs) and right pulmonary arteries (RPAs).

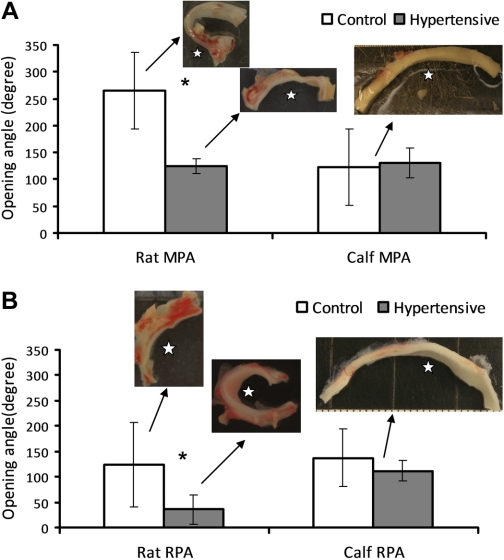
Three-point measurements for OA (OA₁) are compared between control and hypertensive groups of both rat and calf from the MPA and RPA in Fig. 4, A and B, respectively. The insets in these two plots are the representative images of the opened arteries or sectors. The chronic hypoxia intervention did not significantly change the OA of either calf MPA or RPA (P = 0.664 and 0.225 for MPA and RPA, respectively). Moreover, there is no significant difference in OA between calf MPA and RPA for either the control or hypertensive group (P = 0.518 and 0.566 for control and hypertensive groups, respectively), and the average of these OAs is 127 ± 39°. For this reason, a single representative image is provided for both control and hypertensive calf MPA or RPA groups. For the rat, however, OAs decrease from 265 ± 68° to 122 ± 14° and from 125 ± 35° to 35 ± 30° respectively, for MPA and RPA in response to chronic hypoxia, and these changes are significantly different (P < 0.001 and P = 0.007 for MPA and RPA, respectively). Finally, OAs are significantly different between rat MPA and RPA for both control and hypertensive groups (P = 0.0015 and P < 0.001 for control and hypertensive groups, respectively).

Fig. 4.

Comparisons of opening angle (OA₁) from 3-point measurement between control and hypertensive groups of rat and calf for MPA (A) and RPA (B). Insets: representative images of the opened arteries. Open stars (☆) in the images of the opened PA rings indicate the side of the inner wall of PAs. Bars represent means ± SD. *P < 0.05.

Thickness-to-ID ratio.

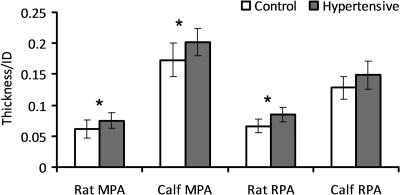
The arterial wall thickness-to-ID ratios for both rat and calf MPA and RPA rings at the no-load state are shown in Fig. 5. Due to chronic hypoxia, the ratio increased significantly for all the PAs except for the calf RPA (P < 0.05, except for P = 0.074 for the calf RPA), but there was still an increasing trend in the mean of the ratio for the calf RPA. The ratios are smaller than 0.1 for both groups of the rat PAs, but larger than 0.1 for both groups of the calf PAs.

Fig. 5.

Comparisons of the arterial wall thickness-to-inner diameter (ID) ratio between control and hypertensive groups of rat and calf MPA and RPA. Bars represent means ± SD. *P < 0.05.

Histology.

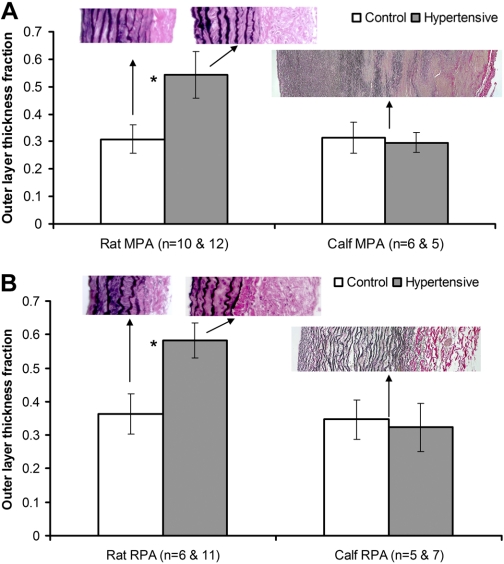
Figure 6 presents the comparisons of the outer layer thickness fraction of the MPA (Fig. 6A) and RPA (Fig. 6B) between control and hypertensive groups for both calf and rat. The insets in these two figures are the representative histological images of both rat and calf PA tissues stained with VVG. In response to chronic hypoxia, the outer layer thickness fraction did not change significantly in either calf MPA or RPA with an average of 0.320 ± 0.057 for all calf PAs (P = 0.568 and 0.560 for the calf MPA and RPA, respectively), but increased statistically significantly in both rat PAs from an average of 0.308 ± 0.052 to 0.543 ± 0.085 and from an average of 0.363 ± 0.060 to 0.583 ± 0.052 for MPA and RPA, respectively (P < 0.001 for both rat MPA and RPA). Because no significant change between control and hypertensive groups was seen in either calf MPA or RPA, a single representative histological image was provided for calf MPA or RPA as shown in Fig. 6.

Fig. 6.

Comparisons of outer layer thickness fraction between control and hypertensive groups in rat and calf for MPA (A) and RPA (B); n is the number of histological images with the left value in the bracket indicated for control group and the right one for hypertensive group. Insets: representative histological images of PAs across the arterial wall. Collagen and elastin appear red and black, respectively. Bars represent means ± SD. *P < 0.05.

Two-layer model.

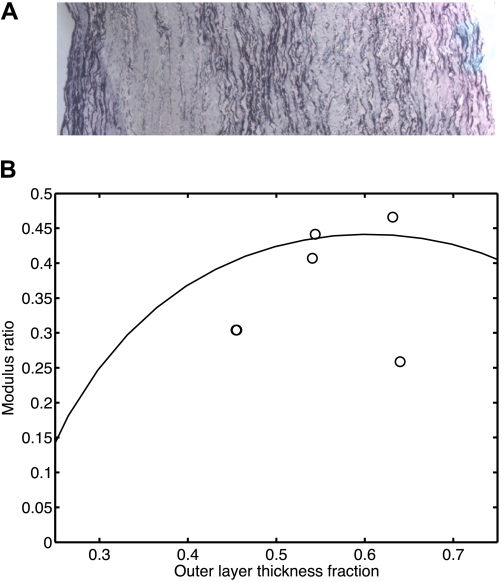
The histological study of the remaining tissues obtained from removing the collagen-rich layers of the adult bovine MPAs confirms that these remaining tissues were elastin-rich and the collagen-rich layers were cut off (Fig. 7A). By using the in vitro uniaxial tests on both intact and inner tissues and their geometry data, the modulus ratios (f_m) were estimated, and the relationship between the modulus ratio (f_m) and the outer layer thickness fraction (f_t) is plotted in Fig. 7B. Also shown in Fig. 7B is the relationship computed by using the mean arterial ring thickness, ID, and residual stretch distribution values from the control calf MPAs. The model prediction is reasonably consistent with our results from in vitro uniaxial tests on control adult bovine MPAs. In the range of 0.25 < f_t < 0.75, the modulus ratios (f_m) from model prediction and experimental results are <0.5. At the measured mean outer layer thickness fraction of control calf MPAs of 0.31 ± 0.056, the modulus ratio (f_m) is estimated to be around 0.26 from model prediction. Similar relationships between f_m and f_t are also seen for calf MPA and rat MPA and RPA.

Fig. 7.

Representative histological images of inner cross-sectional tissues from adult bovine MPA after collagen-rich layer was cut off (A), and the modeled relationship between modulus ratio (f_m) and outer layer thickness fraction (f_t) for control calf MPA group (solid line) and experimental results on MPAs of control adult bovines (circles) (B). Note that 2 data points are nearly coincident at f_t ≈ 0.45 and f_m ≈ 0.3.

Stiffness ratio.

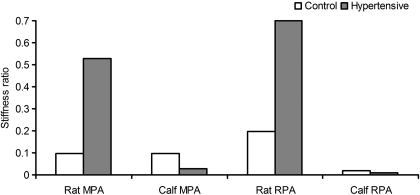
By using the proposed two-layer model as described in the previous section, the stiffness ratio (SR) of the outer to inner layer can be calculated. For the calf, the outer layer thickness fractions (f_t) are not significantly different between control and hypertensive groups; we used the respectively pooled average for calf MPA and RPA in the calculation of SR. For the rat, however, we used the separate group means in the calculation of SR because the outer layer thickness fraction (f_t) changed significantly in response to chronic hypoxia. As shown in Fig. 8, the estimated SRs are 0.096 and 0.029, respectively, for the calf MPA control and hypertensive groups; 0.019 and 0.010, respectively, for calf RPA control and hypertensive groups; 0.097 and 0.528, respectively, for rat MPA control and hypertensive groups; and 0.196 and 0.699, respectively, for rat RPA control and hypertensive groups.

Fig. 8.

Stiffness ratios (SRs) of the outer to inner layer of the MPA and RPA in both rat and calf predicted from model.

OA vs. SR.

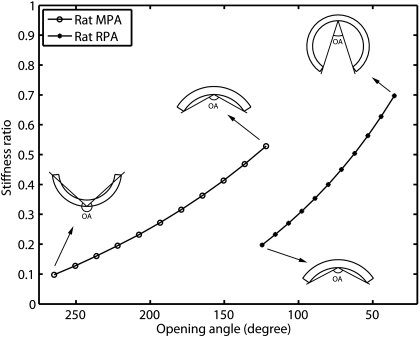
OAs and SRs in the calf MPAs and RPAs do not show substantial changes from control to hypertensive groups (Figs. 4 and 8); as a result we do not plot the relationship between SR and OA since the calf PA curves would not provide any interesting information. However, SRs in the rat MPAs and RPAs show substantial increases, which may correlate to the significant decreases of OA due to chronic hypoxia. The relationships between the SR and OA for both rat MPA and RPA as predicted from the model are presented in Fig. 9. The insets illustrate the schematic plot of OA of the artery at each condition. As seen from the predicted result, when OA decreases in response to chronic hypoxia, SRs increase approximately linearly for both rat MPA and RPA.

Fig. 9.

Relationship between SR and OA for rat MPA and RPA predicted from model.

DISCUSSION

Understanding changes in arterial geometry and mechanical properties at their zero-stress and no-load states and relating these to arterial histology are critical steps toward evaluating variations in arterial in vivo mechanical behavior due to vascular growth and remodeling. This paper investigates changes in arterial geometry at the zero-stress and no-load states and the histology of proximal PAs in response to chronic hypoxia, compares these changes between calf and rat, and proposes a mechanical model to link OA to the mechanics and histology. It is found that rat PA remodeling has a more dramatic impact on the arterial geometry and histology than that seen in calf PAs. and the change of SR corresponds to the change of OA based on the model prediction. These results are discussed in more details as follows.

OA measurement methods.

OA can be estimated directly from the opened artery ring image with three-point measurement or calculated from the opened artery ring dimensions (inner and outer circumferences and thickness). Both methods have been used in the literature, and theoretically, the results should be exactly the same. However, the difference in results between these two methods is primarily due to the imperfect annular-sector shape of the opened artery ring. This study performed these two methods on calf PAs and found that there is little bias between the two methods but with a fair amount of variation. Therefore, either method can be used to estimate OA.

Geometric changes due to remodeling.

For the calf MPA and RPA in response to 2 wk of hypoxia, only the arterial wall thickness and the thickness-to-ID ratio increased, while ID, OA, and the residual stretches at the inner and outer walls did not change significantly. The increase in thickness and unchanged ID in response to chronic hypoxia were also found in a previous study by our group (20). However, for the rat MPA and RPA in response to 3 wk of hypoxia, all the geometry parameters increased significantly and OA decreased significantly. An increase in wall thickness was also found in mouse RPA in response to 10 days or 15 days of hypoxia (19) and in rat MPA and RPA in response to >2 days of hypoxia (16). Further, a decrease of OA in rat PAs in response to chronic hypoxia is consistent to the study of rat MPA and LPA by Huang et al. (16). The small value of the thickness-to-ID ratio in rat PAs implies that rat PAs can be assumed to be a thin wall for both control and hypertensive groups, which is consistent with the mice proximal PAs (19), while for the calf PAs the thick wall assumption may be more appropriate.

Our results show that the outer layer thickness fraction measured from histological images does not change significantly in the calf PAs but increases dramatically in the rat PAs. During arterial remodeling, SMCs, elastin, and collagen all increase in volume, which results in an increase in arterial wall thickness. Deposition of these arterial components does not change the outer layer thickness fraction in calf PAs with an average of 0.320 ± 0.057 for all calf MPAs and RPAs, but does yield an increase in the outer thickness fraction from ∼0.33 to ∼0.56 in the rat PAs. The great increase in the rat appears to be due to much more deposition of collagen in the outer layer of rat PAs as seen in the histological images. These results of adventitial layer thickness fraction in rats agree with the previous findings in rats that showed increases from 0.35 to 0.55 and 0.42 to 0.56 for rat MPA and LPA, respectively, after 21 days of hypoxia (16).

Stenmark et al. (26) demonstrated different cellular and molecular response mechanisms to chronic hypoxia exposure between calf and rat. In response to chronic hypoxia, the adventitia in rat PAs undergoes early and dramatic thickening with media remodeling in a later stage (26); while in the calf, nonmuscle cells and immature SMCs in PA media may respond rapidly with proliferation and production of matrix proteins (26), leading to the thickening of both media due to cell proliferation and adventitia due to collagen deposition. Therefore, different impact of chronic hypoxia on PAs would be expected between the two species. Our work complements these findings, in that it suggests these different biological responses are associated with unique geometric and mechanical consequences, namely different changes of the in vivo stress-strain state and the pressure-diameter behavior of PAs. This also complements our previous work that found different changes in the in vitro PA stiffness between these models (20, 21) and thus different changes in right ventricular afterload. Nevertheless, such different response between the two species as observed in this study could be also due to the different vascular structure and the phenotype and function of cells in PAs in the different developmental stages (28) as the calves and rats were young and adult, respectively, during the test, resulting in different remodeling mechanisms at the molecular and cellular levels. While it will be of great interest to investigate such difference between the two species, it is not within the focus of this study.

Relationship between OA and SR.

The in vitro uniaxial tests on the adult bovine MPAs show that the outer layer of PA has a lower elastic modulus than the inner layer at small strains, which is consistent with the two-layer model prediction as shown in Fig. 7B. Although only control MPAs were tested for model validation, the model is assumed valid for calf MPAs in the hypertensive condition and rat MPAs and RPAs in both conditions thanks to the structural similarity of artery (i.e., 2 layers with different elastic moduli) between MPAs and RPAs, between rat and calves, and between control and hypertensive conditions. Moreover, the fact that the collagen-rich outer layer is softer than the elastin-rich inner layer before collagen engages has been indicated in many previous studies (14, 15, 25). Therefore, it is appropriate to use the proposed two-layer model in this study given that the largest residual stretches measured here are far less than the collagen engagement stretch for either animal model, at either condition (20, 21). Although the two-layer concept has been employed in many previous studies to simulate arterial mechanical behavior, this is the first work to apply this concept to link histological and mechanical aspects together and thus to provide further insight into mechanobiological correlations.

The two-layer model predicts that the SRs are <0.1 for calf PAs and change with small amounts (−0.067 and −0.009, or by −70% and −48% for MPA and RPA, respectively) in response to chronic hypoxia, which correlate to the insignificant measured changes of OAs (6° and −25°, or by 4.9% and −18%, for MPA and RPA, respectively). Although the percent changes in SRs are larger than that in OAs, the changes in SR absolute values are small. These small changes in SRs estimated from the model could be due to the measurement errors in the calf PA geometry data used in the model and can be neglected within the measurement error. In rat PAs, however, SRs substantially increase by 0.43 and 0.50, or by 442% and 257%, for MPA and RPA, respectively, and are predicted to be approximately linear to the corresponding OAs. This can be explained as follows. During PA remodeling in the rat, collagen is preferentially deposited over elastin, which increases the outer layer thickness fraction (f_t). This preferential deposition could also increase the outer layer elastic modulus at small stretches, which would yield increase of the outer-to-inner modulus ratio (f_m). The increase of f_m is also predicted from our two-layer model as seen in Fig. 7B when the outer layer thickness fraction (f_t) increases (note that Fig. 7B is for control calf MPA, but similar curves are also found for rat PAs). As a result of the increases of both f_m and f_t, SRs for both rat MPA and RPA increase, which means that the outer layer becomes stiffer in the hypertensive condition than in the control condition, which could further constrain the artery opening process. This would be reflected in a decrease in OA, which was observed in our study. This relationship with SR is yet another means by which the change in OA can reveal structural changes in the artery (9, 16).

Limitations.

There are several limitations in our study. First with regard to imaging, not every calf PA has its histological image for the measurement of the outer layer thickness fraction, while for the rats, our opened arterial sector images have insufficient resolution to measure the circumferential lengths of the inner and outer walls for the calculation of the residual stretches. This lack of the data prevents the calculation of the SR for each PA. As a result, our study only estimates one SR for each rat and calf group with the measured mean data and the estimated residual stretches; however, interindividual differences could be very great. Second, the measurement uncertainty in the OA is not quantified. For OA estimated from the geometry data, its uncertainty depends on the accuracy of the measured arterial thickness and circumferential lengths. For OA estimated from the three-point measurement, its uncertainty depends on the chosen middle point of inner layer. However, during the OA measurement, several points around the middle point of inner layer were chosen as the middle point to obtain several OAs and it was found that these estimated OAs for the same artery in general had differences <5°. Thus the uncertainty in OA estimated from the three-point measurement may be negligible. OA uncertainty would be useful especially when OA is used to estimate the residual stretches. Third, our layerwise in vitro uniaxial tests were performed on adult bovine MPAs, although our PH model is in the neonatal calf. Future work is needed for the layerwise tests on the neonatal calf PAs and/or rat PAs to validate the proposed two-layer model. Fourth, data from adult rats and neonatal calves were compared and the differences between the two species could be due to the different stages of development in these two species. Future studies are needed to investigate the differences between the two species in the same stage of development. Finally, the proposed two-layer model assumes that the material in each layer is uniform through the arterial wall thickness and has a linear stress-strain relationship in the small strain range. In fact, the artery is very complex with nonuniform distribution of arterial components (elastin, SMCs, collagen, etc.), and the stress-strain curve is slightly nonlinear even within the small strain range. A more robust and sophisticated model may be required to fully characterize the mechanical behavior of artery. All these limitations remain to be considered in future studies.

Conclusion.

We have quantified the geometrical and histological changes of calf and rat conduit PAs in response to arterial remodeling in chronic hypoxia and their interspecies differences. Further, we proposed a two-layer model to link the change of OA to the SR of the outer to inner layer, which is a combination quantity of the outer layer thickness fraction and the outer-to-inner layer modulus ratio. Although the two-layer model or concept is not new, to the best of our knowledge this study is the first application of the model to quantitatively relate OA to the mechanical and histological properties of the two layers, which can establish a relationship between these parameters that cannot be measured directly or easily. Our results show that there are great differences in the arterial remodeling between rat and calf PAs. As a result of remodeling due to chronic hypoxia, the OA does not change significantly in calf PAs but decreases dramatically in rat PAs. Correspondingly, the outer layer thickness fraction does not change significantly in calf PAs but increases dramatically in rat PAs. Our proposed two-layer model predicts that a change in OA may be linked to a change in SR. Therefore, the OA is linked to the histological structure and mechanics of the artery, and studying the OA and artery residual stretch provides insight into the functional changes of the artery in remodeled conditions.

GRANTS

This study was supported in part by grants from the National Institutes of Health (R01-HL067393, T32-HL072738, K24-HL081506, K25-HL094749, and SCCOR-HL084923) and the American Heart Association (09SDG2260194).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).