Simultaneous measurement of glucose transport and utilization in the human brain

Abstract

Glucose is the primary fuel for brain function, and determining the kinetics of cerebral glucose transport and utilization is critical for quantifying cerebral energy metabolism. The kinetic parameters of cerebral glucose transport, K_M^t and V_max^t, in humans have so far been obtained by measuring steady-state brain glucose levels by proton (¹H) NMR as a function of plasma glucose levels and fitting steady-state models to these data. Extraction of the kinetic parameters for cerebral glucose transport necessitated assuming a constant cerebral metabolic rate of glucose (CMR_glc) obtained from other tracer studies, such as ¹³C NMR. Here we present new methodology to simultaneously obtain kinetic parameters for glucose transport and utilization in the human brain by fitting both dynamic and steady-state ¹H NMR data with a reversible, non-steady-state Michaelis-Menten model. Dynamic data were obtained by measuring brain and plasma glucose time courses during glucose infusions to raise and maintain plasma concentration at ∼17 mmol/l for ∼2 h in five healthy volunteers. Steady-state brain vs. plasma glucose concentrations were taken from literature and the steady-state portions of data from the five volunteers. In addition to providing simultaneous measurements of glucose transport and utilization and obviating assumptions for constant CMR_glc, this methodology does not necessitate infusions of expensive or radioactive tracers. Using this new methodology, we found that the maximum transport capacity for glucose through the blood-brain barrier was nearly twofold higher than maximum cerebral glucose utilization. The glucose transport and utilization parameters were consistent with previously published values for human brain.

glucose is the primary fuel for brain function. It is transported from the blood to the brain via facilitated diffusion through the lumenal and ablumenal endothelial membranes of the blood-brain barrier (BBB) by the GLUT1 glucose transporter protein (23, 30). Following entry into the brain, glucose is transported from the interstitial fluid into neurons primarily via GLUT3 and into glia primarily via GLUT1 transporters (37). This transport into the intracellular compartment is relatively rapid, making the BBB the rate-limiting barrier for glucose entry into brain cells (2, 16, 23). Therefore, glucose has been traditionally considered a single pool past the BBB, as also evidenced by its homogeneous distribution in the brain tissue (32). Once inside the cells, a fraction of the glucose molecules gets irreversibly phosphorylated to glucose 6-phosphate by hexokinase, enters the glycolytic pathway, and is almost completely oxidized to CO₂ and H₂O in the TCA cycle. Under normal physiology, glucose transport is not rate limiting for phosphorylation, which is saturated at the euglycemic brain glucose levels of 1–1.5 mmol/l due to a hexokinase K_M of ∼50 μmol/l.

Quantifying the kinetics of glucose transport into and eventual utilization in the brain is critical for assessing cerebral energy metabolism under normal and pathological conditions. The kinetic parameters for glucose transport and the rates of its metabolism in the brain have typically been obtained from separate experiments, for example, measurements of brain glucose concentrations by ¹H NMR as a function of blood glucose to extract transport parameters (6, 19) and MR and PET tracer studies to estimate net glucose uptake/oxidation (11, 20, 42). In glucose transport measurements by ¹H NMR, the kinetic parameters of cerebral glucose transport are obtained traditionally by fitting steady-state models to steady-state brain glucose concentrations obtained as a function of plasma glucose concentrations. This way, K_M for transport (K_M^t) and the ratio of V_max for transport (V_max^t) to cerebral metabolic rate of glucose (CMR_glc) are obtained, and, assuming a constant CMR_glc from prior work, V_max^t is calculated (6, 19). The standard irreversible Michaelis-Menten model has been used widely in these studies (16, 23), whereas more recently reversible Michaelis-Menten kinetics (5) were shown to describe the relationship between blood and brain glucose at high blood glucose levels up to 30 mmol/l more accurately (19). The reversible Michaelis-Menten model posits that net glucose transport into the brain is reduced by glucose present in the brain and results in a linear relationship between brain and blood glucose up to these high blood glucose levels. A more sophisticated four-state carrier model that accounts for known features of the GLUT1 transporter, such as trans-acceleration and asymmetry (2), was also used recently to fit in vivo NMR data (10). However, this model did not account for experimental data any better than the reversible Michaelis-Menten model for plasma glucose concentrations less than 25 mmol/l while increasing the number of fitted parameters (10).

Steady-state measurements of brain vs. blood glucose concentrations contain enough information to extract K_M^t and V_max^t/CMR_glc. However, they do not take advantage of the additional information available in dynamic data. Thus, an early NMR study of cerebral glucose transport demonstrated the feasibility of obtaining K_M^t, V_max^t, and CMR_glc, rather than only two parameters, from dynamic glucose measurements in the brain (16). More recently, the feasibility of determining all four kinetic parameters for cerebral transport and utilization (K_M^t, V_max^t, K_M^util, V_max^util) by fitting both dynamic and steady-state data was demonstrated for acetate (7). However, this approach has not thus far been applied to glucose transport and utilization.

Therefore, the aims of the current study were to 1) measure the change in brain glucose concentrations when blood glucose levels are increased in a step function, 2) fit a non-steady-state, reversible Michaelis-Menten model to these data together with steady-state brain vs. blood glucose concentration data from literature (6, 19), and 3) determine the reliability of the extracted kinetic parameters for cerebral glucose transport and utilization as well as their consistency with values reported previously from separate experiments under the same conditions.

MATERIALS AND METHODS

Participants and study design.

Five healthy volunteers [3 males and 2 females, age 31 ± 16 yr, BMI 22.4 ± 1.4 kg/m² (means ± SD)] were studied after they gave informed consent, using procedures approved by the Institutional Review Board: Human Subjects Committee of the University of Minnesota. On the morning of the study, subjects reported at 7 AM to the Center for Magnetic Resonance Research in the fasting state. An intravenous (iv) catheter placed antegrade in an antecubital vein was used for glucose infusion. An additional iv catheter was placed retrogradely in the foot for blood sampling. Upon placement in the scanner, a baseline MR spectrum was obtained from the occipital lobe. Then the volunteers received a 40- to 60-ml iv glucose bolus (50 g/100 ml solution) over 1–2 min to raise their blood glucose in a step function. The bolus was followed by continuous infusion of glucose (20 g/100 ml solution) as necessary to maintain the plasma concentration at ∼17 mmol/l for ∼2 h (typically started at 360 ml/h and then dropped to 270 ml/h after 20–30 min), and MR spectra were acquired continuously throughout the infusion. Blood samples were obtained every 5 min to measure plasma glucose concentration on an automatic glucose analyzer. Additional blood samples were obtained every 20 min and frozen for the later determination of plasma insulin concentrations by a chemiluminescent assay (Immulite; Diagnostic Products, Los Angeles, CA).

NMR spectroscopy.

All measurements were performed on a 4 tesla (4 T), 90-cm bore magnet (Oxford Magnet Technology, Oxford, UK) with an INOVA console (Varian, Palo Alto, CA) and a standard body gradient coil (Sonata; Siemens, Erlangen, Germany), as described previously (40). Briefly, subjects were positioned supine on the patient bed with the occipital lobe just above a quadrature 14 cm ¹H coil (1). Subjects wore earplugs to minimize exposure to gradient noise and were positioned in the coil holder, using cushions to minimize head movement. A 3 × 2.5 × 3 or 3 × 3 × 3 cm³ volume of interest (VOI) was selected in the occipital cortex based on axial magnetic resonance imaging using a multislice rapid acquisition with relaxation enhancement sequence [repetition time (TR) = 4 s, echo train length = 8, echo time (TE) = 60 ms, 7 slices]. All first- and second-order shim terms were adjusted using FASTMAP with echo-planar readout (18). Localization was achieved with an ultrashort stimulated echo acquisition mode sequence (TE = 5 ms, TR = 4.5 s, mixing time TM = 42 ms). Water suppression was achieved using eight variable power RF pulses with optimized relaxation delays, which were interleaved with outer volume suppression to improve localization performance (41). Spectra were acquired and saved as single scans, which were individually frequency and phase corrected to minimize the effects of motion on spectral linewidths and signal-to-noise ratio (SNR). The baseline MR spectrum was acquired with 128 transients over 10 min. MR spectra continuously acquired during the glucose infusion were summed over every 32 scans to provide 2.5-min resolution.

Metabolite quantification.

Metabolites were quantified using LCModel (33), as described previously (40). The model spectra for alanine, aspartate, ascorbate/vitamin C, glycerophosphocholine, phosphocholine, creatine, phosphocreatine, γ-aminobutyric acid, glucose (Glc), glutamine, glutamate, glutathione, myo-inositol, lactate, N-acetyl aspartate (NAA), N-acetyl aspartylglutamate, phosphoethanolamine, scyllo-inositol, and taurine (Tau) were simulated on the basis of previously reported chemical shifts and coupling constants (15, 39). Macromolecule spectra were acquired from the occipital cortex of five other healthy volunteers using an inversion recovery technique (TR = 2 s, inversion time = 0.675 s) (40). To be able to include the 5.23-ppm resonance of Glc in the LCModel fitting, the residual water was removed by adding a simulated peak at the water frequency with the same intensity and opposite phase of the residual water signal. Metabolite concentrations were obtained relative to an unsuppressed water spectrum acquired from the same VOI, assuming a water content of 82% (36). Metabolites quantified with Cramér-Rao lower bounds (CRLB; estimated error of metabolite quantification) >50% were classified as not detected. At 4 T, the correlation between Glc and Tau may be high (correlation coefficient less than −0.5) depending on SNR and spectral resolution, making the determination of their individual concentrations unreliable (27). The cross-correlation of Glc and Tau was found to be low (correlation coefficient greater than −0.5) in all spectra acquired from the occipital cortex in the current study thanks to the high SNR and excellent resolution obtained in this brain region, resulting in reliable estimates of Glc concentrations from these spectra.

Modeling glucose transport and utilization.

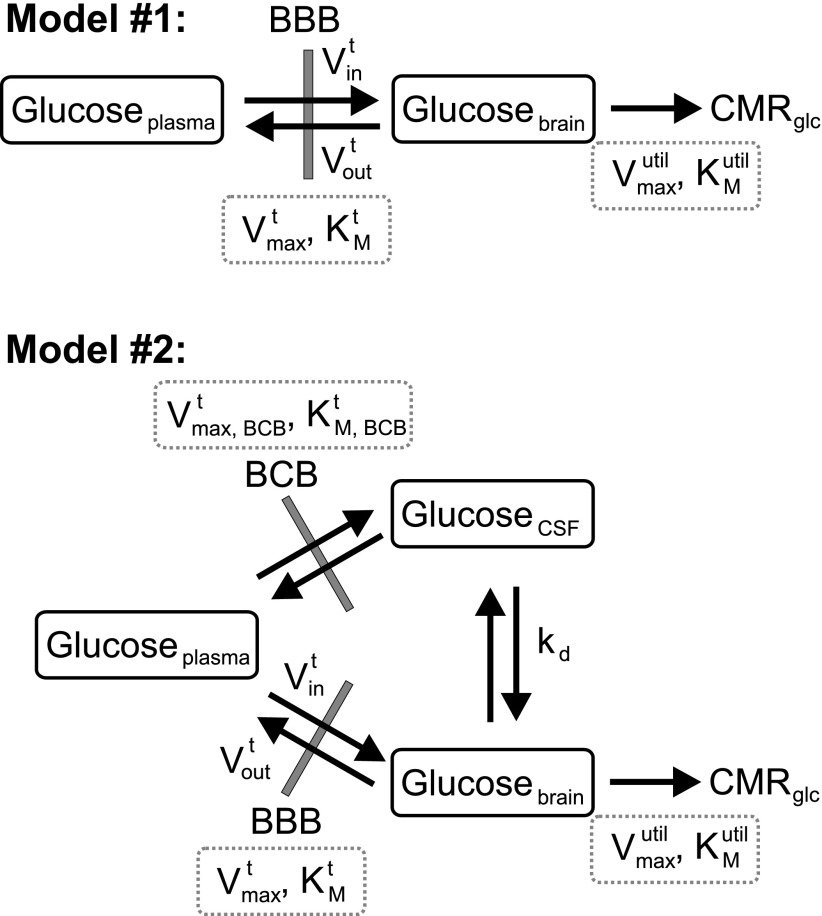
Two kinetic models utilized to extract kinetic parameters for cerebral glucose transport and utilization are shown in Fig. 1. In model no. 1, only plasma and brain glucose are considered, whereas model no. 2 also takes into account the contribution of cerebrospinal fluid (CSF) and blood glucose to the acquired MR signal. The CSF contribution to the VOI was assumed to be 9% based on our prior data acquired from an identical voxel in young, healthy volunteers (12), and the vascular contribution was assumed to be 3.5% (34). Whereas at steady state the Glc concentration in CSF can be assumed to be ∼0.65 times Glc concentration in plasma (6, 22), under non-steady-state conditions where plasma glucose is increased in a step function, the time course of CSF glucose has to be estimated because equilibration of glucose between plasma and CSF is not rapid (13). In both models, glucose transport through the BBB or blood-CSF barrier (BCB) via the endothelial glucose transporter GLUT1 assumes reversible symmetric Michaelis-Menten kinetics, and glucose utilization in brain tissue assumes irreversible Michaelis-Menten kinetics. As in prior studies (6, 19, 23), the endothelial cell compartment with its two membranes is replaced by a single membrane because of the limited volume and metabolism in this compartment and because the single membrane assumption describes glucose transport through the BBB as well as the double-membrane assumption (10). We assumed a single pool for glucose in the brain tissue because a homogeneous distribution was demonstrated for intra- and extracellular glucose in brain (32).

Fig. 1.

The reversible Michaelis-Menten models utilized to extract kinetic parameters for cerebral glucose transport and utilization. The extracted kinetic parameters are shown in dotted boxes. BBB, blood-brain barrier; BCB, blood-cerebrospinal fluid (CSF) barrier; V_in^t, blood-to-brain glucose transport rate; V_out^t, brain-to-blood glucose transport rate; V_max^t, maximal glucose transport rate through the BBB; K_M^t, the glucose concentration for half-maximal transport through the BBB; V_max,BCB^t, maximal glucose transport rate through the BCB; K_M,BCB^t, the glucose concentration for half-maximal transport through the BCB; k_d, transport coefficient for diffusion between CSF and brain tissue; V_max^util, maximal brain glucose utilization rate; K_M^util, brain glucose concentration for half-maximal utilization; CMR_glc, cerebral metabolic rate of glucose utilization.

Brain glucose concentration at steady state is dependent on the relative rates of glucose transport and utilization in the brain. In other words, the difference between plasma and brain glucose concentration at steady state depends on the relative rates of utilization and transport (CMR_glc/V_max^t) such that if CMR_glc is zero, the plasma and brain glucose concentrations would be equal. In contrast, how fast brain glucose concentration changes in response to a change in plasma glucose concentration is also dependent on the absolute rates of glucose utilization in the brain (CMR_glc) and glucose transport into and out of the brain (V_in^t and V_out^t, respectively). Hence, in model no. 1, the differential equation describing the time-dependent brain glucose concentration Glc_brain is given by

$$\frac{d[Gl{c}_{\text{brain}}]}{dt}=V_{\text{in}}^t-V_{\text{out}}^t-CM{R}_{glc}=\frac{V_{\text{max}}^t[Gl{c}_{\text{plasma}}]}{K_M^t+[Gl{c}_{\text{plasma}}]+[Gl{c}_{\text{brain}}]/V_d}-\frac{V_{\text{max}}^t[Gl{c}_{\text{brain}}]}{(K_M^t+[Gl{c}_{\text{plasma}}])V_d+[Gl{c}_{\text{brain}}]}-CM{R}_{glc},$$ (1)

where the terms V_in^t and V_out^t describe the influx of glucose from plasma to brain and efflux of glucose from brain to plasma, respectively, K_M^t is the Michaelis-Menten constant for transport of glucose through the BBB, V_max^tis the maximal transport rate of glucose through the BBB, and V_d is the physical distribution volume for brain glucose (0.77 ml/g) (14, 23). CMR_glc is the time-dependent cerebral metabolic rate for glucose consumption and is modeled by irreversible Michaelis-Menten kinetics:

$$CM{R}_{glc}=\frac{V_{\text{max}}^{\text{util}}[Gl{c}_{\text{brain}}]}{K_M^{\text{util}}\cdot V_d+[Gl{c}_{\text{brain}}]},$$ (2)

where K_m^util and V_max^util represent the Michaelis-Menten constant and the maximal rate for glucose utilization, respectively. The four unknown parameters in these equations are K_M^t, V_max^t, K_M^util, and V_max^util, and the measured data sets are [Glc_plasma] and [Glc_brain] under steady-state conditions and as a function of time in dynamic experiments.

The steady-state Michaelis-Menten model was first fitted to steady-state data [Glc_brain] as a function of [Glc_plasma], [Glc_brain] = f([Glc_plasma]) to extract K_M values for transport and utilization. The steady-state data included both previously published data from literature (6, 19) and steady-state data obtained in the current study (by utilizing up to 3 steady-state experimental [Glc_brain] vs. [Glc_plasma] values for every subject). Because the steady-date data constitute a single data set, the errors for fitted K_M values were obtained by Monte-Carlo simulations. These K_M values were then used to fit the time courses of [Glc_brain](t) using [Glc_plasma] = f_input (t) as input function obtained in the current study to extract V_max values for transport and utilization.

In model no. 2, reversible glucose exchange/transport between CSF and brain tissue is modeled to occur by passive diffusion (Fig. 1). The differential equation describing the time-dependent brain glucose concentration Glc_brain is given by (with a term added to Eq. 1 for CSF-brain transport)

$$\frac{d[Gl{c}_{\text{brain}}]}{dt}=V_{\text{in}}^t-V_{\text{out}}^t-CM{R}_{glc}+r_{cb}{R}^t=\frac{V_{\text{max}}^t[Gl{c}_{\text{plasma}}]}{K_M^t+[Gl{c}_{\text{plasma}}]+[Gl{c}_{\text{brain}}]/V_d}-\frac{V_{\text{max}}^t[Gl{c}_{\text{brain}}]}{(K_M^t+[Gl{c}_{\text{plasma}}])V_d+[Gl{c}_{\text{brain}}]}-CM{R}_{glc}+r_{cb}{R}^t,$$ (3)

where R^t is the net transport rate between CSF and brain by passive diffusion and r_cb = V_csf/M_brain is the ratio of CSF volume to brain mass. CMR_glc is modeled by irreversible Michaelis-Menten kinetics as in model no. 1 (Eq. 2). R^t is given by

$$R^t=k_d\left(\left[Gl{c}_{csf}\right]-[Gl{c}_{\text{brain}}]/V_d\right),$$ (4)

where k_d is the diffusion transport coefficient that incorporates permeability/diffusion and effective surface area. This passive diffusion is a nonsaturable process and depends linearly on glucose concentrations in CSF and brain tissue. The differential equation describing the time-dependent CSF glucose concentration is given by

$$\frac{d[Gl{c}_{csf}]}{dt}=\frac{V_{\text{max},\text{BCB}}^t[Gl{c}_{\text{plasma}}]-V_{\text{max},\text{BCB}}^t[Gl{c}_{csf}]}{K_{M,\text{BCB}}^t+[Gl{c}_{csf}]+[Gl{c}_{\text{plasma}}]}-R^t,$$ (5)

where V_max,BCB^t and K_M,BCB^t are the maximal rate and Michaelis-Menten constant for glucose transport through the BCB, respectively. At BBB and BCB the same GLUT1 transporter is operational (38); hence K_M^t = K_M,BCB^t. As such, the six unknown parameters in these equations are K_M^t, V_max^t, K_M^util, V_max^util, V_max,BCB^t, and k_d, and the measured data sets are [GLc_plasma] and [GLc_brain] under steady-state conditions and as a function of time in dynamic experiments.

The steady-state Michaelis-Menten model was first fitted to steady state [Glc_brain] as a function of [Glc_plasma], [Glc_brain] = f([Glc_plasma]) from literature data (6, 19) combined with steady-state data obtained in the current study to extract K_M values for transport through BBB and utilization as for model no. 1. Values for V_max,BCB^t and k_d were obtained by fitting literature data for dynamic CSF glucose measurements as a function of plasma glucose in healthy humans (13). The errors for these fitted V_max,BCB^t and k_d values were obtained by Monte-Carlo simulations within the experimental errors (13). These K_M^t, K_M^util, V_max,BCB^t, and k_d values were then used to fit the time courses of [Glc_brain](t), using [Glc_plasma] = f_input(t) as input function obtained in the current study to extract V_max values for transport through the BBB and utilization.

Simplex, Broyden-Fletcher-Goldfarb-Shanno, and Levenberg-Marquart algorithms were used to extract kinetic parameters by minimization of the cost function as defined by the least-square difference between model simulation and experimental data.

Monte-Carlo simulations to estimate the dependence of the precision of glucose transport and utilization rates on experimental noise.

To estimate the variation of V_max^t and V_max^util as a function of signal to noise in the glucose time courses, time courses of brain glucose concentration were generated with 40 time points as a function of input plasma glucose with assumed V_max and K_M values. Gaussian noise with a mean of zero and different standard deviations (SD) was then added to the brain glucose curve. Model no. 1 was fitted to this synthetic brain glucose curve to obtain estimates for V_max^t and V_max^util. The fit was repeated 200–500 times each with different noise realizations to get the distribution of V_max^t and V_max^util. These V_max distributions were characterized by their SD.

The experimental noise level was calculated as SD of differences between experimental and fitted time courses of brain glucose concentration.

RESULTS

Reliability of glucose concentration measurements by ¹H NMR.

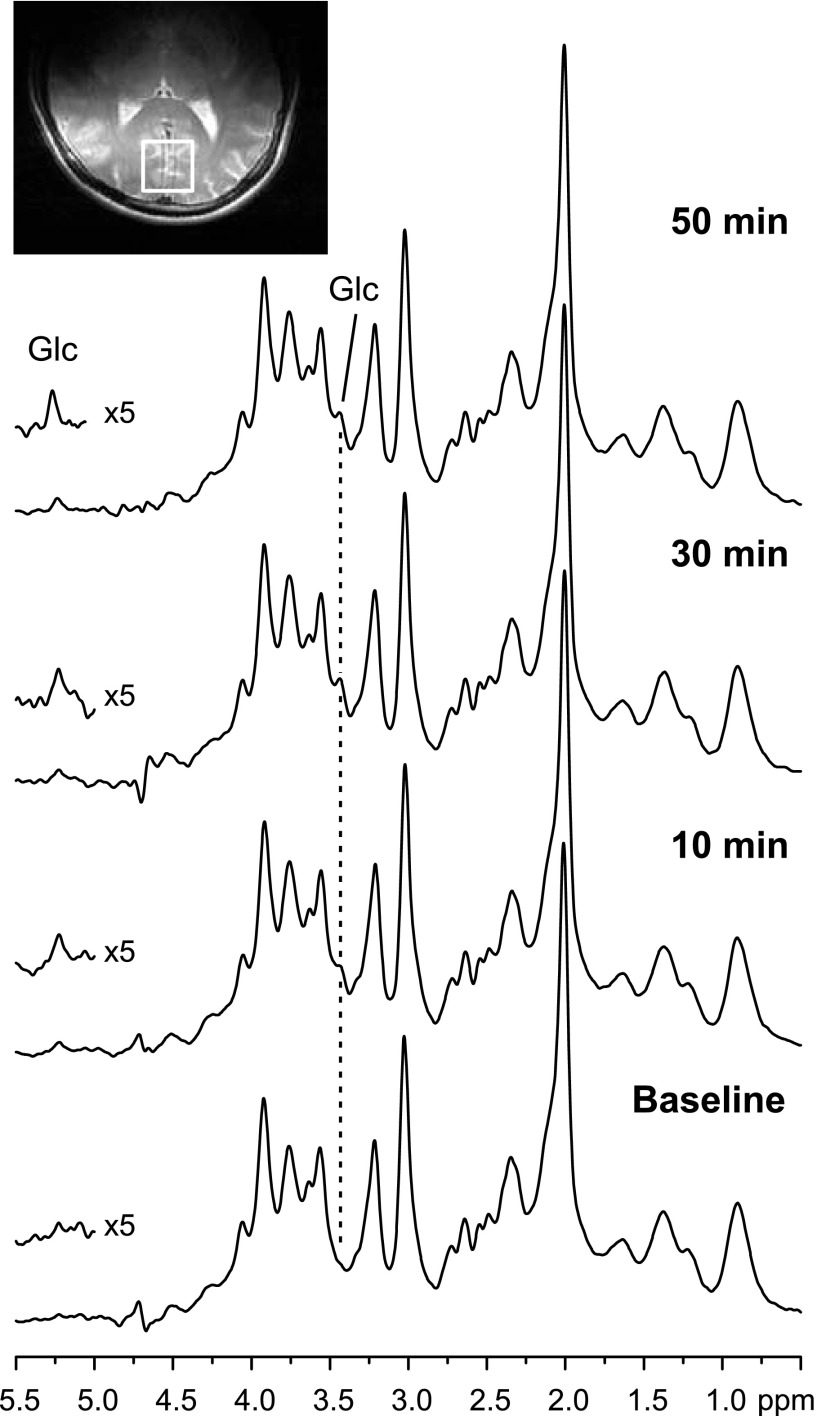
The spectral quality obtained with 2.5-min time resolution is shown in Fig. 2. The increase in brain glucose concentration during the glucose infusion was apparent from both the resolved 5.23-ppm resonance and the 3.44-ppm resonance. To quantify glucose by LCModel, the full spectral pattern, including the 5.23-ppm resonance, was utilized after removal of the water peak. When only the 4.2- to 0.5-ppm spectral range was utilized for LCModel analysis, glucose concentrations were on average only 1.6% higher, indicating that inclusion of the 5.23-ppm resonance does not substantially contribute to the estimation of glucose concentrations. Average CRLB for glucose were 34% at baseline and dropped to ∼10% within 15 min of the start of glucose infusion due to the rise in concentrations and hence, improved precision of the concentration estimate. They stayed below 10% for the remainder of the time courses, indicating excellent reliability.

Fig. 2.

¹H MR spectra acquired at 4 T from 1 volunteer before (baseline) and during infusion of glucose (Glc) at selected time points. The voxel position is shown on a T₂-weighted image. The increase of the 3.44- and the 5.23-ppm glucose resonances over time is visible in the spectra. Spectra were acquired with a stimulated echo acquisition mode sequence [repetition time (TR) = 4.5 s, echo time (TE) = 5 ms] and weighted with a Gaussian function prior to Fourier transformation. No baseline correction was applied. The residual water peak was removed. Each spectrum consists of 32 transients; i.e., they were acquired over 2.5 min.

Blood and brain glucose concentrations during glucose infusion.

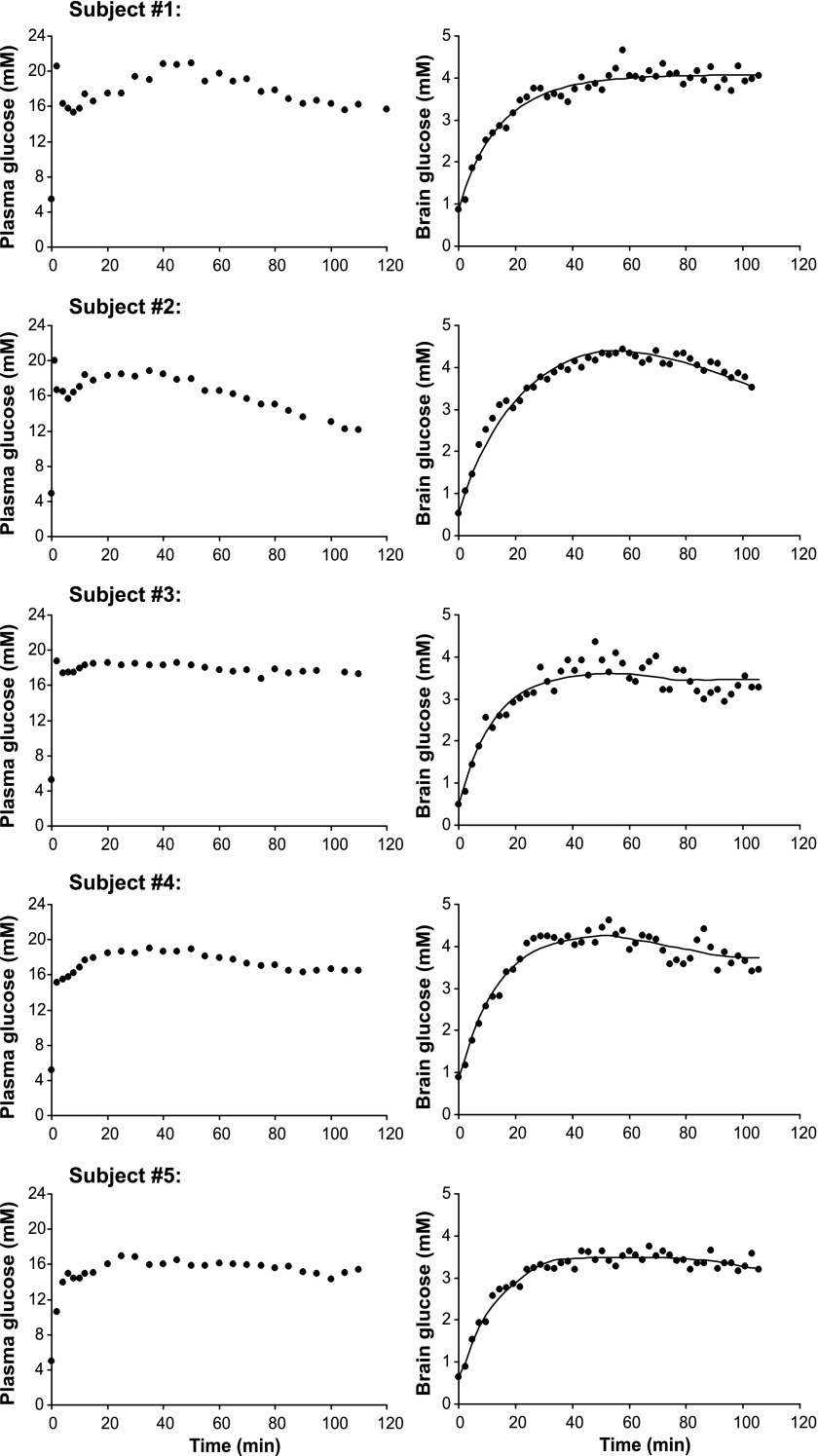
Figure 3 shows that the blood glucose concentrations of all subjects were successfully raised to target levels with the bolus infusion within 2 min and then maintained fairly stable by adjusting the glucose infusion rate. Plasma insulin levels increased in response to the glucose infusion and stayed within 700 pmol/l on average throughout the 2 h of infusion.

Fig. 3.

Plasma and brain glucose concentrations in each of the 5 healthy volunteers. Also shown are the best fits of the non-steady-state, reversible Michaelis-Menten model (model no. 1) to the time courses of brain glucose concentrations. ●Plasma (left) and brain (right) glucose concentrations.

Brain glucose concentrations increased with a delay relative to blood glucose and reached steady-state levels within 30–40 min (Fig. 3). None of the other quantified neurochemicals showed a trend during the glucose infusion.

Modeling glucose transport and utilization.

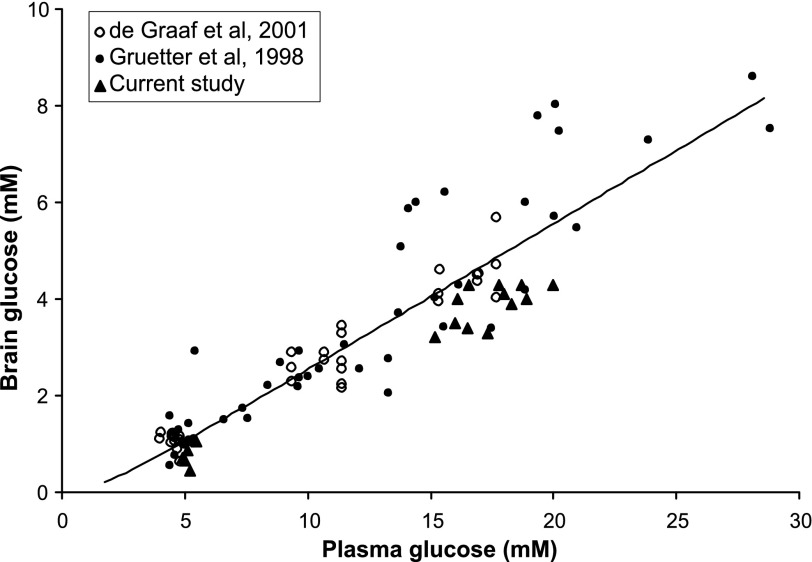
Because our glucose infusion experiments employed a single hyperglycemic target of 17 mmol/l plasma glucose, resulting in steady-state brain glucose concentrations only around two plasma glucose levels (5 and 17 mmol/l), we utilized literature steady-state brain glucose concentrations obtained in similar occipital VOIs as a function of blood glucose (6, 19). These data, in addition to our steady-state values, provided brain glucose concentrations over a wide range of plasma glucose concentrations (Fig. 4). The solid line in Fig. 4 represents the best fit of a steady-state Michaelis-Menten model that included reversible BBB glucose transport and hexokinase activity. The in vivo Michaelis-Menten constants extracted from this fit were K_M^t = 2.1 ± 2.0 mmol/l and K_M^util = 0.1 ± 0.3 mmol/l (means ± SD). These Michaelis-Menten constants were then used to fit our dynamic data with the two models depicted in Fig. 1.

Fig. 4.

Steady-state brain vs. plasma glucose concentrations from literature (6, 19) and the current study. Also shown is the best fit of the steady-state, reversible Michaelis-Menten model to these steady-state data.

Figure 3 shows the best fits of model no. 1 to brain glucose time courses. The model fit the data well for the entire time course for all subjects. The resulting fitted V_max values for transport and utilization, as well as the extracted CMR_glc at euglycemia, are shown in Table 1.

Table 1.

Parameters extracted from fitting models no. 1 and 2 to the dynamic brain glucose data

	Vmaxt	Vmaxutil	CMRglc*
Model no. 1	0.97 ± 0.24	0.50 ± 0.14	0.43 ± 0.12
Model no. 2	0.83 ± 0.22	0.49 ± 0.14	0.41 ± 0.13

Values are means ± SD between subjects (n = 5) and in μmol·g⁻¹·min⁻¹. V_max^t, maximal rate for glucose transport; V_max^util, maximal rate for glucose utilization; CMR_glc, cerebral metabolic rate of glucose utilization.

^*At euglycemia.

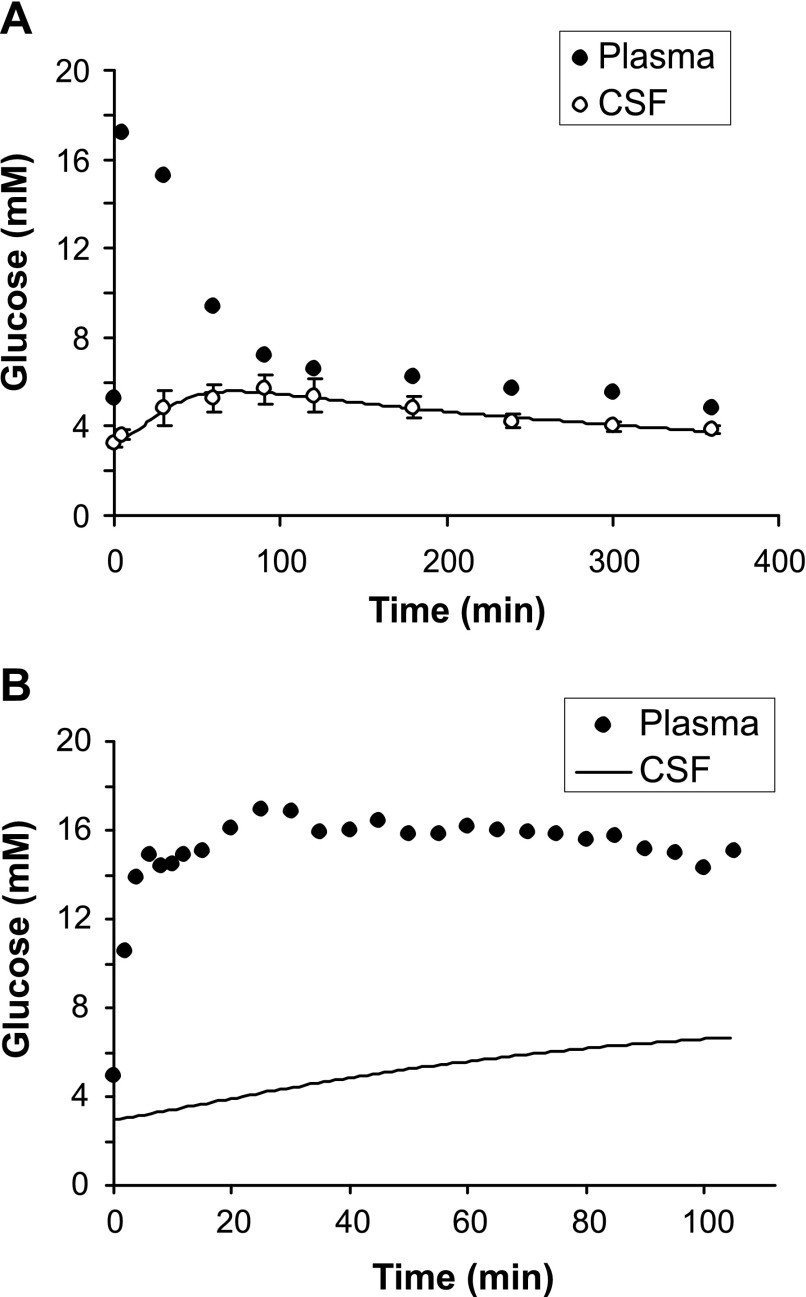
To assess the influence of CSF and vascular contributions to the MR signal on the kinetic parameters for glucose transport and utilization, the same data were fitted with model no. 2. First, V_max,BCB^t and k_d parameters (Eq. 5) were evaluated by fitting literature data for average CSF glucose concentrations obtained in response to a bolus intravenous glucose infusion from healthy volunteers (13). The baseline steady-state CSF glucose concentration in these data was ∼65% of plasma glucose level, consistent with other reports (22). These experimental data and the best fit are shown in Fig. 5A. This fit indicates a maximal rate through BCB, V_max,BCB^t = 0.10 ± 0.04 μmol·ml⁻¹·min⁻¹ and k_d = 0.0054 ± 0.0002 min⁻¹. These values were then used to fit our dynamic experimental data, which resulted in intersubject average V_max values and CMR_glc at euglycemia shown in Table 1. Model no. 2 fit the data better than model no. 1 (Fig. 3), as assessed by cost function, for three of the five subjects, but not the other two subjects. The V_max and CMR_glc values obtained with model no. 2 were within the SD of those obtained with model no. 1 (Table 1). However, note that the values obtained with model no. 1 represent glucose transport and utilization in the whole VOI, whereas those obtained with model no. 2 represent glucose transport/utilization only in the brain tissue.

Fig. 5.

A: average glucose concentrations obtained in CSF and plasma in response to a bolus intravenous glucose infusion in 5 healthy volunteers from literature; error bars are SD (13). The line represents the best fit of model no. 2 (Fig. 1) for glucose transport through the BCB. B: time course of plasma glucose concentration in subject no. 5 together with CSF glucose concentration predicted based on model no. 2 and values of BCB transport determined in A.

To assess the sensitivity of the final V_max values on the two K_M values obtained from the steady-state data (for both models) and on the values of V_max,BCB^t and k_d obtained from literature CSF data (for model no. 2), we performed sensitivity analyses by varying these values within the error ranges determined by the Monte-Carlo simulations (Table 2). For example, a K_M^t of 2.1 mmol/l was obtained from the steady-state data with an error of 2.0 mmol/l estimated by Monte-Carlo simulations, and therefore, we changed K_M^t from 0.1 to 4.0 mmol/l while keeping all other parameters estimated from steady-state glucose data or literature CSF data (K_M^util, V_max,BCB^t, and k_d) fixed and fitted the dynamic data of subject 5 to models no. 1 and 2 to obtain V_max^t and V_max^util (Table 2). The V_max values were not very sensitive to V_max,BCB^t and k_d. Maximum sensitivity was found for V_max^t on the setting of K_M^util with model no. 2, namely V_max^t decreased from the value obtained with K_M^util = 0.1 mmol/l by 25% for K_M^util = 0.4 mmol/l, a highly unlikely value based on reported hexokinase rates in literature (21).

Table 2.

Sensitivity analysis for V_max^t and V_max^util using dynamic data from subject 5

	Model No. 1, μmol·g−1·min−1		Model No. 2, μmol·g−1·min−1
	Vmaxt	Vmaxutil	Vmaxt	Vmaxutil
KtM, mmol/l
0.1	0.93	0.53	0.79	0.53
0.5	0.98	0.55	0.84	0.55
1.0	1.00	0.55	0.89	0.57
1.5	1.09	0.58	0.93	0.58
2.0	1.13	0.59	0.98	0.60
3.0	1.23	0.62	1.07	0.62
4.0	1.36	0.65	1.16	0.64
KMutil, mmol/l
0.05	1.18	0.61	1.04	0.62
0.10	1.16	0.60	1.00	0.60
0.20	1.04	0.55	0.86	0.54
0.30	0.97	0.53	0.79	0.50
0.40	0.93	0.52	0.74	0.49
Vmax,BCBt, μmol·ml−1·min−1
0.05			0.90	0.53
0.10			1.00	0.60
0.15			1.02	0.63
kd, min−1
0.0040			0.98	0.59
0.0054			1.00	0.60
0.0060			1.00	0.60

K_M^t, K_M for transport; V_max,BCB^t, maximal rate for glucose transport through the blood-cerebrospinal fluid barrier (BCB); k_d, diffusion transport coefficient.

An ∼13% increase in CMR_glc at 17 mmol/l plasma glucose was predicted relative to euglycemia. Numerical simulations with the fitted parameters also predicted an ∼12% decrease in CMR_glc during hypoglycemia (3 mmol/l plasma glucose) compared with euglycemia. In addition, model no. 2 allowed us to predict temporal CSF glucose profiles for all subjects based on the fitted parameters, as shown in Fig. 5B. The model estimated that CSF glucose concentrations increased more slowly than brain glucose concentrations, indicating that CSF glucose levels have not reached steady state during 100 min of glucose infusion.

Finally, to determine the feasibility of extracting kinetic parameters of glucose transport and utilization in smaller VOI with less SNR, we estimated the variation of V_max^t and V_max^util as a function of noise of the glucose time courses using Monte-Carlo simulations (Table 3). The average experimental noise of the current data sets was 0.2 μmol/g, corresponding to an average spectral SNR of 105 between subjects (calculated on the basis of the NAA peak in non-weighted spectra acquired in 2.5 min). The simulations indicated that noise levels up to 0.5 μmol/g are acceptable to obtain V_max values with errors within ∼20%. Further increases of noise in the glucose measurements also resulted in substantial overestimation of the V_max values (Table 3).

Table 3.

Monte-Carlo simulations for V_max^t and V_max^util as a function of the noise of the brain glucose time course

Noise SD, μmol/g	Vmaxt	Vmaxutil
0.1	1.00 ± 0.04 (4%)	0.50 ± 0.02 (4%)
0.2	1.00 ± 0.07 (7%)	0.50 ± 0.04 (8%)
0.3	1.00 ± 0.12 (12%)	0.50 ± 0.06 (12%)
0.4	1.02 ± 0.15 (14%)	0.51 ± 0.08 (15%)
0.5	1.05 ± 0.22 (21%)	0.53 ± 0.12 (22%)
0.6	1.04 ± 0.26 (25%)	0.52 ± 0.14 (26%)
0.7	1.08 ± 0.40 (37%)	0.54 ± 0.21 (38%)
0.8	1.15 ± 0.95 (83%)	0.58 ± 0.51 (88%)

Values are means ± SD (%SD) and in μmol·g⁻¹·min⁻¹.

DISCUSSION

Here we report the first simultaneous measurement of the kinetic parameters for glucose transport and utilization in the human brain. The methodology involves dynamic measurements of brain glucose as a function of blood glucose by widely used ¹H NMR acquisition techniques and metabolic modeling of these data. In addition to providing simultaneous measurements of glucose transport and utilization, the advantages over other methods to obtain the same kinetic parameters include that CMR_glc does not need to be assumed constant and that infusions of expensive or radioactive tracers are not required. The kinetic parameters obtained using the methodology were consistent with previously published results for the human brain.

Use of and comparison with prior brain vs. blood glucose data obtained by NMR.

Although we could have utilized only our experimental data for modeling, we chose to take advantage of literature data available from the same region of interest (6, 19) that cover a wider range of plasma glucose concentrations (Fig. 4). For future studies that utilize this methodology to study glucose transport and utilization in other brain regions or under different pathological conditions, different hyperglycemic targets need to be chosen in different subjects to populate the steady-state brain vs. blood glucose curve. For example, three hyperglycemic targets of ∼11, 17, and 22 mmol/l, with three to five subjects per target, are expected to provide sufficient steady-state and dynamic data sets to enable measurements of glucose transport and metabolism in a different brain region or in disease states. Alternatively, a two-step glucose infusion protocol can be utilized, leading to three steady-state glucose levels in each subject, as was done previously (6). Such a two-step procedure would reduce the necessary number of subjects; however, it would also require longer acquisition times that may not be tolerable by patient populations. However, note that, although we utilized glucose infusions of up to 2 h in the current study, our data demonstrate that an ∼1-h infusion is sufficient to reach and maintain steady state for ∼20 min (Fig. 3). Therefore, future studies with patients will only necessitate ∼1.5-h scanning sessions (∼30-min imaging, power calibrations, acquisition of baseline spectrum + 1-h data acquisition during glucose infusion) for a single blood glucose target. These data also show that it is feasible to achieve two hyperglycemic targets within the study duration we utilized if the subjects can tolerate the ∼2.5-h scanning session.

Unlike the prior studies of cortical glucose transport (6, 19), we did not infuse somatostatin to suppress endogenous insulin secretion in the current study because plasma insulin concentrations up to ∼670 pmol/l do not change brain glucose concentrations (35).

The methods to obtain cerebral glucose concentrations in the current study were similar but not identical to those used in the prior studies. For example, Gruetter et al. (19) utilized only the αH1-glucose resonance at 5.23 ppm and quantified glucose relative to total creatine concentration set to 10 mmol/l, whereas de Graaf et al. (6) utilized the full spectral pattern of glucose and quantified it relative to known NAA concentrations in gray and white matter. We utilized the full glucose spectral pattern and found that the 5.23-ppm resonance does not contribute substantially to the glucose concentration estimate. We used the unsuppressed water peak acquired from the same VOI as an internal reference to forego assumptions about NAA or creatine concentrations. Despite these methodological differences, the steady-state brain glucose concentrations obtained in the current study were within the range of those obtained in the prior studies at the same blood glucose levels (Fig. 4) (6, 19). The current values were slightly lower than the prior values on average, which may be due to the different assumptions made for the reference signals or because our voxel contained primarily gray matter. Namely, when de Graaf et al. (6) distinguished the contributions of gray and white matter to the total glucose signal, they found lower glucose levels in gray matter.

Data quality.

Although the glucose clamps were maintained only by adjusting the glucose infusion rate, plasma glucose levels were increased in a step function and maintained successfully at the target levels with few fluctuations in each volunteer (Fig. 3). With this protocol, the omission of the somatostatin infusion avoided the associated nausea and hence, increased subject comfort. Thanks to the consistent spectral quality throughout the infusions (Fig. 2), glucose levels were obtained with CRLB <10% for most of the time course. In addition, the 2.5-min time resolution provided sufficient data density to detect any substantial deviations from the best fits of the tested models (Fig. 3). On the other hand, Monte-Carlo simulations demonstrated that, assuming an inverse linear relationship between spectral SNR and the noise in the glucose time courses, which is indicated by our data, spectral SNR levels 2.5-fold lower than in the current study, i.e., VOI sizes of ∼10 ml (instead of 22–27 ml used here), can be utilized at 4 T while still keeping the time resolution at 2.5 min and the errors of the extracted V_max values within ∼20% (Table 3). Note that the intersubject SDs in the extracted parameters (25–30%; Table 1) were higher than the %SD predicted with Monte-Carlo simulations at the current noise level (7–8%; Table 3), indicating that the errors of the extracted parameters were dominated by interindividual differences rather than experimental measurement errors. Therefore, even smaller VOIs are possible without the experimental errors exceeding the interindividual differences. Future multivolume NMR or magnetic resonance spectroscopic imaging studies with even smaller VOIs could produce regional glucose transport and metabolism maps similar to PET scans, from glucose maps obtained during glucose infusions, as was demonstrated in the rodent brain (25).

Modeling glucose transport and utilization.

The lag in the rise of cerebral glucose relative to plasma glucose was reported previously (16). Although this early study suffered from technical limitations, such as the unavailability of absolute brain glucose concentrations from the ¹H NMR measurements (hence, utilizing relative glucose increases over the time course or assumptions on brain glucose concentration from other studies), it was the first to demonstrate the additional information content for cerebral glucose transport and utilization in dynamic data. Hence, the standard irreversible Michaelis-Menten model was fit to the time course of relative brain glucose signals while plasma glucose was increased in this prior study (16) to obtain K_M^t, V_max^t, and CMR_glc (assumed constant) instead of only K_M^t and the ratio of V_max^t to CMR_glc that is obtained from steady-state measurements. We expanded on the idea of utilizing dynamic data in the current study and fitted reversible Michaelis-Menten models to cortical glucose concentrations as a function of plasma glucose to obtain K_M and V_max for both transport and utilization without assuming a constant CMR_glc.

Note that the V_max values extracted from such modeling are apparent values since, for example, CMR_glc can be decreased substantially by anesthesia (4, 26) and increased by seizures (31) at a given blood glucose level, whereas the V_max^util reported here would not allow such substantial increases in CMR_glc. This is because inhibitory and activating factors are not taken into account in the metabolic modeling. In addition, the V_max^util reported represents the glucose consumption for the region of interest and does not distinguish between astrocytic and neuronal glucose consumption. Also note that the V_max^util obtained with the current methodology represents total (oxidative + nonoxidative) glucose utilization, unlike prior ¹³C NMR studies in which only oxidative glucose consumption is obtained from label transfer from infused [¹³C]glucose to metabolites that are in exchange with the TCA cycle. This is a small difference since glucose is almost completely oxidized in the brain tissue, with an oxygen-to-glucose uptake ratio of ∼5.5 in resting state.

The first model we tested was the standard reversible Michaelis-Menten model that utilized the total glucose concentrations obtained in the NMR voxel. The second model also took into account the contributions of CSF and blood glucose to the MR signal, and therefore, it likely represented cerebral glucose transport and utilization kinetics more accurately. We did not observe a substantial improvement of the fit of model no. 2 to the data (not shown) relative to model no. 1 (Fig. 3), although the extracted kinetic parameters were somewhat affected, as expected (Table 1). However, note that these values represent an extreme case because the 3.5% estimate for vascular contribution is likely an overestimate for the actual plasma glucose contribution to the MR signal due to the reduction of the vascular signal by diffusion and the crusher gradients in the pulse sequence (6, 19). Therefore, the true kinetic parameters are likely between those extracted from models no. 1 and 2 (Table 1). The CSF contribution is relatively minor for healthy brain but may become more significant in disease states. In future studies it may be possible to further reduce the contribution of the vascular and CSF signals by adding diffusion gradients to the pulse sequence and taking advantage of the difference in diffusion properties of glucose in tissue vs. in blood and CSF.

The transport parameters we obtained were similar to those reported in previous studies using reversible Michaelis-Menten kinetics (6, 19), and the CMR_glc estimated at euglycemia was consistent with previously reported values in the human brain as well (17, 24, 42). Similar to prior studies (6, 19), the K_M values extracted from the steady-state data were low but not well determined (large SDs); i.e., the fit was largely insensitive to K_M due to lack of data in the hypoglycemic blood glucose regime (Fig. 4). In addition, the experimental errors for the combined steady-state data from literature and the current study were high (SD of experimental noise was ∼1 mmol/l), resulting in high SDs for the K_M parameters.

The data indicated that maximum transport capacity for glucose through the BBB was nearly twofold higher than maximum cerebral glucose utilization rate (Table 1). Interestingly, a slight increase in CMR_glc was estimated at hyperglycemia, as one might expect from ∼90–94% hexokinase saturation at euglycemia (based on the extracted K_M^util and 1–1.5 μmol/g brain glucose concentrations). Also, a reduction in CMR_glc was estimated at hypoglycemia on the basis of the extracted kinetic parameters. Taken together, these data indicated that at high plasma glucose concentrations (∼10 mmol/l and above) glucose metabolism is rate limited after entry of glucose into the brain (at hexokinase level) rather than at the BBB, whereas at hypoglycemia transport through the BBB may influence the glucose utilization rate and could be rate limiting, especially for activated states.

In model no. 2, the time course of CSF glucose had to be modeled (instead of approximating these at 0.65 times plasma glucose levels at all times) in light of literature that demonstrated a lag for the rise in CSF glucose levels relative to blood glucose (13), similar to the situation in the brain tissue. This was expected considering that the same GLUT1 transporter system is operational at the BBB and BCB. However, the lag in CSF glucose is more substantial than the lag in brain glucose relative to plasma glucose (Fig. 5B), as also reflected by the approximately ninefold difference in V_max^t values between BBB and BCB. This difference between the blood-to-brain and blood-to-CSF transport capacity is likely due to a difference in the number of GLUT1 transporters on each barrier. Therefore, these data indicate that assuming CSF glucose levels at 0.65 times plasma glucose may be inaccurate even for steady-state studies unless the hyperglycemic plasma glucose levels are maintained for a very long time. For example, when temporal CSF glucose profiles were predicted for increasing plasma glucose from 5 to 17 mmol/l, as was done in the current study, it took ∼200 min to reach 90% of the new steady-state CSF glucose levels.

Limitations.

This study did not distinguish between gray and white matter and assumed a %CSF contribution to the MR voxel based on prior data from our group (12). Glucose concentrations in gray and white matter were found to be the same in one prior study (35) and different in another (6). Therefore, future investigations should ideally measure the gray matter, white matter, and CSF content in all VOIs by image segmentation. Another limitation of the current study was that the contribution of glycogen metabolism to glucose kinetics was omitted because turnover of glycogen constitutes ∼1% of CMR_glc in both humans (29) and rodents (3) in resting state. However, future improvements on the model should also include glycogen metabolism because such non-steady-state modeling is also expected to contribute to the understanding of glycogen metabolism, particularly in experiments where the synthesis and breakdown of glycogen may not be equal (28). In addition, high rates of glycogen turnover have been implicated with activation in rodent studies (8, 9), and therefore, the contribution of glycogen metabolism to glucose kinetics may not be negligible in activated states. Finally, note that if the additional CSF-related parameters provided by model no. 2 are desired under different physiological states, e.g., in disease states, it will be necessary to obtain CSF glucose levels as a function of plasma glucose in the same study populations.

Conclusions.

The new ¹H NMR and metabolic modeling methodology can be utilized to simultaneously obtain kinetic parameters for glucose transport and utilization in any brain region as long as dynamic glucose profiles are obtained with multiple hyperglycemic plasma glucose targets that cover a wide range of plasma glucose values. This methodology is expected to enable investigations of altered cerebral glucose transport and metabolism within the same experiment.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grants R01-NS-035192 (E. R. Seaquist) and R01-NS-38672 (P. G. Henry). The Center for MR Research is supported by National Center for Research Resources (NCRR) Biotechnology Research Resource Grants P41-RR-008079 and S10-RR-023730 and Neuroscience Center Core Blueprint Award P30-NS-057091. The General Clinical Research Center is supported by NCRR Grant no. M01-RR-00400.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.