Impedance control is selectively tuned to multiple directions of movement

Abstract

Humans are able to learn tool-handling tasks, such as carving, demonstrating their competency to make movements in unstable environments with varied directions. When faced with a single direction of instability, humans learn to selectively co-contract their arm muscles tuning the mechanical stiffness of the limb end point to stabilize movements. This study examines, for the first time, subjects simultaneously adapting to two distinct directions of instability, a situation that may typically occur when using tools. Subjects learned to perform reaching movements in two directions, each of which had lateral instability requiring control of impedance. The subjects were able to adapt to these unstable interactions and switch between movements in the two directions; they did so by learning to selectively control the end-point stiffness counteracting the environmental instability without superfluous stiffness in other directions. This finding demonstrates that the central nervous system can simultaneously tune the mechanical impedance of the limbs to multiple movements by learning movement-specific solutions. Furthermore, it suggests that the impedance controller learns as a function of the state of the arm rather than a general strategy.

many common tasks requiring tools such as chiseling or drilling are unstable. This instability amplifies the effects of motor noise (Hamilton et al. 2004; Harris and Wolpert 1998) and can lead to unpredictable and unsuccessful action (Burdet et al. 2006). For instance, the hand of an apprentice carpenter may slip when chiseling a piece of rough wood. However, with practice he will learn to control movements with suitable force and impedance in all directions and carve skillfully. To develop these skills, he will need to tune his limb impedance (Burdet et al. 2001; Gomi and Kawato 1996; Hogan 1984, 1985) to the instabilities that may vary across the workspace. To modulate the limb impedance, he can either change the limb posture (Hogan 1985; Rancourt and Hogan 2001; Trumbower et al. 2009), modulate feedback control (Krutky et al. 2010; Loram et al. 2011, 2009; Morasso 2011), or coactivate muscles (Damm and McIntyre 2008; Hogan 1984; Milner 2002). In an unstable or unpredictable environment, the central nervous system (CNS) learns to co-contract suitable muscle pairs involved in the movement (Burdet et al. 2001; Franklin et al. 2007a, 2003b) stabilizing the limb end point and minimizing the production and effect of motor noise (Selen et al. 2005, 2009). However, all previous studies investigating impedance control in reaching movements examined only a single movement direction (Burdet et al. 2001, 2006; Franklin et al. 2003a, 2008; 2007a, 2003b, 2007b; Osu et al. 2003, 2002; Takahashi et al. 2001; Wong et al. 2009a,b). Can humans learn impedance control models to compensate for different directions of instability across the workspace?

Adaptation to stable dynamics takes place in the joint coordinates of the neuromuscular system (Shadmehr and Mussa-Ivaldi 1994) and generalizes across the workspace (Conditt et al. 1997; Gandolfo et al. 1996; Malfait et al. 2005, 2002; Shadmehr and Moussavi 2000; Shadmehr and Mussa-Ivaldi 1994). When different dynamics or visuomotor transformations are learned one after another, interference between the two learned models results (Brashers-Krug et al. 1996; Caithness et al. 2004; Karniel and Mussa-Ivaldi 2002; Mattar and Ostry 2007; Osu et al. 2004; Shadmehr and Brashers-Krug 1997), making it difficult to learn independent internal models. Exceptions have only been found for sufficiently different environments (Krakauer et al. 1999) and in bimanual movements where the context allows independent learning of multiple models (Howard et al. 2008, 2010; Nozaki et al. 2006). However, when different force directions are learned as a function of different movement directions, no interference occurs (Shadmehr and Mussa-Ivaldi 1994; Thoroughman and Taylor 2005) as a single model of the overall environment is learned.

If impedance control uses similar neural structures as learning stable dynamics, it should be possible to independently control limb stiffness across the workspace. To examine this hypothesis, subjects reached to two different targets with instability applied orthogonally to each trajectory (lateral instability). We examined whether end-point stiffness adaptation occurred in the same manner whether subjects moved to a single target with one direction of instability or randomly to one of two targets, each with its own instability direction. If only a single co-contraction model is learned, then the stiffness in the multiple movement direction condition would not be optimal for both directions. However, if the impedance controller can learn a single model generalizing across the workspace or switches between multiple models for each direction of movement, then subjects may learn the optimal stiffness for adaptation to each direction.

MATERIALS AND METHODS

Simulation of general and selective end-point stiffness.

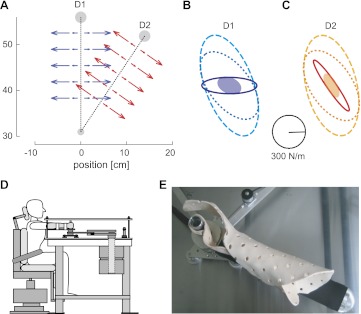
Simulations were performed to examine how the CNS may adapt end-point stiffness of the arm when lateral instability is applied on the hand during planar movements in different directions (Fig. 1A). The simulated task (identical to the experimental task) consisted of performing two 25-cm long point-to-point movements: from (0, 31) cm relative to the shoulder to (0, 56) cm for the D1 movement and from the same start to (14, 52) cm for the D2 movement (which is separated from D1 by 35° clockwise). The simulations explored possible strategies for the CNS to move successfully in the lateral instability caused by a divergent force field (DF), orthogonal to the movement trajectory (Fig. 1A), defined by:

$$\left[\begin{array}{c}{F}_{\perp }\\ F_{\parallel }\end{array}\right]=\left[\begin{array}{c}\zeta x_{\perp }\\ 0\end{array}\right]$$ (1)

where F_⊥ and F_∥ indicate the force components normal and parallel to the straight line from start to end points, respectively, ζ = 300 N/m, and x_⊥ is the lateral deviation of the hand from this straight line. The end-point stiffness necessary to compensate for this instability was simulated at the middle of the movement.

Fig. 1.

Strategies that the central nervous system (CNS) could use to compensate for lateral instability in 2 different directions of movement. A: an unstable force field that creates instability perpendicular to the movement was created for movements in 2 directions (D1 and D2). B and C: predicted end-point stiffness in movement direction D1 and D2, respectively. To adapt to environmental instability, subjects could increase the end-point stiffness in several methods to stabilize the interaction with their limbs. All simulated end-point stiffness matrices maintain the net stiffness at or above the level of the null field stiffness (shaded ellipse) after compensating for the instability. Dashed ellipses indicate the predicted end-point stiffness from a uniform co-contraction of all muscle pairs such that the stiffness in both movement directions is larger than the instability in each direction. In this case, only a single contraction term needs to be learned to perform movements in each direction of movement. Dotted ellipses represent the predicted end-point stiffness for a selective increase of co-contraction, which compensates exactly for both instability directions simultaneously. Overall metabolic cost is much lower than for the uniform co-contraction condition. Solid ellipse indicates the predicted end-point stiffness for selective co-contraction tuned independently for each movement direction for the instability. Note that the stiffness ellipse area is minimal in the latter possibility, which thus requires least co-contraction. However, in this case, either 2 separate impedance control models are required, or the CNS must learn a single impedance control model which generalizes across the workspace. D: experimental setup. Subjects sat in an adjustable chair, with their forearm and hand attached to the robotic manipulandum. E: top view close-up of the forearm attachment to the robotic manipulandum (shown without subjects arm). This coupling of the subject's forearm to the robotic manipulandum is performed by creating an individual thermoplastic mold that fits around the subjects arm and robot handle. Straps attach this thermoplastic cuff to the supportive forearm brace which is a part of the robotic manipulandum.

A simplified version of the muscle limb model from (Selen et al. 2009) was used to predict both the baseline null field (NF) stiffness and theoretical adaptations to the instability. The force attributed to each muscle (F_m) was solved for such that the minimal summed muscle activation was produced that could both result in the required end-point force and sufficient end-point stiffness in the direction perpendicular to the movement direction. Six muscles were simulated: two single joint shoulder muscles, two single joint elbow muscles, and two biarticular muscles. Muscle forces were required to produce the joint torques (T) that created the appropriate end-point forces F for each direction of movement:

$$\text{F}={\left({\text{J}}^T\right)}^{-1}\text{T}={\left({\text{J}}^T\right)}^{-1}{\text{D}}^T{\text{F}}_m$$ (2)

where J is the Jacobian matrix of the limb configuration and D is a 6 × 2 matrix of the moment arms of the muscles around the shoulder and elbow joints. The end-point stiffness (K) for a given muscle activation pattern was found using:

$$\text{K}={\left({\text{J}}^T\right)}^{-1}\left({\text{R}}_{base}+{\text{D}}^{T}diag\left(c_m{\text{F}}_m\right)\text{D}-\frac{d{\text{J}}^T}{d\theta }\text{F}\right){\text{J}}^{-1}$$ (3)

where c_m is the stiffness scaling constant. As in Selen et al. (2009), we used c_m = 75 m⁻¹ for all muscles, which was based on published joint torque stiffness (Franklin and Milner 2003; Gomi and Osu 1998) and muscle force stiffness (Edman and Josephson 2007) regressions. The matrix R_base is a 2 × 2 matrix [3.18 2.15; 2.34 6.18] Nm/rad containing the baseline joint stiffness found experimentally (Gomi and Osu 1998) when the muscle activation is zero.

To examine the predicted changes in end-point stiffness, the baseline value of end-point stiffness of the limb for NF movements needs to be determined. Previous studies have demonstrated that the NF end-point stiffness is usually ∼200 N/m in the direction perpendicular to that of the movement (Franklin et al. 2004), which may be due to the interaction between stiffness and movement variability (Burdet et al. 2001, 2006; Lametti et al. 2007). The simulated end-point stiffness for each movement direction was solved subject to the constraint that the end-point stiffness perpendicular to the movement was >200 N/m. This produced stiffness ellipses qualitatively similar to those previously measured (Franklin et al. 2003a, 2004), which we used for the baseline stiffness. For the predictions in the unstable force fields, the stiffness constraint was such that the end-point stiffness perpendicular to the movement was >500 N/m. This produced end-point stiffness that compensated for the lateral instability (−300 N/m) such that the net end-point stiffness was maintained (Burdet et al. 2001; Franklin et al. 2004). The optimal muscle activation pattern (F_m) producing no change in end-point force was solved for each prediction using the fmincon function MATLAB (2007a; Mathworks) on Eq. 3. Additional constraints are specifically detailed for each prediction below.

To adapt movements in two directions simultaneously, one possible strategy for the CNS is to learn to co-contract all antagonistic pairs of muscles equally such that movements in both directions would be stabilized. To simulate this global co-contraction strategy, a single co-contraction term, which increased the activation of all muscles, was found such that the stiffness perpendicular to the movement direction was sufficient to compensate for the instability of the force field for both movement directions. Specifically, the increase in each element of F_m was constrained to be equal (ΔF₁ = ΔF₂ = ΔF₃ = ΔF₄ = ΔF₅ = ΔF₆) and occurred for adaptation to both directions of movement (ΔF_m in D1 = ΔF_m in D2).

Alternatively the CNS may be able to learn to selectively control the end-point stiffness to counteract the effect of lateral instability as in previous work (Burdet et al. 2001), but only able to learn a single end-point stiffness or set of muscle activations. To simulate this strategy, we solved for the optimal set of muscle activations that would produce the required end-point stiffness for both movement directions simultaneously. Specifically, the same increase in each element of F_m occurred for adaptation to both directions of movement (ΔF_m in D1 = ΔF_m in D2).

Finally, the possibility is that the CNS adapts end-point stiffness optimally to the instability specific to each direction of movement. This would mean that either the CNS could switch from one learned impedance model to another dependent on the movement state or learns an impedance model that can be modulated across the workspace. To simulate this strategy, the optimal muscle activations were solved independently for each movement direction. Specifically, no constraint was applied on the change in muscle force, such that independent patterns could be learned for each movement direction (ΔF_m in D1 was not constrained to be equal to ΔF_m in D2).

Experimental methods.

Ten right-handed male subjects without any known neurological problem (aged 19–34 years) participated in the study. The institutional ethics committee approved the experiments and subjects provided informed consent.

Subjects sat on an adjustable chair with harness over their upper trunk, which prevented movement of the trunk (Fig. 1D). A subject specific custom-molded thermoplastic cuff was used to restrict motion of the wrist and firmly attach the subject's hand and forearm to the manipulandum (Fig. 1E). The forearm and cuff were coupled to the handle of the parallel-link direct drive air magnet floating manipulandum (PFM; Gomi and Kawato 1996, 1997). The coupling of the forearm to the manipulandum was such that measurements could be made and movements could be performed without subjects explicitly grasping the handle. Detailed figures of the PFM and the experimental setup are found in Franklin et al. (2007b). The arm was restricted to planar motion of the shoulder and elbow, where the positive x and positive y directions correspond to the right and forward of the subject, respectively. Hand position was estimated from the PFM joint encoders (409,600 pulse/rev), and force exerted on/by the hand was measured using a force sensor (resolution 0.006 N) placed between the handle and the manipulandum's links. Both force and position signals were sampled at 500 Hz.

Subjects were instructed to perform point-to-point movements from a starting circle (1.5-cm diameter) centered at (0, 31) cm relative to the shoulder and towards two targets denoted by D1 and D2, respectively, within 600 ± 100 ms. Each target was a 2.5-cm diameter circle that was 25 cm apart from the starting point. D1 movements were performed to a target at (0, 56) cm straight-ahead of the shoulder and D2 movements towards a circle centered at (14, 52) cm, which was at 35° clockwise rotation from the first target. A cursor representing the actual hand position was beamed from a ceiling mounted projector onto an opaque cover that prevented subjects from seeing their hands or the robot. Start circle and the selected target circle were also displayed before and during each trial to indicate the movement subjects needed to make. A screen in front of subjects displayed feedback about successful and nonsuccessful movements after each trial. An unsuccessful trial was indicated by “out of target,” “too slow,” or “too fast” on a monitor placed in front of subject after the trial. All movements were recorded during the experiment, whether successful or not. There was no time constraint as to when the following trial should start, and so subjects could rest between trials. Subjects were required to bring the cursor inside the start circle before a beep sound signaled start of the movement. Each time the cursor was brought within the start circle, a trial was initiated by three beeps at 500-ms intervals. Subjects were instructed to start moving their hand at the third beep and reach the specified target circle by the fourth beep, 600 ms later. Finally, two subsequent beeps, 500 ms apart, indicated that the trial had finished.

Subjects produced movements in either a NF environment where only the robot's dynamics were felt (Burdet et al. 2006; Tee et al. 2004) or in a DF where the robot applied an unstable force field on the hand producing a force perpendicular to the movement (Fig. 1A) as defined by Eq. 1. During trials in the DF, a safety boundary was implemented when the hand deviated by >5 cm perpendicularly from the straight line between start and end targets. The safety boundary was implemented by large damping replacing the negative stiffness of Eq. 1. There was no force field inside the start and end circles.

Subjects started by familiarizing themselves with the PFM and the task by performing NF reaching movements. They had to practice on the robot at least 1 day before starting the experiment, by performing movements in both the D1 and D2 directions. Targets were randomly mixed, and subjects had to achieve 30 successful trials in each direction. The experiment was then conducted on 3 separate days for each subject. On day 1, subjects learned movements in one direction, while they performed movements towards the other direction on day 2, and on day 3 they practiced in both directions simultaneously. Subjects were separated into two groups of five to study any possible confound associated with learning one direction of movement before another. Subjects in group I performed D1 movements on day 1 and D2 movements on day 2, whereas the counterbalanced order was performed by subjects in group II.

On each of day 1 and day 2, subjects first performed 20 successful NF trials followed by a further 100 successful NF trials in which perturbations were applied to measure end-point stiffness. Then, subjects had to learn the DF by performing 100 successful trials. After this learning phase, stiffness was estimated while subjects made a further 148 successful trials. On day 3, the movement directions were selected randomly. Subjects performed trials with the same phases as on day 1 and day 2 subject to the requirement that the minimum number of successful trials was achieved in each direction. For example, in the first phase, subjects had to produce 20 successful D1 trials and 20 successful D2 trials.

The method for the stiffness estimation is described by Burdet et al. (2000). Briefly, subjects first completed 20 successful trials in whichever force field was being tested. After this, half of the additional trials were randomly selected for stiffness estimation. On each of these trials, a 300-ms displacement was applied near the midpoint of the movement in one of eight equally spaced directions, encompassing the full 360°. The displacement consisted of a smooth 100-ms ramp-up, 100-ms hold, and a smooth 100-ms ramp-down segment.

This study was performed by constraining the wrist for each subject, which was necessary to allow end-point Cartesian stiffness measurement. However, during normal object manipulation, humans are free to change the wrist or limb posture depending on the task, another method that the sensorimotor control system could use to adapt to the environment and one that may be of importance during tool manipulation. However, the focus of this work is not to explain tool-use but instead to investigate the mechanisms available to the sensorimotor control system.

Data analysis.

The hand path error (Osu et al. 2003)

$$E={\displaystyle {\int }_0^T\left|x_{\perp }\right|\left|{\dot{x}}_{\parallel }\right|dt}$$ (4)

was used to examine learning, where x_⊥ is the perpendicular component of the deviation to the straight line from the start to the target and ẋ_∥ is the parallel velocity component. The hand-path error is the area between the realized path and the straight line from start to target. It was calculated from time 0 (75 ms before crossing a hand-velocity threshold of 0.05 ms⁻¹) to time T (when curvature exceeded 0.07 mm⁻¹). If the movement deviated for >5 cm from the straight line (outside the safety boundary), it was assumed that the position of the hand followed the 5-cm parallel line until the movement end.

Previous work has shown that adaptation to unstable divergent fields occurs with no change in the end-point force unlike adaptation to velocity dependent force fields (Franklin et al. 2003a). As changes in end-point force can significantly change the end-point stiffness (Gomi and Osu 1998; McIntyre et al. 1996; Milner and Franklin 1998; Perreault et al. 2001, 2004), it is important to also examine the end-point force to determine whether any change in stiffness was produced as a byproduct of a net change in force (such as occurs after adaptation to velocity dependent force fields; Franklin et al. 2003a) or was being controlled directly. In addition, it should be mentioned that the end-point stiffness measured during movements in the NF such as in this work as well as previous studies (Burdet et al. 2001; Franklin et al. 2003a, 2007a, 2007b, 2004) will not be equivalent to the end-point stiffness measured with no external force in the static condition (Flash and Mussa-Ivaldi 1990; Gomi and Osu 1998; Mussa-Ivaldi et al. 1985; Tsuji et al. 1995). This is due to the fact that while the movement is in the NF condition, there are still forces that the subject produces to move the arm, which are different depending on the direction of movement. As we know from several studies (Franklin and Milner 2003; Gomi and Osu 1998; McIntyre et al. 1996; Perreault et al. 2001, 2004), the end-point stiffness changes as the direction and magnitude of the force changes. This means that the NF stiffness will be different for different directions of movement. To examine any differences in the end-point force after adaptation to the force fields, the end-point force was measured using the first 10 successful trials in the stiffness measurement session. The mean force in the middle of each unperturbed movement corresponding to the time of stiffness estimate (80 ms) was obtained for each trial to see if subjects changed the end-point force as a mechanism to adapt to the divergent force field.

Stiffness was computed using the perturbed trials. The average force and displacement measured during the final 80 ms of the hold period were used to estimate the end-point stiffness matrix K:

$$\left[\begin{array}{c}\Delta F_{\perp }\\ \Delta F_{\parallel }\end{array}\right]=\text{K}\left[\begin{array}{c}\Delta x_{\perp }\\ \Delta x_{\parallel }\end{array}\right].$$ (5)

The mean changes in the end-point force in displacement, in the normal and perpendicular directions ΔF_⊥, ΔF_∥, Δx_⊥, and Δx_∥ relative to the unperturbed trials, were used to estimate the components

$$\text{K}=\left[\begin{array}{cc}{K}_{\perp \perp }& K_{\perp \parallel }\\ K_{\parallel \perp }& K_{\parallel \parallel }\end{array}\right]$$ (6)

using a least square fit of Eq. 5. For instance, K_⊥∥ is the stiffness in the normal direction due to a hand displacement in the parallel direction. End-point stiffness was visualized by an ellipse (Mussa-Ivaldi et al. 1985), whose size, shape, and orientation were computed from singular value decomposition (Gomi and Osu 1998). The joint stiffness matrix R was computed from the hand space stiffness K using the relationship (McIntyre et al. 1996):

$$\text{R}={\text{J}}^T\text{KJ}+\frac{\partial {\text{J}}^T}{\partial \theta }\text{F}.$$ (7)

Data was analyzed using MATLAB (2007a; The Mathworks), while statistical analysis was performed using the general linear model in SPSS 10.0 (SPSS, Chicago, IL) to perform ANOVA. Statistical significance was considered at the 0.05 level.

RESULTS

Simulation of general and selective end-point stiffness.

Simulations were performed to examine how the CNS may adapt end-point stiffness of the arm when lateral instability is applied on the hand during planar movements in two different directions labeled as D1 and D2 (Fig. 1A). The predictions of three possible impedance learning strategies to perform successful movements to simultaneous directions were investigated. First, the CNS may learn a single strategy for both directions of movement involving globally co-contracting all muscle pairs sufficiently to produce successful movements in both directions (dashed lines in Fig. 1, B and C). However, as illustrated by the large ellipse size, this means a large physical effort to compensate for the external instability. Another possibility is that the CNS learns to selectively increase co-contraction of only the muscles required to compensate for the instability in both directions simultaneously (dotted lines in Fig. 1, B and C). This strategy would require less energy expenditure relative to the global strategy but still not predict the changes in the end-point stiffness that were found previously for a single movement direction (Burdet et al. 2001; Franklin et al. 2003a, 2004). Finally, it is possible that the CNS might be able to selectively co-contract muscles pairs to tune impedance to the environment instability for every movement direction (solid lines in Fig. 1, B and C). This strategy provides optimal adaptation to the instability but requires that the brain is able to learn independent muscle strategies for each movement direction and switch between them.

Learning is not affected by the order of learned movements.

Results were first analyzed for the two groups separately, where the subjects from group I started by training with D1 on day 1 and then with D2 on day 2 and conversely for the subjects of group II. However, statistical analysis showed that subjects from the two groups performed similarly in the same direction on day 1 and day 2 and that they also performed similarly on day 3. An ANOVA showed that there was no main effect of group for hand-path error [F(1,192) = 1.038; P = 0.309] or end-point force in either the x-axis [F(1,64) = 2.002; P = 0.162] or y-axis [F(1,64) = 0.078; P = 0.781]. Examination of the stiffness ellipses found no significant main effect of group for orientation [F(1,64) = 2.770; P = 0.101] or size [F(1,64) =1.380; P = 0.244]. Similarly, no main effect of group was found for Cartesian end-point stiffness (K) [F(1,256) = 0.110; P = 0.741] or joint stiffness (R) [F(1,256) = 0.745; P = 0.389]. Based on these results, we determined that both groups of subjects adapted in the same manner to the force fields. Therefore, data from both groups were collapsed together and the following analysis presents the results across all subjects in both groups.

Evidence and characteristics of learning.

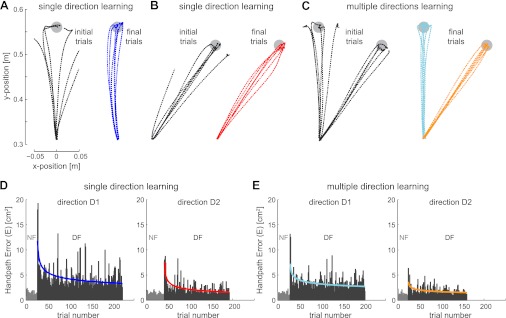
In both D1 and D2 directions, initial hand trajectories in the divergent field deviated to either side of the straight line joining start and end targets (Fig. 2, A–C), often exiting the safety zone. However, with repeated trials, trajectories became straighter and similar to those in the NF. Hand-path error, representing the area between hand movement and the straight-line between start and target points, was examined during repeated trials in NF and DF. The mean error over the subjects decreased as subjects continued to experience the DF (Fig. 2, D and E), as shown by the significant decrease of mean error between the first five and last five trials in both directions and on every day [F(1,9) = 33.670; P < 0.001]. This shows that there was learning on every day and in both D1 and D2, which was corroborated by a large improvement of the success rate, i.e., the moving average of success in 10 consecutive trials [F(1,9) = 55.561; P < 0.001].

Fig. 2.

Initial and final reaching movements in the divergent force field (DF) during the learning experiment. A: initial and final 6 trajectories in the DF for movement direction D1 when only a single direction of movement was learned. Trajectories are shown from a single representative subject for all conditions. A virtual safety zone was implemented, outside of which the force field was turned off. The safety zone was implemented on DF trials if the lateral position exceeded 5 cm relative to the straight-line joining the start and target positions. B: initial and final 10 trajectories in the DF for movement direction D2 when only a single direction of movement was learned. C: initial and final 6 trajectories for learning the DF simultaneously in both D1 and D2. D: hand-path error in null field (NF; grey bars) and DF (black bars) when learning to adapt to a single direction of movement in either movement direction D1 (left) or D2 (right). Hand-path error is calculated for all learning trials (both successful and unsuccessful) averaged across subjects. Thin colored lines represent a power-model fit to the data. E: hand-path error in the NF and DF when learning to adapt simultaneously to movement directions D1 (left) and D2 (right). While trials in the two directions were intermingled in the experiment, they have been separated in the results for clarity.

Subjects were required to produce 100 successful movements in each direction and on each day during the learning session. The average ± SD number of trials performed by subject was 197 ± 44 when learning the DF in D1 only and 151 ± 25 trials when learning in D2 only. On day 3, when both directions of movements were made, 174 ± 38 and 136 ± 20 trials were required in D1 and D2, respectively. This suggests that movements were easier in the D2 direction and that learning in the two single directions on day 1 and day 2 facilitated performance in these directions on day 3. These two observations were confirmed by ANOVA of the hand-path error. The two movements D1 and D2 were characterized by different levels of error in the five initial [F(1,9) = 19.911; P = 0.002] movements. Furthermore, for a given direction, the error level in five initial trials was different between single and multiple directions learning [F(1,9) = 6.067; P = 0.036], showing that subjects retained learning from the first 2 days going into the third day of the experiment.

However, these differences were not found after learning. The difference in hand-path error in the two movements D1 and D2 in the last five trials was not statistically significant [F(1,9) = 4.114; P = 0.073]. Moreover, the error level in the last five trials was not significantly different between single and multiple direction learning [F(1,9) = 0.673; P = 0.433]. This suggests that subjects reached the same level of adaptation to the force fields when learning in one direction only compared with learning in two directions simultaneously. Subjects had no particular difficulty in performing movement towards two directions simultaneously.

End-point force.

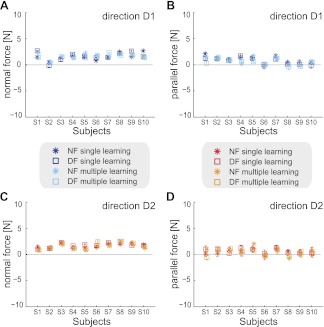
The end-point force applied by the subjects in the movements was analyzed to determine if changes in the end-point force could be responsible for changes in the measured stiffness of the limb. The mean end-point force was calculated over the interval in the middle of the movement where stiffness was estimated in the NF and DF for each subject (Fig. 3). Similar levels of end-point force were produced in the divergent field as was produced in the NF. With the use of the first 10 unperturbed trials during stiffness measurement, an ANOVA showed that there was no main effect of force field on the force applied by the subject in either the x-axis [F(1,9) = 0.116; P = 0.742] or y-axis [F(1,9) = 0.626; P = 0.449]. This indicates that any change in the end-point stiffness that was produced during adaptation to the DF was not due to a change in the end-point force. This finding was also supported by the reduction in hand-path error after learning, indicating that subjects make fairly straight movements, which would then have little change in end-point force compared with the NF movements.

Fig. 3.

End-point force was not modified during adaptation to the instability. Means and SD of the end-point force after learning for each subject, measured in the middle of the movement. A: mean force normal to the direction of the movement in direction D1. Values are shown for the NF and DF both in single and multiple directions of learning. B: mean force parallel with the direction of the movement in direction D1. C: mean force normal to the direction of the movement in direction D2. D: mean force parallel with the direction of the movement in direction D2. There was no change between force applied in NF (star) and DF (square) for either direction of movement in any experimental condition.

End-point stiffness adaptation.

To examine how subjects adapted the impedance of their limb to the instability produced by the DF, end-point stiffness was estimated mid-movement by displacing the hand relative to a prediction of the trajectory, and measuring the restoring force (Burdet et al. 2000). Figure 4 visualizes end-point stiffness geometry through stiffness ellipses, averaged across subjects, in NF and DF for both the D1 and D2 movement directions. In both cases, the stiffness ellipses after adaptation to the DF are elongated primarily orthogonal to the movement direction, along the direction of instability.

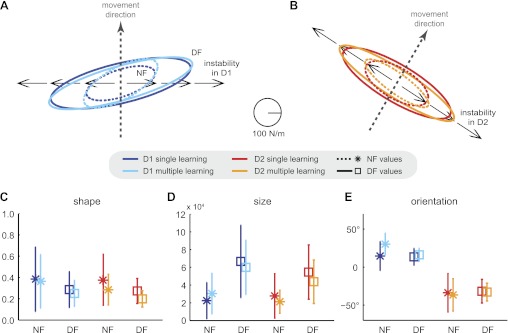
Fig. 4.

End-point stiffness increased in the direction of the instability after adaptation to the DF. A: mean end-point stiffness ellipses for movements in direction D1 in both the NF (dotted) and after adaptation to the DF (solid) while performing either only in a single direction (dark blue) or simultaneously in multiple directions (light blue). Direction of instability (black arrows) is perpendicular to the direction of movement (grey dashed line). B: mean end-point stiffness ellipses for movements in direction D2 while performing either only in a single direction (red) or simultaneously in multiple directions (green). In both conditions, the end-point stiffness increases primarily along the direction of instability. C: means and SD of the stiffness ellipse shape. D: means and SD of the size of the stiffness ellipses. E: means and SD of the stiffness ellipse orientation.

Differences across the conditions were examined by testing the geometric characteristics of the stiffness ellipse. The shape of stiffness ellipse, i.e., the ratio of smaller to larger singular values, was not significantly different in DF than in NF [F(1,9) = 4.147; P = 0.072; Fig. 4C]. The size of the ellipse (proportional to the product of the singular values) was significantly larger in DF than in NF across both movement directions [F(1,9) = 24.924; P < 0.001; Fig. 4D]. The orientation was not found to be significantly different between the NF and the DF [F(1,9) = 0.701; P = 0.424; Fig. 4E]. However, the orientation of the stiffness ellipses in the DF was significantly different in the two directions of movement D1 and D2 [F(1,9) = 86.804; P < 0.001], and tended to align with the direction of instability. Most critically, none of these features were significantly different between single or multiple direction learning [shape: F(1,9) = 2.992; P = 0.118, size: F(1,9) = 0.450; P = 0.519, and orientation: F(1,9) = 2.475; P = 0.150], indicating that similar changes occurred for adaptation to instability in either a single direction of movement or multiple directions of movement.

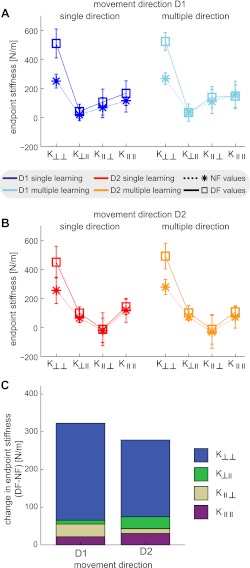
To further investigate the changes in end-point stiffness that occurred during the adaptation to environmental instability, changes in each component of the end-point stiffness matrix were examined (Fig. 5). In movement direction D1 (Fig. 5A), the DF stiffness was significantly increased relative to the NF stiffness in K_⊥⊥ [F(1,9) = 108.649; P < 0.001], but no significant differences were found between DF and NF stiffness for any of the other three terms of the stiffness matrix [K_⊥∥: F(1,9) = 0.752; P = 0.408] [K_∥⊥: F(1,9) = 2.251; P = 0.168] [K_∥∥: F(1,9) = 1.182; P = 0.305]. For all four terms of the stiffness matrix, no significant main effect was found between single or multiple direction learning [F(1,9) ≤ 2.825; P ≥ 0.127]. In movement direction D2 (Fig. 5B), there were significant increases in the DF stiffness compared with the NF stiffness both for the K_⊥⊥ [F(1,9) =197.738; P < 0.001] and K_⊥∥ [F(1,9) = 7.136; P = 0.026] elements. However, no significant difference was found in the other two elements of the stiffness matrix [K_∥⊥: F(1,9) = 0.717; P = 0.419] [K_∥∥: F(1,9) = 2.192; P = 0.173]. No significant difference was found between single and multiple direction learning [F(1,9) ≤ 1.768; P ≥ 0.216] except for K_∥∥ [F(1,9) = 13.479; P = 0.005]. However, in this case, the decrease in stiffness for the multiple direction learning was present in both the NF and DF conditions [no significant interaction effect between the field and number of movements learned; F(1,9) = 0.139; P = 0.718]. The relative changes in end-point stiffness after adaptation that occurs in all components of the stiffness matrix were examined (Fig. 5C). Overall, the largest increase in stiffness in the DF occurred in the K_⊥⊥ component of the stiffness matrix in both directions of movement. This component directly acts to compensate for the added environmental instability.

Fig. 5.

Changes in the end-point stiffness matrix components after adaptation to the unstable environmental dynamics. For comparisons across the 2 movement directions, the stiffness matrix has been solved for relative to the movement direction (see materials and methods for description). A: end-point stiffness components in the NF (stars) and DF (squares) for movement direction D1. Lines have been draw joining the four components in the same condition (dark blue: single direction) (light blue: multiple directions) for clarity. B: end-point stiffness components in the NF (stars) and DF (squares) for movement direction D2 (red: single direction) (orange: multiple directions). C: changes in the end-point stiffness after adaptation to the DF (data replotted from A and B but collapsed across the conditions). Each bar indicates the total change (K_DF − K_NF) in the end-point stiffness after adaptation in movement directions D1 and D2. Color indicates the stiffness component responsible. In both movement directions almost all of the change in the end-point stiffness occurred in the K_⊥⊥ component, compensating directly for the added environmental instability.

Previous work has shown that subjects compensated almost “exactly” for the DF, such that the net stiffness (end-point stiffness − environmental instability) was similar to the stiffness in the NF (Burdet et al. 2001; Franklin et al. 2004). In movement direction D1, the net stiffness K_⊥⊥ in the DF was not significantly different from that in the NF [F(1,9) = 2.992; P = 0.118] similar to previous results. However, in movement direction D2, the net stiffness K_⊥⊥ in the DF was significantly smaller than that in the NF [F(1,9) = 44.233; P < 0.001]. This may be related to the significant increase found in the K_⊥∥ component after adaptation to the force field in this direction, which also contributes to stabilize the limb-environment interaction. F(1,9)

Joint stiffness adaptation.

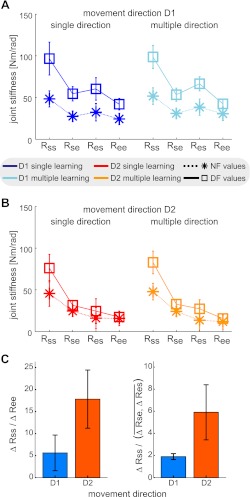
Joint stiffness was computed from end-point stiffness to examine the contribution of different muscle pairs. The contributions of muscle pairs to each element of the joint stiffness matrix can be seen in (McIntyre et al. 1996). In particular, the single joint shoulder and elbow muscles only influence the diagonal components, whereas the biarticular muscles influence all four components of the matrix. In direction D1 (Fig. 6A), we found significant increases in all components of the joint stiffness matrix [R_ss: F(1,9) = 92.156; P < 0.001] [R_se: F(1,9) = 82.949; P < 0.001] [R_es: F(1,9) = 64.395; P < 0.001] [R_ee: F(1,9) = 46.135; P < 0.001] but no significant effect of single or multiple directions of movement for any of the four terms [F(1,9) ≤ 4.362; P ≥ 0.066]. In direction D2 (Fig. 6B), we found significant increases in three of the components of the joint stiffness matrix [R_ss: F(1,9) = 136.457; P < 0.001] [R_se: F(1,9)=19.323; P = 0.002] [R_es: F(1,9) =18.833; P = 0.002]. However, there was no significant change in the elbow joint stiffness [R_ee: F(1,9) = 1.487; P = 0.254], suggesting that the adaptation in the two directions of movement was produced by different patterns of joint stiffness. Again in D2, there was no significant effect of single or multiple directions of movement for any of the four terms [F(1,9) ≤ 5.030; P ≥ 0.052].

Fig. 6.

Joint stiffness demonstrates that different adaptation strategies were used in each movement direction. A: joint stiffness components in the NF (stars) and DF (squares) for movement direction D1. Lines have been draw joining the four components in the same condition for clarity. B: joint stiffness components in the NF (stars) and DF (squares) for movement direction D2. C: ratios of the change in shoulder joint stiffness (R_ss) relative to either the change in elbow joint stiffness (R_ee; left plot) or the change in cross joint stiffness (R_se and R_es; right plot). Ratios are smaller for adaptation to the DF in movement direction D1 rather than movement direction D2. This indicates that the limb stiffness was independently modulated for the instability in each direction of movement.

The results of the joint stiffness suggested that two different strategies were used to adapt to instability in the two different directions of movement. In D1, the biarticular muscles may have been predominately utilized, resulting in increases across all four components of the joint stiffness matrix. In contrast, in movement D2, the increase was mainly found in the shoulder joint stiffness, suggesting that most of the adaptation was produced by co-contraction of the shoulder joint muscles (although some contribution of biarticular muscles would be required to increase the cross joint terms of the stiffness matrix). To test the theory that different patterns of joint stiffness were produced in each of the two movement directions, the ratios of the change in shoulder stiffness relative to that of the cross-joint stiffness and elbow stiffness were examined (Fig. 6C). The ratio of the change in shoulder (R_ss) to elbow (R_ee) stiffness was larger in D2 than in D1 [F(1,9) = 5.889; P = 0.038]. This would suggest that there was a larger contribution to the limb stiffness produced by shoulder joint muscles than by elbow joint muscles in D2 compared with D1. Similarly the ratio of the change in shoulder stiffness (R_ss) to cross joint stiffness (R_es and R_se) was much larger in D2 than D1 [F(1,9) = 8.933l; P = 0.015]. This suggests that there was a larger contribution to the limb stiffness produced by single shoulder joint muscles than by double joint muscles in D2 compared with D1. Importantly, there was no significant difference between learning a single direction of movement and learning multiple directions of movement for either the shoulder to elbow ratio [F(1,9) = 0.652; P = 0.440] or shoulder to cross joint ratio [F(1,9) = 0.930; P = 0.360]. These results demonstrate that adaptation to the instability in each of the two directions of movement was produced by different changes in the joint stiffness, independently controlled for each movement direction. Moreover, these differences in the method of adaptation for each movement direction were not changed by performing multiple directions of movement.

DISCUSSION

Subjects adapted to two directions of environmental instability, each of which was associated with a single direction of movement. On the first two days, subjects learned to adapt to each direction separately, and on the third day, subjects switched randomly between the two directions of movement. End-point stiffness of the arm was estimated in the NF before learning and after learning the DF. In both directions of movement the end-point stiffness increased in the direction of instability with little or no change in the perpendicular direction. No difference was found between performing either only a single direction of movement or simultaneously performing movements to two different targets. The joint stiffness demonstrated that different patterns of adaptation were used for adaptation to each direction of movement.

The initial learning in each direction was performed on 2 consecutive days with a counterbalanced order of the two target directions between two groups of subjects. This was followed on the third day by performing movements to both targets randomly intermixed. The results showed that the two groups learned similarly for each direction, although movements were performed on the first day for one group and on the second day for the other group. This suggests that learning to compensate for the instability in one direction neither helped nor hindered the learning of compensating for the instability in the other direction. In other words, there was no evidence that compensating for the instability transferred to the other movement direction as has been seen for stable force fields (Donchin et al. 2003; Thoroughman and Shadmehr 2000). This also indicates that impedance control learning does not generalize in trajectory-based coordinates, as both force fields had instability perpendicular to the direction of movement. This might suggest that impedance control, like force control (Shadmehr and Mussa-Ivaldi 1994), is learned in joint coordinates. The results also show that there was no interference between the learning of the two different unstable force fields while earlier studies for stable force fields showed strong interference (Brashers-Krug et al. 1996; Caithness et al. 2004). This was not entirely unexpected as the two fields were separately presented for two different trajectories for which limited interference was previously found (Thoroughman and Taylor 2005). However, even in the case of smoothly varying stable force fields, some interference has been shown as the angle between the two directions becomes larger (Donchin et al. 2003; Thoroughman and Shadmehr 2000).

On the other hand, training in the two directions on the first 2 days resulted in better initial performance in both directions on the third day. Although only the generalization from single directions to multiple directions of movement was examined, these findings suggest that learning to compensate for instability in a movement was retained to some degree and could be used to successfully perform this movement on later days. Furthermore, the subjects were able to make the synthesis of these two different force field models so as to successfully switch from one movement to the next using the suitable control. Not only was there no evidence of interference between the two movements, but the subjects were able to combine the two learned movements in an efficient, movement-specific manner.

This study investigated adaptation to an unstable force field amplifying lateral deviations, when reaching movements were performed to two directions separated by 35°. In contrast, previous studies (Burdet et al. 2001; Franklin et al. 2007a; Takahashi et al. 2001) had investigated the adaptation to unstable or unpredictable dynamics along only a single direction of movement. Compensating for instability in different directions requires the CNS to coordinate the muscles carefully, taking into account changing moment arms and the nonlinear properties of muscles (Murray et al. 2000, 1995), although we should note that this is true even for a single movement of any reasonable length. However, the results show for the first time that subjects are able to learn to perform movements in unstable dynamics in several directions simultaneously.

The simulations (Fig. 1) proposed three possible methods of adaptation to two directions of movement. The first model suggested that, unlike previous studies examining only a single direction of movement (Burdet et al. 2001; Franklin et al. 2003a, 2007a; Franklin et al. 2004), selective control of the end-point stiffness for two different instability directions might not be possible to learn. Instead subjects might be required to globally co-contract their arm muscles to produce enough stiffness to compensate for both directions of movement. This would have produced an increase in all four terms of the end-point stiffness matrices, which was not found. Instead, the major increase in the end-point stiffness was produced along the direction of instability. The second model proposed that subjects would still be able to learn the optimal end-point stiffness of the limb, reducing the metabolic cost, but that only a single model of the required impedance could be learned. This would mean that the same change in joint stiffness and muscle activity would be produced in both directions of movement. The results clearly demonstrated that movements in each direction in the DF were associated with significantly different changes in joint stiffness and muscle activity. Therefore, this model is also demonstrated to be incorrect. The third model, which proposed selective control of end-point stiffness independently for each direction, is supported by the results. Clear differences in the change in joint stiffness were found for each direction of movement. Moreover, there were no significant differences between the mechanisms of adaptation to multiple directions of movement and single directions of movement. Subjects were instead able to produce the appropriately tuned end-point stiffness (without superfluous stiffness increase in stable directions) for each direction of movement and switch between these.

The simulations used to explain and predict the changes in limb stiffness only consider feedforward control of muscle activation as a method of modulating stiffness. However, reflex excitability changes during adaptation to environments (Akazawa et al. 1983; Asai et al. 2009; Damm and McIntyre 2008; Doemges and Rack 1992a,b; Krutky et al. 2010; Perreault et al. 2008). Moreover there is some evidence for reflex contributions to changes in end-point stiffness during movement (Franklin et al. 2007a). An alternative explanation therefore is that the adaptation to the instability occurs through modulation of the long latency feedback pathways, which have been shown to be sensitive to the task goals (Kurtzer et al. 2008; Pruszynski et al. 2008). Short-latency reflex responses could contribute to the limb impedance but tend to modulate very little with task (Pruszynski et al. 2008) and occur too early to contribute to our measured stiffness [short latency contributions to EMG: 20–50 ms (Lewis et al. 2006; Matthews 1991; Pruszynski et al. 2008, 2011); force responses delayed by a further 25 ms (Ito et al. 2004)]. However, this alternative explanation does not change the findings of this study. First, reflex actions, similar to feedforward muscle co-activation, cannot produce different changes in joint stiffness for the same perturbations unless a task-dependent reflex modulation, independent for each movement direction, was learned. Thus the simulations based on muscle actions are still useful for interpreting the results of this study. Secondly, several studies have shown that large increases in muscle activation relative to the NF occur during adaptation to unstable force fields in movement (Franklin et al. 2003a, 2007a). Thus we predict that both reflexive and intrinsic adaptation contribute to the modification of end-point stiffness in this study.

The results clearly indicate that distinct control over the end-point stiffness in the DF was produced for each direction of movement. Subjects were able to switch between these depending on the movement direction. How was this learning represented computationally within the brain? One possibility is that subjects gradually formed a single feedforward model of the external dynamics, i.e., a mapping from a state space to muscle activation, compensating for the force and instability encountered during movements in any direction. Such a model would be roughly equivalent to models that map the state space of the limb to end-point force or joint torque for stable adaptation (Donchin et al. 2003; Hwang et al. 2003; Thoroughman and Shadmehr 2000). Using information about the intended motion velocity, the CNS may be able to infer the direction of instability that is normal to the movement. Simulations have shown that it is indeed possible to learn a model to deal with environmental instability valid in multiple directions based on state information (Kadiallah 2008). Alternatively, the CNS might acquire two distinct dynamic models and switch between them using contextual information (Haruno et al. 2001; Wolpert and Kawato 1998). Evidence for such switching depending on contextual information has been shown for certain conditions (Howard et al. 2008; Nozaki et al. 2006; Osu et al. 2004).

In summary, these results show that humans are able to adapt to instability in multiple movement directions and can alternate between these movements with good performance. This simultaneous adaptation occurred despite the fact that instability in each movement direction required different compensation in terms of the limb stiffness. Within each movement, the correct pattern of muscle activation was produced such that the required impedance to compensate for the environment instability was achieved tuned independently for each direction of instability. This finding suggests that minimal extraneous stiffness or co-contraction was produced in each movement, which could indicate that the sensorimotor control system finds a solution with a minimal metabolic cost. This ensured a stability margin similar to movements in the NF condition. This may explain how humans are able to learn to work with tools requiring the control of instability in a range of directions.

GRANTS

A. Kadiallah was supported by a scholarship from the Algerian ministry of higher education for Ph.D. studies. This research was supported by the Wellcome Trust, the EU FP7 VIACTORS project and the Strategic Research Program for Brain Sciences “Brain Machine Interface Development” by the Ministry of Education, Culture, Sports, Science and Technology of Japan.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).