Modulation of inhibitory strength and kinetics facilitates regulation of persistent inward currents and motoneuron excitability following spinal cord injury

Abstract

Spasticity is commonly observed after chronic spinal cord injury (SCI) and many other central nervous system disorders (e.g., multiple sclerosis, stroke). SCI-induced spasticity has been associated with motoneuron hyperexcitability partly due to enhanced activation of intrinsic persistent inward currents (PICs). Disrupted spinal inhibitory mechanisms also have been implicated. Altered inhibition can result from complex changes in the strength, kinetics, and reversal potential (E_Cl⁻) of γ-aminobutyric acid A (GABA_A) and glycine receptor currents. Development of optimal therapeutic strategies requires an understanding of the impact of these interacting factors on motoneuron excitability. We employed computational methods to study the effects of conductance, kinetics, and E_Cl⁻ of a dendritic inhibition on PIC activation and motoneuron discharge. A two-compartment motoneuron with enhanced PICs characteristic of SCI and receiving recurrent inhibition from Renshaw cells was utilized in these simulations. This dendritic inhibition regulated PIC onset and offset and exerted its strongest effects at motoneuron recruitment and in the secondary range of the current-frequency relationship during PIC activation. Increasing inhibitory conductance compensated for moderate depolarizing shifts in E_Cl⁻ by limiting PIC activation and self-sustained firing. Furthermore, GABA_A currents exerted greater control on PIC activation than glycinergic currents, an effect attributable to their slower kinetics. These results suggest that modulation of the strength and kinetics of GABA_A currents could provide treatment strategies for uncontrollable spasms.

spasticity, including exaggerated stretch reflexes (hyperreflexia) and muscle hypertonia, often develops after chronic spinal cord injury (SCI) (Young 1994) and many other central nervous system disorders (e.g., multiple sclerosis, stroke). In many cases, it can significantly affect the quality of life. Chronic incomplete SCI results in reduced supraspinal drive to some spinal neurons and tonic facilitation of others (Heckman 1994). While spinal circuitry caudal to injury is preserved, impaired spinal inhibition is commonly observed (Neilsen et al. 2007). Moreover, α-motoneurons (α-MN) providing the final common motor output become hyperexcitable. Specifically, they show prolonged self-sustained afterdischarge in response to brief sensory stimuli, thereby contributing to uncontrollable muscle spasms (Gorassini et al. 2004; Norton et al. 2008).

Brain stem-derived serotonin (5-HT) is an important modulator of spinal motoneuron excitability. Activation of 5-HT₂ receptors enhances intrinsic low-voltage-activated persistent inward Ca²⁺ and Na⁺ currents (PICs) that produce plateau potentials and self-sustained firing (SSF) (Harvey et al. 2006a, 2006b; Hounsgaard et al. 1988; Li et al. 2007). PIC activation substantially amplifies both synaptic excitation and inhibition and is critical for the dynamic transformation of synaptic inputs to motoneuron frequency code (Hultborn et al. 2003; Lee and Heckman 2000; Prather et al. 2001). Inhibitory synaptic inputs can exert considerable control over α-MN discharge by regulating intrinsic PIC activation/deactivation, especially due to a shunting effect when the synapses colocalize with PIC channels (Bui et al. 2008b).

Despite a loss of brain stem-derived 5-HT with chronic SCI, PICs are enhanced due to compensatory upregulation of spontaneously active 5-HT₂ receptors (Murray et al. 2010). This PIC enhancement can cause motoneuron hyperexcitability and uncontrollable spasms. Impairment in many spinal inhibitory pathways has been implicated in spasticity (Boorman et al. 1996; Katz 1999; Mazzocchio and Rossi 1997) after chronic SCI and may be related to reduced GABAergic and glycinergic inhibitory neurotransmission/reception (Shapiro 1997). Specifically, GABA_A receptor expression appears more sensitive to supraspinal sources of 5-HT (Sadlaoud et al. 2010) than glycinergic receptors, suggesting a potential therapeutic value of modulating GABA_A-mediated inhibition for SCI-induced spasticity. Indeed, pharmacological management of spasticity often includes GABA_A receptor agonists [e.g., diazepam (Gracies et al. 1997)]. Alternatively, the reduced efficacy of inhibition of motoneurons after chronic SCI could result from a depolarized chloride reversal potential (E_Cl⁻) due to downregulation of potassium chloride cotransporter (KCC2) such that increasing inhibitory conductance may actually intensify hyperexcitability under some conditions (Boulenguez et al. 2010). Therefore, it is important to evaluate a combination of factors that ultimately restores inhibitory regulation of motoneurons. Since PICs are enhanced after chronic SCI, it is essential to understand how GABA_A and glycine receptor-mediated inhibition regulate 5-HT-activated PICs and motoneuron discharge and to examine the role that changes in E_Cl⁻ play in this regulation. We addressed this exploration with a computational approach. We first developed a computational model for a SCI motoneuron with a hyperexcitable dendrite (mediated by enhanced PICs). We then examined the effect of concomitant changes in inhibitory strength (conductance) and E_Cl⁻ on PIC activation/deactivation and the associated SSF. Using a simple network model of the α-MN and its recurrent inhibition, we examined the role of realistic dendritic GABA_A and glycinergic inhibition in PIC control. Our analyses indicate that dendritic inhibition can effectively regulate PIC activation/deactivation and that increasing inhibitory strength can compensate for moderate E_Cl⁻ depolarization. Moreover, inhibitory strength is proportional to its decay time constant (τ_decay), and GABAergic inhibition with larger τ_decay than glycine exerted greater control on PICs. We suggest that therapeutic measures targeting spinal GABAergic inhibition may be effective strategies for spasticity management.

MATERIALS AND METHODS

SCI α-MN model.

A two-compartment motoneuron model (with soma and dendrite) was developed to reproduce the firing properties resulting from exaggerated dendritic plateau potentials reported in SCI motoneurons (Bennett et al. 2001). This formulation allowed dendritic confinement of plateau-causing PICs and investigation of the regulation of plateau development and termination by dendritic inhibition, unlike a previous single-compartment model (Graham et al. 2005). The somatic compartment includes the action potential (I_Na, I_Kdr)-and medium afterhyperpolarization (I_CaN, I_KCa)-producing currents (see Fig. 1A). The dendritic compartment includes the plateau-generating low-threshold L-type calcium (I_CaL) and persistent sodium currents (I_NaP), together termed PIC (Li and Bennett 2003). Although anatomical evidence exists for the dendritic distribution of Ca(v) channels mediating the I_CaL, dendritic localization of I_NaP is based on indirect evidence (Li et al. 2004a). Based on the time dependency of plateau activation in normal cat motoneurons, it has been suggested that I_CaL activates with a time constant in the order of 100 ms (cf. Powers 1993; Schwindt and Crill 1984). We noted that a faster time constant of 40 ms as used in the Booth and Rinzel motoneuron model (cf. Booth et al. 1997) also generated the expected firing characteristics, such as counterclockwise current-frequency (I-f) hysteresis and bistability, and produced a reasonably well-matched slope of secondary range frequencies in response to ramp current injection as observed in rodent SCI motoneurons (Bennett et al. 2001; Li et al. 2004a). A slower activation with a time constant of 100 ms did not significantly alter these characteristics (simulation not shown). Hence, we chose the faster 40-ms time constant. Since I_NaP also contributes to a negative slope region in the current-voltage (I-V) relationship obtained during a slow voltage ramp (Li and Bennett 2003; Li et al. 2004a), further suggesting a dendritic origin of these currents, we assumed a similar activation time constant for I_NaP with a relatively slower inactivation time constant. The activation of I_NaP is likely faster than what is assumed in our model (cf. Li et al. 2004a), although there are no definitive measures. In other simulations (not shown), we have observed that even instantaneous activation of I_NaP merely results in nominal speeding up of plateau development. The inactivation of I_NaP was set in the order of seconds (τ_NaP^h = 1 s) as seen in other mammalian neurons (Rybak et al. 2004). This slow inactivation allows very slow firing before spike termination during the down ramp of somatic triangular ramp current injection (Li and Bennett 2003). Reflecting measurements in SCI motoneurons (Li and Bennett 2003), the voltage threshold for I_NaP activation was set lower than that for I_CaL (θ_NaP^threshold = −48 mV, θ_CaL^threshold = −39 mV). Choosing a lower activation threshold for I_NaP allowed slow subthreshold acceleration of membrane potential before spike onset (Li and Bennett 2003). The choice of maximal conductance values for PICs was based on their relative ratio (∼1.772) in SCI motoneurons (Li et al. 2004a). Recently, Li and Bennett (2007) showed that the nimodipine-sensitive I_CaL activates a subset of sustained potassium currents, perhaps of dendritic origin, in intact and SCI motoneurons. Therefore, we modeled a sustained L-type calcium-activated potassium current (SK_L) in the dendritic compartment. Maximal conductance for the SK_L currents was chosen on the basis of the emergent firing characteristics in the computational model and ensured that the amplitude of SK_L currents was a smaller fraction of the I_CaL (see Li and Bennett 2007). We further note that the dendritic SK_L currents could serve as an important intrinsic mechanism for limiting PICs (Venugopal et al. 2010), although the present study focuses on the effect of inhibitory synaptic inputs. We excluded other hyperpolarization-dependent potassium currents such as the transient potassium current (I_A) and mixed inward cation current (I_h) in the current model. Neonatal studies suggest that spinal motoneurons show a significant I_h (Kjaerulff and Kiehn 2001), and SCI-induced increases in I_h lead to elevated resting potential (cf. Li et al. 2007). Although this may reduce the action potential threshold and cause early recruitment of the motoneuron (cf. Kiehn et al. 2000), available evidence suggests that elimination of I_h does not alter estimations of 5-HT-induced Ca²⁺ PICs after SCI (Li et al. 2007). However, this may not preclude a potential interaction between I_h and I_NaP that activates near spike threshold. The depolarization provided by I_h activation may promote NaP-mediated slower repetitive firing (cf. Li and Bennett 2003), but it is unlikely that such activity could induce spasm like high-frequency discharge in motoneurons (e.g., Li et al. 2004a). With the above considerations, the two-compartment motoneuron model reproduces salient firing properties seen in SCI motoneurons such as self-sustained firing, counterclockwise I-f hysteresis, delay in plateau/PIC activation, membrane bistability, and slow acceleration of somatic membrane potential before spike onset (Bennett et al. 2001; Li and Bennett 2003; Li et al. 2004a).

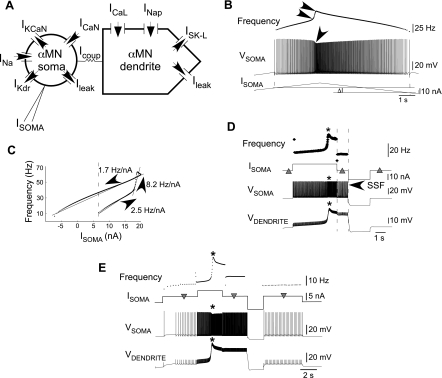
Fig. 1.

Spinal cord injury (SCI) motoneuron model schematic and firing properties. A: model schematic showing the intrinsic and synaptic currents of the α-motoneurons (α-MN). Currents included in the model are the spike-generating fast sodium (I_Na) and delayed rectifier-type potassium currents (I_Kdr), medium afterhyperpolarization (mAHP)-generating N-type calcium (I_CaN) and N-type calcium-activated potassium currents (I_KCaN), leak potassium currents essential for stable resting potential (I_leak), L-type calcium (I_CaL) and persistent sodium (I_NaP) persistent inward currents (PIC), sustained L-type calcium-activated potassium current (I_SK-L), α-MN soma-injected current (I_soma), and α-MN soma and dendrite coupling current (I_coup). B: voltage (V_soma) and frequency responses to somatic injection (I_soma) of triangular ramp current. Single arrow on V_soma denotes spike acceleration, and double arrowheads on frequency denote a nonlinear increase in instantaneous spike frequency. I_soma needed to initiate discharge exceeds the value required to sustain discharge (ΔI), which is self-sustained (Bennett et al. 2001). C: injected current-frequency (I-f) relationship showing counterclockwise hysteresis and primary, secondary, and tertiary frequency ranges. The I-f slopes in the 3 frequency ranges are indicated. PIC activation accounts for the frequency augmentation in the secondary range and supports self-sustained α-MN discharge (frequencies to left of dashed vertical line). D: initial zero I_soma (left triangle) produces no α-MN discharge. A following depolarization activates dendritic plateau/PICs; somatic spikes concomitantly speed up, and firing frequency jumps up (note asterisks on V_dendrite, V_soma, and frequency traces). A subsequent return of I_soma to zero (middle triangle) results in self-sustained firing (SSF) due to the sustained plateau (demarcated by dashed vertical lines). A subsequent hyperpolarization turns the plateau off and returns somatic and dendritic voltages to rest as I_soma again returns to zero (right triangle). E: I_soma without PIC activation (left inverted triangle) produces low-frequency firing; a subsequent greater I_soma activates PICs (near asterisk). Sustained PIC activation produces higher firing frequencies when I_soma is returned to its previous smaller value (middle inverted triangle). A subsequent hyperpolarization inactivates PICs, restoring low frequencies after I_soma returns to its original smaller value (right inverted triangle).

A previous report on rat triceps surae motoneuron morphology indicates that the dendrites constitute >90% of the total surface area (Chen and Wolpaw 1994). Hence, the ratio of somatic area to the total surface area of the motoneurons was set to p_area = 0.1 (also see Booth et al. 1997). The soma-dendrite electrotonic coupling conductance g_coup = 0.1 mS/cm² was chosen to provide fairly weak coupling that was essential for the generation of bistable membrane behavior (Booth and Rinzel 1995; Booth et al. 1997). Reports on SCI-induced changes in motoneuron morphology are inconsistent and injury and motoneuron specific (Bose et al. 2005; Gazula et al. 2004; Kitzman 2005). Moreover, potential effects of morphology changes on PIC-mediated SSF were shown to be rather weak in a similar SCI motoneuron model (Kurian et al. 2011). Therefore, we did not consider changes in the above morphometric parameters as factors integral for PIC-induced hyperexcitability.

The α-MN model equations follow conductance-based Hodgkin-Huxley formalism. The complete list of equations for the model is provided in the Appendix.

Synaptic inputs.

The recurrent inhibitory input to α-MN consists of GABA_A and glycinergic components. The decay kinetics of GABA_A currents are approximately three to four times slower (Jonas et al. 1998) (also see Venugopal et al. 2007). The synaptic currents follow conductance-based formalism (see Appendix). The recurrent inhibitory synaptic current (I_RC) consists of GABAergic and glycinergic currents (see results). The decay time constant of the GABA_A current was ∼3.6 times longer than that of glycinergic currents (GABA_A ∼50 ms, glycine ∼14 ms) (Jonas et al. 1998). Although the co-contribution of GABA_A and glycinergic currents in the recurrent inhibition of α-MNs is fairly well established (Cullheim and Kellerth 1981; Jonas et al. 1998), the relative contribution of these currents is yet uncertain. Various values have been reported previously for their relative contributions toward the dual inhibitory postsynaptic currents in motoneurons (Cullheim and Kellerth 1981; Schneider and Fyffe 1992). We assumed similar maximal conductances for both currents in this study, although an ∼30% variability in the relative contributions still yielded the observed differential effects on PIC-mediated motoneuron firing due to GABA_A and glycine inhibition (see results). The values for maximal conductances were similar to experimentally determined values and those used in previous modeling studies (Bui et al. 2008a; Maltenfort et al. 2004).

The excitatory cholinergic input from α-MN to a recurrent Renshaw cell (RC) was modeled with a 10–90% rise time of 1 ms and a decay time constant of 5 ms as noted in neonatal rat spinal cord recordings (Dourado and Sargent 2002). The magnitude of the maximal conductance was chosen to yield amplitudes of excitatory postsynaptic current in the order of 0.1–0.3 nA (Dourado and Sargent 2002).

The firing behavior of the RC model shows a linear steady-state I–f relationship (Ross et al. 1976) obtained using a simpler single-compartment model with action potential-generating currents (I_Na and I_Kdr) along with a leak potassium current (I_leak).

Protocols and simulations.

The voltage and frequency responses of the α-MN were studied during somatic current injection (I_soma) similar to intracellular current injection experiments (Bennett et al. 2001; Hounsgaard et al. 1988; Turkin et al. 2010). Three types of current injection protocols were used for the motoneuron: 1) triangular ramp I_soma (5 nA/s), 2) ramp I_soma (0.7 nA/s), and 3) pulse I_soma, with values indicated in the corresponding figures (see results). The I_pool train stimulation of RC in Fig. 4 had a 250-ms pulse width, 500-ms interpulse duration, and 10-nA pulse height. Tonic inhibition was created by setting the presynaptic voltage-dependent variables s_GABAA and s_glycine to constant values between 0 and 1 (see Appendix). The excitatory synaptic activation in Fig. 6 consisted of a tonic constant dendritic current I_ex = 0.4 nA. Model simulations were performed using XPPAUT software (Ermentrout 2002), and MATLAB was used to plot results. Instantaneous frequencies were determined using custom-written scripts in MATLAB.

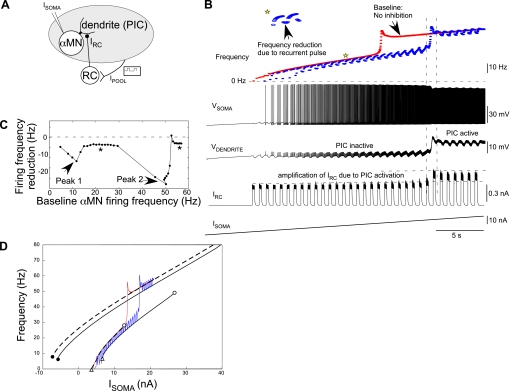
Fig. 4.

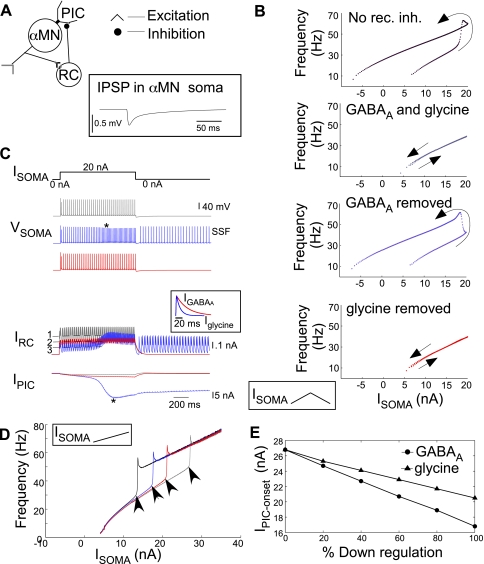
PIC-mediated amplification of dendritic inhibition. A: schematic representation of a classic experimental protocol mimicked to examine the effects of dendritic inhibition on α-MN discharge and PIC activation. I_pool represents the excitatory drive to the inhibitory Renshaw cell (RC) neuron posited via antidromic activation of the motoneuron pool. An RC neuron activated by I_pool provides the inhibitory input to the α-MN. B: V_soma and V_dendrite during an increasing ramp I_soma.. The instantaneous frequencies (blue) show acceleration concomitant with the dendrite turning ON. RC-induced inhibitory synaptic current in the α-MN (I_RC) is amplified as V_dendrite/PIC turns ON. Inset (top) shows a magnified view of frequency reduction during an I_pool pulse (down and up arrows denote onset and offset, respectively). The baseline α-MN discharge frequencies (α-MN with no inhibition) are shown in red. C: RC-mediated reduction in α-MN frequencies plotted against baseline firing frequencies of α-MN with no inhibition. Inhibition is more effective in reducing α-MN frequencies near motoneuron recruitment (peak 1) and during PIC activation (peak 2). Note the otherwise nominal and constant frequency reduction (asterisks). D: black solid and dashed lines are steady-state α-MN frequencies with and without recurrent inhibition, respectively, with superimposed I-f responses from B (baseline frequencies in red, those during recurrent pulsatile inhibition in blue). I_soma values corresponding to α-MN recruitment, PIC onset, and PIC offset are denoted by white triangles, white circles, and black circles, respectively.

Fig. 6.

Effect of selective increases in GABAergic and glycinergic inhibition on the deactivation of synaptically activated plateau/PIC and SSF. A: schematic of the α-MN-RC network construct. I_ex is a tonic dendritic excitation of the α-MN. B: excitatory input (duration marked by open horizontal bars) activated dendritic plateau (asterisk) and induced soma firing. Plateau activation and SSF persisted after removal of the excitatory input under default levels of GABA_A and glycinergic inhibitory conductances. C: 2-fold increase in GABA_A conductance (horizontal black line) completely deactivated the plateau and inhibited SSF. D: 2-fold increase in glycinergic conductance did not completely deactivate the plateau, and SSF ensued. V_den, dendritic voltage.

RESULTS

Model α-MN mimics SCI motoneuron firing.

Chronic SCI enhances plateau potentials and SSF in many sacrocaudal rat motoneurons (Li et al. 2004b). These responses were associated with exaggerated PICs (Bennett et al. 2001; Li and Bennett 2003; Li et al. 2004a). During somatic current injection, the current-firing frequency (I-f) relationship showed PIC-mediated counterclockwise hysteresis, a response that contrasted a linear I-f relationship observed after acute spinal transections where plateaus were also rarely observed (Bennett et al. 2001). These changes in motoneuron firing properties following chronic spinalization were reproduced in the physiologically realistic motoneuron model (Fig. 1A). Figure 1B illustrates the spike discharge during a somatic triangular ramp current (I_soma) injection (see somatic membrane voltage, V_soma). Spike acceleration occurred (arrow) during the rising phase of I_soma, and SSF was noted during the falling phase [see legend; similar to Fig. 2B in Bennett et al. (2001)]. Spike acceleration marks PIC activation, and persistently active PICs produce the SSF. The I-f relationship in Fig. 1C shows a counterclockwise hysteresis (Bennett et al. 2001) and is fit with three piecewise linear segments corresponding to a primary range (slope 2.5 Hz/nA) before PIC activation, a steeper secondary range (slope 8.2 Hz/nA) during PIC activation, and a shallow tertiary range (slope 1.7 Hz/nA) after PICs are fully activated. The sustained PIC activation giving rise to tertiary frequencies mediates the SSF frequencies to the left of the dashed vertical line in Fig. 1C. Steady-state analyses detailed in the following section validate these results and determine the threshold values for injected current I_soma at which discharge begins (I_recruitment), PIC activates (I_PIC-onset) and deactivates (I_PIC-offset), and the conditions for producing SSF. SSF exists in the I_soma range between I_PIC-offset and I_recruitment provided I_PIC-offset < I_recruitment. As further illustrated in Fig. 1D, a depolarizing I_soma evokes discharge and eventually activates PICs (asterisk) and the dendritic plateau (see V_dendrite). The plateau sustains even after I_soma returns to zero (see V_dendrite between dashed vertical lines). This noninactivation of plateau/PICs supports the self-sustained discharge in V_soma. A hyperpolarizing pulse returns the somatic and dendritic voltages to rest, suggesting plateau/PIC deactivation [as also noted in SCI rat (Bennett et al. 2001) and decerebrate cat motoneurons (Hounsgaard et al. 1988)]. Thus SSF produces bistability wherein stable resting and firing states coexist for the same I_soma value based on whether PICs are activated. PICs can mediate another bistable behavior wherein two stable firing states (low and high frequencies) coexist for the same input, as illustrated in Fig. 1E. In this example, somatic current injection (left inverted triangle) initially produced low-frequency firing. Higher I_soma activated dendritic plateau/PICs (asterisk), resulting in higher firing frequencies after I_soma returned to its original lower value. Again, a subsequent hyperpolarization reset the dendrite and deactivated PICs, returning discharge frequencies to their original lower values. Hence, PICs mediate amplification of depolarizing inputs, in turn controlling motoneuron discharge frequencies (Hultborn et al. 2003).

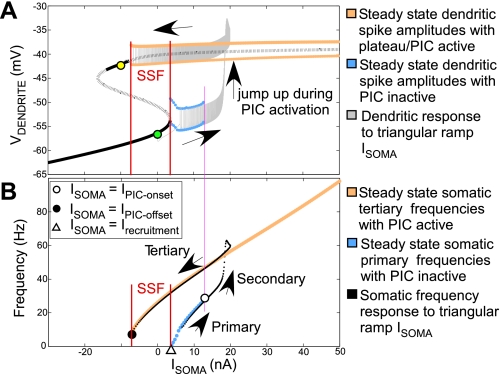
Fig. 2.

Analyses of PIC activation/deactivation and SSF. A: steady-state dendritic current-voltage curve (black) with solid and dotted lines denoting stable and unstable steady states, respectively. Red vertical lines denote range of I_soma in which SSF exists. Pink line marks I_soma value at PIC onset (I_PIC-onset). An overlay of the dendritic response to triangular ramp I_soma is shown in gray (ramp begins at green circle and ends at yellow circle). Arrows show direction of change in V_dendrite during the triangular ramp I_soma. B: I-f curves: steady-state frequencies are show in blue and orange. White triangle marks I_soma value at motoneuron recruitment (I_recruitment); white circle corresponds to dendritic PIC onset. An overlay of I-f response to triangular ramp I_soma (black dotted curve) shows the transitory secondary frequencies during dendritic plateau development. The termination of tertiary frequencies (black circle) marks deactivation of plateau at I_soma = I_PIC-offset. SSF exists in the range of I_soma values between I_PIC-offset and I_recruitment provided I_PIC-offset < I_recruitment. Arrows show directionality of frequency changes during triangular ramp I_soma.

Steady-state analyses of motoneuron firing properties.

Steady-state analysis is useful to determine the theoretical input thresholds for the various regimes of motoneuron firing, namely, the primary, secondary, and tertiary ranges, using dynamical systems methods (cf. Ermentrout and Terman 2010). To do so, we present the theoretical steady-state of the dendritic voltage in response to somatic current injections that is experimentally intractable and has not been specifically dealt with in similar previous modeling reports (Booth et al. 1997; Elbasiouny et al. 2006); however, see Booth and Rinzel (1995). Figure 2A shows the steady-state dendritic I-V relationship (black). The lower branch of the steady-state curve corresponds to “low” dendritic states without plateau/PIC activation, whereas the upper branch corresponds to “high” dendritic states with plateau/PICs activated. A switch from the low to high states occurs during PIC activation. The steady-state dendritic spike amplitudes in the low state are demarcated by upper and lower blue curves. These spikes are produced by I_soma-induced somatic discharge in the primary frequency range. Similarly, in the high state, steady-state dendritic spikes have amplitudes demarcated by upper and lower orange curves. Such spikes would occur in the tertiary somatic frequency range. This steady-state diagram further reveals bistability underlying SSF, in which the low stable resting states and high tertiary firing states coexist between the red vertical lines. This description of model bistability corresponds well with the fully bistable motoneurons described by Lee and Heckman (1998). The following analysis provides a theoretical basis for experimentally estimated current thresholds for PIC onset and offset (Lee and Heckman 1998), further validating the model.

A dendritic response to triangular ramp I_soma is shown by the overlay (in black) on the steady-state diagram (ramp begins at the green circle and ends at the yellow circle). When this response is observed in conjunction with the soma frequency responses (Fig. 2B), we note that the dendritic voltage begins at an initial resting state. As increasing ramp I_soma recruits the motoneuron (i.e., somatic firing begins), dendritic spikes driven by primary range somatic spikes are observed. At the end of the primary range (marked by the pink vertical line), dendritic voltage begins to jump up (PIC onset) and a plateau develops, giving way to secondary range soma firing. V_dendrite reaches the upper branch of the S-shaped curve marking full activation of plateau/PICs, and dendritic spikes corresponding to tertiary somatic frequency range are seen. As the triangular ramp I_soma decreases, dendritic spikes eventually terminate at a hyperpolarizing I_soma value marking PIC offset. Thus the transition of dendritic voltage from a low to a high state during PIC activation results in the secondary range soma firing.

Figure 2B shows steady-state primary (blue) and tertiary (orange) α-MN somatic frequencies corresponding to the steady-state low and high dendritic states, respectively. The I_soma value corresponding to the white triangle marks α-MN recruitment, henceforth called I_recruitment. The primary frequency range continues up to an I_soma value at which PIC onset occurs (white circle intersecting with pink vertical line). This value is referred as I_PIC-onset. In the tertiary range, deactivation of PICs is marked by the black circle, and the corresponding I_soma is called I_PIC-offset. SSF exists for the range of I_soma values between I_PIC-offset and I_recruitment provided I_PIC-offset < I_recruitment. Overlay of the I-f response (in black) to a triangular ramp I_soma shows transitory secondary frequencies during dendritic plateau development/PIC activation. Since PICs appear to activate in a threshold-dependent manner for I_soma > I_PIC-onset, an “all-or-none” PIC activation underlies the I-f hysteresis (Venugopal et al. 2009a, 2009b). In the following section, we examine the effect of dendritic inhibition on PIC activation/deactivation and SSF.

Dendritic inhibition modulates PIC activation/deactivation and SSF.

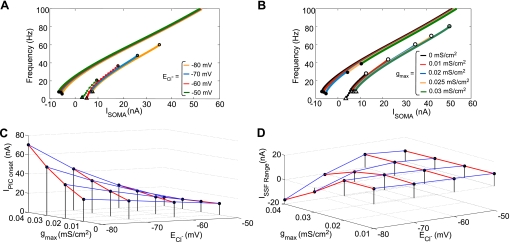
Prolonged motoneuron discharge in response to brief sensory stimulation of chronic SCI human subjects suggests PIC activation and lack of inhibitory regulation of the same (Norton et al. 2008). Therefore, we examined the effect of steady (tonic) dendritic inhibition on PIC onset (activation), offset (deactivation), and SSF by examining changes in I_PIC-onset, I_PIC-offset, and I_recruitment. The steady-state α-MN I-f curves now consist of primary and tertiary frequencies before and after PIC activation, respectively; the transitory secondary range is absent. First, to mimic an effect of KCC2 downregulation, we depolarized E_Cl⁻ from a default value of −80 mV to −50 mV in steps of 10 mV. Steady-state I-f curves in Fig. 3A indicate that depolarizing shifts in E_Cl⁻ considerably reduced I_PIC-onset and facilitated PIC activation. However, there were only nominal, nonmonotonic changes in current threshold for PIC offset (I_PIC-offset) and the recruitment current (I_recruitment) such that the range for SSF given by I_{SSF range} = I_recruitment − I_PIC-offset was virtually unaffected. Alternatively, we tested the effect of impairment in inhibition on PIC onset and SSF by varying the strength of inhibition given by the maximal inhibitory synaptic conductance (g_max) at the default E_Cl⁻ value. Figure 3B illustrates that increases in inhibitory conductance prevented early onset of PICs by producing significant increases in I_PIC-onset. Starting with a default g_max = 0.02 mS/cm², decreases in g_max produced nominal changes in I_PIC-offset and I_{SSF range} similar to those from depolarizing shifts in E_Cl⁻ noted earlier. However, increasing inhibitory conductance significantly reduced SSF due to large increases in I_PIC-offset wherein a 50% increase in g_max completely abolished SSF. Since SCI can alter both the strength of inhibition (g_max) and E_Cl⁻, we next studied the interaction of these two factors in regulating I_PIC-onset and I_{SSF range}. In the three-dimensional plot in Fig. 3C, the iso-g_max lines (blue) show that the efficacy of a given maximal inhibitory conductance in controlling PIC onset is reduced as E_Cl⁻ depolarizes. Nonetheless, the iso-E_Cl⁻ lines (red) show that increasing inhibitory conductance can counter this effect by increasing PIC onset threshold due to shunting. However, note that at a higher depolarized E_Cl⁻ value of −50 mV, inhibition switches to excitation wherein increases in inhibitory conductance would facilitate PIC activation (right-most red line in Fig. 3C). We note, however, that the value of E_Cl⁻ = −50 mV is more depolarized than suggested by depolarizing shifts in E_Cl⁻ based on studies in neonatal rats with SCI (Boulenguez et al. 2010). Therefore, whether such E_Cl⁻ values are physiologically attained following SCI and could be associated with spasticity remains speculative. The three-dimensional plot in Fig. 3D shows that SSF exists, and the iso-g_max lines (blue) and iso-E_Cl⁻ lines (red) indicate that the I_{SSF range} is roughly invariant at small g_max (0.01 and 0.02 mS/cm²) or at higher depolarized E_Cl⁻ levels of −60 and −50 mV. However, the I_{SSF range} significantly decreases and SSF is eliminated at larger g_max values (0.03 and 0.04 mS/cm²) with E_Cl⁻ close to control levels (−80 and −70 mV). In summary, dendritic inhibition regulates PIC onset and offset; increases in inhibitory strength can compensate for moderate depolarizing E_Cl⁻ shifts by limiting PIC activation (a shunting effect) and SSF.

Fig. 3.

Effect of changes in inhibitory synaptic conductance (g_max) and chloride reversal potential (E_Cl⁻) on PIC activation and SSF. A and B: steady-state I-f curves with respect to changes in E_Cl⁻ and maximal strength of g_max, respectively. I_recruitment, I_PIC-onset, and I_PIC-offset are denoted by white triangles, white circles, and black circles, respectively. In A, g_max is set to a default value of 0.02 mS/cm² while E_Cl⁻ is varied as indicated; in B, E_Cl⁻ is set to a default value of −80 mV while g_max is varied as indicated. C: PIC onset threshold I_PIC-onset for different values of E_Cl⁻ and g_max. Each red line is an iso-E_Cl⁻ line. Note that increasing g_max increases I_PIC-onset with larger effects at lower E_Cl⁻ values; at E_Cl⁻ = −50 mV, however, there is a nominal decrease in I_PIC-onset with increasing g_max. D: range of injected current values for which SSF exists for various combinations of g_max and E_Cl⁻, where I_{SSF range} = I_recruitment − I_PIC-offset. Each red line is an iso-E_Cl⁻ line. Gray surface indicates the boundary above which SSF exists. Increasing the strength of inhibition eliminated SSF at E_Cl⁻ values of −80 and −70 mV; at further depolarized E_Cl⁻, the I_{SSF range} was nominally reduced as the strength of inhibition increased.

Model offers insights into PIC mediated amplification of synaptic inhibition.

Next, we investigated the effect of physiologically realistic dendritic inhibitory inputs (both GABA and glycine) on PIC regulation and α-MN discharge. We modeled the recurrent inhibition of α-MN, since it employs both GABA_A and glycinergic receptors on α-MNs (Schneider and Fyffe 1992) whose expressions might be altered after SCI (Bareyre and Schwab 2003). Renshaw cells (RC) mediating recurrent inhibition are the only known interneurons that are directly activated by α-MN discharge and provide regulatory feedback of motoneuron activity. The location of Renshaw synapses overlaps the probable sites of dendritic PIC channels, suggesting a potential interaction of PICs with Renshaw inputs to set α-MN excitability (Bui et al. 2008a; Fyffe 1991).

Recurrent inhibition was evoked in the α-MN by activating the model RC by a train of current pulses (I_pool) mimicking a classic experimental approach (Hultborn et al. 2003) (see schematic in Fig. 4A). I_pool represents the excitatory drive to RC posited from the motoneuron pool antidromically activated by peripheral nerve stimulation. The model α-MN refers to a test motoneuron in the pool, driven by somatic ramp current injection during simultaneous RC activation by I_pool. In this configuration the excitation from α-MN to RC was set to zero, since this input is negligible compared with antidromic stimulation. The α-MN somatic and dendritic voltages and the corresponding firing frequencies are shown in Fig. 4B (cf. Bennett et al. 1998). The postsynaptic recurrent inhibitory current (I_RC) is also shown. Increasing I_soma leads to PIC activation and a concomitant amplification of I_RC (demarcated by horizontal dashed lines). The α-MN frequencies undergo reductions during RC inhibition (see inset at asterisk). These somatic frequency reductions relative to the baseline α-MN firing (i.e., motoneuron firing in the absence of inhibition; see red curve in Fig. 4B) are plotted against baseline α-MN frequencies in Fig. 4C. The frequency reductions showed two peaks corresponding to primary baseline frequencies near recruitment (peak 1) and secondary baseline frequencies during PIC development (peak 2); they were otherwise nominal and constant (see asterisks). Thus RC inhibition was stronger in the primary range near motoneuron recruitment and in the secondary range during PIC development, as in experimental results described by Granit et al. (1960) and Hultborn et al. (2003), respectively.

Analyses of the effect of inhibitory inputs on motoneuron discharge.

How does inhibition produce amplification of frequency reductions? To address this question, we utilized the steady-state α-MN frequency responses to somatic current injection, as described earlier, in the presence and absence of tonic dendritic inhibition. Figure 4D shows steady-state I-f curves for the primary (lower black curves) and tertiary (upper black curves) frequencies with (solid line) and without (dashed line) inhibition. The corresponding I_recruitment (white triangles), I_PIC-onset (white circles), and I_PIC-offset (black circles) values are marked. Inhibition increases the α-MN recruitment and PIC onset thresholds (compare white triangles and white circles with and without inhibition). The frequency responses to somatic ramp current during pulsatile RC inhibition (blue curve) and the baseline frequencies with no inhibition (red curve) illustrated in Fig. 4B are also overlaid on the steady-state frequency curves. Near recruitment between the two white triangles, the α-MN is toggling between a firing state while RC inhibition is off and a subthreshold resting state (zero frequency) during pulsatile RC inhibition. The emergent frequency reductions underlie peak 1 in Fig. 4C. As I_soma increases beyond baseline I_PIC-onset (left white circle), PICs are recruited and secondary range α-MN frequencies are initiated (upswing in red curve). These frequencies eventually approach the baseline tertiary frequencies (upper dashed curve). However, with pulsatile RC inhibition (blue curve), appearance of secondary frequencies is delayed, since the amplified I_RC shunts PICs as they are recruited. The emergent frequency reductions during this delay (between upswing of red and blue curves) underlie peak 2 in Fig. 4C. Increasing I_soma nonetheless produces incremental PIC recruitment in between the pulsatile RC inhibition, which eventually fully activates and results in the tertiary range of α-MN discharge.

GABAergic inhibition exerts greater control on PICs than glycinergic inhibition.

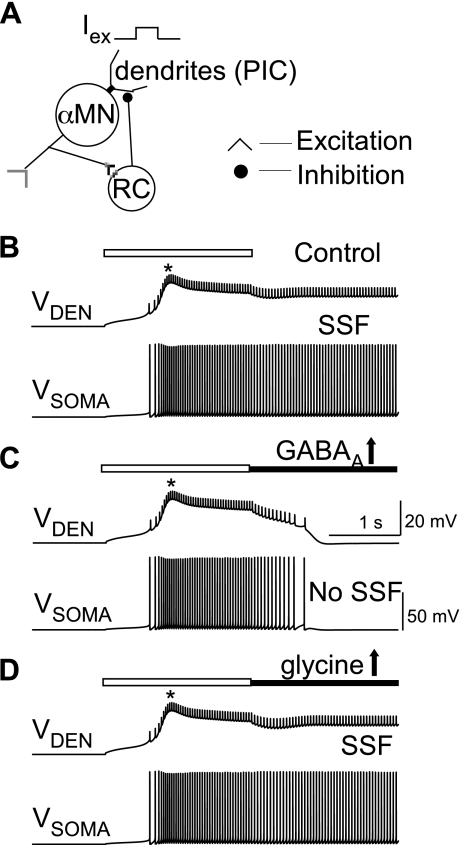
GABA_A and glycinergic postsynaptic potentials and receptors on motoneurons show differential plasticity after SCI that is sensitive to loss of brain stem-derived 5-HT (Sadlaoud et al. 2010). Moreover, GABA_A inhibition shows greater efficacy than glycine in the control of motoneuron firing as reported for brain stem motoneurons (Russier et al. 2002). Therefore, we tested the hypothesis that GABA_A inhibition exerts greater control on PICs than glycine. The network construct consisted of a self-inhibitory α-MN-RC circuit wherein RC inhibition varied in proportion to motor activity, as expected under normal physiological conditions. The schematic of this circuit is shown in Fig. 5A. The inset shows an inhibitory postsynaptic potential produced in the α-MN by a single RC spike (cf. Hamm et al. 1987; McCurdy and Hamm 1994; Van Keulen 1981). We specifically tested the selective influence of GABA_A and glycinergic inputs on PIC onset that leads to I-f hysteresis and SSF. In Fig. 5B, the I-f response to a triangular ramp I_soma shows hysteresis in the absence of recurrent inhibition (black trace). The hysteresis is absent when both GABAergic and glycinergic components of recurrent inhibition are present, suggesting a lack of PIC activation (gray trace). Selective removal of GABAergic inhibition allowed PIC activation, although with a delay (blue trace). In contrast, the I-f hysteresis/PIC activation was suppressed following selective removal of glycinergic inhibition alone. The mechanism of differential control of PIC activation by GABA_A and glycine currents is illustrated in Fig. 5C. An I_soma pulse was injected under control conditions (with both glycine and GABA_A inhibitory currents present, gray traces) or with selective elimination of GABA_A (blue) or glycine (red) currents. V_soma traces show PIC activation resulting in SSF with removal of GABAergic currents. GABA_A currents produced greater average inhibition compared with glycine as shown by the dashed lines on I_RC traces under the three conditions. The slower decay rate of GABA_A currents (see inset) helped maintain a greater average inhibition during ongoing firing of RC and prevented PIC activation. To compare the effect of removal of GABA_A currents vs. glycine on I_PIC-onset, we injected a higher maximal I_soma (ramp up to 35 nA) and examined the I-f responses (Fig. 5D). Removal of GABA_A currents reduced the I_PIC-onset considerably more than removal of glycinergic inputs. Furthermore, selective downregulation of GABA_A currents produced greater reductions in I_PIC-onset than similar decreases in glycinergic currents (Fig. 5E). Alternatively, a twofold increase in the strength of GABA_A conductance terminated the PIC-mediated SSF induced by a constant dendritic excitation, whereas a similar increase in glycinergic conductance failed to terminate the plateau and SSF (see Fig. 6). These results demonstrate the benefit of enhancing GABA_A conductance in controlling motoneuron hyperexcitability.

Fig. 5.

Differential effect of GABA_A and glycinergic currents on PIC onset and I-f hysteresis. A: schematic of the self-inhibitory α-MN-RC network where RC activity varies in proportion to α-MN activity as normally expected. Inset shows an inhibitory postsynaptic potential (IPSP) in the motoneuron due to a single RC spike. B: α-MN I-f responses during triangular ramp I_soma. Top to bottom: counterclockwise hysteresis marking PIC activation under default condition with no RC inhibition; RC inhibition with both GABA_A and glycinergic currents suppressed hysteresis, resulting in a linear I-f response; removal of GABA_A currents uncovered I-f hysteresis; and removal of glycine did not result in I-f hysteresis. No rec. inh., no recurrent inhibition. C: responses to pulse I_soma (20 nA) under 3 simulated conditions of ongoing recurrent inhibition by both GABA_A and glycine RC currents (gray traces), with GABA_A currents removed (blue traces), and with glycinergic currents removed (red traces). Asterisk on I_PIC and V_soma marks PIC activation resulting in SSF in the absence of GABAergic inhibition. Dashed lines 1, 2, and 3 show average I_RC for the respective cases; inset shows the relative kinetics of GABA_A (I_GABAA) and glycine currents (I_glycine). D: I-f responses to increasing ramp I_soma up to 35 nA under the 4 different conditions in B shows the different I_PIC-onset (arrowheads) in the respective cases. E: changes in I_PIC-onset plotted against percent selective downregulation of recurrent GABA_A and glycine currents.

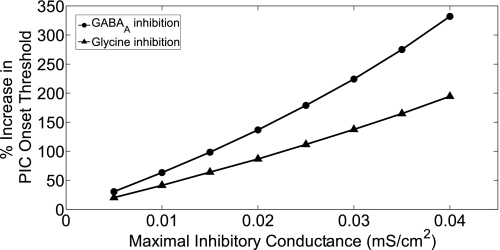
To illustrate the importance of decay kinetics of inhibition that produced relatively greater efficacy of GABA_A inhibition, we maintained a tonic firing rate (∼100 Hz) of the inhibitory neuron, independent of motoneuron firing. For a given maximal inhibitory conductance (g_max), the τ_decay was set to 50 and 14 ms to simulate GABAergic and glycinergic decay kinetics, respectively. The threshold I_soma required to activate dendritic PICs (i.e., I_PIC-onset) was determined for various conductance values. The percent increase in I_PIC-onset values with the different strengths of inhibition with respect to no inhibition was computed as shown in Fig. 7. We note that the percent increase in I_PIC-onset required to activate PICs was greater for GABA_A inputs than for glycine at all conductance values, and this efficacy improved as the strength of inhibition (conductance value) increased. On the basis of these observations, modulation of GABA_A kinetics offers a novel target for spasticity management.

Fig. 7.

Comparison of the efficacy of slower decay kinetics of GABA_A inhibition at similar strengths of glycinergic inhibition in increasing the activation threshold of PICs. The percent increase in PIC onset threshold (I_PIC-onset) for a range of conductance values of GABA_A (circles) and glycinergic (triangles) inputs with respect to the control value of I_PIC-onset with no inhibitory input are illustrated. The inhibitory inputs to the α-MN occurred at a fixed rate of ∼100 Hz.

DISCUSSION

Our results demonstrate the dependence of PIC activation on the strength and decay kinetics of dendritic inhibition, suggesting that modulation of these factors could restore inhibitory regulation of PICs following SCI. Consistent with the recent evidence for increased motoneuron excitability due to depolarizing shifts in E_Cl⁻ (Boulenguez et al. 2010), we noted that depolarized E_Cl⁻ also weakened the ability of dendritic inhibition to control PIC activation. However, increasing the inhibitory conductance produced a compensatory effect for moderate E_Cl⁻ depolarization. Although depolarized E_Cl⁻ can impart excitatory actions to GABA_A/glycine synapses, this action depends on the separation of the locations of the synapses and excitatory current (Boulenguez et al. 2010; Jean-Xavier et al. 2007). Provided that GABA_A/glycine synapses spatially overlap with PIC channels, inhibitory synaptic conductance continues to exert control over PIC activation and inactivation following E_Cl⁻ depolarization. Moreover, the strength of this inhibitory effect was proportional to the decay time constant of inhibitory inputs. In particular, a slower decay time constant resulted in greater average inhibition and enhanced the shunting effect of inhibition. Furthermore, increases in maximal inhibitory conductance augmented this effect of the decay time constant.

We utilized and analyzed realistic recurrent α-MN inhibition as a model system to investigate the role of dendritic inhibition in PIC control. Results of simulating recurrent inhibition were consistent with previous physiological studies, and model analyses provided further insight into recurrent inhibitory control of motoneuron discharge. Within the primary range of α-MN discharge frequencies, recurrent inhibition is most effective in controlling recruitment. After recruitment and with increasing excitation, recurrent inhibition produces only nominal reductions in firing frequencies, consistent with assessments based on effective synaptic current (Lindsay and Binder 1991). This predominant effect on motoneuron recruitment could limit neuronal activity to the most strongly activated motor pools by shutting off weakly activated synergists during coactivation of multiple motoneuron pools (cf. Brooks and Wilson 1958). In the secondary range during PIC activation, PIC-mediated amplification of RC currents and RC-induced α-MN frequency reductions were observed (also see Bui et al. 2008b; Hultborn et al. 2003). The increased driving force of inhibition produced by depolarizing PICs (Bui et al. 2008b) further delayed frequency transitions into the secondary range that significantly extended the primary range, similar to data shown in Fig. 2B in Bennett et al. (1998), further validating the model. Once PICs were fully activated, increasing recurrent inhibition resulted in PIC deactivation (Bui et al. 2008b) and termination of SSF. As we demonstrate in Fig. 3, A and B, and Fig. 4D, tonic inhibition extends the primary range. In a case where the PICs are activated at or below the threshold of discharge and the motoneurons do not show a primary range, as observed by Bennett et al. (1998) and Lee and Heckman (1998), the presence of ongoing inhibitory drive such as a recurrent inhibition early during recruitment would tend to delay PIC activation. It would introduce a regime of lower firing frequencies corresponding to the primary range and in turn allow a more graded PIC activation. This can be seen in Fig. 4D (blue vs. red trace). With respect to the steady-state diagrams shown in Fig. 2, the lack of a primary range implies that there are no stable frequencies (as shown by blue circles) near the lower branch of the S-shaped curve. Introducing tonic inhibition could uncover such stable primary range frequencies, depending on the balance of synaptic excitation and inhibition received by the motoneuron.

An important limitation of our model is its representation of the motoneuron pool with one model motoneuron and the Renshaw cell pool with one single-compartment interneuron. Due to the use of this simple model design, replication of asynchronous input to either motoneuron or Renshaw cell was not attempted. However, within the constraints of this model, we have simulated conditions that are suitably realistic with regard to strength of input between motoneuron and Renshaw cell. Accordingly, synaptic strengths and neuron characteristics were set to match parameters for Renshaw responsiveness and recurrent inhibitory conductance of the cited published studies (e.g., Dourado and Sargent 2002; Maltenfort et al. 2004; Ross et al. 1976). Under these conditions, each motoneuron spike produced at most two Renshaw spikes, as shown in Fig. 5, rather than the high-frequency burst associated with antidromic motor volleys in classic studies of Renshaw cells. At these rates, inhibitory synaptic current in the motoneuron from the Renshaw cell (Fig. 5C) is small and consistent with the study by Maltenfort et al. (2004) and previous determinations of recurrent inhibitory current such as Lindsay and Binder (1991). Importantly for this study, the time course of development of PICs is relatively slow (Carlin et al. 2000; Li and Bennett 2003), with a time constant of 40 ms, such that PIC activation is relatively insensitive to small variations in spike timing of the Renshaw cell. Therefore, as is evident in Fig. 5C, PIC development occurs over several cycles of motoneuron and Renshaw cell discharge. Given this relative insensitivity to spike timing, the most critical features of the model for the present purpose concern the magnitude of inhibitory conductance and current produced in motoneurons by Renshaw cells. Functions of recurrent inhibition in which spike timing is important, such as a potential role in motoneuron synchrony, on the other hand, clearly could not be explored in any meaningful way with the current model. We further demonstrated the importance of inhibitory kinetics in PIC control. GABAergic inhibition showed greater efficacy in controlling both PIC activation and deactivation thresholds than glycine. Greater efficacy of GABA_A inhibition over glycine in the control of motoneuron firing has been reported in brain stem motoneurons (Russier et al. 2002). Our analyses show that the relatively slower decay rate increased the average inhibition with GABA_A currents compared with glycinergic currents, delineating a mechanism that can underlie such greater efficacy. Interestingly, the decay rate of GABA_A (and not glycinergic) currents was significantly greater following neonatal SCI (Sadlaoud et al. 2010). Moreover, plasticity in GABA_A receptor expression on motoneurons was markedly dependent on supraspinal influences, particularly to serotonergic projections that potentially activate PICs, whereas glycinergic plasticity was independent of such influences. Although the mechanisms underlying this plasticity are unknown, these reports indicate the potential for altering GABA_A receptors and their kinetics.

Prior studies have associated impaired GABAergic neurotransmission/reception with pathological hyperexcitability (Kakinohana et al. 2006; Knopp et al. 2008). However, there is little direct evidence for such changes leading to α-MN hyperexcitability and hyperreflexia following SCI. Downregulation of GABA_A receptors may partially underlie such impairment (e.g., Adams and Hicks 2005; Bareyre and Schwab 2003; Shapiro 1997). Alternatively, altered intrinsic properties such as downregulation of the KCC2 cotransporter can reduce the driving potential of inhibition and lead to α-MN hyperexcitability. Although E_Cl⁻ remains well below spike threshold following SCI (Boulenguez et al. 2010), E_Cl⁻ depolarization may reduce the excitation required for activity if the sources of excitation and inhibition have separate loci (Boulenguez et al. 2010; Jean-Xavier et al. 2007). Dendritic sources of inhibition colocalized with PICs, like recurrent inhibition, would continue to oppose PIC activation and assist PIC inactivation as shown presently, although these actions weaken with E_Cl⁻ depolarization. Consequently, modulation of dendritic inhibition, particularly with slower kinetics, would retain the ability to counter some intrinsic sources of increased motoneuron excitability following SCI, such as E_Cl⁻ depolarization and increased PICs through constitutive activity of 5-HT₂ receptors (Murray et al. 2010). Other potential effects produced by KCC2 downregulation, such as loss of rate-dependent depression of monosynaptic reflexes (Boulenguez et al. 2010), might not be countered as effectively by dendritic inhibition.

The role of inhibitory pathways in functional recovery following SCI is complex and poorly understood. Despite the potential for downregulation of inhibitory receptors to contribute to motoneuron hyperexcitability, as noted above and from observations supporting this possibility after neural injury and disease (Katz and Pierrot-Deseilligny 1998), evidence has been presented for increased inhibition following SCI (Shefner et al. 1992). Moreover, application of the GABA_A receptor antagonist bicuculline improved locomotor performance in spinalized cats (Khristy et al. 2009; Robinson and Goldberger 1986). Khristy et al. (2009) recently showed either increases or decreases in the levels of GABA_A receptor subunit expression on motoneurons in spinalized rats dependent on muscle functional identity; these levels were restored to their control values with step training. The changes in inhibition shown in these various studies imply adaptive mechanisms following SCI that remain to be identified. As demonstrated in this study, the potential of dendritic inhibition to control PIC activation following injury suggests new avenues for development of antispastic drugs, spinal neurotechnology applications, and perhaps other therapeutic measures as these mechanisms come to be understood.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant R01-NS054282 to R. Jung and funds from the Barrow Neurological Foundation to T. M. Hamm.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

APPENDIX

The α-MN somatic and dendritic membrane potentials follow the standard Hodgkin-Huxley formalism with the following current balance equations:

$$\begin{array}{c}{C}_{\text{m}}\frac{\text{d}{V}_{\text{soma}}}{\text{d}t}=-I_{\text{leak}}-I_{\text{Na}}-I_{\text{Kdr}}-I_{\text{CaN}}-I_{\text{KCaN}}-I_{\text{coup}}+I_{\text{soma}}\\ C_{\text{m}}\frac{\text{d}{V}_{\text{dendrite}}}{\text{d}t}=-I_{\text{leak}}-I_{\text{CaL}}-I_{\text{Nap}}-I_{\text{SK-L}}-I_{\text{coup}}-I_{{\text{GABA}}_{\text{A}}}-I_{\text{glycine}}\end{array}$$

where C_m = 1 μF/cm² as for most cells. See Fig. 1A for description of currents.

The ion channel gating kinetics of α-MN soma are governed by the following equations:

$$\begin{array}{l}\frac{\text{d}{h}_{\text{Na}}}{\text{d}t}=\frac{h_{\text{Na}\infty }\left(V_{\text{soma}}\right)-h_{\text{Na}}}{{\tau }_{\text{Na}}\left(V_{\text{soma}}\right)};{\tau }_{\text{Na}}\left(V_{\text{soma}}\right)=\frac{30}{\left\{e^{\frac{\left[V_{\text{soma}}-\left(-50\right)\right]}{15}}+e^{\frac{\left[V_{\text{soma}}-\left(-50\right)\right]}{16}}\right\}}\hfill \\ \frac{\text{d}{n}_{\text{Kdr}}}{\text{d}t}=\frac{n_{\text{Kdr}\infty }\left(V_{\text{soma}}\right)-n_{\text{Kdr}}}{{\tau }_{\text{Kdr}}\left(V_{\text{soma}}\right)};{\tau }_{\text{Kdr}}\left(V_{\text{soma}}\right)=\frac{7}{\left\{e^{\frac{\left[V_{\text{soma}}-\left(-40\right)\right]}{40}}+e^{\frac{\left[V_{\text{soma}}-\left(-40\right)\right]}{50}}\right\}}\hfill \\ \frac{\text{d}{m}_{\text{CaN}}}{\text{d}t}=\frac{m_{\text{CaN}\infty }\left(V_{\text{soma}}\right)-m_{\text{CaN}}}{{\tau }_{\text{CaN}}^m};\frac{\text{d}{h}_{\text{CaN}}}{\text{d}t}=\frac{h_{\text{CaN}\infty }\left(V_{\text{soma}}\right)-h_{\text{CaN}}}{{\tau }_{\text{CaN}}^h}\hfill \end{array}$$

where τ_CaN^m = 4 ms and τ_CaN^h = 40 ms are the activation and inactivation time constants, respectively, for N-type calcium currents similar to those described by Booth et al. (1997).

The dendritic ion channel gating kinetics are as follows:

$$\frac{\text{d}{m}_{\text{CaL}}}{\text{d}t}=\frac{m_{\text{CaL}\infty }\left(V_{\text{dendrite}}\right)-m_{\text{CaL}}}{{\tau }_{\text{CaL}}^m};\frac{\text{d}{m}_{\text{NaP}}}{\text{d}t}=\frac{m_{\text{NaP}}\left(V_{\text{dendrite}}\right)-m_{\text{NaP}}}{{\tau }_{\text{NaP}}^m};\frac{\text{d}{h}_{\text{NaP}}}{\text{dt}}=\frac{h_{\text{NaP}\infty }\left(V_{\text{dendrite}}\right)-h_{\text{NaP}}}{{\tau }_{\text{NaP}}^h}$$

where the activation time constant for L-type calcium current is τ_CaL^m = 40 ms (Booth et al. 1997). The activation time constant of persistent sodium currents was chosen similar to L-type calcium, τ_NaP^m = 40 ms, whereas the inactivation time constant was in the same order of magnitude as in other mammalian neurons with τ_NaP^h = 1,000 ms (also see methods).

The intracellular calcium concentration in the somatic compartment (Ca_soma) is modeled to depend on the high-voltage-activated CaN calcium currents, whereas that in the dendritic compartment (Ca_dendrite) is modeled to depend explicitly on L-type Ca²⁺ PIC (also see methods), as follows:

$$\begin{array}{c}\frac{{\text{dCa}}_{\text{soma}}}{\text{d}t}=f\left(\alpha I_{\text{CaN}}-K_{\text{Ca}}{\text{Ca}}_{\text{soma}}\right)\\ \frac{{\text{dCa}}_{\text{dendrite}}}{\text{d}t}=f\left(\alpha I_{\text{CaL}}-K_{\text{Ca}}{\text{Ca}}_{\text{dendrite}}\right)\end{array}$$

where the constant f = 0.01 is the percentage of free to bound calcium, α = 0.009 mol·C⁻¹·μm⁻¹ converts the total calcium current in each compartment to Ca²⁺ concentration, and K_Ca = 2 ms⁻¹ is the calcium removal rate, assumed to be similar in both compartments [values are similar to those reported by Booth et al. (1997)].

Somatic currents are as follows:

$$\begin{array}{c}{I}_{\text{leak}}=g_{\text{L}}\left(V_{\text{soma}}-V_{\text{K}}\right)\\ I_{\text{Na}}=g_{\text{Na}}{\left[m_{\text{Na}\infty }\left(V_{\text{soma}}\right)\right]}^3{h}_{\text{Na}}\left(V_{\text{soma}}-V_{\text{Na}}\right)\\ I_{\text{Kdr}}=g_{\text{Kdr}}{\left(n_{\text{Kdr}}\right)}^4\left(V_{\text{soma}}-V_{\text{Kdr}}\right)\\ I_{\text{CaN}}=g_{\text{CaN}}{\left(m_{\text{CaN}}\right)}^2{h}_{\text{CaN}}\left(V_{\text{soma}}-V_{\text{Ca}}\right)\\ I_{\text{KCaN}}=g_{\text{KCaN}}\frac{{\text{Ca}}_{\text{soma}}}{0.2+{\text{Ca}}_{\text{soma}}}\\ I_{\text{coup}}=g_{\text{coup}}\frac{\left(V_{\text{dendrite}}-V_{\text{soma}}\right)}{P_{\text{area}}}\end{array}$$

where the maximal ionic conductances are (in mS/cm²) g_L = 0.51, g_Na = 80, g_Kdr = 100, g_CaN = 14, and g_KCaN = 6. The ratio of somatic area to the total surface area of the motoneurons is p_area = 0.1, the soma-dendrite coupling conductance is g_coup = 0.1 mS/cm²(see methods), and the ionic reversal potentials are (in mV) V_K = −80, V_Ca = 80, and V_Na = 55.

The dendritic ionic currents are as follows:

$$\begin{array}{c}{I}_{\text{leak}}=g_{\text{L}}\left(V_{\text{dendrite}}-V_{\text{K}}\right)\\ I_{\text{CaL}}=g_{\text{CaL}}{m}_{\text{CaL}}\left(V_{\text{dendrite}}-V_{\text{Ca}}\right)\\ I_{\text{NaP}}=g_{\text{NaP}}{m}_{\text{NaP}}{h}_{\text{Nap}}\left(V_{\text{dendrite}}-V_{\text{Na}}\right)\\ I_{\text{SK}-\text{L}}=g_{\text{SK}-\text{L}}\frac{{\text{Ca}}_{\text{dendrite}}}{0.2+{\text{Ca}}_{\text{dendrite}}}\\ I_{\text{coup}}=g_{\text{coup}}\frac{\left(V_{\text{soma}}+V_{\text{dendrite}}\right)}{1-p_{\text{area}}}\end{array}$$

where the maximal ionic conductances are (in mS/cm²) g_CaL = 0.25, g_NaP = 0.1, and g_SK-L = 1 (see methods) with the same ionic reversal potentials as for soma.

Soma steady-state voltage-dependent channel gating functions are

$$\begin{array}{c}{m}_{\text{Na}\infty }\left(V_{\text{soma}}\right)=\frac{1}{1+e\left(\frac{V_{\text{soma}}-{\theta }_{m\text{Na}}}{K_{m\text{Na}}}\right)}\\ h_{\text{Na}\infty }\left(V_{\text{soma}}\right)=\frac{1}{1+e\left(\frac{V_{\text{soma}}-{\theta }_{h\text{Na}}}{K_{h\text{Na}}}\right)}\\ {\tau }_{\text{Na}}\left(V_{\text{soma}}\right)=\frac{30}{e\left[\frac{V_{\text{soma}}-\left(-50\right)}{15}\right]+e\left[\frac{V_{\text{soma}}-\left(-50\right)}{16}\right]}\\ n_{\text{Kdr}\infty }\left(V_{\text{soma}}\right)=\frac{1}{1+e\left(-\frac{V_{\text{soma}}-{\theta }_{n\text{Kdr}}}{K_{n\text{Kdr}}}\right)}\\ {\tau }_{\text{Kdr}}\left(V_{\text{soma}}\right)=\frac{7}{e\left[\frac{V_{\text{soma}}-\left(-40\right)}{40}\right]+e\left[\frac{V_{\text{soma}}-\left(-40\right)}{50}\right]}\\ m_{\text{CaN}\infty }\left(V_{\text{soma}}\right)=\frac{1}{1+e\left(-\frac{V_{\text{soma}}-{\theta }_{m\text{CaN}}}{K_{mCaN}}\right)}\\ h_{\text{CaN}\infty }\left(V_{\text{soma}}\right)=\frac{1}{1+e\left(-\frac{V_{\text{soma}}-{\theta }_{h\text{CaN}}}{K_{h\text{CaN}}}\right)}\end{array}$$

where the half-activation and inactivation voltages for the somatic channel gating functions are (in mV) θ_mNa = −35, θ_hNa = −55, θ_nKdr = −28, θ_mCaN = −30, and θ_hCaN = −45. The voltage sensitivities of activation and inactivation are (in mV) K_mNa = 7.8, K_hNa = 7, K_nKr = 12, K_mCaN = 5, and K_hCaN = 5.

Dendritic steady-state voltage-dependent channel activation and inactivation functions are

$$\begin{array}{c}{m}_{\text{CaL}\infty }\left(V_{\text{dendrite}}\right)=\frac{1}{1+e\left(\frac{V_{\text{dendrite}}-{\theta }_{m\text{CaL}}}{K_{m\text{CaL}}}\right)}\\ m_{\text{NaP}}\left(V_{\text{dendrite}}\right)=\frac{1}{1+e\left(\frac{V_{\text{dendrite}}-{\theta }_{m\text{NaP}}}{K_{m\text{NaP}}}\right)}\\ h_{\text{NaP}\infty }\left(V_{\text{dendrite}}\right)=\frac{1}{1+e\left(\frac{V_{\text{dendrite}}-{\theta }_{h\text{NaP}}}{K_{h\text{NaP}}}\right)}\end{array}$$

where the half-activation and inactivation voltages for the dendritic channel gating functions are (in mV) θ_mCaL = −39, θ_mNaP = −48, θ_hNaP = −35 (also see methods) and the voltage sensitivities of gating functions are (in mV) K_mCaL = 7, K_mNaP = 3, and K_hNaP = 6.

The scalar equation describing the rise and decay kinetics of excitatory α-MN input to RC is given by

$$\frac{\text{d}{s}_{\text{MN}}}{\text{d}t}={\alpha }_{\text{MN}}\left(1-s_{\text{MN}}\right)s_{\infty }\left(V_{\text{soma}}\right)-{\beta }_{\text{MN}}{s}_{\text{MN}}$$

where α_MN = 2 is a positive constant related to rise of s_MN and β_MN = 0.05 is a positive constant related to the decay of s_MN. The function s_∞(V_soma) is given by

$$s_{\infty }\left(V_{\text{soma}}\right)=\frac{1}{1+e\left(\frac{V_{\text{soma}}-{\theta }_{\text{sth}}}{K_s}\right)}$$

where synaptic voltage threshold θ_sth = −15 mV and the corresponding voltage sensitivity K_s = 0.02.

Equations for the RC model are as follows:

$$C_{\text{m}}=\frac{\text{d}{V}_{\text{RC}}}{\text{d}t}=-I_{\text{leak}}-I_{\text{Na}}-I_{\text{Kdr}}-I_{\alpha \text{MN}}$$

$$\frac{\text{d}{n}_{\text{Kdr}}}{\text{d}t}=\frac{n_{\text{kdr}\infty }\left(V_{\text{RC}}\right)-n_{\text{Kdr}}}{{\tau }_{\text{Kdr}}\left(V_{\text{RC}}\right)}$$

$$\begin{array}{c}\frac{\text{d}{s}_{{\text{GABA}}_{\text{A}}}}{\text{d}t}={\alpha }_{{\text{GABA}}_{\text{A}}}\left(1-s_{{\text{GABA}}_{\text{A}}}\right)s_{\infty }\left(V_{\text{RC}}\right)-{\beta }_{{\text{GABA}}_{\text{A}}}{s}_{{\text{GABA}}_{\text{A}}}\\ \frac{\text{d}{s}_{\text{glycine}}}{\text{d}t}={\alpha }_{\text{glycine}}\left(1-s_{\text{glycine}}\right)s_{\infty }\left(V_{\text{RC}}\right)-{\beta }_{\text{glycine}}{s}_{\text{glycine}}\end{array}$$

where C_m = 1 μF/cm² and α_GABAA = α_glycine = 1 are positive constants related to the rate of rise of s_GABAA and s_glycine, respectively. Similarly, β_GABAA = 0.025 and β_glycine = 0.09 are positive constants related to the rate of decay of s_GABAA and s_glycine, respectively. The resultant rise and decay kinetics of GABAergic and glycinergic currents are shown in Fig. 4E and are similar to those reported by Jonas et al. (1998). I_leak, I_Na, and I_Kdr are defined similarly to those of the α-MN soma. The nonlinear voltage-dependent functions are as follows:

$$\begin{array}{c}{m}_{\text{Na}\infty }\left(V_{\text{RC}}\right)=\frac{1}{1+e^{\left(\frac{-40-V_{\text{RC}}}{7}\right)}}\\ m_{\text{Kdr}\infty }\left(V_{\text{RC}}\right)=\frac{1}{1+e^{\left(\frac{-45-V_{\text{RC}}}{15}\right)}}\end{array}$$

$$\begin{array}{c}{\tau }_{\text{Kdr}}\left(V_{\text{RC}}\right)=\frac{28}{e^{\left(\frac{V_{\text{RC}}+50}{\text{20}}\right)}+e^{-\left(\frac{V_{\text{RC}}+50}{\text{20}}\right)}}\\ s_{\infty }\left(V_{\text{RC}}\right)=\frac{1}{1+e^{\left(\frac{V_{\text{RC}}-{\theta }_{\text{sth}}}{K_{\text{s}}}\right)}}\end{array}$$

where θ_sth = −15 mV and the corresponding K_s = 0.02.

The inhibitory synaptic currents from RC to α-MN are

$$\begin{array}{c}{I}_{{\text{GABA}}_{\text{A}}}=g_{{\text{GABA}}_{\text{A}}}{s}_{{\text{GABA}}_{\text{A}}}\left(V_{\text{dendrite}}-V_{\text{i}}\right)\\ I_{\text{glycine}}=g_{\text{glycine}}{s}_{\text{glycine}}\left(V_{\text{dendrite}}-V_{\text{i}}\right)\end{array}$$

where maximal GABAergic and glycinergic synaptic conductances are g_GABAA = 0.01 mS/cm² and g_glycine = 0.01 mS/cm², respectively, and the chloride reversal potential is V_i = −80 mV.

The excitatory synaptic current from α-MN to RC is

$$I_{\alpha \text{MN}}=g_{\alpha \text{MN}}{s}_{\alpha \text{MN}}\left(V_{\text{RS}}-V_{\text{e}}\right)$$

where maximal synaptic conductance is g_αMN = 0.15 ± 30 mS/cm² and the reversal potential for cholinergic currents is V_e = 50 mV (Dourado and Sargent 2002).