Patterns of hypermetria and terminal cocontraction during point-to-point movements demonstrate independent action of trajectory and postural controllers

Abstract

We examined elbow muscle activities and movement kinematics to determine how subjects combine elementary control actions in performing movements with one and two trajectory segments. In reaching, subjects made a rapid elbow flexion to a visual target before stabilizing the limb with either a low or a higher level of elbow flexor/extensor coactivity (CoA), which was cued by target diameter. Cursor diameter provided real-time biofeedback of actual muscle CoA. In reversing, the limb was to reverse direction within the target and return to the origin with minimal CoA. We previously reported that subjects overshoot the goal when attempting a reversal after first having learned to reach accurately to the same target. Here we test the hypothesis that this hypermetria results because reversals co-opt the initial feedforward control action from the preceding trained reach, thereby failing to account for task-dependent changes in limb impedance induced by differences in flexor/extensor coactivity as the target is acquired (higher in reaching than reversing). Instructed increases in elbow CoA began mid-reach, thus increasing elbow impedance and reducing transient oscillations present in low CoA movments. Flexor EMG alone increased at movement onset. Test reversals incorporated the initial agonist activity of previous reaches but not the increased coactivity at the target, thus leading to overshoot. Moreover, we observed elevated coactivity in reversals upon returning to the origin even though coactivity in reaching was centered at the goal target. These findings refute the idea that the brain necessarily invokes distinct unitary control actions for reaches and reversals made to the same target. Instead, reaches and reversals share a common control action that initiates trajectories toward their target and another later control action that terminates movement and stabilizes the limb about its final resting posture, which differs in the two tasks.

this report is the third in a series of studies in which we used cross-adaptation paradigms to isolate and characterize the elementary control actions comprising point-to-point reaching movements of the arm (a reach task) and out-and-back reversal movements made between the same spatial locations (a reversal task) (Ghez et al. 2007; Scheidt and Ghez 2007). Those studies were undertaken to determine whether the entire realized trajectories of point-to-point reaching movements could be considered as resulting from the implementation of unitary control actions, a frequent assumption of learning models seeking to account for adaptation to visuomotor transformations and/or dynamic loads (cf. Fagg et al. 1997; Franklin et al. 2008; Kawato and Gomi 1992).

In our previous studies, we provided subjects with selective visual feedback of either the movement's ongoing trajectory or its final position as they adapted to visuomotor rotations while reaching or reversing in the horizontal plane (Ghez et al. 2007; Scheidt and Ghez 2007). We quantified whether a learned rotation transfers from one task to the other. Within each task, we found that learning was confined to the movement feature used to drive adaptation. Moreover, adaptations to visually rotated trajectory directions acquired in reversals did not enable subjects to correctly terminate reaches at the rotated targets. Adaptation to rotated final positions in reaching resulted in highly abnormal reach trajectories and no transfer to the initial stroke of reversal movements (although partial transfer to the final stabilized position in reversals was observed in Ghez et al. 2007). We also observed systematic overshoot (hypermetria) when subjects made a reversal movement after having learned to reach accurately to the same target. This effect was also asymmetric in that we observed no corresponding reach errors after reversal training. None of these observations could be explained if reaches were to represent unitary control actions. Instead, we were able to account for all our findings by assuming that realized trajectories of goal-directed reaches are driven by two distinct but partially redundant control actions that superimpose during movement execution (Scheidt and Ghez 2007). In our model, one control action (assumed to be the output of a limb trajectory controller) specifies the torques required to generate the desired trajectory throughout its time course while the other control action (the output of a limb posture controller) specifies the desired equilibrium position and impedance to be achieved at the end of movement. We assumed that the two control actions could be adjusted by separate estimates of kinematic error derived from visual feedback received during and after movement. As such, the limb trajectory and limb posture controllers can specify final intended position redundantly and independently in our model.

Redundancy and independence of final intended position create the potential for errors due to unexpected interactions between the posture and trajectory control actions. If agonist/antagonist coactivity increases at the end of a reach to increase joint stiffness (Gribble et al. 2003; Lametti et al. 2007; see also Hannaford and Stark 1985), for example in anticipation of a possible environmental perturbation (cf. Hogan 1984; Loeb et al. 1990), then muscle activity early in the movement must also change if movement kinematics are to be preserved (Scheidt and Ghez 2007) primarily because agonist/antagonist coactivation increases joint viscosity as well as joint stiffness (Gomi and Osu 1998; Lacquaniti et al. 1993). Such change in the feedforward control of reaches should have no impact on subsequent reversals if subjects use independent unitary control actions for the two tasks (cf. Wolpert and Kawato 1998). However, if subjects use the same initial control action to launch the hand toward the target in both reaches and reversals, overshoot could result if the viscoelasticity previously produced by coactivity in reaching were no longer present as the hand approached the reversal target. That is, postreach hypermetria in reversals is predicted by the two-component limb control model only if the initial control action in reversals is influenced by reach practice such that it fails to account for the magnitude of joint impedance to be implemented as the hand acquires its goal in the middle of the same movement. This is logically possible only if independent control actions initiate a trajectory toward a spatial target and instantiate a stable limb posture about a (potentially different) final position.

The present study explored the interactions between limb trajectory and postural impedance planning in single-joint goal-directed elbow movements, in which kinematics are more readily related to patterns of muscle activations than in two-joint planar motions or movements through free space. We instructed subjects to move the handle of a single degree-of-freedom (DOF) robot so as to move a cursor between targets on a video screen with a prescribed level of terminal coactivity in elbow muscle antagonists. We gained direct experimental control of joint impedance at the end of reaching movements by varying target diameter to indicate the desired level of coactivity and by varying cursor diameter (independent of its position) to indicate the actual real-time coactivity value. Successful performance in reaching required subjects to capture the target for a brief time interval, during which coactivity was also to be maintained at a low or a higher level in separate blocks of trials. We first asked whether the level of terminal coactivity influenced positional accuracy (the performance variable explicitly demanded by the task) at the end of reaches generated without visual feedback. We also asked how this coactivity influenced uninstructed performance variables such as limb impedance at movement termination, limb kinematics prior to achieving steady state, and, importantly, the pattern of agonist muscle activity initiating movement. We then used a task-switching paradigm to determine whether variations in terminal impedance produced by instructed cocontraction training in reaching influenced subjects' abilities to generate accurate reversal movements. The presence of elevated agonist muscle activity and systematic overshoot errors in the initial stroke of reversal movements (relative to corresponding strokes performed during pretraining blocked reversal practice) would be consistent with the predictions of our two-component model of limb control. In contrast, the absence of a systematic trend would be predicted if subjects learned and implemented different unitary control actions to generate the two different movements, as suggested in a previous comparison of reach and reversal movements (Gottlieb 1998) and as assumed in context-specific (Wolpert and Kawato 1998) and optimal control models of goal-directed reaching (Flash and Hogan 1985; Franklin et al. 2008; Kawato and Gomi 1992; Uno et al. 1989). Finally, we asked whether high levels of coactivity instructed at the reach target would transfer to the terminus of a subsequent reversal movement (i.e., back at the origin of the hand's movement sequence). This would be expected if coactivity was associated with the act (but not location) of movement termination in the previously trained control action (i.e., if coactivity and final position control at movement termination were linked) but not if terminal coactivity training in reaching adapted a common control action specifying both trajectory and terminal impedance. If this last were the case, movement kinematics and muscle activities at the end of postreach reversals should not differ from those observed at the end of reversals performed during pretraining blocked practice. We conclude by discussing how cross-adaptation experiments such as those we describe here may be necessary to isolate constituent “motor primitive” control actions, elements that subjects may combine sequentially to form the observed kinematics of goal-directed movements. Portions of this work have appeared in abstract form (Asnani et al. 2008; Scheidt 2008).

METHODS

Ten neurologically normal, right-handed subjects (age 20–41 yr; 4 men, 6 women) provided written informed consent to participate in these experiments. Experimental protocols were institutionally approved in accord with the Declaration of Helsinki. All subjects had normal or corrected-to-normal visual acuity. Seated subjects grasped the instrumented handle of a 1-DOF electromechanical manipulandum with their dominant hand (Fig. 1A) and performed 340 movements during a single experimental session lasting ∼2 h.

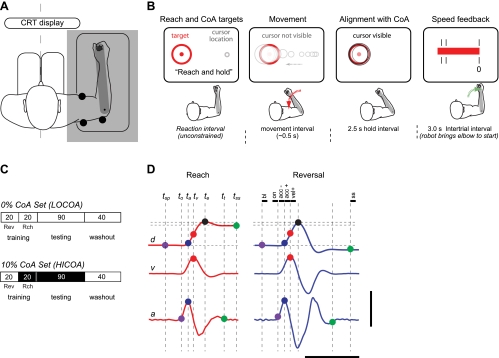
Fig. 1.

Schematic diagram of experimental setup. A: the seated subjects grasped the manipulandum and viewed a computer monitor. An opaque screen blocked direct view of the moving arm. B: visual display configuration. See more details in text. CoA, coactivity. C: structure of trial sequences for the 2 trial supersets comprising the experimental session. Visual feedback of cursor motion was always available during training and washout blocks, comprised of 20 trials each of reach and reversal movements. [Reversals (Rev) preceded reaches (Rch) in training, whereas task presentation order was pseudorandomized during washout.] 10% CoA was cued during trial sets indicated with shading. D: elbow joint angular displacement (d), velocity (v), and acceleration (a) for a typical reaching (left) and reversal (right) movement. Kinematic traces were analyzed to identify the timing of critical events in the movement, including time of peak movement extent (t_e, black), peak velocity (t_v, red), peak acceleration (t_a, blue), the joint angle 200 ms before movement onset (t_o, violet), as well as the steady-state hand position (200 ms after movement's end, t_ss). The vertical scale bar corresponds to a change in joint angle of 50°, a change in velocity of 500°/s, and a change in joint angular acceleration of 5,000°/s². The horizontal scale bar represents 500 ms. t_sp, starting point; t_t, movement termination; bl, t_o − 200 ms to t_o − 150 ms; on, t_o − 50 ms to t_o; acc−, t_a − 50 ms to t_a ms; acc+, t_a to t_a + 50 ms; vel+, t_v to t_v + 50 ms; ss, t_t + 100 ms to t_t + 150 ms.

The robotic device is powered by a low-inertia, brushless DC motor (D061A DC; Kollmorgen, Radford, VA). An integrated resolver transduces joint angle with a resolution better than 2.5 arc sec. A 6-DOF load cell (model 67M25A-I40-A-200N12; JR3, Woodland, CA) measures forces and torques applied to an adjustable arm support and handle. All control and data sampling operations were performed with 16-bit resolution at 1,000 Hz. Upper arm and forearm segment lengths were measured at the beginning of each experimental session, and the robot handle was adjusted for fit. Rigid mechanical stops constrained the subject's arm such that the motor's rotational axis was aligned with that of the elbow and so that motion of the upper arm was minimal. The shoulder was abducted 80–90° at 0° of horizontal flexion. Subjects could move the handle along an arc within the horizontal plane by contracting elbow flexor and extensor muscles.

A vertical computer monitor was located 60 cm in front of the subject. It displayed a circular cursor that moved along a horizontal axis in direct proportion to instantaneous elbow flexion angle. Two additional circles (0.5-cm diameter minimum) displayed the required origin for the movements (90° elbow flexion) and a goal target located 15 cm to the left of the origin (corresponding to an elbow angle of 120°; a flexion movement of 30°) (Fig. 1B). The goal's color (red or blue) cued which of two tasks subjects were to perform. The goal's diameter cued the amount of elbow flexor/extensor muscle coactivity subjects were to achieve as they acquired the target (see below). Cursor diameter was modulated by a signal that varied with elbow muscle coactivity. A line of text provided task instructions below these graphical display elements.

We recorded electromyographic (EMG) signals from arm muscles with differential surface electrodes (Delsys DE-2.1 electrodes and Delsys Bagnolli 8 system; Delsys, Taunton, MA). Monitored muscles included an elbow flexor [biceps brachii, short head (BIC)], an elbow extensor [lateral triceps (TRI)], as well as a shoulder horizontal flexor [anterior deltoid (ADL)] and a shoulder horizontal extensor [posterior deltoid (PDL)]. Although other shoulder and elbow muscles were also monitored, we report data from just these two muscle pairs because they sufficed to capture the behavioral phenomena we describe. EMG signals were band-pass filtered from 10 to 450 Hz, amplified (×1,000), and sampled with 16-bit resolution at 1,000 Hz prior to being stored off-line for further analysis.

At the beginning of each experiment, we asked subjects to perform a set of maximum voluntary contractions (MVCs) to obtain data later used to normalize EMG recordings during task performance. MVC trials included three each of quasi-isometric elbow flexions, elbow extensions, shoulder flexions, and shoulder extensions. Digitized EMG signals obtained during these trials were low-pass filtered with a 250-ms sliding window that computed the instantaneous root-mean-square (RMS) value. The maximum RMS value of this signal (EMG_MAX^RMS) was identified for each muscle across all MVC trials. During the experiments, we used the same sliding window to process EMGs in real time. We normalized each muscle's instantaneous EMG value by dividing by EMG_MAX^RMS to obtain a measure of relative muscular effort (EMG_NORM^RMS) represented as a percentile of MVC value.

We then computed a real-time index of elbow muscle coactivity, CoA(t), by taking the minimum instantaneous value of the normalized RMS values from BIC and TRI:

$$\text{CoA}\left(t\right)=\min \left[{\text{BIC}}_{\text{NORM}}^{\text{RMS}}\left(t\right),{\text{TRI}}_{\text{NORM}}^{\text{RMS}}\left(t\right)\right]$$ (1)

This time-varying signal represents the magnitude of normalized EMG that is equal in the antagonist pair of elbow muscles (cf. Suminski et al. 2007). We used this signal to modulate the diameter of the visual cursor, which ranged from a minimum diameter of 5 mm (corresponding to 0% CoA) to a maximum diameter of 55 mm (corresponding to 20% CoA). The mapping from CoA(t) to cursor size was linear.

Reach and Reversal Tasks

Prior to each trial, the text box on the display instructed the subject to “relax” as the robot brought the handle slowly to the origin and maintained it there for 1.0 s, following which the holding force was gradually reduced to zero over 500 ms. Then, an endpoint target appeared on the screen. The target's color (red or blue) cued subjects to perform one or the other of two tasks.

When the target was red, the subject was to “perform a single 30° point-to-point elbow flexion movement from the origin to goal target as smoothly and accurately as possible.” The text “Reach And Hold” appeared at the bottom of the screen, reinforcing verbal instruction. For reaches, the goal included a concentric circle that either bounded the target (5-mm diameter) or surrounded it (30-mm diameter), thus cueing subjects to acquire the target with either 0% or 10% cued CoA (the LOCOA and HICOA conditions, respectively). During most movements, the cursor disappeared when the target and textual cue appeared (Fig. 1B, 2nd panel) and reappeared at the end of flexion (i.e., 100 ms after the angular acceleration dropped and stayed below 4 rad/s²; Fig. 1B, 3rd panel). In reaching, subjects were further instructed to “make the cursor appear and maintain it centered on the target for 2.5 s while matching cursor size to the target's concentric circle.”

When the target was blue, the subject was to “move out-and-back,” first to the target and then back to the origin, “in one smooth motion, reversing direction as accurately as possible within the target circle without pause.” For these reversal movements, only 5-mm-diameter targets were presented such that only 0% CoA (LOCOA) reversals were cued. The text “Go Out and Back” appeared with the target to reinforce verbal instruction. Visual feedback conditions for reversal movements are described in detail below. As in reaching, we continued to record joint kinematics and EMG data throughout a 2.5-s hold interval following the end of movement.

To promote consistent movement speed across the two tasks, a graphical display of peak flexion velocity was displayed during the 3-s intertrial interval following the stabilization period (Fig. 1B, 4th panel). Subjects were encouraged to adjust their movements so that the leftmost edge of the feedback bar fell within the target zone (peak elbow flexion speed of 5 rad/s ± 10%).

Experimental Design and Feedback Conditions

This study required that subjects perform 95 reaching movements in which they cocontracted elbow flexors and extensors and that they do so without substantial fatigue. We performed a series of pilot experiments and found that subjects could perform 95 reaches without fatigue only if coactivity was below 20% MVC. We therefore limited cued CoA values to 10% MVC.

Each subject performed two supersets of 170 trials requiring either minimal (LOCOA: 0% MVC; Fig. 1C, top) or modest (HICOA: 10% MVC; Fig. 1C, bottom) elbow CoA upon target acquisition in reaching. Each superset consisted of three blocks of trials. The first 40 trials (the training block) consisted of 20 consecutive reversals followed by 20 consecutive reaches, all performed with continuous visual feedback of the cursor. In the next 90 trials (the testing block), subjects performed reaching movements in which the cursor feedback was eliminated prior to and during movement, was reinstated 100 ms after movement termination, and remained visible throughout the 2.5-s hold interval. One of every six trials in this block (selected pseudorandomly) required subjects to make a single reversal movement without any cursor feedback. This allowed us to determine how prior practice during reaching with and without terminal cocontraction might influence accuracy in the reversal task. Finally, a washout block interleaved 20 trials each of LOCOA reaches and reversals in order to minimize potential carryover effects from the first to the second superset of trials. Cursor feedback was available throughout movement for both reaches and reversals during washout. The presentation order of the two supersets was counterbalanced across subjects.

To verify that the two levels of cued elbow coactivity resulted in different levels of joint impedance, we imposed small torque perturbations to the handle during the 2.5-s hold interval following one of every five randomly selected training block reaches. These unpredictable torques (sum of 2.1- and 3.5-Hz sinusoids; 2 Nm peak to peak) were unbiased (zero mean) and were phased in smoothly over a period of 250 ms immediately after movement termination. The robot's motor was turned off at all other times during the trials and therefore did not impede or assist in the performance of the cued tasks.

Data Analysis

Analysis of movements during the training block focused on the last 10 trials of each type (reach and reversal). Analysis of movements from the testing block focused on the last 10 reversal trials and the reaches immediately preceding them in the trial sequence. Washout phase movements were not analyzed.

Joint angular trajectories were low-pass filtered with a second-order, zero-lag Butterworth filter with 20-Hz cutoff before joint angular velocities were computed. Velocities were filtered similarly before joint angular accelerations were computed. We identified several kinematic features with the use of an automated algorithm within the MATLAB programming environment (The Mathworks, Natick, MA) (Fig. 1D). Each was verified visually and manually adjusted if necessary. The hand's starting point (θ_sp) was defined as its angular location 200 ms before movement onset. Movement onset (t_o) was identified as the moment when elbow flexion acceleration exceeded and remained above 4 rad/s² for 50 ms at the beginning of a trial. The peak angular acceleration point consisted of the elbow flexion angle (θ_a) and peak angular acceleration taken at the time when elbow acceleration reached its maximum positive value in the flexion phase of movement (i.e., at time t_a). The peak angular velocity point consisted of the elbow flexion angle (θ_v) and peak angular velocity taken at the time when the elbow joint reached its maximum positive velocity in the flexion phase of movement (i.e., at time t_v). Movements from all subjects exhibited overshoot in movement extent. Therefore, the peak extent point (θ_e) was defined as the elbow angle attained at maximum displacement from the home position in the flexion phase of movement in both reach and reversal movements. The time at which this occurred was defined as t_e. Movement termination (t_t) was identified as the moment when the magnitude of elbow acceleration last exceeded 4 rad/s² at the end of a trial. Finally, the steady-state position in reaching (θ_ss) consisted of the joint angle 150 ms after movement termination (t_ss; just 50 ms after visual feedback of cursor position and size was provided).

We derived a pair of secondary measures to characterize task performance. Percentage overshoot (PO) was computed as 100 × (θ_e − θ_ss)/(θ_ss − θ_sp). Because reaches in all subjects overshot the target to some degree before settling into steady state, we assumed that these movements were dominated by an underdamped, second-order response to a step change in desired hand position. We estimated the limb's relative damping ratio (ζ) using the well-known relationship between this quantity and PO for underdamped, second-order systems (Kuo 1987):

$$\zeta =\left|\ln \left(\text{PO}/100\right)\right|/\sqrt{{\pi }^2+{\ln }^2\left(\text{PO}/100\right)}.$$ (2)

EMG signals were postprocessed for statistical comparison of muscle activation patterns between conditions within subjects. Postprocessing involved band-pass filtering from 30 to 300 Hz followed by full-wave rectification. These signals were normalized by their maximum values recorded during the MVC trials after the same postprocessing. Trials were then aligned in time by t_o. We were particularly interested in understanding how initial agonist muscle activity in occasional reversal movements would be impacted by prior training in reaching with different levels of terminal postural coactivation. We therefore defined six time periods within which EMG activities in the different muscles were averaged. The first window quantified premovement, resting baseline activity (bl: t_o − 200 ms to t_o − 150 ms), allowing us to assess signal quality. The second window quantified the magnitude of the initial onset agonist activity (on: t_o − 50 ms to t_o). The third and fourth windows assessed activity within the periods from t_a − 50 ms to t_a ms (acc−) and from t_a to t_a + 50 ms (acc+) and thus are sensitive to temporal modulation of the magnitude and duration of the initial agonist burst (often referred to in the literature as AG₁; Brown and Cooke 1990; Dijkstra and Denier van der Gon 1973; Ghez 1979; Hallett and Marsden 1979; Hannaford and Stark 1985; Marsden et al. 1983; Terzuolo et al. 1973; Wadman et al. 1979, among others). The fifth window (vel+: t_v to t_v + 50 ms) was sensitive to activity in the deceleration phase of movement (including the second agonist burst AG₂). The final window was sensitive to task-related differences in reaches and reversals at steady state (ss: t_t + 100 ms to t_t + 150 ms).

Statistical testing was carried out within the Minitab computing environment (Minitab, State College, PA). Data values in the text are reported as means ± SD. Error bars in figures represent ±SE. Repeated-measures analyses of variance (ANOVA) and multivariate ANOVA (i.e., MANOVA) were used to compare performance measures across tasks, experimental blocks (training vs. testing), and trial supersets (LOCOA vs. HICOA) while accounting for substantial intersubject variation. Note that because subjects received ongoing visual feedback of cursor motion during the training block but only terminal visual feedback of cursor motion during testing block reaches, the “experimental block” factor also assessed the influence of visual feedback condition on measured performance. Post hoc Bonferroni paired t-tests and Dunnett simultaneous paired comparisons were applied where appropriate. Effects were considered statistically significant at the α = 0.05 level.

RESULTS

Subjects followed our instructions and made either single flexions or a sequence of flexion-extension movements depending on whether a reach or reversal trial was cued. Task errors accounted for <5% of all trials and were excluded from further analyses. We examine first how the level of required CoA influenced instructed displacements and elbow muscle coactivity, the two steady-state variables governed by task instruction and available visual feedback. We then show that the level of instructed coactivity also influenced other performance features that were not explicitly specified by the task (e.g., limb trajectory kinematics and phasic muscle activation patterns in both elbow and shoulder muscles). Finally, we show that kinematic accuracy and elbow muscle activity in reversals depended contextually on cued CoA level during prior reach training. In particular, we highlight evidence that reversals co-opt the initial BIC activity and terminal stabilizing impedance from trained reaches immediately preceding them in the trial sequence, even though this was to compromise movement accuracy and violate explicit task instruction.

In Reaching, Terminal HICOA Instruction Increases Joint Impedance, Dampens Terminal Oscillations, and Influences Muscle Activity Early in the Movement

Subjects reliably performed reaching movements that were smooth with unimodal bell-shaped velocity profiles in all cases. All subjects stabilized elbow joint angle within the required 30 ± 3° window under both CoA conditions (average reach trajectories for a representative subject are shown in Fig. 2A, top). Steady-state accuracy in reaching was similar during training with ongoing visual feedback (blocked training phase) and with only terminal visual feedback (transfer assessment phase): Two-way repeated-measures ANOVA found no main effect of either cued CoA level [F_(1,27) = 0.37, P = 0.55] or experimental phase [F_(1,27) = 1.61, P = 0.215] and no interaction between factors [F_(1,27) = 0.21, P = 0.654]. Similarly, two-way repeated-measures ANOVA found that movement duration (t_t − t₀) did not differ across CoA levels [F_(1,27) = 0.12, P = 0.735] or experimental phase/feedback conditions [F_(1,27) = 0.00, P = 0.957]. Again, we found no evidence for interaction between factors [F_(1,27) = 0.74, P = 0.398]. The across-subject average duration of reaching movements was 0.41 ± 0.05 s.

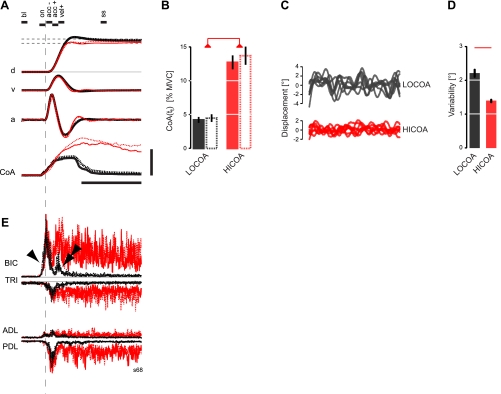
Fig. 2.

Effect of cued elbow muscle coactivation and “online” visual cursor feedback on performance variables during reaching. A, top: average kinematics of reaching movements with continuous visual feedback of the cursor (solid) or only after movement (dashed) from a single representative subject: 0% cued elbow CoA (heavy black), 10% cued CoA (red). CoA, realized elbow BIC/TRI coactivation values (see text for details). Vertical scale bar: 25°, 150°/s, 1,500°/s², and 10% change in CoA. Horizontal scale bar: 500 ms. Horizontal dashed lines correspond to the cued target region. B: population analysis (n = 10) of average realized coactivity values at the end of reaching. Line type and color encoding as in A. Horizontal red bar highlights statistically significant differences (P < 0.05, corrected for multiple comparisons). C: kinematics during the 2.5-s elbow joint postural stabilization period after the end of reaching in perturbed training trials with 0% cued CoA (top) and 10% cued CoA (bottom) for a representative subject. Variations in elbow angle during hold periods without perturbation were typically <0.1° peak to peak. D: population analysis of elbow joint angle variability during terminal postural stabilization. E: average EMG activities (n = 10 each trace) recorded during the same movements and plotted on the same time scale as in A. Line type and color encoding are also as in A. Single arrowhead, AG₁; double arrowhead, AG₂. BIC, biceps brachii; TRI, triceps, lateral head; ADL, anterior deltoid; PDL, posterior deltoid. Vertical scale bar in A also corresponds to a 10% maximum voluntary contraction (MVC) change in EMG activity. Error bars indicate ±SE in all panels.

Subjects readily achieved different levels of elbow flexor/extensor muscle coactivity levels as cued. CoA at movement termination (t_t) was markedly increased in the HICOA condition relative to the LOCOA condition [2-way repeated-measures ANOVA: F_(1,27) = 136.99, P < 0.0005] regardless of trial block [training vs. testing: F_(1,27) = 0.68, P = 0.417] (Fig. 2B). The absence of main or interaction effect of trial block or CoA condition implies that neither visual feedback (present during training but not during testing) nor the greater amount of prior reach practice in the testing block had measurable impact on instructed performance variables. Subjects exceeded the instructed CoA level somewhat at t_t, averaging 13.2% ± 3.7% CoA and 4.4% ± 1.6% CoA in the (10%) HICOA and (0%) LOCOA conditions. This surplus activity persisted at steady state, averaging 11.5% ± 3.0% CoA and 2.5% ± 1.1% CoA in the HICOA and LOCOA conditions. Terminal CoA in the LOCOA condition was significantly greater than premovement resting baseline values in both end-of-movement time windows (paired t-tests; t_t: T = 6.72, P < 0.0005; t_ss: T = 4.31, P = 0.001) even though subjects were provided real-time biofeedback of CoA along with explicit instructions to minimize it at movement's end for these trials. Because coactivity contributes importantly to the control of limb stability (Milner and Cloutier 1998), it is possible that subjects generated modestly elevated CoA values in the LOCOA condition because we applied unpredictable torque perturbations at the end of training block reaches with 20% probability. It is also possible that subjects chose to generate a modest level of coactivity as a solution to the conflict between the on-screen instructions (to “Reach and Hold” at the target) and the target size (specifying 0% terminal CoA), although no such confusion was evident during baseline blocked practice.

In the subset of training trial reaches in which we applied perturbations (Fig. 2C), induced hand displacements were significantly larger for LOCOA than for HICOA reaches (2.2 ± 0.6° vs. 1.4 ± 0.2°) (Fig. 2D), thus validating our use of CoA as a proxy for joint impedance. This finding is consistent with the increase in joint stiffness and viscosity reported in tasks associated with increased coactivation of antagonists (Gomi and Osu 1998; Hogan 1984; Laquaniti et al. 1993) and supports the idea that subjects reduce hand position variability at the end of reach by increasing joint impedance through cocontraction (Gribble et al. 2003; Lametti et al. 2007).

The pattern of EMG activity during transport differed for the two CoA conditions. With LOCOA (Fig. 2E), transport was associated with the well-known triphasic bursting pattern, which mirrored acceleratory and deceleratory phases of joint displacement. The pattern was present both in the training block with continuous visual feedback and in the testing block with only terminal cursor feedback. As seen for a representative subject, BIC shows two agonist bursts (AG₁, AG₂) separated by a distinct silent period, whereas TRI shows a single burst during the agonist silent period. With HICOA, this triphasic pattern was no longer apparent (e.g., Fig. 2E). Instead, the agonist silent period was partially “filled in”; agonist and antagonist EMGs both increased phasicly before and during transport and then declined to asymptotic levels several hundred milliseconds after positional stability was achieved. Across both CoA conditions, BIC activity began 60–80 ms before the onset of kinematic changes and was similar until the time of peak acceleration (when the EMG traces began to diverge). EMGs remained systematically greater in the HICOA condition until the end of the trial (i.e., long after movement had ceased). Extensor EMG activity (TRI) began slightly later than in flexors and peaked at t_a or shortly thereafter. It was similar for the two CoA conditions until just after the time of peak acceleration, when it became greater at HICOA. Silent periods and later bursts in flexors and extensors were either indistinct or absent in the HICOA trials. Unlike flexors, where peak AG₁ amplitude was similar across CoA conditions, extensor activation values were higher at HICOA than at LOCOA in several subjects. Both shoulder muscles ADL and PDL showed instruction-dependent patterns of phasic and tonic EMG activity that closely resembled those of the single-joint elbow muscles BIC and TRI. This was surprising since we neither instructed subjects to modulate shoulder muscle activity nor provided them with visual biofeedback motivating them to do so. In all muscles and training blocks, EMG values were close to zero at rest for each subject (<1.0 ± 0.2% MVC) and were thus uncorrupted by obvious noise sources.

We found similar patterns of muscle activation in all subjects. Figure 3A shows the means and SE of EMG activity obtained by first averaging sampled EMGs across training phase (but within subject) and then computing across-subject population statistics in successive sampling intervals during movement (see methods and Fig. 1). Three-way repeated-measures MANOVA found that the activities of elbow muscles (BIC, TRI) and shoulder muscles (ADL, PDL) varied as a function of temporal sampling window [Wilks' F_(4,101) = 28.09, P < 0.0005], task [HICOA vs. LOCOA; F_(1,101) = 58.09, P < 0.0005], but not trial block/feedback condition [training vs. testing block; F_(1,101) = 1.59, P = 0.178]. An interaction between sampling window and CoA level was also revealed [F_(4,101) = 6.008, P < 0.0005], but all other two- or three-way interactions failed to reach significance (P > 0.86 in each case). These findings imply that the temporal patterns of EMG activity we report were not influenced by factors that varied with trial block (e.g., availability of ongoing visual feedback or amount of training).

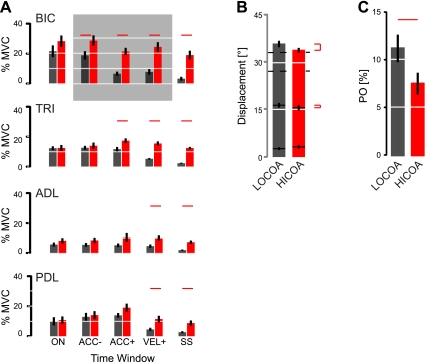
Fig. 3.

Effect of cued elbow muscle coactivation level on uninstructed performance variables during reaching. Black, LOCOA; red: HICOA. A: population analysis of EMG activity within the 6 sampling intervals of interest. Red horizontal markers indicate significant differences across training conditions identified via repeated-measures ANOVA and post hoc Bonferroni t-tests. B: population analysis of limb displacements at t_e, t_v, and t_a as a function of cued CoA level. Red markers on right indicate significant difference. C: population analysis of percentage overshoot (PO) in the underdamped response to a step change in desired joint angle. Error bars indicate ±SE in all panels.

Post hoc paired t-tests showed CoA-dependent differences in EMG during movement for all monitored muscles (Fig. 3A). In the elbow flexor BIC, instruction-dependent differences were significant already within the 50-ms sampling window preceding t_a. Significant differences appeared later in elbow extensor TRI (the window succeeding t_a). Differences were evident in all monitored muscles by t_v and were maintained throughout the hold period at the end of movement.

These CoA-dependent differences in EMG were reflected in highly consistent differences in kinematic variables that were not contingent on any aspect of task instruction during the reach (Fig. 3B). Two-way repeated-measures ANOVA found that peak arm displacements θ_e were systematically reduced at HICOA relative to those at LOCOA [F_(1,27) = 11.90, P = 0.002] without a main effect of training phase [F_(1,27) = 0.20, P = 0.660] or interaction between the two factors [F_(1,27) = 0.22, P = 0.639]. A similar main effect of CoA instruction (not training phase) was observed for arm displacements at t_v [F_(1,27) = 5.19, P = 0.031] but not t_a [F_(1,27) = 3.37, P = 0.078].

Effective Joint Impedance.

The task dependence of peak displacement—but not of steady-state joint angle described above—implies that instructed CoA level had a significant influence on limb dynamics. Indeed, two-way repeated-measures ANOVA found percentage overshoot in flexion (PO) to vary with CoA instruction [F_(1,27) = 6.06, P = 0.020] but not training phase [F_(1,27) = 0.02, P = 0.893] without interaction between factors [F_(1,27) = 0.22, P = 0.644] (Fig. 3C). This effect was not due to differences in speed across CoA conditions, because we observed no CoA dependence in peak velocity (LOCOA: 264 ± 18°/s, HICOA: 266 ± 13°/s; paired t-test: P = 0.736). Under the assumption that elbow kinematics are dominated by second-order dynamics (cf. Fig. 2A, top), the PO values in the two CoA conditions (11.2 ± 4.6% vs. 7.5 ± 3.6%) correspond to effective elbow joint damping values of 0.53 ± 0.15 and 0.64 ± 0.07 in the LOCOA and HICOA cases, respectively. Note that the lack of main or interaction effects involving training phase implies that neither visual feedback condition nor amount of training had a measurable impact on uninstructed performance variables of interest, including effective joint impedance.

Transfer Effects: Influence of Prior Reach Practice on Accuracy and Muscle Activity In Reversals

In the paragraphs that follow, we show that subjects use the same initial agonist EMG activity and the same initial flexion accelerations for test reversals as they used for the reaches immediately preceding them in the trial sequence. In the HICOA test block, this led to a mismatch between the effective joint impedance generated as the target was approached in reversals and that encountered during the preceding reach. This mismatch suffices to explain hypermetria in the two-joint reversal movements described previously (Scheidt and Ghez 2007) as well as in the single-joint elbow reversals made by the present subjects.

Movement kinematics and realized CoA.

Subjects made smooth reversal movements as instructed, with bimodal velocity profiles and trimodal acceleration profiles in all conditions (Fig. 4A: representative subject data). By the end of the training blocks, subjects captured the target accurately (Fig. 4A, top): Peak arm displacements averaged 33.2 ± 4.2° and 34.3 ± 3.8° across subjects in the LOCOA and HICOA supersets, respectively. These values did not significantly exceed the target boundaries of 27–33° (P > 0.31 in both cases). By contrast, test block reversals (interspersed among successive reaches) systematically overshot the target at both CoA levels (LOCOA: 40.1 ± 3.6°, HICOA: 40.7 ± 4.9°; e.g., Fig. 4A, top), implying a relatively weak maintenance of the motor representation obtained in baseline reversal training. Two-way repeated-measures MANOVA found that the raw arm displacements at t_e, t_v, and t_a varied with trial block [training vs. testing blocks: Wilks' F_(3,25) = 12.88, P < 0.0005] but, surprisingly, not with cued coactivation level [F_(3,25) = 0.98, P = 0.417] (Fig. 4B). (We will revisit this point in Fig. 5.) No interaction between factors was indicated [F_(3,25) = 0.68, P < 0.576]. Post hoc ANOVA found that the trial block difference was already evident by time of peak flexion acceleration [F_(1,27) = 14.44, P = 0.001], which occurred only 3.0 ± 0.7° and 70.2 ± 7.0 ms into the movement. The timing of these differences precludes a simple visual reaction time response and therefore reflects errors in movement planning rather than differences in visual feedback conditions across the training phases (i.e., continuous cursor feedback in the baseline training condition vs. no cursor feedback in the test condition).

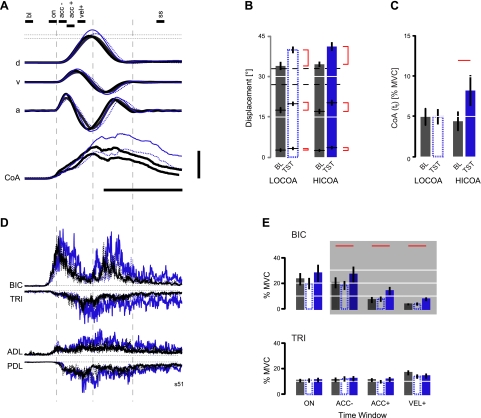
Fig. 4.

Effect of coactivation training on the kinematics and EMG of reversals. A: average kinematics (n = 10 each trace) from a representative subject performed before (heavy solid black traces: both baseline blocks) and after reach training without (dashed blue: LOCOA) and with terminal coactivation (solid blue: HICOA). Scale bars and time indicator lines are as in Fig. 2. The time windows used for EMG averaging and analysis are shown at top. B: population analysis of peak elbow movement amplitude in reversal movements of training (BL) and test (TST) trials in the 0% and 10% CoA supersets. C: population analysis of realized CoA values at movement's termination. D: average EMG activities from the same movements as in A. For this panel, the vertical scale bar in A corresponds to a change in EMG of 20% MVC. E: population analysis of EMG activity within the 4 sampling intervals spanning flexion movement. Error bars indicate ±SE in all panels.

Fig. 5.

Comparisons of kinematics and EMG activities in reaches with HICOA (red), interspersed test reversals (blue), and baseline reversals (heavy black) (representative subject). A: ensemble averages (n = 10 trials). Scale bars and time indicator lines are as in Fig. 2. Black line segments above traces indicate time windows used for EMG analysis in E. B: population analysis of primary flexion amplitudes in both movement tasks during the testing block of the 0% and 10% supersets (right) and for reversals in the training blocks (left). C: change in peak displacement in reversals after reach training with 0% (LOCOA) and 10% (HICOA) CoA. D: average EMG activities recorded during the same movements as in A. Scale bars and time indicator lines are as in Fig. 2. E: population analysis of EMG activity within the sampling intervals spanning flexion movement as well as steady state. Error bars indicate ±SE in all panels.

Muscle activation patterns during reversals are influenced by prior reach training.

As in LOCOA reaching, terminal BIC/TRI CoA values in training block reversals averaged slightly less than 5% MVC (4.9 ± 2.6%), a value significantly greater than premovement baseline resting values (T = 4.74, P = 0.001) (Fig. 4C). This was despite the fact that starting and goal target sizes were such that all reversals were to be performed with 0% cued CoA. In contrast, CoA was dramatically elevated (8.2 ± 5.3% MVC) at the end of reversals made immediately after 10% CoA reaches but not after 0% CoA reaches (4.4 ± 2.6% MVC). Elevated coactivity here is not the result of a control action preparing for the contingency of perturbation (cf. Hogan 1985; Loeb et al. 1990), because the likelihood of perturbation in the baseline and testing trial blocks was identical across CoA training sets. Thus stabilization performance in reversal movements depended contextually on terminal elbow muscle coactivation produced during prior reach training.

Virtually identical patterns of alternating bursts in BIC and TRI were present during the initial baseline training block reversal movements from both the HICOA and LOCOA supersets (representative subject data shown in Fig. 4D). BIC activity began before elbow flexion and preceded activity in all other monitored muscles. It peaked around t_o and then decreased to a trough around t_v. As in reaching, TRI activity was also evident early during the initial flexor phase of reversals, peaking later than activity in BIC (around t_v). The subsequent decline in TRI activity (starting around the time of maximum extensor acceleration) was coincident with the onset of phasic BIC activity, which was then followed by a brief acceleration into flexion. The correspondence between the reciprocal activation of TRI and the pause in BIC was seen in every subject. EMG activity at the end of reversals decayed gradually in both elbow muscles after t_t. Importantly, these phasic features of BIC and TRI activity were both increased in amplitude and prolonged in duration when reversals were embedded in a series of consecutive reaches (testing block) compared with reversals produced after blocked practice (training block) (Fig. 4D).

Two-way repeated-measures MANOVA showed that BIC and TRI EMGs varied in training block reversals only as a function of the time window used for sampling [on, acc−, acc+, vel+: Wilks' F_(6,124) = 13.708, P < 0.0005] but not trial superset [F_(2,62) = 0.574, P = 0.566] and with no interaction between the two factors [F_(6,124) = 0.799, P = 0.573] (data not shown in Fig. 4). Thus any influence of prior reach training was effectively “washed out” prior to data recording for reversals in the second superset. We therefore averaged EMGs across supersets to obtain muscle activity estimates for stably accurate training block reversals (Fig. 4D). We compared these estimates to those obtained after reach training at 0% and 10% cued CoA, using separate two-way repeated measures ANOVA for BIC and TRI (Fig. 4E). For BIC, reversal EMGs varied as a function of both sampling window [F_(3,99) = 47.00, P < 0.0005] and testing condition [F_(2,99) = 9.52, P < 0.0005]. Post hoc, pairwise, within-window comparisons of test block BIC activity to BIC activity in the blocked training control condition showed that reaching with 10% terminal CoA induced a dramatic increase in BIC EMG magnitude in subsequent reversals, whereas reach training with 0% CoA did not (Dunnett simultaneous paired t-tests: horizontal red lines in Fig. 4E indicate significant differences). EMG increases in the 10% trial set were already apparent within the 50-ms window preceding t_a and persisted throughout the remainder of the flexion phase of movement. These increases mirror those observed during reaches made with 10% CoA (shaded comparisons in Figs. 3A and 4E). In contrast, reversal activity in TRI varied only with sampling window [F_(3,99) = 8.97, P < 0.0005] but not testing condition [F_(2,99) = 0.69, P < 0.507]. No interaction between factors was found for either muscle.

Muscle activation patterns after movement termination.

Terminal EMGs at t_t were elevated when reversals were embedded within a series of reaches performed at 10% CoA (BIC: 4.5 ± 4.0%, TRI: 4.8 ± 3.2%) compared with reversals performed in the training blocks (BIC 2.7 ± 3.3%, TRI: 2.5 ± 1.4%) (BIC: T = 3.29, P = 0.005; TRI: T = 3.47, P = 0.004). This was not the case for reversals embedded within a series of 0% CoA reaches (BIC: 2.5 ± 2.6%, TRI: 2.9 ± 2.0%) (BIC: T = 0.35, P = 0.633; TRI: T = 1.48, P = 0.087). Thus terminal coactivity transferred from the reach to the reversal task, even though the final position of the hand differed dramatically in the two cases.

Trajectory kinematics and muscle activations in test reaches and reversals reveal that modifications to initial trajectory control actions that were implemented to counter elevated joint impedance at the target in reaching were applied inappropriately to the initial trajectory plan for subsequent reversal movements, in which joint impedance was not elevated at the target. Figure 5A shows average elbow joint trajectories and CoA values from test block reaches and reversals performed by a representative subject in the HICOA superset. Data from training block reversals (presented above) are overlaid for comparison. Note that test reaches were highly accurate at both peak extent and steady state. The same was true for peak extent in training block reversals. In contrast, test block reversals exhibited dramatic overshoot when the previous movement was an accurate reach with elevated flexor/extensor coactivation in proximity to the target.

Peak arm displacements in test block reaches differed between the two supersets (0%: 35.75 ± 3.07°, 10%: 33.52 ± 2.62°; T = 2.00, P = 0.038) (Fig. 5B). We therefore computed the difference in peak extent between reversals and the reaches immediately preceding them in each test block to control for possible time-dependent variations in aim (Fig. 5C). Paired t-test found this difference to depend strongly on cued CoA level (T = 3.37, P = 0.004), with reversals exceeding reaches by 4.3 ± 3.0° in the 0% CoA case and by 7.3 ± 4.1° in the 10% case. In this way, reversal kinematics depended on the level of coactivity required in the most recent reaching movements.

EMG activity in test block reversals also varied with the level of cued coactivity in the most recent reach. As shown for a representative subject in Fig. 5D, the earliest phasic BIC activities in test reaches and reversals of the 10% CoA superset were strikingly similar to activity seen in training block reversals. However, between t_o and t_v, BIC activity declined rapidly in training block reversals but remained high for test reaches and for test reversals (in which activity was indistinguishable from that observed in the immediately preceding reach; Fig. 5D, shading). From about t_v onward, BIC activity in test reversals diverged from test reach activity (which declined gradually throughout the stabilization period) and instead followed the envelope of activity seen in training block reversals, albeit with visibly greater magnitude. Test reaches and reversals both exhibited elevated steady-state activities that persisted well after positional stability was achieved. As noted above, antagonist activity in TRI increased and peaked earlier in reaches than in reversals. TRI activity also exhibited elevated steady-state activities in test block reaches and reversals. The apparent increase in terminal elbow muscle coactivity in test block reversals is interesting because the final arm postures were different in the reach and reversal tasks (separated by 30° of elbow flexion) and because transfer of a planned equilibrium posture from reach to reversal could have interfered with the reversal's motion back to the starting posture (which was never observed; cf. Fig. 4A). Rather, the amount of terminal coactivity in reversals appears to reflect the magnitude (but not locus) of coactivity generated in previous reaches. This, then, implies that terminal coactivity was planned and executed independent of the equilibrium joint angle about which elevated impedance was desired.

These results were confirmed by population analysis (Fig. 5E): Paired t-tests comparing BIC EMGs in training block reversals to those in test reaches and test reversals showed that initial EMG activities during 0% test movements did not differ measurably from those in training reversals for any time window. On the other hand, BIC EMG magnitude increased for all 10% test movements (reaches and reversals) in the on, acc−, and acc+ sampling windows (P < 0.003 in each case). Moreover, test block reversal activities did not differ from those in the immediately preceding reaches in these sampling windows (P ≥ 0.473 in each case). Thus it can be inferred that subjects used the same initial agonist commands in the test block reach and reversal trials.

BIC activity in 10% test block reversals tended to exceed levels seen in the training blocks from t_v onward, although this activity failed to achieve significance according to our conservative Bonferroni criterion. Not unexpectedly, these activities were lower than those in the immediately preceding reaches (P < 0.001 in time periods following t_v). We therefore infer that agonist commands in the reach and reversal tasks diverged around the time of t_v.

As we discussed for Fig. 4D above, we found no significant increase in elbow extensor activity prior to target acquisition in test block reversals relative to those in the training blocks. The increased BIC activity in test reversals after 10% CoA reaching therefore was not typically balanced by a corresponding increase in TRI activity. As shown previously (Scheidt and Ghez 2007), a mismatch between the effective joint impedance generated as the target is approached in reversals and that encountered during the preceding reach suffices to explain the hypermetric reversal movements after reach training in Fig. 5, A–C.

DISCUSSION

These experiments examined component control actions contributing to single-joint elbow movements by probing the interaction between planned trajectory and limb impedance in two target capture tasks (reach and reversal movements). After practicing the two tasks, subjects had become proficient in satisfying explicit spatial accuracy demands in both. They also had learned to use a novel biofeedback display to produce specified levels of coactivity upon acquiring the target in reaching. Increasing coactivation at the end of a reach had the anticipated effect of increasing joint impedance about the goal target (Fig. 2C and Fig. 3C) (cf. Gomi and Osu 1998; Hogan 1984; Lacquaniti et al. 1993). Increasing terminal coactivation also exerted systematic influence over uninstructed performance variables including the limb's trajectory during movement and, importantly, the agonist muscle activation patterns used to initiate the reach (Fig. 3, A and B, and Fig. 2E). As predicted by computer simulations (Scheidt and Ghez 2007), subjects increased their initial agonist activity in reaching to compensate for the increase in effective joint viscoelasticity produced by increased terminal coactivation (Fig. 3A). Prior reach training also induced dramatic overshoot errors in “surprise” reversals; these errors varied with the amount of trained reach BIC/TRI coactivation (Fig. 4A). This overshoot occurred because the same agonist EMG and acceleration used to make the reach were also applied to generate the initial flexor movement required in the reversal task (Fig. 5, D and E). This increase was not matched by the corresponding increase in TRI activity seen in reaching, leading to overshoot. Thus, after reach training, modifications to initial trajectory control actions that were implemented to counter elevated joint impedance at the target were applied inappropriately to the initial trajectory plan for subsequent reversal movements, in which joint impedance was not elevated at the target (which was instead to be a via-point to begin the second movement segment of the reversal task). After reach training with CoA at the goal target, subjects also generated elevated BIC/TRI coactivity in reversals upon returning to the home position after reach training. Thus, after reach training, learned modifications to limb impedance about the final resting posture were applied to the plan specifying final limb posture for subsequent reversals despite the fact that in reversals the limb was stabilized far from the trained reach stabilization point. In other words, the amount of terminal coactivity in reversals reflected the magnitude (but not locus) of coactivity generated in previous reaching trials. This finding provides strong evidence linking impedance control to the context of terminating movement rather than with any single trained equilibrium position. It also provides evidence that terminal coactivity commands can be planned and executed independent of trajectory control commands in goal-directed arm movements. Moreover, hypermetria of reversals after reach training implies that without the fine-tuning that comes with practice, initial trajectory plans in reversals do not account for the timing and/or magnitude of joint impedance changes to occur later in the same movement, changes induced by an intervening return stroke in reversals but not reaches. If the trajectory and impedance controllers had cross-knowledge, hypermetria should not have occurred. Instead, initial agonist activity in reversals appears to be based on commands used most recently to move to a given target, even though those plans were formed in the reach task. Taken together, our findings indicate that these two tasks share the same initial control action and terminate with another common control action, even though the limb is stabilized about different steady-state joint angles.

In practice, subjects readily mastered the simultaneous control of cursor location and size; undoubtedly this was because the eye was already focused on the cursor when movements slowed down to capture the target. Whether or not this task required more attention or cognitive effort than the reversal tasks, an increase in attentional demand cannot account for the overshoot errors of the reversal movements or the elevated coactivity in the HICOA reach training block, because the test reversals were blind, i.e., performed without visual feedback. Thus any hypothetical increase in attentional demand would not have been present. Moreover, dynamic overshooting also characterized baseline reaches in the LOCOA superset. These reaches were similar in attentional demands to the HICOA reaches, and the LOCOA reach overshoots were not corrected in the course of repeated movements to the same targets until subjects were given cues to increase coactivity when capturing the target. Only when provided the CoA feedback did the subjects successfully dampen the reach overshoot.

Component Control Actions in the Composition of Reaching and Reversal Movements

A fundamental question in motor behavior is whether the brain manages the contrasting objectives of limb posture and movement control through a single robust control process (Feldman 1986; Gribble et al. 1998; Mussa-Ivaldi and Bizzi 2000) or whether a specialized process subserves each goal (Brown et al. 2003; Humphrey and Reed 1983; Kurtzer et al. 2005; see also Franklin et al. 2002). On the basis of motor unit and single-unit motor cortical recordings in monkeys, Humphrey and Reed proposed that the brain implements separate control over limb trajectory and limb posture. In one study, monkeys grasped and stabilized the handle of a motorized manipulandum that delivered slowly or rapidly oscillating torque perturbations (Humphrey and Reed 1983). Slow torque oscillations (0.2–0.6 Hz) were compensated by graded, reciprocal activation of slow-twitch motor units in the flexor/extensor muscles, whereas fast oscillations (1.0–1.5 Hz) were compensated by a combination of tonic coactivation of slow-twitch flexor/extensor units and by reciprocal activation of fast-twitch motor units in flexors and extensors. Single-unit cortical recordings revealed two distinct populations of task-related cells in the motor cortical zone with lowest threshold for intracortical microstimulation activation of wrist flexor and extensor muscles. One group of cells (modulated or “M-class” cells) was centered within the posterior part of the wrist area and was “organized for the control of single muscles or groups of synergists acting about the wrist; it receives somatotopically precise sensory input from joint and cutaneous receptors in the wrist and hand.” The second group of cells (SΔ-cells) had discharge rates characterized by shifts (Δ) in steady (S) or “tonic” background level. This group of cells “occupies overlapping cortical space, but is centered a bit more anteriorly; it co-activates antagonist muscles at the wrist, and perhaps also at adjacent joints in the more proximal arm. This system receives significantly less somatosensory input than the first, and unit receptive fields are more complex and diffuse” (see also Cheney and Fetz 1980). Humphrey and Reed proposed that the M-class system is most likely used to produce smooth controlled joint movements, whereas the SΔ system provides central control of joint stiffness. However, the authors clarify that this interpretation is not necessarily equivalent to the view that movement and posture are controlled independently because single-muscle activations mediated by the M-class system may be used either to produce movement or to maintain a constant joint posture in the face of slow perturbations, whereas coactivation of antagonist muscles during the movement of a joint may stabilize the limb's trajectory throughout the course of movement (see also Burdet et al. 2001; Franklin et al. 2007). Moreover, they note that while some pyramidal tract neurons elicit clear coactivation behavior, major coactivation effects could also be exerted by way of brain stem or even cerebellar pathways that were not examined in their study.

More recently, Kurtzer and colleagues reexamined the posture/movement question by examining the sensitivity of primary motor cortical cells to changes in environmental load as monkeys stabilized and/or moved their arms within a horizontal plane (Kurtzer et al. 2005). In a posture task, monkeys stabilized the limb against constant loads that induced nine combinations of shoulder/elbow flexion/extension torques. In a movement task, monkeys moved the hand from a central starting location to eight radial targets while experiencing velocity-dependent torques that impeded joint motion at the shoulder, elbow, both, or neither joint. In a combined task, the monkeys first stabilized a constant load at the starting location and then moved the hand between targets while still opposing the load. The guiding hypothesis for the experiments was that if individual neurons contribute similarly to both postural stabilization and trajectory generation, then their responses to mechanical load should be invariant across tasks. Instead, Kurtzer and colleagues found “a profound shift in load-related cortical processing during posture and movement tasks, providing direct evidence for distinct control processes underlying the two behaviors.” Moreover, in the combined task, they found that within single movement trials, individual M1 neurons demonstrated systematic changes in load sensitivity from postural stabilization before (and after) movement to the perimovement period. These findings strongly support the notion of distinct control processes for posture and movement and that both contribute to the production of goal-directed arm movements.

Our previous two studies also support the existence of specialized processes controlling limb postural impedance and trajectory. In the first, subjects adapted to a visuomotor rotation of cursor motion about the hand's starting location as they performed reach and reversal movements to eight targets in the horizontal plane (Scheidt and Ghez 2007). In reaching, cursor feedback was provided only after movement ended, to isolate learning of final position from trajectory direction. As in the present study, we asked whether learning acquired in one task would transfer to the other, because transfer would suggest that the hand's entire trajectory, including its endpoint, was controlled with a common spatial plan. Instead we found minimal transfer, suggesting that the brain used different representations of target position to specify the hand's initial trajectory and its final stabilized position. We tested this hypothesis in the second study by examining how learning in the two tasks generalizes both to movements made from untrained initial positions and to movements directed toward untrained targets (Ghez et al. 2007). Shifting initial hand position had differential effects on spatial accuracy in the two tasks: Trajectory directions remained unchanged and reversal locations were displaced in the reversal task, whereas the final hand positions of both reaches and reversals were relatively unchanged. Moreover, generalization across directions in reversals was consistent with a hand-centered representation of the desired reversal point as demonstrated previously for this task (Krakauer et al. 2000; Pine et al. 1996), whereas the distributions of final positions in both tasks were consistent with an eye-centered representation as found previously in studies of pointing in three-dimensional space (Admiraal et al. 2003; Crawford et al. 2004; Flanders and Soechting 1990; McIntyre et al. 1997; Soechting and Flanders 1989). These results indicate that the limb's intended trajectory and final position are represented in different coordinate frames, a conclusion that is not inconsistent with the idea that the neural mechanisms controlling limb trajectory and posture are lateralized to the dominant and nondominant hemispheres, respectively (Bagesteiro and Sainburg 2002, 2003; Sainburg 2002; Sainburg and Kalkanis 2000, Sainburg and Schaefer 2004; Sainburg and Wang 2002).

By requiring subjects to adapt their motor commands in reaching to the presence of increased joint impedance caused by their own agonist/antagonist muscle coactivations later in the same movement, the present study provided a further test of our hypothesis that a limb's trajectory may be planned independently of the final stabilized posture. We found that when switching tasks, subjects formed the initial segment of reversal movements by co-opting the muscle activations used to initiate prior reaches and that they also terminated reversals with postural impedance values influenced by those same reaches. This strongly suggests that the nervous system composes movement sequences using trajectories and stabilized postures as elementary learned control actions. Gottlieb was the first to address this question by comparing well-practiced reach and reversal movements similar to those performed in our baseline training conditions. Gottlieb assessed whether reversal movements might be viewed as a staggered superposition of two reaches in opposite directions. As also shown here, Gottlieb found that elbow extensor activity in practiced reversals was more modest than expected given the observed extensor acceleration. (In Fig. 4 and Fig. 5 black traces, compare initial biceps activity and its associated initial flexor acceleration to triceps activity and the extensor acceleration in reversals.) He therefore concluded that reversal movements could not be viewed as a simple concatenation of reaches, and our results support this conclusion. But whereas Gottlieb then suggested that the brain plans movements directly in terms of different muscle activation patterns for each task, we believe his rejection of the idea that reversal movements may be composed of more primitive control actions may have been premature because he did not consider the possibility that reaches themselves are composed of two separate control actions. Indeed, our findings support the idea that the brain uses different mechanisms to plan hand trajectories and final positions in point-to-point movements, that it implements these control actions sequentially in composing reach and reversal movements, and that trajectory planning does not account for specific limb impedance values to be implemented about goal positions to be acquired later in that same movement. Further experiments are needed to determine the control policies that people use to combine trajectory and postural control actions in the composition of complex as well as simple motions.

Adjustment of Control Actions and Modeling of Motor Learning

The importance of both trajectory and impedance control in the generation of stable point-to-point movements is widely acknowledged (Burdet et al. 2001; Feldman 1980, 1986; Franklin et al. 2002). Recognizing that increases in impedance entail undesirable energetic cost, Franklin and colleagues recently proposed an interesting model of motor learning that concurrently reduces kinematic errors and energy costs as subjects adapt to dynamic perturbations of two-joint reaching movements (Franklin et al. 2008). Incorporating Feldman's earlier ideas (Feldman 1980, 1986), this model proposes that responses to performance errors are generated through two separate but coupled controllers: One generates reciprocal activation of antagonistic muscle groups to control net joint torque, while the other coactivates the same muscles to control joint stiffness. By using an iterative algorithm that asymmetrically increases both responses in proportion to hand path error integrated throughout the entire previous trial, these authors could model the changes in hand path kinematics and energy costs progressively in a way that fit recordings from a sample of shoulder muscles as subjects adapted to both predictable and unpredictable dynamic perturbations during goal-directed reaches.

Although Franklin and colleagues claim their model to be general and comprehensive (Franklin et al. 2008), it does not admit the possibility that agonist/antagonist coactivity about a desired final location may be controlled independently of (and in addition to) an automatic adaptive response to trajectory error. It explicitly excludes the possibility that realized kinematics may reflect the phase of movement. As described, Franklin's model determines the amount of agonist/antagonist coactivation based only on the magnitude of trajectory error integrated throughout the entire trajectory, the ratio of slopes on two arms of a V-shaped learning function, and a deactivation parameter that reduces muscle activity when errors are small. Consequently, the model does not (and indeed cannot) explain asymmetric transfer of a learned visuomotor rotation between reach and reversal movements both during and at the end of movement, as observed in our previous studies of horizontal planar movements (Scheidt and Ghez 2007). Because the model does not admit the possibility of distinct trajectory and postural control actions, it cannot explain why visuomotor adaptations of reaches and reversals elicit different patterns of generalization within different spatial reference frames when rotated cursor feedback is timed to coincide with final positions in reaches and trajectories in reversals (Ghez et al. 2007). Regarding the single-joint movements studied here, neither the selective damping of reach trajectory overshoot by instructed increases in terminal CoA nor the corresponding upregulation of initial agonist activation would be expected if impedance and trajectory control were linked in the way described by Franklin's model. Neither would the model predict the increased agonist EMG activity and overshoot errors we observed when subjects switched between reaching and reversal tasks in our study. Indeed, it is not clear how Franklin's model should be modified to account for voluntary modulation of elbow flexor/extensor CoA at the end of reaching movements. All of our present subjects easily mastered this ability, demonstrating that the model is not, in fact, comprehensive.

Although we found that terminal accuracy in reaching was not affected by CoA instruction, the resulting change in joint impedance produced by the HICOA instruction caused systematic reduction in the overshoot and oscillations that otherwise preceded final stabilization (Fig. 2A). Since subjects were instructed to generate movements that were “smooth” and to “reach and hold their hand at the target,” overshoot and oscillation were undesirable features of movement that CoA instruction enabled subjects to minimize. This reduction resulted from the feedforward damping induced by cocontraction and not from online feedback corrections, because peak and steady-state displacements were unchanged by the presence or removal of online cursor vision (compare Fig. 2A solid vs. dashed lines). Either the subjects did not attend to overshoot errors in the LOCOA condition or they did not attempt to correct them. This did not reflect an inability to adaptively adjust the initial peak displacement, since subjects did do so in blocked baseline practice. It therefore seems surprising that subjects did not increase coactivity on their own during reaching to eliminate overshoot and that it required explicit CoA instruction for them to increase mechanical damping. Without such cueing, subjects simply allowed the underdamped elbow dynamics to settle at the target angle. These observations demonstrate that among the hypothetical “equilibrium positions” that may give rise to a realized trajectory, terminal positions appear to be controlled more precisely than positions specified during movement (see also Feldman et al. 1995). This emphasis on the reduction of terminal but not transient positioning errors is at variance with the pattern proposed by Franklin and colleagues (Franklin et al. 2008), in which trajectory updating is driven by errors integrated throughout the entire movement, with emphasis on errors made midmovement when the hand was moving fastest.

Possible Benefits of Separate Posture- and Movement-Control Processes

One benefit of implementing separate control over limb posture and the movements between postures would be a simplification of the computational requirements of control. Hollerbach and Flash suggested that neural planning may be simplified if the brain implements two control mechanisms, one concerned with accounting for limb dynamics and another that compensates for posture-dependent factors such as torques due to gravity (Hollerbach and Flash 1982). These authors showed that inertial and interaction joint torque profiles remain substantially the same at different movement speeds, and it is therefore possible to scale the duration of a learned movement by a factor of r by generating inertial and interaction joint torque profiles that are scaled versions of the original profiles (magnified by a factor of r²). Because posture-dependent torques do not depend on either movement speed or acceleration, they do not scale with movement speed. Motor command generation could be simplified if rate-dependent components of torque (i.e., those specifying movement trajectory) were computed independent of the gravity-dependent and other posture-dependent torques, which would be added in separately.

Another potential benefit would be resilience to variations or errors in the initial trajectory plan (Ghez et al. 2007). As demonstrated in horizontal planar reaching (Gordon et al. 1994), compensation for direction-dependent variations in limb dynamics is imperfect, even for relatively unperturbed movements. Specification of a final equilibrium posture independent of an initial trajectory plan would minimize the kinematic consequence of unmodeled dynamics as the hand approached its target. This control scheme could also allow for dramatic simplification of movement initiation. In one extreme proposal, Karst and Hasan proposed that subjects use a simple kinematic rule to select initial acceleratory EMG activations, not rules that account for either limb statics or dynamics (Karst and Hasan 1991). This proposal was based on analyses of EMG activity recorded while people initiated point-to-point reaching movements in the horizontal plane. Karst and Hasan identified which shoulder and elbow muscles were activated first in any given movement (those they defined as movement agonists) and analyzed these activities as a function of two kinematic parameters: the initial elbow angle (θ_E^init) and the spatial direction (ψ) of the final hand position with respect to the initial forearm orientation. They found distinct regions in this parameter space in which movements were always initiated with either flexor or extensor activations. They compared the boundaries between regions with those predicted if subjects had initiated movements so as either to exert an initial hand force in the direction of the target or to accelerate the hand in the direction of the target. Whereas the first rule predicts boundaries based on statics, the second rule predicts boundaries based on dynamics. Neither rule predicted the boundaries used by subjects at both the shoulder and elbow joints. Instead, the kinematic parameter ψ alone predicted initial muscle activity. We suggest that by specifying a final equilibrium posture independent of the initial trajectory plan, a dual control scheme would minimize the kinematic consequence of errors in initial limb acceleration, regardless of what control rule gave rise to them.

Summary and Conclusions

In summary, our findings support the conclusions that 1) the brain uses different mechanisms to plan the arm's initial trajectory, final position, and final limb impedance about that position in point-to-point movements; 2) it implements the respective control actions staggered in time; and 3) accuracy in goal-directed movements generally requires fine coordination between feedforward trajectory and postural control mechanisms. The findings are important both because they challenge the commonly held (and theoretically appealing) notion that limb posture and movement are controlled with a common neural substrate (Crammond and Kalaska 1996) and because they also begin to explain why patients can exhibit differential impairment of limb posture and movement control in their contralesional (Scheidt and Stoeckmann 2007) and ipsilesional (Schaefer et al. 2009) limbs after stroke. Although untested, the use of terminal coactivity training in physical therapy might be useful in the remediation of impaired limb control in some patients with neurological disorders. For example, training cerebellar ataxia patients to increase terminal cocontraction while reaching might mitigate inaccuracy of intended movements in these individuals. Because ataxia selectively impairs control of hand trajectories and the adaptive adjustment of feedforward commands without corresponding impairment in posture control, it may be possible to train such patients to increase the accuracy of movements by increasing limb impedance at the desired goal through procedures emphasizing voluntary cocontraction.

GRANTS

This work was supported by National Science Foundation Grant BES 0238442 and National Institute of Child Health and Human Development Grant R01-HD-53727.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).