Mechanisms of the contextual interference effect in individuals poststroke

Abstract

Although intermixing different motor learning tasks via random schedules enhances long-term retention compared with “blocked” schedules, the mechanism underlying this contextual interference effect has been unclear. Furthermore, previous studies have reported inconclusive results in individuals poststroke. We instructed participants to learn to produce three grip force patterns in either random or blocked schedules and measured the contextual interference effect by long-term forgetting: the change in performance between immediate and 24-h posttests. Nondisabled participants exhibited the contextual interference effect: no forgetting in the random condition but forgetting in the blocked condition. Participants at least 3 mo poststroke exhibited no forgetting in the random condition but marginal forgetting in the blocked condition. However, in participants poststroke, the integrity of visuospatial working memory modulated long-term retention after blocked schedule training: participants with poor visuospatial working memory exhibited little forgetting at 24 h. These counterintuitive results were predicted by a computational model of motor memory that contains a common fast process and multiple slow processes, which are competitively updated by motor errors. In blocked schedules, the fast process quickly improved performance, therefore reducing error-driven update of the slow processes and thus poor long-term retention. In random schedules, interferences in the fast process led to slower change in performance, therefore increasing error-driven update of slow processes and thus good long-term retention. Increased forgetting rates in the fast process, as would be expected in individuals with visuospatial working memory deficits, led to small updates of the fast process during blocked schedules and thus better long-term retention.

during neurorehabilitation after brain injury, but also in activities such as sports, technical training, and music, one must often learn, or relearn, multiple motor tasks within a given period. Intermixing the learning of different tasks via random schedules reduces performance during training but enhances long-term retention compared with blocked schedules, (e.g., Schmidt and Lee 1999; Shea and Morgan 1979; Tsuitsui et al. 1998). This phenomenon is known as the contextual interference (CI) effect.

Despite close to a century of research (Pyle 1919), however, the mechanism underlying the CI effect are unclear. According to the “forgetting-reconstruction” hypothesis of the CI effect, short-term forgetting between successive presentations of the same task during random training requires the learner to “reconstruct the action plan at each presentation,” resulting in stronger memory representations (Lee and Magill 1983; Lee et al. 1985). Recent computational models similarly suggest a crucial role of working memory in the CI effect. It has notably been proposed that motor adaptation occurs via simultaneous update of a fast process that contributes to fast initial learning but forgets quickly and a slow process that contributes to long-term retention but learns slowly (Joiner and Smith 2008; Smith et al. 2006). We recently extended this model to account for multiple task adaptation (Lee and Schweighofer 2009). In our model, a single fast process is arranged in parallel with multiple independent slow processes switched via contextual cues. During adaptation, motor errors simultaneously update fast and slow processes in a competitive manner. In a situation where tasks are intermixed during training, our model predicts that the decay in the fast process due to both time and interference from other tasks leads to greater update of the slow process. Thus random schedule training should lead to less long-term forgetting than blocked schedule training, as in the CI effect.

Individuals with unilateral stroke-related damage in the sensorimotor areas often exhibit deficits in visuospatial working memory (Winstein et al. 1999). Accordingly, the integrity of visuospatial working memory may play a role in the CI effect in individuals poststroke. The two previous attempts at testing the CI effect in stroke individuals with motor impairments were inconclusive. Specifically, Hanlon (1996) reported a CI effect; the effect of schedules could not be unequivocally determined in this study, however, because the practice sessions were of variable lengths. On the contrary, Cauraugh and Kim (2003) reported no CI effect; the tasks used in this study were strengthening tasks (such as wrist/finger extension), however, not goal-directed tasks that required acquisition of new skills. Thus it is unclear whether these contrasted results are due to either, or both, the experimental design or the heterogeneous grouping of all stroke individuals poststroke with potential differences in working memory, thus masking the CI effect.

The goals of this study are thus to provide a mechanistic explanation for the CI effect using our previous model (Lee and Schweighofer 2009), notably to study the role of the fast process in the CI effect and to test the CI effect in individuals poststroke with visuospatial working memory deficits, providing behavioral support for the model. For this purpose, we designed an experiment in which young nondisabled participants and individuals at least 3 mo poststroke learned how to produce three specific force patterns in either a random or a blocked schedule practice condition. The CI effect was measured by long-term forgetting, the change in performance between two retention tests given immediately and 24 h following training, respectively.

MATERIALS AND METHODS

Participants

Nondisabled participants.

Twenty-four young participants (12 females) with no reported neurological deficits were randomly assigned to either a blocked training schedule or a pseudorandom training schedule (n = 12 in each group; because of problems with the recording device with 1 participant, we analyzed data for 11 participants in the random group and 12 in the blocked group for the retention results). The participants met the following inclusion criteria: >18 yr of age and right hand dominant. A summary of the demographic data for nondisabled individuals is reported in Table 1.

Table 1.

Characteristics of nondisabled individuals

Characteristics	Blocked	Random	P Value
No. of individuals	12	11
No. of men	6	6	>0.1
Age, yr	25.5 ± 1.86	26.7 ± 2.65	>0.1
Power force, N	863 ± 99	794 ± 111	>0.1
Wechsler figural score (max 10)	8.58 ± 0.29	8.33 ± 0.33	>0.1

Values are means ± SE. Max value indicates the maximum score for the Wechsler figural test.

Individuals poststroke.

Twenty-five participants (8 females) with stroke at least 3 mo from onset were randomly assigned to either a blocked training schedule or a pseudorandom training schedule (n = 12 in blocked group, n = 13 in random group). To be included in the study, the participants needed to fulfill the following inclusion criteria: 1) >18 years of age, 2) at least 3 mo poststroke, 3) stable medical condition, 4) an upper extremity (UE) Fugl-Meyer score no less than 33 (Fugl-Meyer et al. 1975); 5) the ability to produce at least 10 N of force in power and 2 N in precision grasp, 6) a score at least 10 out of 17 on the Functional Test of the Hemiparetic Upper Extremity (FTHUE; Wilson 1984), and 7) a score of no less than 25 on the mini mental state exam (MMSE). The participants were excluded from the study if they 1) demonstrated excessive pain in any joint of the more affected extremity that could limit ability to participate in the grasping tasks or 2) had any previous history of surgery of fracture in the affected extremity that might impair their ability to perform the task. A summary of the demographic data for individuals poststroke is reported in Table 2.

Table 2.

Characteristics of individuals poststroke

Characteristics	Blocked	Random	P Value
No. of individuals	12	13
No. of men	8	9	>0.1
Age, yr	61.25 ± 13.92	54.58 ± 13.39	>0.1
No. with left hemiparesis	6	4	>0.1
No. with concordance	7	5	>0.1
Time postonset, mo	39.25 ± 16.45	25.83 ± 22.32	>0.1
Power force, N	462 ± 67	326 ± 29	0.082
UE Fugl-Meyer score
ROM (max 24)	22.58 ± 1.83	22.25 ± 1.76	>0.1
Pain (max 24)	24.00 ± 0.00	23.25 ± 2.30	>0.1
Sensory (max 12)	12.00 ± 0.00	11.00 ± 2.23	>0.1
Motor (max 66)	55.00 ± 8.98	54.00 ± 7.01	>0.1
Wrist (max 10)	9.10 ± 2.81	8.00 ± 3.28	>0.1
Hand (max 14)	12.25 ± 1.54	11.58 ± 2.31	>0.1
FTHUE	14.50 ± 3.53	14.91 ± 2.94	>0.1
MMSE (max 30)	29.25 ± 1.21	29.41 ± 0.90	>0.1
Wechsler digital score (max 24)	16.83 ± 4.71	16.08 ± 3.17	>0.1
Wechsler figural score (max 10)	6.16 ± 1.69	6.67 ± 1.97	>0.1

Values are means ± SE. Max value indicates the maximum score for the indicated test. UE, upper extremity; ROM, range of motion; FTHUE, Functional Test of the Hemiparetic Upper Extremity; MMSE, mini mental state exam.

All participants (nondisabled individuals and individuals poststroke) signed an informed consent to participate in this study, which was approved by the Institutional Review Board at the University of Southern California.

Experimental Design and Procedures

A critical impairment after stroke is the inability to generate precise force output at moderate levels with sufficiently rapid force rise. We thus designed a learning experiment that required learning to exert three force patterns with unique magnitude and timing in response to three visually distinct target force profiles. Participants were pseudorandomly assigned to either a blocked schedule condition or a random schedule condition.

The participants came to our laboratory for two sessions on 2 consecutive days. The first session consisted of physical and cognitive tests, a training session, and an immediate retention test (see below). A delayed retention tests was given 24 h following the first (immediate) retention test. During the training session, all participants were trained on the 3 motor tasks, with 50 trials per task. In the blocked schedule condition, there were 3 blocks of 50 consecutive trials, with a single task within a block. Task order was counterbalanced across participants. In the random schedule condition, there were 50 blocks of 3 trials, with each task occurring once per block at a random order within the block. The initial task order was counterbalanced across participants.

The participants were instructed to reach and grasp a plastic cylinder and to exert a force profile with a power grasp that matched one of three target profiles displayed on a computer screen in both magnitude and timing (Fig. 1). Participant poststroke were instructed to use their affected hand. Nondisabled participants were instructed to use their dominant hand. Force data was acquired through a sensor embedded in the cylinder sampling at a rate of 100 Hz.

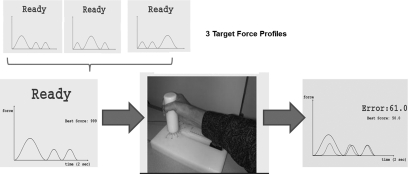
Fig. 1.

Motor task. At each trial, 1 of 3 target force profiles was shown during the “ready” period. The specific force profile was selected according to a predetermined schedule (random or blocked). Two seconds later, a “GO” signal appeared and the participant was instructed to reach and grasp the apparatus and modulate the power grip force to approximate the target profile that lasted 2 s. The computer screen then became blank for 4 s, and feedback was shown for 4 s. Feedback included the actual force profile superimposed with the desired profile, the root mean squared error (RMSE) between the 2 profiles, as a well as a “best score,” which reflected the smallest error so far and was included for motivational purposes.

At the beginning of each trial, one of the three target force profiles was shown. Two seconds later, the target profile disappeared, a “GO” signal was displayed, and the participants were instructed to produce a force trajectory that matched the target force profile. If the participant did not grasp the cylinder within the 2 s of the “GO” signal, the message “Next time move faster” was displayed.

In training trials, feedback was provided 4 s after the end of the target display. Specifically, the actual force trajectory was shown superimposed on the desired trajectory (Fig. 1). An error value was also displayed indicating the total root mean squared error (RMSE) between the desired and actual force trajectory.

To assess performance after training, retention tests were given immediately and 24 h following training. Each test consisted of five trials per task, with each trial similar to training trials but without feedback. In the immediate test for the blocked schedule group, the test for each task was given immediately following the 50 training trials. In the immediate retention tests for the random schedule group, as well in the delayed tests for both groups, the order of the three tasks was randomized.

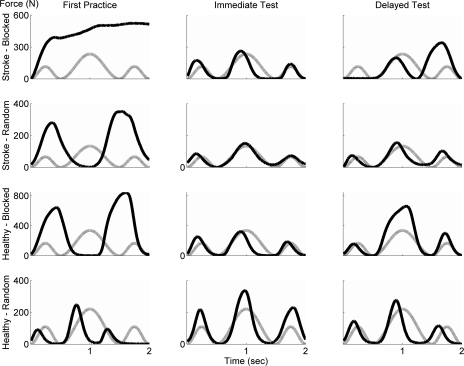
For each participant, maximal force was recorded with the apparatus in three separate trials and averaged before training. The maximum magnitude of each target force profile was set at 40% of maximum force for each participant. Figure 2 shows examples of the force profiles and the actual force trajectories for one force pattern for a representative participant in each group (stroke blocked, stroke random, nondisabled blocked, nondisabled random) for the first trial of training, for the first trial of the immediate test, and for the first trial of the delayed retention test.

Fig. 2.

Examples of force trajectories for 4 participants for 1 task for the first trial of practice (left), the first trial of the immediate retention test (middle), and the first trial of the delayed test (right). Representative data are from a participant poststroke in blocked schedule (stroke-blocked), a participant poststroke in random schedule (stroke-random), a nondisabled participant in blocked schedule (healthy-blocked), and a nondisabled participant in random schedule (healthy-random). The gray line indicates the desired force profile; the black line indicates the actual force (in N) exerted by the participant during 2 s.

Visuospatial Working Memory Test

In our task, participants exerted grip forces based on line-drawing cues visually displayed 2 s previously and not available during force modulation. Furthermore, visual feedback was provided 4 s following force modulation. Thus visuospatial working memory was needed to link the visual information provided as cue and feedback to the actual movement generated. We assessed visuospatial working memory for each participant with the figural memory subtest of the Wechsler memory test revised (Wechsler 1987). In the figural memory test, a target geometrical pattern is presented to the participant. After a 6-s delay, both the target pattern and alternative patterns are shown. The participant is asked to identify the correct pattern. The maximum score for the figural test is 10. The figural test has been used in previous research studies with various clinical populations to assess visual-visuospatial working memory (e.g., Hawkins et al. 1997; Nixon et al. 1987; Winstein et al. 1999). The digital memory subtest of the Wechsler memory score was also given for comparison purpose.

Data Analysis

To compare performance across two schedules and across young nondisabled and stroke individuals, we computed performance at each trial as 1 minus a normalized root mean square error (nRMSE) averaged across the tasks. We normalized the RMSE for each task: we divided the RMSE at each trial by the difference between the maximum RMSE (often but not always on the first trial) and the minimum RMSE generated during training. The nRMSE for subject i at trial n is thus given as nRMSE_i(n) = [RMSE_i(n) − min(RMSE_i)]/[max(RMSE_i) − min(RMSE_i)], where min(RMSE_i) and max(RMSE_i) are calculated for subject i across training trials for all three tasks.

Our main dependent measure was “long-term forgetting.” Long-term forgetting was computed as the difference in task performance between the immediate and the 24-h test. As a measure of retention performance in the immediate and delayed retention tests, we used the average performance in the first trial for the three tasks. We did not use all five trials of each task in the retention test because we noted that performance largely improved during the test even without feedback in the nondisabled participant group (e.g., immediate group, average of 3 tasks, repeated ANOVA for the 5 test trials: P < 0.001 in blocked condition, P = 0.04 in random condition).

All data (and residuals for regression models) used were tested for normality with the Shapiro-Wilks' test and for equality of variance with the Levene's test. For group comparisons, when the data were normally distributed and when the sample size was ≥10 in each group, we used t-tests for independent measures and paired t-tests for repeated measures. Otherwise, we used the Mann-Whitney test for independent measures. In repeated ANOVA, nonspherical data were corrected using Greenhouse-Geisser correction. Differences between groups in participants' baseline characteristics were tested with t-tests when the data were numerical (e.g., age) and with χ² tests when the data were categorical (e.g., sex). We classified the individuals with stroke as “high” and “low” function in visuospatial working memory, based on a cutoff of 7 on the figural Wechsler score (the cutoff value was chosen because it yielded nearly equal group sizes in our data set) and compared the effect of practice schedules for high- and low-level groups. Our significance level in all tests was set at P < 0.05.

Computer Modeling

It has been proposed that motor adaptation occurs via simultaneous update of a fast process that contributes to fast initial learning but forgets quickly and a slow process that contributes to long-term retention but learns slowly (Joiner and Smith 2008; Smith et al. 2006). We recently extended this model to account for multiple task adaptation (Lee and Schweighofer 2009). In our model, a single fast process is arranged in parallel with multiple independent slow processes switched via contextual cues. During adaptation, motor errors simultaneously update the fast and the selected slow processes in a competitive manner. Because the model was specifically developed to account for multiple task-adaptation, it can be used to simulate the changes in performance resulting from different task schedules. We therefore tested in what conditions, if any, the model could reproduce the CI effect.

The model contains one fast process and N slow processes, with N being the number of tasks, all organized in parallel (the model is thus called a 1-fast N-slow parallel model). The model output and the state update rules are given by Eqs. 1 and 2, respectively:

$$y\left(n\right)=x_{\text{f}}\left(n\right)+{\text{x}}_{\text{s}}{\left(n\right)}^T\text{c}\left(n\right)$$ (1)

$$\begin{array}{l}{x}_{\text{f}}\left(n+1\right)=A_{\text{f}}{x}_{\text{f}}\left(n\right)+B_{\text{f}}e\left(n\right)\\ {\text{x}}_{\text{s}}\left(n+1\right)=A_{\text{s}}{x}_{\text{s}}\left(n\right)+B_{\text{s}}e\left(n\right)\text{c}\left(n\right)\end{array}$$ (2)

where n is the trial number. The motor error determined by the difference between an external perturbation f(n) and the motor output y(n) at time step n is e(n) = f(n) − y(n), x_f is the state of the fast process, x_s is the state vector of the slow process, and c is the contextual cue vector, with both x_s and c vectors having a length equal to the number of tasks, N. Because we assumed no interference and perfect switching among states in the slow process in the model, c is a unit vector with a single non-zero element. A_f is the forgetting rate of the fast process, A_s is the forgetting rate of the slow processes, B_f is the learning rate of the fast process, and B_s is the learning rate of the slow processes. Default parameters in the model in the current simulations were A_f = 0.8, B_f = 0.2, A_s = 0.995, and B_s = 0.04, and they were hand-tuned to qualitatively reproduce the learning curve of the nondisabled subjects in the blocked and random schedule.

At trial n, the motor output is generated by the sum of the fast process and the corresponding slow process, according to Eq. 1. After a task is presented, if the motor error is not zero, both the fast state and the corresponding slow state are updated according to Eq. 2. Because of the gating by the contextual input, the slow states for other (nonpresented) tasks are not updated after this trial but instead decay with forgetting rate A_s. When no tasks are presented, such as after training, for instance, all fast and slow processes decay toward zero. Forgetting in the fast processes is rapid (in the order of tens of seconds), but forgetting in the slow processes is more long-lasting (in the order of tens of minutes). Although we do not model long-term retention (in the order of days), it has been shown that for adaptation to one task, the amount of long-term retention is predicted as the level of activity in the slow process at the end of training (Joiner and Smith 2008). Thus, to compare computer simulations with in our experimental data, performance for the first task at the end of training was taken as immediate retention performance; level of the slow process for the first task at the end of training was taken as long-term retention at 24 h.

In the present work, the competition between the fast and slow processes for errors is crucial to explain the differential effects of blocked and random schedules. Such competition stems from the model's parallel architecture. In our previous work (Lee and Schweighofer 2009), we showed that only the parallel 1-fast N-slow architecture, and not the serial 1-fast N-slow architecture, could account for adaptation data in a random schedule. Because of this parallel architecture of the model, the fast and slow processes compete for motor errors at each trial. Thus, in a blocked task presentation, there is no interference in the fast process, which is only updated by the errors of the task presented in the block. Because the fast process as a high learning rate (compare the values of the parameters B_f and B_s and above), errors will be quickly reduced. In a random schedule, however, there are large interferences in the fast process; if the two perturbations have equal magnitude but opposite signs, for instance, the fast process will have activity oscillating around zero. As a result, the changes in performance during training will be driven mostly by the slow process. See Lee and Schweighofer (2009) for additional details of the model.

In addition, we made the simplifying assumption that, in the model, the integrity of visuospatial working memory is linked to the rate of decay of the fast process, with larger rates of decay linked to poorer visuospatial working memory. We thus modeled the integrity of visuospatial working memory by modulating the time constant τ_f in the fast process, with τ_f = 1/(1 − A_f)T, where A_f is the fast process forgetting rate given in Eq. 2 and T corresponds to a simulated trial length, which was 12 s as in the experiment. The default “normal” forgetting rate A_f = 0.8 gives τ_f = 60 s. A small time constant, which indicates fast decay in the fast process (small value of forgetting rate A_f), is used to model poor working memory. The default “poor” working memory forgetting rate was A_f = 0.4, which gives τ_f = 20 s.

RESULTS

The CI Effect in the Computational Model

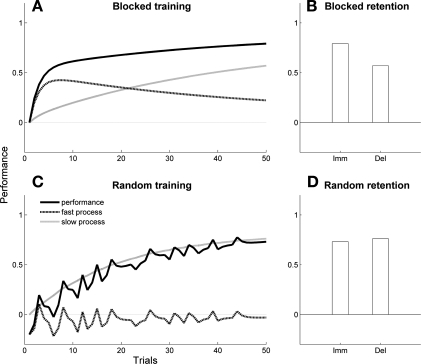
Our computational model reproduced the CI effect: slower improvements in performance during training (Fig. 3, A and C, black lines) and less long-term forgetting following training in random schedules than in blocked schedules (Fig. 3, B and D). During blocked presentations, the fast process exhibited high activity levels (Fig. 3A, dotted line) because there was little long-term forgetting during the short intervals between presentations of the same task. Because fast and slow processes compete for errors, the high activity levels of the fast process leads to relatively little update of the slow process (Fig. 3A, gray line). As a result, there was fast adaptation during training but large long-term forgetting in delayed retention (Fig. 3B). In contrast, during random presentations, the fast process exhibited low and jittered activity levels (Fig. 3C, dotted line); this occurred because interferences between tasks was high and the passage of time between presentations of the same task was relatively long. This led to relatively large update of the slow process (Fig. 3C, gray line). As a result, there was relatively slow adaptation during training but little long-term forgetting in delayed retention (Fig. 3D, compare with B). Specifically, at the end of training and for task 1 for the blocked schedule, performance was 0.79 and the slow process was 0.57 (performance is equal to the slow process at long-term retention; see materials and methods); for the random schedule, performance was 0.73 and the slow process was 0.76.

Fig. 3.

Computer simulations: contextual interference (CI) effect in the nondisabled model. Performance (black line), fast process (dotted line), and slow process (gray line) are shown during blocked (A) and random schedule training (C). Immediate and long-term retention are shown following blocked (B) and random schedule training (D). Imm, immediate test; Del, 24-h delayed test. Notice the large forgetting following blocked training and slower performance improvement during random than during blocked training. The jitter in the fast process memory (reflected in performance) during random training in C was due to both decay and interferences between the tasks.

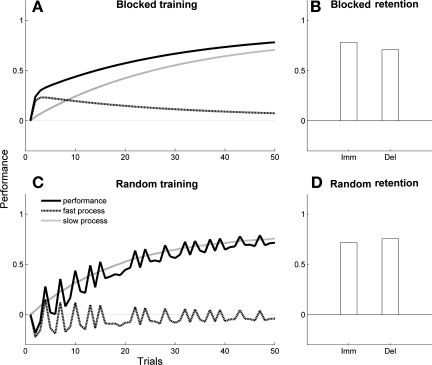
Our model makes the prediction that the integrity of visuospatial working memory differentially affects delayed retention in blocked and random schedules. In Fig. 4, a simulated participant with poor visuospatial working memory (parameter A_f = 0.4) showed little long-term forgetting following either blocked or random schedule training (B and D). During blocked schedule training (Fig. 4A), compared with the simulated participant with normal visuospatial working memory in Fig. 3A, there was reduced update of the fast process because of large long-term forgetting from one trial to the next. However, because of the competition between fast and slow process, there was an enhanced update of the slow process (Fig. 4A, gray line). Long-term forgetting following blocked training was then minimal (Fig. 4B). During random schedule training (Fig. 4C), the update of the slow process was nearly identical to that of the normal simulated participant (Fig. 3C). Specifically, at the end of training and for task 1 for the blocked schedule, performance was 0.78 and the slow process was 0.71 (performance is equal to the slow process at long-term retention, see materials and methods); for the random schedule, performance was 0.72 and the slow process was 0.75.

Fig. 4.

Computer simulations: reduced CI effect in a model with poor visuospatial working memory. Performance (black line), fast process (dotted line), and slow process (gray line) are shown during blocked (A) and random schedule training (C). Immediate and long-term retention are shown following blocked (B) and random schedule training (D). In blocked schedules, there was little forgetting in the delayed retention test (B; compare with Fig. 3B) because of relatively higher buildup of slow process and lower buildup of fast process during training (A; compare with Fig. 3A). In random schedules, there was little difference during training (C) and testing (D) compared with the normal model (compare with Fig. 3, C and D).

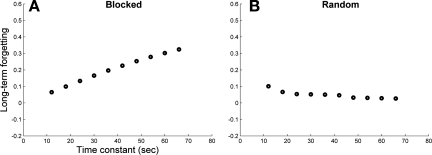
In the model, long-term forgetting following blocked schedule training positively correlates with the time constant of visuospatial working memory: for small time constants (i.e., poor visuospatial working memory), there was little long-term forgetting in the delayed test (Fig. 5A, left), because much short-term forgetting happened between presentations during training (as in Fig. 4A). For larger time constants (i.e., good visuospatial working memory), there was large long-term forgetting in the delayed test (Fig. 5A, right), because little short-term forgetting happened between presentations during training (as in Fig. 3A). In contrast, long-term forgetting following random schedule training did not correlate with this time constant (Fig. 5B): because of interference between tasks during training, there was little buildup of fast process.

Fig. 5.

Computer simulations: forgetting measured at the delayed retention test as a function of the time constant of decay of fast process after either blocked (A) or random schedule (B) for 2 tasks. Overall, and notably for larger time constants, there was less forgetting following random schedule than blocked schedule. However, for smaller time constants, forgetting was comparable following random and blocked schedule.

The CI Effect in Nondisabled Individuals

We first examined whether the typical CI effect was replicated with our tasks in our young nondisabled sample. There was no difference in baseline characteristics between the two nondisabled groups for sex, age, maximal power grip force, and Wechsler figural score in nondisabled participants (see Table 1).

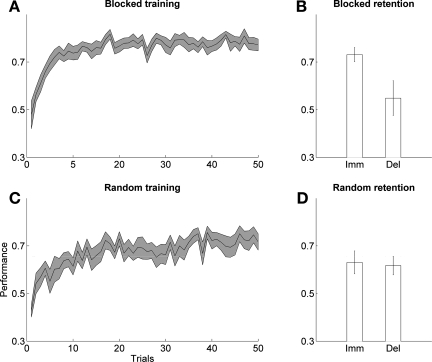
Long-term forgetting was positive following blocked training (0.183 ± 0.063; P = 0.011, 1-sample t-test) but not following random training (−0.0004 ± 0.041; P = 0.99, 1-sample t-test). Furthermore, long-term forgetting was greater following blocked schedule than following random training (P = 0.023, t-test) (see Fig. 6, B and D).

Fig. 6.

Data: CI effect in nondisabled participants. Performance (mean and SE) is shown during blocked (A) and random training (C). Immediate and long-term retention are shown following blocked (B) and random training (D).

The performance of participants in both groups improved during training in both conditions (repeated-measures ANOVA, 10 blocks of 5 trials: P ≤ 0.0001 for both blocked and random groups) (Fig. 6, A and C). There was no difference in performance in the first block of five trials between groups (P = 0.129, t-test), no difference in the last block of five trials (P = 0.233, t-test), and no difference in the overall change in performance between the first and the last block of five trials (P = 0.763, t-test). However, performance continued to improve in the random group after the first five trials, but not in the blocked group. To show this, we regressed the performance from trials 6 to 50 as a function of trial number for each participant: the slopes were positive in the random group (mean 0.0051 ± 0.0006 trial⁻¹) but near zero in the blocked group (mean 0. 0015 ± 0.0011 trial⁻¹) and larger in the random group compared with the blocked group (P = 0.008, t-test).

The CI Effect in Individuals Poststroke

There was no difference in baseline characteristics between the two groups for sex, age, side of paresis, concordance of stroke (i.e., whether the stroke affected the dominant hand), time postonset, maximal force, any of the UE Fugl-Meyer subscale scores [range of motion (ROM), pain, sensory, arm motor, hand, wrist], FTHUE, MMSE, and Wechsler figural score (all values are given in Table 2). The only marginally non-zero difference between groups was maximal power grip force (blocked: 462 ± 67 N; random: 326 ± 29 N; P = 0.082, t-test).

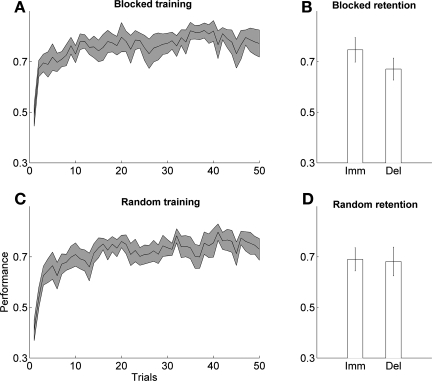
We first examined the CI effect for all individuals poststroke (i.e., without dividing the participants into subgroups based on their figural memory test scores). Long-term forgetting was marginally positive following blocked training but not following random training (blocked: 0.076 ± 0.040, P = 0.085; random: 0.0085 ± 0.063, P = 0.89, 1-sample t-tests) (see Fig. 7, B and D). Furthermore, long-term forgetting was not different following blocked and random training (P = 0.342, t-test). We verified that there was no correlation between maximal power grip force and long-term forgetting in either group (blocked: P = 0.97; random: P = 0.75, Pearson).

Fig. 7.

Data: CI effect in participants poststroke. Performance (mean and SE) is shown during blocked (A) and random training (C). Immediate and long-term retention are shown following blocked (B) and random training (D).

The performance of participants in both groups improved during training in both conditions (repeated-measures ANOVA, 10 blocks of 5 trials: P < 0.0001 for both groups, Greenhouse-Geisser corrections) (Fig. 7, A and C). There was no difference in performance in the first trial between groups (P = 0.12, t-test). Furthermore, there was no difference in performance in the first block of five trials between groups (P = 0.13, t-test), no difference in the last block of five trials (P = 0.67, t-test), and no difference in the overall change in performance between the first and the last block of five trials (P = 0.19, t-test). There was no difference in slopes between group in the regression model of performance vs. trials 6–50 (P = 0.63, t-test; see above for details of analysis).

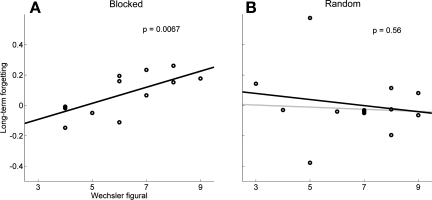
Our simulations predict that visuospatial working memory integrity influences the degree of long-term forgetting after blocked schedules but not after random schedules. Figure 8A illustrates the strong dependency of the figural Wechsler score on long-term forgetting in the blocked schedule (compare Figs. 5A and 8A). A repeated ANOVA model with test as repeated factor and figural Wechsler as covariate showed significant long-term forgetting in the blocked schedule (P = 0.025) and a significant effect of the figural Wechsler on long-term forgetting (P = 0.0067). A similar analysis show no long-term forgetting in the random schedule (P = 0.55) and no effect of the figural Wechsler score on long-term forgetting (P = 0.56), again as predicted by our computer simulations (compare Figs. 5B and 8B).

Fig. 8.

Data: forgetting in individuals poststroke in a 24-h posttraining period is shown as a function of Wechsler visual memory score (figural) following training in either blocked (A) or random schedule (B) in the individuals poststroke who participated in the study. Black lines are regression lines; the gray line in B is a robust regression line (with default weighting function in Matlab robustfit function); the robust regression line is superimposed on the regression line in A. Compare with the computer simulations of Fig. 5.

The influence of visuospatial working memory on long-term forgetting is well illustrated by classifying stroke individuals between high and low visuospatial working memory based on a cutoff of 7 on the figural Wechsler memory score. The difference between long-term forgetting in blocked and random schedules was significant in the high spatial working memory subgroups (n = 5 high spatial working memory in blocked, n = 8 high spatial working memory in random; P = 0.042, Mann-Whitney test). However, there was no difference in long-term forgetting in the low spatial working memory subgroups (P = 0.40, Mann-Whitney test).

Finally, we verified that in the individuals poststroke enrolled in the study, there was no correlation between the figural Wechsler memory score and any motor and sensory variables (maximum power force, P = 0.482; UE Fugl-Meyer ROM, P = 0.480; UE Fugl-Meyer pain, P = 0.825; UE Fugl-Meyer sensory, P = 0.316; UE Fugl-Meyer motor, P = 0.839; UE Fugl-Meyer wrist, P = 0.330; UE Fugl-Meyer hand, P = 0.615; FTHUE, P = 0.839). There was no correlation of the figural memory score with the digital Wechsler memory score (P > 0.87). The only significant correlation between the figural score was with the MMSE (r = 0.70, P < 0.0005). Furthermore, there was no correlation between long-term forgetting and any motor and sensory variables (maximum power force, P = 0.66; UE Fugl-Meyer ROM, P = 0.34; UE Fugl-Meyer pain, P = 0.98; UE Fugl-Meyer sensory, P = 0.79; UE Fugl-Meyer motor, P = 0.2; UE Fugl-Meyer wrist, P = 0.31; UE Fugl-Meyer hand, P = 0.44; FTHUE, P = 0.56). Since the MMSE contains working memory components, this validates the use of the Wechsler figural memory score as a visuospatial working memory test in our study. These results indicate that it is the integrity of figural visuospatial working memory, not any motor or sensory impairment after stroke, that leads to the observed changes in long-term forgetting following blocked training.

DISCUSSION

In this study, we have replicated the CI effect in nondisabled participants and present novel evidence that the CI effect can hold in participants with stroke affecting the motor system but is modulated by the integrity of visuospatial working memory. Our results indicate that individuals with stroke with normal visuospatial working memory, like nondisabled individuals, exhibit less long-term forgetting of visuomotor skills acquired in random training schedules than in blocked training schedules. In contrast, individuals with stroke with low visuospatial working memory exhibit little long-term forgetting after either random or blocked schedules. Our results may explain why previous studies reported conflicting results on the CI effect in individuals with stroke (Cauraugh and Kim 2003; Hanlon 1996), since participants were not separated by low and high working memory capabilities.

The rather counterintuitive effect of the integrity of visuospatial working memory on long-term retention following blocked schedules (the better the working memory, the worse the long-term retention!) was predicted on a theoretical basis with our previous computational model of motor memory (Lee and Schweighofer 2009). Furthermore, we found no other motor or sensory variables that correlated with long-term forgetting after training in the blocked schedule or with the integrity of visuospatial working memory. Thus our combined computational and experimental results suggest that the integrity of visuospatial working memory is a crucial factor underlying the modulation of the CI effect in participants poststroke in our experiment.

Although the CI effect has led to a considerable amount of research over almost a century (Magill and Hall 1990), its underlying mechanism has remained unclear. Three nonexclusive hypotheses have been proposed to explain the CI effect in motor learning. First, according to the “elaboration-distinctiveness” hypothesis, random training schedules allow intertask comparisons during the planning stage that lead to distinctive memory representations (e.g., Cross et al. 2009; Immink and Wright 2001; Lin et al. 2008; Shea and Morgan 1979). Second, according to the “deficient processing” hypothesis, blocked repetitions lead to reduced rehearsal or attention in later presentations (e.g., Callan and Schweighofer 2010; Hintzman et al. 1973). Third, according to the “forgetting-reconstruction” hypothesis of the CI effect, forgetting between successive presentations of the same task during random training results in stronger memory representations (Lee and Magill 1983; Lee et al. 1985).

In this report, we propose a novel mechanistic account of the CI effect in motor learning. Like in the forgetting-reconstruction hypothesis, our account of the CI effect relies on forgetting between presentations of the same task during training. The specific mechanisms underlying the enhancement of long-term memory differ in the forgetting-reconstruction hypothesis and in our model, however. According to the forgetting-reconstruction hypothesis, forgetting in working memory between spaced presentations necessitates retrieval from long-term memory, which increases long-term retention. In our model, forgetting in visuospatial working memory between spaced presentations during training leads to slower improvements in performance in random schedule than in blocked schedules. The resulting greater errors during training benefit the update of the slow process, leading to better long-term retention. Note that our account of the CI effect does not exclude additional explanations such as the elaboration-distinctiveness and the deficient processing theories; further studies are needed to dissociate the possible contributions of such mechanisms. Moreover, further studies are needed to determine the putative neural substrates for the slow and fast processes. For example, we recently showed that the neural substrates of memory consolidation depend on practice structure (Kantak et al. 2010).

Our results have implications for rehabilitation of patients with stroke. Although there is good evidence that task training is effective for improving upper extremity function after stroke (Butefisch 1995; Kwakkel et al. 1999; Wolf et al. 2002, 2006), none of these studies addresses the “microscheduling” of individual tasks. Thus, although the use of random task schedule during training has been advocated (Krakauer 2006), physical and occupational therapists rely on guidelines that simply suggest inclusion of extensive and variable training without weighing heavily on individual capability (e.g., Bach-y-Rita and Balliet 1987; Lee et al. 1991). Our results suggest that patients with stroke with normal visuospatial working memory should receive training schedules that mix tasks randomly. Because such training is hard to implement in normal therapeutic situations and places high demand on the therapists, robots that can present functional tasks and that can easily switch between these tasks during training could be developed; see our preliminary work in this direction (Choi et al. 2009). On the contrary, and in a rather counterintuitive manner, our results suggest that individuals with stroke with poor visuospatial working memory can receive blocked training schedules with no compromise to long-term retention.

Our experiment has a number of limitations that need to be addressed in future work. First, our study included only a relatively small number of participants in each group and needs replication with a larger sample size and different populations, such as the elderly. In the current study, we chose to study young healthy subjects as a control population and not (older) age-matched controls because the elderly show decreased working memory capability, which might have led to a reduced CI effect in this population (see Anguera et al. 2011). Two CI studies have found a CI effect in motor tasks in older adults (Lin et al. 2007, 2010). Lin et al. (2010) directly compared young and elderly subjects on a serial reaction time task and found the CI effect in both groups. Lin et al. (2007) found a CI effect in a subject population of ages similar to those of our participants poststroke with motor tasks similar to ours in that subjects were to produce different force patterns as a result of specific visuomotor patterns. Second, although the young participants in our study were instructed to use their dominant hand, the participants poststroke were instructed to use their most affected hand, which was or was not their affected hand before stroke. There is therefore the slight possibility that our results are due to not-controlled handedness, although concordance was balanced across groups (see Table 2). Third, a prediction of the model is that poor visuospatial working memory will reduce the rate of performance improvement during acquisition in blocked practice. We found no correlation between the figural memory and the rate of learning in the stroke group, however. This can be due to the large variability between and within participants at each trial during training in the stroke group compared with the nondisabled group (compare the shaded areas of Figs. 6A and 7A). Increasing the sample size in motor tasks that lead to less trial-by-trial variability may be desirable. Fourth, because visuospatial working memory is thought to have a limited capacity (e.g., Cowan 2001), it is possible that in addition to, or in lieu of, shortened time span, limited visuospatial working memory in our participants is due to a deficit in the number of items that can be stored in memory (our current model of motor memory cannot account for such limited storage mechanism). Fifth, we were only able to obtain the MRI scans for a small subset of our participants. In future work, it would be most interesting to relate stroke characteristics, such as locations and volumes, to the amount of CI effect that can be induced.

Similarly, our model, because of its simplicity, has a number of important limitations. First, like others (e.g., Kording et al. 2007; Smith et al. 2006), we only attempted to model the common neuronal mechanism of error-driven motor adaptation or learning, not the mechanism for specific types of motor adaptation or learning. As such, the model accounts for dual-adaptation data in eye movement, visuomotor rotation, and force field adaptation (see Lee and Schweighofer 2009). However, our model does not account for the effect of physiological factors, such as muscle mechanics, etc., of our specific experimental tasks. Second, although our computation model is a model of motor adaptation (where “adaptation” is the change in motor performance that allows the motor system to regain its former capabilities in altered circumstances), we used it in this study to account for visuomotor learning of novel tasks. Such extension from adaptation to motor learning requires us to make two assumptions about motor learning in our experiment. The first assumption is that learning in our experiment is error driven. Since we provided an error measure in the form of the actual force trajectory superimposed on the desired trajectory (Fig. 1), this appears reasonable. In addition, there is also a large body of evidence that supports the fact that skill learning is at least in part driven via errors (reviewed for instance in Hikosaka et al. 2002). The second assumption is that skill learning, like motor adaptation, results from a combination of fast and slow memory processes; there is a large body of evidence that supports this view (see for review Anguera et al. 2009, 2010, 2011). The final and perhaps most crucial limitation of our model in the current context is that our model assumes that there is no interference/generalization between tasks in the slow processes. Thus our model cannot reproduce any transfer of learning effect across tasks. This is clearly an oversimplification in light of the similarities between the three tasks in our experiment (see Fig. 2), and this prevented us from using the participant data to estimate the model parameters (which had to be hand-tuned instead). However, our simulation results show that our model well accounts for the CI effect when performance across tasks are averaged. Further work is needed to determine whether the CI effect occurs when several unique tasks, such as a force task, a digit manipulation task, and a bimanual task, etc., are given.

In summary, our combined theoretical and experimental results suggest a relationship between the integrity of visuospatial working memory and motor learning. Such a relationship between working memory and motor learning has been previously reported in a number of recent studies (e.g., Anguera et al. 2010; Boyd and Winstein 2004; Keisler and Shadmehr 2010); our results add to and extend this body of work by showing that working memory is involved in the CI effect. Causal evidence for a role of visuospatial working memory in the CI effect in motor learning may be obtained via virtual lesion of the areas involved in visuospatial working memory via repetitive transcranial magnetic stimulation (see related, Tanaka et al. 2010).

GRANTS

This work was funded by National Institute of Child Health and Human Development Grant R03 HD050591-02 and National Science Foundation Grants IIS 0535282 and PAC 1031899 to N. Schweighofer.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).