Representation of limb kinematics in Purkinje cell simple spike discharge is conserved across multiple tasks

Abstract

Encoding of movement kinematics in Purkinje cell simple spike discharge has important implications for hypotheses of cerebellar cortical function. Several outstanding questions remain regarding representation of these kinematic signals. It is uncertain whether kinematic encoding occurs in unpredictable, feedback-dependent tasks or kinematic signals are conserved across tasks. Additionally, there is a need to understand the signals encoded in the instantaneous discharge of single cells without averaging across trials or time. To address these questions, this study recorded Purkinje cell firing in monkeys trained to perform a manual random tracking task in addition to circular tracking and center-out reach. Random tracking provides for extensive coverage of kinematic workspaces. Direction and speed errors are significantly greater during random than circular tracking. Cross-correlation analyses comparing hand and target velocity profiles show that hand velocity lags target velocity during random tracking. Correlations between simple spike firing from 120 Purkinje cells and hand position, velocity, and speed were evaluated with linear regression models including a time constant, τ, as a measure of the firing lead/lag relative to the kinematic parameters. Across the population, velocity accounts for the majority of simple spike firing variability (63 ± 30% of R_adj²), followed by position (28 ± 24% of R_adj²) and speed (11 ± 19% of R_adj²). Simple spike firing often leads hand kinematics. Comparison of regression models based on averaged vs. nonaveraged firing and kinematics reveals lower R_adj² values for nonaveraged data; however, regression coefficients and τ values are highly similar. Finally, for most cells, model coefficients generated from random tracking accurately estimate simple spike firing in either circular tracking or center-out reach. These findings imply that the cerebellum controls movement kinematics, consistent with a forward internal model that predicts upcoming limb kinematics.

multiple studies have consistently concluded that the simple spike discharge of Purkinje cells encodes movement kinematics. Correlations with movement position, direction, amplitude, velocity, and speed are found in a variety of single-joint and multijoint limb movement tasks, particularly for Purkinje cells located in the intermediate and neighboring lateral zones around the primary fissure (Coltz et al. 1999; Fortier et al. 1989; Fu et al. 1997; Harvey et al. 1977; Mano and Yamamoto 1980; Marple-Horvat and Stein 1987; Pasalar et al. 2006; Roitman et al. 2005; Thach 1970). Eye position, velocity, and acceleration signals dominate the discharge of flocculus Purkinje cells during smooth pursuit and ocular following (Gomi et al. 1998; Medina and Lisberger 2009; Shidara et al. 1993; Stone and Lisberger 1990). During passive limb movements, position and velocity are signaled in the simple spike firing of anesthetized or decerebrate cats and rats (Giaquinta et al. 2000; Kolb et al. 1987; Rubia and Kolb 1978; Valle et al. 2000).

Conversely, evidence is limited that Purkinje cell discharge encodes the motor command needed to execute hand movements. Early electrophysiology studies demonstrated that Purkinje cell simple spikes exhibit reciprocal activity with single-joint movement timing and muscle activity, but the muscle activity was not dissociated from the movement kinematics (Frysinger et al. 1984; Gilbert and Thach 1977; Smith 1981; Thach 1968, 1970). In visuomotor tracking, the simple spike firing exhibits stronger correlations with arm kinematics than with EMG activity (Coltz et al. 1999; Roitman et al. 2005). Similarly, in a button pushing task, on average, only 6–7% of the variability in the simple spike firing is accounted for by EMG activity (Holdefer and Miller 2009). Although brief changes in simple spike discharge occur when switching from a resistive to an assistive force during elbow rotation, it remains to be determined whether this transient change in simple spike firing encodes specific joint torques and/or muscle forces (Yamamoto et al. 2007). However, when kinetic encoding was directly tested in a manual tracking task that explicitly controls kinematics while varying loads and force fields, the large majority of Purkinje cell simple spike firing does not modulate with the type (e.g., viscous or elastic) or magnitude of the force field (Pasalar et al. 2006). Therefore, evidence that anterior lobe Purkinje cells encode kinetic parameters and/or muscle activity is still lacking.

Many theories have been proposed to explain how the cerebellum might use representations of movement kinematics to produce accurate, coordinated movements. One prominent hypothesis is that the cerebellum acts as a forward internal model, transforming the motor command and the current state of the limb into a prediction about the future state of the limb, such as the upcoming movements or errors (Kawato 1999; Kawato and Wolpert 1998; Wolpert et al. 1998). These predictions of the upcoming movements would likely be expressed in terms of sensory consequences and kinematic variables (Wolpert et al. 1995).

A forward internal model by definition would require feedforward and predictive control (Bastian 2006; Ebner and Pasalar 2008). Many previous studies used highly predictable tasks in which monkeys were given cues about upcoming task parameters and the trajectory paths were relatively fixed, allowing the animals to easily anticipate and plan subsequent movements (Coltz et al. 1999; Fortier et al. 1989; Fu et al. 1997; Marple-Horvat and Stein 1987; Roitman et al. 2005). These paradigms result in highly stereotypical movements with relatively few task-related errors in which Purkinje cell simple spike discharge largely leads arm/hand kinematics (Fu et al. 1997; Marple-Horvat and Stein 1987; Roitman et al. 2005). However, the predictable movements and relatively few task errors make it difficult to determine whether the observed leads reflect the subject's anticipation and planning for the upcoming trial or direct control of the current movement trajectory. A task with minimal predictability is necessary to answer this question.

Another important issue is the degree to which a single Purkinje cell invariantly signals the same information for different movements. This question is central to the hypothesis that the cerebellar cortex is the site of multiple internal models (Imamizu et al. 2003; Kawato and Wolpert 1998; Wolpert et al. 1998). If signals in the simple spike discharge differ greatly for different tasks, this would reflect a nonparametric representation consistent with the concept of multiple internal models for specific movements. Conversely, if the signals present in a particular type of movement can be used to predict the firing in different tasks, this would suggest that Purkinje cells have a parametric representation of limb kinematics that can generalize over a wide range of behaviors. Our previous study showed that estimates of the kinematic signals obtained during circular tracking were able to predict with modest accuracy the simple spike firing during the target intercept period (Roitman et al. 2005). However, circular tracking and other previously tested behavioral tasks provide only limited coverage of the kinematic workspace, which limits the robustness of any firing models created from the data sets. Rigorous testing of invariant encoding requires firing models built from data that extensively explore the kinematic workspace, so that model bias is minimized when applied to different movements.

Previous studies also typically relied on substantial data averaging, both across trials and time, to assess the signals present in the simple spike firing (Coltz et al. 1999; Fu et al. 1997; Marple-Horvat and Stein 1987; Medina and Lisberger 2009; Pasalar et al. 2006; Roitman et al. 2005; Shidara et al. 1993). While providing significant insights into the parameters signaled, averaging firing data discards information in the data set, leading to regression coefficients that are likely biased (Freund 1971; Zar 1999). Conclusions about the nature of the signals encoded in the firing cannot be ensured to generalize to other movements or tasks. Furthermore, averaging is guaranteed to increase the R² value by removing variability in the sample. The increase is deceptive because models based on averaged data (also called aggregate models) describe the grouped behavior rather than the effects of individual time points or trials (Kenny 1979). Therefore, the goal should be to understand the nature and the strength of the signals carried in the instantaneous firing rate, rather than striving to simply maximize the variance that a model can account for (O'Grady 1982).

In this study, we developed a behavioral paradigm in which monkeys were trained to manually track a target that moved pseudorandomly at unpredictable speeds and directions. Although used to study the encoding of information in the motor cortex (Paninski et al. 2004a, 2004b), deficits in cerebellar stroke (Boyd and Winstein 2004), and cerebellar activation during neuroimaging (Imamizu et al. 2000), a random tracking paradigm has not been utilized in an electrophysiology study targeting the cerebellum. Random tracking has several advantages. The task provides excellent coverage of the position, velocity, and speed workspaces (Paninski et al. 2004a) and eliminates the confound of predictability. Random tracking also reduces the statistical dependencies among the kinematic parameters and requires continuous control of the movement throughout the task (Paninski et al. 2004a). Purkinje cell simple spike firing recorded during a random tracking task was evaluated for position, velocity, and speed encoding. Timing relationships between the firing and these parameters were also characterized. We compared regression model results using averaged versus nonaveraged data to determine whether these kinematic variables are reliably encoded in the firing at the level of individual trials. Finally, Purkinje cell firing was evaluated in two additional tasks, to determine whether the signals present in random tracking generalize to either circular tracking or center-out reach.

METHODS

The experimental protocol was approved and monitored by the University of Minnesota Institutional Animal Care and Use Committee and conformed to the “Guiding Principles for the Care and Use of Vertebrate Animals in Research and Training” of the American Physiological Society.

Behavioral Paradigms

Two rhesus monkeys [Macaca mulatta; female monkey N (6.3 kg), male monkey I (6.2 kg)] were trained, with their heads fixed, to perform three different movement paradigms (Fig. 1). Each monkey used a two-joint robot manipulandum (In Motion 2, Interactive Motion, Boston, MA) in the horizontal plane to control a cursor and track targets displayed on a vertically oriented video screen placed 50 cm in front of the animal. The animal received an automated juice reward after successful trial completions. During each recording session, a monkey performed the random tracking paradigm and at least one of the other two tasks (circular tracking or center-out reach) so that each cell's firing was evaluated in multiple tasks requiring different movement strategies. The animals typically executed 100–200 trials of the random tracking task and 80–150 trials of circular tracking or center-out reach tasks during a recording session.

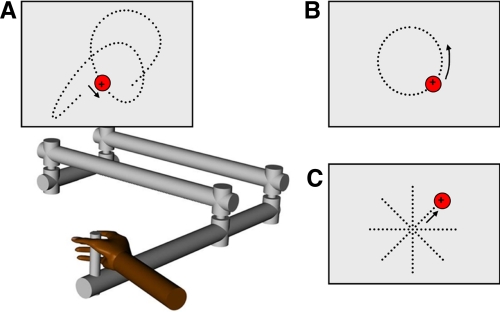
Fig. 1.

Behavioral paradigms. Monkeys used a 2-joint manipulandum to control a “+”-style cursor viewed on a video screen. All 3 tasks begin when the animal holds the cursor within a circular “start” target (located at screen center for circular tracking and center-out reach or randomly positioned for random tracking) for a variable time period (1–2 s). A: random tracking: the cursor is maintained within the target as it moves at pseudorandomized directions and speeds across the workspace; brief excursions (<500 ms) outside of the target are permitted to make the task achievable. B: circular tracking: a moving yellow “cue” target (not shown) first indicates target direction and speed (±60 or 80°/s) as it moves along a circular path (5-cm radius) for 180°. When the cue target turns red, animals move the cursor to intercept and track the target for 360°. Brief excursions are again permitted to match random tracking constraints. C: center-out reach: a red target appears at 1 of 8 randomized locations spaced 5 cm from the workspace center. Targets can be intercepted immediately, without further cues or constraints on movement speed. All 3 tasks end with maintaining the cursor inside a motionless “final hold” target for 1 s. Note that the dotted lines and arrows are only shown to illustrate typical target paths and are not normally visible.

All tasks began with an initial hold period requiring the monkeys to move to and hold a “+” style cursor (0.5 × 0.5 cm) within a red “start” target for a randomized time (1,000–2,000 ms). All targets for center-out reach and circular tracking were 2.5-cm-diameter circles, and the start target was always located at the center of the workspace. In random tracking, target size was enlarged to 3.0 cm because of the increased task difficulty, and the start target was positioned randomly within the 12 cm × 12 cm workspace viewed on the screen.

Random tracking.

After the initial hold period, the target began moving pseudorandomly so that the monkey had no knowledge of the upcoming trajectory (Fig. 1A). To ensure that the task was achievable (i.e., no abrupt changes in curvature or speed), target trajectories were generated a priori with sum of sine waves (Imamizu et al. 2000; Paninski et al. 2004a) and smoothed with a low-pass filter. Trajectories with a sharp turn (i.e., angle >75° between adjacent 50-ms segments of the binned trajectory) were discarded. Speed was controlled along the entire target path with the equation speed = cK^−1/3, where K is the curvature of the current path and the constant c was chosen to yield an average speed of 4 cm/s. This is an implementation of the two-thirds power law found to govern natural arm movements (Lacquaniti et al. 1983; Viviani and Terzuolo 1982). Additional filtering was used to prevent rapid speed increases at the onset of tracking. At the end of each trajectory, the target ceased moving and the animal was required to maintain the cursor within the target for a “final” hold period (1,000 ms). Because of the difficulty of the task, brief excursions (<500 ms) outside of the target were permitted. Longer excursions during any trial period automatically aborted the trial. A set of 100 trajectories, 6–10 s in duration, were predefined and randomly presented at each recording session.

Circular tracking.

As described previously (Pasalar et al. 2006; Roitman et al. 2005), after the initial hold a yellow cue target appeared at one of four initial angles (0°, 90°, 180°, or 270°) and moved at constant speed along a 5.0-cm-radius circular path at 60°/s (5.2 cm/s) or 80°/s (7.0 cm/s) in either the clockwise (CW) or the counterclockwise (CCW) direction (Fig. 1B). After 180° of travel, the cue target changed color (yellow to red), signaling the onset of interception. The monkey had 65° of target travel to intercept the moving target, and then continued tracking the target for an additional 360°. A “final” hold period required that the animal maintain the cursor within the unmoving target for a brief time (1,000 ms). To be comparable to the random tracking task, trials were again aborted if at any time the cursor deviated from the target for >500 ms.

Center-out reach.

This paradigm was also described in prior studies (Fortier et al. 1989; Fu et al. 1997; Georgopoulos et al. 1982). After the initial hold, a red cue target appeared in one of eight directions spaced at 45° intervals and 5.0 cm from the workspace center (Fig. 1C). The animal had 1,500 ms to intercept the cue target with the cursor, and then maintained cursor position inside the target for an additional 500-ms “final” hold period.

Surgical Procedures

Head restraint hardware and a recording chamber were chronically implanted in each animal with aseptic techniques and full surgical anesthesia (Coltz et al. 1999; Pasalar et al. 2006; Roitman et al. 2005). The head was restrained during training and recording experiments with a circular stainless steel halo attached to the skull with three or four surgical steel posts and screws. The recording chamber was placed over the right parietal cortex (both animals were trained to use their right hands for movement tasks) and stereotaxically positioned over a 2.0-cm-diameter craniotomy to target recordings from lobules IV–VI of the intermediate and lateral cerebellar zones (Coltz et al. 1999; Pasalar et al. 2006; Roitman et al. 2005), where hand- and arm-related Purkinje cells have been described (Fortier et al. 1989; Fu et al. 1997; Mano and Yamamoto 1980; Ojakangas and Ebner 1992; Pasalar et al. 2006; Roitman et al. 2005; Thach 1968; Yamamoto et al. 2007). The two monkeys used in this study have not been euthanized and are subjects in another experiment.

Anatomical Modeling

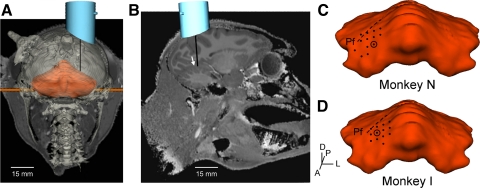
Microelectrode recording positions were reconstructed for each monkey (Fig. 2) based on electrode penetration coordinates and individual CT scans obtained after recording. It was not possible to acquire MRI data from either monkey because the metal recording hardware created large artifacts and both animals are still being studied in another experiment. Instead, whole brain MRI images (T1-weighted with a voxel size of 0.5 × 0.5 × 0.5 mm³) were collected from a similarly sized monkey with a custom-built monkey coil and a 7-T MR scanner (Siemens) equipped with a head gradient coil (80 mT/m G-maximum, 200 mT·m⁻¹·ms⁻¹). With the software Monkey Cicerone v1.2 (Miocinovic et al. 2007), each monkey's CT scan was coregistered with the MRI images by using the eye sockets, mandible, skull, nasal turbines, and teeth as landmarks (Fig. 2A). A custom anatomical model of the rhesus monkey cerebellum and primary fissure was created from the whole brain MRI data with three-dimensional (3D) volume rendering (AVIZO software, Visualization Sciences Group, Burlington, MA). The anterior and posterior commissures were also modeled as landmarks for aligning the cerebellum model with each monkey's coregistered imaging data. With the anatomical data aligned, a virtual recording chamber was placed on the skull, using the stereotaxic surgery coordinates. Model microelectrodes were inserted through the chamber at the angle, positions, and depths at which the Purkinje cell recordings were obtained. The virtual microelectrode penetrations were exported along with the cerebellum model to visualize the recording locations.

Fig. 2.

Microelectrode recording positions. A: bony landmarks were identified and used to coregister each monkey's CT images with high-resolution MRI data from a similarly sized rhesus macaque. Virtual microelectrodes were inserted through a recording chamber (positioned by using the surgical stereotaxic coordinates and CT landmarks) at the angle, positions, and depths used to record this data set. A posterior view of the coronal images shows that an electrode inserted in the chamber center falls in the intermediate zone of the cerebellum model (shown in orange). B: a sagittal MRI slice shows that the same center electrode has a trajectory anterior to the primary fissure (white arrow). C and D: all electrode penetrations from which at least 2 cells were successfully recorded are indicated with dots on the cerebellum surface. The circle denotes the recording chamber center, and a dashed line represents the primary fissure (Pf). Axes illustrate the anterior (A), posterior (P), dorsal (D), and lateral (L) orientations.

Electrophysiological Recordings and Data Collection

After full recovery of the animal, Purkinje cells were recorded extracellularly with quartz-platinum/tungsten single microelectrodes (1–2 MΩ impedance; Thomas Recording) that were inserted through the dura with a guide tube (22 gauge) and then advanced with a hydraulic microdrive (Narishige, Japan) to depths of 22.5–33.8 mm. Purkinje cells were identified by the presence of complex spikes (Fu et al. 1997; Ojakangas and Ebner 1992; Pasalar et al. 2006; Roitman et al. 2005; Thach 1968). Conventional techniques were used to amplify and filter (30-Hz to 3-kHz band pass, 60-Hz notch) the spike waveforms prior to the discrimination of simple spikes. Because of the long duration of the experiments (3–5 h), recordings focused on optimizing the discrimination of the simple spikes. Discrimination was performed online with the Multiple Spike Detector system (Alpha-Omega Engineering, Israel), and the resulting spike trains were digitized and stored at 1 kHz. The raw electrophysiological data were also digitized at 32 kHz and stored to disk. The spike trains were transformed to a continuous firing rate using fractional intervals with downsampling to 50 Hz and low-pass filtering (12th-order Butterworth with a 12-Hz cutoff). All data channels (kinematic and firing) were then merged and aligned on movement onset for each trial. For regression analyses, the mean firing rate for each trial was subtracted from the instantaneous firing rate.

Hand position was acquired by optical encoders at each robot joint and used to display cursor position in real time on the vertical screen. Hand position and target position data were both written to disk at 200 Hz. Velocity, speed, and direction of movements and other kinematic variables were calculated from the stored position data (Pasalar et al. 2006; Roitman et al. 2005).

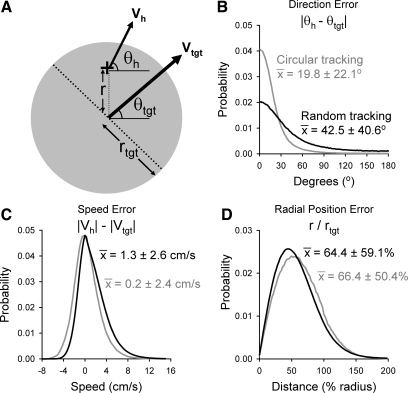
Kinematic Data Analyses

Stored kinematic data were downsampled to 50 Hz and low-pass filtered (12th-order Butterworth with a 12-Hz cutoff). The filtered data were used to calculate instantaneous kinematic error (e) measures (see Fig. 5A) that included the differences in movement direction (Direction_e = |θ_h − θ_tgt|) and speed (Speed_e = |V_h| − |V_tgt|; bold type denotes vectors) between the hand (h) and target (tgt). Radial position errors were assessed by calculating the distance from target center (r), which was normalized by target radius (r_tgt) to account for the different target sizes between random and circular tracking (Radial Position_e = r/r_tgt). Hold periods and the circular tracking intercept period were excluded from the analyses, so that only tracking movements were evaluated. The probability of each error measure was determined, and χ²-tests assessed whether an association exists between the error counts and the tracking task (e.g., random or circular). These results were also averaged for each recording session to obtain a mean direction and speed error for each recording session. One-way within-subject ANOVAs (α = 0.05) were conducted to compare the effects of the behavioral paradigm (e.g., random or circular tracking) on error.

Fig. 5.

Kinematic errors. A: diagram of the instantaneous hand (h) and target (tgt) kinematics used to calculate the kinematic errors. Gray circle is the target; cursor position is denoted by “+”. B–D: the probability distribution functions of the errors were determined from all successfully completed random (black) and circular (gray) tracking trials (from both animals and all recording sessions). Distributions of the probability of the direction (B), speed (C), and radial position (D) errors are plotted. For each plot, the mean ± SD of the error is shown.

Cross-correlation analyses were used to calculate time leads or lags (kinematic τ values) that describe the timing relationships between hand and target trajectories over a complete trial for both random and circular tracking. For position, τ values were determined as the time corresponding to the maximum cross-correlation between the hand and target position (X_h vs. X_tgt and Y_h vs. Y_tgt) from −500 to 500 ms with 20-ms resolution. The τ values describing the timing relationships between target V_tgt (Vx_tgt, Vy_tgt) and hand V_h velocity (Vx_h, Vy_h) trajectories were calculated in the same way. Negative τ values imply that the hand leads the target. χ²-Tests evaluated whether an association exists between the τ value counts and the task (e.g., random or circular).

Models of Simple Spike Firing

On the basis of qualitative analyses of the averaged simple spike firing data and previous studies (Coltz et al. 1999; Fu et al. 1997; Mano and Yamamoto 1980; Marple-Horvat and Stein 1987; Pasalar et al. 2006; Roitman et al. 2005), the simple spike firing was fit to a multiple linear regression model including terms for hand position (P_h), velocity (V_h), and speed (S_h). We refer to this as the PVS regression model (Eq. 1). An additional model parameter, τ, was incorporated to estimate the lead or lag between simple spike firing (f) and the kinematics. Parameters b_o and ε, respectively, depict baseline firing and the residual error.

$$\text{f}\left(t+\tau \right)={\text{b}}_{\text{o}}+{\text{b}}_{\text{P}}{\text{P}}_{\text{h}}\left(t\right)+{\text{b}}_{\text{V}}{\text{V}}_{\text{h}}\left(t\right)+{\text{b}}_{\text{S}}{\text{S}}_{\text{h}}\left(t\right)+\epsilon$$ (1)

Two similar models were also constructed to evaluate the contributions of direction, speed, and velocity. A PŪS regression model (Eq. 2) used hand position (P_h), unit velocity (i.e., direction, Ū_h), and speed (S_h), while the PV regression model (Eq. 3) simplified the PVS model by eliminating the speed term.

$$\text{f}\left(t+\tau \right)={\text{b}}_{\text{o}}+{\text{b}}_{\text{P}}{\text{P}}_{\text{h}}\left(t\right)+{\text{b}}_{\text{U}}{\overline{\text{U}}}_{\text{h}}\left(t\right)+{\text{b}}_{\text{S}}{\text{S}}_{\text{h}}\left(t\right)+\epsilon$$ (2)

$$\text{f}\left(t+\tau \right)={\text{b}}_{\text{o}}+{\text{b}}_{\text{P}}{\text{P}}_{\text{h}}\left(t\right)+{\text{b}}_{\text{V}}{\text{V}}_{\text{h}}\left(t\right)+\epsilon$$ (3)

The firing data from each Purkinje cell were fit to the above models with a five-bin partition for each kinematic parameter. This resulted in a 5 × 5 grid of 2.4 × 2.4-cm bins for the position workspace (−6 to 6 cm) and a 5 × 5 grid of 4.8 × 4.8 cm/s bins for the velocity workspace (−12 to 12 cm/s; see Figs. 9 and 10). Direction was computed as the unit velocity vector (Ūx_h, Ūy_h) and again binned in a 5 × 5 grid of 0.4 × 0.4-unit bins (−1 to 1 unit) to match the velocity binning. The speed workspace (0–12 cm/s) was partitioned into five bins of 2.4 cm/s. Hand kinematics were sorted and averaged within the bins, along with the associated simple spike firing rates, to generate an average kinematic value (i.e., position, velocity, or speed) and firing rate for each bin. For each cell, regressions fitting the averaged data from each bin to the models were performed across multiple τ values (−500 to 500 ms in 20-ms increments). The τ value providing the best fit (i.e., highest R_adj²) for each cell was identified as the optimal τ value and used for modeling. Negative τ values imply that the firing leads hand kinematics. Semipartial correlation coefficients were also calculated to approximate how much of the firing variance was described by each term in the PVS model at the optimal τ value (Zar 1999).

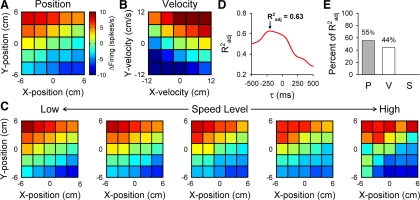
Fig. 9.

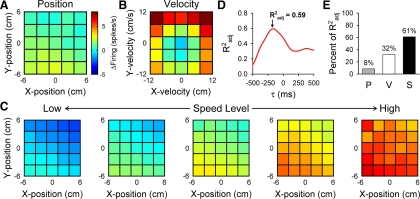
Example position and velocity Purkinje cell. Hand kinematics and simple spike firing data were binned and averaged across position (A) and velocity (B) to create plots of the cell firing. Color code illustrates the deviation from the mean firing, in which dark red represents increased firing and blue decreased firing. Simple spike firing increases when hand position is in the upper left quadrant of the workspace (A) and with higher velocities in both the X- and Y-directions (B). C: plots of averaged firing across position at different speed levels (0–12 cm/s, binned in increments of 2.4 cm/s) show almost no variance in firing with speed. D: R_adj² values are plotted vs. the time leads or lags (τ values). In this cell, a τ value of −200 ms yields a maximal R_adj² value of 0.63. E: semipartial R² values indicate that the position and velocity terms account for most of this cell's firing variability, with almost no contribution from the speed term.

Fig. 10.

Example speed cell. A and B: this cell displays minimal positional preference (A), while the velocity plot (B) exhibits a ringlike pattern of increased firing rates, suggesting that the simple spike firing is speed modulated. C: plots of averaged firing across position at different speed levels confirm that firing increases with speed irrespective of movement direction. D: a maximal R_adj² of 0.59 results when τ equals −180 ms. E: semipartial R² values corroborate that the simple spike firing is highly speed modulated, while the velocity term also describes some of the firing variability. Layout and conventions are as in Fig. 9.

Averaged vs. Nonaveraged Regression Models

As shown in results, the PVS regression model provided the best description of the simple spike firing, and cross-correlograms of hand position (P_h), velocity (V_h), and speed (S_h) averaged across all trials and sessions confirmed that these parameters were only weakly correlated (see Fig. 8) and, therefore, could be used in a multiple linear regression model (Belsley et al. 1980; Freund and Littel 2000; Zar 1999). Three additional analyses were conducted with this PVS model. First, the effects of averaging the data were evaluated. The PVS regression model was computed for each cell with the instantaneous hand kinematics and the instantaneous firing (20-ms bins) instead of the averaged data. Again, the τ value providing the best fit (i.e., highest R_adj²) for each cell was determined. Resulting R_adj², τ, and coefficient values from the regressions based on the nonaveraged data were plotted against those based on the averaged data. The correlation coefficients and slope of these plots were determined to compare the regression results obtained from the averaged and nonaveraged data.

Fig. 8.

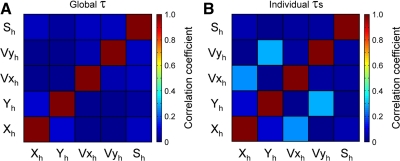
Relative independence of regression model parameters. Matrix plots show the average cross-correlation coefficient for each of the 5 kinematic parameters used in the PVS model, based on the hand kinematics across all recording sessions. A: average correlations among the kinematic parameters at a 0-ms lead/lag were obtained from the PVS regression model and correspond to the single global τ. B: average correlations among the kinematic parameters were also evaluated at the individual optimal τ values.

The second additional analysis evaluated whether curvature altered the optimal τ value, as previous studies in the motor cortex suggest that firing leads or lags may change relative to the curvature, k (Eq. 4), of the hand movement path (Moran and Schwartz 1999).

$$k=\left(\dot{x}\ddot{y}-\ddot{x}\dot{y}\right)/{\left({\dot{x}}^2+{\dot{y}}^2\right)}^{3/2}$$ (4)

The instantaneous curvature of the hand movement data (20-ms bins) was determined and divided into 10 bins ranging from −9.9 to 9.9 cm⁻¹ or five bins ranging from 0 to 9.9 cm⁻¹ for unsigned curvature (absolute value of k) so that each bin included a similar number of data points. The nonaveraged kinematic and firing data in each bin were fit to the PVS model, and the optimal τ value was identified. An ANOVA determined whether there were any significant differences across the τ values for each bin.

Individual τ Values

The initial PVS regression model (Eq. 1) only evaluates τ as a global time lead or lag for the ensemble of kinematic terms. Therefore, we performed a third additional analysis that determined the optimal τ for each parameter. Ideally, this would be calculated by using a single regression model with independent τ values for each parameter, but this approach was computationally prohibitive. Analysis of a single Purkinje cell across all τ values would require 51 iterations of the regression model for each of the five model parameters (51⁵ = 345,025,251 iterations per cell). Instead, we performed single linear regressions for each of the five PVS model parameters by restricting Eq. 1 to fit one kinematic variable at a time. The same five-bin partition described above for the PVS model was used. This resulted in five different R_adj² profiles per cell (1 for each model parameter) from τ = −500 to 500 ms. The individual profiles were then summed and compared with the global profile by using the root mean square deviation (RMSD). We then examined a modified version of the PVS model (Eq. 1) that incorporated these individual τ values in place of the global τ. The resulting model R_adj², β regression coefficients, and semipartial correlation coefficients were computed for each cell and compared with the original PVS model.

Invariant Encoding Across Tasks

For each cell, the optimal τ value and PVS model regression coefficients obtained from the nonaveraged random tracking data were used to estimate the firing in the circular tracking or center-out reach tasks. The neural activity recorded during circular tracking was sorted and averaged with 10° bins (0–360°) corresponding to the angular hand position. Data recorded during the center-out task were averaged across trial direction, smoothed with a 10-point sliding average window, and aligned to the maximum speed with a time window of −600 to 600 ms. The neural data were preprocessed as described for the random tracking task. Correlation coefficients were employed to measure the fit between the estimated and recorded neural activity.

RESULTS

Microelectrode Recording Locations

Anatomical modeling of the recording chamber and electrode positions shows that an electrode placed in the center of monkey N's chamber would project to the intermediate zone of the cerebellum (Fig. 2A). Sagittal MRI slices illustrate that the center electrode trajectory lies just anterior to the primary fissure (Fig. 2B). Very similar electrode positioning was found for monkey I. All electrode positions from which at least two cells were successfully recorded were plotted on the surface of the 3D cerebellum model (Fig. 2, C and D). In both monkeys, penetrations are mostly in lobules IV–V of the intermediate zone and anterior to the primary fissure, a region strongly implicated in the control of the arm (Fortier et al. 1989; Fu et al. 1997; Mano and Yamamoto 1980; Ojakangas and Ebner 1992; Pasalar et al. 2006; Roitman et al. 2005; Thach 1968).

Behavior and Kinematic Data Analyses

Random tracking fully covers kinematic workspace.

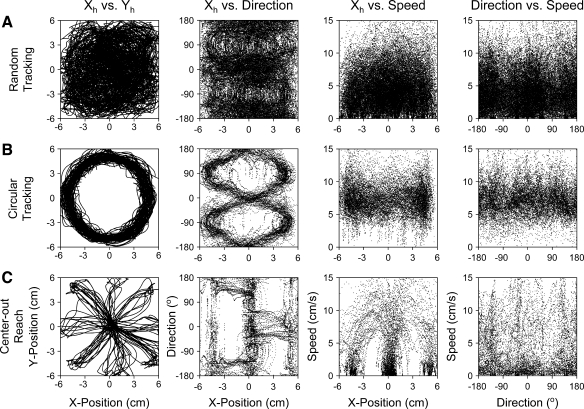
Hand kinematics from a typical recording session are plotted in Fig. 3 and illustrate differences in workspace coverage between the three tasks. Random tracking hand trajectories (X_h vs. Y_h) thoroughly cover the position workspace (Fig. 3A). All directions and speeds from 0 to 12 cm/s are executed across the entire X-position workspace. Additionally, the full range of speeds is applied to all movement directions. Results are similar for the Y-position data (not shown).

Fig. 3.

Coverage of the kinematic workspace. A: an example of hand kinematics collected from a typical 100-trial random tracking recording session. Plotted left to right are 1) hand position trajectories (X_h vs. Y_h) across the 12 × 12-cm workspace, 2) hand position (X_h, −6 to 6 cm) vs. hand movement direction (−180° to 180°), 3) hand position (X_h) vs. hand speed (S_h, 0–12 cm/s), and 4) hand movement direction vs. hand speed (S_h). B: similar plots for 100 trials of circular tracking are shown and include both clockwise and counterclockwise tracking directions. C: plots for 100 trials of center-out reach movements. Comparable results were observed for the Y-position data (not shown) in all 3 tasks.

In comparison, both the circular tracking (Fig. 3B) and center-out reach (Fig. 3C) tasks leave large areas of the position workspace untraversed. Plots of hand position (X_h) vs. direction or speed demonstrate coupling between the position and velocity vectors for these two movement paradigms. For circular tracking, movements span the complete range of directions (−180° to 180°) but are mostly limited to a narrow speed range of 5–10 cm/s. Similarly, center-out reach covers the low speed range but is limited to the positions of the cue and intercept targets. Fast movements (i.e., high speed range) are limited to the eight directions corresponding to the intercept targets. Again, similar findings are observed for direction or speed versus hand Y-position (Y_h). Collectively, these results reaffirm the limits of previous movement paradigms (Coltz et al. 1999; Fortier et al. 1989; Fu et al. 1997; Roitman et al. 2005) and demonstrate that the random tracking task achieves one of its major aims of providing more complete coverage of the kinematic workspace (Paninski et al. 2004a).

Kinematic error measures.

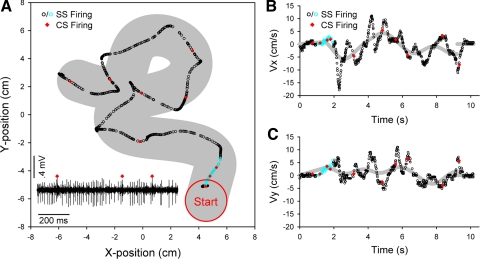
Figure 4 depicts Purkinje cell simple and complex spike occurrences and hand kinematics superimposed on the hand path (Fig. 4A) or hand velocity (Fig. 4, B and C) during a single trial of random tracking. Recorded neural activity from the first second of hand movement (Fig. 4A, bottom left) includes three complex spikes that produced brief pauses in simple spike firing (Bloedel and Roberts 1971; McDevitt et al. 1982). This 1 s of example firing is labeled blue for simple spike firing in the corresponding kinematics plots. Comparison of the hand and target paths show that the hand briefly went outside the target three times during this trial, illustrating the task difficulty (Fig. 4A). Mismatches between hand and target velocity were also prevalent and suggest that the animals were unable to fully predict future target movement directions or speeds (Fig. 4, B and C). Qualitative interpretation of the relationship between the raw firing and hand kinematics is challenging because each trial of the random tracking task produced unique target trajectories and different hand kinematics. Additionally, the spacing between kinematic data points (and thus the overlaid simple or complex spike occurrences) is greater during periods of fast movements and smaller during slow movements, potentially giving the misleading perception of differences in simple spike firing with curvature or acceleration.

Fig. 4.

Tracking performance and electrophysiology data. A: the red “start” target is drawn at the beginning of the target trajectory, with the target path (X_tgt, Y_tgt) shown in gray (target diameter = 3 cm). Simple (SS) and complex (CS) spikes are superimposed upon the hand position (X_h, Y_h) at the time of occurrence. Blue symbols denote simple spikes from the first 1 s of hand movement, and these raw electrophysiology data (shown at bottom left) include 3 complex spikes (red diamonds). B and C: similarly, target velocity (gray) in the x-direction (Vx_tgt; B) or y-direction (Vy_tgt; C) was plotted vs. time, with the simple and complex spikes superimposed upon the hand velocity (Vx_h or Vy_h).

Instantaneous error measures, including direction, speed, and radial position error, were calculated from hand and target kinematic data of successfully completed circular and random tracking trials across all recording sessions (Fig. 5A). Direction errors (θ_h − θ_tgt) show that the hand and target mostly move in the same direction (mode = 0.5° for both tasks; Fig. 5B). However, large direction errors (i.e., hand movements opposite the direction of target movement) are more frequent during random tracking (mean = 42.5 ± 40.6°) than circular tracking [mean = 19.8 ± 22.1°, X²(179, n = 10,909,856) = 511,130.96, P < 0.0001; Fig. 5B]. Hand speeds overall exceed target speeds (V_h − V_tgt) for random tracking (mean = 1.3 ± 2.6 cm/s; Fig. 5C), which is consistent with observations that both monkeys frequently made quick catch-up movements to compensate for tracking errors (see velocity plots, Figs. 4 and 6). In circular tracking, the mean speed error approaches zero (mean = 0.2 ± 2.4 cm/s; Fig. 5C), suggesting that the monkeys are better able to predict and, therefore, match target movements. Conversely, the speed errors for random tracking are larger than in circular tracking [X²(88, n =10,903,151) = 344,254.18, P < 0.0001]. Excursions outside of the target (i.e., radial errors > 100%) occur ∼10% of the time in both tasks. These radial position errors (r/r_tgt; Fig. 5D) are slightly greater for circular tracking (mean = 66.4 ± 50.4% target radius) than random tracking [mean = 64.4 ± 59.1% target radius, X²(99, n = 10,738,785) = 31,768.87, P < 0.0001]. Consequently, direction, radial position, and speed errors are strong performance indicators and provide evidence that random tracking is the less predictable, more difficult task.

Fig. 6.

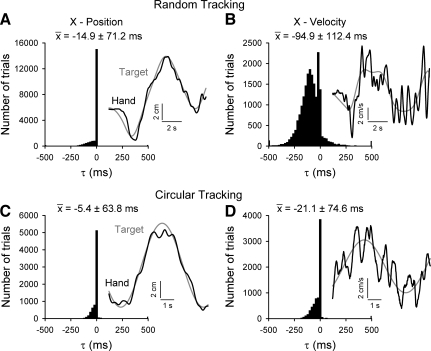
Timing between hand and target kinematics. Hand kinematic data were compared with target kinematic data across individual trials by using cross-correlation analyses to determine the kinematic τ values that describe the time of maximal correlation between the hand and target movements. A and B: histograms of τ values for the X-position and X-velocity trajectories during random tracking. Insets: example hand (black) and target (gray) trajectories from 1 trial. C and D: similar τ value histograms and insets for the X-position and X-velocity trajectories during circular tracking. Similar results were obtained for position and velocity measures in the Y-direction in both tasks (not shown). Histograms represent all successfully completed random and circular tracking trials from both animals and all recording sessions. For each histogram, the mean ± SD of the τ values is shown.

To examine hand and target relationships across longer time intervals, the cross-correlation between hand and target position or velocity profiles was evaluated for individual random and circular tracking trials (Fig. 6, insets). As described in methods, the profiles were shifted across multiple τ values (−500 to 500 ms in 20-ms increments) to determine the time lead or lag that results in the maximum correlation coefficient. Hand and target paths are highly correlated in both tracking tasks (mean random ρ_Px = 0.96 ± 0.13, ρ_Py = 0.96 ± 0.12; mean circular ρ_Px = 0.98 ± 0.11, ρ_Py = 0.97 ± 0.13). For both random and circular tracking, hand and target position are similar across the entire length of the trial (Fig. 6, A and C). The mean τ values tend toward zero (mean random τ_x = −14.9 ± 71.2 ms, τ_y = −14.1 ± 68.4 ms; mean circular τ_x = −5.4 ± 63.8 ms, τ_y = −8.9 ± 76.8 ms), although the hand lags the target more in random than in circular tracking [τ_x X²(24, n = 26,810) = 636.90, P < 0.0001; τ_y X²(20, n = 26,786) = 1,308.55, P < 0.0001]. This is expected, as the task constraints require hand position to closely match target position for successful trials. Hand and target velocity profiles, however, are less closely coupled, especially for the random tracking task (mean random ρ_Vx = 0.65 ± 0.14, ρ_Vy = 0.69 ± 0.14; mean circular ρ_Vx = 0.87 ± 0.12, ρ_Vy = 0.88 ± 0.13). Figure 6, B and D, insets, illustrate the “intermittent” nature and rapid changes that occur in hand velocities (Roitman et al. 2009). Random tracking velocity τ values (Fig. 6B) are highly skewed negatively (mean τ_Vx = −94.9 ± 112.4 ms; τ_Vy = −115.6 ± 117.4 ms), indicating that the hand often lags the target considerably during changes in velocity. In contrast, circular tracking velocity τ values are only slightly skewed toward negative values (mean τ_Vx = −21.1 ± 74.6 ms; τ_Vy = −26.8 ± 87.5 ms), and for a large fraction of the trials (57.1%) the τ value is zero. These cross-correlation results further confirm that the random target movements are more difficult to predict, causing more tracking errors to be made during random tracking than circular tracking [τ_Vx X²(24, n = 26,828) = 6,284.23, P < 0.0001; τ_Vy X²(24, n = 26,785) = 6,346.87, P < 0.0001].

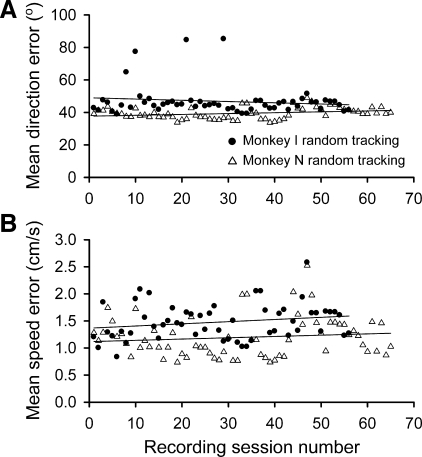
We also evaluated whether there was any evidence for learning or improvement in motor performance during random tracking. The direction and speed errors (Fig. 7) were averaged for each recording session, plotted chronologically, and fit to a linear regression to evaluate performance. The mean errors remain fairly constant across days, and nearly all mean error coefficient confidence intervals contain zero for both monkeys (i.e., the slopes are not different from zero). The one exception is that the mean direction error coefficient (β_direction) for monkey N is 0.054 [R² = 0.09, F(1,63) = 5.87, P = 0.018], indicating that performance minimally worsened over the course of the recording period. In comparison, the direction error slope coefficient in monkey I is not significantly different from zero [R² = 0.02, F(1,54) = 0.96, P = 0.332]. Overall, there is no evidence that the animals improved their performance or learned the target trajectories over time.

Fig. 7.

Movement performance and learning over time. Direction and speed errors were plotted chronologically by recording session and fit to a linear regression (thin lines) for each monkey during random tracking. A: mean direction errors for monkey I show no significant trend (i.e., confidence intervals for the linear regression slope coefficients contain 0). Monkey N slightly increases in direction error over time, that is, performance worsens. B: similar plots for mean speed errors show no significant changes with time for either monkey.

Simple Spike Firing

Comparison of regression models.

The PV model resulted in a higher mean R_adj² than the PŪS model [PV R_adj² = 0.33 ± 0.19, PŪS R_adj² = 0.30 ± 0.16, t(119) = 4.17, P < 0.0001], suggesting that decomposing velocity into direction (i.e., unitary velocity) and speed does not provide as good a description of the simple spike modulation. However, the PV model could not sufficiently describe ∼10% of Purkinje cells in which the simple spike activity was predominantly modulated by speed (see below and Fig. 10). In random tracking movements, velocity and speed are independent regressors and can be used together in the same linear regression model (see Fig. 8). The PVS model had the greatest mean R_adj² (0.35 ± 0.19) and captured speed-related modulation. It was therefore judged the best of the three models in describing the simple spike discharge.

Simple spike firing was recorded from 120 Purkinje cells during the random tracking task and additionally from either circular tracking or center-out reach. Qualitative examination (see Figs. 9 and 10) of the average simple spike firing binned as described in methods revealed modulation with position (P), velocity (V), and speed (S). Correlation analyses of the hand kinematics across all sessions confirmed that these three parameters were not highly correlated. For the PVS model in which a single global τ was used for all kinematic terms, one only needs to assess the correlation at a lead/lag of 0 ms, because all kinematic terms are shifted together in determining the optimal τ. The highest correlation among these variables was between X_h and Y_h (ρ = 0.08, Fig. 8A), allowing these terms to be incorporated into a multiple linear regression model describing simple spike firing of individual Purkinje cells.

PVS regression model.

An example Purkinje cell is shown in Fig. 9 in which the simple spike firing is simultaneously tuned to both position and velocity. For each position or velocity bin (see methods), simple spike firing is averaged to obtain a visual representation of position (Fig. 9A) and velocity (Fig. 9B) encoding. Position modulation is shown by the increases in simple spike firing when the hand moves in the upper left quadrant (negative X and positive Y coordinates) of the workspace and decreases in the lower right quadrant (Fig. 9A). Velocity modulation is evident by the increases in firing for positive Vx_h and Vy_h, with relative decreases for negative Vx_h and Vy_h (Fig. 9B). Plots of simple spike firing across positions at different speed levels show almost no modulation with speed (Fig. 9C). The time lead or lag between simple spike firing and hand kinematics is calculated with the PVS model (Eq. 1) and regressing across multiple τ values. In this cell, a τ value of −200 ms yields the maximal R_adj² value of 0.63 (Fig. 9D), suggesting that simple spike firing leads hand kinematics. In agreement with the visual representations, semipartial R² values (Fig. 9E) indicate that the position (55% of R_adj²) and velocity (44% of R_adj²) terms account for nearly all this cell's firing variability, with very little contribution from the speed term (<1% of R_adj²).

In several Purkinje cells (11/120), the speed term described >40% of the explained firing variability. Figure 10 shows an example “speed cell.” Modulation with hand position is weak (Fig. 10A), while the velocity plot (Fig. 10B) exhibits a semiring pattern of maximal firing along the outer borders that represent the greatest speeds. This demonstrates the presence of speed modulation that cannot be reduced to a linear combination of the velocity terms. Plots of averaged firing across position (Fig. 10C) verify that movement speed highly influences the firing rates. The optimal τ value of −180 ms (Fig. 10D) suggests that the discharge leads hand kinematics. Semipartial R² values (Fig. 10E) verify that this cell is highly speed modulated (61% of R_adj²), with velocity (32% of R_adj²) also describing some of the firing variability. Position (8% of R_adj²) contributes little to changes in simple spike firing.

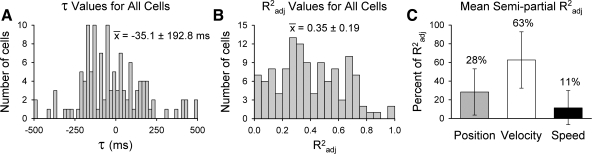
A wide range of sensitivities to PVS model parameters were observed across the population of Purkinje cells. Optimal τ values (Fig. 11A) are skewed toward negative numbers (mean = −35.1 ± 192.8 ms) and confirm that the firing of most cells (72/120) leads hand kinematics. However, 38% (45/120) of the cells have a positive τ value, suggesting that simple spike firing also encodes feedback about hand movements. Remaining cells (3/120) lie within the τ = 0 ms bin that neither leads nor lags hand kinematics. The mean R_adj² value shows that the parameters in the PVS model account for ∼35% of the simple spike firing variability (Fig. 11B). Mean semipartial R² values (Fig. 11C) indicate that, on average, velocity (63 ± 30% of R_adj²) describes more of the firing variability than position (28 ± 24% of R_adj²) or speed (11 ± 19% of R_adj²). Importantly, τ values were not highly correlated with the model R_adj² (ρ = −0.034), demonstrating that the firing leads and lags obtained from the PVS model explained comparable amounts of variability. Similarly, τ values were not highly correlated with the semipartials (ρ_P = −0.052; ρ_V = 0.066; ρ_S = −0.020), indicating that the τ values are not biased by a single parameter (e.g., cells with strong velocity signals do not have more negative τ values.)

Fig. 11.

Population summary of firing data from all 120 cells recorded during random tracking. A and B: distributions of the optimal firing τ values (A) and R_adj² values (B) resulting from the PVS linear regression model with averaged kinematic data. C: bar plots and SD of the mean semipartial R² values for all cells.

Averaged vs. nonaveraged regression models.

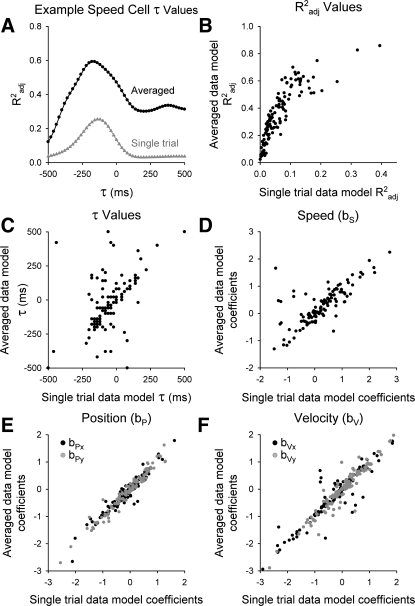
To evaluate whether the same kinematic parameters are reliably encoded in single trial observations, the instantaneous single trial (nonaveraged) simple spike firing data for each cell were fit to the same PVS regression model (Eq. 1) across multiple τ values (see methods). Results from an example Purkinje cell show that R_adj² as a function of the τ has similar profiles for the averaged and nonaveraged data (Fig. 12A). As expected, maximal R_adj² values are smaller when nonaveraged, single trial data are used, but the R_adj² values scale down similarly across all cells (Fig. 12B; ρ = 0.84, slope = 2.54). Across the population of Purkinje cells, comparisons of regression model coefficients (Figs. 12, D–F) illustrate that the speed (b_S, ρ = 0.78, slope = 0.64), position (b_P; x: ρ = 0.96, slope = 0.98; y: ρ = 0.98, slope = 1.02), and velocity (b_V, x: ρ = 0.95, slope = 0.93; y: ρ = 0.95, slope = 1.00) terms are highly correlated with slopes near 1, confirming that regression models based on nonaveraged data capture the same relationships as the models based on averaged data. The optimal τ values are also consistent between averaged vs. nonaveraged data (Fig. 12C; ρ = 0.52, slope = 0.75), but the strength of the correlation is less than for the coefficients, suggesting that averaging can influence the timing relationships.

Fig. 12.

Averaged vs. nonaveraged firing models. A: R_adj² values arising from different τ values of the PVS regression model are plotted for the example speed cell (Fig. 10) using averaged data (black) or nonaveraged single trial data (gray). B: maximal R_adj² values resulting from the averaged data regression model (y-axis) are plotted vs. the nonaveraged data regression model (x-axis) for each cell. C: similar plots show that optimal τ values are consistent between averaged vs. single trial data. D–F: plots of the averaged vs. nonaveraged regression model coefficients for the speed (b_S; D), position (b_P; E), and velocity (b_V; F) terms also demonstrate tight linear relationships.

Curvature.

Prior studies in the motor cortex suggest that firing leads or lags change with the curvature of the hand movement (Schwartz and Moran 1999), leading us to investigate the influence of trajectory curvature on the optimal τ value. As described in methods, both curvature (−9.9 to 9.9 cm⁻¹) and absolute curvature (0–9.9 cm⁻¹) were calculated for the hand trajectory and divided into 10 bins. The data from each bin were fit to the PVS model, and the optimal τ was identified for each bin. An ANOVA showed no significant difference across the mean τ for each bin regardless of whether curvature [F(9,1190) = 0.32, P = 0.970] or absolute curvature [F(4,595)= 0.49, P = 0.745] was used for the comparison. Therefore, as opposed to the properties of neurons in the motor cortex, the lead or lag of the simple spike firing does not appear to be related to the curvature.

Prediction of simple spike firing in different tasks.

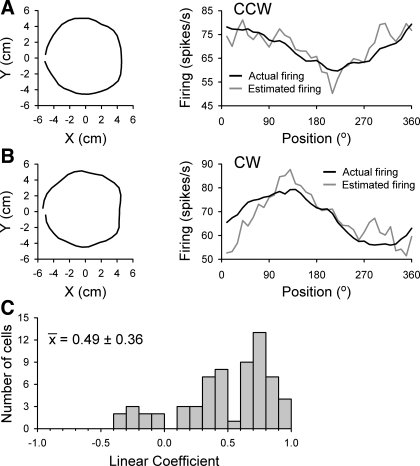
For each Purkinje cell, the τ value and regression coefficients calculated from random tracking data were used to estimate the simple spike firing rates for the kinematics recorded during circular tracking or center-out reach. Importantly, we elected to use regression coefficients obtained from the nonaveraged data, although the coefficients were mostly equivalent between the two models (Fig. 12). Estimates of firing during CCW and CW circular tracking for an example cell are shown in Fig. 13. Although the averaged hand paths are similar for both tracking directions (Fig. 13, A and B, left), there is a large shift (∼90°) in the position of maximal firing (Fig. 13, A and B, right), indicating that this neuron encodes both position and direction information (Roitman et al. 2005). Regression coefficients from the PVS linear regression model for random tracking (Eq. 1) provide an accurate estimate of the simple spike firing for both directions of movement (Fig. 13, A and B, right; ρ_CCW = 0.80, ρ_CW = 0.78). Correlation coefficients from all 32 circular tracking cells in both tracking directions (mean = 0.49 ± 0.36; Fig. 13C) indicate that most cells encode hand kinematics invariantly for both random and circular tracking.

Fig. 13.

Estimation of circular tracking firing based on the model using random tracking data. A and B, left: average hand position (X_h, Y_h) traces for 360° of counterclockwise (CCW; A) or clockwise (CW; B) circular tracking recorded from an example Purkinje cell. Right: binned and averaged actual recorded simple spike firing rates (black traces) against the estimated firing activity (gray traces). Firing was estimated by applying the τ value and PVS linear regression model coefficients (nonaveraged model) computed from the random tracking data to the circular tracking hand kinematics. C: distribution of the correlation coefficients from the 32 Purkinje cells. Correlation coefficients are plotted for each direction of tracking, resulting in twice the number of coefficients than cells.

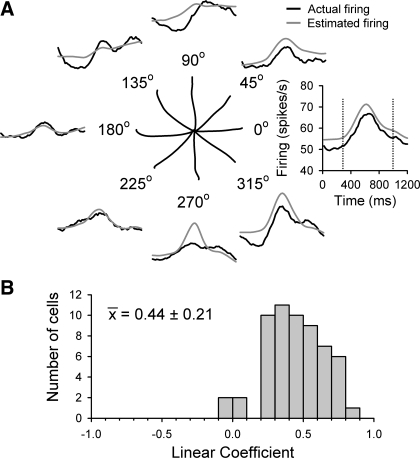
Similar accuracy was achieved for estimation of firing during center-out reach, despite vastly different movement strategies and kinematics. Typical center-out reach movements are fast, ballistic, relatively straight trajectories (Fig. 14A, center plot) during which the early part of the reach uses feedforward control (Beaubaton et al. 1978; Keele and Posner 1968; Ojakangas and Ebner 1991). In contrast, tracking tasks continually utilize error feedback to make numerous, small corrective movements. In the example cell shown, the PVS model coefficients and τ value calculated from the random tracking data successfully estimate the actual firing for all eight directions of center-out reach (Fig. 14A, outer plots). The estimates accurately capture the temporal profile for the six reach directions between 180° and 45°. The average correlation coefficient is 0.88 for all eight directions. The mean correlation coefficient for the 58 Purkinje cells studied in the center-out task is ρ = 0.44 ± 0.21 (Fig. 14B), indicating that many cells encode hand kinematics invariantly for both random tracking and center-out reach. Therefore, the regression model coefficients attained from nonaveraged random tracking data can faithfully predict the simple spike firing in other movements for a majority of Purkinje cells.

Fig. 14.

Estimation of center-out reach firing based on the model using random tracking data. A: center plot depicts averaged hand position (X_h, Y_h) traces for the 8 directions of center-out reach. Binned and averaged actual recorded firing data (black trace) from an example Purkinje cell are plotted against the estimated firing rate (gray trace) for each direction of reaching. Firing was estimated by applying the τ value and PVS linear regression model coefficients (nonaveraged model) computed from the random tracking data to the center-out reach hand kinematics. B: distributions of the averaged correlation coefficients from all 58 cells.

Global vs. individual τ values.

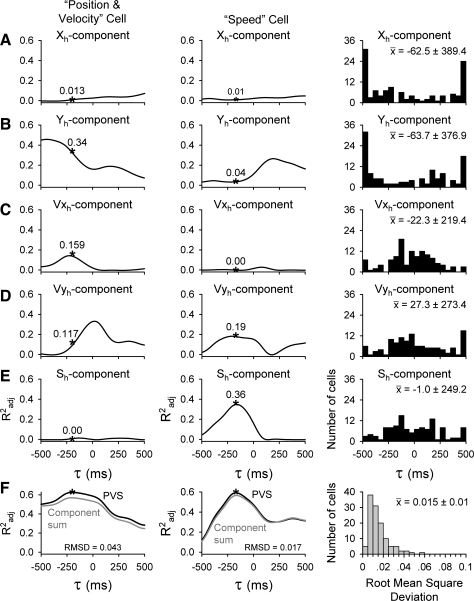
To investigate the influence of individual model parameters on the timing relationship between simple spike firing and hand kinematics, the firing was fit to the five parameters of the PVS model individually (see methods). Figure 15 shows the R_adj² temporal profiles for each term of the PVS model (Fig. 15, A–E, left and center), a single global τ (black traces in Fig. 15F), and the summed individual temporal profiles (gray traces in Fig. 15F) for the two example cells described previously (Figs. 9 and 10). For both cells, the temporal profiles and best individual τ values vary greatly between parameters (Fig. 15, A–E) and do not necessarily align with the global τ values (Fig. 15F), suggesting that each parameter may be encoded at independent lead/lags. However, note that the global τ is often very close to the individual τ of the parameter with the highest semipartial R_adj² value (indicated by *), and the summed individual profiles (Fig. 15, A–E) provide an excellent approximation of the temporal profile for the global τ model (gray traces in Fig. 15F). Similarity between the global τ profile and summation of the individual parameter profiles was quantified by the RMSD and confirmed that the individual kinematic representations are highly additive for the example cells (position/velocity cell: RMSD = 0.043; speed cell: RMSD = 0.017).

Fig. 15.

Optimal τ values for individual PVS model parameters. A–E: plots of R_adj² vs. τ arising from X_h (A), Y_h (B), Vx_h (C), Vy_h (D), and S_h (E) are provided for the 2 example position/velocity and speed cells (left and center) shown previously in Figs. 9 and 10, along with the individual τ value distributions for all 120 cells (right). Star indicates the semipartial contribution of each variable at the time of the optimal global τ. F, left and center: R_adj² vs. τ for the example cells from both a single global τ model (black traces) and summation of the individual parameter profiles (gray traces). The similarity between these 2 traces was quantified by the root mean square deviation (RMSD). The distribution of RMSD values for all 120 cells is shown at right.

The additive property of the individual profiles is conserved at the population level, as demonstrated by the distribution of RMSD values (Fig. 15F, right). The mean RMSD for the cell population was 0.015 ± 0.01, supporting the assumption that the kinematic parameters are effectively independent. Furthermore, the distributions of individual parameter optimal τ values (Fig. 15, A–E, right) suggest that the velocity and speed components were comparable to those obtained for the global τ model. That is, there is a mixture of cells with simple spike firing leading and lagging the hand kinematics. Positional lead/lag distributions differ from the velocity and speed distributions, exhibiting clustering at the ±500 ms limits.

It was necessary to assess whether using individual τ values introduced unacceptable correlations among the regressors. Therefore, the correlations among the hand kinematics were reevaluated, using the times of the individual τ values (Fig. 8B). The average correlations remained low, with the greatest correlations between Y_h and Vy_h (ρ = 0.30) and X_h and Vx_h (ρ = 0.27). These values are still consistent with the assumption of independence required by multilinear regression modeling (Belsley et al. 1980; Freund and Littel 2000).

This allowed us to evaluate a modified version of the PVS model (Eq. 1) in which the individually calculated τ values replaced the global τ parameter. This modified model assesses how the individual leads/lags alter the contributions of the different parameters. The overall R_adj² values were highly correlated between the two models (ρ = 0.97), and the mean R_adj² values were nearly identical (global τ: R_adj² = 0.35 ± 0.19, individual τ: R_adj² = 0.34 ± 0.19), further confirming that the contributions of the individual kinematic terms are relatively independent and can sum linearly. Regression model coefficients for the five model parameters remained highly correlated between both models for the position (b_P, x: ρ = 0.91, slope = 1.40; y: ρ = 0.95, slope = 1.27), velocity (b_V, x: ρ = 0.98, slope = 1.06; y: ρ = 0.97, slope = 1.20), and speed (b_S, ρ = 0.94, slope = 1.13) terms. Further analyses revealed that the individual τ model coefficients were more broadly distributed compared with the global τ model coefficients (i.e., the individual β coefficients for all 5 parameters no longer peaked around zero and positive model coefficients generally increased in magnitude while negative coefficients decreased), which accounts for the positive slopes when comparing coefficients. Therefore, incorporating the individual τ values captures more of the firing variability, especially in the position and speed terms that need not peak at the global τ value. The mean semipartial R² values also validate this, as position increased from 28 ± 24% to 38 ± 26% of R_adj² when the individual τ values were used in the model. The average semipartial R² for speed also increased from 11 ± 19% to 16 ± 19%, while the velocity contribution decreased from 63 ± 30% to 44 ± 25%.

DISCUSSION

Random tracking provides a useful paradigm for assessing the motor signals present in the discharge of neurons (Paninski et al. 2004a, 2004b). As shown, random tracking provides greater coverage of the position, direction, speed, and velocity kinematic workspaces compared with the center-out reach or circular tracking paradigms previously used to characterize the signals in Purkinje cell simple spike discharge (Coltz et al. 1999; Fortier et al. 1989; Fu et al. 1997; Marple-Horvat and Stein 1987; Roitman et al. 2005). Random tracking results in extensive combinations of position, direction, and speed, delivering a robust data set to assess the encoding of kinematic signals. Most importantly, these parameters are minimally correlated during the random tracking movements (see Fig. 8), allowing for use of linear regression models without the problems of correlated predictors (Belsley et al. 1980; Freund and Littel 2000; Zar 1999).

As expected, random target movements are difficult to predict. Errors in hand movement speeds and directions relative to the target are significantly greater in random tracking than in circular tracking. Comparisons of random tracking kinematic profiles across time show that hand velocity lags target velocity by ∼95 ms, a significantly greater lag than with circular tracking (∼21 ms). These analyses confirm that the random tracking task is a feedback-dependent, highly unpredictable task.

In random tracking, the monkeys appear to use a strategy of controlling position. This is expected, as the task requires maintaining the cursor within the moving target. Hand and target position are highly correlated, and, in a large fraction of the trials, hand position had a zero time lag with target position. Similar results were obtained for circular tracking. Both findings suggest that position is highly controlled in these two tracking tasks.

Encoding of Kinematics

Analyses of the simple spike firing focused on finding kinematic parameters that are relatively independent. This approach allows for unambiguous statements about the relationships between firing and the specific kinematic variables of position, velocity, and speed. It also differs from our previous studies that allowed interaction terms and did not rigorously assess the degree of correlations between model parameters (Coltz et al. 1999; Fu et al. 1997; Roitman et al. 2005). Similar to previous findings, the velocity term explains the greatest amount of the firing variability, with position also contributing considerably (Mano and Yamamoto 1980; Marple-Horvat and Stein 1987; Roitman et al. 2005). Psychophysical studies show that humans and monkeys use a combination of velocity and position information to intercept and track targets (Engel and Soechting 2000; Roitman et al. 2004). These results provide further support that position and velocity are key control parameters during visually guided tracking tasks.

Global vs. Individual τ Values

For many Purkinje cells, the global τ analysis found that simple spike firing led hand movements (Fig. 11A). This finding is consistent with other electrophysiology studies that have found that Purkinje cell simple spike firing mostly leads hand kinematics during manual tracking (Coltz et al. 1999; Roitman et al. 2005) or center-out reaching (Fu et al. 1997; Marple-Horvat and Stein 1987) and supports the concept that Purkinje cells encode feedforward or predictive signals (Bastian 2006; Ebner and Pasalar 2008; Wolpert et al. 1998). Unlike prior tasks, monkeys performing random tracking had no knowledge of the upcoming movements. The present results demonstrate that the firing leads are not a function of task predictability and that the simple spike firing from a majority of Purkinje cells provides feedforward kinematic signals irrespective of the task demands.

We also determined the optimal individual τ values for each PVS model parameter by computing individual regressions for each of the five parameters. The sum of the R_adj² profiles from the individual regressions closely matched the profile obtained by using a single global τ, verifying the validity of the model and the independence among the regression parameters. Estimates of the individual leads/lags for the velocity and speed terms demonstrate a mixture of feedforward and feedback signals, similar to the global τ. Distributions of the τ values for the position parameters differ from velocity and speed, with clusters at the limits of the ±500 ms time window. Position signals vary slowly compared with velocity (Fig. 4), limiting the temporal resolution at which changes can be reliably detected. It is yet unclear whether this property has physiological relevance, reflecting longer time relationships between the position signals and their neural representations.

Using the individually determined τ values in the PVS model alters the weighting and variability explained by the individual terms, so that across the cell population the model is less influenced by the dominant term. Using a global τ tends to exaggerate the contribution of the parameter that has its peak at or near that τ value. The individual τ model increased both the position and speed semipartial R² values, suggesting that use of a global τ overemphasizes the velocity contribution. Improved analytical techniques as well as experimental paradigms are needed to further dissect out the timing of the individual parameters.

As in prior studies (Fu et al. 1997; Marple-Horvat and Stein 1987; Roitman et al. 2005), the distribution of τ values is wide and includes cells in which firing lags hand kinematics. These findings are consistent with processing sensory feedback. It should not be surprising that Purkinje cells may dually encode both feedforward and feedback signals, as visually guided tasks, like tracking, rely heavily on performance feedback. Imaging studies reveal that cerebellar activation is related to feedback signals such as motor errors (Diedrichsen et al. 2005; Flament et al. 1996; Grafton et al. 2008; Miall and Jenkinson 2005). The cerebellum could potentially support both feedforward and feedback control because of numerous bidirectional connections with the motor cortex (Ito 1984; Kelly and Strick 2003) and extensive sensory inputs (Bloedel and Courville 1981). Factors influencing the timing relationships of the signals are unknown. The task itself appears to have little effect, as the range of τ values are similar between single-joint wrist flexion/extension (Mano and Yamamoto 1980), center-out reach (Fu et al. 1997; Marple-Horvat and Stein 1987), manual tracking (Roitman et al. 2005), and reach-to-grasp (Dugas and Smith 1992). Possibly, the resultant leads or lags reflect hard-wired circuitry. For example, cells with greater lead times tended to be recorded from more lateral locations in the cerebellar cortex during limb movements (Gray et al. 1993; Marple-Horvat and Stein 1987). However, the information on timing is too limited to make strong inferences.

Generalization of the Signals to Other Tasks

For many Purkinje cells, the kinematic signals extracted from the simple spike firing in random tracking were able to estimate firing rates in either circular tracking or center-out reach. It is worth reemphasizing that this estimate was based on the PVS model using nonaveraged firing and kinematics data. Even model fits with positive τ values (suggesting that the cell processed sensory feedback) were still able to provide good estimates of cell firing for the other tasks. These results further support conclusions that most Purkinje cells provide a parametric representation of movement kinematics in which simple spike activity reflects kinematic parameters irrespective of the movement or task.

For a limited number of Purkinje cells, the results show that model coefficients are not effective in estimating the simple spike discharge in other tasks. For a few cells, the prediction even resulted in a negative correlation. Good fits between the estimated and actual firing do not correlate with model R_adj² or τ values, and low R_adj² values cannot account for all of the poor predictions. Therefore, some Purkinje cells may change their signaling with different tasks.

Averaged vs. Nonaveraged Data

Overall, the total R_adj² explained by the PVS model is somewhat less than in previous reports. Three major differences contribute to the lower R² values. First, as noted above, the PVS model is limited to parameters that are minimally correlated, which was not the case for our two previous manual tracking studies (Coltz et al. 1999; Roitman et al. 2005). Also, whereas the PVS model is restricted to linear fits, previous models were based on regression analyses that included a number of interactive and nonlinear terms (Coltz et al. 1999; Roitman et al. 2005). In one study, the interaction terms resulted in a complex model with nine predictors (Roitman et al. 2005), whereas only five predictors are used in this PVS model. Second, random tracking covers larger parts of the kinematic workspace compared with other tasks, greatly increasing the variability in the data. The firing model was fit to the entire kinematic data set as opposed to specific segments of the data, as used in some studies (Gomi et al. 1998; Medina and Lisberger 2009; Shidara et al. 1993).

The third, and potentially most important difference, is the extent of averaging used. It is well established that averaging artificially reduces the inherent variability of the data set (Kenny 1979; Zar 1999), so that the model error cannot accommodate expected levels of noise. As a result, linear regression models may be biased and have poor predictive performance (Freund 1971). Therefore, any conclusions about the nature of the signals encoded in the firing cannot be ensured to generalize to other movements or tasks. Averaging may also alter the timing relationships between firing and kinematics, and limit understanding of the signals at the level of single trials. In the present study, the regression analysis based on averaged data divided the position, velocity, and speed workspaces into 3,125 (5⁵) bins compared with 32 bins in Coltz et al. (1999) and 360 bins in Roitman et al. (2005). A small number of bins was also used in previous center-out reach studies (Fortier et al. 1989; Fu et al. 1997). The effects of averaging can be appreciated by using the same model parameters and only changing the bin resolution. The average R_adj² of the PVS model is 0.35 when the workspace is partitioned into 5⁵ bins compared with 0.31 or 0.46 when partitioned into 6⁵ or 3⁵ bins, respectively. Further averaging, by restricting the regression analysis to only velocity (Vx_h, Vy_h), results in a mean R_adj² of 0.70. Similarly, limiting the regression variables to position parameters (X_h, Y_h) inflates the mean R_adjj² to 0.64. Therefore, the extent of the bin size and the degree of averaging heavily influence the model R².

The regression analyses performed without averaging further illustrate this issue. Using the instantaneous simple spike firing and hand kinematics without binning results in smaller R² values (Fig. 12). However, the regression coefficients and τ values obtained from the nonaveraged data were highly correlated to those obtained by using the averaged, binned data. No additional physiological information is gained by using averaged data for regression modeling. Instead, models based on nonaveraged data provide a better understanding of the real-time signals contained in the firing of individual Purkinje cells.

The use of nonaveraged firing data raises questions about the encoding of signals in the simple spike discharge of Purkinje cells. It might be argued that an R² value of 0.05 or 0.1 for the PVS model implies a poor fit to the data or that the instantaneous firing is inherently noisy, limiting the encoding. However, the results suggest otherwise and show that explaining even a small fraction of the firing variability is highly relevant. As demonstrated, random tracking model coefficients with modest R² values can adequately estimate the simple spike firing in reaching and circular tracking, even though the tasks differ substantially in their properties and workspace coverage. Therefore, the magnitude of the R² is not likely to be the most important indicator of model validity, as has been suggested for biological data sets (O'Grady 1982). Conversely, the small model R² and conserved encoding of kinematic signals suggest that Purkinje cell simple spike discharge could encode numerous parameters. This would be consistent with the 100,000–200,000 parallel fiber synapses on a single Purkinje cell (Napper and Harvey 1988) and the fact that only 100–200 parallel fiber synapses are needed to generate a simple spike (Barbour 1993; Isope and Barbour 2002). If, as found in this study, each signal does not need to account for a large percentage of the firing variability but only be highly conserved, a single Purkinje cell could provide a wealth of information and participate in a large number of behaviors.

Implications for the Forward Internal Model Hypothesis

Several of the findings are consistent with Purkinje cells acting as the output of a forward internal model that predicts upcoming kinematics (Kawato 1999; Kawato and Wolpert 1998; Wolpert et al. 1995). The first is that Purkinje cell simple spike firing is highly correlated with movement kinematics. Given the evidence that Purkinje cells do not encode kinetics or muscle activity in other manual tracking tasks (Coltz et al. 1999; Pasalar et al. 2006; Roitman et al. 2005), the signals undoubtedly represent kinematics. Second, for the majority of Purkinje cells, simple spike firing leads the kinematics as required by a forward model. Third, the future kinematic signals are present in an unpredictable task, in which the monkey is not provided any information about the upcoming target movements, yet Purkinje cell activity signals future hand kinematics. We argue that this is a strong test of the forward model. If the cerebellum acts as a forward internal model (Wolpert et al. 1998), it will combine the motor command with feedback about the present state of the arm and transform the output into a prediction of the movement consequences, irrespective of whether the task is dominated by feedback or feedforward characteristics. Therefore, finding kinematic signals encoded prior to the actual movements in random tracking is solid support for a forward internal model.

GRANTS

This work was supported in part by National Institutes of Health Grants NS-18338, NS-071686, DK-70106, RR-008079, GM-008244, and NS-057091.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).