Comparison of Generalized Estimating Equations and Quadratic Inference Functions in superior versus inferior Ahmed Glaucoma Valve implantation

Abstract

BACKGROUND:

The celebrated generalized estimating equations (GEE) approach is often used in longitudinal data analysis While this method behaves robustly against misspecification of the working correlation structure, it has some limitations on efficacy of estimators, goodness-of-fit tests and model selection criteria The quadratic inference functions (QIF) is a new statistical methodology that overcomes these limitations.

METHODS:

We administered the use of QIF and GEE in comparing the superior and inferior Ahmed glaucoma valve (AGV) implantation, while our focus was on the efficiency of estimation and using model selection criteria, we compared the effect of implant location on intraocular pressure (IOP) in refractory glaucoma patients We modeled the relationship between IOP and implant location, patient's sex and age, best corrected visual acuity, history of cataract surgery, preoperative IOP and months after surgery with assuming unstructured working correlation.

RESULTS:

63 eyes of 63 patients were included in this study, 28 eyes in inferior group and 35 eyes in superior group The GEE analysis revealed that preoperative IOP has a significant effect on IOP (p = 0 011) However, QIF showed that preoperative IOP, months after surgery and squared months are significantly associated with IOP after surgery (p < 0 05) Overall, estimates from QIF are more efficient than GEE (RE = 1 272).

CONCLUSIONS:

In the case of unstructured working correlation, the QIF is more efficient than GEE There were no considerable difference between these locations, our results confirmed previously published works which mentioned it is better that glaucoma patients undergo superior AGV implantation.

Most of the researches in epidemiology and medical sciences are based upon longitudinal designs; where individuals repeatedly measured over time. The primary interest of a longitudinal study is to explore the pattern of change over time; which includes time or covariate effects. In longitudinal data analysis, the correlation between successive measurements has to be accounted for in order to make a valid statistical inference.¹,²

One of the methodologies that extensively used for analyzing longitudinal data is the marginal models. The purpose of marginal models is to estimate the population-average effect of covariates on response of interest. The term marginal means that the model for mean response depends only on the covariates of interest, not on any random effects or previous responses.²

The generalized estimating equation (GEE) approach is the most popular method in marginal models that extends the capabilities of generalized linear models (GLM) for analyzing longitudinal data. In this method the correlation between successive measurements is modeled by assuming a working correlation matrix. This assumption facilitates the estimation of model parameters. Using an optimum or correct working correlation matrix increases the efficacy of the parameter of interest; hence it is preferable to choose a working correlation matrix that fits the data better. If the working correlation matrix is not correctly specified, the model parameter estimates that are obtained from GEE are inefficient but consistent.³

Moreover, the GEE method has limitations on choosing the best model and goodness-of-fit tests. In addition, in the presence of contaminated measurements or outlier values, the GEE method cannot produce consistent estimators.⁴,⁵

Wang and Carey⁶ showed that appropriate specification of correlation structures in longitudinal data analysis improves estimation efficiency and leads to more reliable statistical inferences.

In order to improve the efficiency of model parameter estimators when the working correlation structure of the GEE is misspecified, Qu et al ⁷ proposed quadratic inference function (QIF) as an alternative. QIF is a relatively new and simple statistical methodology that provides efficient estimators irrespective of the true underlying correlation structure. Furthermore, the inference function of QIF enables it to provide goodness-of-fit test, simultaneous hypothesis tests and applying model selection criteria such as AIC (Akaike Information Criterion) or BIC (Bayes Information criterion).⁷

While many articles showed the superiority of QIF over GEE,⁵,⁷,⁸ a literature review cited on PUBMED yielded only one study that illustrated the use of QIF for analyzing correlated data.⁹

The aim of this paper is to encourage the use of QIF approach in analyzing longitudinal data. As an illustration, we applied QIF and GEE methodologies to analyze data from a longitudinal study, previously analyzed without considering the correlation between successive measurements. In this illustration we want to see if any differences exist between the two locations of implant on intraocular pressure (IOP) after Ahmed Glaucoma Valve (AGV) implantation and after adjusting some desired factors and accounting for correlation between successive measurements. We model the relationship between response variable IOP and covariates such as implant location, patient's age and sex, best corrected visual acuity (BCVA), preoperative IOP, history of cataract surgery and months after surgery.

Methods

GEE and QIF Approaches

We briefly recall here the description of these methods. Liang and Zeger³ first introduced the idea of using working correlation matrix with small set of nuisance parameters in order to avoid determination of within-subject correlation in quasi-likelihood equation. In fact, the term “working” shows our uncertainty about correlation matrix. The most common types of working correlation structures are independence, exchangeable, auto-regressive of order 1 (AR-1) and unstructured working correlation structure.

The details of correlation structure and a model for the mean of the response variable are included in quasi-likelihood equation; this equation is iteratively solved to obtain parameter estimates.³

Fitzmaurice et al¹⁰ showed that in order to improve the efficiency of the regression coefficients in quasi-likelihood inference, it is necessary to specify the working correlation matrix that is as close as possible to the true one. However, the GEE methodology gives inefficient parameter estimators, if the correlation structure is not correctly specified.³ Moreover, the difficulty with this approach is that to obtain the model parameter estimators consistently, the estimators of nuisance (correlation) parameters have to be existent and consistent.² However several papers¹¹,¹² showed that in some simple cases the estimator of the nuisance parameter does not exist, and in the case of the misspecified working correlation the estimator of nuisance parameters may not be consistent. The advantages and limitations of using GEE are summarized in table 1.

Table 1.

Summary of the advantages and limitations of GEE and QIF methodologies

The QIF methodology has some useful properties over GEE that were pointed out in table 1. In this method the inverse of working correlation matrix is approximated by a linear combination of known basis matrices and unknown constants. This linear combination would be put in place of working correlation matrix in quasi-likelihood function and the generalized method of moments¹³ is used to obtain an objective function. Therefore, the QIF methodology does not directly involve the estimation of correlation parameters, and remains optimal even if the working correlation structure is misspecified.⁷

In the case of unstructured working correlation, Qu and Lindsey¹⁴ have found that using variance matrix of responses instead of basis matrices provides an approximately optimal inference function. This variance matrix can be estimated by the sample covariance matrix of responses, which updates along with the updating of regression coefficients in the iterative algorithm.

QIF is a powerful alternative to the celebrated GEE, nevertheless, it has some limitations (highlighted in table 1); only two statistical software packages are available for QIF analyzing including SAS MACRO QIF¹⁵ and R's package.¹⁶ Both of them cannot support unequally spaced repeated measurements⁸,¹⁶ ; and established only for four types of commonly used working correlation structures including Independence, Exchangeable, AR-1 and Unstructured.⁸ Moreover the current versions of QIF R's package can only support equal cluster sized data typed (balanced data).¹⁶ However, it is worth mentioning that unlike R's package the SAS MACRO QIF can deal with unbalanced data (this macro was developed under SAS 9.1.3).

AGV Implantation Data

Glaucoma is the name of a group of diseases characterized by specific damage of the optic nerve head, often accompanied by elevated IOP and followed by specific glaucomatous visual field loss.¹⁷

Ahmed Glaucoma Valve (AGV) (New World Medical Inc., Rancho Cucamonga, CA) was introduced in 1993 for management of refractory glaucoma. The recommended site for AGV implantation by the manufacturer is the superotemporal quadrant and generally, the inferior quadrant is less commonly used as the primary sites for implantation unless it is not feasible to do implantation on superior quadrant. The superior and inferior AGV are known to be safe and effective in controlling IOP on patients with refractory glaucoma.¹⁸

We used a longitudinal data set comparing AGV implantation in superior and inferior quadrants. Details concerning this dataset study design and data collection can be found else-where.¹⁸ Briefly, this study is a prospective parallel cohort study that had been conducted on 106 eyes of 106 refractory glaucoma patients who underwent AGV implantation from August 2004 to September 2007; 58 eyes underwent superior AGV implantation and 48 eyes underwent inferior AGV implantation. The postoperative follow-up visits were scheduled at 1 week and 1, 3, 6 and 12 months after surgery. The clinical variables of interest are patient's age and sex, history of cataract surgery, BCVA, and IOP; where IOP and BCVA are measured during one year after surgery.

In this study we compared the effect of implant location on IOP after AGV implantation along with above desired factors and accounting for correlation between successive measurements. To do this, we used the QIF R's package. In order to deal with the limitations of this software, we made two modifications on data. First, in this study 39.65% of patients who underwent superior AGV implantation and 41.67% of patients who underwent inferior AGV implantation did not complete the study and had incomplete data on one or more scheduled follow-ups and dropped out of analysis for making the data equally cluster sized. Second, we interpolated the clinical data on the 9^th month after surgery in order to make data equally spaced. This interpolation was done using XIXtrFun.dll¹⁹ in Excel for IOP and BCVA based on the information from before surgery, week 1 and months 1, 3, 6 and 12 after surgery.

Statistical Analysis

All statistical analyses were performed using freely available R statistical software (version 2.10.1). P value less than 0.05 were considered statistically significant. Summary statistics were used to provide a description of patients in each group. T-test was used for quantitative variables and Fisher's exact test for qualitative variables. The marginal model with identity link function was used, where IOP is expressed as a function of implant location, sex, age, pre-operative IOP, history of cataract surgery, BCVA and months after surgery using GEE and QIF methodologies. We fitted the two models (Figure 1).

Figure 1.

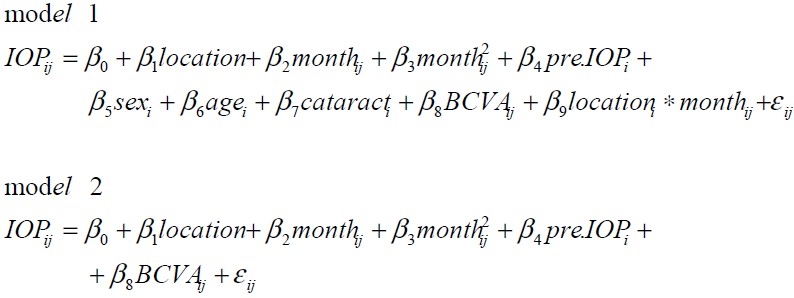
Two marginal models with identity link function used for statistical analyses

While “location” stands for implant location, with 1 or 0 for patient underwent superior or inferior AGV implantation, respectively; “cataract” stands for history of cataract surgery, with 1 if the patient had a history of cataract surgery and 0 otherwise; and “months” stands for number of months after surgery and the possible values of “months” are 3, 6, 9 and 12. “Sex” is 1 or 0 for males or females, respectively; we treated the preoperative IOP as “pre.IOP” here.

Goodness-of-fit test available in QIF was used for model assessment. Extensions of Q statistics such as AIC and BIC were used to select the best fitting model. Smaller AIC and BIC indicate better fit.

Parameter estimates obtained from GEE and QIF were compared with respect to relative efficacy.

Results

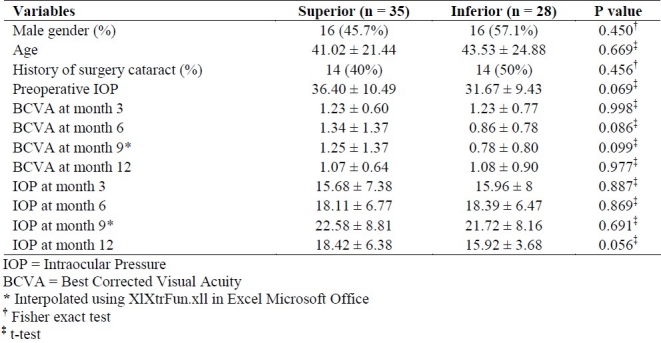
A total of 63 eyes of 63 patients were included in this study; 28 eyes in inferior group and 35 eyes in superior group. General characteristics of the study participants are shown in table 2. No significant differences were observed between two groups regarding considered variables. Although the preoperative IOP and IOP at month 12 after surgery were higher in the superior. Moreover based on the graph obtained from mean of IOP for each group at selected follow-ups, it was revealed that the trend of IOP changes does not have linear manner. In both groups, the mean of IOP appeared to increase until month 9 after surgery, and then decrease. Moreover, during the first 6 months after surgery the mean of IOP in inferior group is higher than superior group, but in the second 6 month the mean of IOP for superior group is higher than inferior group and diverge as months after surgery go further. For this reason we included the interaction term in model 1. Also, this figure shows that a quadratic term is required to improve the model fit (this graph were not shown).

Table 2.

General characteristics of study participants (% or Mean ± SD)

Model Fitting Using GEE and QIF Methodologies

The correlation between successive measurements on IOP is shown in table 3. It is appeared that the unstructured working correlation is a good choice for this data. In order to use an appropriate working correlation, we followed the method that was proposed by Song² and fit a marginal GLM under the independence correlation structure, compute the pairwise Pearson correlation between residuals, and match the sample correlation matrix with one of the commonly used working correlation matrices. Again, we obtained the same result (the results were not shown).

Table 3.

The correlation matrix between IOPs measured at selected months after AGV implantation

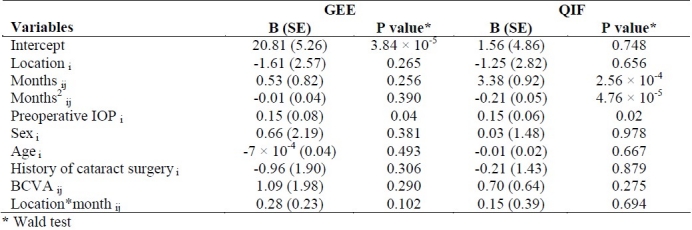
table 4 provides point estimates, standard errors, and p values based on Wald test using model 1 with GEE and QIF under unstructured working correlation structure; according to table 4, preoperative IOP is significantly associated with IOP, after adjusting for other variables using both GEE and QIF approaches. Moreover, our results using QIF method showed months after surgery and squared months have significant effects on IOP.

Table 4.

Regression coefficient estimates based on GEE and QIF for model 1

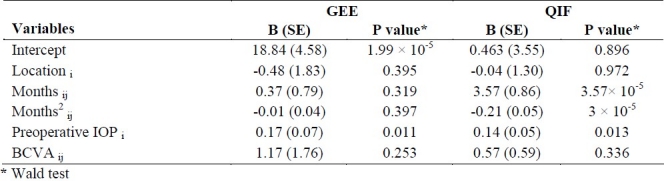
Since some variables did not show any significant effect on IOP after implantation, we decided to fit a simpler model. Many models have been fitted and among those models, model 2 was selected as a simpler model in comparison with model 1. The results from fitting model 2 using GEE and QIF are summarized in table 5. Again we obtained the same results on significant variables as table 4.

Table 5.

Regression coefficient estimates based on GEE and QIF for model 2

In addition, the QIF provides direct measure of goodness-of-fit. These measures are shown in table 6. According to the Q statistic, it is concluded that the above two models are adequate to describe the observed data. This statistic enables us to do simultaneous test hypotheses, and see if the simpler model is as predictive as the full model. Like the likelihood ratio test, the difference between these Q statistics is asymptotically Chi-squared, regardless of the true correlation structure.⁷ Based on table 6, the difference between the Q statistic for model 1 and model 2 (1.955-0.468 = 1.487) follows the Chi-squared distribution with 4 degrees of freedom, the p value associated with this statistic is 0.916. Therefore, we concluded that model 2 is equivalent as model 1 and we could ignore the effect of variables sex, age, history of cataract surgery and interaction term between months after implantation and implant location in predicting IOP after implantation.

Table 6.

QIF goodness-of-fit test for models 1 and 2

Moreover, the smaller AIC and BIC in model 2 compared to model 1 indicates the better fit of model 2.

GEE Versus QIF

Overall the results from GEE and QIF were consistent on the strength of relationship between considered variables and the response of variable IOP (Tables 4 and 5). However GEE and QIF produce different conclusions on the effects of months and squared months after surgery.

In comparison with the efficiency of parameter estimates, we used the relative efficacy (RE) formula (presented by Qu et al⁷) and obtained 1.823 and 1.271 for model one and two, respectively. This implies that the QIF paramter estimates are more efficient than the GEE estimates in both models.

Discussion

In the present study, we exemplified the use of QIF for analyzing one longitudinal data set. We obtained the effect of some desired factors on IOP control after AGV implantation while considering the correlation between successive measurements.

This study is the first one to compare the efficacy of parameter estimates from GEE and QIF using unstructured working correlation. Odueyungbo et al⁹ compared GEE and QIF using data from National Longitudinal Survey of Children and Youth (NLSCY) with assuming AR-1 and exchangeable working correlation structures and showed that the estimators from QIF are more efficient than GEE. Although Qu et al⁷ previously had obtained the same results with simulated data. Also, this paper is the first one which compares the effect of implant location on IOP after AGV implantation while accounting for the correlation between successive measurements. There has been one previous study that compared the safety and efficacy of AGV implantation in superior and inferior quadrants. Their findings showed that these locations have similar efficacy in term of IOP control. Moreover, in that study the generalized linear regression model at month 12 after AGV implantation showed that there was a borderline difference between superior and inferior AGV implantation, which was slightly in favor of inferior group: a mean of 2.24 mmHg (CI 95%, -0.32 to 4.82, p value = 0.086) showed greater decrease in IOP after adjustment for possible confounding factors.¹⁸ However, our results (based on table 5) showed a slightly decrease in mean of IOP for superior AGV implantation group and this result is consistent with the proposed site by the manufacturer for AGV implantation, which is the superotemporal quadrants.¹⁹

Overall, we obtained similar results comparing GEE and QIF. However, there were some differences between them which can be expressed by the useful properties of QIF over GEE in analyzing longitudinal data.

Based on the results of tables 4 and 5, we see that the parameter estimates using GEE and QIF are similar, besides the estimators from QIF are more efficient than GEE.

The difference between two methods regarding the effects of months after surgery and squared months is appeared to be due to the inverse of the unstructured working correlation in QIF. Qu and Lindsay¹⁴ proposed a linear approximation inverse for unstructured working correlation that uses a consistent estimator of the variance matrix of response variable. Furthermore, Qu and Song⁵ showed that QIF has a redescending property and automatically downweights through the inverse of the weighting matrix. Thus, the weights that assigned to each observation varied by each other, and if the residual of one observation is large this observation takes smaller weight in model fitting process. But in GEE all observations take the same weight.

Our results showed the greater efficiency of parameter estimates from QIF in comparison with GEE and were consistent with the findings of Qu et al⁷ and Odueyungbo.⁹

The strength of this study is the longitudinal nature of the data set and accounting for the correlation between successive measurements. Besides, there were some limitations concerning available QIF R's package that was used. We removed 43 patients and interpolated for month 9 in order to make data equally cluster sized and equally spaced. According to Lee et al (2007)²⁴ it is recommended that one used GEE only if the number of subjects were at least 30, and if 3 to 5 data points per participants were evaluated. This recommendation is derived from the fact that the GEE is based on the large sample theory, or asymptotic properties of regression parameter estimators. However, there is no recommendation on the needed sample size for QIF, but Song et al (2009)⁸ showed that to achieve the same power in hypothesis test for treatment effects in a longitudinal study, the QIF requires a smaller sample size than GEE. Based on these we think that our sample size was adequate. It is worth noting that, one of the advantageous of using cubic spline in XIXtrFun.dll is that it's third degree piecewise polynomial curve goes through all knots and all knots are required to define all polynomials that make up the entire curve; thus changing any one of the knots changes all the interpolated values that are between knots.

Conclusions

In the present study, based on all above analysis we found that, after accounting for the correlation between successive measurements, there is no difference between the superior and inferior AGV implantation on IOP control; and we confirmed the findings from previously published works, that it is better for glaucoma patients to undergo superior AGV implantation.

Authors’ Contributions

RKK has proposed and performed the study and is the corresponding author. BG has managed and supervised the project until her sudden death, after that KM continued supervision on behalf of her. MM and SN provided assistance in data analysis and discussion. MP provided the data. All authors have read and approved the content of the manuscript.