Ba₄KFe₃O₉: A Novel Ferrite Containing Discrete Six-member Rings of Corner-sharing FeO₄ Tetrahedra

Abstract

Single crystals of a new iron containing oxide, Ba₄KFe₃O₉, were grown from a hydroxide melt and the crystal structure was determined by single crystal x-ray diffraction. This ferrite represents the first complex oxide containing isolated 6-member rings of corner sharing FeO₄ tetrahedra. Mössbauer measurements are indicative of two tetrahedral high-spin Fe³⁺ coordination environments. The observed magnetic moment (~3.9 BM) at 400 K is significantly lower than the calculated spin-only (~5.2 BM) value indicating the presence of strong antiferromagnetic interactions in the oxide. Our density functional calculations confirm the strong antiferromagnetic coupling between adjacent Fe³⁺ sites within each 6-member ring and estimate the nearest neighbor spin exchange integral as ~200 K; next nearest neighbor interactions are shown to be negligible. The lower than expected effective moment for Ba₄KFe₃O₉ calculated from χT data is explained as resulting from the occupation of lower lying magnetic states in which more spins are paired. X-band (9.5 GHz) electron paramagnetic resonance (EPR) spectra of powder sample consist of a single line at g~2.01 that is characteristic of Fe³⁺ ions in a tetrahedral environment, thus, confirming the Mössbauer results. Further analysis of the EPR line shape reveals the presence of two types of Fe₆ magnetic species with an intensity ratio of ~1:9. Both species have Lorentzian line shapes and indistinguishable g-factors but differ in the peak-to-peak line widths (δB_pp). The line width ratio δB_pp(major)/δB_pp(minor) ~ 3.6 correlates well with the ratio of the Weiss constants, θ_minor/θ_major ~ 4.

Introduction

Among extended oxide compounds, structures containing rings of transition metal-oxygen polyhedra are uncommon, with the exception of silicates and germanates, where they are ubiquitous. Natural silicate minerals like beryl and tourmaline have 6-member rings of corner-sharing SiO₄ tetrahedra,¹ while some germinates, such as Ge₉O₁₉(OH)₂(N₂C₂H₁₀)₂(N₂C₂H₈)_0.5•H₂O, contain both 8- and 11-membered rings of corner-sharing GeO₄ tetrahedra.² In contrast, only a small number of iron-containing oxides adopt ring structures. The room temperature AFeO₂ (A = K, Rb and Cs) structures are of the KGaO₂ type and contain six member rings of corner-sharing FeO₄ tetrahedra that are connected to adjacent rings by additional corner-sharing.³ Na₁₄Fe₆O₁₆ contains linked 4- and 6-member rings of corner sharing FeO₄ tetrahedra,⁴ while in Ba₃NbFe₃Si₂O₁₄, FeO₄ tetrahedra form trimers that are interconnected via NbO₆ octahedra.⁵ Other iron containing ring structures include Na₁₀Fe₄O₉,⁶ and Ba₃Fe₂O₆⁷ In most iron containing oxides the rings are interconnected but exceptions exist, including the FeO₄ tetrahedra trimers in Ba₃NbFe₃Si₂O₁₄,⁵ and the 12-member rings in Ba₃Fe₂O₆.⁷

A number of molecular inorganic ring structures are known⁸ and are of interest both for the aesthetics of the structures⁹ as well as for potential applications in catalysis and gas adsorption.¹⁰ Furthermore, when such rings contain magnetic ions, such as manganese, molybdenum or iron, they typically exhibit complex magnetic interactions.¹¹ Over the years, a number of iron containing molecular ring structures, referred to as ferric wheels,^12,13 have been crystallized via solution routes, including [Fe(OMe)₂(O₂CCH₂Cl)]₁₀,¹³ [Fe₁₄O₁₀(OH)₄(Piv)₁₈ (HPiv = pivalic acid)¹⁴ and [Fe(OH)(C₃₀H₃₈N₂O₈)Fe₂(OCH₃04(O₂CCH₃)₂]6.¹⁵

We have been exploring the crystallization of iron containing complex oxides using high temperature solutions, including carbonate and hydroxide melts, and have synthesized complex oxides containing di-, tri- and tetravalent iron centers.^16,17 Of the fluxes used, the molten hydroxides work especially well for the crystal growth of complex oxides,¹⁸ as noted by other groups that have also investigated the crystal growth of iron containing oxides out of hydroxide fluxes.¹⁹

Recently, we succeeded in using hydroxide melts to crystallize a new iron containing oxide, Ba₄KFe₃O₉. To our knowledge, this is the only reported complex iron oxide containing isolated 6-member rings. We have structurally characterized this new oxide and have collected Mössbauer spectroscopy, EPR and magnetic data to investigate the magnetic interactions between the iron centers. To supplement these data, we have carried out density functional calculations to study the magnetic coupling between adjacent iron centers. Herein we report the crystal growth of Ba₄KFe₃O₉, its structure determination and the investigation of its magnetic properties.

Experimental Section

Crystal Growth

Single crystals of Ba₄KFe₃O₉ were grown from molten hydroxides. In a typical synthesis 1.9 g of dehydrated Ba(OH)₂ (prepared by heating Ba(OH)₂·8H₂O (Alfa Aesar, 98%) at 280°C for 3 h), 2.5 g of KOH (Fisher, reagent grade), and 0.4 g of Fe₂O₃ (Alfa Aesar, 99.998%) were loaded into an alumina crucible, which was then covered with a lid. The crucible was placed into a box furnace, heated to 750 °C in 5 h, held at that temperature for 5 h, cooled to 600 °C in 32 h, and finally cooled to room temperature by turning off the furnace. Upon completion of the reaction, removal of the crucible lid revealed a bed of loose crystals. The crystals were twice washed with 36 ml iso-propanol under N₂ to remove any remaining flux particles and then, since the crystals are very moisture sensitive, stored in a glovebox.

Structure Determination

X-ray data from an irregular shape black-looking single crystal were obtained at 150(2) K using a Bruker SMART APEX (Billerica, MA) diffractometer (Mo Kα radiation, λ = 0.71073 Å).²⁰ The crystal was separated from a rough chunk covered with 1 mL of decane right after the reaction. When thin enough to transmit light, the crystals appear dark brown. The data collection covered 100% of the reciprocal space to 2θ_max = 66.3°, with an average redundancy of 23.2 and R_int = 0.0995 after absorption correction. Raw area detector data frame integration was performed with SAINT+.²⁰ Final unit cell parameters were determined by least-squares refinement of 5628 reflections from the data set in the range 6.8°<2θ<64.9°. Direct methods structure solution, difference Fourier calculations and full-matrix least-squares refinement against F² were performed with SHELXTL.²¹

The compound crystallizes in the cubic space group Pa 3̄ (No. 205), as determined uniquely by the pattern of systematic absences in the intensity data. There are three barium, two iron, one potassium, three mixed K⁺/Ba²⁺ positions and six oxygen atom positions in the asymmetric unit. All atoms are in general positions (Wyckoff symbol 24d) except Ba3, K1, and K2/Ba2A (8c, site symmetry 3), K3/Ba3A (4a, site symmetry 3̄) and Ba4/K4A (4b, site symmetry 3̄). Unreasonably large or small displacement parameters were observed for sites K2/Ba2A (8c), K3/Ba3A (4a) and Ba4/K4A (4b) if refined as fully occupied by Ba²⁺ or K⁺, respectively. Trial refinement of the affected site occupancies always showed significant deviations from the unit occupancy by a single atom type. Each site was therefore refined as a mixture of Ba²⁺/K⁺, with total occupancy of each site constrained to sum of unity. The refined occupancy values are 0.569(5)/0.431(5) for K2/Ba2A, 0.934(5)/0.066(5) for K3/Ba3A, and 0.962(5)/0.038(5) for Ba4/K4A Occupancies of the other metal atom sites deviated from full occupancy by less than 3%, and were not refined. The site mixing model results in a formula of Ba_3.97K_1.03Fe₃O₉. This formula implies a small excess negative charge of 0.03 e⁻ per formula unit (assuming all Fe³⁺). This is very close to electro-neutrality and supports the site mixing model over a vacancy model. All atoms were refined with anisotropic displacement parameters. The largest residual electron density extrema are +1.88 and −2.07 e⁻/Å located 0.61 and 0.01 Å from Ba2 and Ba4/K4A, respectively. The reported atomic coordinates were standardized with the StructureTidy program implemented in PLATON.²²

Magnetic Susceptibility

The magnetic susceptibility χ of powder samples of Ba₄KFe₃O₉ was measured as a function of temperature T using a Quantum Design PPMS (San Diego, CA) equipped with a vibrating sample magnetometer (VSM) attachment. The sample was contained in a gelatin capsule and held in place using small pieces of tissue paper. The capsule was fastened inside a plastic straw that was connected to the PPMS sample holder. χ(T) were collected in an applied magnetic field of 1 kG under both field-cooled (FC) and zero-field cooled (ZFC) conditions. ZFC data were collected in the temperature range 2 – 400 K, while FC data were collected in the temperature range of 2 – 300 K. An empty capsule was prepared in the identical fashion and its χ(T) was collected in order to correct the collected data for the contribution of the sample holder.

Heat Capacity

A representative group of crystals were weighed and placed in an aluminum Tzero sample pan that was coated on the inside with a thin layer of Apiezon N grease to increase thermal contact. The pans were hermetically sealed under helium, which provides further thermal contact with the small crystals. Heat capacity measurements were conducted between 5 and 300 K in zero magnetic field using a Quantum Design PPMS. The lattice contribution was not subtracted from the heat capacity.

Mössbauer

The ⁵⁷Fe transmission Mössbauer spectrum was measured at room temperature using a γ-ray source from ⁵⁷Co embedded in a rhodium matrix. The sample was sealed within 2 mylar tapes in a glove box before the measurement. The spectrum was fitted with Lorenzian lines by the MOSFIT program. The isomer shift was referenced to metallic α-Fe at 293 K.

Electron paramagnetic resonance (EPR) spectroscopy

Ba₄KFe₃O₉ powder was placed in a 3×4 mm (i.d. × o.d.) quartz EPR tube (Wilmad, Vineyard, NJ), filled with nitrogen gas and flame-sealed. EPR spectra were collected at ~9.5 GHz (X-band) in the 190 K – 360 K temperature range using a Bruker Elexsys 580 spectrometer equipped with an ER4131 variable temperature unit (all from Bruker Biospin, Billerica MA). Electronics g-factors, peak-to-peak line widths (δB_pp) and double-integrated intensities (I) were obtained by performing a Levenberg-Marquardt least-squares fitting of the EPR spectra to a two-component model using EWVOIGTN program.^23,24

Results and Discussion

Crystal structure

Single crystals of Ba₄KFe₃O₉ were grown out of molten KOH and carefully isolated to prevent exposure to atmospheric moisture to avoid rapid decomposition. Any exposure to moisture causes the structure to visibly degrade, as evidenced by a color change to light brown and the appearance of additional diffraction lines in the powder X-ray diffraction pattern. This extreme moisture sensitivity is likely directly related to this structure type that contains isolated anionic Fe₆O₁₈ rings held in a salt like environment made up of barium and potassium cations.

The crystallographic data and atomic coordinates are summarized in Table 1 and Table 2. The structure consists of a complex cubic barium/potassium framework in which Fe₆O₁₈ rings are located. One Fe₆O₁₈ ring consisting of corner shared FeO₄ tetrahedra that encapsulates a potassium ion is shown in Figure 1a. There are two different tetrahedral iron sites in the ring structure that are arranged such that each Fe(1)O₄ tetrahedron shares one corner with each of two Fe(2)O₄ tetrahedra and vice-versa. The two FeO₄ tetrahedra are slightly distorted and each has four different Fe-O bond lengths, ranging from 1.83 – 1.89 Å with O-Fe-O angles from 102.7 to 106.9° (Table 3). The 6-membered ring has a shape similar to the chair-conformation of cyclohexane and holds one potassium cation, K(1), in the middle (Figure 1b). Unlike other FeO₄ tetrahedra-based 6-membered ring structures, the rings in this compound are isolated from each other (Figure 2). Each Fe₆O₁₈ ring has a formal charge of 18-, which is balanced by the Ba²⁺ and K⁺ counterions. The ionic radii for 9-coordinate Ba and K are quite similar, 1.47 and 1.55 Å, respectively. Hence, it is not surprising that some of the counterion sites have mixed Ba²⁺ and K⁺ occupancy. The cation site in the middle of the Fe₆O₁₈ ring is, however, occupied by potassium only. In this structure, the coordination numbers for Ba²⁺, K⁺, and mixed occupied metal sites range from 9 to 10.

Table 1.

Crystal and refinement data

Empirical formula	Ba3.97Fe3K1.03O9
Formula weight	897
Temperature	150(2) K
Wavelength	0.71073 Å
Crystal system	Cubic
Space group	Pa-3
	a = 16.7644(2) Å α = 90°
	b = 16.7644(2) Å β = 90°
Unit cell dimensions	c = 16.7644(2) Å γ = 90°
Volume	4711.55(10) Å3
Z	16
Density (calculated)	5.058 Mg/m3
Absorption coefficient	17.030 mm−1
F(000)	6270
Crystal size	0.12 × 0.08 × 0.06 mm3
Theta range for data collection	2.10 to 33.14°.
Index ranges	−25<=h<=25, −25<=k<=25, −25<=l<=25
Reflections collected	104498
Independent reflections	3008 [R(int) = 0.0995]
Completeness to theta = 33.14°	100.00%
Absorption correction	Semi-empirical from equivalents
Max. and min. transmission	1.0000 and 0.3407
Refinement method	Full-matrix least-squares on F2
Data/restraints/parameters	3008/0/108
Goodness-of-fit on F2	1.078
Final R indices [I>2sigma(I)]	R1 = 0.0314, wR2= 0.0632
R indices (all data)	R1 = 0.0451, wR2= 0.0679
Extinction coefficient	0.000018(3)
Largest diff. peak and hole	1.878 and −2.073 e.Å−3

Table 2.

Atomic coordinates (× 10⁴) and equivalent isotropic displacement parameters (Ų × 10³). U(eq) is defined as one third of the trace of the orthogonalized U^ij tensor.

	x	y	z	U(eq)	Occupancy
Ba(1)	1227(1)	3811(1)	3881(1)	9(1)
Ba(2)	1359(1)	3712(1)	1374(1)	15(1)
Ba(3)	3754(1)	3754(1)	3754(1)	12(1)
Ba(4)	5000	5000	5000	12(1)	0.962(5)
K(4A)	5000	5000	5000	12(1)	0.038(5)
Fe(1)	145(1)	180(1)	2542(1)	8(1)
Fe(2)	42(1)	2407(1)	2374(1)	8(1)
K(1)	1236(1)	1236(1)	1236(1)	21(1)
K(2)	2559(1)	2559(1)	2559(1)	10(1)	0.574(3)
Ba(2A)	2559(1)	2559(1)	2559(1)	10(1)	0.426(3)
K(3)	0	0	0	12(1)	0.937(5)
Ba(3A)	0	0	0	12(1)	0.063(3)
O(1)	2332(2)	4074(2)	2821(2)	14(1)
O(2)	56(2)	2575(2)	1262(2)	12(1)
O(3)	1025(2)	2710(2)	2757(2)	13(1)
O(4)	166(2)	4861(2)	3453(2)	12(1)
O(5)	1297(2)	2424(2)	4964(2)	12(1)
O(6)	235(2)	4745(2)	1521(2)	20(1)

Figure 1.

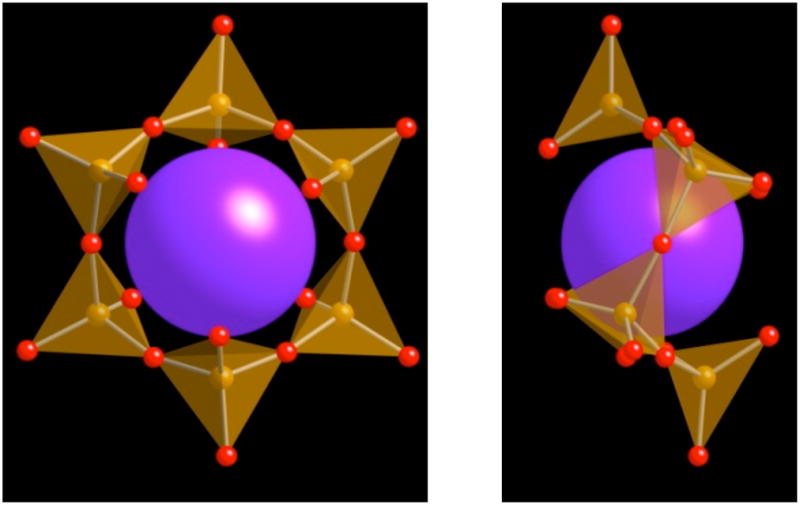
(a) One 6-member Fe₆O₁₈ ring with K atom in center viewed straight on (left) and (b) sideways to emphasize chair-configuration (right). FeO₄ tetrahedra are shown in orange, oxygen atoms in red and potassium atoms in purple.

Table 3.

Selected bond lengths (Å) and bond angles (°)

Fe(1)-O(4)#15	1.828(3)
Fe(1)-O(6)#15	1.846(3)
Fe(1)-O(2)#9	1.885(3)
Fe(1)-O(5)#16	1.898(3)
Fe(2)-O(1)#2	1.831(3)
Fe(2)-O(3)	1.840(3)
Fe(2)-O(2)	1.885(3)
Fe(2)-O(5)#16	1.896(3)
O(4)#15-Fe(1)-O(6)#15	124.20(15)
O(4)#15-Fe(1)-O(2)#9	106.19(13)
O(6)#15-Fe(1)-O(2)#9	105.92(15)
O(4)#15-Fe(1)-O(5)#16	105.73(14)
O(6)#15-Fe(1)-O(5)#16	107.95(15)
O(2)#9-Fe(1)-O(5)#16	105.53(13)
O(1)#2-Fe(2)-O(3)	126.48(14)
O(1)#2-Fe(2)-O(2)	102.77(14)
O(3)-Fe(2)-O(2)	106.97(13)
O(1)#2-Fe(2)-O(5)#16	105.23(13)
O(3)-Fe(2)-O(5)#16	105.67(13)
O(2)-Fe(2)-O(5)#16	108.94(14)

Symmetry transformations used to generate equivalent atoms:

#1 −z+1/2,x+1/2,y

#2 y−1/2,z,−x+1/2

#3 y,−z+1/2,x+1/2

#4 −x,y+1/2,−z+1/2

#5 z,−x+1/2,y+1/2

#6 y,z,x

#7 x,−y+1/2,z−1/2

#8 z,−x+1/2,y−1/2

#9 z,x,y

#10 x+1/2,y,−z+1/2

#11 −y+1,z+1/2,−x+1/2

#12 z+1/2,−x+1/2,−y+1

#13 −x+1/2,−y+1,z+1/2

#14 −x+1,−y+1,−z+1

#15 −x,y−1/2,−z+1/2

#16 z−1/2,x,−y+1/2

Figure 2.

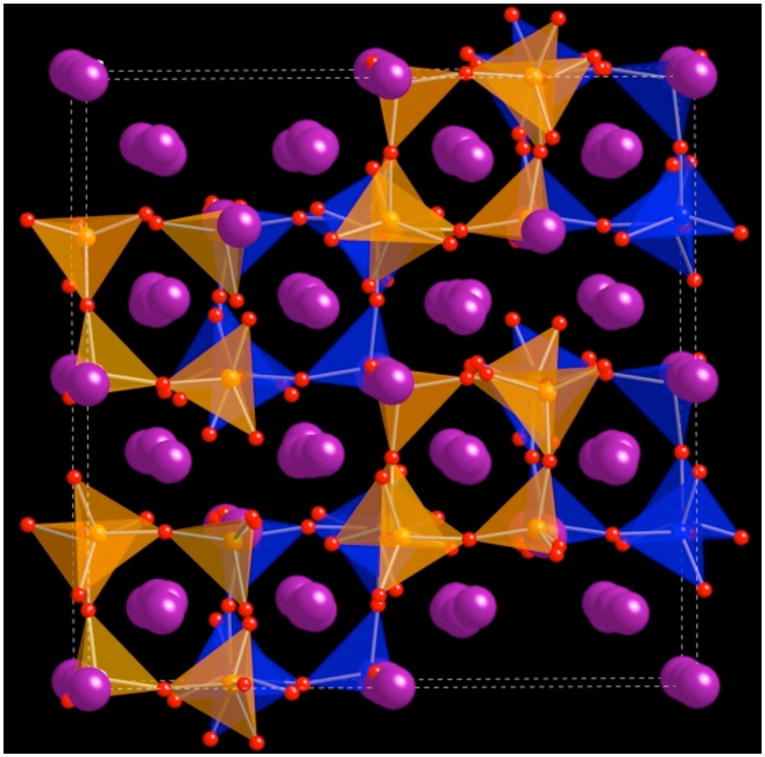
Crystal structure of Ba₄KFe₃O₉ depicting the isolated nature of the 6-member rings. FeO₄ tetrahedra belonging to different rings are shown in orange and blue to illustrate the isolated nature of the rings. Ba and K atoms are both shown in purple.

The counterions (Ba²⁺, K⁺, and Ba²⁺/K⁺ mixed sites) form the cubic framework shown in Figure 3, within which the Fe₆O₁₈ rings are located. The cation arrangement is best related to a defect body centered cubic structure, where the atoms at the corners of the cubes (K(1)) are located in the middle of the ring, while the atoms at the body center of the cubes lie adjacent to the rings. By comparison, in RbFeO₂, an oxide with connected 6-membered FeO₄ tetrahedra rings, the Rb⁺ counterions arrange in a diamond structure ²⁵

Figure 3.

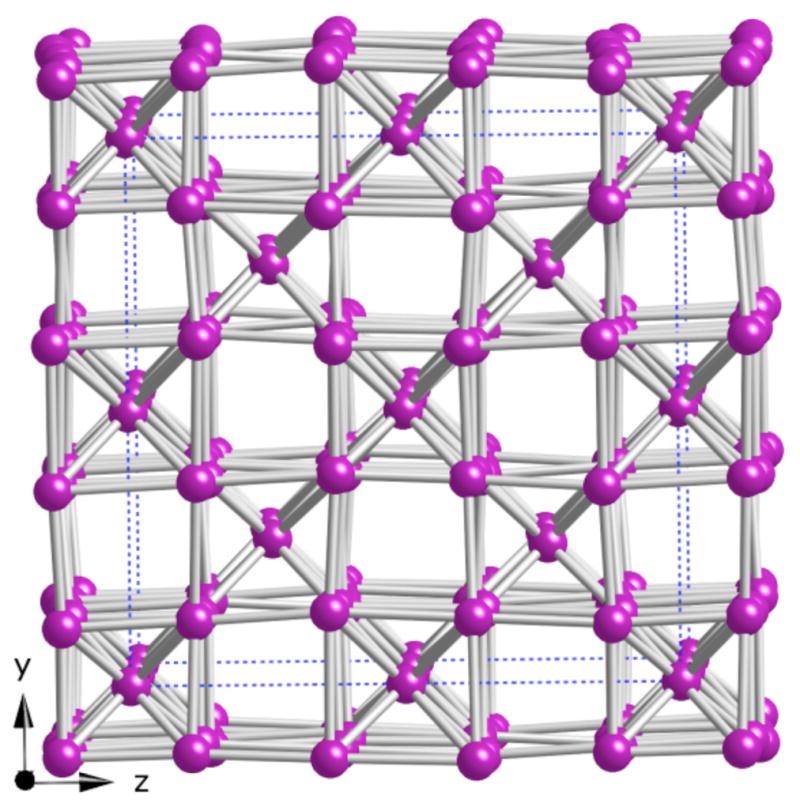
The arrangement of Ba and K atoms. Ba and K atoms are both shown in purple.

Mössbauer, Magnetic Susceptibility and Heat Capacity

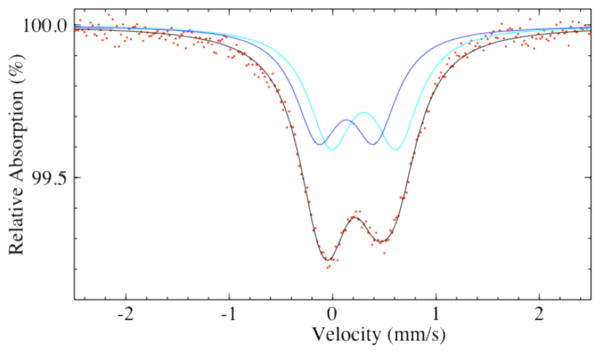
The room temperature Mössbauer spectrum of Ba₄KFe₃O₉ (Figure 4) is composed of two quadrupole doublets with isomer shifts and quadrupole splittings (δ₁ = 0.41 mm/s, ΔEQ₁ = 0.64 mm/s) and (δ₂ = 0.25 mm/s, ΔEQ₂ = 0.55 mm/s) consistent with Fe(III) in a high-spin state and tetrahedral coordination environment.¹⁷ The ratio between these two sites is 0.52/0.48 and is in agreement with the crystal structure. No magnetic hyperfine interactions are observed, consistent with reports for other cyclic iron structures.¹²

Figure 4.

Mössbauer spectrum of Ba₄KFe₃O₉.

To investigate the possible existence of long-range magnetic order in this oxide, magnetic susceptibility data, χ(T), were collected between 2 K and 400 K. The χ vs. T and χ⁻¹ vs. T plots are shown in Figure 5, and do not contain any feature indicative of a long-range magnetic order. The inverse susceptibility plot is non-linear over the entire temperature range measured and cannot be readily fit to the Curie law. Furthermore, the χT vs. T plot shows a complex change in the moment as a function of temperature. The observed effective magnetic moment ${\mu }_{\text{eff}}(=\sqrt{8\chi T})$ of ~3.933 μ_B(Bohr magneton) at 400 K is lower than the expected spin-only value of 5.92 μ_B (for g = 2) for a tetrahedral high spin Fe³⁺ ion. This behavior indicates the presence of antiferromagnetic interactions between Fe³⁺ ions within the Fe₆O₁₈ ring. A similar effect was observed for [Fe₁₄O₁₀(OH)₄(Piv)₁₈] where the room temperature moment was only about 20% of the spin-only value.¹⁴

Figure 5.

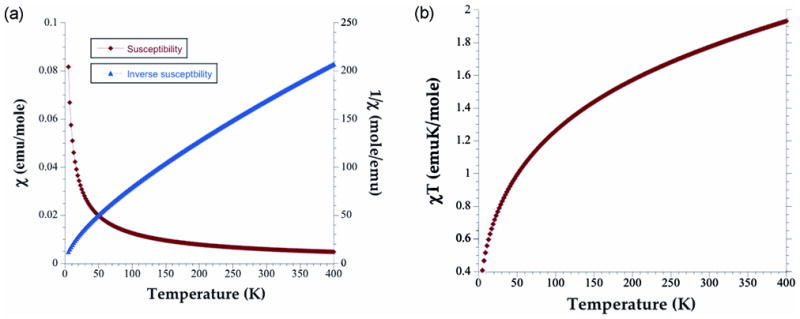
(a) Magnetic Susceptibility and inverse susceptibility vs. Temperature plot per mole of Fe³⁺ for Ba₄KFe₃O₉ (left), (b) χT vs. Temperature plot for per mole of Fe³⁺ for Ba₄KFe₃O₉ (right).

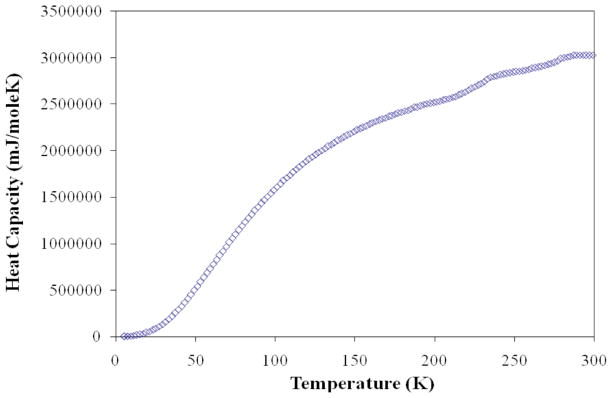
It has previously been observed that the measured effective magnetic moment is much smaller than the theoretical magnetic moment not only in molecular ring structures but also in related iron and cobalt oxides such as, for example, BaKFeO₃¹⁹ and Ba₃Fe₂O₆⁷ as well as Co(IV) compounds Cs₂CoO₃, Rb₂CoO₃ and K₂CoO₃.²⁶ In some of these cases, it was suggested that the large difference between the observed and theoretical magnetic moments is due to a long-range antiferromagnetic ordering with Néel temperatures above the upper limit of the magnetic measurement temperature.^7,19 It is unlikely that this scenario applies to our system, because a long-range antiferromagnetic order was not detected in the Mössbauer spectrum. Nonetheless, in order to investigate a possibility of a magnetic order we collected the heat capacity data shown in Figure 6. The data give no indication of an identifiable magnetic ordering transition between 5 and 300 K.

Figure 6.

Zero –field heat capacity data for Ba₄KFe₃O₉.

EPR spectroscopy

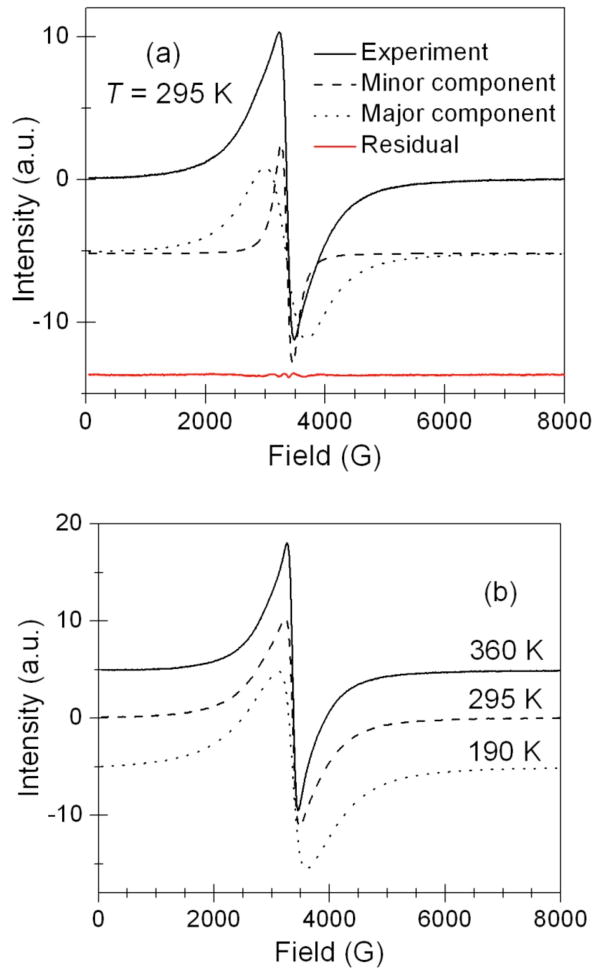
Figure 7a shows a typical room temperature X-band EPR spectrum from Ba₄KFe₃O₉ powder. The spectrum consists of a single line at g~2.01 and this g-factor is characteristic of Fe³⁺ ion in a tetrahedral environment.^27,28 The line is sharp at the center but has some broad wings and cannot be fitted to a single Lorentzian line shape (not shown). EPR spectra with broad wings were previously observed for other types of strongly-coupled spin systems^29,30 and were explained by either a dipolar broadening²⁹ or a two-component Lorentzian model.³⁰ It was found that Ba₄KFe₃O₉ EPR spectra over the entire temperature range studied could be modeled as a superposition of two Lorentzian shapes that have the same field position but differ in widths with one component by a factor of ~3.6 broader than the other one (see Fig. 7a). Note that the number of electronic spins is proportional to the double integral of the corresponding EPR spectra. Further, for the first-derivative components appear to be of comparable peak-to-peak amplitudes (Fig. 7a), the spectra of the same (Lorentzian) shape, such as shown in Fig. 7, the double integral will be proportional to the square of the peak-to-peak width. Then, even though the two components appear to be of comparable peak-to-peak amplitudes (Fig. 7a), the double integrated intensity of the broad component represents ~90% of all the electronic spins because the peak-to-peak width is broader by a factor of ~3.6. Therefore this component is further referred as ‘major’ whereas the narrower component, which accounts for the remaining ~10% of the double integrated intensity, is referred to as ‘minor’. Both components are attributed to Fe³⁺ species based on g-factor g_major = g_minor ≈ 2.01. Based on the x-ray structure, we assign the major component in the EPR spectra to Fe₆ clusters with an encapsulated K⁺ ion in the chair conformation. One may consider a possibility that the two crystallographically distinct tetrahedral Fe³⁺ ions could give rise to the two distinct EPR spectral peaks observed experimentally (Fig. 7). However, we believe that this is not the case. X-ray studies show only single type of Fe₆ ring with two crystallographically distinct Fe³⁺ ions in equal amounts i.e., each ring is made-up of three ions of each type of Fe³⁺ ion. This does not match the 9:1 ratio of the EPR double-integrated intensities. Furthermore, even though the two crystallographically distinct tetrahedral Fe³⁺ ions could yield distinguishable anisotropic EPR spectra for isolated ions, we show that the adjacent Fe³⁺ sites within the 6-member rings are strongly spin exchange coupled. Then in the limit of strong spin exchange all the anisotropic features of Fe³⁺ EPR spectra and, hence, the differences between the EPR spectra corresponding to two crystallographically distinct Fe³⁺ sites would average out yielding an isotropic Lorentzian shape observed in our experiment. Thus, the presence of the two crystallographically distinct Fe³⁺ sites was ruled out as the origin of the two Lorentzian EPR components. It is more likely that the minor component would originate from a small fraction of a polymorph in the sample or even a partially decomposed sample due to its extreme moisture sensitivity. It is worthwhile to note here that the ability to resolve two components in EPR spectra reinforces the statue of EPR spectroscopy as one of the best analytical tools for detecting and differentiating the electronic spin environments in various systems.

Figure 7.

(a) Room temperature X-band EPR spectrum (black solid line) of Ba₄KFe₃O₉ powder along with the major (dotted line) and minor (dashed line) components. The fit residual (red solid line), a difference between the experimental and simulated spectra, demonstrates an exceptional quality of the two-component model. The two components and the residual are displaced along the ordinate for clarity, (b) X-band EPR spectra of Ba₄KFe₃O₉ powder at three representative temperatures.

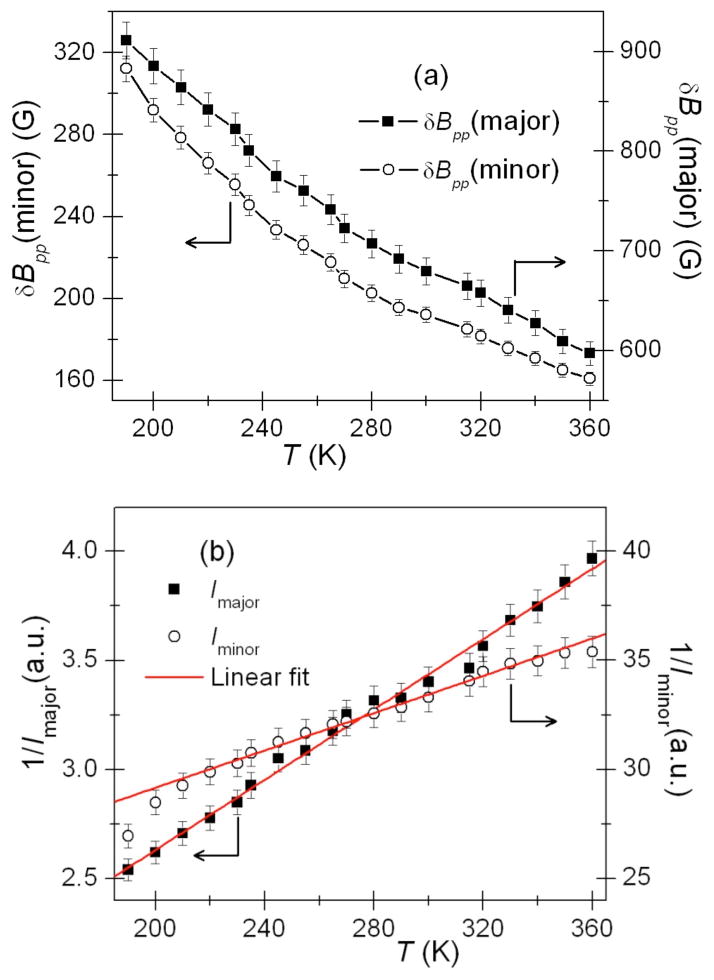
To further understand the spin environment in Fe₆ clusters and estimate the nearest neighbor spin exchange integral, J_nn, we have performed variable temperature EPR studies from 190 to 360 K (see Figure 7b for representative EPR spectra). Figure 8a shows that the peak-to-peak line width (δB_pp) of both the major and the minor components decreases monotonously as the temperature increases while maintaining the δB_pp(major)/δB_pp(minor) ratio of ~3.6. The observed line narrowing with temperatures is attributed to further averaging of the local magnetic fields caused by an increased rate of spin fluctuations.

Figure 8.

(a) Peak-to-peak EPR line width (δB_pp) as a function of temperature for the major and minor components. The solid lines are guides to the eye. (b) Inverse EPR double-integral signal intensity of the major and minor components as a function of temperature. Solid red lines are the best linear fit to the Curie-Weiss law. See the text for further details.

The isotropic exchange integral J can be estimated from δB_pp(T) according to the Anderson-Weiss (AW) EPR line width theory.³¹ In a system with strong spin exchange interactions and containing a uniform distribution of magnetic ions in a simple cubic lattice, the δB_pp parameter is related to the dipolar and spin exchange fields as:³¹

$$\delta B_{pp}=\left(\frac{2}{\sqrt{3}}\right)\left(\frac{10B_d^2}{3B_{ex}}\right)$$ (1)

$$B_d^2=5.1\left(g{\mu }_{\text{B}}/r^3\right)S(S+1)$$ (2)

$$B_{ex}=1.68\left(J_{nn}/g{\mu }_B\right){[S(S+1)]}^{1/2}$$ (3)

where B_d is the dipolar field, B_ex is the spin exchange field, g is the g-factor, μ_B is the electronic Bohr magneton, r is the distance between the magnetic ions, S is the spin of the magnetic ion, and k the Boltzmann constant. Finally, the 10/3 factor in Eq. 1 accounts for additional broadening contributions to the line width from other magnetic interactions such as zero-field splitting from crystal field interactions, hyperfine interactions, etc.³¹

Let us now assume that the minor component in the EPR spectra originates from a very similar Fe₆ cluster but with different J_nn and that these clusters are non-interacting with each other. Since the EPR spectral line shapes of both components of Ba₄KFe₃O₉ are Lorentzian, the spin exchange field in Fe₆ clusters must be sufficiently strong to average out the magnetic anisotropy and local dipolar fields. Therefore, it is reasonable to apply the AW theory to estimate, at least qualitatively, the J_nn from Eqs. 1 – 3. Since our sample contains discrete Fe₆ wheels as opposed to the uniform distribution of Fe³⁺ ions expected in the AW model, we assume that (i) the effective dipolar field B_d at each Fe³⁺ site of the Fe₆ cluster is the sum of dipolar fields due to the remaining Fe³⁺ ions in the Fe₆ cluster (see Figure 9). (ii) The Fe₆ clusters corresponding to the minor and major components have essentially identical bond lengths and angles resulting in very similar effective dipolar fields B_d. (iii) Since the density functional calculations, vide infra, show that the intra-cluster next nearest neighbor interaction J_nnn ≪ J_nn, only the two intra-cluster nearest neighbors are considered in calculating J_nn. (iv) Note that Eqs. 1 – 3 are only valid for the regime of the extreme narrowing of the line width due to large spin exchange interactions. Thus, only the lowest experimental δB_pp values were used for estimating numerical values of J_nn. Table 4 lists the J_nn values corresponding to the major and minor components calculated using g_major = g_minor ≈ 2.01 and S_major = S_minor = 5/2.

Figure 9.

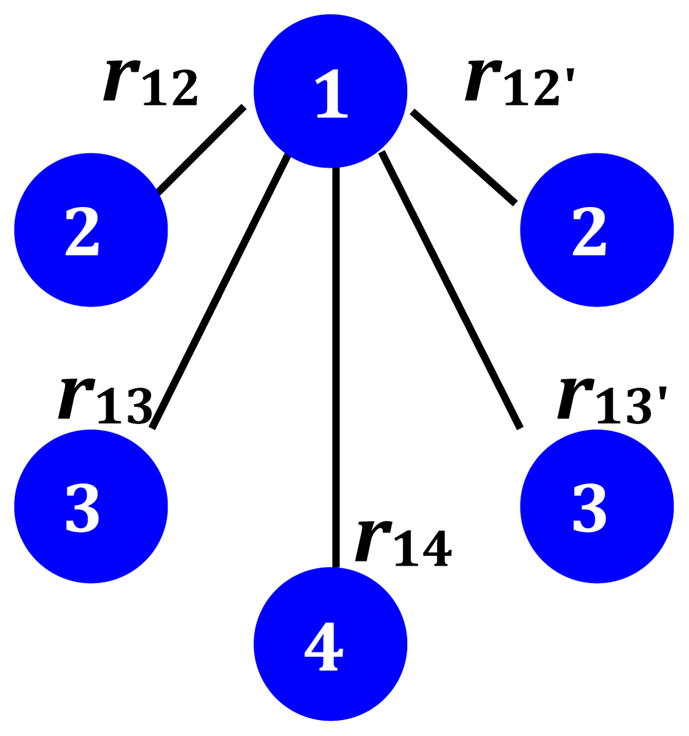
A diagram depicting dipolar interactions considered in estimating the total dipolar field B_d. r_ij is the distance between i^th and j^th ions and is assumed to be same for both minor and major components of Ba₄KFe₃O₉. The distances are: r₁₂ = r_12′ = 3.750 Å, r₁₃ = r_13′= 5.642 Å, and r₁₄ = 6.745 Å.

Table 4.

The Curie-Weiss temperature θ obtained from the Curie-Weiss fits (Eq. 4) of the EPR intensities as a function of temperature (Fig. 8b) and the nearest neighbor spin exchange integrals J_nn calculated from Eq. 5. The last column lists the |J_nn| values calculated from the Anderson-Weiss theory of EPR line width (Eqs. 1 – 3). The error in θ and J_nn is ±5 K.

	I(T)		δBpp (T)
	Θ (K)	Jnn (K)	|Jnn| (K)
Major component	−125	−21	12
Minor component	−470	−81	38

Figure 8b shows a plot of inverse of the double-integrated EPR intensity (I) as a function of the temperature for both the major and the minor components. Notably, I_major/I_minor remains at ~10 over the entire temperature range, thus, reinforcing the validity of the two-component model. As long as the thermal energy kT ~ J,J can be estimated from the I(T) measurements.²⁸ Since the double-integrated EPR intensity is proportional to the paramagnetic component of magnetic susceptibility χ, I_major(T) and I_minor(T) of Ba₄KFe₃O₉ could be fitted to the Curie-Weiss law²⁷ (cf. Eq. 4) to extract the J_nn according to the molecular field theory (MFT) (cf. Eq. 5):²⁷

$$\frac{1}{\chi }=\frac{(T-\theta )}{C}$$ (4)

$$\theta =\frac{{zJ}_{nn}S(S+1)}{3k}$$ (5)

where, θ is the Weiss constant, C is the Curie constant and z (=2 for our Fe₆ clusters) is the number of the nearest neighbors. The solid lines in Figure 8b are the best fits to the Eq. 4 with parameters shown in Table 4 along with the J_nn values obtained from the MFT relation shown in Eq. 5.

It is worth noting that the spin exchange integral ratio J_nn(minor)/J_nn(major) ~ 3 – 3.5, determined from 1/I vs T plot as well as the AW model, correlate well with the observed line width ratio δB_pp(major)/δB_pp(minor) ~ 3.6. Indeed, if all the parameters of the AW theory are the same with exception of J_nn, then δB_pp ~ 1/J_nn ~ 1/θ. Thus, the major difference in the two magnetic environments corresponding to the narrow and broad EPR components is likely to be in the spin exchange J_nn integral with the rest of parameters being about the same. We speculate that the observed discrepancy in J_nn obtained from the AW theory and the Curie-Weiss fits is either due to the assumptions (i) – (iv) adapted for our Fe₆ clusters or the inherent simplifications of the AW model. In fact, (δB_pp)_observed/(δB_pp)_calculated ~ 2 was expected by the authors of the AW model³¹ and noticed in other experiments³². Authors in references [32] attributed this discrepancy to the truncated Lorentzian line shape employed in the AW theory. We also note that the AW theory neglects the partial averaging of the dipolar fields due to spin-flips on the time scale of EPR experiment.

Spin exchange interactions

To better understand the magnetic properties of the Ba₄KFe₃O₉, we examined the spin-exchange interactions within the iron hexamer ring by performing energy-mapping analysis based on density functional electronic band structure calculations.^33–35 Since the cation disorder was observed for some positions of Ba/K, we assumed an ordered stoichiometric arrangement of Ba/K for our calculations by arranging them with largest distance from each other, unless the occupancies of their positions are higher than 0.9. Only the intra-ring spin-exchange interactions were considered, namely, the nearest-neighbors (J_nn) and next-nearest-neighbors (J_nnn) exchanges within each iron hexamer, while the inter-ring spin exchange interactions are expected to be negligible. To further simplify our discussion, it was assumed that all the nearest-neighbor interactions J_nn are identical, and so are the next-nearest-neighbor interactions J_nnn.

To determine the values of J_nn and J_nnn, we first consider the relative energies of the three ordered spin states (AF1, AF2 and AF3) of each iron hexamer ring shown in Figure 10 on the basis of density functional calculations. The calculations employed the projector-augmented wave (PAW) method encoded in the VASP code³⁶ with the generalized-gradient approximation (GGA)³⁷ for the exchange–correlation functional, the plane-wave cutoff energy of 485 eV, and either a set of 2×2×2 k-points or one k-point (i.e., Γ point). To consider the electron correlation associated with Fe 3d states, GGA plus on-site repulsion (GGA+U) calculations³⁸ with U = 3 eV were also carried out. In evaluations of J_nn and J_nnn, the optimized crystal structure of Ba₄KFe₃O₉ was employed. With the lattice parameters kept constant, the atomic positions of Ba₄KFe₃O₉ were relaxed by GGA+U calculations (with U = 3 eV) using the AF1 state until the force acting on each ion is reduced below 0.01 eV/Å.

Figure 10.

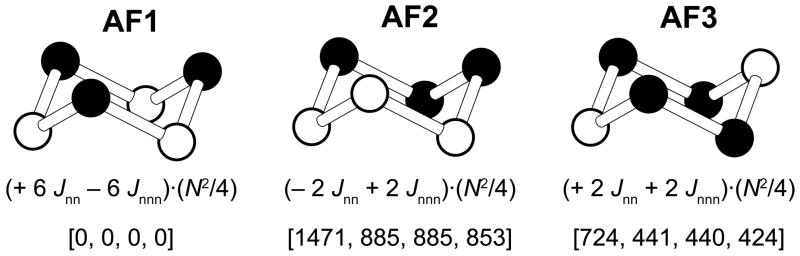
Three ordered spin arrangements of each iron hexamer ring used for the energy-mapping analysis, where the filled and empty circles represent down-spin and up-spin Fe³⁺ sites, respectively. For each state, the expression of the total spin exchange energy per hexamer ring is given, where N is the number of unpaired spins at each Fe³⁺ site (i.e., N = 5), and the four numbers in the square bracket from left to right are the relative energies in meV per unit cell in the order of the entry given in Table 5.

The relative energies of the AF1, AF2 and AF3 states obtained from our GGA+U calculations are summarized in Figure 10. The total spin exchange energies of these states, per hexamer ring, can be expressed in terms of the spin Hamiltonian Ĥ = −Σ_i<j J_ijŜ_i · Ŝ_j, where J_ij = J_nn, J_nnn. By applying the energy expressions obtained for spin dimers with N unpaired spins per spin site (in the present case, N = 5),³⁹ the total spin exchange energies of the three ordered spin states per six-membered ring are written as summarized in Figure 10. Therefore, we determine J_nn and J_nnn by mapping the relative energies of the three ordered states obtained from the GGA+U calculations onto those expected from the total spin exchange energies (Table 5).

Table 5.

Values in K of the spin exchange parameters J_nn and J_nnn obtained from GGA+U calculations for the experimental (Exp) and optizmized (Opt) crystal structures of Ba₄KFe₃O₉.

U (eV)	Structure	k-points	Jnn	Jnnn
0	Exp	Γ	−347	−5.3
3	Exp	Γ	−206	−0.9
3	Exp	2×2×2	−207	−1.3
3	Opt	2×2×2	−199	−1.0

In all cases, J_nn is strongly antiferromagnetic (of the order of −200 K), and J_nnn is negligible. It should be noted that since S = 5/2 for the high-spin Fe³⁺ ions, the effective nearest-neighbor spin exchange is given by J′_nn = S²J_nn = 25J_nn/4. The width of the magnetic energy spectrum of Ba₄KFe₃O₉ scales as J′_nn, and hence should spread over a wide range of energy. Then, even at room temperature the Boltzmann distribution favors the occupation of lower-lying magnetic states in which more spins are paired resulting in lower moments. Consequently, the effective moment calculated from χT will be much smaller than expected from the paramagnetic state in which all the allowed magnetic states are equally occupied. As a result, the effective moment calculated from χT decreases continuously with lowering the temperature. In general, this kind of observation should be expected not only for magnetic oxides made up of corner-sharing FeO₄ tetrahedra with Fe³⁺ (S = 5/2) ions but also for those made up of corner-sharing CoO₄ tetrahedra with Co⁴⁺ (S = 5/2) ions as found for Cs₂CoO₃, Rb₂CoO₃, and K₂CoO₃.²⁵

The value of J_nn ≈ −200 K obtained from the present GGA+U calculations is stronger than J_nn ≈ −20 K for the major component estimated from the EPR measurements by an order of magnitude. In general, GGA+U electronic structure calculations overestimate the magnitude of spin exchange interactions by a factor approximately up to four to five.^{34, 35, 40} Thus, we cannot exclude the possibility that our EPR analysis underestimated the value of J_nn by a factor of two or greater.

Conclusion

In summary, a new ferrite containing discrete 6-member rings of FeO₄ tetrahedra has been synthesized and characterized experimentally and theoretically. In spite of the relatively short Fe-O-Fe contacts, no evidence of long-range magnetic order has been found in the magnetic susceptibility, Mössbauer, or the heat capacity data. X-band EPR indicated presence of two different magnetic species, with the Fe₆ clusters in Ba₄KFe₃O₉ accounting for ~90% of the total spin count. The temperature dependence of the EPR signal intensity of the Fe₆ clusters is analyzed in terms of the Curie-Weiss law yielding the Weiss constant of ~ −125 K. This corresponds to the spin exchange integral J_nn of ~ −20 K that agrees well with |J_nn|~12 K estimated from the Anderson-Weiss EPR line shape theory. Our density functional calculations reveal that all nearest neighbor magnetic interactions are strongly antiferromagnetic, while next nearest neighbor interactions are negligible. The lower than expected effective moment calculated from χT is explained as resulting from the occupation of lower lying magnetic states in which more spins are paired, resulting in a lower moments.