Dual Processes in Decision Making and Developmental Neuroscience: A Fuzzy-Trace Model

Abstract

From Piaget to the present, traditional and dual-process theories have predicted improvement in reasoning from childhood to adulthood, and improvement has been observed. However, developmental reversals—that reasoning biases emerge with development —have also been observed in a growing list of paradigms. We explain how fuzzy-trace theory predicts both improvement and developmental reversals in reasoning and decision making. Drawing on research on logical and quantitative reasoning, as well as on risky decision making in the laboratory and in life, we illustrate how the same small set of theoretical principles apply to typical neurodevelopment, encompassing childhood, adolescence, and adulthood, and to neurological conditions such as autism and Alzheimer's disease. For example, framing effects—that risk preferences shift when the same decisions are phrases in terms of gains versus losses—emerge in early adolescence as gist-based intuition develops. In autistic individuals, who rely less on gist-based intuition and more on verbatim-based analysis, framing biases are attenuated (i.e., they outperform typically developing control subjects). In adults, simple manipulations based on fuzzy-trace theory can make framing effects appear and disappear depending on whether gist-based intuition or verbatim-based analysis is induced. These theoretical principles are summarized and integrated in a new mathematical model that specifies how dual modes of reasoning combine to produce predictable variability in performance. In particular, we show how the most popular and extensively studied model of decision making—prospect theory—can be derived from fuzzy-trace theory by combining analytical (verbatim-based) and intuitive (gist-based) processes.

Biases in adult reasoning and decision making have been well documented (Evans, 2003; Gilovich, Griffin, & Kahneman, 2002; Tversky & Kahneman, 1986; Wason & Johnson-Laird, 1972). In order to explain such biases, dual-process theorists have posited an evolutionarily primitive system of thought that relies on intuition and emotion rather than reflection and analysis (e.g., Chaiken & Trope, 1999; Epstein, 1994; Evans, 2008; Tversky & Kahneman, 1983). According to standard dual-process theories, intuitive thinking is quick, automatic, and unconscious, whereas analytical thinking is the opposite (i.e., slow, controlled, and conscious). Stanovich and West (e.g., 2000) dubbed these collections of attributes System 1 and 2, respectively, capturing the order of their appearance phylogenetically and ontogenetically. Developmental neuroscientists make similar distinctions between early emerging emotional and reward systems (e.g., limbic structures such as the ventral striatum) and later developing cognitive control systems (e.g., the prefrontal cortex) (e.g., Somerville, Jones, & Casey, 2010; Steinberg, 2008).

From Piaget to the present, developmental theories have predicted improvement in the ability to reason from childhood to adulthood (Bjorklund, 2012; Haines & Moore, 2003). The mechanisms of improvement differ among neo-Piagetian, information-processing, developmental-neuroscience, and standard dual-process theories: better logical and analytical skills, larger working memory capacity, enhanced inhibitory capabilities, increased myelination (and, hence, faster processing speed), or greater metacognitive awareness. These mechanisms have been used to explain why reasoning ought to progressively conform to the canons of logic and mathematics, including probability theory. However, the endpoint of development, the adult logician-scientist of developmental theory, evolving away from intuitive thought, does not resemble the intuitive adult of the judgment-and-decision-making literature. The disparity is not between ideal competence versus actual performance, but between different views of competence: As Reyna and Brainerd (1994) concluded, “the heuristics and biases research and the developmental research imply diametrically opposed views of adult competence” (p. 264).

Adult variability of this kind is grist for the mill for dual-process theories, which were designed to accommodate it. However, none of the traditional or standard dual-process theories predict that reasoning biases should increase from childhood to adulthood. (Indeed, they predict that reasoning becomes more analytical and less intuitive, e.g., Stanovich, Toplak, & West, 2008). Nevertheless, beginning in 1991 with findings by Jacobs and Potenza, a growing list of studies provide evidence for surprising developmental reversals, showing that children reasoned better than adults did (De Neys & Vanderputte, 2011; Morsanyi & Handley, 2008; see Table 3 in Reyna & Farley, 2006). Although some of these findings can be explained in terms of developmental differences in knowledge (e.g., about social stereotypes; Stanovich, West, & Toplak, in press), many reversal effects cannot be explained this way (e.g., Brainerd, Reyna, & Ceci, 2008; Davidson, 1991; Reyna & Ellis, 1994; Reyna, Estrada, et al., in press). These developmental reversals are not explained simply by alternative modes of processing; in these tasks, performance does not become more variable, but, rather, declines systematically from childhood to adulthood.

Because traditional and standard dual-process theories cannot supply mechanisms for developmental reversals, they are left with post hoc rationalizations of such findings (see Stanovich, West, & Toplak, this issue). These post hoc rationalizations (of better performance among children than adults) also do not explain why adults fail to override System 1 biases with System 2 reasoning, especially given that adults have the needed analytical competence. Certainly, dual-process theories are on the right track in assuming that there are multiple modes of reasoning, but post hoc classification of reasoning is a poor substitute for prediction. As we discuss, it is possible to conserve features of standard dual-process models, address some of the recent criticisms of those models (e.g., Keren & Schul, 2009; Kruglanski & Gigerenzer, 2011), and retain the predictive power of models that motivated studies of developmental reversals in the first place.¹

Specifically, in this article, we explain how fuzzy-trace theory predicts both adult variability and developmental reversals in reasoning and decision making. We draw on evidence from research on logical and quantitative reasoning (e.g., probability judgment), as well as on risky decision making in laboratory tasks and in real life. We then illustrate how these theoretical principles apply to neurodevelopment, encompassing childhood, adolescence and adulthood, and their implications for neurological conditions, such as autism and Alzheimer's disease. These theoretical principles are summarized and integrated in a new mathematical model that specifies how dual modes of reasoning combine to produce predictable variability in performance. In particular, we show how the most popular and extensively studied model of decision making—prospect theory—can be derived from fuzzy-trace theory by combining analytical (verbatim) and intuitive (gist) processes.

The Fuzzy-Processing Framework

Core Constructs

Based on evidence from a wide variety of tasks (e.g., Reyna, 1995, 1996; Reyna & Adam, 2003; Reyna & Brainerd, 1995), we have identified five components of processing in reasoning and decision making: (a) stored knowledge and values; (b) mental representations of problems or situations; (c) retrieval of knowledge and values; (d) implementation of knowledge and values; and (e) developmental and individual differences in monitoring and inhibiting interference (e.g., from emotional arousal, wrong representations, or overlapping classes) (for overviews, see Reyna, 2004, 2008). Each of these components has been found to contribute to reasoning and decision making.

Stored knowledge and values refer to what a person has stored in long-term memory by virtue of education and experience, including culturally transmitted values. For example, individuals with low levels of numeracy cannot understand and use numbers, and thus reason and make decisions involving numbers differently than those with high levels of numeracy (Peters, Slovic, Vastfjall, & Mertz, 2008; Reyna, Nelson, Han, & Dieckmann, 2009). Similarly, cultural values (e.g., for human life or family) are learned and later retrieved to influence judgment and decision making (Rokeach, 1973; Wang, 2002). Research has shown that these values are not stored in a highly articulated form (e.g., Reyna, 2008). This view differs from theories that assume that values are constructed anew in every situation (e.g., Lichtenstein & Slovic, 2006). Fuzzy-trace theory accounts for variability in the application of values to problems or decisions in two ways, by assuming that values are mentally represented imprecisely in long-term memory, and then instantiated (or recognized) in the situation (a variable process) and by assuming that retrieval of values depends on cues that vary across situations.

Mental representations refer to how people perceive the problem or situation that they face. According to fuzzy-trace theory, there are two types of representations. Verbatim representations capture the exact surface form of problems or situations, how they are perceived literally (e.g., the exact words or the precise numbers). Gist representations capture the bottom-line meaning of the problem or situation. In contrast to verbatim representations, which are precise (and quantitative, if they involve numbers), gist representations are vague and qualitative. For example, social knowledge can affect how the gist of a problem or situation is interpreted (Davidson, 1995; Jacobs & Potenza, 1991; De Neys & Vanderputte, 2011; Reyna, 1996; Reyna & Adam. 2003). The gist of a problem or situation is its subjective interpretation based on emotion, education, culture, experience, and worldview, that is, anything that affects essential meaning.

According to this theory, merely having an appropriate mental picture or representation of a problem is not sufficient for good reasoning or decision making. Rather, people must access what they know and believe in (or value) when that knowledge or value is relevant (i.e., in the situation). Even highly overlearned knowledge and deeply held values are sometimes not retrieved in relevant situations, producing variability in reasoning and decision making. Representation plus retrieval, however, are also not sufficient by themselves. Implementation, or how people put together what they perceive about a situation (mental representation) with what they know and value (retrieved from long-term memory), accounts for additional variance in reasoning and decision making.

Last, in studies of memory, reasoning, and decision making, there is evidence for a separate factor of monitoring or inhibition, not unlike Ricco and Overton's (in press), Moshmans' (2004), and Frederick's (2005) metacognitive reflection or Stanovich and West's (2000) need-for-cognition (Reyna, 1995; Reyna & Mills, 2007). Epstein (1994) also employs the concept of need-for-cognition as a measure of rationality (i.e., as a desire to engage in analytical thought). Contrary to standard dual-process approaches, however, inhibition is not a reasoning mode (a System 2 censor) in fuzzy-trace theory, but instead operates to withhold thoughts and actions (Carver & White, 1994; Gray, 1987; 1990; Hare et al., 2008). Developmental neuroscience research supports the conclusions that inhibition (or cognitive control) increases from childhood to young adulthood, and that this increase is associated with maturation of the prefrontal cortex, including increased white-matter connectivity between cortical and subcortical limbic areas of the brain (e.g., Casey, Getz, & Galvan, 2008).

Domains of Application

The kinds of data explained by this fuzzy-processing framework include recognition and recall (e.g., true and false memory, and effects of emotion, Brainerd, Holliday, Reyna, Yang, & Toglia, 2010; Brainerd & Reyna, 2005); comprehension and reasoning (e.g., transitive inference, pragmatic inference, moral reasoning, and metaphor comprehension; Reyna & Casillas, 2009; Reyna & Kiernan, 1994, 1995); probability judgment (e.g., conjunction and disjunction fallacies, base-rate neglect, hindsight bias, denominator neglect, and conversion errors in conditional probability judgment; Reyna & Adam, 2003; Wolfe & Reyna, 2010); and decision making (e.g., framing effects and preference reversals; Gonzalez, Dana, Koshino, & Just, 2005; Kuhberger & Tanner, 2010; Reyna, 2008; Reyna, Estrada, et al., in press;).

For example, consider two treatments for a disease, one in which 200 lives were saved out of 400 treated and another in which 2000 lives were saved out of 4500 treated. The 200 and 2000 lives are nested within the 400 and 4500 treated, respectively, which produces confusion about which classes are relevant to the decision (Reyna & Mills, 2007). Interference from nested or overlapping classes in probability judgment or other ratio problems must be inhibited; otherwise, reasoners tend to neglect denominators and focus only on relative frequency of numerators (2000 saved vs. 200 saved; Reyna & Brainerd, 2008). Therefore, the appropriate gist of the numbers (e.g., 2000 is less than half of 4500; Spinillo & Bryant, 1991), retrieval of knowledge (e.g., the rule that ratios of both numerator and denominator must be compared to judge probability; Acredolo et al., 1989), and inhibition of interference from wrong representations (e.g., 2000 is more than 200) and from overlapping classes are all necessary to select the right treatment (Reyna, 1991; Reyna & Brainerd, 2008). These predictions of fuzzy-trace theory have been borne out in independent investigations (e.g., Garcia-Retamero, Galesic, & Gigerenzer, 2010; Stone et al., 2003).

Semantic and pragmatic knowledge combine to support extraction of gist from novel metaphors, transitive inferences (A > B, B > C, therefore A > C), and categorical syllogisms (All A are B, All B are C, therefore All A are C) (Evans, 2008; Reyna & Brainerd, 1990; Reyna & Kiernan, 1994, 1995). Mental representations thus contain content or meaning, rather than being purely abstract, accounting for effects such as “belief bias” in which factual knowledge influences judgments of logical validity. Mental representations include such gist as relative magnitude (A is more than B, which could be longer, taller, more numerous and so on) or linear ordering (A is more than B is more than C). Logical rules or principles (perhaps more akin to heuristics because they do not apply universally) are retrieved with some variability, depending on cues in the problem, and then applied to the mental representations of the gist of the problem information. Categorical syllogisms are also subject to class-inclusion confusion, or interference from overlapping classes, just as probability judgment is. Simultaneously considering the A's that are B's and the A's that are not B's produces confusion, and neglect of parenthetical classes. Contrary to assumptions, performance in logical and pragmatic inference tasks tends to be independent of working memory capacity for verbatim information, but dependent on memory for gist (e.g., relative magnitude, such as which class is bigger or more numerous).

Main Ideas

These results support five core ideas of fuzzy-trace theory that are relevant to reasoning and decision making: First, both verbatim and gist representations are extracted in parallel, and both verbatim-based analysis of precise details and gist-based intuition operate in parallel. (Different kinds of mental representations support different kinds of processing; verbatim representations provide the level of detail needed for analysis and gist representations facilitate the fuzzy, impressionistic processes of intuition.) How the two kinds of processing “communicate” with one another to produce a response is modeled below.

Second, meaning is at the center of adult cognition. Most adults have a fuzzy-processing preference. That is, they favor, as a default, the simplest gist representations that allow them to reason or decide. This preference is the opposite of what information processing theories assume, which is that precise and elaborate reasoning proceeds until excessive cognitive load forces simpler processing. Thus, global gist, not verbatim details, generally determines how information is interpreted and acted on. For example, a risk of breast cancer of 16% can be interpreted as “large” relative to an average or base rate of 13% and as “small” relative to 50% or more, which determines whether women seek cancer screening (Fagerlin. Zigmund-Fisher, & Ubel, 2005; Reyna, 2008). Precision does not necessarily clarify meaning (Reyna et al., 2009).

Third, both verbatim-based analysis and gist-based intuition develop during childhood, and sometimes the latter develops at an even faster rate than the former (e.g., Brainerd, Reyna, & Zember, 2011). The preference for operating on gist in reasoning and decision making also increases during this period (Reyna & Kiernan, 1994; 1995). Hence, the net contribution to reasoning and decision making is more gist-based in adolescence and adulthood, compared to childhood. Figure 1 presents illustrative data from a memory experiment with elementary schoolers using sentences presented in short narratives. Correcting for response bias (bias also changes with age so must be corrected for), children erroneously recognized gist-consistent sentences more often as they got older. In many studies, verbatim memory also improves across age during childhood. Thus, we do not claim that gist-based intuition replaces verbatim-based analysis; as also assumed in standard dual-process theories, both modes of reasoning remain available to advanced reasoners.

Figure 1.

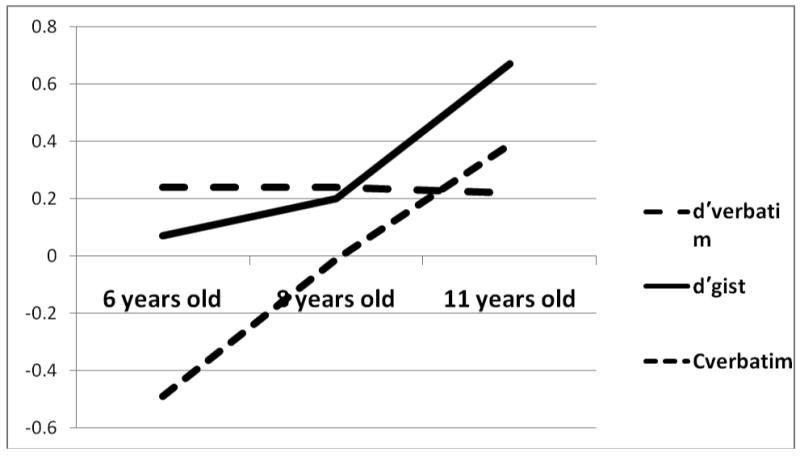
Children were presented with sentences as part of 12 short narratives (The bird is in the cage. The cage is under the table. The bird has yellow feathers; Brainerd & Mojardin, 1998). After a buffer task, they were given recognition tests; they were instructed to only say “yes” to exact matches of presented sentences. The “gist” measure refers to false alarms (saying “yes” to paraphrases of presented sentences, such as The cage is below the table).

Fourth, consistent with the direction of development (to rely more on gist), advanced reasoning is generally gist-based, not verbatim-based, which is the opposite of what standard dual-process theories assume (e.g., Reyna & Ellis, 1994; Reyna & Lloyd, 2006). (Reasoning is judged to be “advanced” based on criteria of coherence and correspondence or accuracy; see Adam & Reyna, 2005; Reyna & Adam, 2003.) Expert cardiologists, for example, processed fewer dimensions of cardiac risk compared to generalist physicians and medical students in deciding whether to admit patients to the hospital. Experts were also more likely to make all-or-none decisions: discharging patients or admitting them to intensive care. Nevertheless, experts were more accurate than generalists or students in discriminating low from high risk patients, based on practice guidelines. In fuzzy-trace theory, developmental comparisons of children and adults are analogous to expert-novice comparisons, and provide further evidence that advanced reasoning is gist-based.

Finally, multiple gist representations that vary in precision (or vagueness) are usually encoded, which produces cognitive options (Reyna & Brainerd, 1995). Task calibration ensures that the requirements of the task influence the precision of the representation used to accomplish that task. For example, choosing between two comparable apartments might not require discriminating much beyond high versus low rent, but deciding on exactly how much rent one is willing to pay for each apartment requires more fine-grain processing. Thus, task calibration accounts for preference reversals based on changes in response format (e.g., from forced choice to estimating the amount one is willing to pay; Fischer & Hawkins, 1993).

Fuzzy-Trace Theory and Standard Dual Processes

Fuzzy-trace theory is a dual-process approach, and shares features of standard dual-process approaches. For example, the theory distinguishes between intuition (gist-based) versus analysis (verbatim-based). As in standard dual processes, intuition generally operates quickly, automatically, and unconsciously, and the opposite is true for verbatim processing. This conclusion is supported by results of empirical tests of mathematical models; the models that make these assumptions fit the data, but models incorporating alternative assumptions did not (e.g., Brainerd, Reyna, & Mojardin, 1999; Brainerd, Reyna, Wright, & Mojardin, 2003). In addition, like standard dual-processes, specific biases are attributed to intuitive processes (although some biases are also attributed to retrieval failure and to interference). Hindsight bias, for example, in which people falsely remember that they predicted an outcome once they know that it occurred, depends on both gist memories (subjective interpretations of events influenced by outcomes) as well as a failure to retrieve verbatim memories of what was actually predicted (Bayen, Pohl, Erdfelder, & Auer, 2007; Bernstein, Erdfelder, Meltzoff, Peria, & Loftus, 2011; Reyna, 2005).

Fuzzy-trace theory also incorporates effects of emotion on reasoning and decision making. For example, gist representations frequently incorporate emotion (or affect), coloring the perception of risks and benefits and, hence, determining risk-taking (Rivers, Reyna, & Mills, 2008). Research has also shown that valence (good-bad or positive-negative) is encoded automatically and persists over time in memory, hallmarks of gist representations (Ashby, Isen, & Turken, 1999; Osgood, Suci, & Tannenbaum, 1957; Zajonc, 1980). Valence, derived from experience, supplies intuitions that protect adults from harm (e.g., Bechara, Damasio, Tranel, & Damasio, 2005). Both valence and arousal have been found to promote gist-based “false” memories (Brainerd et al., 2010; Brainerd, Stein, Silveira, Rohenkohl, & Reyna, 2008). Also similar to standard dual process-theory, and discussed above, fuzzy-trace theory predicts that inhibition varies developmentally and across individuals in adulthood. Neurobiological theories posit similar positive arousal (reward sensitive or go) and negative inhibitory (stop) systems (Gray, 1987, 1990; Hare et al., 2008).

Despite such similarities, standard dual process theory is subject to criticisms that do not apply to fuzzy-trace theory (e.g., Keren & Schul, 2009; Kruglanski & Gigerenzer, 2011). Importantly, key predictions of some dual-process theories have been disconfirmed. Epstein's (1994) cognitive-experiential self theory (CEST) was developed to account for so-called ratio bias (e.g., preferring a 9 out of 100 chance to win over a 1 in 10 chance to win, which is accounted for in fuzzy-trace theory through the concept of denominator neglect caused by confusion about overlapping classes). However, despite the development of a sophisticated survey instrument for assigning people to intuitive or analytical reasoning styles, those styles did not consistently predict ratio bias (e.g., Pacini & Epstein, 1999). Paradoxical effects of numeracy, thought to represent analytical thinking, have also been observed. People with more precise numerical representations performed worse on numerical reasoning problems, an effect that has been replicated in multiple studies (for a review, see Reyna et al., 2009). Conversely, standard dual-process theory has difficulty predicting superior performance based on intuition when that has been observed, as opposed to post-dicting accidental accuracy based on intuition.

Further, standard dual process theory cannot predict that adolescents who trade off risks and benefits (i.e., they analyze risky options) take more risks and have poorer outcomes, compared to those who rely on crude intuition (e.g. Mills et al., 2008; Reyna, Estrada et al., in press; Reyna & Farley, 2006). Intuition, rather than focusing on details, also seems to aid decision making in experts and among older reasoners (e.g., Mikels et al., 2010; Reyna, & Lloyd, 2006; Strough, Mehta, McFall, & Schuller, 2008). Also, as discussed, intuitive biases seem to emerge with development; advanced reasoners use gist-based intuition despite accurate memory for details and despite analytical competence. Thus, in contrast to standard dual processes, gist-based intuition is not merely associative, not rote, and not primitive in fuzzy-trace theory.² Nevertheless, the most basic assumption of dual-process models—that there are independent dual processes—has been confirmed. This dual-process assumption has been rigorously tested and modeled mathematically in fuzzy-trace theory (e.g., Brainerd et al., 1999, 2003; Reyna & Kiernan, 1994).

Overview

More generally, fuzzy-trace theory resembles dual-process approaches in incorporating intuition, but intuition occupies a more central place in the theory. Intuitionism (thinking as intuition) in fuzzy-trace theory is contrasted with Piagetian logicism (thinking as logic), and with information-processing formalism (thinking as computation). By “intuition” we mean fuzzy, impressionistic thinking using vague gist representations, but we distinguish mindless impulsive reaction from insightful intuition that reflects understanding.³ Thus, there are two kinds of fast and simple ways of thinking: a stupid kind that represents the most primitive form of thinking and a smart kind that represents the highest form of thinking, insightful intuition. In the foundations of mathematics, intuition is a similarly advanced form of thinking. Fuzzy-trace theory draws on evidence for independent gist and verbatim-memory representations of information, but differs from other dual-process models in emphasizing that there are degrees of rationality and that intuition is an advanced form of reasoning. Such claims are based on empirical evidence comparing reasoning by children and adolescents to that of adults and reasoning of adult novices to that of experts. The theory predicts parallel development of verbatim-based analysis and gist-based intuition, which produces developmental reversals (e.g., children outperform adults) under specific circumstances. As an example, despite increasing competence in reasoning, some biases in judgment and decision making grow with age, producing more “irrational” violations of coherence among adults than among adolescents and younger children. The latter phenomena are linked to developmental increases in gist processing with age in childhood and adolescence (e.g., Reyna, Lloyd, & Brainerd, 2003; Reyna & Rivers, 2008).

Gist-based Intuition Explains Risky Decision Making

Any developmental theory must accommodate the repeated finding that reasoning and decision making seem to become more sophisticated from childhood to adulthood (e.g., Barrouillet in press, this issue; Evans in press, this issue; Ricco & Overton, this issue). At the same time, developmental theory must also accommodate repeated findings of developmental reversals (that children outperform adults). The former findings are hardly surprising: children learn to count and to multiply in school, facilitating consistent performance in such tasks as area judgment (area = length × width) and expected-value preference (expected value = probability of getting a reward × size of the reward). Before they learn to multiply, children estimate magnitudes (e.g., of probabilities and rewards) by examining colored areas of spinners (to estimate the probability of winning a reward) and how big a pile of rewards appears to be (to estimate reward magnitude). By the age of about six, children can reliably choose a .50 chance of winning 2 toys over a .33 chance of winning 2 toys (although the “noisiness” of performance declines, and ability to calculate continues to improve, during childhood, Figner et al., 2009; Kokis, Macpherson, Toplak, West, & Stanovich, 2002; Rakow & Rahim, 2009; Reyna & Brainerd, 1994).

Thus, the story of developmental improvement can be described as “dog bites man,” unremarkable and probably overdetermined by traditional assumptions about development. The story of developmental reversals can be described as “man bites dog,” especially informative when it can be predicted from theoretical mechanisms for which there is independent evidence. Therefore, we focus on the latter findings of developmental reversal, showing how they have been predicted by fuzzy-trace theory.

The Gist of Representations in Framing

Recall the theoretical principle discussed earlier that reasoners initially represent information at the lowest, or least precise, level of gist (for a detailed discussion of how these translate into developmental levels, see Reyna, Lloyd, & Brainerd, 2003). For numbers, this simplest level is a nominal or categorical scale; there is no quantity or there is some quantity. A more precise representation of number would be ordinal (as opposed to nominal): less versus more (e.g., Mills et al., 2008; Reyna & Brainerd, 1995). For example, we might ask whether Farmer Brown has no cows or some cows (nominal scale, or yes-no answer concerning the quantity of cows) or whether she has more cows than sheep (ordinal scale, some is differentiated into less vs. more). Moving up the hierarchy of gist, finer and finer distinctions regarding quantity could be made, in principle, until the precision of numbers was achieved (e.g., she has 10 cows and 7 sheep, exactly 3 more cows than sheep; Brainerd & Gordon, 1994; Reyna & Brainerd, 1993). Probabilities are also numbers and can be similarly dichotomized.

According to fuzzy-trace theory, people begin with the simplest level, nominal (i.e., categorical) gist.⁴ We can apply this gist to the following classic decision problem, a choice between a sure thing and a gamble of equal expected value:

Assume that 600 people are expected to die from an outbreak of disease. You have a choice between two programs to combat the disease: (a) 200 people will be saved (certain option) versus (b) a 1/3 probability that 600 people will be saved and a 2/3 probability that no one will be saved (gamble option) (Tversky & Kahneman, 1986).

Most people prefer the sure option in this framing of the decision. The same options, however, can be framed as losses:

Assume that 600 people are expected to die from an outbreak of disease. You have a choice between two programs to combat the disease: (c) 400 people will die (certain option) versus (d) a 1/3 probability that nobody will die and a 2/3 probability that 600 people will die (gamble option).

In the loss frame, the gamble is the popular choice. Taken together, the choice of the sure thing in the gain frame (lives saved) and the gamble in the loss frame (lives lost) violates axioms of rationality in decision making. One can be risk averse (choose the sure option) or risk seeking (choose the gamble), but shifting from one to the other means that preferences are incoherent--and, thus, they violate rationality (Tversky & Kahneman, 1986).

Armed with the lowest, or least precise, level of gist for numbers, we can translate the decision problems as follows: In the gain frame, the options boil down to choosing between (a) saving some people or (b) saving some people or saving no one. Probabilities as well as outcomes are represented dichotomously, as certain (one thing can happen) versus uncertain (more than one thing can happen; Reyna, 2008). Given that people value human life (i.e., saving some people is better than saving none), they retrieve that value in the decision context, and they apply it to options a and b, they will choose option a (the sure thing). Translating the loss problems in exactly the same way (dichotomizing outcomes into none and some and dichotomizing probabilities into certain and uncertain) yields a choice between (c) some people die or (d) some people die or none die. Retrieving the value that no one dying is better than some people dying, and applying it to the options, produces a preference for option d (the gamble).

Predictions of Prospect Theory

Although this fuzzy-trace theory account makes sense and it produces the framing effect (greater risk seeking in the loss frame than the gain frame), prospect theory also predicts the framing effect. Therefore, in 1991, Reyna and Brainerd performed some critical tests pitting predictions of prospect theory against those of fuzzy-trace theory. These tests have been replicated independently with highly similar results (for a recent review, see Kuhberger & Tanner, 2010). In order to appreciate the implications of those tests, it is necessary to briefly present prospect theory.

According to prospect theory, the perception of quantities such as numbers of lives or amounts of money is nonlinear, akin to the psychophysics of light or sound (Kahneman, 2003; Kahneman & Tversky, 1979). If the perception of quantity were linear, the expected value of 200 lives would equal the expected value of 1/3 of 600 lives (and people would be indifferent between options a and b in the gain frame). In prospect theory, however, the perception of quantity is a power function that falls under the linear function (its exponent is less than 1). Therefore, the perceived value of a quantity diverges more and more from its linear value as its magnitude increases, creating the familiar psychological phenomenon of diminishing returns as numbers get large. That is, the psychological difference between $1000 and $1100 is less than the same numerical difference between $0 and $100.

Analogously, in the disease problem, if the perceived value of 600 lives (farther from the origin) is less than 600, it is easy to see that 1/3 of that lesser value will be smaller than 200 lives (closer to the origin), which favors the sure option. The same logic can be applied to the loss function, which is nonlinear but convex rather than concave. Because 600 dying is discounted more than 400 dying, fewer are perceived as dying in the gamble relative to the sure option, prompting choice of the gamble. Additional assumptions are made in prospect theory about nonlinear probability functions, namely, that “moderate” probabilities such as 1/3 and 2/3 are discounted (or underestimated), which also contributes to framing effects.

Tests of Prospect Theory and Fuzzy-Trace Theory: Nonnumerical Framing Effects

Applying fuzzy-trace theory, Reyna and Brainerd (1991) tested whether the perception of numbers was necessary or sufficient to observe framing effects. First, for different groups of subjects, they removed some of the numbers (just the outcomes or just the probabilities) or all of the numbers (both outcomes and probabilities) in framing problems. The numbers were replaced with vague gist (e.g., “some” replaced every instance of a number other than zero for the both-deleted problems). Obviously, this replacement should eliminate framing effects because the psychophysical function of numbers (e.g., in prospect theory) can no longer operate. However, significant framing effects were obtained in the absence of numbers, and, most counterintutitively, were largest when all numbers were deleted (90% chose the sure option in the gain frame and 86% chose the gamble in the loss frame). These effects were replicated for lives and money problems, and when problems were presented repeatedly, mixed together with other decision problems over eight blocks of trials (Reyna & Brainerd, 1995). In fact, framing effects increased over blocks for all types of problems (intact and numbers-deleted). Despite the vagueness of these problems with missing numbers, people rated confidence in their selections as pretty high (routinely greater than 5 on a 7-point scale), and confidence was also surprisingly high when the scale ranged from 0 to 20 to provide better resolution.

More Critical Tests: Selective Focusing Effects

These non-numerical framing effects demonstrated that numbers, and the psychophysics of numbers, were not necessary to observe the framing effect. In a second series of experiments, we tested the hypothesis that the psychophysics of numbers was sufficient to observe framing effects. The entire decision—all of the information—was presented to subjects. However, attention was focused on either the contrast between the numbers, relevant for predictions of prospect theory, or on the contrast between none and some, relevant for predictions of fuzzy-trace theory (for replications of these critical tests of fuzzy-trace theory, see also Betsch & Krauss, 1999; Kuhberger, 1995; Kuhberger & Tanner, 2010; Mandel, 2001; Stocke', 1998).

For example, in the studies cited above, subjects were offered a choice in the disease problem between (a) 200 people will be saved versus (b) a 1/3 probability that 600 people will be saved. (The same truncation of the zero complement was applied to the loss frame problems, as in 400 die vs. 2/3 probability that 600 die.) According to prospect theory, all the quantities needed to produce framing effects (outcomes and probabilities) are present in this formulation of the problem. The zero complement in the gamble option literally contributes nothing to predictions of prospect theory (or other utility theories) because the value of zero is set at zero (and anything multiplied by zero is also zero, so that the zero complement disappears from consideration). The information about the 2/3 probability was placed in the preamble (with the other information about how many were expected to die altogether and so on). Subjects were later asked about the information provided in the preamble to ensure that they had not misunderstood or skipped over that information; the subjects were aware of that information (i.e., the problems were not ambiguous).

When these problems were presented, focusing on the key numerical information according to prospect theory (removing only the zero complement from the focus of attention), framing effects disappeared. However, the opposite truncation of the gamble produced large framing effects (i.e., removing the numbers but leaving the entire zero complement to highlight the some-none contrast that is essential to predictions of fuzzy-trace theory). Thus, as predicted by fuzzy-trace theory, 200 saved was strongly preferred compared to a 2/3 probability that no one will be saved, despite knowing that there was a 1/3 probability that 600 would be saved (and vice versa in the loss frame). These effects, too, have been replicated by others (see Kuhberger & Tanner, 2010, for a recent summary of studies showing these effects). These effects have also been obtained within subjects for a variety of money and lives problems, as shown in Figure 2.

Figure 2.

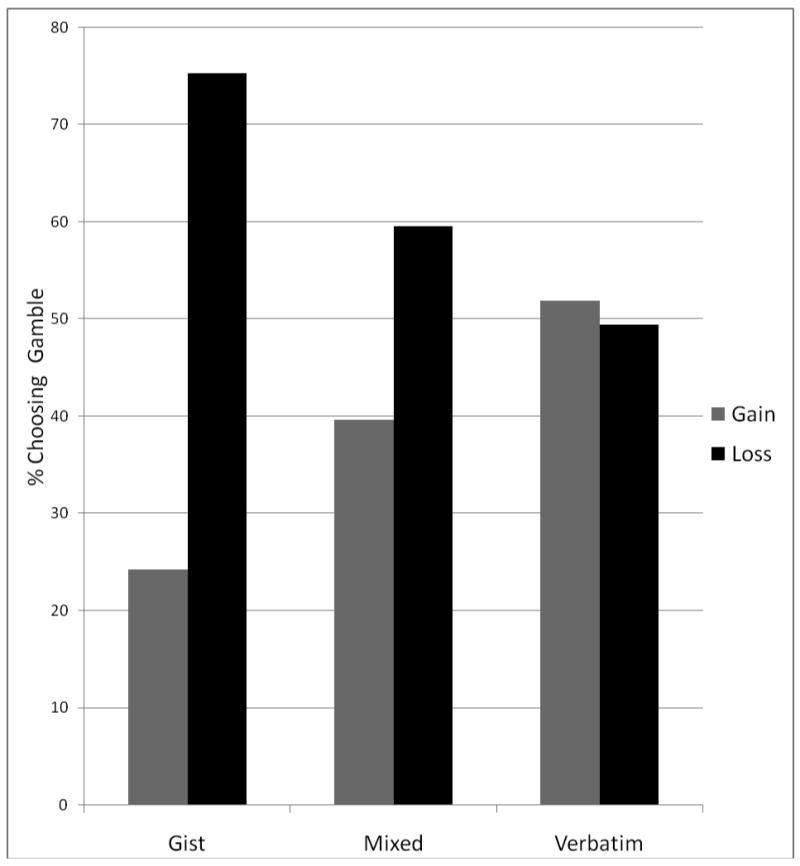
Sixty money and lives framing problems (30 gain and 30 loss) were presented within subjects to 38 adults. Two sets of materials were constructed; subjects saw the gains problems from one set and the loss problems from the other set. The mixed versions were the traditional complete framing problems as they are typically presented. The gist versions juxtaposed the zero complement of the gamble (e.g., 2/3 probability that no one will saved) and the sure thing (e.g., 200 saved for sure), whereas the verbatim versions juxtaposed the non-zero complement (e.g., 1/3 probability that 600 will be saved) and the sure thing (e.g., 200 saved for sure). Non-focal complements were presented as part of the preamble to each problem, eliminating ambiguity.

Still More Critical Tests: Variations on Framing and the Allais Paradox

Variations on framing problems that either preserve the possibility of a zero outcome, or remove that zero outcome, produce effects that would be expected by fuzzy-trace theory (Keren, 1991). For example, when subjects are told that their selection will be repeated many times, framing effects decline or disappear. Repeating the gamble many times means that the possibility of a zero outcome becomes miniscule: a 1/3 chance of saving 600 lives and 2/3 chance of saving no one repeated 100 times saves no one only if the zero outcome comes up all 100 times. Removing the realistic possibility of no one being saved removes the none-some contrast between the sure option and the gamble, attenuating framing effects according to fuzzy-trace theory. In addition, when outcomes are experienced according to their probabilities (e.g., for the gamble, $600 is won on 1/3 of trials, and nothing is won on 2/3 of the trials), rather than verbally described, people also do not show framing effects (Weber, Shafir, & Blais, 2004). Again, fuzzy-trace theory says that this is because there is effectively no zero outcome when the gamble is repeated, removing the some-none contrast that produces risky choice framing effects. The result that one-time decisions behave differently than repeated decisions has been explained by analogy to the biblical tale of Solomon and the baby (Reyna & Brainerd, 1995). When choices are made one time, people are saved or not and money is won or not; these are categorically or qualitatively different states of the world rather than matters of degree. In the same way, cutting the baby in two, giving each mother 50%, is not equivalent to giving one mother all of the baby and the other none, although, just like expected value, it is equivalent “on average.”

Although we have focused on framing problems, these principles of gistification, that is, that reasoners begin with the simplest categorical distinctions and then make finer distinctions only if necessary, apply broadly to decision making. Consider predictions when zero outcomes are present in not only one option (as in framing problems and in Decision 1 of the Allais paradox, Table 1) but in both options, for example, when choosing between two gambles (as in the second part of the Allais paradox, Table 1; see Reyna, in press). (As the colored sections in Table 1 illustrate, Option B is embedded in Option A, so choices should be consistent for Decision 1 and 2; however, most people prefer A for Decision 1 and B for Decision 2.) In Decision 2, a choice between winning $1 million with 11% probability and $5 million with 10% probability boils down to winning some money with some probability for both options, which produces a stalemate. The next rung on the gist ladder must then be ascended, so that an ordinal (rather than categorical) differentiation is achieved. Winning less money with some probability can be rejected in favor of winning more money with some probability (Reyna & Brainerd, 1995). Even more fine-grained distinctions are required if the response format demands it (e.g., How much would you pay for a lottery ticket with an 11% probability to win $1 million?). These principles explain preference reversals and risk aversion, but loss aversion, that losses hurt more than gains feel good, may also produce a greater willingness to gamble when zero outcomes are not present (Johnson, Gachter, & Hermann, 2010; Tversky & Kahneman, 1986).

Table 1. Example of the Allais Paradox: Choosing between a Sure Thing and a Gamble and between Two Gambles.

Decision 1				Decision 2
Option A		Option B		Option A		Option B
Winnings	Probability	Winnings	Probability	Winnings	Probability	Winnings	Probability
$1 million	100%	$1 million	89%	Nothing	89%	Nothing	90%
		Nothing	1%	$1 million	11%
		$5 million	10%			$5 million	10%

Summary

In sum, experiments have demonstrated that framing effects in adults are explained by the processing of simple, categorical gist, rather than processing exact (verbatim) numbers (with a psychophysical function or even processing numbers at all). Although we did not present evidence that cuing different values can produce different results for framing problems, others have shown this. For example, Wang (e.g., 2002) has shown that cuing values such as equity (e.g., everyone should have the same chance at life) increases choices of the gamble in the gain frame (see also Reyna & Brainerd, 1992; Reyna & Casillas, 2009; Wang, Simons, & Brédart, 2001). Numbers, which are essential to predictions of prospect theory and all other utility theories (expected utility theory, subjective expected utility theory, cumulative prospect theory, etc.), were not necessary to observe effects; when they were removed, framing effects increased rather than decreased. In addition, focusing processing on these numbers made framing effects disappear. Thus, numbers are neither necessary nor sufficient for framing effects. In contrast, focusing on some-none dichotomies, despite the fact that “none” literally contributes nothing to preferences in standard theories, enhanced framing effects. When decision makers had a chance to reflect because the same one-shot decisions were presented repeatedly, framing effects became bigger, suggesting that these are not impulsive choices. However, when told that the choices will be executed many times, effectively removing zero outcomes, framing effects disappeared. When problems and response formats demanded it, finer distinctions were made, climbing the ladder of gist as required—but beginning with the simplest level first. Each of these results supports predictions of fuzzy-trace theory.

Gist-based Intuition Increases with Age and Experience

Having established that risky decisions in adults are explained by simple, qualitative gist processing, as opposed to quantitative analysis of exact (verbatim) numbers via a psychophysical function, we are ready to turn to developmental predictions. Many studies have shown that young children can process verbatim numbers in decision tasks (e.g., for a review, see Reyna & Brainerd, 1994). Based on fuzzy-trace theory, we would predict that as decision makers develop, they should move from a reliance on more precise verbatim analysis toward fuzzier gist-based processing of outcomes and probabilities. Precise quantitative processing of degrees of risks and magnitudes of rewards (e.g., multiplying .5 × 2 toys to yield an expected value of 1 toy) should give way to qualitative processing that captures the gist—or bottom-line meaning—of decision options (e.g., choosing the gamble entails that one might win nothing).

Developmental Differences in Decision Making

In the first experiment conducted on framing effects in children, Reyna and Ellis (1994) presented 9 gain and 9 loss problems to subjects ranging in age from four to eleven years old (order of gain and loss blocks was counterbalanced). By presenting multiple problems, level of reward and level of risk can be varied, which is essential to diagnose decision strategies. In this study, three levels of reward (1, 4, or 30 prizes) were combined with three levels of risk (1/2, 2/3, and 3/4 chances to win nothing or to lose something).

Precise instructions and task formats are required so that children understand the task and remember the information (otherwise misleading results are obtained). Rather than read problems aloud, information is presented visually. Spinners with colored sections (e.g., 1/3 blue and 2/3 red) conveyed probabilities of winning or losing prizes (Reyna & Brainerd, 1994; Schlottmann, 2001). (To ensure comparability, the same task has also been presented to adults, e.g., Reyna, Estrada, et al., in press.) Prizes were placed in transparent bags directly on the corresponding colored section of the spinner. For example, in the gain frame, children might decide between winning 1 prize for sure versus a 1/3 chance to win 3 prizes if the spinner lands on blue (2/3 chance to win nothing, represented by an empty transparent bag on the red section of the spinner).

For loss frame problems, children were given an “endowment” of prizes (e.g., 3 prizes) and chose between such options as losing 2 prizes for sure versus a 2/3 chance to lose 3 prizes (1/3 chance to lose nothing). Although different numbers of prizes could be lost in different problems, the endowments ensured that net outcomes were identical across gain and “loss” frames. Children did not need to know how to subtract. Instead, losses were acted out by removing smaller transparent bags of prizes from larger transparent bags so prizes to be kept were displayed in front of the child (outcomes to be lost were also visible and were placed opposite the child, on the experimenter's side of the table). In both frames, children did not experience outcomes (which produces carryover effects to subsequent trials), although the operation of the spinner was demonstrated prior to the first trial to ensure awareness that outcomes were random (Gigerenzer, Hell, & Blank, 1988). Choices were “incentive compatible” because all participants were instructed that at the end of the game that they would win real prizes based on their choices in the game.

Reyna and Ellis (1994) found that the youngest group of children (preschoolers) treated the gain and loss frames as though they were paying attention to quantitative information. These children did not show framing differences when net quantitative consequences were identical. However, they did not gamble all of the time. Instead, they systematically modulated risk preferences according to degree of risk and amount of reward (see also Levin & Hart, 2003; Levin et al. 2007; Reyna, 1996; Schlottmann, 2001; Schlottmann & Anderson, 1994). Their responses were roughly consistent with multiplying risk and reward, resembling multiplicative responding in other studies of proportional reasoning (i.e., in proportional reasoning, quantitative dimensions trade off, such as length and width in area judgment; Acredolo, O'Connor, Banks, & Horobin,1989; Kerkman & Wright, 1985).

Somewhat older children also did not show framing effects, and they too gambled judiciously depending on the levels of risk and reward—except when differences between rewards were large. Second graders preferred the larger gains (in the gamble) and preferred the smaller losses (in the sure thing). This response pattern is called “reverse framing” because it is the reverse of the adult framing pattern, namely, greater preference for gambling in the gain than the loss frame. The pattern is consistent with paying attention mainly to one rather than to two quantitative dimensions, the dimension of rewards. Although overall expected value was always equal for these decisions, more rewards were available in the gamble and fewer rewards would be lost in the sure thing. (If one is thinking quantitatively, the zero outcomes in the gamble multiply out to zero and, thus, do not matter.) Young adolescents also exhibited reverse framing effects when differences between rewards were large, but this was also the age level at which standard framing first appeared. Between early and late adolescence, the standard framing pattern emerges and becomes dominant (e.g., Chien et al., 1996; Reyna & Ellis, 1994; Reyna, Estrada et al., in press). Adults rarely show reverse framing (e.g., Levin, Gaeth, Schreiber, & Lauriola, 2002; Reyna, Estrada et al., in press).

This general developmental trajectory—from quantitatively processing two dimensions (no framing shift) to processing one dimension (reverse framing) to ultimately reasoning qualitatively (standard framing)—has been replicated in multiple studies (e.g., Chien, Lin, & Worthley, 1996; Levin, Weller, Pederson, & Harshman, 2007; Reyna & Mattson, 1994; Rice, 1995; Reyna, 1996; Reyna & Farley, 2006, Figures 6 and 7). Young children are able to process both probability and outcome information in making risky choices, although quantitative performance improves from childhood to adulthood (e.g., Boyer, 2006; Figner et al., 2009; Harbaugh, Krause, & Vesterlund, 2002; Levin, Hart, Weller, & Harshman, 2007; Reyna & Ellis, 1994; Rice, 1995; Schlottmann & Tring, 2005). Responsiveness to quantitative differences in expected value between options, for example, increases with age and framing effects diminish in adults when expected values counter standard framing preferences (e.g., when the gamble has higher expected value in the gain frame; Fischhoff, 2008; Levin, Weller, et al., 2007; Reyna & Brainerd, 1995). Both trends, developmental increases in preferences for gist accompanied by parallel increases in analytical proficiency, were predicted by fuzzy-trace theory (e.g., Reyna & Brainerd, 1994; Reyna & Ellis, 1994). These kinds of contradictory developmental trends cannot be accounted for without assuming the existence of some kind of dual processes. An increase in analytical ability, for example, cannot plausibly produce a growth in framing effects without conjuring tortured arguments.

Additional Evidence that Gist-Based Intuition is Advanced

As these developmental predictions imply, fuzzy-trace theory differs from standard dual-process accounts in suggesting that gist-based intuition is an advanced mode of processing. In addition to evidence that experts rely on gist more than novices do (cf. Ashby, Ennis, & Spiering, 2007), developmental evidence for a growth in gist-based intuition in framing and other problems supports the hypothesis that such intuition is advanced (see Adam & Reyna, 2005; Reyna & Adam, 2003; Reyna & Farley, 2006; Reyna, Lloyd, & Brainerd, 2003, concerning the relevance of using developmental trends in judging rationality). Further evidence can be gleaned by considering the relation between gist-based intuition and unhealthy risk taking.

Although risk taking (e.g., choosing the gamble over the sure thing) generally declines in laboratory tasks during childhood, adolescents take more risks than adults do in real life (Institute of Medicine, 2010; Reyna & Farley, 2006). If fuzzy-trace theory's account of framing is correct, risk aversion in the gain frame is caused by qualitative thinking (e.g., considering the categorical possibility of gaining nothing), whereas quantitative thinking promotes risk taking (e.g., comparing differences in magnitudes of rewards). Therefore, Reyna and Farley (2006) argued that verbatim-based analysis, as in reverse framing, would promote real-life risk taking because (a) most adolescents operate in a gain frame in developed countries (e.g., choosing between less fun and less risk vs. more fun and more risk) and (b) objective risks are often low, so benefits compensate for risks (if one is thinking quantitatively; see also Reyna, Adam, Poirier, LeCroy, & Brainerd, 2005). For instance, the probability of pregnancy from a single instance of unprotected sex is objectively low. A review of the literature supported this conclusion. Across risk-taking domains (e.g., alcohol use, unprotected sex), degree of perceived risks and benefits predicted risk taking, suggesting a reasoned route to risk taking in adolescence (as opposed to only a reactive or emotional route in which behavior would occur impulsively in spite of perceived risk).

This prediction was further tested by developing different survey instruments to measure categorical or gist-based thinking and verbatim-based analytical thinking about risk taking (see Table 2; Mills et al., 2008; Reyna, 2008). For example, the Categorical Thinking Scale includes such items as “It only takes ONCE to get pregnant (or to get someone pregnant).” Agreement with these kinds of gist-based items in young adolescents predicted lower levels of sexual initiation, lower sexual intentions, and fewer numbers of sexual partners. Traditional decisionmaking approaches make the opposite prediction, that beliefs such as “it only takes once” are insufficiently precise and, thus, risk-promoting (Downs, Bruine de Bruin, Murray, & Fischhoff, 2004). However, more “complex” or precise distinctions in thinking about risk (e.g., making distinctions about specific consequences using a 100-point scale) were associated with greater risk taking (Table 2; Mills et al., 2008; Reyna, Estrada et al., in press).

Table 2. Examples of Items from Verbatim and Gist Scales Assessing Perceptions of Risks and Benefits.

Gist Measures
Gist principles	Avoid risk. Better safe than sorry.	(number endorsed)
Categorical risk	It only takes ONCE to get HIV-AIDS.	(agreement ratings)
Global benefits	Overall, for YOU, which of the following best describes the benefits of having sex?	(none, low, medium, high)
Global risks	Overall, for YOU, which of the following best describes the risks of having sex?	(none, low, medium, high)
Verbatim Measures
Specific risk	I am likely to have HIV-AIDS in the next 6 months	(agreement ratings)
Quantitative risk	What are the chances that you have a sexually transmitted disease?	(0%, no chance at all, to 100%, absolutely sure)
Reverse framing	# gambles chosen in the gain frame – # gambles chosen in the loss frame	(+9 to -9)

Moreover, in a subsequent study with adolescents and young adults employing principal components analyses, instruments that assessed global perceptions of risk with crude response formats loaded on a gist-thinking factor and instruments that assessed specific perceptions of risk with precise response formats loaded on a separate verbatim-thinking factor (Table 2; Reyna, Estrada, et al, in press). These risk perceptions correlated in opposite directions with behavior (replicating results of Mills et al., 2008, and supporting dual-process predictions). In addition, response patterns on framing tasks were related within subjects to assessments on these thinking scales and to self-reported risk taking. As predicted, the tendency to engage in reverse framing loaded together with superficially different but conceptually similar verbatim thinking items in principal component analyses. Orthogonal verbatim and gist factors each contributed unique variance in predicting unhealthy risk taking: Again, gist-based intuition was associated with less risk taking and verbatim-based thinking was associated with more risk taking. Gist and verbatim factors accounted for significant variance in risk-taking, controlling for emotional reactivity and impulsivity scale scores, which loaded on additional factors. The latter findings illustrate that verbatim and gist factors cannot be reduced to a simple dichotomy between emotion versus inhibition (or censoring), and that each of these factors contributes unique variance to predictions.

Summary

In sum, although children as young as four or five (but certainly by six) can roughly estimate multiplicative trading off of risks and rewards, this quantitative approach recedes from childhood to adulthood, with qualitative processing emerging in adolescence. However, adolescents are in transition. When rewards are large, they revert to reverse framing, which reflects verbatim-based analysis of rewards. Supporting that idea, reverse framing loads with other measures of verbatim thinking about risk in principal components analysis, whereas gist measures load together on a separate factor. Verbatim-based thinking was associated with increased risky behaviors and intentions. Gist-based thinking was a significant protective factor in all analyses of behaviors and intentions, accounting for unique variance beyond neurobiological factors such as reward sensitivity and behavioral inhibition. Contrary to traditional theories of decision making, fuzzy gist-based thinking seems more adaptive than verbatim-based thinking in the sense that it promotes healthy outcomes for adolescents.

Neurodevelopment and Decision Making

Childhood and Adolescence

Risk taking and decision making are among the most heavily researched areas in developmental neuroscience (e.g., Reyna, Chapman, Dougherty, Confrey, in press; Somerville et al., 2010; Steinberg, 2008; Van Leijenhorst et al., 2010; Vartanian & Mandel, 2011). Neurobiological theories have focused on developmental and individual differences in inhibition and reward sensitivity, and how these explain risky decision making (Crone & van der Molen, 2004; Galvan et al., 2006, 2007; Luna & Sweeney, 2004). Children and patients with lesions to the ventral medial prefrontal cortex seem to have difficulty learning from outcomes (rewards and punishments) in a risky decision making task and both groups do not modulate their risk taking as well as intact adults do to differences in expected value (Levin et al., 2007; Weller et al., 2007). These results underline that preference for quantitative reasoning (higher in childhood) is not the same as performance (lower in childhood).

Although the dual-process model has been controversial in the adult neuroscience literature (e.g., Kable & Glimcher, 2007), there is widespread agreement in the developmental literature that cognitive control and inhibitory networks (e.g., prefrontal cortex, anterior cingulate, and amygdala, which is down-regulated by frontal areas) develop later in adolescence and young adulthood, relative to areas responsible for motivation and reward sensitivity, such as the ventral striatum (e.g., Casey et al., 2008; Somerville et al., 2010: Van Leijenhorts et al., 2010). Within the striatum, the nucleus accumbens (which responds proportionately to the magnitude of rewards) has been found to be more responsive to anticipation of reward in adolescents, compared to adults (e.g., Galvan, et al., 2006; 2007). Analogous findings have been reported for sensation seeking, which peaks in adolescence (Romer, 2003; Steinberg et al., 2008). Because the subcortical reward systems develop sooner than prefrontal cortical control systems, this is thought to produce an imbalance that is most acute in adolescence and that drives risk taking. During adolescence, white matter develops, connecting frontal areas and limbic reward systems, presumably inhibiting risk-taking in most adults (Casey et al., 2008; Galvan et al., 2007; Institute of Medicine, 2010). When that control is deactivated by transcranial magnetic stimulation to the lateral prefrontal cortex, adults resemble adolescents; they take risks and are less likely to delay gratification in response to immediate rewards (Figner et al., 2010).

Interestingly, framing effects seem to engage dual processes, although areas do not completely overlap those identified in developmental studies. For example, De Martino et al. (2006) found that increased activation in the amygdala was associated with standard framing effects, interpreted as an “affect heuristic” related to the emotional system. When subjects made occasional selections that ran counter to standard framing (e.g., reverse framing), there was enhanced activity in the anterior cingulate cortex (ACC). Moreover, across subjects, orbital and medial prefrontal cortical activity was related to reduced susceptibility to framing effects. This pattern of activation was interpreted in terms of opposing neural systems, with ACC activation consistent with the detection of conflict between analytical responses versus a more emotional amygdala-based system (see also Roiser et al., 2009; Zheng, Wang, & Zhu, 2010).

Autism, Aging, and Alzheimer's Disease

In a critical test of predictions of fuzzy-trace theory, De Martino et al. (2008) showed that subjects with autism spectrum disorder were less susceptible to framing effects than control subjects. Autism is a neurodevelopmental condition in which individuals focus on parts rather than global aspects of objects, have difficulty integrating information into a meaningful whole, and tend to process language (e.g., metaphors or proverbs) literally (Frith & Happé, 1994; Happé & Booth, 2008). Frith (1989) noted that non-autistic individuals prefer processing higher-level meaning, achieved by establishing a gestalt, context, or gist (akin to the “fuzzy processing preference” in fuzzy-trace theory; Reyna & Brainerd, 1998). This capacity for “central coherence” is diminished in autism so that processing lacks higher-order meaning or gist. Thus, the weak central coherence hypothesis predicts that autistic individuals will experience disadvantages when required to integrate elements, but experience advantages in situations when required to process in a local or piecemeal way. This cognitive portfolio can be also characterized as diminished gist-based intuition, but higher verbatim analytical processing. Therefore, according to fuzzy-trace theory, those with autism should be less susceptible to framing effects because framing effects depend on gist-based intuition. Using the task administered in the magnet in the 2006 study, De Martino et al. (2008) found the predicted result, superior performance among those with autism relative to controls. On the same grounds, fuzzy-trace theory would predict that other gist-based biases and heuristics—those that emerge with age in normally developing individuals—would also elicit less biased performance among those with autism. These predictions simultaneously test our explanation of reasoning and decision biases and test our characterization of cognitive processing in autism.

Autism has been associated with brain overgrowth and delayed maturation, and an absence of long connections, in contrast to typical developmental increases in connectivity and integrative processing (e.g., Just, Cherkassky, Keller, Kana, & Minshew, 2007). One of the most surprising results from anatomical neuroimaging scans performed at different ages of normal development is that substantial pruning of gray matter occurs from childhood through young adulthood (e.g., Giedd, et al., in press). Reyna and Rivers (2008) pointed out that pruning along with increased myelination would facilitate rapid recruitment of simple gist, especially during heightened emotional arousal, in concert with parallel development of behavioral inhibition in prefrontal cortex that reduces impulsive responding (Reyna & Casillas, 2009; Reyna & Mills, 2007; Rivers et al., 2008; see also Figner et al., 2009).

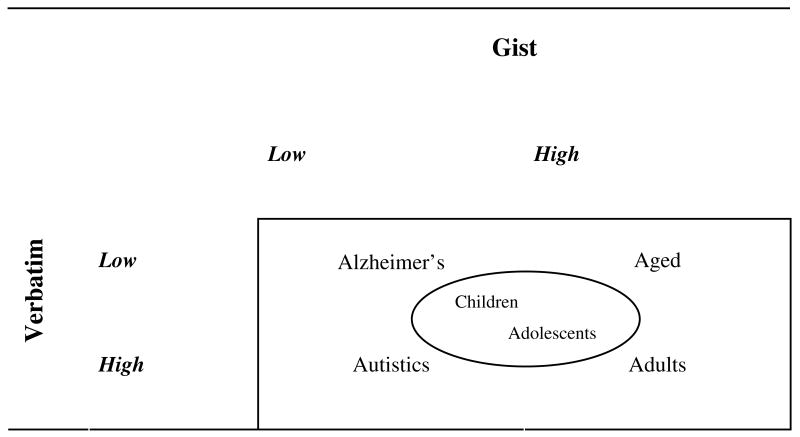
At the other end of the lifespan, normal aging has been associated with declines in verbatim memory, but conservation of gist memory (e.g., Brainerd, Reyna, & Howe, 2009). However, hypothesized age declines in hippocampal volume have proved surprisingly elusive (Van Petten, 2004). Consistent with conserved gist processing in aging and our explanation of framing effects, older adults were more susceptible to framing effects compared to younger adults in one study (Kim, Goldstein, Hasher, & Zacks, 2005) and as susceptible (i.e., they do not differ from young adults) in other studies (Mayhorn, Fisk, & Whittle, 2002; Rönnlund, Karlsson, Laggnäs, Larsson, & Lindström, 2005). Verbatim processing is not entirely absent in normal aging, however, and older subjects can be induced to engage in it, which decreases framing (Kim et al., 2005) (see also Löckenhoff & Carstensen, 2004; Mikels & Reed, 2009). Transitions to Alzheimer's disease have been associated with hippocampal atrophy, which then extends outward from the medial temporal lobe as the disease progresses (e.g., Raji, Lopez, Kuller, Carmichael & Becker, 2009). Recent modeling research has isolated loss of gist memory as a key distinction between normal aging and progression to Alzheimer's disease, more predictive than the presence of the E4 allele of the APOE gene (Brainerd et al., 2009; Brainerd, et al., in press; Reyna & Mills, 2007). As would be expected from the decline in both representational systems, decision making in Alzheimer's disease is disorganized (e.g., Delazer et al., 2007). Gist and verbatim differences in Alzheimer's disease and normal aging, as well as in autism, childhood, adolescence, and adulthood are summarized in Figure 3.

Figure 3.

Summary of gist and verbatim memory abilities in typical and atypical development across the life span. Children are positioned higher in verbatim memory than those with Alzheimer's disease. Adolescents are positioned higher in verbatim memory than children and those with Alzheimer's, but lower in gist memory than younger adults and older adults (aged). Memory abilities constrain processing styles. Therefore, younger adults have the greatest cognitive flexibility.

Thus, developmental neuroscience has identified major changes in brain morphology and connectivity that occur from childhood to young adulthood. These changes are associated with motivational and emotional changes, and with risky decision making. Concurrently, cognitive processes undergo development, which result in better cognitive control and better quantitative reasoning about rewards and about expected value. The overall picture of brain and behavior is broadly consistent with standard dual-process theory, and its emphasis on emotional and inhibitory processes, as well as with fuzzy-trace theory, and its emphasis on gist and verbatim processes. Neurocognitive differences in autism, aging, and Alzheimer's disease fill in important gaps in our knowledge about the consequences of gist-based intuition for reasoning and decision making, as summarized in Figure 3.

An Integrative Model: Verbatim + Gist = Prospect Theory

The heart of traditional decision theory is the concept of expected value, which implies that outcomes and probabilities trade off. For example, the expected value of the gamble in the gain frame of the disease problem is 1/3 probability × 600 lives = 200 lives. This basic multiplicative framework has been adopted in expected utility theory and its descendants, such as prospect theory (Tversky & Kahneman, 1986). Recently, scholars have proposed dual-process models in which processing conformed either to expected value (or expected utility) versus prospect theory (e.g., Loewenstein & O'Donoghue, 2005; Mukherjee, 2010). However, as discussed, robust and replicated effects rule out prospect theory; indeed, the entire family of expected value and expected utility models has been rejected. Furthermore, psychophysical theories, such as prospect theory, have been criticized because they lack an underlying process model, begging the question of why the psychophysics shapes up as a power function as opposed to something else. To be sure, scores of studies have been published that seemingly support the familiar power function of prospect theory (Tversky & Kahneman, 1992; see also Birnbaum, 2004). However, tweaking the functional forms or adding parameters are insufficient to address the evidence produced by the critical tests we have discussed.

In the following section, we show that the power function of prospect theory will be produced if decision makers are combining a linear process (i.e., numerical values are processed precisely) and a discrete process (i.e., numerical values are processed imprecisely using categorical or ordinal gist). In this view, the power function of prospect theory is not, in itself, a description of underlying processes of valuation. Instead, the power function reflects a compromise between verbatim and gist processes. Without making any additional assumptions, the power function of prospect theory is delivered free, as a consequence of starkly different underlying processes. This formalization shows how both verbatim analysis (the linear process) and gist-based intuition (the discrete process) operate simultaneously and how the interplay between them produces linear or curvilinear forms of the valuation function. The model is also used to explain developmental contradictions, such as the early emergence of verbatim analysis, as well as gist-based developmental reversals.

A Fuzzy-Trace Model of Decision Making

The prospect theory value function for gains and losses can be derived from fuzzy-trace theory's proposal that subjective value is controlled by two processes, one that is quantitative and linear and a second that is qualitative and Markovian (discrete state process). We introduce the prospect theory value function first and then show how that same function falls out of the two-process analysis.

In prospect theory, outcomes that are gains are treated separately from outcomes that are losses. (We retain this feature of prospect theory.) The theory specifies a value function for gains and a value function for loses, which are the counterparts of the familiar notion of a utility function, u(x), from economics. That is, the prospect theory value functions for gains and losses, which are based on ideas borrowed from psychophysics, are psychological versions of the utility function (e.g., the psychological value of $200). The specific forms of the gain and loss value functions for an outcome x are

$$u(x)=\{\begin{array}{lll}{x}^{\alpha }\hfill & \text{for}\hfill & x\ge 0\hfill \\ -\lambda (-x^{\alpha })\hfill & \text{for}\hfill & x<0\hfill \end{array}$$ (1)

Certain constraints are imposed on Equation 1 in order to yield two standard findings about risky prospects (see Figure 4). First, people are normally risk avoidant for gains (they prefer certainty over taking a chance when x is positive) but risk seeking for losses (they prefer taking a chance over certainty when x is negative). So that the value function will behave accordingly, the constraint α < 1 is imposed in prospect theory. Second, people are normally less sensitive to gains than to losses. So that the value function will behave accordingly, the constraint λ > 1 is imposed. (The slope λ is often estimated to be about 2 to 2.5, producing a steeper slope for losses than gains, and, hence, loss aversion; Kahneman, 2003.) Next, we show that Equation 1 can be represented as the combination of a linear valuation process, together with a Markovian valuation process.

Figure 4.

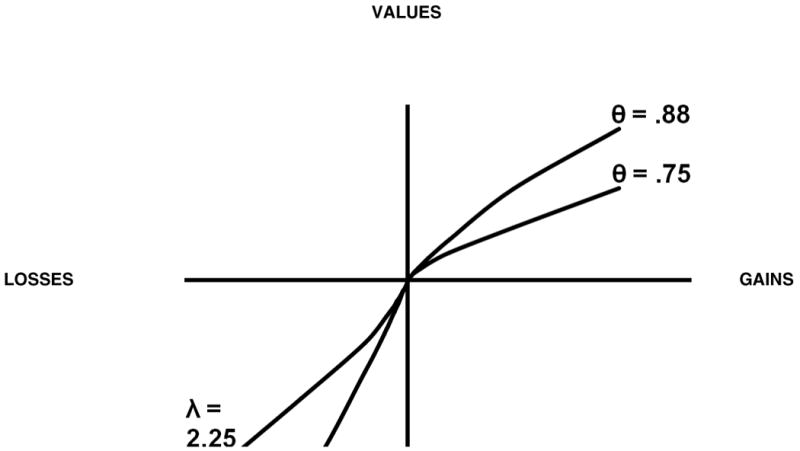
Illustrating different probabilities of transitioning from the some-none state to the some-more state for the discrete (gist) process, which produce the prospect theory value function for gains and losses. As shown in the figure, higher values of theta approach linearity, the verbatim process.

The first thing to note about Equation 1 is that it is linear under a certain limiting condition—specifically that α = 1. This constraint means that u(x) increases linearly with the value of x for gains, with a slope of 1 and an intercept of 0, and that u(x) increases linearly with the value of x for losses, with a slope of λ and an intercept of 0. Fuzzy-trace theory assumes that, when α = 1, the value function is linear with slope 1 and slope > 1 over gains and losses, respectively, unless a second psychological process operates, which drives the value of α below 1. This second process is Markovian, a discrete state-change process.

Fuzzy-trace theory assumes that when people are confronted with choices between different outcomes, each outcome (e.g., $200) is assigned a value by the linear process. In parallel, people gistify the outcomes by imposing a qualitative distinction between outcomes, a categorical or ordinal gist. In particular, people interpret the problem outcomes in one of two ways: The first and simpler interpretation is what will be called the some-none state, by which we mean that the gist of the task is that, psychologically, numerical outcomes are “worth something” while zero outcome(s) are “worth nothing.” (People are indifferent to gaining or losing x when an outcome is perceived to be worth nothing.) As discussed in an earlier section, this simple qualitative distinction is sufficient to deliver a clear preference in many types of problems, such as framing problems and the first decision of the Allais paradox (Table 1). However, it does not do that for options in other problems, such as the second decision of the Allais paradox, because both non-zero outcomes are perceived to be “worth something” (i.e., both gambles boil down to “winning something or winning nothing,” which makes the options indistinguishable). To deliver a preference here, fuzzy-trace theory assumes that people can jump from the some-none state to a some-more state. In this more complex state, one outcome is perceived to be worth more than the other non-zero outcomes, which are represented as some.

The change in value representation that results from this second process involves movement through a discrete space. That is, it is Markovian. For a particular value of x, say x_i, which is associated with a particular outcome in a particular problem, the probability that a subject is in the some-none state (SN) is π and the probability that the subject is in the some-more state (SM) is 1- π. For that problem, then, the probability of choosing either option is a joint function of the values that are assigned by the linear process together with the proportions of subjects who are in the two qualitative representational states. This starting value, π, changes when the reasoner begins with different biases; for example, more adults are likely to begin in the some-none state, relative to younger subjects, because of the fuzzy-processing preference. Then, as the value of x increases, by changing the outcomes in a particular problem (e.g., stepping up values in one option, making expected values unequal), two things happen. First, the linear process assigns a higher value, based on the gain or loss function, and second, subjects transition upward, with some probability (θ), to the more complex some-more state. The second process can now be presented in standard Markov form as:

W(i) = [SN(i), SM(i)] = [π, 1- π];

(2)

W(i) is a starting vector that gives the proportions of subjects who are in the SN and SM representational states when x = x_i, and M is a transition matrix that specifies how subjects move through this state space as x increases. This matrix has two features. The first is the transition parameter θ, which is the interstate transition rate. According to the bottom row of the matrix, each time x is increased by 1 unit (the definition of a unit may vary from problem to problem, e.g., money or lives), subjects who are in the SN representation state jump to the higher SM representational state with probability θ or remain in the SN knowledge state with probability 1-θ. The other feature is that the matrix is an absorbing process, and specifically, it absorbs in the higher SM state because, according to the top row, if the subject is in SM when x = x_i, the probability that the subject is in that same state when is x = x_i+1 is 1. This directionality is a consequence of the aforementioned fuzzy processing preference, which begins in some-none and absorbs in some-more. Now, we show how the prospect theory value function falls out.

Returning to Equation 1, remember that this is a linear process in the limiting case where α = 1. According to fuzzy-trace theory, this is true whenever the Markov process in Equation 2 does not operate, and thus the linear valuation process drives preferences. When the Markov process operates, this affects α, and specifically, α is the rate of transition through the state space (i.e., α = θ). Thus, the fuzzy-trace theory derivation of the prospect theory value function from the combination of a linear valuation process and a Markovian valuation process is this:

$$u(x)=\{\begin{array}{lll}\hfill x^{\theta }\hfill & \text{for}\hfill & x\ge 0\hfill \\ \hfill -\lambda (-x^{\theta })\hfill & \text{for}\hfill & x<0\hfill \end{array}$$ (3)

Note two important properties of the fuzzy-trace theory value function. First, it is not necessary to impose the α < 1 constraint any longer, in order to obtain risk avoidance for gains and risk seeking for losses, because it falls out of the theoretical analysis: When α = θ, the exponent of the power function must fall in the unit interval because θ is a probability. Second, we said that the fuzzy-trace theory value function is linear as long as the Markov process does not operate. Inspecting M, the Markov process ceases to operate when the interstate transition probability θ approaches 1, which simply means that all subjects remain in their current representational state as x increases because they have entered the absorbing SM state. Note that as θ approaches 1, the exponent of the gain and loss functions in Equation 3 approaches 1 and the function becomes progressively more linear—precisely as the theory assumes should happen: The Markov process ceases to operate because all subjects have entered the absorbing state.

Thus, there are two boundary conditions for this psychological function. On the one hand, when θ = 1, the linear process determines values (and the Markov process has been exhausted). On the other hand, at the other extreme, when θ = 0, there is zero probability of transitioning out of the Markov state, and the some-none state determines values. That is, for θ = 0, all positive values become 1 and all negative values become -1 (i.e., for x > 0, x⁰ = 1; for x < 0, -x⁰ = -1 or other constant as a function of the value of λ). As in prospect theory, the value of x = 0 is always zero (i.e., for x = 0, x^θ = 0). It follows that, in the some-none state, there are two basic, categorical values: some, which is 1, and none, which is 0 (and, because λ is generally > 2.0, losing “some” feels worse than gaining “some” feels good).

A number of psychological implications fall out of this model. First, adults are more likely to transition to the some-more state (i.e., θ is higher), whereas children and adolescents are more likely to wait in the some-none state (θ is lower, and thus 1-θ is higher). Because adults are more likely to transition to some-more as rewards get larger, they should show greater sensitivity to expected value. In other words, when x increases, for example, in the gamble relative to the sure thing so that expected value increases, subjects should transition to the some-more state. Therefore, as x increases, differences in outcomes should matter more and more, especially to adults (or older children relative to younger ones; developmental differences in θ are a matter of degree).

Although adults are more sensitive to differences in quantity (they transition more readily in response to changes in values), they are more likely to begin in the some-none state (i.e., π is high), whereas children are more likely to begin in the some-more state (π is low, and thus 1- π is high). Thus, adults are more discriminating about differences in outcomes despite an initial fuzzy-processing bias that favors some versus none. Because children initially represent the options in terms of some versus more, they should be more likely to show reverse framing (preferring the gamble in the gain frame and sure thing in the loss frame): In the gain frame, when expected values of the two options are equal, the sure thing offers some rewards but the gamble offers more rewards. The starting parameter π may represent motivational differences between children (or adolescents) and adults, whereas θ represents cognitive factors (the ability to discriminate quantities). Children may want more, whereas adults are willing to settle for some (seeking potential as opposed to security, respectively; see Lopes, 1987), but adults are better able to perceive differences between more and some.

For problems either with a sure thing versus a gamble or for problems with two gambles (Table 1), adults begin in the some-none state. However, the probability of transitioning to the some-more state, θ, is higher for the two gambles (i.e., for any two gambles with a zero outcome in both options). Subjects transition to some-more because the two gambles are not distinct in the some –none state; the two options cannot be discriminated from one another. For the two gambles, subjects in the some-none state experience uncertainty, which is aversive (Camerer & Weber, 1999; Ellsberg, 1961; Gneezy, List, & Wu, 2006; Simonsohn, 2009). Subjects can guess, choosing either option, but this discomfiting uncertainty prompts change (increasing θ), much like disequilibrium prompts change in Piagetian theory.

Hence, this account explains and distinguishes a number of important empirical phenomena: loss aversion (λ), ambiguity aversion (epistemic uncertainty when options are not distinct), risk aversion (preferring the sure option over the gamble, attributable to a some-none state), fuzzy-processing preference in adults (attributable to π, the starting default of some-none), standard framing (again, attributable to a some-none state), and reverse framing (attributable to a some-more state). Children should be more motivated by rewards (i.e., by “more,” lower π) than adults, but adults should be more discriminating about differences in reward values than children are (higher θ). Finally, problems in which options cannot be distinguished based on some versus none prompt transitions to a more complex state of some-more (higher θ).

Summary

Summing up, the familiar prospect theory value functions were predicated on psychological conceptions derived from psychophysics; that is, that perceived value behaves like perceived intensity of light or sound, and hence, value functions will be power functions. However, the validity of the psychophysical conception is not demonstrated by data showing that valuation data are well fit by power functions. That is because, as we have just seen, the same power functions fall out of a cognitive interpretation, derived from research on reasoning and memory, which specifies that value functions are combinations of linear and Markovian processes. Discrete states are representations of outcomes, either categorical (some-none) or ordinal (some-more). The linear process operates all the time, which is consistent with children having the capacity to rely on expected value from a young age (Betsch & Lang, 2011; Reyna & Brainerd, 1994). Indeed, linearity operates for all subjects and contributes more as differences in x get larger (e.g., explaining why adults would be more sensitive to differences in expected value). However, the discrete process causes the curve to deviate from linearity, producing the familiar function of prospect theory as a consequence.

Epilogue

René Descartes, who has been called “the first great psychologist of the modern age,” was not the first dual process theorist, but he was among the most influential. Cartesian dualism contrasted the mind, the seat of reason, with the body, through which coursed “animal spirits.” The influence of Descartes is apparent in Freud's distinction between primary processes (primitive drives serving the pleasure principle) and secondary processes (control and self-regulation serving the reality principle), most recently reborn in Epstein's cognitive-experiential self (CEST) theory (e.g., Epstein, 1994).

Similar dualities between reason and emotion, cognition and experience, or analytical and intuitive thought have been used to explain biases in reasoning and decision making. The first process in each of these pairs, but the second process evolutionarily, has been predicted to develop from childhood to adulthood. Developmental reversals, predicted by fuzzy-trace theory, violate those standard expectations. Fuzzy-trace theory differentiates neurobiological factors such as emotion and inhibition from intuition, and grants gist-based intuition a more advanced status in development than verbatim analysis. Ironically, verbatim analysis of risks and benefits promotes unhealthy risk taking because young people do not see the forest for the trees: They trade off rare risks, such as HIV-infection, against the benefits of sex and other rewards, making “rational” and logical decisions that have poor outcomes for individuals.

Applying the simplest categorical distinctions between risk and no risk, or quantity and no quantity, a host of surprising effects in risky decision making can be predicted, effects that violate expected utility and prospect theory. Adults use simplest gist and show framing effects, but young children and individuals with autism make quantitative distinctions and do not show framing effects. A clear lesson from developmental neuroscience is that brain development is not simply about adding more and more capacity, but, rather simplifying and integrating.

The desire and ability to reflect on one's cognition increase with age, but are not necessarily connected to the intuitive processes of advanced cognition, which are often unconscious. Logical and pragmatic inferences are never entirely abstract, as they depend on the gist of information—its content—in addition to the generic values, principles, and heuristics that are applied to representations of content. Thus, children's reasoning progressively conforms to the prescriptions of logic and mathematics, but it also becomes progressively more colored by meaning and intuition. Our fuzzy-trace model incorporates this tension between analysis and intuition, between dual processes that develop independently, operate in parallel, and vary across content and context.

Research Highlights.

• Fuzzy-trace theory predicts improvement and reversals in cognitive development.

• A new model of decision making under risk and uncertainty is introduced.

• We show that prospect theory can be derived from fuzzy-trace theory.

• The theory is applied to neurodevelopment, autism, and Alzheimer's disease.