Characterization and Analysis of Relative Intensity Noise in Broadband Optical Sources for Optical Coherence Tomography

Abstract

Relative intensity noise (RIN) is one of the most significant factors limiting the sensitivity of an optical coherence tomography (OCT) system. The existing and prevalent theory being used for estimating RIN for various light sources in OCT is questionable, and cannot be applied uniformly for different types of sources. The origin of noise in various sources differs significantly, owing to the different physical nature of photon generation. In this study, we characterize and compare RIN of several OCT light sources including superluminescent diodes (SLDs), an erbium-doped fiber amplifier, multiplexed SLDs, and a continuous-wave laser. We also report a method for reduction of RIN by amplifying the SLD light output by using a gain-saturated semiconductor optical amplifier.

I. Introduction

The development and application of optical coherence tomography (OCT) has progressed rapidly since its inception in 1991, and OCT is finding many applications in clinical research and medical diagnostics[1], [2]. System sensitivity and imaging speed are two of the most important parameters used to evaluate the performance of an OCT system. State-of-the-art OCT systems typically operate at ~8–12 dB below shot noise limited sensitivity performance at higher source powers [3]. While this loss is typically attributed to the presence of residual system and relative intensity noise (RIN), the effect of the latter is often not clearly explained. Hence a thorough understanding of all RIN noise is critical to maximize the system sensitivity.

There have been numerous studies on the noise characterization of OCT systems and most of them assume the excess photon noise (often mentioned as RIN) to be inversely proportional to the linewidth of the optical source[4], [5]. This assumption is questionable as this theory cannot be uniformly applied to all sources because the origin of noise in various light sources differs significantly, owing to the different physical nature of photon generation[6]. To the best of our knowledge, no systematic study has been performed to quantitatively measure the RIN contribution of various OCT light sources. In this study, we perform experimental characterization of RIN of several optical sources including a superluminescent diode (SLD), amplified SLD output, an erbium-doped fiber amplifier (EDFA), multiplexed SLDs, and a continuous-wave (CW) semiconductor laser.

II. Theory

Total noise from an optical source mainly consists of three different noise terms: shot noise, thermal noise, and excess photon noise. Shot noise and thermal noise can be expressed as $\langle \mathrm{\Delta }{i}_{\text{sh}}^2\rangle =2q\langle I\rangle \mathrm{\Delta }f$ and $\langle \mathrm{\Delta }{i}_{\text{th}}^2\rangle =4k_{\text{B}}T\mathrm{\Delta }f/R_L$, respectively, where q is the electron charge, 〈 I 〉 is the averaged direct current (dc), Δf is the detection bandwidth, R_L is the load resistance, k_B is the Boltzmann constant, T and is the temperature. Excess photon noise refers to the fluctuations in source light output intensity due to the beating of various spectral components having random phases. Excess photon noise for a purely spontaneous source is given by

$$\langle \mathrm{\Delta }{i}_{\text{ex}}^2\rangle =\left(\frac{(1+{\alpha }^2){\langle I\rangle }^2\mathrm{\Delta }f}{\mathrm{\Delta }{v}_{\text{eff}}}\right)$$ (1)

where α is the degree of polarization, and Δv_eff is the effective linewidth [6], [7]. Though most of the studies analyzing noise in OCT systems use the above-mentioned formula to estimate the effects of RIN, it should be noted that (1) should be restricted to an optical source with purely spontaneous emission [7]–[9]

$$\text{RIN}=\left(\frac{\langle \mathrm{\Delta }{i}_{\text{th}}^2\rangle +\langle \mathrm{\Delta }{i}_{\text{sh}}^2\rangle +\langle \mathrm{\Delta }{i}_{\text{ex}}^2\rangle }{{\langle I\rangle }^2\mathrm{\Delta }f}\right)=\left(\frac{\mathrm{\Delta }{V}^2}{{\langle V\rangle }^2\mathrm{\Delta }f}\right)[{Hz}^{-1}].$$ (2)

By definition, RIN represents the total amount of photon noise per unit bandwidth and can be calculated using (2). However, several studies use the term RIN and excess photon noise interchangeably [4], [10] because typically the excess photon noise is the dominant signal-to-noise ratio (SNR) limiting factor at higher source powers. Hence, it is justifiable to make an approximation that RIN is equal to the excess photon noise in most cases.

III. Experimental Setup and Results

We perform RIN measurements at frequencies of 100 kHz, 500 kHz, and 10 MHz, corresponding to typical detection frequency bandwidth regimes for spectral-domain (SD-OCT), time-domain (TD-OCT), and swept-source (SS-OCT) OCT systems, respectively.

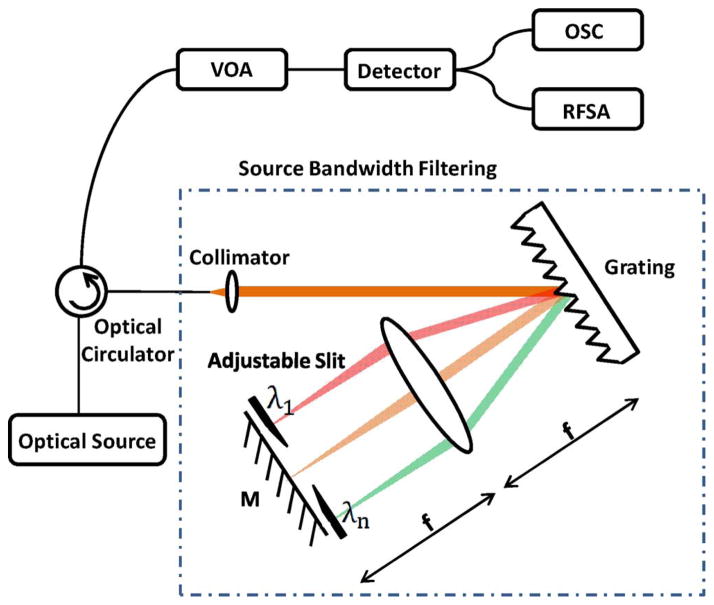
In our RIN measurement setup, attenuated light was incident on a low noise photodetector (New Focus 1817FC) and the detector output was monitored using a radio-frequency (RF) spectrum analyzer (HP 8561E) and oscilloscope (Fig. 1). An oscilloscope recorded the mean dc voltage level and corresponding mean square voltage fluctuation signals (in a 1-Hz bandwidth) were recorded with the RF spectrum analyzer. Optical source power was attenuated to keep the incident power constant, thus avoiding any saturation or nonlinear response from the photodetector. This setup was also used to produce a tunable linewidth output from a light source to study the dependence of RIN on the linewidth of the source. The light output from the light source can be spectrally filtered by using an optical circulator, diffraction grating (Richardson, 1000 g/mm), achromatic lens, mirror, and a slit with an adjustable width, as shown in Fig. 1. The filtered spectral output is then routed to port 3 of the circulator for optical detection.

Fig. 1.

RIN measurement setup. VOA: variable optical attenuator. OSC: oscilloscope. RFSA: RF spectrum analyzer.

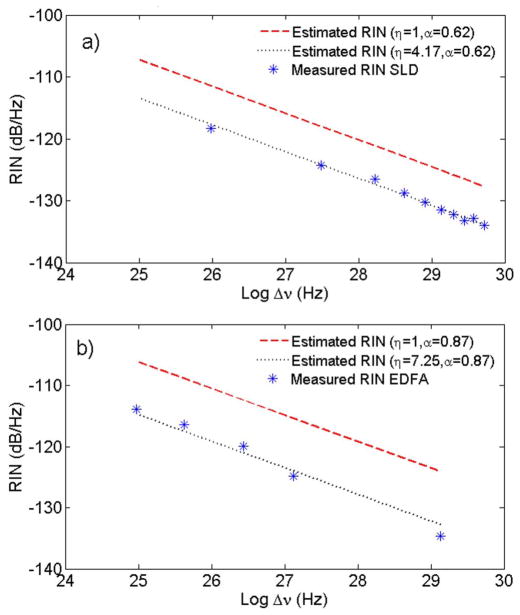
RIN measurements were obtained for an SLD (Covega Inc.) for linewidths ranging from 1.1 to 45.6 nm at the center wavelength of 1.3 μm. The degree of polarization was measured to be α = 0.62 for the SLD. Fig. 2 shows the experimental results along with the estimated results expected from (1) (α = 0.62). While it can be seen that RIN decreases linearly with an increase in linewidth, as (1), there is a constant offset of several decibels/hertz between the measured and expected RIN values. This is expected because the equation for estimating RIN is applicable to a purely spontaneous source, whereas in the amplified spontaneous emission (ASE) output from SLDs, there are contributions due to both spontaneous as well as stimulated photons from the gain-saturated part near the output facet of the diode [11]. We use a modified formula to describe the noise from an SLD as (1 + α²)/(ηΔv_eff); where we introduce a new empirical factor η, defined as the noise suppression factor. We can see that the expected RIN values fit very well with the experimental data when noise suppression factor of η = 4.17 is applied [Fig. 2(a)]. Next we used an EDFA as an alternative source of ASE to explore the dependence of noise on linewidth. RIN measurements were taken for linewidths ranging from 0.55 to 4.55 nm. As shown in Fig. 2(b), the RIN was again found to decrease linearly with an increase in linewidth, but with a different noise suppression factor (η = 7.25). We performed linewidth versus RIN measurements for two other SLD sources and the noise suppression factor (η) values were found to be 5.28 (Menlo Systems; α = 0.77) and 4.65 (Praevium Research, Inc.; α = 0.65), respectively. It is expected that the noise suppression factor (η) may vary from one source to another as different ASE-based sources would have different gain dynamics, waveguide structure, and properties [12].

Fig. 2.

(a) RIN versus linewidth for an SLD source (Covega Inc.) at 100 kHz. (b) RIN versus linewidth for an EDFA at 100 kHz.

In order to further analyze the effect of amplification on noise reduction, we performed another experiment in which attenuated ASE output from one SLD was fed to a semiconductor optical amplifier [(SOA) Covega Inc.], and the RIN of this amplified source was measured. The setup in Fig. 1 was used to produce a 10-nm linewidth output from the first SLD before it was amplified by the SOA. The linewidth of the output was measured to be the same, thereby ensuring that the process was simply the amplification of ASE without any spurious lasing effects. RIN values were measured at frequencies of 100 kHz, 500 kHz, and 10 MHz, as shown in Table I.

TABLE I.

Measured RIN From Amplified ASE

Measurement Frequency	100 kHz (dB/Hz)	500 kHz (dB/Hz)	10 MHz (dB/Hz)
SLD ASE	−122.89	−125.89	−127.59
Amplified ASE	−125.64	−132.54	−136.34

We can clearly see that the noise decreased by up to 9 dB due to the amplification process by using a gain-saturated SOA (driving current = 450 mA). The different amount of noise suppression at different frequencies could be attributed to a nonuniform frequency response of the SOA. However, the measurement is still in accordance with our conclusion that amplification of spontaneous emission could lead to reduced noise. With this configuration, we can easily achieve a lower noise for broadband OCT light sources by using a very basic and simplistic design. This result may have an impact towards making practical and low-noise SLD-based sources for applications in OCT.

To further confirm our findings, we also measured the RIN from a CW fiber ring cavity laser with an SOA as the gain medium. This laser is similar to those used in SS-OCT. However, we operated it in the static mode to measure the RIN for a fixed wavelength band. We measured the RIN to be −142.43 dB/Hz (at 100 kHz), −144.07 dB/Hz (at 500 kHz), and −146.10 dB/Hz (at 10 MHz) for a laser linewidth of 2.6 nm. ASE output from an SLD exhibited an RIN of ~ −120 dB/Hz for the same linewidth. The difference in RIN of more than 20 dB/Hz between the ASE light and stimulated light confirmed our assumption that ASE noise can be reduced by amplification using a gain-saturated SOA.

Multiplexing two or more SLDs to achieve a broader linewidth is a cost-effective method to achieve ultrahigh resolution in OCT imaging [13]. However, its effect on overall spectral stability and noise has not been thoroughly investigated. Table II shows the measured and estimated values of RIN for two individual SLDs (Praevium Research, Inc.) and their combined output. RIN is measured at a frequency of 100 kHz. Previously estimated values for the correction factor and the degree of polarizability were used to calculate the estimated RIN values. It should be noted that the linewidth of a multiplexed SLD system is not simply the summation of linewidths from SLD (A) and SLD (B), as the spectrum is modified due to spectral overlap. We conclude that there is no significant adverse effect on noise levels as a result of multiplexing light outputs from two SLDs.

TABLE II.

Measured RIN From Multiplexed SLDs

	Δλ (nm)	Estimated RIN (dB/Hz)	Measured RIN (dB/Hz)
SLD (A)	80	−140.93	−140.94
SLD (B)	82	−140.41	−141.03
SLD (A+B)	146	−143.32	−141.43

IV. Conclusion

We performed quantitative estimation of RIN in various broadband sources used in OCT. We demonstrated that the existing theory for estimating the RIN of an optical source cannot be applied uniformly to all types of broadband OCT sources. We proposed a corrected formula to estimate excess photon noise by introducing a source-specific noise suppression factor (η). We also demonstrated a design using a cascaded SLD-based source to amplify ASE and obtain light output with much lower noise levels. These quantitative experimental results will help to provide a better understanding of the RIN and its effects on degradation of OCT system sensitivity, and subsequently, aid in designing optimized systems.