Abstract
The buckling and wrinkling of thin films has recently seen a surge of interest among physicists, biologists, mathematicians, and engineers. This activity has been triggered by the growing interest in developing technologies at ever-decreasing scales and the resulting necessity to control the mechanics of tiny structures, as well as by the realization that morphogenetic processes, such as the tissue-shaping instabilities occurring in animal epithelia or plant leaves, often emerge from mechanical instabilities of cell sheets. Although the most basic buckling instability of uniaxially compressed plates was understood by Euler more than two centuries ago, recent experiments on nanometrically thin (ultrathin) films have shown significant deviations from predictions of standard buckling theory. Motivated by this puzzle, we introduce here a theoretical model that allows for a systematic analysis of wrinkling in sheets far from their instability threshold. We focus on the simplest extension of Euler buckling that exhibits wrinkles of finite length—a sheet under axisymmetric tensile loads. The first study of this geometry, which is attributed to Lamé, allows us to construct a phase diagram that demonstrates the dramatic variation of wrinkling patterns from near-threshold to far-from-threshold conditions. Theoretical arguments and comparison to experiments show that the thinner the sheet is, the smaller is the compressive load above which the far-from-threshold regime emerges. This observation emphasizes the relevance of our analysis for nanomechanics applications.
Keywords: pattern formation, thin-film buckling
Thin films are among the ubiquitous examples of flexible structures that buckle under compressive loads. More interestingly, these buckling instabilities usually develop into wrinkled patterns that provide a dramatic display of the applied stress field (1, 2). Wrinkles align perpendicularly to the compression direction, depicting the principal lines of stress and providing a geometric tool for mechanical characterization. Traditional buckling theory is regularly used to understand these patterns in the near-threshold (NT) regime, in which the deformations are small perturbations of the initial flat state. However, it has been known since Wagner (3, 4) that, when the exerted loads are well in excess of those necessary to initiate buckling, the asymptotic state of the plate is very different from the one observed under NT conditions. In this far-from-threshold (FFT) regime, the stress nearly vanishes in the compression direction and wrinkles mark the region where the compressive stress has collapsed.
Two complementary approaches have provided some insight into wrinkled sheets under FFT loading conditions. In a 1961 paper (5), Stein and Hedgepeth computed the asymptotic stress field in infinitely thin sheets under compression by assuming a vanishing component of the stress tensor along the compression direction. They further showed how such an asymptotic stress field yields the extent of wrinkles in several basic examples. A similar formalism that builds on the same assumption was advanced later by Pipkin (6). This approach (often referred to as “tension field” or “relaxed energy” theory) correctly characterizes the stress distribution and the corresponding extent of the wrinkled region, but cannot identify the fine features of the pattern, such as the wavelength (or number) of wrinkles, their amplitude, and the sensitivity to various boundary conditions (BCs). A second approach, which does address the wavelength of wrinkled sheets in the FFT regime, has been introduced recently by Cerda et al. (7, 8), who studied a long rectangular strip under strong uniaxial tension T. Using the simplicity of the stress tensor in this geometry (where the dominant stress component is approximately T everywhere) and assuming a balance of bending, compressive, and tensile forces, these authors derived an asymptotic scaling law for the FFT wavelength and amplitude of wrinkles. Although this idea has been very successful in characterizing the asymptotic wrinkling pattern of tensed rectangular sheets, its implementation in situations characterized by a spatially varying stress distribution, with a wrinkled state spanning a finite region, remains obscure.
The lack of a theoretical setup that enables a quantitative distinction between wrinkling patterns in the NT and FFT regimes has led to confusion in interpreting experimental observations. For instance, the length and number of wrinkles in nanofilms have been measured in ref. 9 with high accuracy, suggesting that these features could be used as an effective indicator for metrology. In another experiment (10), the onset of wrinkling was identified by slowly increasing the exerted loads or modifying the setup geometry. These and other experiments have shown various scaling laws for the length and number of wrinkles. However, it is unclear how many independent parameters control wrinkling in these systems, what is the structure of the “morphological phase space” spanned by these parameters, and consequently, whether the observed wrinkling patterns reflect NT or FFT conditions.
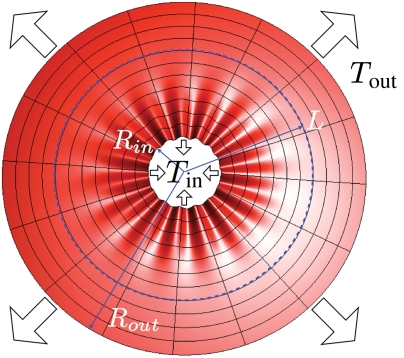
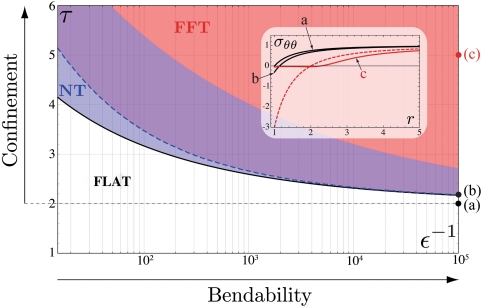
In this paper, we present an FFT theory of wrinkling in very thin sheets that connects the tension field theory (5, 6) to the study of the wrinkle wavelength (7, 8). The essence of our theory is an expansion of the Föppl–von Kármán (FvK) equations around the singular limit of a sheet with vanishing bending modulus (the so-called membrane limit; ref. 4). We show that the extent of the wrinkled region (5) comes from the leading order of that expansion, whereas the wavelength and amplitude of wrinkles (7, 8) result from the subleading order. Furthermore, through a quantitative analysis of the FvK equations, our approach enables a clear identification of the NT and FFT regimes of wrinkling patterns and exposes the subtleties in interpretation of experimental observations. In order to elucidate the basic principles of the theory, we focus on a model problem of fundamental interest: a very thin annular sheet under planar axisymmetric loading (Fig. 1). This system, which was apparently first studied by Lamé (11), possesses the highest possible symmetry of a 2D sheet. The instability of such a sheet, which leads to wrinkles of finite extent, may therefore be considered as the simplest extension of Euler’s instability (which describes sheets confined in a 1D geometry). Our main findings are summarized in Fig. 2, which presents a schematic phase diagram of wrinkling patterns, ranging from NT to FFT conditions.
Fig. 1.
The Lamé configuration: A mismatch between the inner and outer stresses yields a compression, which is relieved by wrinkling, in the region Rin < r < L.
Fig. 2.
A schematic phase diagram of wrinkling patterns in the Lamé geometry. The dimensionless parameters ϵ-1, τ represent, respectively, bendability and confinement (see Eq. 8). Radial wrinkles emerge for ϵ, τ > τc(ϵ), where the threshold curve τc(ϵ), computed similarly to ref. 15, is marked with a black solid line. The NT analysis is valid below the blue dashed line (see text). After a cross-over region (purple), the sheet is under FFT conditions (red). The evolution of the hoop stress as τ increases is shown in the inset for ϵ-1 = 105 using three curves corresponding to points in the (ϵ,τ) phase space indicated in the main figure. Curves a and b show the stress profile as predicted by Eq. 6. However, curve c, which is well within the FFT region, shows that the hoop stress has collapsed in a manner compatible with Eq. 17. To emphasize the collapse of compressive stress, the red dashed line in the inset shows the hoop stress given by Eq. 6 for the same value of τ.
We commence by reviewing the classical Lamé solution for the planar state of stretched axisymmetric sheets, and define the bendability and confinement parameters: ϵ and τ, respectively. Focusing on the high bendability limit (ϵ ≪ 1), we show how the Lamé solution gives rise to scaling laws for the threshold confinement τc(ϵ), at which wrinkling first occurs, and for the extent and number of wrinkles in the NT regime. We then turn to the FFT regime and introduce the “collapsed compressive stress” assumption that yields the asymptotic FFT stress field. We show how the resulting stress field leads to scaling laws for the extent and number of wrinkles, which are markedly different from the NT behavior. In Discussion, we describe the general structure of the (ϵ,τ) phase diagram predicted by our results and address the subtleties of the FvK equations in the FFT regime. We emphasize insights provided by our model, explain experimental observations, and conclude with open questions and future directions.
Near-Threshold Wrinkling
We study the essential differences between the NT and FFT regimes by focusing on the configuration shown in Fig. 1, where an annular film of inner radius Rin and outer radius Rout is stretched differentially by radial forces per unit length Tout at r = Rout and Tin > Tout at r = Rin. Similar geometries have been used to study wrinkling under different types of central loads, such as the impact of fast projectiles (12), the de-adhesion and wrinkling of a thin sheet loaded at a point (13), and the wrinkling and folding of floating membranes (9, 14). However, Fig. 1 exhibits the simplest load distribution that leads to wrinkling with finite extent and wavelength.
The Planar State.
The equilibrium force balance equations are as follows:
| [1] |
| [2] |
The stresses are connected to the radial, hoop, and shear strains by Hooke’s law εij = [(1 + ν)σij - νσkkδij]/Y. Here, Y = Et is the stretching modulus, E is the Young’s modulus, t is the film thickness, and ν is the Poisson ratio. The expressions for the strains in the large deflection, small slope limit (4) are
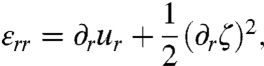 |
[3] |
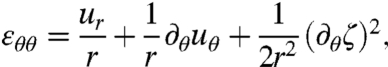 |
[4] |
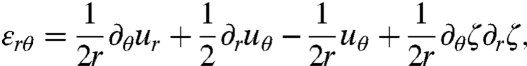 |
[5] |
where ur, uθ, and ζ are, respectively, the radial, azimuthal, and out-of-plane displacements. We included here the shear components, although they will not be required for our analysis. It is a classical problem of linear elasticity (11) to obtain the stress field of the planar, axisymmetric state: uθ = ζ = ∂θur = 0, where εrr = ∂rur, εθθ = ur/r, and εrθ = 0. Focusing for simplicity on the limit Rout≫Rin, one finds
| [6] |
where ΔT = Tin - Tout. In this solution (due to Lamé), the radial stress is tensile everywhere, but if Tin/Tout > 2, the hoop stress becomes compressive for Rin < r < LNT, where
| [7] |
The existence of compression leads to buckling if the film is thin enough that it becomes energetically favorable to relieve the compressive stress by bending. The Lamé problem is thus characterized by two independent dimensionless groups, confinement (τ) and bendability (ϵ-1), where
| [8] |
where B = Et3/12(1 - ν2) is the bending modulus. For a given ϵ, buckling is expected if τ > τc(ϵ) > 2, where τc(ϵ) is the critical loads ratio. As the sheet gets thinner, the energetic cost of bending becomes smaller, hence we expect τc(ϵ) → 2 as ϵ → 0 (see Fig. 2).* Our prime interest is in the high bendability regime, ϵ ≪ 1, that describes very thin sheets. For a given ϵ ≪ 1, we first consider the NT regime, assuming a loads ratio τ sufficiently close to τc(ϵ).†
Threshold, Extent, and Number of Wrinkles.
Standard buckling theory in the NT regime consists of a stability analysis of the first FvK equation (4):
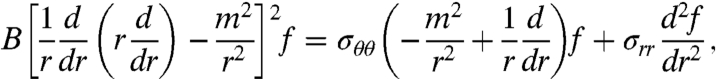 |
[9] |
where the out-of-plane displacement is assumed to be ζ = f(r) cos(mθ), and σrr, σθθ assume their Lamé form [6]. Whereas the energy and wrinkled extent in the NT regime are determined by Eqs. 6 and 7, bifurcation analysis [assuming f(r) is infinitesimal†] yields the value of τc(ϵ) and the number of wrinkles mc(ϵ) of the emerging pattern (15, 16).
Focusing on the high bendability regime (ϵ ≪ 1), a force balance argument yields the NT scaling of τc(ϵ) and mc(ϵ). The forces in Eq. 9 are estimated by using the Lamé solution [6] to approximate the stress in the NT regime: σrr ≈ 2Tout, 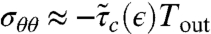 , where we employed the fact that
, where we employed the fact that 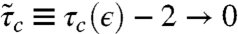 in this limit.† Furthermore, the characteristic (radial) scale over which the amplitude f(r) varies is
in this limit.† Furthermore, the characteristic (radial) scale over which the amplitude f(r) varies is 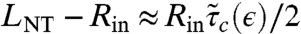 (see Eq. 7). These relations allow us to estimate by inspection the different terms in Eq. 9, thus finding that the three dominant forces are associated with azimuthal bending (
(see Eq. 7). These relations allow us to estimate by inspection the different terms in Eq. 9, thus finding that the three dominant forces are associated with azimuthal bending (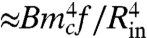 ), azimuthal compression (
), azimuthal compression (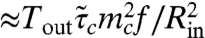 ), and radial tension (
), and radial tension (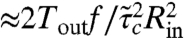 ). Balancing these forces yields the NT scalings:
). Balancing these forces yields the NT scalings:
| [10] |
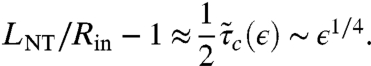 |
[11] |
These scaling relations were obtained in ref. 15 by using numerical and asymptotic analysis (15), but to our knowledge the above force balance argument has not been noted before.‡
Far-From-Threshold Wrinkling
Let us turn now to the main focus of our paper: the FFT regime for very thin sheets (ϵ ≪ 1). Expecting the NT behavior to characterize a zone in the parameter space (ϵ,τ) above the curve τc(ϵ) (see Fig. 2), we assume a fixed value of τ sufficiently above this strip and consider the asymptotic process ϵ → 0, keeping τ fixed.* We will start by finding the asymptotic FFT stress field, and then show how this stress leads to predictions for the extent LFFT and number mFFT of wrinkles in this regime.
The Asymptotic Stress Field.
Motivated by experiments (9, 10) and following the formalism developed in refs. 3, 5, and 6, we assume that the sheet is composed of two parts: a wrinkled region in Rin < r < L with collapsed hoop and shear stresses σθθ, σrθ → 0, and an outer annulus L < r < Rout in which the sheet remains planar with stresses following the Lamé form [6] appropriately modified. We shall prove that for ϵ ≪ 1, a state with L > Rin is energetically favorable compared to the Lamé state, which corresponds to L = Rin. Thus, wrinkling appears as a mechanism for releasing elastic energy in the film. For Rin < r < L, Eq. 1 and Hooke’s law yield
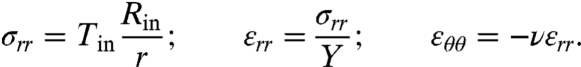 |
[12] |
Continuity of the radial stress shows that the stresses in the outer annulus have the Lamé form [6] with Rin → L and ΔT → ΔT(L) = TinRin/L - Tout. For a given wrinkle extent L, the FFT stresses are now fully characterized by Eqs. 6 and 12. Moreover, the radial displacement ur(L) must also be continuous, and because the Lamé solution at r≥L implies a link between ur(L) and σrr(L), one obtains for r < L,
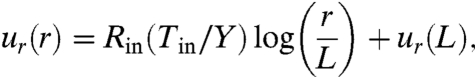 |
[13] |
with ur(L) = [2L(Tout/Y) - (1 + ν)Rin(Tin/Y)]. The wrinkle extent will be determined by minimizing the energy over L.
Before turning to energy calculations, let us highlight some important aspects of the FFT solution. First, as Eq. 12 indicates, there is pure traction along the radial direction, producing a Poisson effect εθθ = -νεrr < 0 in the azimuthal direction and reducing the perimeter at radius r by a total length -2πrνTin/Y. This local contraction shows that, for ν ≠ 0, the film is not inextensible in the azimuthal direction as was assumed in refs. 7 and 8. However, a similar constraint arises: There is an excess in length when this contraction is not compatible with the geometrical shortening of the perimeter length 2πur(r) that is generated by the inwardly radial displacement ur < 0. In order to reduce stretching energy, this excess of length is relieved by out-of-plane displacement that is highly oscillatory in the azimuthal direction. Using the strain-displacement relations, [3] and [4], and the relation εθθ = -νεrr, we obtain
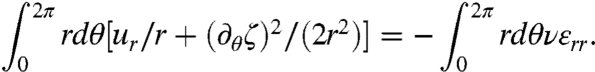 |
[14] |
Assuming again that ζ = f(r) cos(mθ),§ one finds
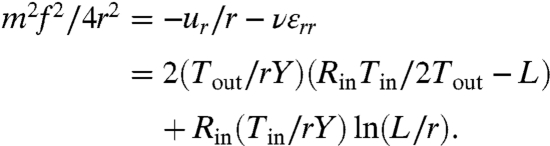 |
[15] |
The positivity of the left-hand side of Eq. 15 shows that wrinkling is possible only if there is an excess of length of the circle perimeter. An analysis of the right-hand side of Eq. 15 shows that wrinkling is possible for Rin < r < L only if L ≤ RinTin/2Tout, thus providing an upper bound for the wrinkled extent.
Finally, let us make two related observations. First, Eq. 15 indicates that the product mf(r) remains finite in the FFT limit, in contrast to the NT regime where f(r) is infinitesimal. Second, Eqs. 4, 12, and 13 imply that the azimuthal variations of the displacement (∂θuθ) are also finite in the FFT limit.¶ These observations underlie the difference between the singular FFT analysis and the NT behavior, which reflects a regular expansion around a planar, axisymmetric state. Indeed, our FFT analysis is based on an asymptotic series in which the expansion parameter is ϵ, in contrast to the NT regime, where the small parameter is the wrinkle amplitude [or equivalently, the distance to threshold τ - τc(ϵ)].
The Extent Of Wrinkles.
In order to determine the wrinkled extent L, we compute the elastic energy 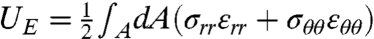 of the FFT stress field. A straightforward calculation using Eqs. 6 and 12 yields to
of the FFT stress field. A straightforward calculation using Eqs. 6 and 12 yields to  :
:
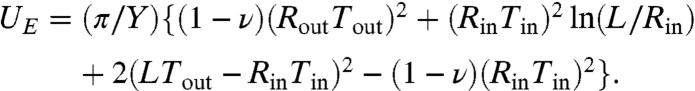 |
[16] |
Note that this energy does not include the costs of bending and out-of-plane stretching of the sheet. We will show below that, in the FFT limit, these are higher-order contributions in ϵ but are nevertheless crucial for obtaining the number of wrinkles m. Because our problem involves constant applied forces at r = Rin, Rout, we must minimize the mechanical energy U = UE - W, where W = 2π[ToutRoutur(Rout) - TinRinur(Rin)] is the exerted work. Minimizing U as a function of wrinkle extent is analogous to fracture mechanics problems, in which the mechanical energy is minimized as a function of crack length under constant load conditions (17). Like cracks, wrinkles provide a route for the release of elastic energy. Using a general result from elasticity theory for bodies under constant external loads (17), we find that W = 2UE, and hence U = -UE. In order to minimize U, we note that its first derivative ∂LU = -π(2LTout - RinTin)2/(YL) ≤ 0 is zero for
| [17] |
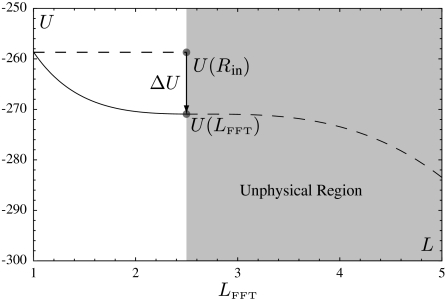
Interestingly, this result coincides with the upper bound implied by the positivity of [15] and also ensures continuity of the hoop stress at r = LFFT. Thus, energy minimization naturally yields a value for the stress at the tip of the wrinkles that smoothly matches the flat region in the film to the wrinkled one. Fig. 3 shows that Eq. 17 corresponds to an inflection point of U, but the upper bound found above guarantees that Eq. 17 provides the actual length in the FFT limit. Fig. 3 also indicates that, in the FFT limit, the energy at the inflection point U(LFFT) is lower than the Lamé value U(Rin). Thus, for τ > 2 and sufficiently small ϵ, there is indeed an energy gain in the FFT regime, with respect to the planar state (Lamé value). Eq. 17 is one of the central results of our analysis. It reflects a linear scaling of the extent of the wrinkles in the FFT regime with the ratio Tin/Tout, in sharp contrast to the square-root scaling that characterizes the NT limit, Eq. 7.
Fig. 3.
The mechanical energy U in the FFT limit (normalized by 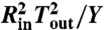 ) as a function of the wrinkle extent L (normalized by Rin) for τ = 5, Rout = 10Rin, and ν = 1/3. An inflection point exists at LFFT = τ/2 = 2.5. ΔU is the energy gain for ϵ → 0 of the FFT energy (inflection point) with respect to the planar, Lamé solution (upper dashed line).
) as a function of the wrinkle extent L (normalized by Rin) for τ = 5, Rout = 10Rin, and ν = 1/3. An inflection point exists at LFFT = τ/2 = 2.5. ΔU is the energy gain for ϵ → 0 of the FFT energy (inflection point) with respect to the planar, Lamé solution (upper dashed line).
Number of Wrinkles.
As noted already, our FFT theory amounts to an asymptotic expansion of the FvK equations around the “membrane limit.” We determined above the wrinkle extent from the leading order in this expansion, whose energetic contribution [16] does not depend on ϵ. This leading order is insensitive, however, to the fine features of the pattern, most importantly the number of wrinkles. In order to determine the number of wrinkles, we turn now to the next (subdominant) order in the expansion, whose energetic contribution will be shown to scale as 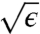 .
.
Whereas Eq. 15 reveals that the product mf(r) must remain finite, we expect |f| to become smaller and hence m to diverge as ϵ → 0,* which agrees with experimental observations (7–9). It is also correlated with the fact (similar to the NT regime) that the out-of-plane forces dominating the first FvK Eq. 9 in the FFT regime are azimuthal bending (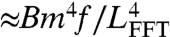 ), azimuthal compression (
), azimuthal compression (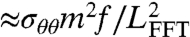 ), and radial stretching (
), and radial stretching (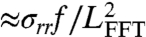 , with σrr given by [12]). Notice that, in contrast to the NT analysis, the FFT force estimates assume the limit ϵ → 0 while keeping the loads ratio τ at a fixed value (and hence, by Eq. 17, fixing LFFT/Rin), and allowing the value of σθθ to vary. Balance of these three forces implies the hoop stress scaling
, with σrr given by [12]). Notice that, in contrast to the NT analysis, the FFT force estimates assume the limit ϵ → 0 while keeping the loads ratio τ at a fixed value (and hence, by Eq. 17, fixing LFFT/Rin), and allowing the value of σθθ to vary. Balance of these three forces implies the hoop stress scaling 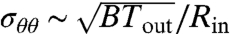 . This result can be expressed as σθθ/Tout ∼ ϵ1/2, whereas the NT result, Eq. 10, yields σθθ/Tout ∼ ϵ1/4. Both scalings show that, for small ϵ, small compressive loads are sufficient to buckle the film. More interestingly, they express the essence of the transition from NT to FFT conditions: a rapid collapse of the compressive stress as the loads ratio is increased beyond threshold (for a fixed, small ϵ). The same force balance implies the FFT scaling of the number of wrinkles:
. This result can be expressed as σθθ/Tout ∼ ϵ1/2, whereas the NT result, Eq. 10, yields σθθ/Tout ∼ ϵ1/4. Both scalings show that, for small ϵ, small compressive loads are sufficient to buckle the film. More interestingly, they express the essence of the transition from NT to FFT conditions: a rapid collapse of the compressive stress as the loads ratio is increased beyond threshold (for a fixed, small ϵ). The same force balance implies the FFT scaling of the number of wrinkles:
| [18] |
for some k(τ), in sharp contrast to the NT scaling [10]. This scaling has already been predicted in refs. 7 and 8 and is supported by experiments on ultrathin sheets, where ϵ is estimated to be below 10-6 (9). Computing the value of the prefactor k(τ) introduces complexities that will be explained later on.
Discussion
The Phase Space Structure.
Focusing on highly bendable sheets (ϵ ≪ 1), our analysis of the NT and FFT regimes yields the schematic phase diagram, Fig. 2. Once the external loads induce sufficient compressive hoop stress, a wrinkled shape will emerge. Here the threshold line was obtained from a linear analysis similar to ref. 15 (albeit with a free edge BC at r = Rin to eliminate a spurious boundary layer near r = Rin).
The stress field and pattern features must change markedly as the loads ratio τ is increased above threshold. Most importantly, the compressive hoop stress decreases [from O(ϵ1/4) to O(ϵ1/2)], the extent of wrinkles increases [from O(ϵ1/4Rin) to Rinτ/2], and the number of wrinkles decreases [from O(ϵ-3/8) to O(ϵ-1/4)]. It is interesting that this rather nontrivial (and arguably, nonintuitive) behavior follows directly from the force balance (FvK) equations for thin sheets supplemented by two rather intuitive assumptions. First, we assume the collapse of the compressive stress in the FFT regime. Second, we assume that the normal force balance (first FvK equation) in highly bendable sheets is dominated by three forces: bending and compression in the azimuthal (transverse to wrinkles) direction and stretching in the radial (along wrinkles) direction. This balance, which explicitly requires the shape to be curved in both spatial directions (and hence precludes translation invariance), underlies the morphological complexity of the planar, axisymmetric Lamé problem, a complexity that is absent in the simpler classical Euler buckling of a sheet confined in 1D geometry.
The existence of clearly distinguished NT and FFT patterns prompts a very practical question: How large is the NT regime that is described by traditional postbuckling theory? Specifically, consider a sheet with fixed thickness, geometry, and external load (hence fixed ϵ) and assume the loads ratio τ is increased above the threshold value τc(ϵ). We ask two related but distinct questions: First, at what value of τ should we expect to observe significant deviations from the NT behavior (Eqs. 10 and 11)? Second, at what value of τ should we begin to observe features of the FFT pattern (Eqs. 17 and 18)? The first question can be addressed through a perturbation theory (in the amplitude |f|) by estimating the characteristic value of τ, where the perturbed stress values become comparable to the prebuckled Lamé stresses (Eq. 6). We find that the width of the NT region shrinks at a rate that scales as ϵ1/2 (dashed blue curve in Fig. 2). The second question is more subtle. Our asymptotic analysis of the FFT regime, which considers the limit ϵ → 0 for a fixed value τ > 2, shows that FFT behavior is expected to emerge above a cross-over regime whose size shrinks with ϵ (the purple region in Fig. 2). However, our analysis is insufficient to predict the actual size of the cross-over zone, nor can it reveal the exact nature of the NT–FFT transition. The above discussion motivates the search for a nonlinear model that will simplify the full FvK equations and will capture the behavior of wrinkling patterns for all values of ϵ and τ > τc(ϵ). The predicted narrowing of the NT regime (and transition to FFT) for ϵ ≪ 1, indicates that experiments would need to be constructed extremely carefully in order to observe the NT regime for highly bendable sheets.
FFT Analysis of the FvK Equations.
Whereas the NT analysis amounts to a regular perturbation around the planar state (15, 16), our FFT analysis introduces an expansion of the FvK equations around the singular membrane limit ϵ = 0. The singular nature of the FFT expansion is further clarified by considering the energy. The leading energy U ∼ (RinTout)2/Y, Eq. 16, approaches a (τ-dependent) value that is independent of ϵ and determines the extent of wrinkles but does not involve their number. By contrast, the subleading energy involves terms such as the bending energy 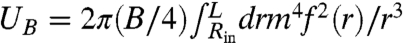 which scale as ϵ1/2U and hence vanish as ϵ → 0.* However, despite its apparent negligibility, the subdominant energy involves m, and hence it selects the number of wrinkles. In this respect, our FFT theory joins two apparently distinct ideas: the approach of refs. 4–6, which yields the asymptotic stress field with collapsed compressive stress and consequently the extent of the wrinkles [17], and the approach of refs. 7 and 8, which yields the asymptotic scaling of the number of wrinkles [18]. Our asymptotic expansion of the FvK equations, which considers the high bendability limit ϵ → 0 for a fixed τ > τc(ϵ), shows that these two approaches are complementary: The first results from the leading order, whereas the second emanates from the next (subleading) order of the expansion. The unusual link between the leading and subleading orders is manifested in Eq. 15, which expresses a constraint on fine features of the pattern [i.e., the product mf(r)] imposed by the FFT stress field. One should notice that phenomena, in which macroscale features are dominated by a leading energy and fine features are governed by a subleading energy, are not unique to elastic sheets. A representative example is the domain structure in the intermediate state of a type-I superconductor (18).
which scale as ϵ1/2U and hence vanish as ϵ → 0.* However, despite its apparent negligibility, the subdominant energy involves m, and hence it selects the number of wrinkles. In this respect, our FFT theory joins two apparently distinct ideas: the approach of refs. 4–6, which yields the asymptotic stress field with collapsed compressive stress and consequently the extent of the wrinkles [17], and the approach of refs. 7 and 8, which yields the asymptotic scaling of the number of wrinkles [18]. Our asymptotic expansion of the FvK equations, which considers the high bendability limit ϵ → 0 for a fixed τ > τc(ϵ), shows that these two approaches are complementary: The first results from the leading order, whereas the second emanates from the next (subleading) order of the expansion. The unusual link between the leading and subleading orders is manifested in Eq. 15, which expresses a constraint on fine features of the pattern [i.e., the product mf(r)] imposed by the FFT stress field. One should notice that phenomena, in which macroscale features are dominated by a leading energy and fine features are governed by a subleading energy, are not unique to elastic sheets. A representative example is the domain structure in the intermediate state of a type-I superconductor (18).
An important consequence of the above discussion pertains to the robustness of patterns in the FFT regime. The small ratio ϵ1/2 between the subleading and leading energies suggests that the wrinkle extent is more robust than the wavelength. This property is manifested when studying the effect of clamped BCs [f(r = Rin) = 0] on the wrinkling pattern.§ Although the dominant energy and hence the extent of wrinkles, Eq. 17, are indifferent to this effect, similar arguments to those underlying Eq. 18 show that a smooth (tension-dominated) wrinkling cascade that emerges near the clamped edge (19) may strongly modify the prefactor k(τ) in Eq. 18.
Another manifestation of the subtlety of our FFT expansion is found when attempting to compute the prefactor k(τ) in the scaling law [18]. To this end (regardless of the assumed BCs at r = Rin), we must use Eqs. 12, 13, and 15 to compute the bending energy UB and the out-of-plane stretching energy 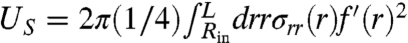 as functions of m, and determine m as the minimizer of these subdominant energies. We find, however, a divergence of f′(r) and US as L → LFFT for all m. Initially, this observation can raise doubts to the validity of our theory. However, careful consideration reveals the source of this divergence: Our matching conditions at r = L assume a direct transition from the planar state at r > L to the collapsed compressive stress region at r < L. The divergence of US can be remedied if the unphysical “pointwise” matching is replaced by a smooth matching of the two regions. The subtle aspects of our analytic approach emphasize once more the necessity of developing model equations that will enable effective and accurate numerical study of wrinkling patterns in the whole (ϵ,τ) phase space.
as functions of m, and determine m as the minimizer of these subdominant energies. We find, however, a divergence of f′(r) and US as L → LFFT for all m. Initially, this observation can raise doubts to the validity of our theory. However, careful consideration reveals the source of this divergence: Our matching conditions at r = L assume a direct transition from the planar state at r > L to the collapsed compressive stress region at r < L. The divergence of US can be remedied if the unphysical “pointwise” matching is replaced by a smooth matching of the two regions. The subtle aspects of our analytic approach emphasize once more the necessity of developing model equations that will enable effective and accurate numerical study of wrinkling patterns in the whole (ϵ,τ) phase space.
Comparison to Previous Experiments.
There are many papers that describe wrinkling phenomena under various geometries and load configurations. The distinction we have drawn here between wrinkling in the NT and FFT regimes is crucial for obtaining a proper understanding of these experiments. We restrict the following discussion to two papers that address thin sheets in configurations similar to the Lamé geometry.
In the experiments of ref. 9, a very thin circular sheet (t ranging from 30–300 nm) floats on water and hence is subject to a surface tension Tout = γ at its perimeter r = Rout. A liquid drop is placed at the center, deforming the sheet beneath it, and exerting an in-plane tensile force Tin at the contact line r = Rin. The problem is thus analogous to the Lamé problem, but determining Tin is a subtle problem that has not yet been fully resolved (20). Typical values of ϵ are less then 10-6, and hence our high bendability analysis seems relevant. The number of wrinkles (figure 2 of ref. 9) shows excellent agreement with the FFT scaling [18], indicating that the experiment corresponds to FFT conditions and that the prefactor k(τ) in Eq. 18 is nearly constant within the range of loads ratios studied. Because Tin is unknown, our result [17] cannot be directly compared to the experiments of ref. 9. Nevertheless, it does resolve a puzzle raised by their empirical observation that the length of wrinkles is approximately 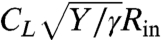 , with CL a numerical constant. The authors of ref. 9 assumed the NT scaling, Eq. 7, and concluded that their results indicate that Tin is “independent of surface tension, which is implausible.” However, the FFT scaling, Eq. 17, shows that the empirical law is consistent with
, with CL a numerical constant. The authors of ref. 9 assumed the NT scaling, Eq. 7, and concluded that their results indicate that Tin is “independent of surface tension, which is implausible.” However, the FFT scaling, Eq. 17, shows that the empirical law is consistent with 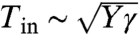 , suggesting instead that the in-plane tension exerted by the drop at the contact line is affected “equally” by the surface tension and the stretching modulus.
, suggesting instead that the in-plane tension exerted by the drop at the contact line is affected “equally” by the surface tension and the stretching modulus.
In contrast to ref. 9, the Lamé geometry was studied in ref. 10 by mechanically stretching an annular sheet in an axisymmetric fashion.∥ We find that the parameter values reported in ref. 10 correspond to a small characteristic value of ϵ ≲ 10-3, but note that the studied range of log(ϵ) is significantly narrower than in ref. 9, and therefore comparison to the predicted scaling laws is less conclusive. Let us discuss first figure 8 of ref. 10, which provides a striking insight into a subtle aspect of wrinkling patterns. The pattern amplitude is plotted there as a function of the control parameter δi (which is proportional to τ¶) and exhibits a square-root dependence, 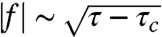 , which is a universal feature of patterns in the NT regime†. However, analysis of our Eq. 15 for L = LFFT and small values of τ - 2 shows that, surprisingly, the same square-root dependence characterizes the FFT regime. Thus, although the stress distribution, as well as the extent and number of wrinkles strongly vary between the NT and FFT regimes, the pattern amplitude does not disclose this dramatic change. Another central result of ref. 10 is presented in their figure 7, where the number of wrinkles m is shown to scale linearly with Rin, in apparent contradiction with both the NT (m ∼ ϵ-3/8, [11]) and the FFT (m ∼ ϵ-1/4, [18]) scalings. However, replotting the data on a log–log scale, we find the relation m ∼ ϵ-c, where c ranges from 0.25 to 0.4. This large uncertainty does not allow a clear distinction between NT and FFT behaviors, and it emphasizes the necessity of a large interval of log(ϵ) values for analyzing wrinkling patterns in thin sheets.
, which is a universal feature of patterns in the NT regime†. However, analysis of our Eq. 15 for L = LFFT and small values of τ - 2 shows that, surprisingly, the same square-root dependence characterizes the FFT regime. Thus, although the stress distribution, as well as the extent and number of wrinkles strongly vary between the NT and FFT regimes, the pattern amplitude does not disclose this dramatic change. Another central result of ref. 10 is presented in their figure 7, where the number of wrinkles m is shown to scale linearly with Rin, in apparent contradiction with both the NT (m ∼ ϵ-3/8, [11]) and the FFT (m ∼ ϵ-1/4, [18]) scalings. However, replotting the data on a log–log scale, we find the relation m ∼ ϵ-c, where c ranges from 0.25 to 0.4. This large uncertainty does not allow a clear distinction between NT and FFT behaviors, and it emphasizes the necessity of a large interval of log(ϵ) values for analyzing wrinkling patterns in thin sheets.
Conclusions
Our paper carries two central messages: First, wrinkles in very thin sheets may appear as two distinct types of patterns, near-threshold and far-from-threshold. In each of these regimes, different asymptotic relations characterize the morphology and stress field. Second, whereas the NT regime can be described with the standard postbuckling approach, analysis of the FFT regime requires a nonstandard perturbation theory around the singular membrane limit. This analysis makes direct use of the collapse of compressive stress in this limit. Our FFT theory unifies the stress field analysis of ref. 5 and the scaling ideas of refs. 7 and 8. We have demonstrated the FFT theory for the Lamé problem—a sheet of axisymmetric geometry and loads, which is the simplest extension of the classical Euler buckling of sheets confined in a 1D geometry. Our analysis makes use of the high degree of symmetry of the Lamé problem, which implies dependence of the patterns on two dimensionless parameters (ϵ,τ) only. Nevertheless, we anticipate that the method introduced here will lead to insights on wrinkling phenomena in setups with a lower level of symmetry (for instance, the indentation experiments of ref. 14).
Our analysis substantiates the analogy discovered by Mansfield between crumpling and wrinkling (4, 21). Similar to our wrinkling pattern, the macroscale features of a crumpled shape are determined by minimizing a dominant energy (22). However, although the dominant energy of a wrinkling pattern consists of stretching [Eq. 16], a crumpling pattern is dominated by a bending energy, whose minimization leads to a stress-focusing shape: line or point singularities that connect strainless regions. Furthermore, in both cases, the subdominant energies consist of a mixture of stretching and bending terms that determine small-scale features of the pattern: wavelength (wrinkling) and the size of stress-focusing zones (crumpling). Recent experiments (23, 24) have shown that this mixture of subdominant energies leads to the complex shapes of curtains: multiscale, hierarchical patterns that interpolate between crumpling- and wrinkling-like shapes.
The classification of wrinkling patterns into NT and FFT regimes provides previously undiscovered insights into the behavior of elastic sheets. Our results raise some interesting problems concerning the nature of the transition between the NT and FFT regimes and crucial aspects of the FFT analysis, such as the computation of the exact wrinkle number, and how it is influenced by boundary conditions. We hope that the ideas introduced in this paper will inspire theoretical and experimental works that will further elucidate the subtleties of wrinkling phenomena and other types of deformations of thin compressed sheets.
Acknowledgments.
We thank P. Bella, R. Kohn, and N. Menon for useful discussions. We thank the Aspen Center for Physics for hospitality during the final stages of this work. We acknowledge support by the Petroleum Research Fund of American Chemical Society (B.D.) and National Science Foundation-Materials Research Science and Engineering Center at University of Massachusetts (R.D.S.). This publication is based on work supported in part by Grant KUK-C1-013-04 made by King Abdullah University of Science and Technology (D.V.). M.A.-B. and E.A.C. acknowledge the support of Centre National de la Recherche Scientifique-Conicyt 2008. E.A.C. is thankful for Fondecyt project 1095112 and Anillo Act 95.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. T.A.W. is a guest editor invited by the Editorial Board.
*The requirement Tin, Tout ≪ Y, necessary to ensure a Hookean (linear elastic) response, implies that the limit ϵ → 0 is to be taken maintaining the constraint (t/Rin)2 ≪ ϵ ≪ 1.
†We assume that the wrinkling instability in the Lamé geometry is supercritical (amplitude vanishes at threshold). This assumption implies that 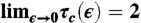 and dictates our NT analysis.
and dictates our NT analysis.
‡While the scaling relations for the threshold loads ratio and critical wrinkles number (our Eq. 10) appear in ref. 15 (their Eq. 19), their expression (Eq. 29) corresponding to the NT extent of wrinkles (our Eq. 11) seems to be wrong because it yields a diverging extent of wrinkles as Rout/Rin → ∞.
§Assuming a single-mode shape in the FFT regime is motivated by experiments (9, 10) and simplifies the analysis. There are indications (9) that this assumption fails near a clamped boundary [e.g., f(r = Rin) = 0], where a wrinkling cascade may emerge, but this does not seem to affect the basic results of our FFT analysis, Eqs. 17 and 18. Hence, we proceed by assuming a BCs at r = Rin that are compatible with Eq. 15. Cascade effects will be briefly mentioned later.
¶The fact that ∂θuθ remains finite in the FFT limit explains why the nonlinear model of ref. 10, which assumes negligibility of this and similar terms, cannot describe this regime.
∥The control parameters in ref. 10 were Rin (their r0), ur(Rout) (their β), and the “access” radial displacement at Rin (their δi). Hence, the tensions Tin and Tout are proportional to the thickness. Using Eqs. 3 and 6 and Hooke’s law, we find 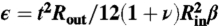 and τ = δiRout(1 - ν)/βRin(1 + ν). The last relation corresponds to the NT regime, which is sufficient for our discussion, but is different in the FFT regime. The sheet thickness in ref. 10 was t = 0.2 mm, and Rout/Rin≥6.
and τ = δiRout(1 - ν)/βRin(1 + ν). The last relation corresponds to the NT regime, which is sufficient for our discussion, but is different in the FFT regime. The sheet thickness in ref. 10 was t = 0.2 mm, and Rout/Rin≥6.
References
- 1.Bowden N, et al. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature. 1998;393:146–149. [Google Scholar]
- 2.Genzer J, Groenewold J. Soft matter with hard skin: From skin wrinkles to templating and material characterization. Soft Matter. 2006;2:310–323. doi: 10.1039/b516741h. [DOI] [PubMed] [Google Scholar]
- 3.Wagner H. Flat sheet metal girders with very thin metal web (Translated from German) Z Flugtechn Motorluftschiffahrt. 1929;20:8–12. [Google Scholar]
- 4.Mansfield E-H. The Bending and Stretching of Plates. Cambridge, UK: Cambridge Univ Press; 1989. [Google Scholar]
- 5.Stein M, Hedgepeth J-M. Analysis of Partly Wrinkled Membranes. Washington: Natl Aeronautics Space Admin; 1961. Technical Note D-813. [Google Scholar]
- 6.Pipkin A-C. The relaxed energy density for isotropic elastic membranes. IMA J Appl Math. 1986;36:85–99. [Google Scholar]
- 7.Cerda E, Mahadevan L. Geometry and physics of wrinkling. Phys Rev Lett. 2003;90:074302. doi: 10.1103/PhysRevLett.90.074302. [DOI] [PubMed] [Google Scholar]
- 8.Cerda E, Ravi-Chandar K, Mahadevan L. Thin films—wrinkling of an elastic sheet under tension. Nature. 2002;419:579–580. doi: 10.1038/419579b. [DOI] [PubMed] [Google Scholar]
- 9.Huang J, et al. Capillary wrinkling of floating thin polymer films. Science. 2007;317:650–653. doi: 10.1126/science.1144616. [DOI] [PubMed] [Google Scholar]
- 10.Géminard J-C, Bernal R, Melo F. Wrinkle formations in axi-symmetrically stretched membranes. Eur Phys J E Soft Matter. 2004;15:117–126. doi: 10.1140/epje/i2004-10041-1. [DOI] [PubMed] [Google Scholar]
- 11.Timoshenko S-P, Goodier J-N. Theory of Elasticity. New York: McGraw–Hill; 1970. [Google Scholar]
- 12.Vermorel R, Vandenberghe N, Villermaux E. Impacts on thin elastic sheets. Proc R Soc Lond Ser A. 2009;465:823–842. [Google Scholar]
- 13.Chopin J, Vella D, Boudaoud A. The liquid blister test. Proc R Soc Lond Ser A. 2008;464:2887–2906. [Google Scholar]
- 14.Holmes D-P, Crosby A-J. Draping films: A wrinkle to fold transition. Phys Rev Lett. 2010;105:038303. doi: 10.1103/PhysRevLett.105.038303. [DOI] [PubMed] [Google Scholar]
- 15.Coman C-P, Bassom A-P. On the wrinkling of a pre-stressed annular thin film in tension. J Mech Phys Solids. 2007;55:1601–1617. [Google Scholar]
- 16.Adams G-G. Elastic wrinkling of a tensioned circular plate using von Karman plate-theory. J Appl Mech. 1993;60:520–525. [Google Scholar]
- 17.Lawn B. Fracture of Brittle Solids. 2nd Ed. Cambridge, UK: Cambridge Univ Press; 2004. [Google Scholar]
- 18.Choksi R, Kohn R-V, Otto F. Energy minimization and flux domain structure in the intermediate state of a type-I superconductor. J Nonlinear Sci. 2004;14:119–171. [Google Scholar]
- 19.Davidovitch B. Period fissioning and other instabilities of stressed elastic membranes. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;80:025202(R). doi: 10.1103/PhysRevE.80.025202. [DOI] [PubMed] [Google Scholar]
- 20.Vella D, Adda-Bedia M, Cerda E. Capillary wrinkling of elastic membranes. Soft Matter. 2010;6:5778–5872. [Google Scholar]
- 21.Mansfield E-H. Tension field theory, a new approach which shows its duality with inextensional theory. Proceedings of the 12th International Congress of Applied Mechanics. 1968. pp. 305–320.
- 22.Witten T-A. Stress focusing in elastic sheets. Rev Mod Phys. 2007;79:643–675. [Google Scholar]
- 23.Huang J, et al. Smooth cascade of wrinkles at the edge of a floating elastic film. Phys Rev Lett. 2010;105:038302. doi: 10.1103/PhysRevLett.105.038302. [DOI] [PubMed] [Google Scholar]
- 24.Vandeparre H, et al. Wrinkling hierarchy in constrained thin sheets from suspended graphene to curtains. Phys Rev Lett. 2011;106:224301. doi: 10.1103/PhysRevLett.106.224301. [DOI] [PubMed] [Google Scholar]