Microscopic Symmetry Imposed by Rotational Symmetry Boundary Conditions in Molecular Dynamics Simulation

Abstract

A large number of viral capsids, as well as other macromolecular assemblies, have icosahedral structure or structures with other rotational symmetries. This symmetry can be exploited during molecular dynamics (MD) to model in effect the full viral capsid using only a subset of primary atoms plus copies of image atoms generated from rotational symmetry boundary conditions (RSBC). A pure rotational symmetry operation results in both primary and image atoms at short range, and within nonbonded interaction distance of each other, so that nonbonded interactions can not be specified by the minimum image convention and explicit treatment of image atoms is required. As such an unavoidable consequence of RSBC is that the enumeration of nonbonded interactions in regions surrounding certain rotational axes must include both a primary atom and its copied image atom, thereby imposing microscopic symmetry for some forces. We examined the possibility of artifacts arising from this imposed microscopic symmetry of RSBC using two simulation systems: a water shell and human rhinovirus 14 (HRV14) capsid with explicit water. The primary unit was a pentamer of the icosahedron, which has the advantage of direct comparison of icosahedrally equivalent spatial regions, for example regions near a 2-fold symmetry axis with imposed symmetry and a 2-fold axis without imposed symmetry. Analysis of structural and dynamic properties of water molecules and protein atoms found similar behavior near symmetry axes with imposed symmetry and where the minimum image convention fails compared with that in other regions in the simulation system, even though an excluded volume effect was detected for water molecules near the axes with imposed symmetry. These results validate the use of RSBC for icosahedral viral capsids or other rotationally symmetric systems.

1 Introduction

Thousands of viruses, including those that cause human disease, have protein shells that display icosahedral symmetry. This protein shell, or viral capsid, exhibits remarkable physical properties,^1,2 which are necessary to promote the virus life cycle. These properties and their functional role in viral pathogenesis have long captured the interest of experimental and computational researchers.

All-atom MD simulations provide the most rigorous and detailed computational approach to investigate capsid physical behavior. An entire capsid solvated in water consists ≈ 2,000,000 or more atoms. Simulation of such a large system is generally impractical even though a few notable exceptions have been reported.^3,4 The capsid of human rhinovirus, one of the smallest RNA viruses, has ≈ 500,000 atoms, and its diameter is ≈ 300 Å. The computational time for MD simulation can be reduced by exploiting the rotational symmetry of viruses.^5–8 Other macro-molecular assemblies, such as the icosahedral pyruvate dehydrogenase complex,⁹ also display rotational symmetry, as symmetry often confers stability and results in economical usage of basic components.¹⁰ Simulation of these systems can also exploit rotational symmetry to reduce computation time. In the case of icosahedral viruses with three protomers in each of the twenty triangular tiles of an icosahedron, periodic boundary conditions allow simulation of as little as 1/60th of the entire capsid while retaining effects of the whole virus particle.^5–8

With periodic boundary conditions, a primary set of atoms is replicated to produce a neighboring set of atoms, and so model the effect of a larger system. Symmetry related coordinates are generated by transformation of atoms composing the primary unit to image atoms in the neighboring units as follows:

$$\mathbf{x}(k\prime )=\mathbf{R}·\mathbf{x}(k),$$ (1)

where R is one of the operators of the symmetry group. The coordinates of atom k, x(k), are transformed to the coordinates of the image, x(ḱ).

Most uses of periodic boundary conditions in simulations model infinite systems and involve open crystallographic space group symmetry with cubic, truncated octahedron, etc. primary units; however, in the case of icosahedral viruses, closed point group symmetry is used to model a finite system. Thus, we examine here the case where R involves pure rotational operators appropriate for viral capsids. This type of boundary condition is called rotational symmetry boundary conditions (RSBC).

Under RSBC, certain operators (Eq. (1)) lead to short range interactions between copies of both primary and image atoms near a rotational symmetry axis. Thus, as outlined in Section 2.2, there are unavoidable occurrences of an atom in the primary unit near a rotational symmetry axis such that the distance to its own image atom (self-image), as well as distances to both primary and image atoms of neighboring atoms (replicate-image), are within the nonbonded interaction distance. The minimum image convention, typically used to evaluate nonbonded interactions in periodic boundary systems, fails in regions near such rotational symmetry axes. Nonbonded interactions must be determined by explicit treatment of image atoms as implemented with the general image facility in the CHARMM program.^11,12 The explicit treatment of image atoms allows the correct calculation of forces in rotationally symmetric systems; duplicate forces are avoided with the proper counting of nonbonded interactions.^11,12 While the enumeration of nonbonded interactions near such rotational symmetry axes is algorithmically correct, there is an unavoidable imposed symmetry in the forces from self-images and effects from the symmetry related to replicate-images. Such microscopic symmetry is nonphysical but inherent to MD simulations under RSBC. Given the importance of RSBC for exploring molecular behavior of large systems with icosahedral symmetry, we executed an MD study to determine if artifacts on the dynamics exist with icosahedral RSBC due to the inherent microscopic symmetry on the force contributed by self-image and replicate-image interactions.

We conducted RSBC MD simulations on pure TIP3 water within a spherical shell using icosahedral symmetry and on the solvated capsid of human rhinovirus14 (HRV14). For both systems, the primary atoms in the simulation corresponded to five icosahedral asymmetric subunits or 1/12th of the icosahedron, and the symmetry-related image atoms were generated according to Eq. (1) from a group of five icosahedral operators. The use of this pentameric primary unit allows the operator R to be selected so that the minimum image convention fails at only certain rotational axes but not others (described below). Therefore, the properties assessed from regions near symmetry axes where the minimum image convention fails can be compared with those from regions near axes of the same symmetry but without imposed microscopic symmetry in the forces. In addition, the comparison is determined from one trajectory. This system is in contrast to the primary simulation unit being one asymmetric subunit, or the viral protomer equivalent to 1/60th of the icosahedron, for which symmetrical interactions would be imposed at all symmetry axes and such a comparison would not be possible.

We show here from analysis of a variety of physical properties that the imposed symmetry of forces has negligible influence on the resulting dynamics. An excluded volume for water molecules exists near axes with imposed symmetry; however this excluded volume did not perturb water structure or dynamics. Moreover, because protein atoms do not on average lie on a symmetry axis, no excluded volume effects were apparent in the simulation of HRV14. Based on the similarity in the dynamics and structural properties for region with and without symmetry imposed in the forces we conclude that RSBC simulations do not suffer from artifacts due to microscopic symmetry imposed near certain rotational axes and RSBC is a reliable approach for reducing a simulation system with rotational symmetry.

2 Methods

2.1 Computer Simulations

All molecular dynamics (MD) calculations were performed using the CHARMM program^11,12 with constant volume and energy (NVE ensemble). A force switching function¹³ was used to smoothly truncate electrostatic and van der Waals nonbonded forces at a cutoff of 14.0 Å. The covalent bonds to hydrogen atoms were constrained by the SHAKE algorithm. The equations of motion were integrated using the Verlet leap-frog algorithm with a time step of 1 fs. Icosahedral boundary conditions implemented with the IMAGES facility within CHARMM were employed as described below. Image atoms within 16.0 Å of a primary atom were included in the nonbonded pair list. Updates of image and nonbonded lists were made heuristically. All the simulations were performed using a parallel version of CHARMM 35b2 running on a super-computing cluster containing 893 8-core Dell 1950 processors. Each simulation was performed on single node containing 8 cores that shared 16 GB of RAM.

2.2 Rotational symmetry boundary conditions

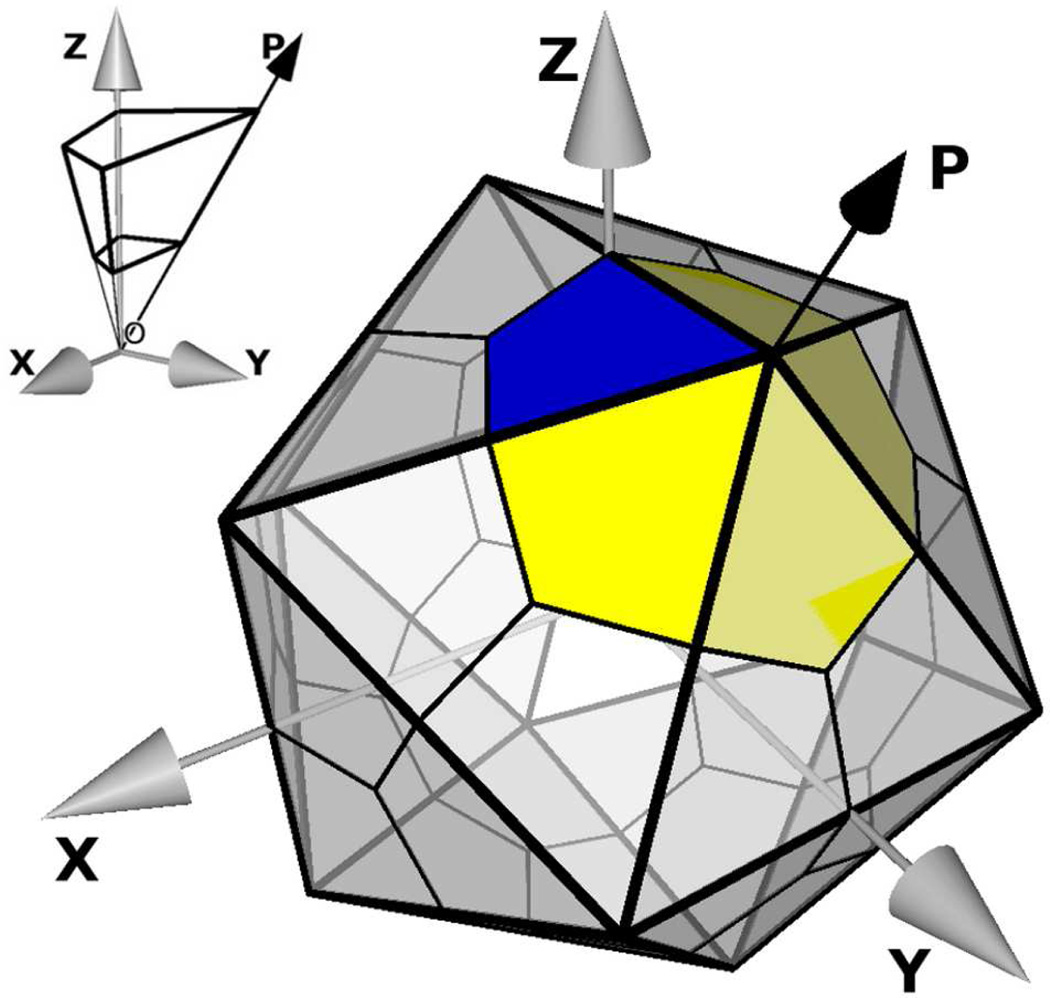
The simulation system for both bulk water and solvated HRV14 capsid was an icosahedral shell rather than a solid icosahedron. Water molecules were constrained within the outer and inner radii by applying spherical quadratic potentials¹⁴ referenced to 60 Å and 30 Å, respectively, for bulk water; and 170 Å and 85 Å, respectively for the solvated HRV14 capsid. The spherical quadratic potential was setup with a well depth of −0.25 kcal/mol at 1 Å from the reference distance followed by a smoothly rising repulsion. The lack of solvent in the central sphere of the icosahedron reduced the number of water molecules and avoided symmetrical interactions near the center.

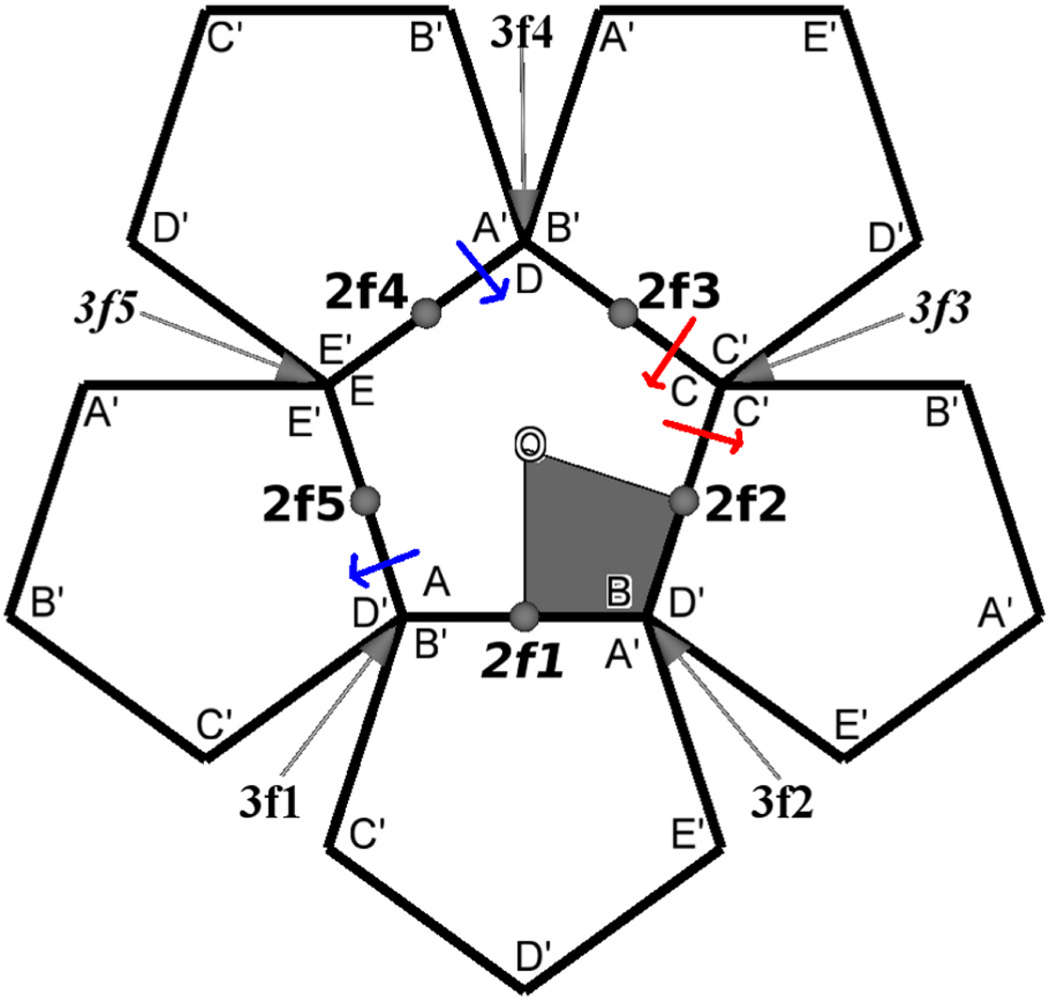
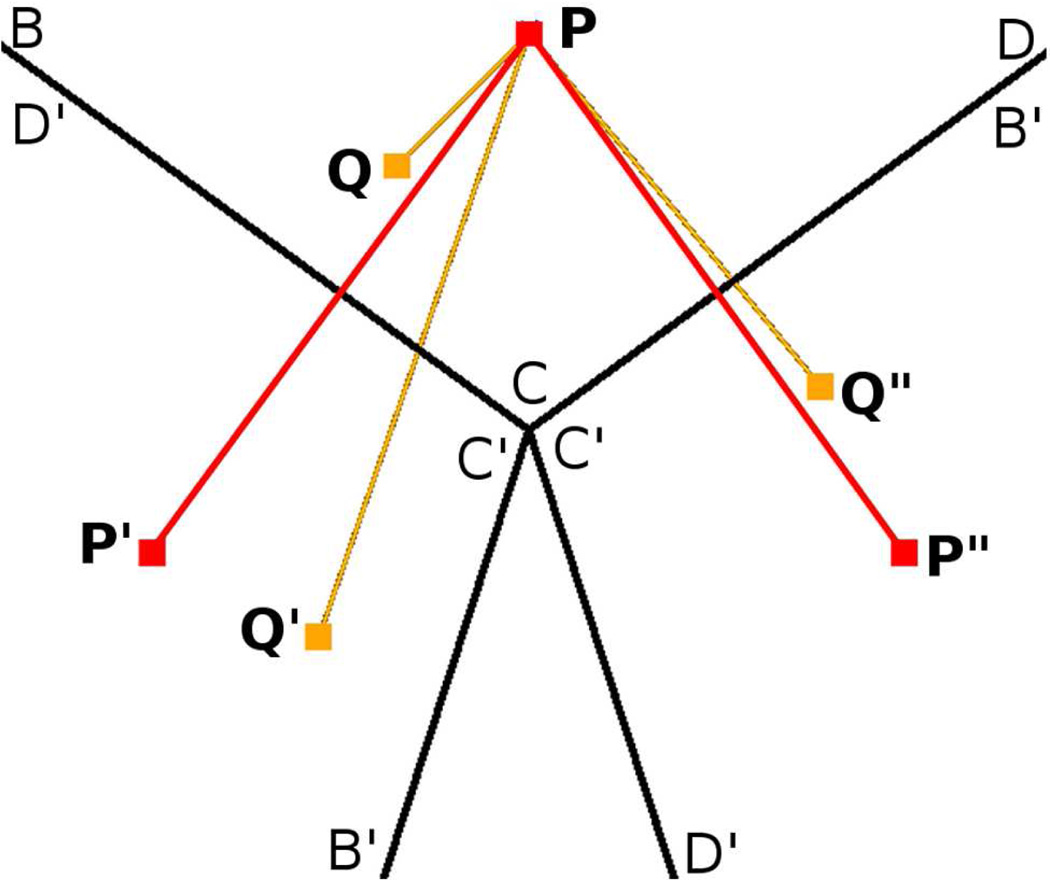
The RSBC system was established from a subset of the 60 transformations for icosahedral symmetry listed in Table 1. The initial coordinates for the pentameric primary unit were generated by symmetry operations in the first row of Table 1 applied to a solvated HRV14 protomer (Figure 1 blue area). The solvated HRV14 protomer system, comprising four polypeptides (VP1, VP2, VP3 and VP4), was generated as described elsewhere.^6,7 Water molecules near the center of the icosahedron were removed to model an icosahedral shell. This primary unit for the HRV14 simulation system therefore comprises five protomer units around the 5-fold symmetry axis of icosahedron (Figure 1 blue and yellow areas). Coordinates for explicit atoms in the five nearest image units were generated by transformation of the primary atomic coordinates using the five rotational operators shown in boldface in Table 1. This selection of rotational symmetry operators from Table 1 uniquely satisfies the requirements for RSBC simulation. (See supporting information for a detailed explanation of the selection of symmetry operators from Table 1.) The resulting simulation system of a pentameric primary unit and the five nearest-neighbor image units is shown projected in two dimensions in Figure 2. Recall that because the central pentamer is the primary unit, each corner, labeled A through E, is distinct from the other corners. As needed for periodic boundary conditions, the crossing of a boundary between the primary unit and an image unit is equivalent for all occurrences (illustrated by the blue or red arrows). These operators generate regions with imposed microscopic symmetry in the forces from self-image and replicate-image interactions near three symmetry axes (2f1, 3f3 and 3f5), while regions around the remaining seven symmetry axes do not have such interactions. These axes are italicized through the paper to distinguish them from the other 2-fold and 3-fold axes. Self-image and replicate-image interactions are illustrated using the 3f3 axis in Figure 3. For the pure water simulation, a pentameric primary unit and image units were similarly generated from a spatial unit of bulk water analogous to the viral protomer.

Table 1.

Icosahedral symmetry operators^a

	1	2	3	4	5
1	I (1,1)	F1 (1,5)	F2 (1,4)	F3 (1,3)	F4 (1,2)
2	Z (2,1)	ZF1 (6,2)	ZF2 (11,4)	ZF3 (9,1)	ZF4 (5,1)
3	X (3,1)	XF1 (8,1)	XF2 (12,1)	XF3 (10,4)	XF4 (7,2)
4	Y (4,1)	YF1 (4,2)	YF2 (4,3)	YF3 (4,4)	YF4 (4,5)
5	F1Z (2,5)	F1ZF1 (6,1)	F1ZF2 (11,3)	F1ZF3 (9,5)	F1ZF4 (5,5)
6	ZF1Z (5,2)	ZF1ZF1 (2,2)	ZF1ZF2 (6,3)	ZF1ZF3 (11,5)	ZF1ZF4 (9,2)
7	XF1Z (7,1)	XF1ZF1 (3,5)	XF1ZF2 (8,5)	XF1ZF3 (12,5)	XF1ZF4 (10,3)
8	YF1Z (3,2)	YF1ZF1 (8,2)	YF1ZF2 (12,2)	YF1ZF3 (10,5)	YF1ZF4 (7,3)
9	F2Z (2,4)	F2ZF1 (6,5)	F2ZF2 (11,2)	F2ZF3 (9,4)	F2ZF4 (5,4)
10	ZF2Z (12,4)	ZF2ZF1 (10,2)	ZF2ZF2 (7,5)	ZF2ZF3 (3,4)	ZF2ZF4 (8,4)
11	XF2Z (11,1)	XF2ZF1 (9,3)	XF2ZF2 (5,3)	XF2ZF3 (2,3)	XF2ZF4 (6,4)
12	YF2Z (3,3)	YF2ZF1 (8,3)	YF2ZF2 (12,3)	YF2ZF3 (10,1)	YF2ZF4 (7,4)

^aRotational operators of icosahedral symmetry. I is identity; F_1,2,3,4 are rotations around the 5 fold symmetry axis (OP) (Figure 1) by 72°, 144°, 216°, 288° respectively; X,Y,Z are rotations by 180° around X,Y,Z axes respectively. The 1st and 2nd numbers inside the parenthesis following the operator indicates the row and column numbers respectively of the inverse of that operator. Five operators in each row transform the protomer coordinates to 5 protomers for the pentameric primary unit used in this study. Neighboring images of the pentameric unit are generated by the five operators in boldface.

Figure 1.

Schematic of an icosahedron with twenty triangular tile. O is at the center of the icosahedron. Each tile has three asymmetric units corresponding to a protomer of the HRV14 capsid (blue area. The Z axis is coincident with one of the 2-fold symmetry axis. In this study the pentamer, or five protomers centered around a 5-fold symmetry axis, is the primary unit cell (blue and yellow areas). The volume occupied by a protomer solvated in water, used in earlier studies,^6–8 is shown in the inset. Here water molecules were removed from center of the icosahedron and a shell of water is used to solvate a protomer (thicker lines on inset). Symmetry operators in the 1st row of Table 1 generate a solvated pentamer from the solvated protomer.

Figure 2.

Two-dimensional projection of the pentamer and its neighbors generated by the set of symmetry operators shown in bold face in Table 1. The central pentamer represented by ABCDE, is the primary simulation unit. Pentamers represented by A′B′C′D′E′ are nearest-neighbor images. The area spanned by a protomer is represented by the shaded area. Three-fold symmetry axes are 3f1 to 3f5 and two-fold symmetry axes are 2f1 to 2f5. O is the five-fold symmetry axis. The Z axis is coincident with 2f1. Self-image and replicate-image interactions are present at one 2-fold symmetry axis, 2f1, and two 3-fold symmetry axes, 3f3 and 3f5.

Figure 3.

Illustration using the 3f3 axis of self-image and replicate-image interactions at a 3-fold symmetry axis of an icosahedron. BCD is part of the primary unit. B′C′D′ are images of BCD and produced by rotating BCD around 3 fold symmetry axis. P and Q are two atoms in primary unit and P′, P” and Q′, Q” are their images respectively. Minimum image convention is violated as Q, Q′ and Q” are all within nonbonded interaction distance of P (replicate-image interaction). P also interacts with its own images P′ and P” (self-image interaction). Microscopic symmetry is imposed on P as positions and velocities of P′, P”, and Q′, Q” are solely determined by positions and velocities of P and Q respectively.

2.3 Bulk water simulations and analysis

A shell of TIP3 water, with an inner and outer radius of 30 Å and 60 Å respectively, was modeled using a primary set of atoms corresponding to a pentameric shape with 2325 water molecules, and the five nearest image sets of atoms were generated using icosahedral symmetry operators as described above. Initial velocities were assigned randomly corresponding to 100 K, and the system was heated to 300 K over a time of 20 ps, and then equilibrated for 180 ps. Velocities were reassigned during the equilibration period to maintain the target temperature. Analysis was done over the subsequent 800-ps trajectory period, during which the average temperature remained constant without velocity reassignment.

The oxygen-oxygen radial distribution function for water, g(r), was computed using water molecules within a certain distance of a symmetry axis for the origin of integration. The g(r) was determined for water molecules surrounding five 2-fold symmetry axes, five 3-fold symmetry axes, one 5-fold symmetry axes of icosahedral water shell, and for an arbitrary axis through the spherical water shell from an MD simulation of TIP3 water calculated without RSBC. Two cutoff distances were used to select water molecules at the origin for g(r) integration: 5 and 10 Å. The average number of water molecules within 5 Å was 28 near the 3-fold axes, 43 closest to the 2-fold axes, 86 near the 5-fold axis of icosahedral water shell, and 86 near an arbitrary axis through the spherical shell of water. Histograms of bin width 0.1 Å were used to estimate g(r).

To investigate whether the symmetrical forces imposed by RSBC affect the dynamical behavior of water molecules, we calculated the survival probability function,¹⁵ S_w(t), of water molecules in the vicinity of the axes of rotational symmetry. S_w(t) gives the percentage of water molecules that remain in the vicinity of a symmetry axis after time t. To obtain S_w(t), we compute the conditional probability P_i(t_n, t) for each ith water molecule of the system. P_i(t_n, t) takes the value of 1 if the ith water is in the vicinity of a symmetry axis between times t_n and t_n + t, and it has the value zero otherwise. The survival probability is then:

$$S_w(t)=\frac{100}{S_w(0)n_t}{\displaystyle \sum _{n=1}^{n_t}}{\displaystyle \sum _i}{P}_i(t_n,t),$$ (2)

Here, n_t is the number of simulation time-frames, S_w(0) is the average number of water molecules in the vicinity of a symmetry axis. If the oxygen atom of a water molecule is within a certain radial distance of a symmetry axis we consider the water molecule to be within the vicinity of that symmetry axis. Image atoms were also considered while counting water molecules. With the choice of symmetry operators indicated by Figure 2, the symmetry axes 3f1, 3f2 and 3f4 correspond to equivalent regions (A,B,D) and will therefore will have same density of water. The micro-environment and hence the number of water molecules near the 3-fold symmetry axis 3f1 will be exactly that near 3f2 and 3f4. Similarly the count near 2-fold symmetry axis 2f2 will be exactly that near 2f3 and 2f4 will be exactly that near 2f5.

We used an orientational order parameter (Q)¹⁶ to investigate the structure of water.

$$Q\equiv 1-\frac{3}{8}{\displaystyle \sum _{j=1}^3}{\displaystyle \sum _{k=j+1}^4}{(\text{cos }{\psi }_{\mathit{\text{jk}}}+\frac{1}{3})}^2$$ (3)

where ψ_jk is the angle formed by the lines joining the oxygen atom of a given water molecule and those of nearest neighbors j and k. For the purpose of this study, we limit our attention to the four oxygen atoms nearest to a given oxygen atom. Here, Q is slightly modified from previous work¹⁷ to have the value 〈Q〉 = 0 (〈…․〉 denotes the ensemble average) in ideal gas phase¹⁶ and Q = 1 for a perfect tetrahedral configuration. Thus, Q measures the degree of tetrahedrality in the distribution of the four nearest oxygen atoms around a central oxygen atom.

We considered effects on the instantaneous temperature, which depends on the root mean square speed, (V_rms).

$$V_{\mathit{\text{rms}}}\equiv \sqrt{\frac{{\displaystyle {\sum }_{i=1}^n}{m}_i{v}_i^2}{{\displaystyle {\sum }_{i=1}^n}{m}_i}}$$ (4)

where n is number of atoms and m_i and v_i are mass and magnitude of velocity of ith atom.

2.4 Solvated HRV14 capsid simulations

Coordinates of the HRV14 protomer (protein data bank: 4RHV¹⁸) were used to generate the pentamer composing the primary set of atoms with the operators of row 1, Table 1 as described above. Missing virus coordinates were modeled based on homologous residues in human rhinovirus 16 (protein data bank: 1AYM¹⁹) or polio virus (protein data bank: 1HXS²⁰). The energy of the modeled residues was minimized while maintaining the known HRV14 crystallographic coordinates fixed. Keeping the known atomic positions fixed, in vacuum NVE MD simulations were performed to raise the temperature of the modeled regions over a 490-ps period from 100 K to 5000 K, the system was annealed at 5000 K for a 50-ps period, and then cooled to 300 K over a 980-ps period.

Electron density at the 3-fold and 5-fold symmetry axes has been interpreted to be a calcium ion.²¹ Following simulated annealing one calcium ion each was therefore placed at the crystallographic position on 5-fold symmetry axis and 3-fold symmetry axis 3f1 in Figure 2. Symmetry operations generated images of calcium ion on 3f2 and 3f4 from calcium ion on 3f1. Modified calcium ions, with one third of charge and mass of a calcium ion as described elsewhere,⁶ were placed at their crystallographic position on the 3-fold symmetry axes 3f3 and 3f5. The HRV14 pentamer with calcium ions was solvated following a known protocol. The charge of the solvated pentamer was neutralized by randomly replacing the appropriate number of water molecules with counter ions, and the interior and exterior of the viral capsid were neutralized independently. The energy of the final primary unit, comprising 25596 water molecules and a total of 142456 atoms, was minimized using the protocol described elsewhere.⁶ Velocities corresponding to 100 K were assigned randomly to the charge neutralized viral capsid and heated to 300 K over a time of 20 ps. The solvated capsid was then allowed to equilibrate over a 980-ps period. A further 2-ns period of MD simulation was performed for analysis. Properties investigated in this article depend on magnitude of atomic velocities, the density of atoms within a shell of different thickness near a symmetry axis and distribution of ϕ, ψ dihedral angles. All of these values were well converged during the 2-ns MD production period (see supporting information).

3 Results and Discussion

3.1 Bulk Water

A shell of bulk water was simulated under RSBC using TIP3 water. Icosahedral symmetry restraints were set up as shown in Figure 2 with the primary unit equivalent to an icosahedral pentamer, and the surrounding five replicated image units. Explicit image atoms were generated according to the operators shown in Figure 2. Symmetry is imposed on the forces from self-image and replicate-image interactions that occur near the axes 2f1, 3f3 and 3f5. Interactions at the other 2-fold and 3-fold axes are uniquely determined and without imposed symmetry. Potential effects due to the non-physical microscopic symmetry imposed 2f1, 3f3 and 3f5 in RSBC MD simulations of bulk water were assessed by comparing structural and dynamic properties evaluated from water molecules near these symmetry axes with the same properties evaluated near other icosahedral symmetry axes.

3.1.1 Influence on structural properties

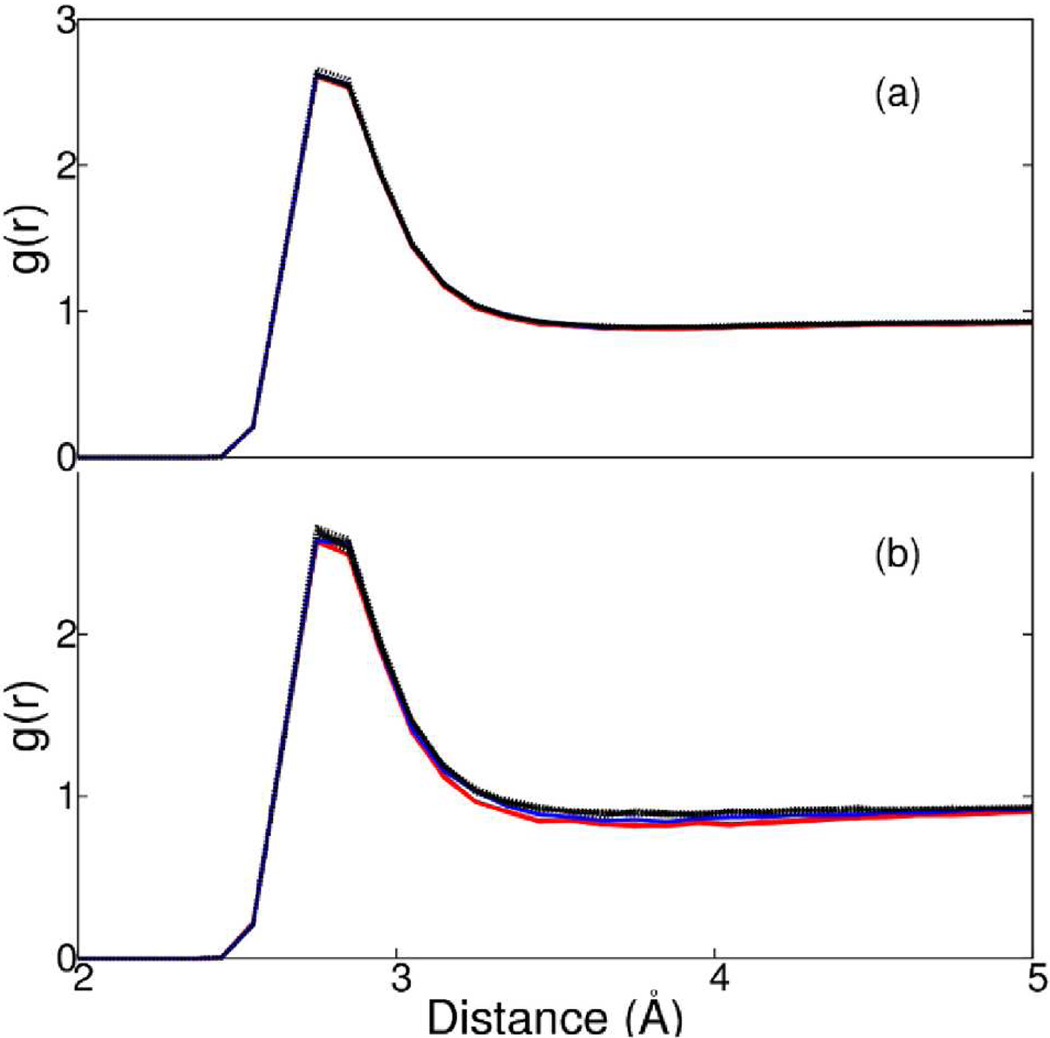
The g(r) functions are plotted for averages over water molecules within 10 Å (Figure 4a) or 5 Å (Figure 4b) of a symmetry axes. The plots in Figure 4a are indistinguishable for distributions within 10 Å of any of the twelve axes, including those with imposed microscopic symmetry. Considering distributions for water molecules positioned within 5 Å of an axis, g(r) is only somewhat perturbed by the imposed symmetry. Between 3 and 5 Å the density is slightly lower for regions near 2f1 (blue), 3f3 and 3f5 (red) than regions near the other symmetry axes (Figure 4b).

Figure 4.

Radial distribution function of O-O distances for water molecules within (a) 10 Å or (b) 5 Å of 3f3 and 3f5 (red); 2f1 (blue); other 2-fold, 3-fold and 5-fold symmetry axes of icosahedron shell of water and an arbitrary axis through spherical shell of water (black).

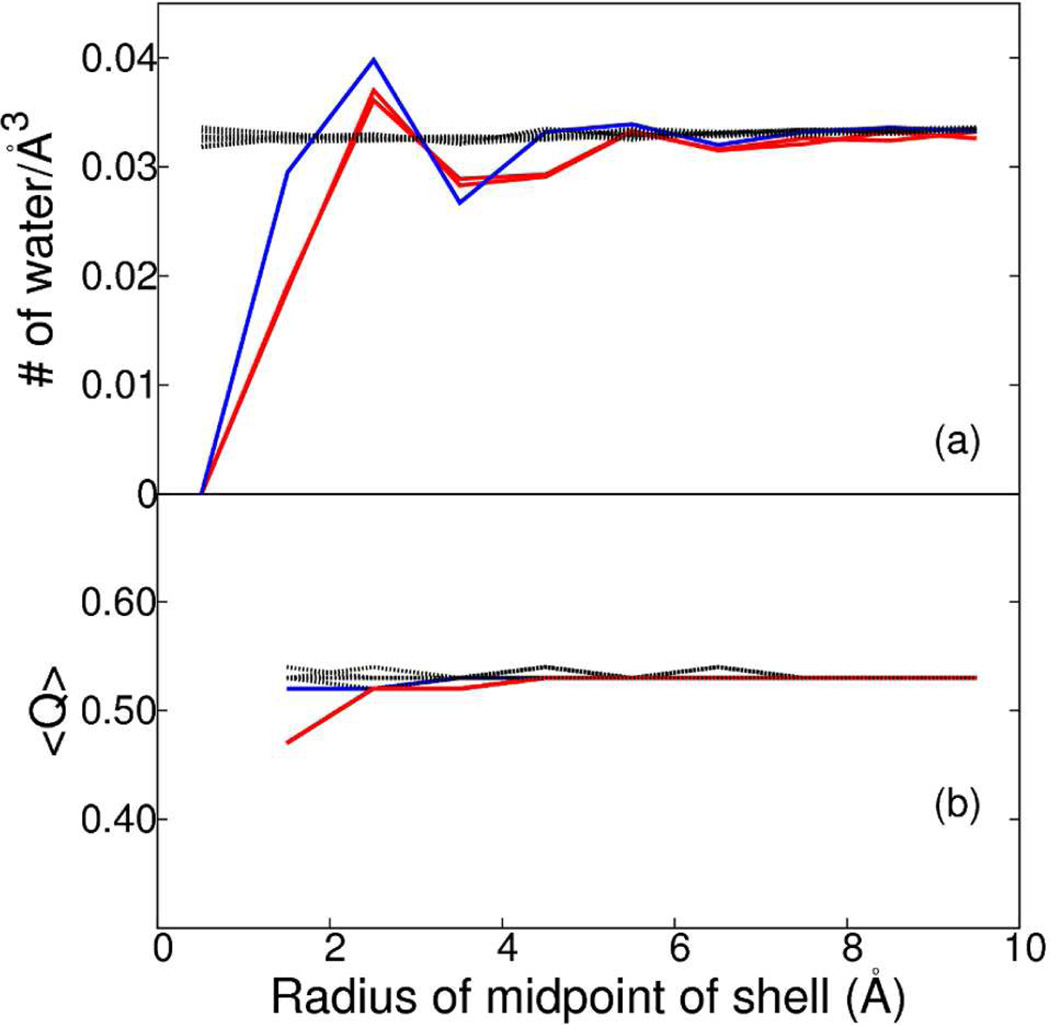
An inevitable consequence of the imposed symmetry surrounding the 2f1, 3f3 and 3f5 axes is that an atom can not occupy this region in space due to steric collision with its own image. As a result, an excluded volume of cylindrical shape surrounds 2f1, 3f3 and 3f5 in the simulation system. The excluded volume was characterized by determining the water density in 1 Å thick cylindrical shells from 0.5 to 9.5 Å radii, in 1 Å increments, around each of the 2-fold, 3-fold and 5-fold symmetry axes of the RSBC simulation of a water shell and around an arbitrary axis for the spherical water shell simulation. The coordinate of the water oxygen was used to specify occupancy. The water density averaged over the simulation time period is plotted as a function of the cylindrical radius in Figure 5a for each of the twelve axes defined in methods. There is no water molecule within 1 Å of the 2f1, 3f3 or 3f5 axis. The radius of the excluded cylindrical volume is between 1 and 2 Å and is slightly larger for the 3-fold symmetry axes than the 2-fold symmetry axis. The total excluded volume is about 0.01% of the icosahedral pentameric water shell. The excluded volume at the 2f1, 3f3 and 3f5 axes is compensated by increased density between 2 and 3 Å of those symmetry axes, so that beyond 6 to 7 Å (less than the dimension of two water molecules), the density of water at 2f1, 3f3 and 3f5 is unperturbed relative to that bulk water and that near the other symmetry axes.

Figure 5.

Density and orientational order parameter, Q, of water within cylindrical shells of 1 Å width around the 3f3 and 3f5 (red); 2f1 (blue); other 2-fold, 3-fold and 5-fold symmetry axes of icosahedron shell of water and an arbitrary axis through spherical shell of water (black). (a) The density of water at X Å is calculated from the average number of water molecules between X − 0.5 Å and X + 0.5 Å over the simulation time period for X from 0.5 Å to 9.5 Å in 1 Å intervals. (b) 〈Q〉 within a cylindrical shell of 1 Å width is calculated by averaging Q of individual waters within the shell over the simulation time period.

To examine whether the excluded volume and variation in water density (Figure 5a) effected the water structure in the vicinity of these symmetry axes, we examined the value of Q (see Methods). The ensemble averaged values 〈Q〉 for water molecules within cylindrical shells of varying radii are shown in Figure 5b. 〈Q〉 is between 0.52 and 0.53 for water molecules near all symmetry axes except those close to 3f3 and 3f5. The value for 〈Q〉 is 0.47 for averaging over water molecules within 2 Å of 3f3 and 3f5, but reaches 0.52 for averaging waters at a distance greater than 2 Å from those axes. Thus, only the first layer of water near 3f3 and 3f5 deviates slightly from the tetrahedrality of bulk water measured by Q.

3.1.2 Influence on dynamical properties

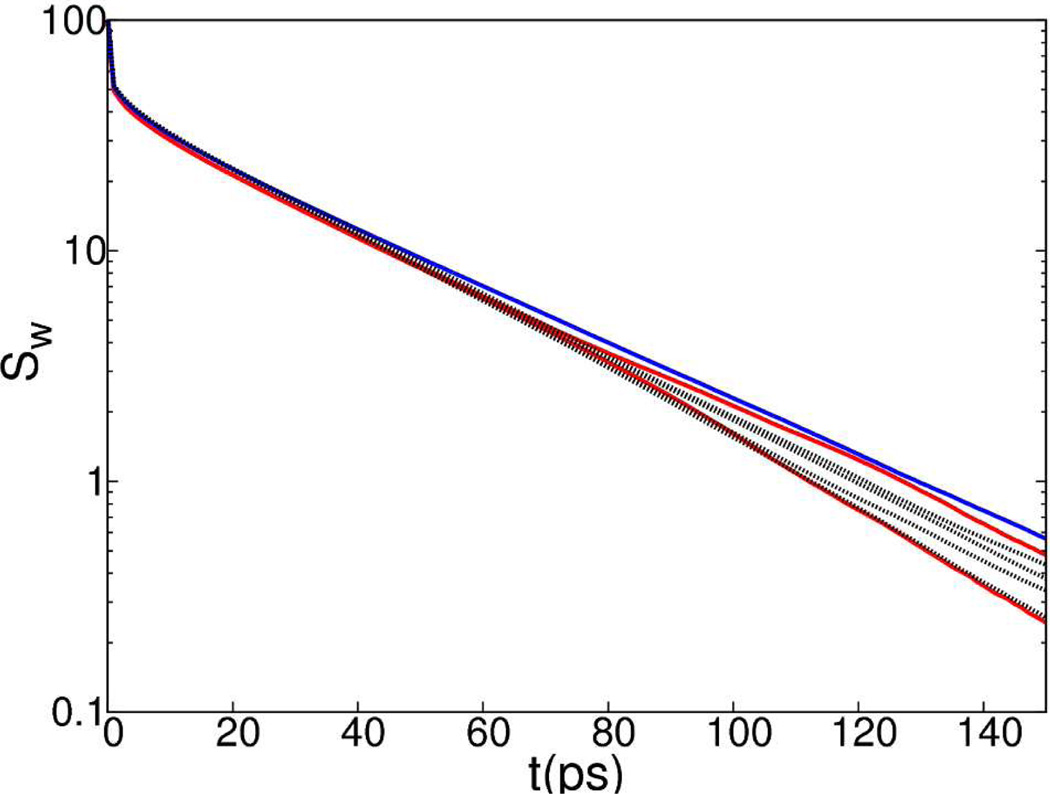
To investigate whether the symmetry imposed by RSBC affects the dynamical behavior of water molecules, we calculated the survival probability, S_w(t), of water within 10 Å of symmetry axes (Figure 6).

Figure 6.

Survival probabilities of water molecules within 10 Å of 3f3 and 3f5 (red); 2f1 (blue); other 2-fold, 3-fold and 5-fold symmetry axes (black) from simulation of an icosahedron shell of water.

The differences in the S_w(t) of water, near the 2f1, 3f3 or 3f5 axes relative to that for the other symmetry axes, are not greater than the differences among the other symmetry axes. The spread in curves in Figure 6 at 150 ps is less than 1 water molecule, and there is no clear trend in the spread that would indicate water molecules reside for longer or shorter times near the 2f1, 3f3 or 3f5 axes compared to the other symmetry axes. Even though the density of water is lower near the 2f1, 3f3 and 3f5 axes, the survival probability of water is not changed near these symmetry axes.

A comparison of the fluctuations in instantaneous temperature for the water molecules near the 2f1, 3f3 and 3f5 axes with symmetry imposed in nonbonded forces to the fluctuations for the rest of the system should also indicate potential artifacts in the dynamical behavior of water. Fluctuations in temperature arise from fluctuations in magnitude of atomic velocities, δV_rms. The δV_rms values for water molecules in a cylinder of 5 Å radius around symmetry axes listed in Table 2 are nearly equivalent, indicating no differences in fluctuation of instantaneous temperature.

Table 2.

Root mean square speed (V_rms) and flux of water^a

	Vrms Å/ps	δVrms Å/ps	Φ(S1) 1/ps/Å2	δΦ(S1) 1/ps/Å2	Φ(S2) 1/ps/Å2	δΦ(S2) 1/ps/Å2
2f1	0.32	0.02	0.00	0.02	-	-
2f2,2f3,2f4,2f5	0.32	0.02	0.00	0.02	-	-
3f3	0.32	0.03	0.00	0.02	0.00	0.02
3f5	0.32	0.02	0.00	0.02	0.00	0.02
3f1,3f2,3f4	0.32	0.02	0.00	0.02	0.00	0.02

^aRoot mean square speed (V_rms) and their fluctuations (δV_rms), flux through adjacent surfaces (Φ) and their fluctuations (δΦ) of water molecules within 5 Å of a symmetry axes. For a 3-fold symmetry axis, the flux through individual two adjacent surfaces (S₁, S₂) of the primary unit edge, was determined. For a 2-fold symmetry axis, the flux through the primary unit surface (S₁) containing the symmetry axis was determined.

The flux, Φ, through two adjacent surfaces of primary unit defining the corner near the 3-fold symmetry axes and the surface of primary unit containing the 2-fold symmetry axes was also calculated. The flux does not diverge near 2f1, 3f3 and 3f5 as no net flux of water molecules were observed through the adjacent surfaces of those three symmetry axes (Table 2).

Overall, the results from MD simulation of bulk water including RSBC indicate the symmetrical force from self-image interactions and other replicate-image nonbonded interactions imposed by an axis of rotational symmetry do not give rise to artifacts other than the presence of an excluded volume of radius between 1 and 2 Å at the symmetry axes, which alters the density of no more than two water layers. RSBC changes the structure of the first water layer somewhat near the region of excluded volume, but no differences were observed in the dynamical behavior of water molecules near these rotational axes.

3.2 HRV14 capsid

As an asymmetric molecule, the protein atoms approach an axis of rotational symmetry but, on average, cannot lie on an axis. In the energy-minimized crystal structure, the closest heavy-atom distance to a 3-fold symmetry axis is 2.5 Å, and 2.8 Å on average, while the distance to a 2-fold axis is 1.1 Å, and 1.6 Å on average. In further contrast to water molecules, given the mass and covalent structure, protein atoms do not experience overall translational motion and reorientation within the simulation boundaries. Accordingly, the protein structure and dynamics would seem less susceptible to the influence of imposed symmetry from RSBC, and effects such as the excluded volume apparent for water molecules would be diminished for a protein molecule.

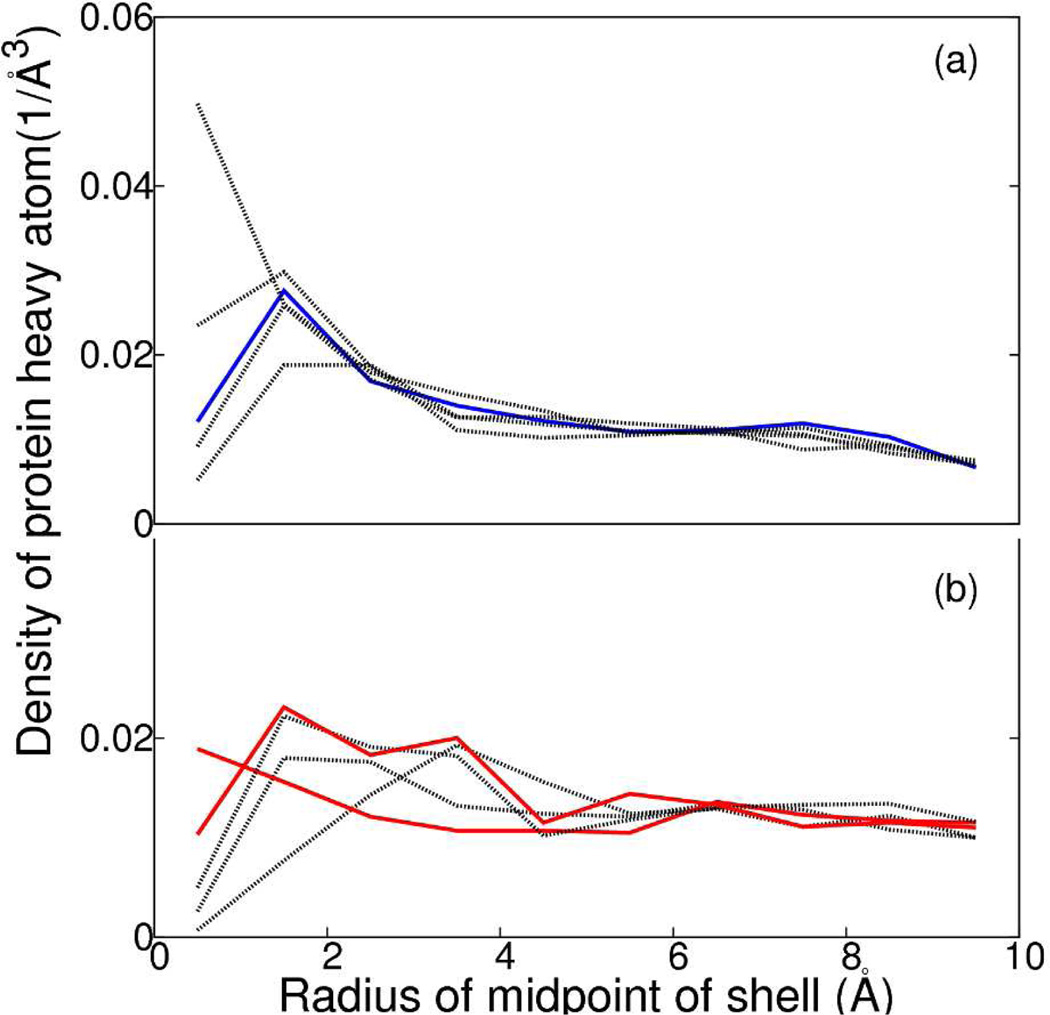
The density of HRV14 atoms was determined as a function of the radial distance from the axes of rotational symmetry in the fashion outlined above for water molecules. Densities of HRV14 heavy atoms within cylindrical shells 1 Å thick around the 2-fold and 3-fold symmetry axes are shown in Figure 7a and Figure 7b, respectively. The variation among the density profiles for all the axes is as large between those without symmetry imposed as it is between those with and without symmetry imposed, and no trend in the profiles distinguishes the density of the protein atoms surrounding the 2f1, 3f3 and 3f5 axes from that surrounding the other axes. The profile around one of the 2-fold axes exhibits an interesting increase at short distance, which shows a microscopic breakdown of symmetry due to a conformational fluctuation that moves the protein toward the region of the symmetry axes. Although this type of fluctuation would be less probable at the 2f1 axis, the overall behavior shown in Figure 7 shows no differences from RSBC.

Figure 7.

Density of protein within a cylindrical shell of 1 Å width around (a) 2-fold symmetry axes - 2f1 (blue); other 2-fold symmetry axes (black), and (b) 3-fold symmetry axes - 3f3 and 3f5 (red), other 3-fold symmetry axes (black). The density of water at X Å is calculated by calculating average density of protein atoms between X − 0.5 Å and X + 0.5 Å over the simulation time period. The density was calculated for X from 0.5 Å to 9.5 Å in 1 Å interval.

If the self-image interactions of the protein molecule near 2f1, 3f3 and 3f5 generate artificial forces, fluctuation of instantaneous temperature of the protein residues near those axes should increase. We examined the V_rms of residue 117 of VP2, which is nearest to the 3-fold symmetry axes. Fluctuation of V_rms for VP2 117 from each of the five protomers in the pentameric set of primary atoms shown in Table 3 and indicate no significant differences in trend for VP2 117 near the 3f3, 3f5 or other 3-fold symmetry axes.

Table 3.

Root mean square speed (V_rms) of protein^a

3 fold symmetry axes	Vrms Å/ps	δVrms Å/ps
3f1	0.37	0.06
3f2	0.37	0.06
3f3	0.38	0.06
3f4	0.38	0.06
3f5	0.37	0.06

^aRoot mean square speed (V_rms) and their fluctuations (δV_rms) of residue 117 of VP2 near five 3-fold symmetry axes. Interactions near the symmetry axes 3f3 and 3f5, violate the minimum image convention.

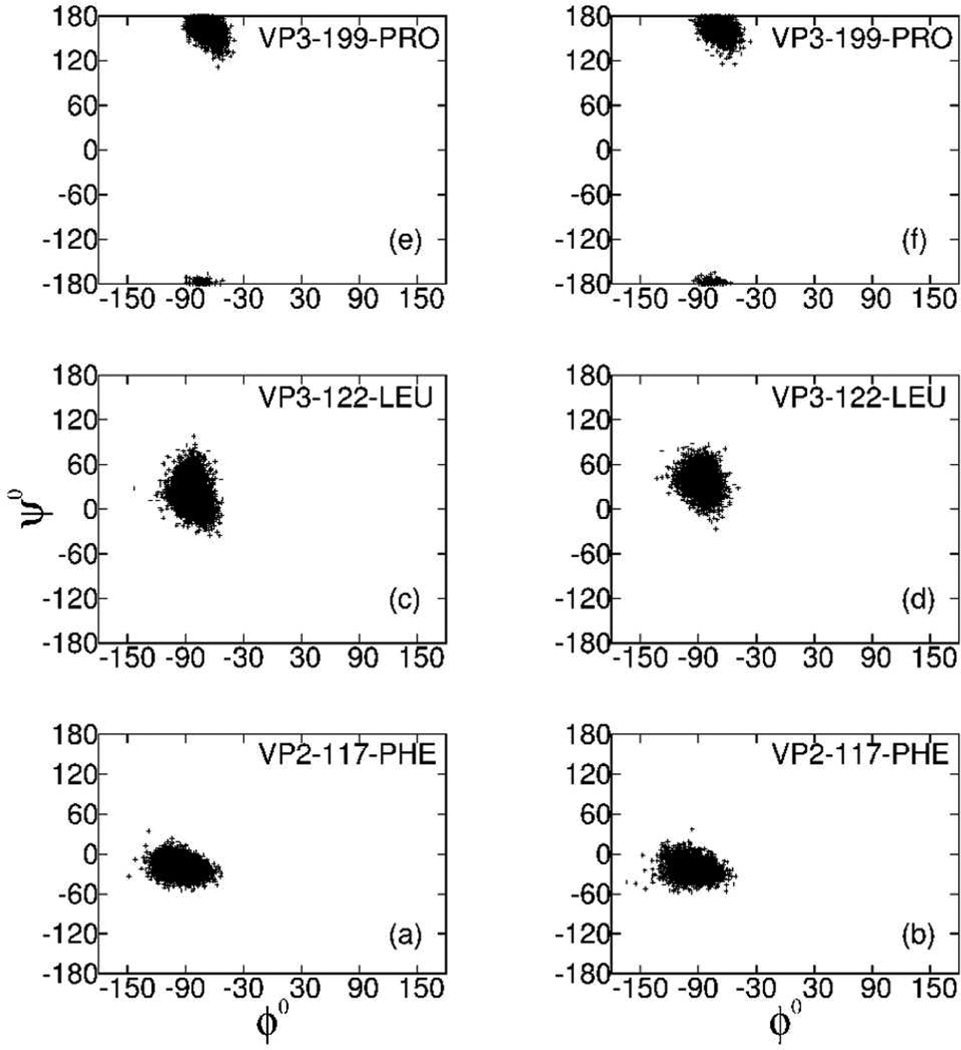
We also examined structural features of residues near the five 3-fold axes. The distribution of the main chain ϕ, ψ dihedral angles are shown for the residues 117 of VP2, and 122 and 199 of VP3 in Figure 8. These Ramachandran plots reveal that the distributions for these residues positioned near the 3f1, 3f2 or 3f4 axes (Figure 8a, c and e) do not differ from those at 3f3 or 3f5 axes (Figure 8b, d and f), and thus the protein main-chain conformation is not effected by self-image interactions.

Figure 8.

Ramachandran plot of residues closest to 3-fold symmetry axes. The dihedral angles, ϕ and ψ, are plotted for residue 117 of VP2, and residues 122 and 199 of VP3 from protomers located near the 3f1, 3f2 and 3f4 axes (Figure 8a, c and e), or located near the 3f3 and 3f5 axes (Figure 8b, d and f).

Together these results show that neither the structural nor dynamical behavior of the HRV viral capsid is perturbed by self-image or replicate-image interactions imposed by RSBC. The excluded volume effect, demonstrated by the density profile from bulk water simulation (Figure 5), is not manifested by the protein atoms. The fact that protein atoms, on average, cannot lie on a symmetry axis reduces the potential for artifacts induced by RSBC and the inherent excluded volume poses practically no problem.

4 Conclusion

In this article we have studied in depth the effect of the nonphysical microscopic symmetry imposed by RSBC on MD simulations of an icosahedral shell of bulk water and HRV14 viral capsid and examined the effect due to symmetry imposed at certain axes based on similarity of properties that are well converged in the 2 ns simulation period. The approach is a reasonable critical assessment of the resulting forces and dynamics even though longer timescale properties may not be fully converged in the 2 ns simulation. Selection of the primary unit to correspond to five protomers of this virus allowed comparisons within a single trajectory of structural and dynamic properties at rotational axes with and without imposed symmetries. The only significant difference observed is the density of water within 6 Å of a rotational symmetry axis with imposed microscopic symmetry (Figure 5a). This excluded volume is unavoidable given the nonphysical nonbonded interactions to self-images. Nevertheless, the structural and dynamical behavior of water remains without perturbation.

No differences in dynamics or structure due to the volume excluded by self-images were observed for the large protein system of HRV14. As a result of the many contributions to the atomic forces of the system, protein atoms can fluctuate into regions within 1 Å of a symmetry axis where self-image interactions occur (red line in Figure 7b). The sub-Angstrom excluded volume due to self-image interaction neither effected the dynamics nor the structural properties of the viral protein.

In summary, we have validated the usage of RSBC to minimize size of a system with rotational symmetry. Usage of a pentamer as primary unit can minimize the artifacts by avoiding the higher symmetry surrounding the 5-fold axis. While a pentamer as the primary unit will only reduce the size of the system by about 12 fold instead of 60 fold if a protomer were chosen as a primary unit, a pentamer of a viral capsid, with about 65,000 atoms and 26,000 water molecules, is well within the capacity of simulation using modern day computers.