Short abstract
Extensive experimental work on the effects of penetrating annular injuries indicated that large injuries impact axial compressive properties of small animal intervertebral discs, yet there is some disagreement regarding the sensitivity of mechanical tests to small injury sizes. In order to understand the mechanism of injury size sensitivity, this study proposed a simple one dimensional model coupling elastic deformations in the annulus with fluid flow into and out of the nucleus through both porous boundaries and through a penetrating annular injury. The model was evaluated numerically in dynamic compression with parameters obtained by fitting the solution to experimental stress-relaxation data. The model predicted low sensitivity of mechanical changes to injury diameter at both small and large sizes (as measured by low and high ratios of injury diameter to annulus thickness), with a narrow range of high sensitivity in between. The size at which axial mechanics were most sensitive to injury size (i.e., critical injury size) increased with loading frequency. This study provides a quantitative hypothetical model of how penetrating annulus fibrosus injuries in discs with a gelatinous nucleus pulposus may alter disc mechanics by changing nucleus pulposus fluid pressurization through introduction of a new fluid transport pathway though the annulus. This model also explains how puncture-induced biomechanical changes depend on both injury size and test protocol.
1. Introduction
Injuries that penetrate the annulus fibrosus (AF) of the intervertebral disc (IVD) can arise from accumulation of micro-damage or acute events, such as needle puncture. A more mechanistic understanding of the biomechanical effects that penetrating AF injuries have on the intact IVD is a priority since needle puncture has becoming a standard model of inducing degeneration in many small animal models [1,2], and also because needle injection is a likely pathway for injecting therapeutic agents in to IVDs [3,4].
Penetrating AF injuries can affect IVD mechanics via both nucleus pulposus (NP) depressurization and AF fiber breakage. Tensile testing of AF tissue has shown a decrease in stiffness proportional to the number of fibers disrupted by an injury [5]. Fiber breakage alone; however, tends to largely underestimate the effect of injury on whole disc mechanics [6]. This implies that changes in fluid pressurization under load have a large effect on compressive mechanics following injury. The concept that puncture injuries predominantly affect IVD pressurization is supported by studies showing IVD height loss following needle puncture and decreased intradiscal pressure following midplane tears only when the injury fully penetrated the annulus [1,7]. Direct measurements of intradiscal pressure during injection show a decrease in disc rupture pressure with increasing needle size with a decrease in sensitivity at larger needle sizes [8].
There is some disagreement in the literature about the sensitivity of disc axial mechanics to penetrating injuries of increasing size. Under some test conditions, puncture injuries using needles smaller than ∼40% of disc height resulted in changes in axial stiffness which were either insignificant [9] or evident only in the neutral zone while injuries with larger needles had more significant effects on IVD mechanics [10]. These needle-size related effects are somewhat contradictory with other tests that showed similar loss of IVD height in both small and large needle puncture injuries and further demonstrated ∼20% decrease in IVD dynamic axial stiffness [11,12] regardless of needle size. In the rat caudal IVD's tested by Michalek et al. [11], the drop in stiffness following puncture was consistent across a range of needle sizes shown histologically to result in a large difference in AF hole volume. Migration of NP material was thus not likely to be the mechanism of decreased axial stiffness, as stiffness would be expected to decrease proportionally to the amount of material displaced. Additionally, the difference in stiffness between punctured and un-punctured discs was found to depend on disc hydration. Together, these results suggest that the sensitivity of disc mechanics to a penetrating injury may be dependent on testing conditions and hydration state as well as injury size, and provides important justification for an improved understanding of the mechanism of how needle injury affects IVD mechanics.
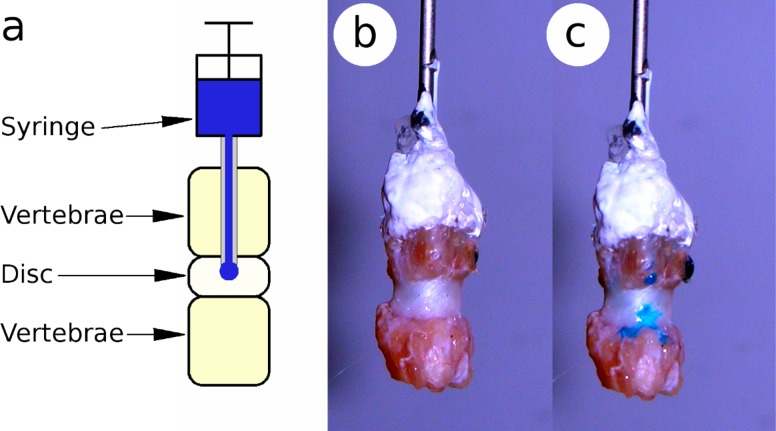
It has previously been proposed that fluid flow into and out of the disc nucleus plays a role in governing disc axial stiffness primarily at short time scales with fluid re-distribution between the nucleus and annulus affecting longer time scales [13]. Needle puncture has also been shown to alter effective permeability when using a fluid transport model to compare punctured and un-punctured discs [14]. A simple pilot study showed that dye injected through the vertebral endplate of a rat caudal IVD will leak through the track of a needle pushed through the AF (Fig. 1). This suggests that a needle puncture injury affects IVD dynamic axial mechanics by altering fluid transport pathways.
Fig. 1.
A pilot study implicated puncture injury as mechanism of altered fluid transport. Schematic of test apparatus (a) and rat caudal IVD before (b) and after (c) puncture with a 30 gauge needle.
We introduce the concept that needle puncture injury in the IVD can create a “pressure vent” through which water may exit the disc more easily than it may through the vertebral endplates, and we develop an analytical model to quantitatively test this hypothesis. It stands to reason that the resistance to fluid flow will decrease as the size of this pressure vent injury increases until it reaches a size above which resistance is effectively zero. However, it is currently unknown what this critical size is for intervertebral discs under physiologically relevant rates and magnitudes of loading. The purpose of this study was to develop an analytical model capable of estimating the sensitivity of small animal IVD dynamic compressive mechanics to penetrating annular injuries. The model was compared to rat caudal motion segments, which are attractive models for in vivo injury studies [14,15] because of their accessibility, simple geometry and composition, and relative ease of monitoring biomechanics prior to animal sacrifice [16].
2. Methods
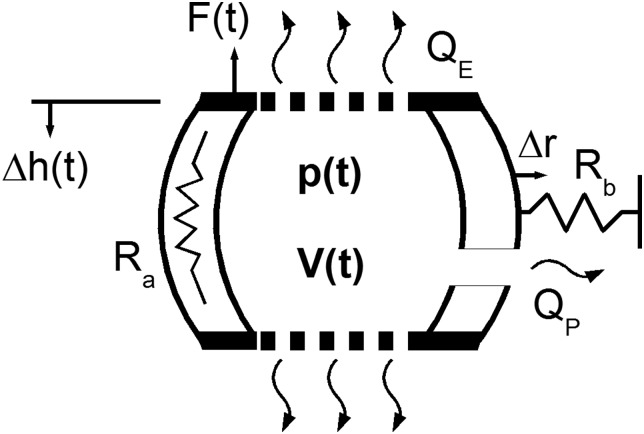
A simplified IVD model is represented as a pressure vessel constrained by axial and radial elasticity, and containing multiple pathways for fluid transport (Fig. 2). A decrease in disc height leads to increased pressure causing fluid to leave the disc through three mechanisms. The first is the injury flow, represented as a pipe of hydraulic diameter, d, which exhibits Poiseuille flow. The second is porous flow, governed by Darcy's Law, with effective permeability, Ke. The third is storage, representing fluid redistributed upon radial bulging restrained by spring, Rb, associated with elasticity of radial bulging of the disc annulus. Axial elasticity is represented by a spring with linear stiffness, Ra. This assumption may be considered valid for compression in the neutral zone, which in the rat IVD may account for over 60% of the disc height [17].
Fig. 2.
Schematic representation of analytical model with penetrating AF injury. This simplified model of the IVD is represented as a pressure vessel constrained by axial, Ra, and radial, Rb, elasticity. This model is capable of three fluid transport mechanisms: injury flow, represented as a pipe of hydraulic diameter, d, which exhibits Poiseuille flow; porous flow, governed by Darcy's Law, with effective permeability, Ke; and storage, representing fluid redistribution upon radial bulging restrained by radial elasticity spring.
The governing equation of axial reaction force due to fluid pressurization, Ff, begins with the assumption that it is proportional to pressure, p, pushing against a disc endplate with area Ae.
| (1) |
Internal pressure in the nucleus may also be defined in terms of its ability to push or pull fluid into or out of the volume, V, at a rate proportional to a constant, Cf.
| (2) |
The fluid volume of the disc nucleus is assumed to be that of a cubic polynomial revolved around the center axis of the disc. The annulus is assumed to be attached flexibly to the endplates at radius, r0, and upon pressurization, Ff/Ae, stretches linearly at its midplane according to compliance Rb. The disc has initial height h0, which changed under applied displacement by Δh.
| (3) |
Taking the time derivative of Eq. (3) and combining with Eq. (2) yields the following nonlinear differential equation that governs the fluid pressurization force.
| (4) |
The fluid flow coefficient, Cf, is derived using Darcy's law for permeable boundaries and fully developed Poiseuille flow in a cylinder to represent the puncture. The resulting constant depends on effective permeability, Ke, injury hydraulic diameter, d, injury length, L, fluid density, ρ, and fluid viscosity, ν. Derivation of Cf is more fully described in the Appendix.
| (5) |
The solid elastic behavior, Fs, of the disc was assumed to be linear and modeled using Hooke's Law, with stiffness, Ra.
| (6) |
Reaction forces for a prescribed displacement, Δh, by using a fourth order Runge-Kutta routine to solve Eq. (4), and adding the solution to the result of Eq. (6). Disc geometric parameters (h0, r0, Ae) were estimated from histological sections, and fluid parameters (ρ, ν) correspond to water at atmospheric pressure and 30 °C.
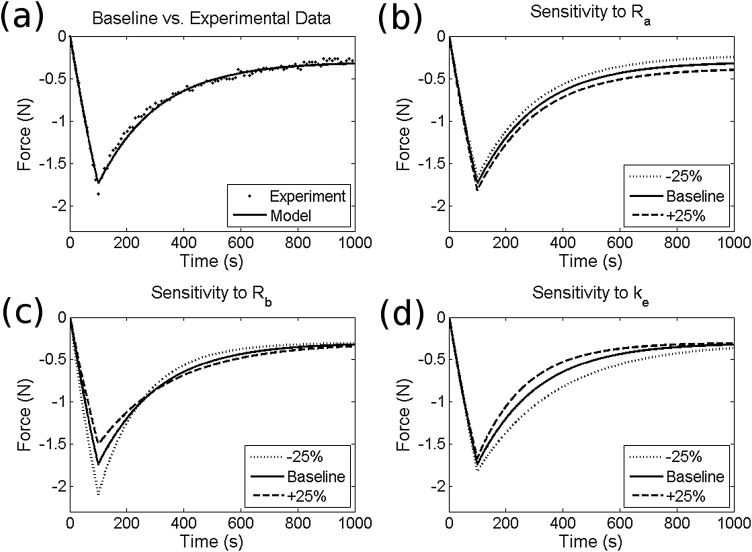
The model was calibrated by varying Ra, Rb, and, Ke to match experimental data (Fig. 3(a)), from five stress-relaxation experiments performed on un-punctured rat caudal motion segments prepared as previously described [13]. The loading protocol consisted of a 100 second ramp to 0.1mm (∼10% of disc height) followed by a 15 min dwell. The resulting baseline parameter values are given in Table 1. A parametric study was performed on the stress relaxation fit in order to evaluate the independence of these three parameters as well as sensitivity to ±25% variations. Using these parameters, the model was run across a range of diameter ratios (injury diameter divided by annulus thickness) in order to predict changes in dynamic compressive properties following puncture. Dynamic stiffness was calculated using a loading input of ten cycles of 0.1 Hz sinusoidal compression ranging from 0 to −10% of initial height, the last of which was used for analysis. The effects of variations in amplitude and frequency of applied displacement on stiffness trends was also investigated.
Fig. 3.
Model validation showing fit to experimental stress-relaxation data (a) and sensitivity to variations in parameters Ra, Rb, and Ke (b)–(d)
Table 1.
Analytical model parameters
| h0 | 1 e−3m | r0 | 1.50e−3m | Ra | 6.24e3 N/m | Rb | 7.60e−10 m3/N |
|---|---|---|---|---|---|---|---|
| ν | 8 e−7 m2/s | ρ | 996 kg/m3 | Ae | 1.40 e−5 m2 | Ke | 1.52e-17 m5/Ns |
3. Results
The sensitivity study (Figs. 3(b)–(d)) confirmed that variations in parameters Ra, Rb, and Ke have independent effects on time dependent response to a prescribed compressive displacement. Specifically, alterations in tissue compressive stiffness, Ra, affected equilibrium compressive reaction force. Annular bulge compliance, Rb, affected peak force, while changes in permeability, Ke, influenced time to equilibrium. Given a cyclic compressive displacement, these parameters produce storage (K’) and loss (K”) stiffnesses of 52 N/mm and 0.78 N/mm, which fall within experimentally measured ranges of 21–70 N/mm and 0.74–4.8 N/mm, respectively [18,19].
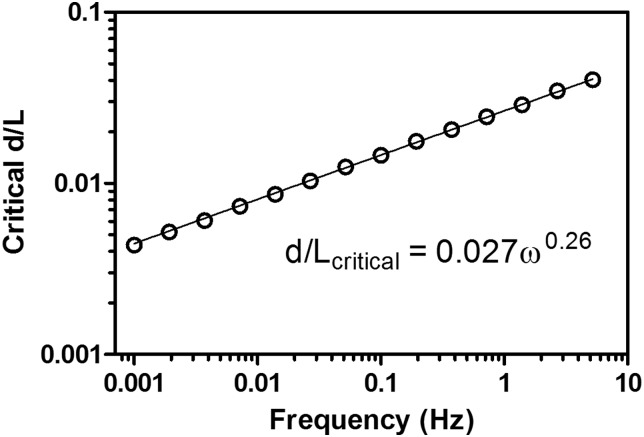
Both storage and loss stiffnesses were relatively insensitive to injury when injuries had small sizes (Fig. 4). As injury diameter relative to AF thickness (defined by diameter ratio d/L) increased, there was a sharp decrease in storage stiffness and a peak in loss stiffness. A critical diameter ratio was defined as the diameter ratio at which the second derivative of storage stiffness with respect to hydraulic diameter was zero. As the diameter ratio increased further, storage stiffness approached a new equilibrium value which was also insensitive to diameter, and loss stiffness returned to its un-injured value. There was a power law dependence of critical diameter ratio on displacement frequency (Fig. 5); critical diameter was not sensitive to displacement amplitude.
Fig. 4.
Dynamic compressive storage stiffness (a) and loss stiffness (b) relative to un-punctured as a function of d/L ratio
Fig. 5.
Critical d/L ratio increases linearly as a function of loading frequency
4. Discussion
This study was performed to provide insights into the effects of penetrating annular injuries on small animal disc axial mechanics due to the importance of needle puncture as a way of inducing degeneration in small animal models and the relevance of needle injection of therapeutics for repair. An analytical model was introduced to quantitatively test the hypothesis that penetrating annular injuries produce a “pressure vent” which enables a new flow pathway. This model accurately described stress relaxation data and patterns of reduced dynamic storage stiffness behaviors following needle puncture, although >80% drop in storage stiffness in the model was larger than the ∼30% drop reported experimentally [11]. The impact of injury size on elastic and viscous behavior showed regions of both insensitivity and of high sensitivity, and the critical needle diameter was frequency dependent, which provides an explanation for apparent differences in the literature with some studies suggesting small needles have a negligible effect on disc mechanics [10] and others indicate that all needle puncture injuries have similar effects on disc mechanics [11,12]. Consequently, the differences in the literature are most likely associated with protocol differences (i.e., loading rate) and/or choice of dependent variables.
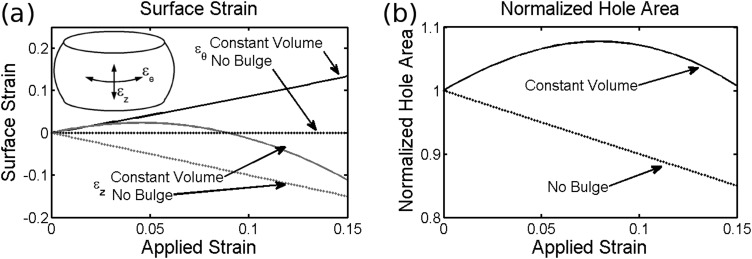
The current model is relevant to axisymmetric discs with gelatinous NPs under uniaxial loading as found in rodents, and such mechanical data from these animals is prevalent in the literature. The model assumes that the annulus fibrosus is a continuous solid which is a reasonable at large injury sizes, yet loses relevance as the injury shrinks to the length scale of the collagen fiber bundle diameter in the AF (0.04–0.33mm in the human disc [20]) since such fine needles will not puncture the AF reliably and it is difficult to estimate such small d/L ratios. The analytical model allows for the approximation of surface strains under load (Eqs. (A37)–(A41) in the Appendix) using Δr to calculate circumferential strain and the arc length of the bulge curve to calculate axial strain, which may be important for model validation or provide some insights for mechanobiological studies. Figure 6(a) shows these strains as a function of applied strain for two bounding cases; constant volume (high loading rate) and constant radius (no bulge/low loading rate). These conceptual situations represent the bounding cases for surface strain, although under experimental conditions “slow” loading will still have some radial bulge and “fast” loading will have some reduction in volume. The model does not account for any changes in hole geometry under load, yet Fig. 6(b) shows the result of the calculated biaxial strain on the area of an elliptical hole through the surface. Depending on the rate of loading and the subsequent degree of radial bulge, the hole may either increase or decrease in area. In either case, the change in area under physiological levels of strain is small and only likely to affect dynamic behavior with punctures close to the critical hydraulic diameter.
Fig. 6.
Calculation of surface strains (a) and resulting effect on the area of an elliptical hole (b) for bounding cases representing fast loading (constant volume) and slow loading (constant radius)
This simple one dimensional model qualitatively supports reported experimental findings and provides a potential mechanism for explaining why some experimental studies demonstrate sensitivity of needle puncture size on axial mechanics while others do not. The model demonstrates that a decrease in dynamic stiffness following puncture is only dependent on needle diameter over a short range around the critical size, and that all else being equal this critical size varies with loading frequency. Notably, the proposed “pressure vent” mechanism requires only a change in fluid flow behavior, rather than solid matrix damage, to produce a loss of dynamic stiffness. Experimental protocols which differ in loading rate and preload, which may alter both initial hydration and tissue permeability, are thus expected to disagree on the extent of injury induced changes in dynamic properties. It should also be noted that prior research has shown measurable localized damage [12,19] and increased risk of degeneration [21] resulting from punctures using needles that are very small relative to the size of the disc and may not drastically affect motion segment scale mechanics. Future refinements are required to move from a hypothetical model to a predictive model, and while the assumptions and limitations of the current model prevent it from being used to make a therapeutic recommendation, the current approach provides a framework for determining biomechanical testing protocols that are sensitive to both acute injury and the efficacy of different repair strategies.
Acknowledgment
This research was supported by grants from the National Institutes of Health (Grant Nos. R01 AR051146 and HL007944) and The NASA Vermont Space Grant Consortium (Grant No. NNX07AK92A).
Appendix
Derivation of Governing Equations.
The total axial force acting on the disc is assumed to be the sum of fluid pressurization force, Ff, and solid matrix, Fs, force.
| (A1) |
Force resulting from fluid pressurization is the product of hydrostatic nucleus pulposus pressure, p, pressing against endplate area, Ae.
| (A2) |
Nucleus pressure results in fluid volume, V, loss through porous and puncture boundaries, and is related by a constant coefficient, Cf.
| (A3) |
Combining Eqs. (A2) and (A3) gives fluid force as a function of fluid flow rate into or out of the disc.
| (A4) |
Nucleus volume in the un-deformed state is assumed to be that of a cylinder initially defined by radius, r0, and height, h0, and varied by radial, Δr, and axial, Δh, deformations. The annulus is connected to the vertebral bodies such that displacements, but not rotations are constrained. The radial deformation of the annulus is defined from the midplane to the upper vertebral body by a function, fr. In order to simplify notation, the position of the upper vertebrae relative to the mid plane, (h0 + Δh)/2, is indicated by X. The boundary conditions are thus:
At h = 0:
| (A5) |
| (A6) |
At h = X:
| (A7) |
| (A8) |
These boundary conditions may be satisfied by a cubic polynomial:
| (A9) |
| (A10) |
| (A11) |
Applying the four boundary conditions, Eqs. (A5)–(A8), yield the following four equations, respectively.
| (A12) |
| (A13) |
| (A14) |
| (A15) |
Solving (A12)–(A13) for the coefficients in Eq. (A9) yields:
| (A16) |
The volume of the top half of the disc is obtained by revolving fr about the z-axis and integrating from the mid-plane to the end-plate.
| (A17) |
Substituting Eqs. (A16) into (A17) and integrating yields:
| (A18) |
Replacing X, and doubling to account for the lower half of the disc:
| (A19) |
Radial deformation is assumed to be linearly proportional to pressure at small displacements and related by compliance, Rb.
| (A20) |
Substituting (A20) into (A19) nucleus volume is given by a function of initial dimensions, fluid pressurization force, annular stiffness, and axial deformation:
| (A21) |
Taking the time derivative of the nucleus volume:
| (A22) |
| (A23) |
Substituting Eqs. (A23) into (A22), the governing equation for fluid force becomes:
| (A24) |
The solid matrix of the disc is assumed to be linearly elastic
| (A25) |
Fluid Flow Coefficient.
The fluid pressurization and venting relationship is derived by summing fluid flow rates through porous (end-plate), Qe, and puncture, Qp, boundaries.
| (A26) |
Flow through the porous boundaries is governed by Darcy's law
| (A27) |
Flow through the puncture is governed by Poiseuille flow, with pressure drop proportional to the square of the volumetric flow rate.
| (A28) |
The proportionality constant, KP is defined by the length, L, and diameter, d, of the puncture, fluid density, ρ, and a friction factor, f.
| (A29) |
The friction factor, f, is proportional to the Reynolds number, Re, for low speed flow, (Re < 2300).
| (A30) |
The velocity term in the Reynolds number may be replaced with flow rate using the following geometric relationship
| (A31) |
The result is a friction factor defined by flow rate, puncture diameter, and fluid viscosity, ν
| (A32) |
Substituting Eqs. (A32) into (A29):
| (A33) |
Substituting (A33) into (A28) and solving for flow rate:
| (A34) |
Substituting Eqs. (A34) and (A27) into (A26), the total discharge from pressurization becomes:
| (A35) |
From (A35), the fluid flow coefficient, Cf in (A3) is given by:
| (A36) |
Surface Strains.
The geometry of an initially circular hole following axial compression was determined by calculating axial (ɛz) and circumferential (ɛq) surface strains on the AF at mid height under two bounding conditions; constant volume and constant radius. For the constant volume case, the disc volume, V0, was first calculated at its initial height using Eq. (A21). Equation (A19) was then solved for the increase in bulge radius, Δr, required to maintain V0 under deformation, Δh.
| (A37) |
This Δr is then substituted into Eq. (A16) to yield a function, fr(z), defining the outer surface of the disc. The axial contour length, s, of the surface is then calculated from fr.
| (A38) |
Axial strain is calculated from the contour length at Δh relative h0/2, and circumferential strain from Δr relative to r0.
| (A39) |
In the constant radius case, circumferential strain is zero and axial strain is calculated from the ratio of disc height to initial height.
| (A40) |
The area of a hole, relative to an initial area of one, is then calculated using strains from Eq. (A39) or (A40) and an assumption of elliptical geometry.
| (A41) |
Contributor Information
Arthur J. Michalek, Department of Molecular Physiology and Biophysics, University of Vermont, Burlington, VT
James C. Iatridis, Professor and Director of Spine Research, Leni and Peter W. May Department of Orthopaedics, Mount Sinai School of Medicine, New York, NY, e-mail: james.iatrdis@mssm.edu.
References
- [1]. Aoki, Y. , Akeda, K. , An, H. , Muehleman, C. , Takahashi, K. , Moriya, H. , and Masuda, K. , 2006, “Nerve Fiber Ingrowth into Scar Tissue Formed Following Nucleus Pulposus Extrusion in the Rabbit Anular-Puncture Disc Degeneration Model: Effects of Depth of Puncture,” Spine, 31(21), pp. E774–E780. 10.1097/01.brs.0000238681.71537.41 [DOI] [PubMed] [Google Scholar]
- [2]. Sobajima, S. , Kompel, J. F. , Kim, J. S. , Wallach, C. J. , Robertson, D. D. , Vogt, M. T. , Kang, J. D. , and Gilbertson, L. G. , 2005, “A Slowly Progressive and Reproducible Animal Model of Intervertebral Disc Degeneration Characterized by Mri, X-Ray, and Histology,” Spine, 30(1), pp. 15–24. 10.1097/01.brs.0000148048.15348.9b [DOI] [PubMed] [Google Scholar]
- [3]. Alini, M. , Roughley, P. J. , Antoniou, J. , Stoll, T. , and Aebi, M. , 2002, “A Biological Approach to Treating Disc Degeneration: Not for Today, but Maybe for Tomorrow,” Eur. Spine J. 2, pp. S215–S220. 10.1016/S1529-9430(02)00156-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Masuda, K. , and Lotz, J. C. , “New Challenges for Intervertebral Disc Treatment Using Regenerative Medicine,” Tissue Eng., 16(1), pp. 147–158. 10.1089/ten.teb.2009.0451 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Adams, M. A. , and Green, T. P. , 1993, “Tensile Properties of the Annulus Fibrosus, I. The Contribution of Fibre-Matrix Interactions to Tensile Stiffness and Strength,” Eur. Spine J., 4(2), pp. 203–208. 10.1007/BF00299447 [DOI] [PubMed] [Google Scholar]
- [6]. Iatridis, J. C. , Michalek, A. J. , Purmessur, D. , and Korecki, C. L. , 2009, “Localized Intervertebral Disc Injury Leads to Organ Level Changes in Structure, Cellularity, and Biosynthesis,” Cellular and Molecular Bioengineering, 2(3), pp. 437–447. 10.1007/s12195-009-0072-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Holm, S. , Ekstrom, L. , Kaigle Holm, A. , and Hansson, T. , 2007, “Intradiscal Pressure in the Degenerated Porcine Intervertebral Disc,” Vet. Comp. Orthop. Traumatol., 20(1), pp. 29–33. [PubMed] [Google Scholar]
- [8]. Wang, J. L. , Tsai, Y. C. , and Wang, Y. H. , 2007, “The Leakage Pathway and Effect of Needle Gauge on Degree of Disc Injury Post Annular Puncture: A Comparative Study Using Aged Human and Adolescent Porcine Discs,” Spine, 32(17), pp. 1809–1815. 10.1097/BRS.0b013e31811ec282 [DOI] [PubMed] [Google Scholar]
- [9]. Boxberger, J. I. , Sen, S. , Yerramalli, C. S. , and Elliott, D. M. , 2006, “Nucleus Pulposus Glycosaminoglycan Content Is Correlated with Axial Mechanics in Rat Lumbar Motion Segments,” J. Orthop. Res., 24(9), pp. 1906–1915. 10.1002/jor.v24:9 [DOI] [PubMed] [Google Scholar]
- [10]. Elliott, D. M. , Yerramalli, C. S. , Beckstein, J. C. , Boxberger, J. I. , Johannessen, W. , and Vresilovic, E. J. , 2008, “The Effect of Relative Needle Diameter in Puncture and Sham Injection Animal Models of Degeneration,” Spine, 33(6), pp. 588–596. 10.1097/BRS.0b013e318166e0a2 [DOI] [PubMed] [Google Scholar]
- [11]. Michalek, A. J. , Funabashi, K. L. , and Iatridis, J. C. , “Needle Puncture Injury of the Rat Intervertebral Disc Affects Torsional and Compressive Biomechanics Differently,” Eur. Spine J., 19(12), pp. 2110–2116. 10.1007/s00586-010-1473-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Korecki, C. L. , Costi, J. J. , and Iatridis, J. C. , 2008, “Needle Puncture Injury Affects Intervertebral Disc Mechanics and Biology in an Organ Culture Model,” Spine, 33(3), pp. 235–241. 10.1097/BRS.0b013e3181624504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Masuoka, K. , Michalek, A. J. , Maclean, J. J. , Stokes, I. A. , and Iatridis, J. C. , 2007, “Different Effects of Static Versus Cyclic Compressive Loading on Rat Intervertebral Disc Height and Water Loss in Vitro,” Spine, 32(18), pp. 1974–179. 10.1097/BRS.0b013e318133d591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Hsieh, A. H. , Hwang, D. , Ryan, D. A. , Freeman, A. K. , and Kim, H. , 2009, “Degenerative Anular Changes Induced by Puncture Are Associated with Insufficiency of Disc Biomechanical Function,” Spine, 34(10), pp. 998–1005. 10.1097/BRS.0b013e31819c09c4 [DOI] [PubMed] [Google Scholar]
- [15]. Rousseau, M. A. , Ulrich, J. A. , Bass, E. C. , Rodriguez, A. G. , Liu, J. J. , and Lotz, J. C. , 2007, “Stab Incision for Inducing Intervertebral Disc Degeneration in the Rat,” Spine, 32(1), pp. 17–24. 10.1097/01.brs.0000251013.07656.45 [DOI] [PubMed] [Google Scholar]
- [16]. Wuertz, K. , Godburn, K. , Maclean, J. J. , Barbir, A. , Donnelly, J. S. , Roughley, P. J. , Alini, M. and Iatridis, J. C. , 2009, “In Vivo Remodeling of Intervertebral Discs in Response to Short- and Long-Term Dynamic Compression,” J. Orthop. Res., 27(9), pp. 1235–1242. 10.1002/jor.20867 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Barbir, A. , Michalek, A. J. , Abbott, R. D. , and Iatridis, J. C. , “Effects of Enzymatic Digestion on Compressive Properties of Rat Intervertebral Discs,” J. Biomech., 43(6), pp. 1067–1073. 10.1016/j.jbiomech.2009.12.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Boxberger, J. I. , Orlansky, A. S. , Sen, S. , and Elliott, D. M. , 2009, “Reduced Nucleus Pulposus Glycosaminoglycan Content Alters Intervertebral Disc Dynamic Viscoelastic Mechanics,” J. Biomech., 42(12), pp. 1941–1946. 10.1016/j.jbiomech.2009.05.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Michalek, A. J. , Funabashi, K. L. , and Iatridis, J. C. , 2010, “Needle Puncture Injury of the Rat Intervertebral Disc Affects Torsional and Compressive Biomechanics Differently,” Eur. Spine J, 19(12), pp. 2110–2116. 10.1007/s00586-010-1473-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Marchand, F. , and Ahmed, A. M. , 1990, “Investigation of the Laminate Structure of Lumbar Disc Anulus Fibrosus,” Spine, 15(5), pp. 402–410. 10.1097/00007632-199005000-00011 [DOI] [PubMed] [Google Scholar]
- [21]. Carragee, E. J. , Don, A. S. , Hurwitz, E. L. , Cuellar, J. M. , Carrino, J. A. , and Herzog, R. , 2009, “2009 Issls Prize Winner: Does Discography Cause Accelerated Progression of Degeneration Changes in the Lumbar Disc: A Ten-Year Matched Cohort Study,” Spine, 34(21), pp. 2338–2345. 10.1097/BRS.0b013e3181ab5432 [DOI] [PubMed] [Google Scholar]