Ultrastructural analysis of hippocampal neuropil from the connectomics perspective

Abstract

Complete reconstructions of vertebrate neuronal circuits on the synaptic level require new approaches. Here, serial section transmission electron microscopy was automated to densely reconstruct four volumes, totaling 670μm³, from the rat hippocampus as proving grounds to determine when axo-dendritic proximities predict synapses. First, in contrast with Peters’ rule, the density of axons within reach of dendritic spines did not predict synaptic density along dendrites because the fraction of axons making synapses was variable. Second, an axo-dendritic touch did not predict a synapse; nevertheless, the density of synapses along a hippocampal dendrite appeared to be a universal fraction, 0.2, of the density of touches. Finally, the largest touch between an axonal bouton and spine indicated the site of actual synapses with about 80% precision, but would miss about half of all synapses. Thus, it will be difficult to predict synaptic connectivity using data sets missing ultrastructural details that distinguish between axo-dendritic touches and bona fide synapses.

Introduction

Reconstructing neuronal circuits on the level of synapses is a central problem in neuroscience. Smaller invertebrate circuits can be reconstructed using serial section transmission electron microscopy (ssTEM) by identifying synapses and manually tracing pre- and post-synaptic neuronal processes to their cell bodies as has been demonstrated for the C. elegans nervous system (White, Southgate et al. 1986; Chen, Hall et al. 2006). However, manually reconstructing vertebrate circuits using ssTEM is impractical and it remains unclear which technology will be capable of achieving this goal. Although automating ssTEM seems promising (Jurrus, Whitaker et al. 2008; Anderson, Jones et al. 2009; Mishchenko 2009), the proof of principle is missing. At the same time, older approaches to reconstruct neuronal circuits are being used (Binzegger, Douglas et al. 2004; Stepanyants and Chklovskii 2005; Stepanyants, Hirsch et al. 2008) and alternative approaches are being developed (Briggman and Denk 2006; Smith 2007; Helmstaedter, Briggman et al. 2008; Luo, Callaway et al. 2008).

In this paper, we used manual (RECONSTRUCT™ (Fiala and Harris 2001; Fiala 2005)) and automated (Mishchenko 2009) ssTEM reconstruction techniques to reconstruct densely four volumes of rat hippocampus neuropil. Although the reconstructed volumes are too small to contain complete circuits, they demonstrate that ssTEM can be scaled through automation. In addition, we used the reconstructed volumes as proving grounds to determine whether other approaches based on proximities between axons and dendrites can yield reliable predictions of synaptic connectivity.

Perhaps the oldest method for inferring synaptic connectivity used light microscopy and relies on counting proximities between axons and dendrites that can be bridged by a spine, or so-called potential synapses (Peters and Feldman 1976; Braitenberg and Schuz 1998; Stepanyants and Chklovskii 2005). As the ratio of actual to potential synapses, which we call the connectivity fraction, is much less than one (Stepanyants, Hof et al. 2002), such a method can predict connectivity only probabilistically. The number of actual synapses, for example, along a dendrite is given by the number of potential synapses times the connectivity fraction. For this method to have practical value, the connectivity fraction must be invariant among dendrites, an assumption known as “Peters’ rule” (Peters and Feldman 1976; Braitenberg and Schuz 1998). By relying on this assumption synaptic connectivity has been estimated in various neuronal circuits (Binzegger, Douglas et al. 2004; Stepanyants and Chklovskii 2005; Jefferis, Potter et al. 2007; Stepanyants, Hirsch et al. 2008),

The validity of Peters’ rule has been explored both anatomically using sparse reconstructions (White and Rock 1981; White 2002; da Costa and Martin 2009) and electrophysiologically using stimulation of neuronal classes (Shepherd, Stepanyants et al. 2005; Petreanu, Mao et al. 2009). These studies revealed two kinds of Peters’ rule violations: different classes of pre-synaptic neurons possess different connectivity fractions onto a given post-synaptic neuron class and different post-synaptic neuron classes have different connectivity fractions with a given pre-synaptic neuron class. Such violations indicate connection specificity among neuronal classes. However, the validity of Peters’ rule within an apparently homogeneous class of neurons could not be tested because it required dense reconstructions.

Among alternative approaches, Serial Block-Face Scanning Electron Microscopy (SBFSEM) (Denk and Horstmann 2004) may benefit from knowing the relationship between proximities and synapses. To outline processes this technique requires high-contrast labeling, which emphasizes the extracellular space, while failing to visualize intra-cellular structures, such as synaptic vesicles and postsynaptic densities that are required for synapse identification. Hence, having a way to identify synapses based on the shape of axons and dendrites and their geometrical arrangement, such as touching, might strengthen the appeal of this and similar approaches for circuit reconstruction.

In reconstructed volumes, we identified all axons, boutons, dendrites, dendritic spines, post-synaptic densities (PSDs) and glial process, and measured the distributions of the dimensions of identified objects. The knowledge of dimensions helped to formulate quantitatively new methods to infer synaptic connectivity. We demonstrate that several formulations of Peters’ rule fail to predict the density of synapses along dendrites because the probability of potential synapses being actual synapses varies among dendrites. We propose two novel methods to predict the density of synapses along dendrites using the density of touches and dendritic shaft caliber. Because the density of synapses is a small fraction (<20%) of the density of touches, the question arises whether touches can predict individual synapses without using synaptic attributes available only in ssTEM. To answer this question, we attempted to predict synapses from touches using their dimensions and found that relative areas of contact among boutons and spines can identify synapses with reasonably high probability approximating 80 percent, although many synapses are missed. The results will also help to evaluate other methods for inferring synaptic connectivity.

Results

1. Reconstruction of neuropil volumes

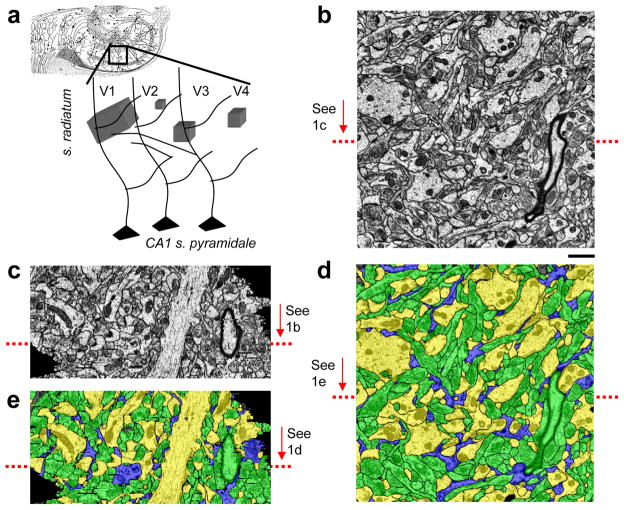
We photographed through ssTEM four volumes of neuropil from the middle of stratum radiatum in hippocampal area CA1 at a spatial resolution of 2.2 nm/pixel and section thicknesses of 45–50 nm (Figures 1a, b). Volumes 1–3 (V1–3) came from a mature and volume 4 (V4) an immature postnatal day 21 rat (see Methods). V1 centered on a radial oblique dendrite; V2 centered on a dendritic spine; V3 centered on an apical dendrite, and V4 was randomly located in s. radiatum (Figure 1a, and Table 1).

Figure 1.

Reconstructed volumes. a) Location of the four volumes (V1–4) relative to CA1 pyramidal neuron dendrites in the hippocampus; b) Typical ssTEM micrograph of the hippocampus neuropil from V1; c) V1 re-sectioned orthogonal to the cutting plane at the location indicated by the red arrow in b. Note that the stack is well aligned and the ultrastructure is visible despite lower z-resolution; d) Electron micrograph from b after automated segmentation and proofreading colored according to the object class: axons - green, dendrites - yellow, and glia processes - blue; e) Segmented re-section from c. Scale bar:1μm (b–e)

Table 1.

Sample volumes and numbers of unique 3D objects in each

Name	Manual	Automated	All 3D Objects	Axons	Dendrites & spine fragments	Glia fragments	Unidentified objects # (%volume)
V1 (“Oblique”)	42 μm3	9.1 × 9.0 × 4.1 = 336μm3	1496	629	66 & 112	151	538 (3.9%)
V2 (“Spine”)	7 μm3	5.4 × 3.8 × 1.7 = 35 μm3	524	345	21 & 80	35	43 (0.7%)
V3 (“Apical”)	167 μm3	6.1 × 6.1 × 4.5 = 167 μm3	597	445	33 & 118	57	0
V4 (PN21)	N/A	6.0 × 4.3 ×5.1 = 132 μm3	548	256	29 & 75	56	132 (3.6%)
Total	219 μm3	670 μm3	3165	1675	149 & 385	243	713 (2.7%)

We partitioned, or segmented, these volumes along plasma membranes into three-dimensional objects using both automated and manual approaches. In the automated approach, the computer performed alignment (Figure 1b,c) and segmentation (Figure 1d, e) (Mishchenko 2009). Then a proofreading facility visually guided the user through serial sections of each object to verify or correct the segmentation. The segmentation was complete meaning that each pixel was attributed to a unique object or to a boundary between objects. In addition, we manually segmented sub-regions of V1–3 into three-dimensional objects using the RECONSTRUCT™ software (Fiala and Harris 2001; Fiala 2005) (http://synapses.clm.utexas.edu); which allowed us to estimate the accuracy and times savings of the automated approach (see below).

We classified reconstructed three-dimensional objects into axons, dendrites, and glial processes, Figures 1d,e, 2a, using the following characteristic features (Peters, Palay et al. 1991; Harris 2008). Axons consisted of thin processes interspersed with boutons containing synaptic vesicles. Dendrites received synapses, both asymmetric (excitatory), recognized by thickened post-synaptic densities (PSDs), and symmetric (inhibitory), recognized by pleomorphic vesicles and uniform thinner densities on pre and postsynaptic sides. Spiny dendrites were further sub-divided into shafts and spines connected to their dendritic shafts through necks and receiving only asymmetric synapses. Small astroglial processes interdigitated irregularly among axons and dendrites, and contained glycogen granules.

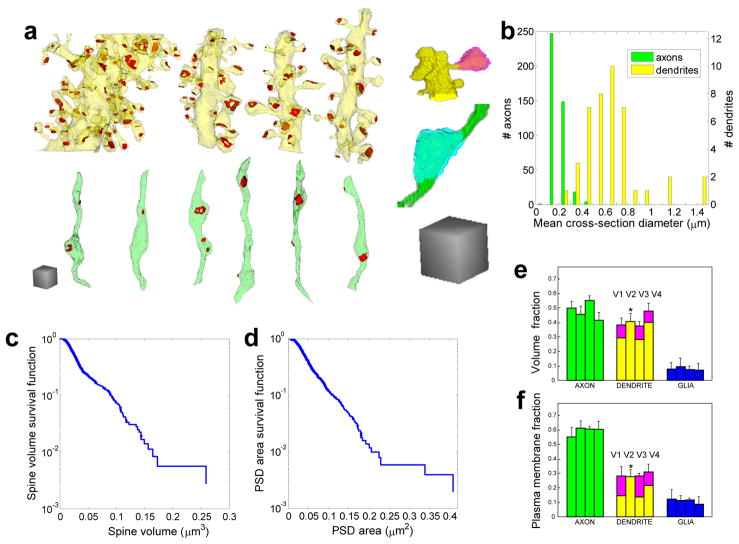
Figure 2.

Shapes and dimensions of various objects in the neuropil. a) Three-dimensional reconstruction of representative objects in V3: dendrites (yellow), axons (green), post-synaptic densities (PSDs) (red), spine (pink), and bouton (cyan); b) Distribution of the effective axonal and dendritic cross-section diameters in V1 and V3; c) Survival function of spine volume, i.e. a fraction of spines whose volume is less than a given value; d) survival function of the PSD area. Only spines and PSDs completely contained within V1 were included in c) and d); e) Distribution of volume among different object classes in the four volumes; f) Distribution of plasma membrane surface area among different object classes. Scale cubes in a) are 1 μm on the side; bars in e) and f) are arranged sequentially V1 → V4 in each object class (axon, dendrite, glia); * in e) and f) - calculations of the volume of spine heads and other analysis were not performed for V2 given its small size.

Because the above characteristic features were absent from many sections in any single ssTEM image, the three-dimensional nature of the reconstruction was essential for object identification. As automated reconstructions, with the exception of V3, extended through the whole image volume, some (<4% by volume) objects that grazed the volume edges did not contain enough features for unequivocal identification, Table 1. Since the manually reconstructed volumes did not extend to the edges of the image volumes, all of the objects could be identified unambiguously by viewing them as they passed beyond the boundaries (Supplemental Figure 1).

Currently, volume reconstruction is limited by time. Tracing is the most time consuming step for the manual process and proofreading is the most time consuming step in the automated process. In both approaches, experience reduced the time needed to follow and identify small objects through sections, establish correct connections, and complete the reconstructions. Proofreading V1 (336 μm³) by an expert (Harris) took approximately 90 hours. Proofreading V3 (167 μm³) by an experienced electron microscopist (Mendenhall), who had limited experience in hippocampal neuropil, took approximately 160 hours: 80 hours to learn and 80 hours to complete. Hence, the average time required to proofread and correct the automatically segmented objects in V1 and V3 was about 10–20 min per μm³. Relative to manual tracing, we estimate a tenfold savings in time.

2. Validation of automated reconstructions

We validated the automated reconstructions by comparing them against manually reconstructed sub-volumes as well as repeat viewing by more than one proofreader. In addition, we measured object dimensions and the partitioning of volume and plasma membrane area among object classes. Comparison of these values among volumes and with those previously reported provided additional validation and confirmed that the volumes were representative of hippocampal neuropil in general.

Reconstruction errors affecting the topology of the circuit, which we name content errors’, typically occurred when objects with dimensions equal to or less than section thickness overlapped and ran tangentially. Thus, the distribution of content errors is non-uniform among different classes of objects (Table 2). No content errors occurred in the reconstruction of thick dendritic shafts. A few spines were lost when their necks were obliquely sectioned and some thin axons were overlapping at some places along their lengths and may have been accidentally merged (Table 2). For example, in V3, this resulted in 26 content errors per 346 spines for an error rate of 0.08 errors per spine; and 45/447 = 0.1 per axon (0.022 errors per micron of axon). We further characterized the content error rate by computing the relative fraction of all contours that had these potential errors (Table 2).

Table 2.

Statistics of potential content errors in automated and manual reconstructions

	Number of potential content errors					# of content errors / # of contours = percentage Auto
Compared Volumes	Dendrites	Spines		Axons
V1 42 μm3	none	3	6	8	9	15/7,500 = 0.2%
V2 7 μm3	none	none	7	none	none	7/1,700 = 0.4%
V3 167 μm3	none	11	26	4	45	71/23,500 = 0.3%

Astroglial processes could often be traced to larger processes with characteristic bundles of intermediate filaments (Ventura and Harris 1999). Sometimes the glial processes could not be linked unambiquously to one another; nevertheless, they likely belonged to one or at most a few astrocytes. This conclusion is based on the observation that astrocytes span regions larger than reconstructed volumes and tile neuropil without substantial overlap between neighboring astrocytes (Bushong, Martone et al. 2002; Livet, Weissman et al. 2007)).

Discrepancies in the 3D shapes of corresponding processes reconstructed by the manual or automated approaches resulted in volume differences of less than 10% (Supplemental Figure 2). The mean deviation between the same contours produced by the manual and automated approaches was 5 nm. Since the automated approach was performed with the images down sampled to a resolution of 4.4 nm/pixel, this value corresponds to a mean deviation of about one pixel. The observed volume difference is consistent with 5 nm variations in the placing of boundary contours along small processes that are 100–200 nm in diameter, which is typical for axons, the most common object in these volumes.

We found that axons, dendrites, and synapses vary widely in their dimensions both within and among classes. Axons ranged in effective cross-section from 0.10 to 0.50 μm, while dendrites ranged from 0.28 to 1.49 μm (Figure 2b; see Methods for the algorithm used to compute the effective cross-section). Spine volumes ranged from 0.003 to 0.26μm³ (Figure 2c), and PSD areas ranged from 0.01 to 0.41μm² (Figure 2d). The breadth of these distributions suggests that the mean values (Table 3) carry only limited information about object dimensions. These distributions motivated the synapse prediction methods described below.

Table 3.

Summary of measured neuropil parameters

Axon diameter (V1 & V3)	0.20 ± 0.06 μm
Dendrite diameter (V1 & V3)	0.67 ± 0.26 μm
Mean PSD area (V1)	0.054 μm2
Exponential decay constant of PSD area (V1)	0.047 μm−2
Mean spine head volume (V1)	0.038 μm3
Exponential decay constant of spine head volume (V1)	0.037 μm−3
Number of axons touching dendritic shaft per μm of dendritic length (V1 & V3)	6 ± 2
Number of axons per μm2 volume cross-section (V1 & V3)	7
Number of axons crossing a cylinder 1 μm from dendritic shaft surface per length of dendrite (V1 & V3)	22 ± 6
Volume density of synapses (V1, V3 & V4)	2.2 ± 0.5 μm−3

To verify that our sample volumes were representative of the general neuropil we computed the fraction of neuropil volume that was occupied by various classes of objects (Figure 2e). We found that axons occupied about 50% and dendrites occupied about 40% of the volume. In the immature neuropil, V4, dendrites occupied a significantly larger fraction of the volume at the expense of axons (p<0.01). Glial processes occupied about 8% of all four volumes (Figure 2e). In volumes 1, 3 and 4, we distinguished spines from dendritic shafts and discovered they occupied about 9% of the total volume.

The relative distribution of plasma membrane surface area among neuropil components (Figure 2f) differed from the volume distributions (Figure 2e), which was not surprising given the differences in dimensions. Nearly 60% of the plasma membrane surface area belonged to axons, a value greater than their corresponding volume fraction consistent with their smaller caliber (Figure 2b). Likewise, the thin and tortuous glial processes provided 10–13% of all plasma membrane surface area (Figure 2f), which was much greater than their corresponding volume fraction (Figure 2e). Dendritic shaft surface area was about 15–20% of total membrane area (Figure 2f), substantially less than its corresponding volume fraction (Figure 2e) but also consistent with their larger caliber (Figure 2b). Spines occupied about 10–12% of the total plasma membrane surface area (Figure 2f).

Overall, the consistency of these results among the adult samples and the general agreement with previous reports (Harris and Stevens 1989; Lisman and Harris 1993; Schikorski and Stevens 1997; Sorra and Harris 2000; Chklovskii, Schikorski et al. 2002) suggests that the chosen volumes are reasonable representatives of dense hippocampal neuropil.

3. Peters’ rule does not accurately predict synapse density

A long-standing proposition for estimating synaptic connectivity, known as Peters’ rule, states that the number of synapses formed along a dendrite is proportional to the number of axons passing within reach of the spines emanating from the dendrite (Peters and Feldman 1976; Braitenberg and Schuz 1998), called potential synapses (Stepanyants, Hof et al. 2002). The coefficient of proportionality was called “filling fraction”(Stepanyants, Hof et al. 2002), and is hereby renamed to “connectivity fraction” to avoid confusion with the volume fractions discussed above. The maximum-reach connectivity fraction was defined as:

$$\text{maximum}\text{reach}\text{connectivity}\text{fraction}=\frac{\#\text{of}\text{axons}\text{presynaptic}\text{to}\text{reference}\text{dendrite}}{\#\text{of}\text{all}\text{axons}(d_{\mathit{spine}\mathit{reach}})},$$ (1)

where d_{spine reach} is the length of the dendrite’s longest spine.

We directly measured the maximum-reach connectivity fractions for the oblique and apical dendrites centered in the manually reconstructed V1 and V3, respectively (Figure 3a–c) and compared them with the theoretical prediction (Stepanyants, Hof et al. 2002). Maximum-reach potential connectivity cylinders’ were empirically constructed around each dendritic segment at a diameter containing the longest spine. For the central oblique dendrite in V1, the cylinder encompassing the longest spine was 4 um in diameter and 3.45 μm long. Of the 159 axons that entered this cylinder, 102 made synapses within the cylinder, but only 28 of these made synapses with the central oblique dendrite for a connectivity fraction of 0.18. For the apical dendrite in V3, the cylinder encompassing the longest spine was 6 μm in diameter and 3.64 μm long. Of the 256 axons that entered that cylinder, 159 made synapses within, but only 54 made synapses with the central dendrite for a connectivity fraction of 0.19. Connectivity fractions for these oblique and apical dendrites are close to each other and to the predicted value of 0.22 (Stepanyants, Hof et al. 2002).

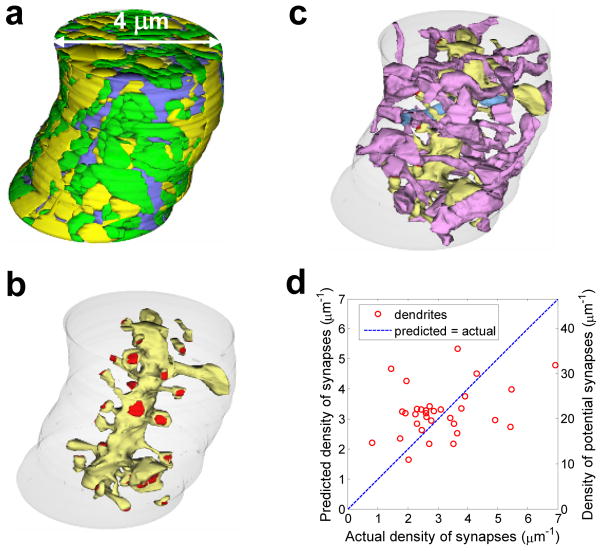
Figure 3.

Comparison of actual density of synapses along individual dendrites in V1 and V3 and predictions based on maximum reach connectivity fraction. a) Manual reconstruction of cylinder centered on the central oblique dendrite coursing through V1 and containing axons (green), dendrites (yellow), and glia (blue). Double arrowed line indicates the diameter of the cylinder. b) Central oblique dendrite (yellow) and its associated synapses (red) located on dendritic spines. The boundary of the smallest neuropil cylinder that contained the selected oblique dendrite and all of its spines is illustrated in light gray. c) Subpopulation of axons (purple, to distinguish from all green axons in a)) that formed synapses with the central oblique dendrite (yellow). Of these 28 axons, 27 made just one synapse and 1 made 2 synapses (light blue axon) on this dendrite. d) Plot of the actual density of synapses for dendrites in V1 and V3 vs. the density of synapses predicted by multiplying the mean maximum-reach connectivity fraction by the local density of potential synapses. This method is a weak predictor (r² ≈ 0.12).

Next, we compared directly measured synaptic densities along dendritic segments in the automated volumes with those estimated using several formulations of Peters’ rule. We considered synaptic density along dendrites rather than the number of synapses, to eliminate the dependence of number on the length of the dendritic segments. First, we calculated the average connectivity fraction by dividing the total number of synapses among all dendrites by the total number of axons within 1 μm from the surface of each dendrite’s shaft, Equation 1. Second, we obtained the predicted density of synapses along each dendrite (per μm of dendrite) by multiplying the mean connectivity fraction and the density of axons (per μm of dendrite) within 1 μm of each dendrite:

$$(\text{predicted}\text{density}\text{of}\text{synapses})=(\text{density}\text{of}\text{axons}\text{near}\text{dendrite})\ast (\text{mean}\text{connectivity}\text{fraction}).$$

Multiplying the local density of axons by the mean maximum-reach connectivity fraction predicted the density of synapses along dendrites rather poorly, Figure 3d. To determine whether the discrepancy could have arisen by chance due to the small numbers of synapses on individual dendritic segments, we calculated the probability of finding this or a greater discrepancy assuming that synapses were drawn with a uniform probability that was set by the connectivity fraction, see Methods. The probability was p<0.05, suggesting that the discrepancy was unlikely to have occurred by chance; hence, the connectivity fraction varied among different dendrites (Supplemental Figure 3a). Therefore, we can reject Peters’ rule using the maximum-reach connectivity function as a tool to predict synaptic densities.

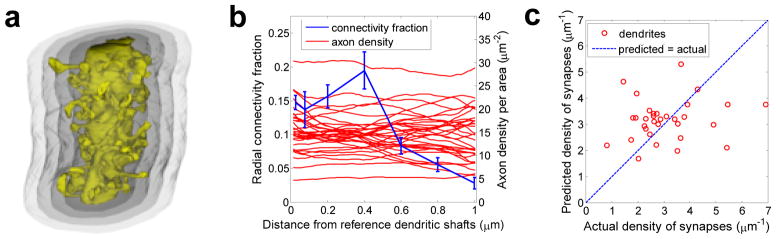
Could the failure of this prediction be due to an over-simplification of the connectivity fraction as being constant up to the maximum spine reach and then dropping to zero? In reality, the connectivity fraction was a smooth function peaking at a distance around 0.4 um from the dendritic shaft, Figure 4a,b. This distance may seem small compared to a typical spine length, yet is consistent with spine length measurements because spines are not necessarily straight, and also do not necessarily synapse at the axon’s nearest point (Harris and Stevens 1989).

Figure 4.

Comparison of actual density of synapses along individual dendrites in V1 and V3 and predictions based on the distance dependent connectivity fraction. a) 3D illustration of one dendritic segment and four radial shells, each following the surface outline of the dendritic shaft after the spines had been truncated. b) Dependence of the mean connectivity fraction and axonal density on the distance from the surface of the dendritic shaft. c) Plot of the actual density of synapses along dendrites in V1 and V3 vs. the density of synapses predicted by convolving the mean distance dependent connectivity fraction (blue line in b) with the local axon density (red lines in b). This method is a weak predictor (r² ≈ 0.02).

We hypothesized that using this distance-dependent connectivity fraction might improve the prediction accuracy of Peters’ rule. Such an approach had an additional benefit because it did not require estimating the maximum spine reach, which fluctuated greatly along dendrites because long spines occur infrequently. Nevertheless, even with the distance-dependent connectivity fraction, Peters’ rule poorly predicted the actual synaptic densities (Figure 4c). To determine whether this discrepancy could have arisen by chance due to the small numbers of synapses on each individual dendrite, we performed a statistical test similar to above, see Methods. The probability was p<0.05, (data not shown) further confirming that the connectivity fraction varies among and along dendrites. Thus, we can also reject Peters’ rule with distance-dependent connectivity fraction as a tool to predict synaptic densities.

4. Axo-dendritic touches and dendritic caliber are good predictors of synapse density

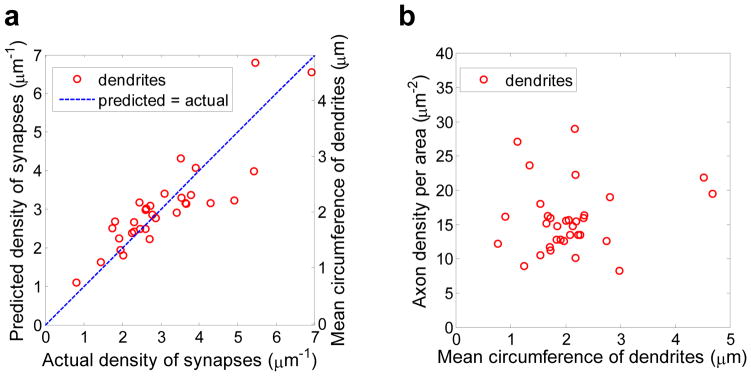
In this section, we report two approaches that predict the density of synapses on a dendrite more reliably than Peters’ rule. First, we considered dendrite caliber as a predictor of synaptic density (Figures 5a). As the shape of dendritic cross-section can be irregular, we quantified the caliber by its circumference length (with spines truncated). Then, synaptic density is proportional to the circumference length. We found, that the remaining discrepancy can happen by chance, p>0.5, Supplementary Figure 3b. Thus, the hypothesis that the synaptic density is linked to dendritic caliber cannot be rejected. Note that the dendrite caliber is not correlated with the density of potential synapses (Figure 5b) suggesting that axon availability is not the source of the caliber - synapse density correlation.

Figure 5.

Relationship between dendritic caliber and the density of actual and potential synapses. a) Plot of the actual density of synapses vs. the density of synapses predicted by multiplying the dendritic circumference by the common coefficient. Dendritic caliber is a strong predictor of actual density of synapses along a dendrite (r² ≈ 0.75). b) Density of available axons (per unit length of dendrite per unit distance from a dendrite) does not correlate with the dendritic caliber (r² ≈ 0.02).

Second, we considered the number of axons touching dendritic spines as a predictor of the number of synapses. We defined a touch as proximity between an axon and a dendritic spine with no other intervening objects. We calculated the density of synapses on a dendrite as a function of the density of touches using a procedure similar to that described in the previous section. First, by dividing the total number of synapses by the total number of touches we calculated the average touch connectivity fraction. Second, we calculated the predicted density of synapses on each dendrite by multiplying the density of touches on that dendrite by the average touch connectivity fraction.

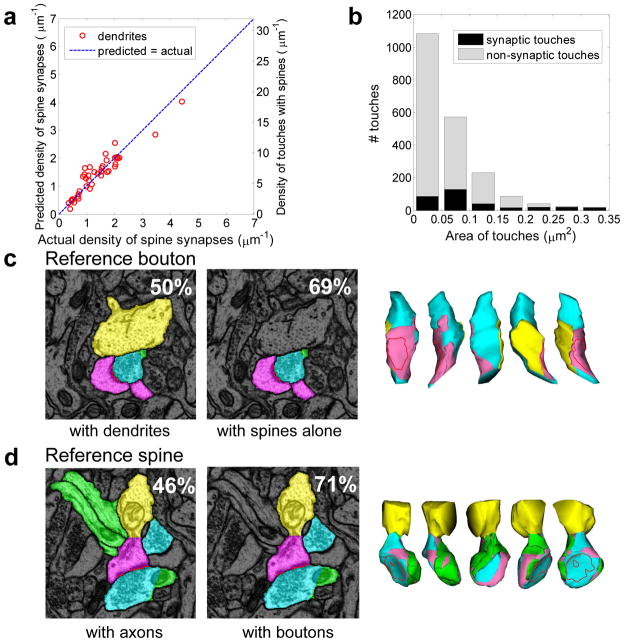
The density of touches predicts the density of synapses well (Figure 6a). To determine whether the remaining discrepancy could have arisen by chance due to small counts of synapses on individual dendrites we applied the multi-hypothesis significance analysis again (see Methods). We found that, for the invariant touch connectivity fraction, the probability of such discrepancy is large, p>0.05, Supplementary Figure 3c. Therefore, the hypothesis that synaptic density is a uniform fraction of the touch density cannot be rejected.

Figure 6.

Relationship between synaptic and non-synaptic axo-dendritic touches in V1. a) Density of spine synapses along a dendrite is proportional to the density of spine touches with axons (r² ≈ 0.88); b) Area distributions of synaptic and non-synaptic touches overlap significantly. c) Reference bouton whose largest touch with a spine corresponds to a synapse. Left: section containing the reference bouton (cyan) with touching dendrite (yellow) and spine (pink). Percentage of boutons with largest dendritic touch corresponding to a synapse is shown. Center: Reference bouton (cyan) and touching spine (pink) form a synapse. Percentage of boutons with largest spine touch corresponding to a synapse is shown. Right: 3D views of the reference bouton colored according to the type of touching object. Visible blue areas are where other axons touched this bouton. d) Reference spine whose largest touch with a bouton corresponds to a synapse. Left: section containing the reference spine (pink) with touching axons (green) and boutons (cyan). Percentage of spines with largest axonal touch corresponding to a synapse is shown. Center: Reference spine (pink) and touching boutons (cyan). Percentage of spines with largest bouton touch corresponding to a synapse. Right: 3D views of the reference spine surface colored according to the type of touching object. Red dotted line: position of the synapse.

The discovered correlations of the synapse density should help to predict it from the density of proximities between one neuron’s axons and other neuron’s dendrites. The dependence of the synapse density on the caliber suggests a modification of the Peters’ rule, where synapse probability is a function of both the number of proximities and the dendritic caliber. The correlation of the synapse density with the touch density may be used in combination with the methods for touch identification such as SBFSEM and GFP Recombination Across Synaptic Partners, or GRASP (Feinberg, Vanhoven et al. 2008) to predict the probability of a synapse.

5. When do axo-dendritic touches predict individual synapses?

Since the density of touches predicts synaptic density, it is natural to ask whether individual touches could reliably predict synapses. As the fraction of touches that correspond to synapses was much less than one (~0.2), additional information is needed to determine which touches correspond to synapses. If the target application for such a method would be a technique other than ssTEM, then, one cannot rely on synaptic attributes, such as vesicles and/or PSDs, and must instead rely on shape and geometrical proximity. We considered whether the area of a touch could predict a synapse but found that it was insufficient because the area distributions of synaptic and non-synaptic touches overlapped completely across the full range of sizes (Figure 6b).

Next, we explored a variation of this approach motivated by the observation that the sizes of boutons, spines and PSD area of a given synapse are correlated (Harris and Stevens 1989; Lisman and Harris 1993; Schikorski and Stevens 1997) (Pierce and Lewin 1994). Moreover, the geometrical dimensions of hippocampal synapses correlate with the physiologically defined synaptic weight (Matsuzaki, Ellis-Davies et al. 2001; Kasai, Matsuzaki et al. 2003). From these observations, we hypothesized that a spine and/or a bouton would not be bigger than that needed to accommodate a synaptic touch. Therefore, we tested i) whether the largest touch a bouton has with adjacent dendrites or spines predicts a synapse; ii) whether the largest touch a spine has with adjacent axons or boutons predicts a synapse; iii) whether a combination of i) and ii) predicts a synapse. In this analysis, we identified spines and boutons based only on their shapes without relying on synaptic ultrastructural attributes (see Methods).

We started by exploring whether the relative area of touches made by a reference bouton with adjacent dendrites could predict a synapse (Figure 6c). We found that the largest-area touch corresponded to a synapse in about half of the cases. Next, we restricted our consideration to the touches among reference boutons and dendritic spines, not dendritic shafts. We found that for 69% of boutons the greatest area touch corresponded to a synapse on a spine (Figure 6c).

Although the majority of boutons’ largest-area touches with spines correspond to synapses, there is a significant fraction of synapses that occur at other touches. These include synapses made with dendritic shafts and at non-largest touches. Moreover, 17–39% of Schaffer collateral boutons are multisynaptic (Sorra and Harris 1993; Shepherd and Harris, 1998; Kirov et al., 1999). This means that a substantial fraction of synapses will be missed by this axo-centric largest-area touch method.

Next, we considered the relative area of touches made by a reference spine with adjacent axons (Figure 6d). The fraction of spines whose largest-area touch with axons corresponded to a synapse was less than half. This method was improved by considering only touches made with boutons, not with typically synapse-free inter-bouton intervals along the axon. For 71% of spines the largest area touch with adjacent boutons was synaptic (Figure 6d). As multisynaptic spines are much rarer (<1%) than multisynaptic boutons in perfusion fixed adult hippocampus (Fiala et al., 1998; Petrak et al.2005), the fraction of spine synapses recovered by this method is also approximately 70%.

Finally, we combined these two approaches by considering a touch area relative to other touches both sharing the same bouton and the same spine. We found that 80% of the touches whose area is greatest among those sharing the same bouton and those sharing the same spine are synaptic. At the same time, this method detects only 46% of all spine synapses. Thus, the relative touch area is also an imperfect predictor of individual synapses on dendritic spines.

Our analysis focused on spine synapses because shaft synapses are rare along principal spiny dendrites in s. radiatum of area CA1. For example, in all of manual volume 3, there were only 17 asymmetric, putative excitatory shaft synapses, and only 12 symmetric, putative inhibitory synapses. Shaft synapses occur frequently along interneuron dendrites (Harris and Landis 1986) but only two short segments of interneuron dendrites passed through volume 3. Hence, despite these being the largest volumes of hippocampal neuropil ever fully reconstructed, we were not able to analyze connectivity of the spine-free interneuron dendrites in this brain region.

Discussion

In this paper, we fully reconstructed an unprecedented volume of hippocampal neuropil using ssTEM and automated registration and segmentation algorithms. Such reconstruction proves the feasibility of automating reconstructions on the scale impractical for manual reconstructions. Although the proofreading speed and the error rates are satisfactory for the analysis of the reconstructed volumes, they require radical improvement – via both hardware and software innovations - to reconstruct complete vertebrate circuits.

Full volume dense reconstruction allowed us to measure directly the numbers of nearby axons and synapses along each dendritic segment. The mean connectivity fraction calculated from these measurements is in agreement with the theoretical predictions based on light microscopy data (Stepanyants, Hof et al. 2002). Yet, the connectivity fraction varied among dendrites enough to make the use of Peters’ rule unsuitable for predicting synaptic density and suggests the need to re-examine previous results (Binzegger, Douglas et al. 2004; Stepanyants and Chklovskii 2005; Jefferis, Potter et al. 2007; Stepanyants, Hirsch et al. 2008). Our measurements indicate possible ultrastructural causes for violations of Peters’ rule obtained from light microscopy and physiology (Shepherd, Stepanyants et al. 2005; Petreanu, Mao et al. 2009).

We found a strong correlation between the density of synapses and dendrite caliber, and no correlation between the caliber and the density of available axons. This finding suggests that the density of synapses is determined not so much by the availability of axons in the local environment, but more by intrinsic properties of the dendrites. The strong correlation previously reported between dendritic cross-sectional area and microtubule number, and microtubule number and spine density further supports this hypothesis (Fiala, Kirov et al. 2003; Harris, Bourne et al. 2007). Interestingly, the scaling of synaptic density with the dendritic caliber implies the existence of a universal shaft membrane area (0.66 μm²) per synapse, cf. (Nicol and Meinertzhagen 1982).

The observed correlation between dendritic caliber and spine density among the segments of different dendrites is consistent with previous reports of spine density along individual dendrites as a function of distance from the cell body. In particular, the density of synapses decreases with the distance from the cell body along a given dendrite (Katz, Menon et al. 2009), which would be expected given that dendrites get thinner with distance from the cell body. Others have shown that the thickest proximal apical dendrites appear spine-free, seemingly in contradiction (Megias, Emri et al. 2001). However, those proximal dendrites receive mostly inhibitory GABAergic synapses (Buhl, Halasy et al. 1994; Megias, Emri et al. 2001) and our volume was taken from the middle of stratum radiatum distal to cell bodies. It will be interesting to learn whether inhibitory synapses also have a caliber to density rule in relationship to intrinsic composition or extrinsic features of the local neuropil.

We measured the distance between adjacent synapses along axons to be 4–5 μm, whereas (Shepherd and Harris 1998) reported a lower inter-synapse interval along axons averaging 2.7 μm. Later it was discovered that the adult hippocampal slices used in (Shepherd and Harris 1998) had nearly 50% more synapses than adult hippocampus fixed by intracardiac perfusion (Kirov, Sorra et al. 1999; Kirov, Petrak et al. 2004), as was used to obtain V1–3 reported here. This difference would account for the discrepancy in these axonal inter-synapse measurements.

We found that touches between axons and dendrites (mostly spines) could be used to predict synapses on two levels. First, the density of synapses along a hippocampal dendrite appears to be a universal fraction, 0.2, of the density of touches. In contrast, the fraction of touches corresponding to synapses reported for the C. elegans nervous system is 0.09 (Durbin 1987). Second, the largest touch shared by a spine and bouton predicts the presence of an actual spine synapse with about 80% precision.

Knowing the relationship between touches and synapses is valuable for techniques that do not contain the information present in ssTEM. For example, automated tracing from SBFSEM is done at lower resolution in combination with extracellular labeling that fails to reveal the two main indicators of synapses: pre-/post-synaptic zones and pre-synaptic vesicles. Another technique that could benefit from knowing the relationship between touches and synapses is GRASP (Feinberg, Vanhoven et al. 2008). Although GRASP can identify synapses rather than touches by relying on synaptic proteins, this is not always done (Feinberg, Vanhoven et al. 2008; Gordon and Scott 2009), and may be undesirable as ectopic expression of synaptic proteins may alter connectivity (Scheiffele, Fan et al. 2000; Biederer, Sara et al. 2002; Zito, Knott et al. 2004). Finally, array tomography (Micheva and Smith 2007) is a promising light microscopy technique with improved vertical resolution that can be used with synaptic markers to identify synaptic contacts. Our results may help one to interpret the observed proximities pre- and post-synaptic puncta.

Although our results provide guidance for reconstructing circuits with lower resolution methods, it is not clear how they would generalize beyond s. radiatum of the hippocampal area CA1. Reconstructing synaptic connectivity for each new brain region or cell type using lower resolution methods, which can be scaled to larger volumes, may require repeating this kind of analysis to determine region and dendrite-specific rules for identifying synapses. For example, the rules for identifying synaptic touches along non-spiny dendrites even within this subregion of the hippocampus, may differ. Furthermore, it is also not clear what rules will apply for shaft synapses occurring on spiny densities, or small-touch synapses on multi-synaptic boutons.

In conclusion, we have shown that ssTEM can be automated, in principle, but will require major advances in data acquisition and analysis to be a viable approach for reconstructing complete vertebrate circuits at the resolution of synapses. Importantly, we have used these dense reconstructions to test whether axo-dendritic proximities predict synaptic connectivity. We found that Peters rule does not predict dendritic spine density because of variations in the connectivity fraction. We found that dendritic spine density is better predicted by spine-bouton touches and dendritic caliber. Furthermore, the relative touch area predicts synapses with about 80% precision when both pre and postsynaptic dimensions of dendritic spines are considered.

Methods

Tissue sources and photographic conditions

All procedures followed NIH guidelines for the humane care and use of laboratory animals. Volumes 1–3 were from hippocampal area CA1 of a perfusion-fixed male rat of the Long-Evans strain weighing 310 g (postnatal day 77, (Harris and Stevens 1989)). Volume 4 was from a hippocampal slice that was prepared from a postnatal day 21 male rat of the Long-Evans strain and maintained in vitro for 3 hours prior to fixation as described (Fiala, Kirov et al. 2003). All volumes were from the middle of s. radiatum about 150 to 200 microns from the hippocampal CA1 pyramidal cell soma. For volume 4, the series was located at a depth between 100 and 200 μm from the cut air surfaces of the slice where excellent tissue preservation occurred.

All series were cut according to our published protocols (Harris, Bourne et al. 2007). Briefly, a diamond trimming tool (EMS, Electron Microscopy Sciences, Fort Washington, PA) was used to prepare small trapezoidal areas ~200 μm wide by 30–50μm high. Serial thin sections were cut at ~45–50 nm on an ultramicrotome, mounted and counter stained with saturated ethanolic uranyl acetate, followed by Reynolds lead citrate, each for 5 min. Individual grids were placed in grid cassettes and stored in numbered gelatin capsules. The cassettes were mounted in a rotating stage to obtain uniform orientation of the sections on adjacent grids and the series were photographed at 10,000× (volume 4) or 5,000× (Volumes 1–3) on a JEOL 1200EX or 1230 electron microscope (JEOL, Peabody, MA).

Manual volume reconstructions

Three-dimensional reconstructions and analyses were performed manually using the software entitled RECONSTRUCT™ (Fiala and Harris 2002; Fiala 2005), which is freely available from http://synapses.clm.utexas.edu. We digitally optimized images for brightness and contrast, and colorized reconstructions to visualize structures of interest. To align manually, we indicated five or more fiducial points on adjacent pairs of serial sections that were in the same location (e.g. cross-sectioned mitochondria or microtubules). Then we chose the minimal algorithm in RECONSTRUCT™ to perform the alignment while blending the adjacent images. Pixel size was calibrated relative to a diffraction grating replica (Ernest F. Fullam, Latham, NY) photographed with each series, and section thickness was computed by dividing the diameters of longitudinally sectioned mitochondria by the number of sections they spanned (Fiala and Harris 2001). Finally, the user manually traced outlines of all objects on each section and identified them as axon, dendrite, glia, spine, or synapse. RECONSTRUCT™ output had calibrated dimensions and 3D displays of reconstructed objects.

Automated registration

Automated registration required two steps. First, the IMOD software (David Mastronarde, U of Colorado, Boulder) was used to obtain pair wise relative affine transforms between adjacent sections. In some cases, manual adjustment using the Midas tool in IMOD was required to initialize the registration algorithm. The pair-wise transforms were propagated through the whole stack and an absolute transform was obtained for each section. The second step was aimed at eliminating registration mis-matches remaining after affine registration. It involved calculating cross-correlations between 200×200 pixel image patches of adjacent sections to find a vector field of remaining miss-registration. We approximated this vector field by local distortion functions and aligned each pair of adjacent sections with sub-pixel precision using the Matlab Image Processing Toolbox (Natick, MA).

Automated segmentation

Automated segmentation of objects used the set of image processing algorithms developed in (Mishchenko 2009) to extract and link the 2D profiles corresponding to different neuronal processes across aligned serial sections. Each image was processed using a multi-scale Gaussian-Smoothed Hessian-based ridge detector to search for plasma membranes as linear dark features of varying width. A fuzzy-logic anisotropic growth of detected membranes was used to bridge short regions where the membranes were grayer due to oblique sectioning or appeared broken. Detected profiles were filtered by retaining only closed contours, corresponding to true cell profiles, to reduce clutter in the images due to darkly stained organelles. Overlapping contours from adjacent sections were compared based on shape and texture cues to determine if they belonged to the same 3D object. All overlapping contours found to belong to the same neuronal processes were automatically grouped across serial sections.

Proofreading of automatic segmentations

To correct errors in automatic segmentation we developed a graphical user interface in Matlab called the ProofReading Tool (PRT) to guide proofreading in a systematic and focused manner. PRT compiled a list of significant 3D objects from the automatic segmentation. The original electron micrographs containing all intracellular organelles were used. An object’s significance depended primarily on its total volume, but also on its average diameter and clarity or composition of the cytoplasm, which influenced brightness. Then the PRT guided a user through this list of processes sequentially in the order of decreasing volumes. The user viewed corresponding neuronal processes through each section of the entire ssTEM stack and either confirmed or corrected them as necessary. Most of the corrections involved grouping together multiple fragments of an axon or attaching spine-necks to dendritic shafts. No manual tracing of boundaries was involved. Fragments of the same neuronal processes were continuously removed from the list so that each process was inspected only once. A final segmentation was produced in which gaps in contours were closed, contours were smoothed and holes were filled using watershed from markers performed on the inverse of the original images, where interiors of proofread objects were used as the markers. From this, a set of single-pixel lines was produced to represent boundaries of neuronal processes in different sections. The final reconstruction was stored as a bitmap of the entire volume, where each pixel carried a numerical label to identify the process containing it. We also generated RECONSTRUCT™ XML series from the final segmentations for visualization or quantification using RECONSTRUCT™.

Distribution of effective cross-section diameters of axons and dendrites

First, we used the Z-trace tool of RECONSTRUCT™ to measure each dendrite’s length across serial sections. A morphological shrinking transformation was applied to each dendritic profile to get central points that were then connected from section to section by the hypotenuse of a right triangle with one side equal to the x-y distance between the two points and the other side equal to the section thickness of 50 nm. The Z-trace length of a dendrite equaled the sum of lengths of all these hypotenuses. Second we computed mean cross-sectional area, A, for each axon and dendrite by dividing the volume for each segment by its length. The effective diameter, d, then was calculated using formula A = π d²/4. The resulting distribution is shown in Figure 2b.

Detection of synapses

We developed a PSD recognition algorithm to detect post-synaptic densities automatically in images by searching for synapses as broader fragments of external cell boundaries with high stain density. For every point on the single-pixel boundary between an axon and a dendrite, we computed three integrals along the direction orthogonal to the boundary at that point, measuring the total integral of the image intensity and the first and the second power moments of the distance from the boundary weighted with the image intensity, out to a specified distance. The first integral measured the total darkness of the boundary at each location, and the other two integrals measured the width of such boundary. For a PSD, the first integral would indicate a very dark region, and the other two would indicate wider than usual membrane. These three measures were used as inputs to a single-layer logit neural network classifier (Haykin 2008) trained to produce PSD-score describing whether the pixel was inside a PSD. The PSD recognition algorithm was trained on 1–2 manually annotated images. For each axon-dendritic pair in contact, the total PSD-score along their contact boundary was produced and used to determine if the pair made the synaptic contact. The algorithm could detect synaptic connections in a volume with 15% false negative and 20% false positive errors. The error-rate was estimated by cross-validating with the manually composed list of synaptic connections. Then, we manually verified all synaptic connections in volumes 1 and 4. By repeating the manual verification process twice, we estimate that these manually verified datasets missed 7–8% of synapses and contained 2–3% false synapses. In volume 3, the PSD recognition algorithm was not used, instead synapses throughout the volume were marked during the process of manual tracing in RECONSTRUCT™.

After identifying the PSD traces, we computed the PSD areas as follows. We interpolated the surface between traces of PSD on adjacent slices with triangles. Then the total PSD area was calculated by adding the areas of these triangles plus the lengths of the two outer most PSD traces times 1/2 of the slice thickness. Compared to (Harris and Stevens 1989), the PSD areas are within range although systematically smaller due to more strict inclusion criteria for the edge pixels of the PSD traces.

Computation of distance-dependent connectivity fraction

Distance-dependent connectivity fractions were calculated for each dendrite as the fraction of potential connections utilized in each radial shell following the surface outline of the dendritic shaft after the spines had been truncated. These quantities were sensitive to boundary effects when radial shells extended partially outside the sample volume. To correct for boundary effects, we divided the number of synapses in each shell by the fraction of the full radial shell actually included in the volume, and the number of axons by the fraction of full radial shell actually included in the volume with respect to one-half of the full shell’s volume (but not greater than one). A factor of one-half was introduced here because each axon traversed the radial shell at two points. Each radial shell was explicitly continued outside of the volume to obtain an accurate estimate of its included fraction. As the fraction of axons grazing the shells was small, treating them the same way did not introduce a significant error. We restricted the sample of dendritic segments to include only those that were longer than 1μm. In V3 and V4 we only included those segments that spent more than 50% of their length farther than 0.5μm away from the volume’s edge. In volume 1 this latter criterion was not necessary because V1 was big enough that dendrites on the boundaries did not affect estimates of connectivity fractions.

Calculation of synaptic density using Peters’ rule with distance-dependent connectivity fraction

Since the calculation of the average distance-dependent connectivity fraction may contain a significant uncertainty, we derived an expression for the density of synapses without explicitly using the dependence of the connectivity fraction on distance by taking advantage of the following observation. With the exception of axons touching dendritic shaft, the density of axons (per unit length of a dendrite per unit distance from a dendrite) as a function of the distance to the dendrite is constant (Figure 4b) in agreement with prior theoretical analysis (Stepanyants, Hof et al. 2002).. Considering only those axons that do not touch the dendritic shaft, then:

$$\text{Synapses}\text{per}\mu \text{m}=\int \text{ds}\text{Density}\text{of}\text{axons}(\text{per}\text{area})(\text{s})\ast \text{connectivity}\text{fraction}(\text{s})$$

As the density of axons is independent of s (Figure 4b), it can be taken out of the integral. Then, even if the connectivity fraction varies with distance from a dendrite, as long as this function is invariant among dendrites, the integral has the same value for all of them. Therefore, we can estimate the integral by dividing the total number of synapses by the total number of axons and use this value to predict the density of synapses on each dendrite.

We also found that the number of axons touching dendritic shafts was not a good predictor of the number of synapses, Supplementary Figure 4. By adding the predictions for axons touching and not touching dendritic shaft, we arrived at the total density of synapses, Figure 4c.

Delineating axonal boutons and spines

The partitioning of axonal boutons from inter-bouton regions relies on their swollen shapes, Supplementary Figure 5a. We computed a 3D distance transform from the surface of each axon inwards. Every voxel inside each axon was assigned the value of the shortest distance to the surface of the process. We calculated the average of the regional maxima and applied a morphological opening operation, which pinches narrow axon processes with distances to the surface shorter than 1.5 times the mean regional maxima. The remains having touches with dendrites are identified as boutons.

The detection of dendritic spines took advantage of their characteristic shapes using the following mathematical procedure. Note that, in a reconstructed dendrite, every voxel connects to the surface of the reconstructed volume by at least one path fully contained within that dendrite. After applying a morphological opening operation to the dendrite, which pinched narrow spine necks, voxels that remained connected to the surface belonged to the shaft, while those disconnected from the volume surface belonged to spines. Supplementary Figure 5b shows an example of spine segmentation. The definition of a spine used here automatically is intermediate between the “spine” and “spine head” previously defined manually.

Multi-hypothesis significance analysis

To evaluate the significance of discrepancy between actual and predicted density of synapses, we calculate the probability of obtaining such discrepancy by chance due to a finite number of synapses per dendrite. We assume that synapses are drawn independently with equal probability set by the connectivity fraction and calculate the probability of observed or greater deviation from the predicted value. In the case of Peters’ rule with maximum-reach connectivity fraction (Figure 3), the number of synapses on each dendrite is governed by a Binomial distribution. To avoid boundary effects, we calculate the p-values only for spiny dendrites with shaft lengths greater than 2 μm and at distances more than 1 μm away from the boundary. Then we apply the Benjamini-Hochberg procedure (Benjamini and Hochberg 1995; Benjamini and Yekutieli 2001), which has greater statistical power than the commonly used Bonferroni correction. The p-values for m dendrites are arranged in ascending order, p₁ ≤ p₂ ≤ … p_m, and adjusted to $p_i^a=min({mp}_i/i,1)$ (Supplemental Figure 3a). The multiple-hypothesis corrected p value $p=min(\{p_i^a\})$ is then compared to the standard false discovery rate α = 0.05. We find that p< 0.05 , implying that the hypothesis of Peters’ rule with maximum-reach connectivity fraction can be rejected. Similar analysis performed on the distance dependent connectivity fraction prediction also yielded p< 0.05 thus rejecting the hypothesis (data not shown).

We performed the same significance analysis on the predictions using the number of axons touching dendrites (Supplementary Figure 3b). As the multiple-hypothesis corrected p > 0.05, we cannot reject this hypothesis.

We performed a similar analysis for the prediction based on mean circumference of dendrites (Supplementary Figure 3c). In this case, we could not use the Binomial distribution because the total number of axons was not known. As the numbers of surrounding axons are usually large (>100) and the connectivity fraction is small (Figure 4b), we approximated the Binomial distribution as a Poisson with mean equal to the predicted number of synapses.