Adaptive Elastic-Net Sparse Principal Component Analysis for Pathway Association Testing

Abstract

Pathway or gene set analysis has become an increasingly popular approach for analyzing high-throughput biological experiments such as microarray gene expression studies. The purpose of pathway analysis is to identify differentially expressed pathways associated with outcomes. Important challenges in pathway analysis are selecting a subset of genes contributing most to association with clinical phenotypes and conducting statistical tests of association for the pathways efficiently. We propose a two-stage analysis strategy: (1) extract latent variables representing activities within each pathway using a dimension reduction approach based on adaptive elastic-net sparse principal component analysis; (2) integrate the latent variables with the regression modeling framework to analyze studies with different types of outcomes such as binary, continuous or survival outcomes. Our proposed approach is computationally efficient. For each pathway, because the latent variables are estimated in an unsupervised fashion without using disease outcome information, in the sample label permutation testing procedure, the latent variables only need to be calculated once rather than for each permutation resample. Using both simulated and real datasets, we show our approach performed favorably when compared with five other currently available pathway testing methods.

1. INTRODUCTION

The advance of high-throughput genomic technologies such as gene expression microarrays, DNA methylation arrays, SNP arrays, and next-generation sequencing enables researchers to make thousands to millions of measurements at the genome level simultaneously. Because of their ultra-high dimensionality and the complex gene-gene correlation patterns, these omics datasets have brought huge challenges for computation and statistical analysis. In particular, for gene expression data, the generation of a differentially expressed gene list is often just the beginning of data analysis and functional interpretation.

Recently, pathway or gene set analyses, which test disease association with pre-defined gene groups jointly instead of testing individual genes, have become popular approaches for analyzing gene expression data. These analyses take advantage of the fact that multiple genes in a functional group typically work cooperatively to fulfill biological functions and test disease associations with groups of genes defined by pathways or gene sets. For example, KEGG Pathway (Kanehisa and Goto, 2000) and Gene Ontology (GO) (Ashburner et al., 2000) are the most commonly used databases for classifying genes into functional groups. This prior biological knowledge on pathways and gene sets can help researchers to obtain functional knowledge about genes.

Many analytical strategies have been proposed for pathway analysis. For example, Gene Set Enrichment Analysis (GSEA) (Mootha et al., 2003; Subramanian et al., 2005) is the one of the earliest approaches to tackle this problem and has been widely used by the research community. Other extended, improved, or related methods include the maxmean statistic (Efron and Tibshirani, 2007), the global test (Goeman et al., 2004), Hotelling’s T² test (Dinu et al., 2007; Tsai and Chen, 2009), mixed models (Wang et al., 2008, 2009) and others. Several recent reviews nicely summarized the progress in pathway analysis and compared the different analysis approaches (Goeman and Buhlmann, 2007; Nam and Kim, 2008, Ackermann and Strimmer, 2009).

Among the pathway analysis methods, performing dimension reduction on gene expression values and computing summary statistics (such as latent variables) for each pathway is an attractive approach. First, an often encountered problem is that the number of genes within a pathway is greater than the number of patients; this can be problematic for traditional statistical modeling which typically assumes that the number of variables is smaller than the sample size. Second, since we expect that the genes in a pathway share similar functions, using one or a few latent variables to represent each pathway also makes sense biologically. Third, beyond testing pathway association with clinical phenotypes, the estimated latent variables can also be used for further analysis such as the prediction of disease outcome or the analysis of pathway-pathway interactions.

In pathway analysis, the latent variables are often constructed based on principal components (PCs) (Tomfohr et al., 2005; Kong et al., 2006; Ma and Kosorok, 2009). Typically, all genes within a pathway are used to estimate the PCs. However, when the number of genes within a pathway is large, association signals from genes unrelated to the clinical outcome may introduce noise and obscure gene set association signal. To increase the power of gene set association testing and to effectively target association signals from functional genes, in this paper, we propose first to discover coherent sub-modules in each pathway by using a data-adaptive approach and then to construct latent variables for the submodules. More specifically, we will use the Adaptive Elastic-net Sparse Principal Component Analysis (AES-PCA) to summarize gene expressions within a pathway. The AES-PCA method removes noisy expression signals and also account for correlation structure between the genes. It is computationally efficient and the estimation of the PCs does not depend on clinical outcomes. Thus, for experiments with complex designs, sparse PCs obtained from AES-PCA can be conveniently integrated into regression models, where additional covariate variables can be simultaneously included in the model.

In section 2, we describe the details of the AES-PCA modeling framework and testing procedures for pathway analysis. In section 3, the AES-PCA is compared with five other widely used pathway analysis approaches using both simulation data and data from two real gene expression experiments. We provide some comments and conclusions in the last section.

2. METHODS

2.1. The adaptive elastic-net

Consider the linear regression model

$$\mathbf{y}=\mathbf{X}\mathit{\beta }+\mathit{\varepsilon }$$ (2.1)

where y is a response vector of length n, X is an n by p matrix, and β is a vector of regression coefficients with length p. Assume both y and columns of X are standardized with mean 0. The lasso estimate is defined b

$${\stackrel{⌢}{\beta }}^{\text{lasso}}=\underset{\beta }{\text{arg}\hspace{0.17em}\text{min}}{\Vert \mathbf{y}-\mathbf{X}\beta \Vert }_2^2+{\lambda }_1\sum _{j=1}^p\left|{\beta }_j\right|,$$ (2.2)

where the L₁ penalty ${\lambda }_1{\sum }_1^p\left|{\beta }_j\right|$ shrinks the coefficients to zero as the tuning parameter λ₁, which determines the path of the coefficient estimates, increases (Tibshirani, 1996).

Lasso can be easily applied to high-dimensional data, but several drawbacks may limit its applications. For example, the number of selected variables is bounded by the sample size. In addition, for a group of highly correlated variables, lasso tends to select one variable and ignores the others. This is undesirable for pathway analysis because when only one variable (i.e. gene) is selected, the gene group effect will be reduced dramatically. To address these limitations, Zou and Hastie, (2005) recently proposed the elastic net estimator. It can be represented as

$${\stackrel{⌢}{\beta }}^{\text{EN}}=(1+{\lambda }_2)\left\{\underset{\beta }{\text{arg}\hspace{0.17em}\text{min}}{\Vert \mathbf{y}-\mathbf{X}\beta \Vert }^2+{\lambda }_2\sum _{j=1}^p{\left|{\beta }_j\right|}^2+{\lambda }_1\sum _{j=1}^p\left|{\beta }_j\right|\right\},$$ (2.3)

which combines both L₁ and L₂ penalties into the model.

Another direction of improvement is to correct bias in estimation by adding weight θ_j for each β_j, which corresponds to different amounts of shrinkage, to the regression coefficients. The weight vector θ can be defined as θ = 1 / |β̂_ols|, and β̂_ols is the coefficient estimator from ordinary least square. This is called adaptive lasso, which has the form

$${\stackrel{⌢}{\beta }}^{\text{Ada}}=\underset{\beta }{\text{arg}\hspace{0.17em}\text{min}}{\Vert \mathbf{y}-\mathbf{X}\beta \Vert }^2+{\lambda }_1\sum _{j=1}^p{\theta }_j\left|{\beta }_j\right|$$ (2.4)

and enjoys the oracle properties (Zou, 2006).

Most recently, Zou and Zhang (2009) proposed the adaptive elastic-net estimator, which combines the two versions of lasso in Equations 2.4 and 2.5 into a single model, and it has the strengths of having both stable estimation and the oracle property. It is defined by

$${\stackrel{⌢}{\beta }}^{\text{AdaEN}}=(1+{\lambda }_2)\left\{\underset{\beta }{\text{arg}\hspace{0.17em}\text{min}}{\Vert \mathbf{y}-\mathbf{X}\beta \Vert }^2+{\lambda }_2\sum _{j=1}^p{\left|{\beta }_j\right|}^2+{\lambda }_1\sum _{j=1}^p{\theta }_j\left|{\beta }_j\right|\right\}.$$ (2.5)

and it has been shown that adaptive elastic-net outperformed lasso, elastic-net and adaptive lasso in terms prediction error and variable selection by simulation studies (Zou and Zhang, 2009).

2.2. Principal component analysis

PCA is one of the most commonly used dimensional reduction techniques for high-dimensional genomic data analysis. The PCs for a data matrix can be computed via Singular Value Decomposition (SVD). Let X be an n × p matrix with p variables (e.g. genes) measured on n samples. The SVD of X, which has centered columns with mean zero, can be written as

$$\mathbf{X}={\mathbf{UDV}}^T$$ (2.6)

where the columns of U and V are PCs (eigen-arrays) and their corresponding loadings (eigen-genes) respectively (Alter et al., 2000). In Tomfohr et al. (2005), the first PC, which accounts for the largest amount of variations in pathway activity among all linear combinations of gene expressions, was used to construct the “metagene” to project the multi-dimensional expression data in a pathway onto a one-dimensional space. Then a t-test was used to compare metagenes for cases and controls for each pathway. Since the first PC may not be sufficient to capture enough information within a pathway, this approach was recently extended to testing a few more PCs using multivariate tests (Kong et al, 2006; Ma and Kosorok, 2009).

However, PCs computed based on all genes in a pathway may not reflect the biological context for a specific experiment or condition. Thus a new method that estimates sparse loadings for the PCs in order to naturally select variables (i.e. genes) relevant to a particular experimental condition would be more desirable for pathway analysis.

2.3. Sparse PCA

Principal components can be derived under regression-type framework. Zou et al. (2006) applied lasso regression optimization to achieve sparse loading of PCs, which is called the sparse PCA approach. For the first k PCs, we have

$$\begin{array}{ll}\left(\widehat{A},\widehat{B}\right)\hfill & =\text{arg}\hspace{0.17em}\text{min}\sum _{i=1}^n{\Vert {\mathbf{x}}_i-{\mathbf{A}\mathbf{B}}^T{\mathbf{x}}_i\Vert }^2+{\lambda }_2\sum _{j=1}^k{\left|{\beta }_j\right|}^2+{\lambda }_1\sum _{j=1}^k\left|{\beta }_j\right|\hfill \\ \hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}{\mathbf{A}}^T\mathbf{A}=I\hfill \end{array}$$ (2.7)

where A_p×k = [α₁,…,α_k], B_p×k = [β₁,…,β_k], p is the number of variables, and x_i is the vector for the ith sample. When the tuning parameter λ₁ equals zero then β̂_j is proportional to V_j (jth standard principal component), and if λ₁ is positive then β̂_j can be normalized in order to obtain the jth sparse principal component. Sparse PCA based on different algorithms including adaptive sparse PCA were also developed recently (Shen and Huang, 2008; Leng and Wang, 2009). In this paper, we use the adaptive elastic-net to estimate the sparse loadings of the PCs for genes within a pathway since adaptive elastic-net has better theoretical properties and empirical performance than elastic-net and adaptive lasso (Zou and Zhang, 2009). Thus, the new objective function is

$$\begin{array}{ll}\left(\widehat{A},\widehat{B}\right)\hfill & =\text{arg}\hspace{0.17em}\text{min}\sum _{i=1}^n{\Vert {\mathbf{x}}_i-{\mathbf{AB}}^T{\mathbf{x}}_i\Vert }^2+{\lambda }_2\sum _{j=1}^k{\left|{\beta }_j\right|}^2+{\lambda }_1\sum _{j=1}^k{\theta }_j\left|{\beta }_j\right|\hfill \\ \hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}{\mathbf{A}}^T\mathbf{A}=I\hfill \end{array}$$ (2.8)

where θ_j = 1 / β̃_j, and β̃_j is the loading coefficients of the jth standard PC. Algorithm 1 in Zou et al. (2006) was used to optimize the equation (2.8). When A = [α₁,…,α_k] is fixed, each adaptive elastic-net estimate β_j can be solved by

$${\beta }_j=\underset{\beta }{\text{arg}\hspace{0.17em}\text{min}}{({\alpha }_j-\beta )}^T{\mathbf{X}}^T\mathbf{X}({\alpha }_j-\beta )+{\lambda }_2{\left|\beta \right|}^2+{\lambda }_1{\theta }_j\left|\beta \right|.$$ (2.9)

Then B and A are updated by computing X^T XB = UDV^T and A = UV^T respectively until convergence. In equations 2.8 and 2.9, represents an N × p_m matrix with p_m genes in the mth a priori known pathway, where m = 1,…,M, and M is the total number of a priori known pathways. The sparse PCA algorithm can be summarized as:

1. Initialize B = [β₁,…,β_k];

2. Iterative until convergence:

   1. Hold B fixed and solve Equation 2.8 with respect to A. The solution takes the form A = UV^T, where UDV^T denotes the SVD of X^TXB;
   2. Hold A fixed and solve with respect to B. It can be shown that the solution also solves Equation 2.9, which can be solved using standard algorithms for the lasso such as LARS or coordinate descent.

In this paper, LARS was used compute the entire solution path with a fixed λ₂ (Efron et al., 2004). Although coordinate descent or other algorithms can be applied to improve the computation efficiency of the procedure, the proposed approach is not very computationally demanding since we process gene expression data by each pathway instead of by the whole transcriptome (Friedman et al., 2007). The tuning parameter λ₂ can be assigned to a small positive number as suggested by Zou et al. (2006). We used BIC to choose tuning parameter λ₁ since BIC has been suggested as an optimal tuning parameter selector (Zou et al., 2007; Wang and Leng, 2007):

$${\text{BIC}}_{{\lambda }_{1}j}=({\widehat{\alpha }}_{{\lambda }_{1}j}-{\widehat{\beta }}_{{\lambda }_{1}j}){\mathbf{X}}^T\mathbf{X}({\widehat{\alpha }}_{{\lambda }_{1}j}-{\widehat{\beta }}_{{\lambda }_{1}j})+\frac{\text{log}\hspace{0.17em}n}{n}{df}_{{\lambda }_{1}j}$$ (2.10)

where df_λ1j is the number of nonzero coefficients in the lasso estimator β̂_λ1j for the jth sparse principal component. This method is referred to as adaptive elastic-net sparse PCA (AES-PCA).

Normally it is difficult to justify that only a few sparse PCs will explain all the transcription activities in the genome well. At the pathway level, however, using sparse PCA to discover latent variables that represent a few different transcription activities within a pathway is more biologically reasonable.

2.4. Current proposal for pathway testing

The following four steps describe the workflow of our proposed pathway association testing method:

1. Map gene expression data to collected pathway database such as KEGG, Biocarta, and others;

2. Summarize gene expression pathway activities for each sample using the first two sparse PCs, which are extracted using the AES-PCA method described in Section 2.3;

3. Test association of sparse PCs with clinical outcomes under the regression modeling framework. More specifically, the generalized linear model, the linear regression model, and the Cox proportional hazards model were applied for categorical, continuous, and survival outcome, respectively, and the deviance can be taken as summary statistic;

4. Estimate p-values via permutation test, by permuting outcome labels 10,000 times and computing the deviance statistic for each permutation sample.

3. SIMULATION STUDIES

The purpose of this simulation study is to examine the test size and power of the proposed approach under different settings of case-control study design. We used a similar simulation study design as in Liu et al. (2007). More specifically, each gene set included 100 genes and the expression values of these 100 genes were generated from a multivariate normal distribution MVN(μ, ∑), where μ is the mean vector and ∑ is the variance-covariance matrix. All elements of μ were generated from uniform distribution U(0,10), and the diagonal elements of the covariance matrix were generated from uniform distribution U(0.1,5). For the correlations between genes in the gene set, we simulated a block diagonal structure for the gene-gene covariance matrix ∑: two blocks consisting of 15 genes each were simulated. In each block, all genes had a pair-wise correlation ρ, which was set at 0.3, 0.5, 0.7, and 0.9.

The 15 genes in the first block and the 15 genes in the second block were selected to be the differentially expressed genes responsible for the differences between case-control groups, so the means for the first 15 genes and the second 15 genes in case group were set at μ + 2γ and μ − 2γ by adding and subtracting a constant γ, respectively. In our study, γ was set at 0, 0.1, 0.2, 0.3, 0.4, and 0.5. The total sample sizes for the study (both case and control groups) were set at 2n = 20, 50 where n is the number of samples per group. There were a total of 2(n) × 4(ρ) × 6(γ) = 48 scenarios, and 1000 replication datasets were generated for each scenario.

We compared the performance of the proposed approach with five other gene set testing methods. These methods included (1) global test (Goeman et al., 2004) with R package globaltest; (2) GlobalAncova (Hummel et al., 2008) with R package GlobalAncova; (3) PCA-based test (Kong et al., 2006) with R package pcot2; (4) GSEA (Subramanian et al., 2005) with GSEA R programs downloaded from the Broad Institute website (www.broadinstitute.org/gsea/downloads.jsp); (5) maxmean test (Efron and Tibshirani, 2007) with R package GSA. The methods (1) - (5) are well-known gene set or pathway analysis tools and are described in Appendix 1.

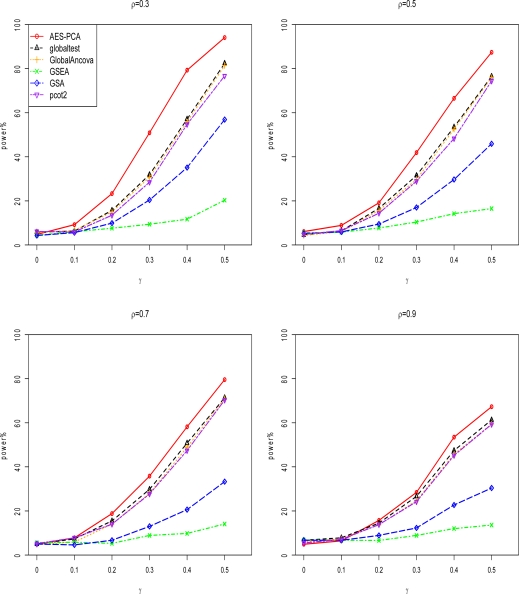
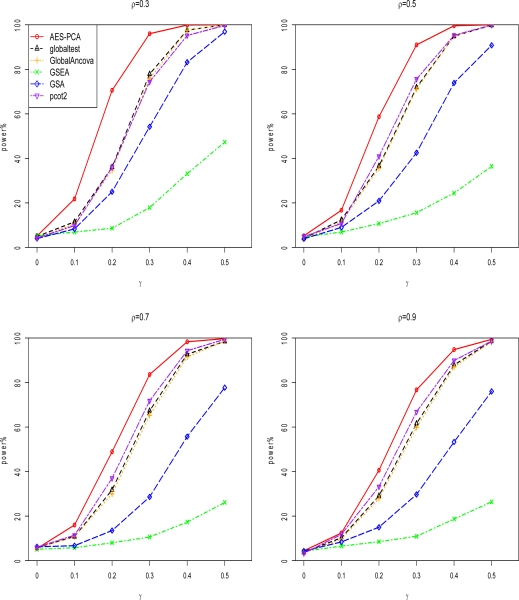
Figure 1 and Figure 2 display the comparison of the seven gene set testing methods for sample size 2n = 20 and 50, respectively. Test sizes and power were compared at nominal p-value 0.05 for each method by estimating the proportion of p-values less than 0.05 for both null gene sets and causal gene sets. The null gene sets were represented by the scenarios where γ = 0. All methods preserved type I error rates at the 0.05 significance level. Because empirical p-values were computed based on sample label permutations in AES-PCA and other 5 methods, as expected, these methods had correct test sizes.

Figure 1.

Power comparisons of six pathway testing methods when sample size 2n=20 in simulation study. ρ represents the pair-wise correlation within causal gene blocks and γ represents the mean difference between case and control groups. The proposed AES-PCA, which is the red line, showed the best power for all scenarios. The other 5 pathway analysis methods are described in Appendix 1.

Figure 2.

Power comparisons of six pathway testing methods when sample size 2n=50 in simulation study. ρ represents the pair-wise correlation within causal gene blocks and γ represents the mean difference between case and control groups. The proposed AES-PCA, which is the red line, showed the best power for all scenarios. The other 5 pathway analysis methods are described in Appendix 1.

In terms of power, the AES-PCA model performed best across all γ levels when compared with the other 5 approaches. The pcot2 test, which was based on the first two PCs of all the genes in each gene set, also showed reasonably good power, especially when the sample size or gene correlation increased. AES-PCA worked well because when estimating sparse PCs (which represented gene expression activities within gene sets), the gene selection step removed noisy signals from irrelevant genes in the gene sets. Both GSEA and GSA showed low power to identify differentially expressed gene sets using our simulation parameters.

4. APPLICATION

4.1. Lung cancer cell lines data

Paclitaxel is an extensively used anti-cancer drug. Gemma et al. (2006) tested for sensitivity of several anti-cancer drugs including paclitaxel on a set of non-small cell lung cancer (NSCLC) cell lines. This study also collected gene expression profiles of the cell lines using the Affymetrix HGU133A platform (GEO Accession No. GSE4127). In our analysis, we tested the association between gene expression levels and growth inhibitory activity (GI50) of paclitaxel in 28 NSCLC cell lines. After data preprocessing and filtering, 4234 genes were mapped to 186 KEGG pathways with minimum pathway size (total number of genes in the pathway) of 5. We applied AES-PCA, globaltest, GlobalAncova, GSEA and GSA for pathway analysis. Pcot2 was not used since it was designed for binary outcome only. For each method, in addition to nominal p-values, we also computed adjusted p-values based on the method of Benjamini and Hochberg (1995) to control false discovery rate (FDR). FDR 0.1 was used as a significance cutoff to select significant pathways.

For GSEA and GSA, all pathways had adjusted p-values greater than 0.5. Similarly, all adjusted p-values from GlobalAncova were greater than 0.15, and the results from globaltest were very similar except one pathway: “taurine and hypotaurine metabolism” with a p-value of 0.04. There were eight genes in this pathway and the gene set significance was mostly influenced by two genes — CSAD and GAD1 — based on the diagnostic plot implemented in the R package globaltest.

In contrast, the AES-PCA method models for association of the outcome with a group of correlated genes instead of a few single genes. Three pathways were selected at FDR 0.1 level by our proposed approach. The most significant one was “DNA replication pathway”, which was directly involved in the anti-cancer mechanism since paclitaxel is a mitotic inhibitor. The other two were “selenoamino acid metabolism pathway” and “renin-angiotesin system (RAS) pathway” with 22 and 16 genes, respectively. Antagonism of RAS can suppress tumor growth and metastasis and has been shown to be effective in several studies recently (George et al., 2010). Thus, our analysis results displayed drug sensitivity associations with several pathways, and these significant pathways can be used as possible molecular signatures to guide therapeutic options.

4.2. Colon cancer survival data

This colon cancer dataset included 55 patients who were diagnosed with colorectal adenocarcinoma from stage I to IV (Smith et al., 2010). The median follow-up time was 50.2 months and disease-free survival time and censoring status were used as survival analysis outcomes. Gene expressions of 55 patients were measured by Affymetrix HGU133 plus 2.0 GeneChip Expression Arrays (GEO Accession No. GSE17537). We had 4796 genes mapped to 186 KEGG pathways with a minimum pathway size of 5.

The purpose of this analysis is to identify pathways associated with survival times. Pathway analysis was conducted for all methods except GlobalAncova and pcot2, which are not applicable to survival outcomes. We followed the same procedures as those for our lung cancer cell lines data analysis described in Section 4.1.

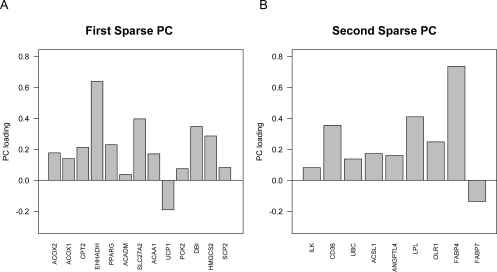
All adjusted p-values from GSEA and GSA were greater than 0.7. The lowest adjusted p-value in globaltest was 0.3184 (for the “type II diabetes mellitus” pathway). AES-PCA identified 46 pathways at FDR 0.05 level. The top eight pathways and genes selected by sparse PC1 and PC2 are listed in Appendix 2. Several top pathways are directly associated with cancer development and metastasis. Much previous experimental evidence suggests that the PPAR pathway, which is the most significant pathway in our list, plays a critical role in colorectal tumor growth. The crucial gene in this pathway is peroxisome proliferator-activated receptor gamma (PPARG). The protein encoded by this gene belongs to the peroxisome proliferators-activated receptor subfamily of nuclear receptors and directly activates a wide range of genes leading to acceleration of colorectal tumor growth (Wu, 2000; Gupta et al., 2001; Gupta et al., 2004). PPARG is regulated by Wnt/β-catenin signaling pathway, which is also important for development of colorectal cancer (Jansson et al., 2005). Another characteristic from the top pathways in Appendix 2 is that epidermal growth factor receptor (EGFR) related genes including ERBB2, KRAS, PIK3 family and MAP2K family were frequently selected by AES-PCA. Anti-EGFR monoclonal antibodies such as cetuximab and panitumumab can block EGFR tyrosine kinase activation and then inhibit the activation of RAS-MAP2K and PI3K-AKT signaling pathways to prevent cancer cell proliferation and invasion (Ciardiello and Tortora, 2008). Mutation status of KRAS is also a predictor of resistance to EGFR monoclonal antibodies in colorectal cancer (Lièvre et al., 2006). These EGFR related genes were likely implicated in targeted therapies in metastasis of colon cancer of 55 patients. In Figure 3, we display the first and second AES-PCs loading for the selected genes in PPAR pathway. For the 68 genes in this pathway, there were 13 genes with nonzero loadings for the first PC and 9 for the second, and none of those genes overlapped between these two PCs, which may represent different biological processes within this pathway.

Figure 3.

Gene plots of first and second adaptive elastic-net sparse PCs for the PPAR pathway.

5. DISCUSSION

In the analysis of gene pathways, it is often advantageous to discover the sub-groups or sub-modules within each pathway before testing pathway association with clinical outcomes because (i) pathway membership information is often based on previous literature and may not be very accurate; (ii) it is biologically meaningful to find multiple groups of genes in a pathway with distinct functions, and gene selection can help researchers focus on a few key players in a large pathway; and (iii) detecting pathway association signals with clinical outcomes by removing noisy signals from irrelevant genes can often improve statistical power.

Principal component analysis is often used as a dimension reduction approach to summarize variations from multiple genes within a pathway while modeling correlations among genes. Constructing PCA scores and testing their association with clinical outcomes after supervised variable (gene) selection was shown to be an effective approach for pathway testing (Chen et al., 2008; Chen et al., 2010). However, correcting for the bias introduced by using outcome information in the gene selection step is not trivial. A permutation test can be used for testing pathway association with clinical outcomes, but because supervised variable selection needs to be performed for each permutation re-sample, the computation can be challenging.

In this paper, we developed a different strategy to do variable (gene) selection and PCA-based dimension reduction for pathway testing. Our approach based on adaptive elastic-net sparse PCA (AES-PCA) is attractive because it can efficiently perform gene selection by capturing the variations and incorporating the correlations of genes in a pathway. In addition, because AES-PCA is an unsupervised procedure that does not use any outcome information in the variable selection step, it is also straightforward to implement a permutation test based on AES-PCA scores.

In the simulation studies, we compared the proposed AES-PCA with five other popular and related pathway testing approaches. Our results showed that AES-PCA has the best power across all scenarios. In particular, in comparison with the PCA-based method from Kong et al. (2006), the better performance of AES-PCA suggests that instead of computing PCA scores based on all genes in a pathway, the variable selection step in AES-PCA helped it gain power by removing noise gene signals from irrelevant genes.

The default setting in the AES-PCA method is to test pathway association based on the first and second PCs, which is the same as the pcot2 approach described in Kong et al. (2006). Although adding more PCs may increase the power of the test, in our simulation study and real datasets analysis, the two AES-PCs implementation showed a satisfactory performance. In addition, the few extracted PCs are relatively easy to interpret biological activities within a pathway.

Another advantage of the proposed AES-PCA pathway testing approach is that it is applicable to different experimental designs. In this paper, we illustrated the analysis for binary, continuous and survival outcomes. For studies with larger sample sizes, future studies can be conducted to fit extracted sparse PCs or latent variables in more complicated models to account for correlations between pathways or to detect pathway-pathway interactions. It would also be interesting to compare the sub-modules in pathways identified by our approach with gene modules identified by gene network methods.

APPENDIX

Appendix 1. Description of pathway testing methods used in simulation studies

We describe the five available pathway analysis methods used in the simulation study. For clarity, we followed the notations in each method’s original paper.

GSEA

Gene set enrichment analysis (GSEA) is one of the earliest developed and a widely used pathway analysis tool (Subramanian et al. 2005). Let N be the total number of genes in a gene expression experiment; k be the number of samples; and S be the pathway or gene set of interest. To calculate enrichment score ES(S): (1) for each gene, compute correlation r_j between gene expression and phenotype, then rank N genes by r_j to have a ranking list L = {g₁,…, g_N}; (2) for each position i in the list L, two running sums for genes within gene set S and outside S can be calculated separately according to the following formula

$$\begin{array}{c}{P}_{\text{hit}}(S,i)=\sum _{\begin{array}{l}{g}_i\in S\\ j\le i\end{array}}\frac{{\left|r_j\right|}^p}{N_R},\hspace{0.17em}\text{where}\hspace{0.17em}{N}_R=\sum _{g_j\in S}{\left|r_j\right|}^p\\ P_{\text{miss}}(S,i)=\sum _{\begin{array}{l}{g}_i\notin S\\ j\le i\end{array}}\frac{1}{(N-N_H)}\end{array}$$

The enrichment score ES(S) is the maximum of P_hit − P_miss over all position i. When p=0, ES(S) is the standard Kolmogorov-Smirnov statistic. The null hypothesis for GSEA of gene set S is: genes in S are randomly distributed in gene list L. The empirical p-value for ES(S) can be computed by permutation of sample labels.

GSA

Efron and Tibshirani (2007) proposed the use of the maxmean statistic as well as combining sample and gene permutations to improve GSEA, especially for the Kolmogorov-Smirnov statistic. The steps are as follows:

1. Compute a summary statistic z_j for each gene, for example two-sample t-statistic;

2. For each gene set S with m genes, define the summary statistic maxmean S_max = max{s̄⁽⁺⁾, s̄⁽⁻⁾}

   where s(z) = (s⁽⁺⁾, s⁽⁻⁾), s⁽⁺⁾ = max(z, 0), s⁽⁻⁾ = − min(z, 0) and ${\overline{s}}^{(+)}=\frac{1}{m}\sum s_j^{(+)},{\overline{s}}^{(-)}=\frac{1}{m}\sum s_j^{(-)}$;

3. Standardize S_max by its randomization mean and standard deviation: S′_max = (S_max − mean_s) / stdev_s where mean_s and stdev_s are the mean and standard deviation of S_max by gene label permutation, respectively;

4. Permute sample labels B times and recompute S′_max each time, then estimate p-values and false discovery rates for all pathways.

Globaltest

Goeman et al. (2004) proposed a generalized linear model for testing the association of phenotype with all genes in a pathway or gene set. Let Y be the n × 1 vector for clinical outcome, for example 0/1 for two-group comparison, and let X_n×m be the gene expression matrix for m genes in a pathway S. The regression model can be written as

$$E(Y_i|\beta )=h^{-1}\left(\alpha +\sum _{j=1}^m{x}_{ij}{\beta }_j\right)$$

where β_j is the regression coefficient for each gene. The null hypothesis for testing pathway association with clinical outcome is

$$H_0:{\beta }_1={\beta }_2=\dots ={\beta }_m=0$$

which states that none of the genes in the pathway is associated with the outcome. To simplify the testing procedure, the authors assume all β are from a common distribution with expectation 0 and variance τ², thus the null hypothesis becomes

$$H_0:{\tau }^2=0.$$

A score test is implemented to test the null hypothesis by assuming a diagonal covariance matrix τ² I_m for vector β (independent genes assumption). Either asymptotic approximaton or permutation test are available in R package globaltest to estimate p-values for pathways.

GlobalAncova

Mansmann and Meister (2005) proposed a pathway testing approach based on the ANCOVA model. In a two-group comparison scenario, let x_ijk denote the gene expression value for the ith group (i = 1,2), jth gene (j = 1,2,…,N_genes) and kth sample (k = 1,2,…M). The linear model can be written as

$$x_{ijk}={\mu }_{ij}+{\theta }_j{z}_{ik}+e_{ijk}$$

where z_ik is the clinical covariate and μ_ij = μ + α_i + β_j + γ_ij with group effect α, gene effect β and interaction effect γ. The null hypothesis is

$${\mu }_{1j}={\mu }_{2j}\iff {\alpha }_i={\gamma }_{ij}=0.$$

Either asymptotic or permutation tests of the F-statistic are available in R package GlobalAncovat to estimate p-values for pathways.

PCOT2

Kong et al. (2006) applied dimension reduction by PCA and Hotelling’s T² test for pathway testing of binary clinical outcomes. Specifically, singular value decomposition was used in each pathway to extract the two-dimensional vector u_ij representing the first and second principal components for the jth sample (j = 1,…, n_i) in the ith group (i = 1,2). The test statistic is based on Hotelling’s T² :

$$T^2=\frac{n_1{n}_2}{n_1+n_2}{({\overline{u}}_1-{\overline{u}}_2)}^t{S}^{-1}({\overline{u}}_1-{\overline{u}}_2)$$

where ū_i is the mean vector and S is the pooled empirical covariance matrix. The null hypothesis is

$$H_0:{\overline{u}}_1={\overline{u}}_2$$

and the test statistic would follow an F-statistic. A permutation test is the default setting for R package pcot2 to calculate p-values.

Appendix 2. Top eight pathways from the AES-PCA method for colon cancer data

KEGG pathways	Size	FDR	Selected Genes
PPAR signaling pathway	68	0.0001	PC1: ACOX1, ACOX2, CPT2, EHHADH, PPARG, ACADM, SLC27A2, ACAA1, UPC1, PCK2, DBI, HMGCS2, SCP2; PC2: ILK, CD36, UBC, ACSL1, ANGPTL4, LPL, OLR1, FABP4, FABP7
ERBB signaling pathway	86	0.0093	PC1: PAK3, MAP2K7, NRG2, CRKL, MAPK8, CAMK2A, MAP2k1; PC2: STAT5B, PAK2, SHC1, PIK3CB, ERBB2, KRAS, MAP2K2, NRAS, GSK3B, ARAF, ABL1
Aldosterone-regulated sodium reabsorption	42	0.0093	PC1: PIK3CA, PIK3R5, PIK3CG, SGK1, ATP1A3, IGF1, PRKCB, HSD11B1; PC2: KCNJ1, PDPK1, KRAS, INS, INSR, PIK3R2, IRS2
Thyroid cancer	29	0.0093	PC1: CDH1, TCF7L2, MAP2K1, RXRB, TP53, MAPK1, NRAS; PC2: TFG, KRAS, CCDC6
Regulation of actin cytoskeleton	208	0.0112	PC1: PIK3CG, PDGFRA, CD14, SSH1, MRAS, ITGB2, ARPC5, ITGB1, ITGA4, PIP4K2A, MYLK, PAK4, MSN, CFL2; PC2: ITGA2B, KRAS, RAC1, FGF1, FGF14, MYL10, FGF21, PPP1CC, ARPC3, PAK3, CRKL, CHRM2, ARPC5L
Neurotrophin signaling pathway	123	0.0124	PC1: RAPGEF1, RELA, MAPK1, MAPKAPK2, PTPN11, RHOA, SHC1, TP53, YWHAE, GSK3B, MAPK14, CRK, CALM1; PC2: MAPK8, KRAS, NTF4, NTRK3, KIDINS220, CRKL, MAP3K1, MAPK12, YWHAQ
Endometrial cancer	52	0.0165	PC1: TP53, CTNNA1, MAPK1, CDH1, SOS2, MAPK2k2, GSK3B; PC2: PEN, PIK3Cb, PIK3CD, ERBB2, ELK1, TCF7L2, KRAS, SOS1, PIK3R5, APC, MAP2K1, ARAF
Endocytosis	179	0.0165	PC1: CHMP4C, CHMP4A, VPS4A, STAM, EGFR, CHMP2A, CHMP2B, SRC, HSPA1L, ADRB3, EPS15, CLTA, LDLR, TSG101, CXCR2, ZFYVE20, RAB4A, RAB11A, STAMBP, VPS25, RNF41; PC2: HLAC, HLAG, ARRB2, ARF6, AP2M1, AGAP2, PSD, EHD1, AP2A1