Electromechanical properties and anisotropy of single- and multi-domain 0.72Pb(Mg_1∕3Nb_2∕3)O₃-0.28PbTiO₃ single crystals

Abstract

Complete sets of elastic, piezoelectric, and dielectric constants of 0.72Pb(Mg_1∕3Nb_2∕3)O₃-0.28PbTiO₃ single crystal poled along [111]_c (single domain) as well as non-polar axes [001]_c and [011]_c (multidomain) have been measured under natural conditions. These data allowed us to evaluate accurately the extrinsic contributions to the superior piezoelectric properties. Very large extrinsic contributions to the unusual anisotropies in multidomain crystals are confirmed. We found that the instability of domain structures is the origin of the low mechanical quality factor Q for the multidomain relaxor-based ferroelectric single crystals. Our results can provide useful guidance in future design of domain engineered materials.

Relaxor-based ferroelectric single crystals, such as (1-x)Pb(Zn_1∕3Nb_2∕3)O₃-xPbTiO₃ (PZN-PT) and (1-x)Pb(Mg_1∕3Nb_2∕3)O₃-xPbTiO₃ (PMN-PT), have been the focus of ferroelectric materials research over the past decade due to their ultrahigh electromechanical properties (d₃₃ > 2000 pC∕N and k₃₃ > 0.9) when they are poled along some nonpolar directions.^{1, 2, 3, 4, 5, 6, 7} There are fundamental research works trying to find out the origin of the giant piezoelectric effects,^{5, 6, 7} and device related research works trying to exploit the large electromechanical properties for medical ultrasonic imaging, sonar transducers, and solid-state actuators.^{4, 8}

It was demonstrated that the high piezoelectric activities of relaxor-PbTiO₃ single crystals along nonpolar directions are from both intrinsic and extrinsic contributions although intrinsic contribution dominates for longitudinal piezoelectric properties. As concluded in Ref. 6, the large intrinsic effects are related to the high level of shear piezoelectric response and large dielectric susceptibility perpendicular to the polarization direction in the monodomain state, which may be understood as due to the flat potential wells in the polar states. Extrinsic contributions are usually responsible for nonlinear field responses, weak-field hysteresis, frequency dispersions of functional properties, and particularly mechanical losses and aging. Despite the intensive efforts of many researchers, the physical mechanism of these engineered domain systems is still not fully understood. The lack of complete physical property data, especially single domain data, is the main hindrance for in depth theoretical studies. Up to date, only 2 self-consistent complete sets of material constants for single domain binary relaxor-PbTiO₃ (relaxor-PT) single crystals have been published.^{9, 10} Both of them were measured under electric bias because their single domain state is unstable. There is only one set of single domain data measured under natural conditions for a ternary system 0.24Pb(In_1∕2Nb_1∕2)O₃-0.49Pb(Mg_1∕3Nb_2∕3)O₃-0.27PbTiO₃.¹¹ Such single domain data would be very useful for the fundamental studies on the origin of the giant piezoelectric properties in the multidoamin binary relaxor-PT single crystals.

In addition to material property variations, it was found that some domain engineered relaxor-PT crystals exhibit lower mechanical quality Q than that of others. This indicates that the mechanical loss of these materials is strongly related to domain structures as well as compositions. Because low mechanical Q factor restricts their usage in high-power applications,^{4, 12, 13} we need to investigate the relationship between mechanical Q-value with domain structures.

Single crystal 0.72Pb(Mg_1∕3Nb_2∕3)O₃-0.28PbTiO₃ (PMN-0.28PT) has a rhombohedral 3 m symmetry at room temperature. We found that this crystal could maintain the single domain state when poled along its spontaneous polarization direction [111]_c. When the crystal is poled along [001]_c or [011]_c directions, the domain patterns form either tetragonal 4 mm or orthorhombic mm2 symmetry. In this letter, we report three self-consistent complete sets of elastic, dielectric, and piezoelectric constants of PMN-0.28PT single crystals poled along [001]_c, [011]_c, and [111]_c, respectively. By using the combined ultrasonic and resonance method, we could obtain the maximum number of materials constant combinations from the least number of samples to achieve self-consistency.^{2, 10, 14} The complete set of material constants of PMN-0.28PT single crystals poled along [001]_c and [011]_c have been reported.^{15, 16, 17} However, those constant sets are not self-consist. The inconsistencies had been analyzed in detail in Refs. ^{18, 19} and it was recommended that they must be re-measured in order to clear out related confusions. One of the objectives of this letter is to provide one set of self-consistent data for PMN-0.28PT. In addition, from ultrasonic measurements, we could obtain both wave velocities as well as ultrasonic attenuation coefficients by fitting the amplitudes of the echoes to an exponential function.

The PMN-PT single crystals used were grown by the modified Bridgman method. All samples were cut from the same wafer and oriented using the Laue x-ray machine with an accuracy of ±0.5°. Each sample was cut and polished into a parallelepiped with three pairs of parallel surfaces along certain defined directions.^{2, 10, 14} For resonance measurements, the dimensions and geometries of samples used were specified by the IEEE standards on piezoelectricity. The resonance and antiresonance frequencies were obtained via an HP4294A impedance-phase gain analyzer. For ultrasonic measurements, 5.0 × 5.0 × 5.0 mm³ cubes were fabricated. A 10 MHz longitudinal wave transducer (Ultran Laboratories, Inc.) and a 20 MHz shear wave transducer (Panametrics Com.) were used for the ultrasonic pulse-echo measurements. The transducers were excited by a 200 MHz pulser∕receiver (Panametrics Com.), and the time of flight between echoes and the amplitudes of echoes were measured using a Tektronix 460 A digital oscilloscope.

Data self-consistency is of vital importance in fundamental studies as well as device designs. As indicated in Refs. ^{18, 19}, lack of self-consistency will lead to undesired confusions. The measured and derived elastic, piezoelectric, and dielectric constants of the PMN-0.28PT single crystals poled along [011]_c, [001]_c, and [111]_c are given in Table TABLE I.. For [111]_c poled (single domain state) case, it was noticed that the dielectric anisotropy, ${\varepsilon }_{11}^T∕{\varepsilon }_{33}^T$ = 8.4, is very strong. This point is confirmed by the measured piezoelectric constants of domain engineered crystals, d₃₃ = 1182 pC∕N and 860 pC∕N for [001]_c and [011]_c poled multidomain single crystals, respectively, which are about 12 and 9 times larger than that of single domain state (d₃₃ = 97 pC∕N).

Table 1.

Measured material properties of single domain and multidomain PMN–0.28PT single crystals.

Elastic stiffness constants: cE, cD(1010 N∕m2)
	$c_{11}^E$	$c_{12}^E$	$c_{13}^E$	$c_{14}^E$	$c_{22}^E$	$c_{23}^E$	$c_{33}^E$	$c_{44}^E$	$c_{55}^E$	$c_{66}^E$
[011]c-poled	19.53	8.30	1.12	—	10.62	8.97	13.82	6.57	0.48	4.45
[001]c-poled	12.04	10.68	9.19	—	—	—	10.35	6.57	—	6.12
[111]c-poled (single domain)	19.10	8.66	4.08	−1.27	—	—	17.02	1.03	—	—
	$c_{11}^D$	$c_{12}^D$	$c_{13}^D$	$c_{14}^D$	$c_{22}^D$	$c_{23}^D$	$c_{33}^D$	$c_{44}^D$	$c_{55}^D$	$c_{66}^D$
[011]c-poled	19.56	8.14	1.55	—	11.51	6.62	20.03	7.98	4.47	4.45
[001]c-poled	22.35	20.99	0.33	—	—	—	17.97	7.03	—	6.12
[111]c-poled (single domain)	21.28	10.50	0.90	−0.03	—	—	22.06	9.99	—	—
Elastic compliance constants: sE, sD(10−12 m2∕N)
	$s_{11}^E$	$s_{12}^E$	$s_{13}^E$	$s_{14}^E$	$s_{22}^E$	$s_{23}^E$	$s_{33}^E$	$s_{44}^E$	$s_{55}^E$	$s_{66}^E$
[011]c-poled	13.40	−21.18	12.67	—	54.36	−33.59	28.02	15.22	147.06	22.47
[001]c-poled	44.57	−28.91	−13.91	—	—	—	34.38	15.22	—	16.34
[111]c-poled (single domain)	8.78	−4.90	−0.93	16.87	—	—	6.32	138.69	—	—
	$s_{11}^D$	$s_{12}^D$	$s_{13}^D$	$s_{14}^D$	$s_{22}^D$	$s_{23}^D$	$s_{33}^D$	$s_{44}^D$	$s_{55}^D$	$s_{66}^D$
[011]c-poled	7.57	−6.19	1.46	—	15.78	−4.73	6.44	12.54	22.35	22.47
[001]c-poled	37.89	−35.58	−0.04	—	—	—	5.57	14.21	—	16.34
[111]c-poled (single domain)	6.22	−3.06	−0.13	0.03	—	—	4.54	10.01	—	—

Piezoelectric constants: d(10−12 C∕N), e(C∕m2), g(10−3Vm∕N), h(108 V∕m)
	d15	d22	d24	d31	d32	d33	e15	e22	e24	e31	e32	e33
[011]c-poled	2162	—	160	447	−1150	860	14.70	—	10.53	1.45	−7.84	20.65
[001]c-poled	122	—	—	−569	—	1182	8.02	—	—	−20.60	—	17.71
[111]c-poled (single domain)	2382	−312	—	−43	—	97	16.62	−2.29	—	−8.13	—	12.89
	g15	g22	g24	g31	g32	g33	h15	h22	h24	h31	h32	h33
[011]c-poled	57.68	—	16.76	13.04	−33.55	25.09	25.80	—	13.37	2.11	−11.42	30.08
[001]c-poled	8.24	—	—	−11.73	—	24.37	5.80	—	—	−50.04	—	43.02
[111]c-poled (single domain)	54.02	−7.07	—	−8.29	—	18.42	53.96	−7.44	—	−24.69	—	39.15
Dielectric constants: ɛ(ɛ0), β(10−4∕ɛ0)
	${\varepsilon }_{11}^S$	${\varepsilon }_{22}^S$	${\varepsilon }_{33}^S$	${\varepsilon }_{11}^T$	${\varepsilon }_{22}^T$	${\varepsilon }_{33}^T$	${\beta }_{11}^S$	${\beta }_{22}^S$	${\beta }_{33}^S$	${\beta }_{11}^T$	${\beta }_{22}^T$	${\beta }_{33}^T$
[011]c-poled	644	890	776	4235	1081	3873	15.53	11.24	12.89	2.36	9.26	2.58
[001]c-poled	1562	—	465	1672	—	5479	6.40	—	21.50	5.98	—	1.83
[111]c-poled (single domain)	348	—	357	4983	—	593	28.74	—	26.88	2.01	—	16.87

Electromechanical coupling constants: k							Density: ρ(kg∕m3)
	kt	k15	k24	k31	k32	k33	8095
[011]c-poled	55%	92%	42%	66%	85%	90%
[001]c-poled	65%	25%	—	44%	—	91%
[111]c-poled (single domain)	48%	94%	—	20%	—	53%

From the single domain data, the intrinsic piezoelectric coefficient $d_{33}^{*}$ of [001]_c poled rhombohedral PMN-0.28PT can be calculated by using coordinate transformation,²⁰

$$d_{33}^{*}=\frac{\sqrt{3}}{9}[2d_{31}+2d_{15}+d_{33}-\sqrt{2}{d}_{22}].$$ (1)

The calculation gives $d_{33}^{*}$ = 1004 pC∕N. Compared to the measured value of $d_{33}^{*}$ = 1182 pC∕N in the multidomain system, the differences is about ∼15%, which is associated with the extrinsic contributions of the engineered domain configuration.

In order to investigate the dissipation properties, ultrasonic attenuations are measured by using ultrasonic pulse-echo method. If the amplitude of the ultrasonic wave is A₀ at the beginning, the amplitude will become A after the wave propagates a distance x, i.e.,

$$A=A_0{e}^{-\alpha x}.$$ (2)

Therefore, the attenuation coefficient α can be extracted from the amplitude measurement based on the ultrasonic echo train,

$$\ln (A∕A_0)=-\alpha x.$$ (3)

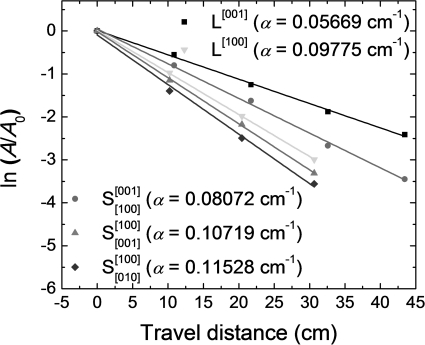
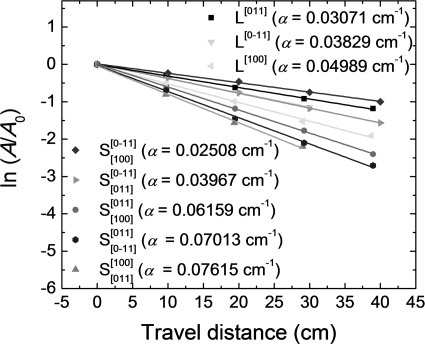
Figures 12 present the value of ln(A∕A₀) as a function of propagation distance x for the ultrasonic waves propagating in both [001]_c and [011]_c poled PMN-0.28PT single crystals. For both cases, the values of α vary considerably with wave propagation directions. For [001]_c and [011]_c poled crystals, the longitudinal ultrasonic waves propagate along the same pseudo-cubic [100]_c direction. But their α values are much different, i.e., 0.09775 cm⁻¹ and 0.04989 cm⁻¹, respectively, for [001]_c and [011]_c poled crystals. The former is almost 2 times as large as the latter. This indicates that the domain structure is an important factor for the ultrasonic attenuation. In other words, the domain structure is vital in controlling the ultrasonic attenuation and the mechanical quality factor Q. In [001]_c-poled crystals, four degenerated engineered domains exist. The domain structure are less stable under external drive and there is also a large hysteresis.²¹ Domain wall movements or breathing motions produce larger piezoelectric effect and lead to larger mechanical loss (or lower mechanical Q). For the [011]_c poled crystals, only two energetically degenerate domains exist, the domain structure is more stable, which leads to smaller piezoelectric response but also less mechanical loss or higher mechanical Q value.

Figure 1.

(Color online) Normalized amplitudes of longitudinal (L) and shear (S) ultrasonic waves as a function of propagation distance for [001]_c poled PMN-0.28PT single crystal.

Figure 2.

(Color online) Normalized amplitudes of longitudinal (L) and shear (S) ultrasonic waves as a function of propagation distance for [011]_c poled PMN-0.28PT single crystal.

It should be noted that the attenuation of shear-mode wave attenuation may also be attributed to the domain structures because domain walls are more susceptible to shear motions, which is the reason why the mechanical quality factor Qs for almost all thickness shear vibration modes are less than 50 in relaxor-PT crystals.⁸

In summary, by using combined resonance and ultrasonic methods, we have measured the elastic, dielectric, and piezoelectric constants of rhombohedral PMN-0.28PT single crystals poled along [001]_c, [011]_c, and [111]_c. The three complete sets of material constants were determined from the same crystal wafer, so that their composition and properties are uniform. It is shown that more than 85% of the large piezoelectric properties of multidomain system come from intrinsic contributions, but the extrinsic contributions are definitely not negligible. The anisotropic attenuation behavior has been experimentally characterized, for which the extrinsic contributions account for more than 50%. The attenuation results obtained shed some light on the key role played by domain walls in the anisotropic characteristics as well as the low mechanical Q values of these domain engineered single crystals.