Paired de Bruijn Graphs: A Novel Approach for Incorporating Mate Pair Information into Genome Assemblers

Abstract

The recent proliferation of next generation sequencing with short reads has enabled many new experimental opportunities but, at the same time, has raised formidable computational challenges in genome assembly. One of the key advances that has led to an improvement in contig lengths has been mate pairs, which facilitate the assembly of repeating regions. Mate pairs have been algorithmically incorporated into most next generation assemblers as various heuristic post-processing steps to correct the assembly graph or to link contigs into scaffolds. Such methods have allowed the identification of longer contigs than would be possible with single reads; however, they can still fail to resolve complex repeats. Thus, improved methods for incorporating mate pairs will have a strong effect on contig length in the future. Here, we introduce the paired de Bruijn graph, a generalization of the de Bruijn graph that incorporates mate pair information into the graph structure itself instead of analyzing mate pairs at a post-processing step. This graph has the potential to be used in place of the de Bruijn graph in any de Bruijn graph based assembler, maintaining all other assembly steps such as error-correction and repeat resolution. Through assembly results on simulated perfect data, we argue that this can effectively improve the contig sizes in assembly.

1. Introduction

The recent proliferation of next generation sequencing with short reads has enabled new experimental opportunities, such as the 10K genomes project, which aims to sequence and assemble the genomes of approximately one species in every vertebrate genus (Genome 10K Community of Scientists, 2009). At the same time, the short read length and sheer demand for powerful assemblers has raised formidable computational challenges. Thus, genome assembly continues to represent one of the most difficult and important algorithmic problems in bioinformatics.

The first generation of assemblers followed the overlap-layout-consensus paradigm, where overlaps were heuristically used to join reads together into contigs (Myers, 1995; Batzoglou et al., 2002). Later, the introduction of de Bruijn graphs led to significant improvements in assembly (Pevzner, 1989; Idury and Waterman, 1995; Pevzner et al., 2001). In contrast to the overlap-layout-consensus approach, these assemblers first constructed a graph where the original genome is spelled by a series of walks through the graph, and non-branching walks correspond to substrings (contigs) of the genome. Compared to the earlier heuristic approaches, de Bruijn graphs produced longer contigs and gave rise to more powerful techniques for correcting errors and resolving repeats—identical, or nearly identical, stretches of DNA (Schatz et al., 2010). Their success led to the development of other types of graphs for sequence assembly: A-Bruijn graphs (Pevzner et al., 2004) and closely related string graphs (Myers, 2005), which together have become an essential part of most modern assembly tools, including EULER-SR (Chaisson and Pevzner, 2008), Velvet (Zerbino and Birney, 2008), ALLPATHS (Butler et al., 2008), ABySS (Simpson et al., 2009), and others.

Despite these advances, the challenge of resolving repeats remains. When the length of a repeat is longer than twice the read length, it becomes difficult to correctly match its upstream and downstream regions. In order to alleviate this problem, sequencing technologies were extended to produce mate pairs (Weber and Myers, 1997)—pairs of reads between which the genomic distance (called the insert size) is well estimated. Because insert sizes could be much longer than the read length, mate pairs were able to span long repeats and could potentially match up the regions surrounding a repeat.

The challenge of algorithmically incorporating mate pair information into de Bruijn graph assemblers was first addressed by Pevzner and Tang (2001), who proposed a heuristic to look for a path between the two reads of a mate pair with a length of the insert size. If exactly one such path was found, then a mate pair transformation could be applied to “unwind” this path in the graph. Essentially, this amounted to transforming two mated reads into one long read where the gap between the mates was filled in with the nucleotide sequence representing the found path, thus potentially connecting the surrounding regions of a repeat. Several other heuristic approaches for utilizing mate pair information in the de Bruijn graph were developed (Zerbino and Birney, 2008; Butler et al., 2008; Medvedev and Brudno, 2008).

Such methods had a great impact on genome assembly, allowing the construction of much longer contigs; however, they could still fail in complex repeat-rich regions, where there are multiple paths between the read pairs. Many current technologies, including Complete Genomics (Drmanac et al., 2010) and Helicos (Harris et al., 2008), still generate very short reads (around 25 nt) for which the resulting de Bruijn graph is very tangled (even for bacterial genomes). In such cases, mate pair transformations often fail because of multiple paths. Additionally, the percentage of mate pairs that can be successfully transformed deteriorates when the insert size is high (Chaisson et al., 2009), and the search for paths between mates becomes prohibitively time-consuming. Unfortunately, these difficulties result in shorter contigs in complex repeat-rich regions. The limitations of the existing heuristics for analyzing mate pairs is thus a major hurdle towards assembling large contigs with short reads.

We believe that the shortcomings of current mate pair algorithms stem from the fact that they are heuristic approaches that are applied after the construction of the de Bruijn graph. The de Bruijn graph does an excellent job of incorporating the sequence information from the single reads; however, it ignores any mate pair information that is available. This information has to be recovered after the graph construction, and only then applied in a heuristic manner. In this article, we propose the paired de Bruijn graph, a generalization of the de Bruijn graph that incorporates the mate pair information into the structure of the graph itself, as opposed to a post-processing step. Just as moving from the heuristic overlap-layout-consensus paradigm to the de Bruijn graph paradigm resulted in better assemblies, we believe that moving from heuristic mate pair algorithms to paired de Bruijn graphs could result in a more effective use of mate pair information. The paired de Bruijn graph is a potential replacement of the de Bruijn graph in existing de Bruijn graph based assemblers; existing assembly stages, including error correction and scaffolding, would not need to be substantially modified.

Through assembly results on simulated perfect data, we argue that when mate pair information is used in this manner, the read length (once above a small threshold) becomes much less relevant (Chaisson et al., 2009). We find that the contig sizes in an assembly are largely dictated by the average insert size—when it exceeds 6000 nt, we can assemble all of E. coli into one contig and most of the human chromosome 22 into 15 contigs. Though this paper falls short of analyzing real data, we believe that, similar to how early error-free studies of de Bruijn graphs laid the foundation for their use in assembly (Pevzner, 1989), the paired de Bruijn graph can become the basis of practical assemblers.

2. From de Bruijn Graphs to Paired de Bruijn Graphs

2.1. Preliminaries

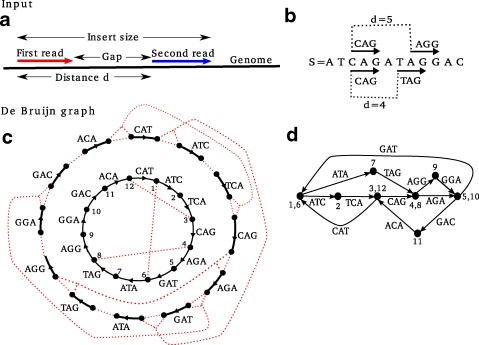
To simplify the presentation, we assume that the genome is a circular string (i.e., one circular, single-stranded chromosome) and that all reads have the same length l; extending our approach for multiple linear chromosomes or varying read length is straightforward. Moreover, we assume that reads are error-free (see Section 5 for a discussion). In this setting, a mate pair is an ordered pair of strings of length l drawn from the genome at positions i and j, respectively. Normally, the relative distance between reads is expressed in terms of the insert size, the number of nucleotides from the first nucleotide of a to the last nucleotide of b: j − i + l. However, for the purposes of our construction, it is more convenient to express it in terms of d = j − i, the difference in their leftmost coordinates. Note that d is the insert size minus one read length (Fig. 1a).

FIG. 1.

Mate pairs and the de Bruijn graph. (a) A mate pair is a pair of reads with a distance of d between their start positions. (b) A circular genome S and two mate pairs, with d = 4 and d = 5. (c, d) The de Bruijn graph construction for k = 2. (c) The outside circle shows a separate black edge for each 3-mer (equivalently, each element of the 3-spectrum). The dotted red lines indicate vertices that will be glued. The inner circle shows the result of applying some of the glues. Note that this is an intermediate step of the construction in which we only show the gluings of vertices arising from the same position of S. (d) The final de Bruijn graph, resulting from all the glues.

As with any de Bruijn graph based approach, our algorithms have a parameter k that dictates the size of the substrings into which the reads are chopped up. Thus, though our input is a set of mate pairs of reads of any length, we immediately chop them up into smaller pieces. Formally, each mate pair of reads is replaced by its constituent l − k (sub-)mate pairs, where the reads of each (sub-)mate pair now have length k + 1. Therefore, for the remainder of the paper, we will assume without loss of generality that the reads are immediately given with length k + 1. We now give some definitions.

A-Bruijn graphs: Let G be a directed graph on m vertices. The gluing of vertices v and w is defined by substituting v and w by a single vertex (called the successor of v and w) and retaining all edges incident to either v or w as edges incident to their successor. Let A be a boolean m × m matrix representing “glues” (Pevzner et al., 2004). The A-Bruijn graph A(G) is obtained by gluing all vertices v and w of G for which A_v,w = 1. One can execute these glues in an arbitrary order under the assumption that each gluing instruction A_{v, w} = 1 is applied to the successors of vertices v and w in the graph resulting from the previous gluing instructions.

Below we describe three A-Bruijn graphs: de Bruijn graphs (for unpaired reads); paired de Bruijn graphs (for mate pairs with an exact distance); and approximate paired de Bruijn graphs (for mate pairs with an approximate distance).

k-mers and labels: Define a k-mer as a string of length k. Below we assume that the parameter k is fixed. Given a circular string 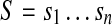, let S_k(i) be the k-mer 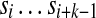(where the index is taken modulo n). The set of all k-mers S_k(i) (for 1 ≤ i ≤ n) is called the k-spectrum of S. For a k-mer 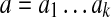, we define two (k − 1)-mers, 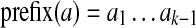(remove last character) and 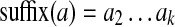(remove first character). We say that k-mer a aligns at position i if a = S_k(i).

(k, d)-mers and bilabels: A bilabel (a|b) is a pair of strings, a and b, of equal length. Define left(a|b) = a and right(a|b) = b. A k-mer bilabel indicates both a and b have length k. Define 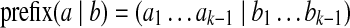and 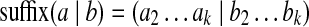. Given an integer d (usually d ≥ k), a (k, d)-mer of S is a pair of k-mers S_k(i) and S_k(i + d) that start exactly d nucleotides apart. We use the bilabel notation (S_k(i)|S_k(i + d)) for (k, d)-mers. For a string S and parameters d and Δ, we say k-mer bilabel (a|b) aligns at position i if a = S_k(i) and b = S_k(i + d + x) for some − Δ ≤ x ≤ Δ. A (k, d, Δ)-mer of S is a bilabel (a|b) that aligns somewhere to S.

2.2. De Bruijn graphs (modeling unpaired reads)

Let C be a set of (k + 1)-mers from a circular string S. We construct an A-Bruijn graph based on C as follows.

• First, we define an initial graph G₀ consisting of m = 2|C| vertices and |C| isolated edges. For each (k + 1)-mer 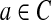, introduce two new vertices u, v and form an edge u → v. Label the edge by the (k + 1)-mer a; label u by the k-mer prefix(a); and label v by the k-mer suffix(a).

• Second, we glue certain vertices of G₀ together, by forming an m × m binary matrix A and setting A_i,j = 1 to indicate that vertices i and j should be glued together. For this construction, we set A_i,j = 1 when vertices i and j have the same label.

The labeled directed graph G = DB(C, k) obtained from these gluings is the de Bruijn graph of C (Pevzner et al., 2004) (Fig. 1b–d). It may be considered as either a simple graph (without parallel edges but with loops), or as a multigraph where the multiplicity of each edge is determined by the number of times the (k + 1)-mer it represents is present in C. Consider a walk through edge/label sequence 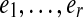. The labels satisfy suffix(e_i) = prefix(e_i+1), and we may define the string of length r + k spelled by this walk as 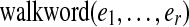by successively overlapping the labels with a shift of one character at a time.

Traditionally, the de Bruijn graph is also defined on a string S by setting the vertex set equal to the k-spectrum of S. For every (k + 1)-mer a of S, define an edge prefix(a) → suffix(a) labeled by a. Explicitly, for each S_k+1(i) of S, define an edge S_k(i) → S_k(i + 1) labeled by S_k+1(i) (for ).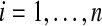

In the case that C is the (k + 1)-spectrum of S, the de Bruijn graph built on C using the gluing approach is identical to the one built directly on the genome S. Moreover, there is a covering cycle that spells S, where a covering cycle is a cyclical walk that visits every edge at least once. In this graph, the cycle is the sequence of edges 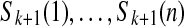. The covering cycle property is crucial for assembly because it implies that all walks whose interior vertices have just one out-neighbor must spell substrings in S (contigs).

2.3. Graph complexity

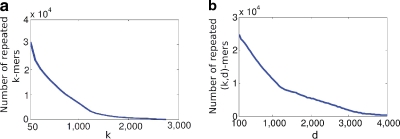
The usefulness of a graph representation of a genome can vary widely. In general, the number of vertices can serve as a rough indicator of how useful the graph is—as the number of vertices grows (and the number of edges stays the same), the graph is likely to become less entangled, and the contigs are likely to become longer. Figure 2a shows that in the de Bruijn graph, the number of repeated k-mers in E. coli drops as k increases, indicating that the de Bruijn graph has more vertices and likely becomes less entangled. Alternatively, consider pairs of k-mers, i.e., (k, d)-mers. Figure 2b shows that, after fixing k = 50, the number of repeated (k, d)-mers drops as d increases. This is not surprising due to the repeat structure of genomes—the bigger the d, the less common it is to have pairs of repeats spaced a distance of d apart. Figure 2a,b illustrates alternatives for improving contig lengths: increasing the read length (pursued by companies such as Pacific Biosciences) versus increasing the insert size, as advocated by Chaisson et al. (2009). While the increase in the read length remains a difficult technological challenge, increasing the insert size (up to tens of thousands of nucleotides) is already within the power of current technologies. Thus, if we could build a graph whose vertices represent (k, d)-mers instead of k-mers, then the length of the contigs is likely to increase as the insert size grows. This is the basic motivation for the paired de Bruijn graph, and, as we will show in Section 3, the contig lengths in the paired de Bruijn graph do in fact increase with d.

FIG. 2.

The effect of increasing k and d. (a) The number of repeated k-mers in the E. coli genome, for various values of k. (b) The number of repeated (k, d)-mers, for various values of d with k = 50.

2.4. Paired de Bruijn graphs (modeling paired reads with exact distance)

We now define a graph modeling mate pairs in the special case that all pairs are exactly the same distance d apart. This is an idealized case unachievable with current sequencing technologies, but the next section will generalize the construction to varying distances. Given a set of (k + 1, d)-mers C (modeling mate pairs), construct an A-Bruijn graph as follows:

• Define an initial graph G₀ on m = 2|C| vertices. For each bilabel 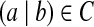(representing a (k + 1, d)-mer), introduce two new vertices u, v and form an edge u → v. Label the edge by (a|b); label u by prefix(a|b); and label v by suffix(a|b).

• Glue vertices of G₀ together when they have the same label. The graph G so obtained is called the paired de Bruijn graph of C.

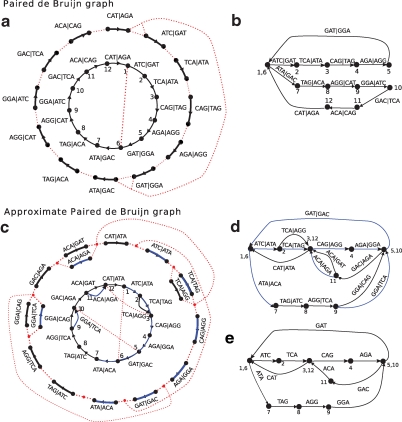
This procedure is illustrated in Figure 3a,b, and Figure 4 gives another example of the graph. An alternate construction of the paired de Bruijn graph is to define the vertex set as the (k, d)-mers present in C, and the edges as connecting prefix(a|b) to suffix(a|b) for every element of C.

FIG. 3.

The (approximate) paired de Bruijn graph: (a, b) The paired de Bruijn construction for k = 2, d = 4 from the same string S as in Fig. 1. In (a), the outer circle has an edge from every element of the (3, 4)-spectrum. (b) The paired de Bruijn graph after all the gluings; notice that it has only one branching vertex, versus four in the de Bruijn graph (Fig. 1d). (c–e) The construction of the approximate paired de Bruijn graph for k = 2, d = 5, Δ = 1. In (c), one possible covering spectrum is shown in the outside circle, with black edges for elements with mate pair distance 6 and blue edges for distance 5. Since Δ = 1, we glue vertices if they have equal left labels and their right labels are a distance at most 2 apart from each other in the de Bruijn graph (Fig. 1d). The final multigraph after all vertex gluings is shown in (d), and the resulting simple graph, used to spell the contigs, is shown in (e). Notice that this graph now has three branching vertices.

FIG. 4.

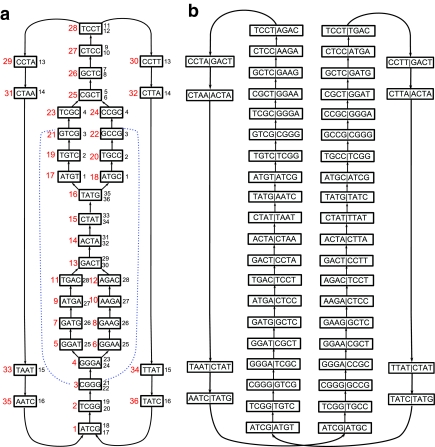
Example of the standard and paired de Bruijn graphs: The reads are the (5,12)-spectrum generated from the cyclic sequence ATCGGGATGACTATGTCGCTCCTAATCGGGAAGACTATGCCGCTCCTT. (a) The de Bruijn graph with edges constructed from the set of 5-mers in the (5,12) spectrum. Each node is a rectangle labeled by a 4-mer with the node ID shown as a large red number on the left of the node. The mate pair information is also presented in the graph: for each node, the node IDs of its corresponding right 4-mers are shown as small numbers on the right of the rectangle. For instance, the right 4-mers (blue dotted lines) of CGGG (node 3) are GTCG (node 21) and GCCG (node 22) and we write 21 and 22 on the right side of node 3. Note that there is not a single mate pair with a unique path between the mates, making mate pair transformations impossible. (b) The paired de Bruijn graph from the (5,12) spectrum is a cycle, representing a single contig. In this example, the paired approach allows for longer contigs than would mate pair transformations (though there are also examples when the opposite is true).

As with the regular de Bruijn graph, in this construction, every vertex of G inherits the label common to all the vertices of G₀ that were glued together to form it, and this label is unique to that vertex. Any walk through the graph on edge sequence 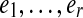spells out an (r + k)-mer bilabel (L|R) where L is formed from the left labels, 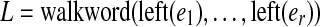, and R is formed from the right labels, .

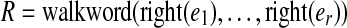The (k, d)-spectrum of a string S is 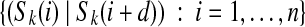. When C is the (k + 1, d)-mer spectrum of S, there is a covering cycle whose left labels spell S in G. The cycle consists of consecutive edges

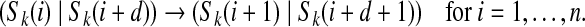Just as with the de Bruijn graph, this is a key property that makes the paired graph useful for spelling contigs.

2.5. Approximate paired de Bruijn graphs (modeling inexact distance)

We now define a graph modeling mate pairs where the distance between the two reads in each pair is only known to lie within some range d ± Δ. The parameter Δ can be estimated based on the mate pair generation protocol.

Let C be an arbitrary set of (k + 1, d, Δ)-mers, representing the input data. The key insight is that if two (k, d, Δ)-mers (a|b) and (a|b′) both arise from the same instance of a in S, then in the de Bruijn graph of S, there is a directed path from b to b′, or vice-versa, with distance at most 2Δ. This insight was used for repeat resolution in Medvedev and Brudno (2008), albeit as a post-construction modification step. We construct an A-Bruijn graph from C as follows:

• The initial graph G₀ consists of |C| isolated edges on 2|C| vertices. For each 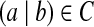, introduce an edge u → v on two new vertices. Label the edge by the (k + 1)-mer bilabel (a|b). Label u by prefix(a|b) and v by suffix(a|b).

• For each k-mer α, glue together all vertices with labels (α|β),(α|β′) if there exists a directed path from β to β′ (or vice-versa) in the de Bruijn graph D = DB(C, k) of length at most 2Δ. Here, we assume that the construction of D implicitly breaks the (k + 1)-mer bilabels of C into independent (k + 1)-mers.

The graph G = APDB(C, k, d, Δ) so obtained is the approximate paired de Bruijn Graph of C (Fig. 3c–e). The effect of this gluing is to merge all vertices (k-mer bilabels) that might align to the same position in the genome; vertices that align to the same position are thus guaranteed to be merged. However, the converse does not hold; vertices aligning to different positions in the genome are sometimes merged, either due to repeats that are not resolved by the given parameters, or due to chance short paths in D.

In the case that k > 2Δ, we observed that if there is a directed path between β and β′ in the de Bruijn graph D of length at most 2Δ, then β and β′ should share an overlap of at least k − 2Δ characters. This observation leads to an alternate rule to glue vertices of G₀: for each k-mer α, glue together all vertices with labels (α|β),(α|β′) if β and β′ share an overlap of at least k − 2Δ characters. Note that this rule can only be used if k > 2Δ and may lead to a different graph; however, it is easier to implement.

Unlike our earlier constructions of the de Bruijn and paired de Bruijn graphs, the vertices of G do not inherit a single label from G₀; the vertices glued together have the same left label, but may have different right labels. In an edge walk 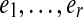on G, the left labels spell the word 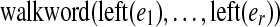. However, the right labels typically do not successively overlap by k − 1 characters as they did for the paired de Bruijn graph. Though we currently ignore these after gluing, we recognize that there is a potentially untapped benefit to using the right labels to later improve the assembly (see Section 5).

A set C of (k + 1)-mer bilabels is a covering spectrum of S if for every position 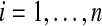, we have 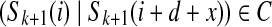for at least one x in the range −Δ ≤ x ≤ Δ. For each position i, there are 2Δ + 1 choices of x. Note that there are many different covering spectra, and different choices of C may lead to different graphs. However, the graph will satisfy the key property of having a covering cycle that spells out S.

Theorem 1

Let S be a circular string, and C a set of (k, d, Δ)-mers that is a covering spectrum of S. Then there is a covering cycle through the graph G = APDB(C, k, d, Δ) that spells out S.

Proof

For 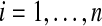, let 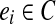be any (k + 1)-mer bilabel in C aligning to position i in S. To prove 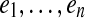is a cycle in G, we need to show that consecutive edges e_i = u_i → v_i with label (a|b), and e_i+1 = u_i+1 → v_i+1 with label (a′|b′), share the connecting vertex, v_i = u_i+1. (Indices are taken modulo n.) Since C is a covering spectrum of S, the graph D is the ordinary de Bruijn graph of S. In G₀, v_i has label (S_k(i + 1), suffix(b)) and u_i has label (S_k(i + 1), prefix(b′)). Since these both align to position i + 1 in S, the distance between the start of b and b′ in S is at most 2Δ. Thus in D, the directed distance from b to b′ (or vice-versa) is at most 2Δ, so these vertices were glued together when forming G.   ▪

3. Results

We implemented a prototype assembly algorithm to test the effectiveness of the (approximate) paired de Bruijn graph approach under the ideal conditions of perfect coverage and error-free reads. We experimented with E. coli (4.6 Mbp) and Human chromosome 22 (35 Mbp after removal of ambigious bases). The reads were generated with perfect coverage, meaning for every position in the genome we generated a single (k, d, Δ)-mer aligning to it. The insert size was picked uniformly at random from the specified range. We report as contigs the (left) words spelled by all maximal walks of the graph whose interior vertices have just one out-neighbor. We validated that any generated contigs mapped perfectly back to the original genome—this was the case for all the contigs.

Constructing the de Bruijn graph and finding all its non-branching paths takes time O(n log n), where n is the number of k-mers. The construction of the approximate paired de Bruijn graph has an additional cost of searching all neighbors within a distance 2Δ of each node. Therefore, the running time of the algorithms is O(n log n + n min{2^Δ, n}), where n is the number of (k, d, Δ)-mers. However, since de Bruijn graphs are sparse, the searches in the graph are usually very fast, and in practice, even the run on chr22 with Δ = 200 took less than 2 hours on an 8-core processor with 16G RAM. Moreover, the algorithm could be easily distributed over a large cluster to deal with larger Δ.

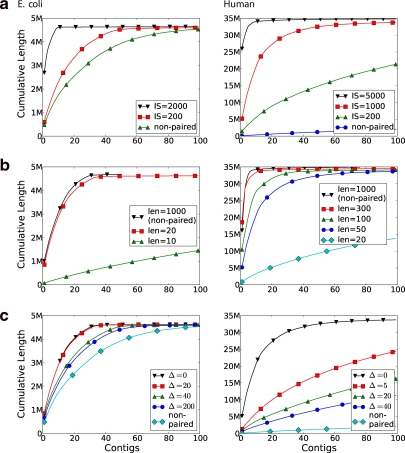
Our motivation for the paired de Bruijn graph approach was that the number of repeated (k, d)-mers quickly drops as d increases (Fig. 2b), and hence the contigs of the paired de Bruijn graph based on these (k, d)-mers could be longer. To test this hypothesis, we generated a set of mate pairs with varying insert sizes and plotted the length of the obtained contigs (Fig. 5a). To isolate the effect of the insert size, the coverage of the data was perfect (the (k, d)-spectrum), the insert sizes were perfect (Δ = 0), and the read length was fixed to 50. We observed that contig lengths improved dramatically as the insert size increased. With an insert size of 6000 nt, all of E. coli was covered with just one contig, while for chr22, an insert size of 5000 nt enabled us to cover 98% of the chromosome with the 15 largest contigs. We thus believe that properly using mate pairs has a strong potential to increase contig lengths.

FIG. 5.

Contig lengths. Cumulative contig lengths (for standard and paired de Bruijn graphs) on simulated data with perfect coverage. Contigs are sorted in order from largest to smallest. Point (x, y) means the largest x contigs have cumulative length y. (a) To analyze the effect of the insert size (IS) on the assembly, we kept the read length fixed at 50, but varied the insert size. We also generated non-paired reads of length 50. For E. coli, the curve for insert size 6000 is not shown because there was only one contig, representing the whole genome. (b) To analyze the effect of read length on contig lengths, we fixed the insert size to 1000 but varied the read length. We also generated non-paired reads of length 1000, giving an upper bound on how good the assembly can be in this case. (c) To analyze the effect of variations in the insert size (Δ), we fixed the mean insert size (1000) and read length (50). We also show the baseline contig lengths in a non-paired dataset, with read length 50 and perfect coverage.

To explore the role that read length plays relative to the insert size, we generated sets of mate pairs with varying read lengths but with a fixed insert size (1000 nt). To isolate the effect of the read length, we had perfect coverage and no variation in the insert size. For E. coli, we found that, for an insert size of 1000 nt, once the read length grew over a small threshold of 10–20 nt, the contig lengths nearly reached the theoretical optimum that could be achieved by simply generating reads of length equal to the insert size (Fig. 5b). For Human, we needed to increase the read length to 300 nt in order to reach the optimum with 1000 nt insert size (Fig. 5b). However, for a longer insert size (5000 nt), a read length of 50 came close (Fig. 5a) to achieving the optimum (which, with 5000 nt reads, was a single contig). Therefore, by properly using mate pairs with large enough insert size, one can significantly reduce the limitations caused by short read length.

We measure the effect of increasing variability in the insert size (Δ) on the assembly. We fix the insert size to be 1000 nt and generate 50-long reads with perfect coverage, while varying Δ (Fig. 5c). We found that the assembly deteriorates with increasing Δ, especially for the Human genome. When Δ is large, the chance of two vertices of the de Bruijn graph being connected increases, and, hence, the number of vertices (bilabels) that do not align but nevertheless get glued together increases. In this situation, the read length is still important in determining the complexity of the (non-paired) de Bruijn graph. Some recent datasets achieve a small Δ, such as the Bentley et al. (2008) human dataset with a mean insert size of 208 nt and a standard deviation of 13 nt. Nevertheless, we see robustness with respect to Δ as an important direction for improving the practical usefulness of our method.

4. Towards a Practical Paired de Bruijn Graph Assembler

We believe that, similarly to early studies of idealized fragment assembly with error-free k-mers (Pevzner, 1989), the (approximate) paired de Bruijn graphs can be of use in practical assemblers that utilize paired reads. Though this paper falls short of analyzing real data, we present here potential ways to remove our simplifications, and to move from the current de Bruijn graph assemblers to (approximate) paired de Bruijn graphs.

Base calling errors in reads. As with regular assembly, reads with base-calling errors may perturb the graph. Error correction algorithms for single reads may be used to improve the accuracy of the reads, while future error correction algorithms may also incorporate the mate pair information. Graph correction algorithms employed by current de Bruijn based assemblers (Chaisson and Pevzner, 2008; Zerbino and Birney, 2008) may also be applied to (approximate) paired de Bruijn graphs.

Insert size outliers. If a small percentage of read pairs are spaced outside the range d ± Δ, they will likely form isolated edges or terminal branches, which can be detected and discarded.

Double strandedness. The approximate paired de Bruijn graph is asymmetric in its treatment of the two reads (a|b), and in the reverse complement, these are switched to (b′|a′) (where a′,b′ are the reverse complements of a and b). This makes existing methods (Kececioglu, 1992; Medvedev et al., 2007; Zerbino and Birney, 2008) for accounting for double-strandedness difficult to apply. However, we may explicitly introduce the reverse complement of every read; perform assembly; match up reverse complement contigs after assembly; and reconcile any differences through a consensus stage.

5. Conclusion

In this article, we introduced the paired de Bruijn graph and motivated its use in genome assembly. Instead of incorporating mate pairs into a post-graph-construction step, we have used them to construct the graph itself. Any procedures that could be performed on the regular de Bruijn graph (e.g., error correction) can be performed in the same manner on the paired de Bruijn graph. For instance, even when there are repeats that the paired de Bruijn graph does not resolve, mate pair transformations can still be applied to the graph to help resolve the remaining repeats.

By formulating an alternative to mate pair transformations, the paired de Bruijn graph approach provides a potential method for assembly with short read mate pairs, like the ones generated by Complete Genomics (Drmanac et al., 2010) and Helicos (Harris et al., 2008). By not requiring unique paths between paired reads in the de Bruijn graph, the paired approach could still resolve repeats despite the short read length (Fig 4). Moreover, the algorithms we describe can be extended to the strobes generated by Pacific Biosciences, which extend the notion of the mate pair to a set of multiple (more than two) reads separated by some distances.

A future direction lies in the use of the right labels on edges of the approximate paired de Bruijn graph. Currently, we spell out each contig using only the left label. The positions of the right labels are only known approximately, but this is often sufficient to form a righthand word displaced approximately d from the lefthand word. Moreover, after encountering an edge (a|b) in a walk, we must encounter some edge (b|c) approximately d edges away (unless it is past the end of the walk). This compatibility requirement may help to narrow the choice of valid paths when encountering branching vertices, thereby resolving longer repeats and improving contig lengths.

Acknowledgments

G.T. and P.M. were supported in part by the NIH (grant 3P41RR024851-02S1).

Disclosure Statement

No competing financial interests exist.