A Bayesian Approach for Determining Protein Side-Chain Rotamer Conformations Using Unassigned NOE Data

Abstract

A major bottleneck in protein structure determination via nuclear magnetic resonance (NMR) is the lengthy and laborious process of assigning resonances and nuclear Overhauser effect (NOE) cross peaks. Recent studies have shown that accurate backbone folds can be determined using sparse NMR data, such as residual dipolar couplings (RDCs) or backbone chemical shifts. This opens a question of whether we can also determine the accurate protein side-chain conformations using sparse or unassigned NMR data. We attack this question by using unassigned nuclear Overhauser effect spectroscopy (NOESY) data, which records the through-space dipolar interactions between protons nearby in three-dimensional (3D) space. We propose a Bayesian approach with a Markov random field (MRF) model to integrate the likelihood function derived from observed experimental data, with prior information (i.e., empirical molecular mechanics energies) about the protein structures. We unify the side-chain structure prediction problem with the side-chain structure determination problem using unassigned NMR data, and apply the deterministic dead-end elimination (DEE) and A* search algorithms to provably find the global optimum solution that maximizes the posterior probability. We employ a Hausdorff-based measure to derive the likelihood of a rotamer or a pairwise rotamer interaction from unassigned NOESY data. In addition, we apply a systematic and rigorous approach to estimate the experimental noise in NMR data, which also determines the weighting factor of the data term in the scoring function derived from the Bayesian framework. We tested our approach on real NMR data of three proteins: the FF Domain 2 of human transcription elongation factor CA150 (FF2), the B1 domain of Protein G (GB1), and human ubiquitin. The promising results indicate that our algorithm can be applied in high-resolution protein structure determination. Since our approach does not require any NOE assignment, it can accelerate the NMR structure determination process.

1. Introduction

Nuclear magnetic resonance (NMR) is an important tool for determining high-resolution protein structures in the solution state. Traditional NMR structure determination approaches (Güntert, 2003; Herrmann et al., 2002; Linge et al., 2003; Huang et al., 2006; Kuszewski et al., 2004) typically use a dense set of nuclear Overhauser effect (NOE) distance restraints to calculate the three-dimensional (3D) coordinates of the protein structure. This process requires nearly complete assignment of both resonances (which serve as IDs of atoms in NMR spectra) and NOE data. Unfortunately, assigning resonances and NOEs is a time-consuming and laborious process, which is a major bottleneck in NMR structure determination. To address this problem, several approaches have been proposed to determine protein structures using sparse experimental data (Hus et al., 2001; Wang and Donald, 2004; Wang et al., 2006; Donald and Martin, 2009; Bowers et al., 2000; Cavalli et al., 2007; Shen et al., 2008; Raman et al., 2010b) or unassigned NMR data (Meiler and Baker, 2003; Raman et al., 2010a; Zeng et al., 2008, 2009, 2010, 2011). These new approaches have shown promising results. In particular, it has been shown that accurate backbone folds can be determined using sparse NMR data, such as residual dipolar couplings (RDCs) (Wang and Donald, 2004; Wang et al., 2006; Donald and Martin, 2009; Hus et al., 2001) or backbone chemical shifts (Shen et al., 2008; Raman et al., 2010b). The question remains: After the backbone structure has been solved, can we also determine accurate side-chain conformations using sparse or unassigned NMR data? In this article, we address this question by using unassigned nuclear Overhauser effect spectroscopy (NOESY) data, which record the through-space dipolar interactions between protons nearby in 3D space. While protein backbones have previously been determined to low resolution (Meiler and Baker, 2003, 2005) or even moderate resolution (Kraulis, 1994; Grishaev and Llinás, 2002a,b; Raman et al., 2010a) using unassigned NOESY data, it has never been shown, prior to our article, that high-resolution side-chain conformations can be computed using only unassigned NOESY data. Since our algorithm does not require any NOE assignment, it can shorten the time required in the NMR data analysis, and hence accelerate the NMR structure determination process.

Protein side-chains have been observed to exist in a number of energetically favored conformations, called rotamers (Lovell et al., 2000). Based on this observation, the side-chain structure determination problem can be formulated as a discrete combinatorial optimization problem, in which a set of side-chain conformations in a given rotamer library are searched over to optimize a scoring function that represents both empirical molecular mechanics and data restraints. Substantial work has been developed for predicting protein side-chain conformations without using experimental data (Tuffery et al., 1991; Desmet et al., 1992; Holm and Sander, 1992; Koehl and Delarue, 1994; Goldstein, 1994; Hwang and Liao, 1995; Bower et al., 1997; Xiang and Honig, 2001; Rohl et al., 2004; Kingsford et al., 2005; Xu and Berger, 2006; Krivov et al., 2009). These side-chain structure prediction approaches might be limited by the approximate nature of the employed empirical molecular mechanics energy function, which might not be sufficient to accurately capture the real energetic interactions among atoms in the protein.

Integration of NMR data with the empirical molecular mechanics energy is a challenging problem. Most frameworks for NMR protein structure determination use heuristic models with ad hoc parameter settings to incorporate experimental data (which are usually assigned NOE data in these approaches) and integrate them with the empirical molecular mechanics energy in an empirical scoring function to compute protein structures. These approaches suffer from the subjective choices in the data treatment, which makes it difficult to objectively calculate high-quality structures. To overcome this drawback, we use a Bayesian approach (Rieping et al., 2005; Habeck et al., 2006; Russell and Norvig, 2002) and cast the protein side-chain structure determination problem using unassigned NOESY data into a Markov random field (MRF) framework. We treat NMR data as an experimental observation on side-chain rotamer states, and use the MRF to encode prior information about the protein structures, such as empirical molecular mechanics energies. The priors in our framework are in essence parameterized by the random variables representing the side-chain rotamer conformations. The MRF modeling captures atomic interactions among residues both from empirical molecular mechanics energies and geometric restraints from unassigned NOESY data. The derived posterior probability combines prior information and the likelihood model constructed from observed experimental data. Unlike previous ad hoc models, our Bayesian framework provides a rational basis to incorporate both experimental data and modeling information, which enables us to develop systematic techniques for computing accurate side-chain conformations.

The side-chain structure determination problem is NP-hard (Pierce and Winfree, 2002; Chazelle et al., 2004). Therefore, a number of algorithms have been developed to address the complexity (Tuffery et al., 1991; Holm and Sander, 1992; Hwang and Liao, 1995; Rohl et al., 2004; Desmet et al., 1992; Looger and Hellinga, 2001; Goldstein, 1994; Georgiev et al., 2008b; Chen et al., 2009; Frey et al., 2010). Stochastic techniques (Tuffery et al., 1991; Holm and Sander, 1992; Hwang and Liao, 1995; Rohl et al., 2004) randomly sample conformation space to generate a set of side-chain rotamer conformations. In contrast, our approach applies deterministic algorithms with provable guarantees (Desmet et al., 1992; Looger and Hellinga, 2001; Goldstein, 1994; Georgiev et al., 2008b; Chen et al., 2009; Frey et al., 2010) to determine the optimal side-chain rotamer conformations that satisfy both experimental restraints and prior information on the protein structures. We first apply a dead-end elimination (DEE) algorithm (Desmet et al., 1992; Looger and Hellinga, 2001; Goldstein, 1994) to prune side-chain conformations that are provably not part of the optimal solution. After that, an A* search algorithm is employed to find the global optimum solution that best interprets our MRF model.

The guarantee to provably find the global optimum using the DEE/A* algorithms enables us to rigorously and objectively estimate the experimental noise in NMR data and the weighting factor between the empirical molecular mechanics energy and experimental data in the scoring function derived in our Bayesian framework. Specifically, we employ a grid search approach to systematically search over all possible grid point values of the noise parameter, and use the DEE/A* search algorithms to compute the optimal solution that minimizes the scoring function for each grid point. We then compare the best solutions over all grid points and find the globally optimal estimation of the weight parameter. The following contributions are made in this article:

1. A novel framework to unify the side-chain structure prediction problem with the side-chain structure determination problem using unassigned NOESY data, by applying the provable dead-end elimination (DEE) and A* search algorithms to find the global optimum solution;

2. A Bayesian approach with an MRF model to derive the posterior probability of side-chain conformations by combining the likelihood function from observed experimental data with prior information (i.e., empirical molecular mechanics energies) about the protein structures;

3. A systematic and rigorous approach to estimate the experimental noise in NMR data, which determines the weighting factor of the data term in the derived scoring function, by combining grid search and DEE/A* search algorithms;

4. Introduction of a Hausdorff-based measure to derive the likelihood function from unassigned NMR data;

5. Promising test results on real NMR data recorded at Duke University.

The source code of our program is available by contacting the authors and is distributed open-source under the GNU Lesser General Public License (2002). The source code can be freely downloaded after publication of this article.

1.1. Related work

In Zeng et al. (2008, 2009), we developed an algorithm, called hana, that employs a Hausdorff-based pattern matching technique to place side-chain rotamer conformations on backbone structures using unassigned NOESY data. The backbone structures were determined by using mainly residual dipolar coupling (RDC) data (Wang and Donald, 2004; Wang et al., 2006; Donald and Martin, 2009), which provides global orientational restraints on the internuclear bond vectors. hana does not completely exploit prior information, nor all the available information from experimental data. For example, hana only uses the back-computed NOE pattern from side-chain rotamers to backbone to calculate the likelihood of a rotamer. In addition, hana does not take into account the empirical molecular mechanics energy when determining the side-chain rotamer conformations. Thus, the side-chain conformations determined by hana may embrace some bad local geometry such as serious steric clashes. Our current Bayesian approach improves over hana by eliminating all serious steric clashes (Table 3). It is a significant extension of the hana module, and can be combined with our previously developed backbone structure determination techniques (Wang and Donald, 2004; Wang et al., 2006; Donald and Martin, 2009; Zeng et al., 2009) to compute complete high-resolution structures, including backbone and side-chains, using a protocol similar to (Zeng et al., 2009).

Table 3.

Comparison between Our Current Bayesian Approach versus Hana and Nasca on the Number of Serious Steric Clash Overlaps (<0.9 Å) in the Determined Side-Chain Conformations.

Proteins	Current Bayesian approach	hana	Nasca
GB1	0	10	14
Ubiquitin	0	16	21
FF2	0	2	14

In Zeng et al. (2010, 2011), we proposed an MRF based algorithm, called Nasca, to assign side-chain resonances and compute side-chain rotamer conformations from unassigned NOESY data without using TOCSY experiments. Similarly to hana, Nasca does not consider the empirical molecular mechanics energy. Thus, it may also produce serious steric clashes in the computed side-chain conformations. On the other hand, compared to our current Bayesian approach, Nasca does not require the side-chain resonances assigned from TOCSY experiments. Nevertheless, our current Bayesian approach provides an example that will be useful for extending the Nasca module to incorporate the empirical molecular mechanics energy with unassigned NOESY data.

Several approaches have been proposed to use assigned backbone chemical shift data (Bowers et al., 2000; Cavalli et al., 2007; Shen et al., 2008; Raman et al., 2010b) or unassigned NOESY data (Kraulis, 1994; Grishaev and Llinás, 2002a,b; Meiler and Baker, 2003, 2005; Raman et al., 2010a) in protein structure determination at different resolutions. These frameworks use a generate-and-test strategy or stochastic techniques such as Monte Carlo (MC), simulated annealing (SA), or highly-simplified molecular dynamics (HSMD) to randomly sample conformation space and compute a set of structures that satisfy the data restraints. These approaches suffer from the problems of undersampling conformation space and overfitting to the data. They cannot provide any guarantee on the convergence to the global optimum. In addition, integration of experimental data with the empirical molecular mechanics energy and the parameter settings in these frameworks are usually performed on an ad hoc basis.

Unlike a previous Bayesian approach in NMR structure determination (Rieping et al., 2005; Habeck et al., 2006), which requires assigned NOE data, our approach works on unassigned NOESY data. Moreover, the Bayesian approach in (Rieping et al., 2005; Habeck et al., 2006) mainly relies on heuristic techniques, such as Monte Carlo or Gibbs sampling, to randomly sample both conformation space and the joint posterior distribution, while our approach employs a systematic and rigorous search method (i.e., a combination of grid search and DEE/A* algorithms) to compute the optimal parameter estimation that is only subject to the resolution used in the grid search.

Markov random fields (MRFs) offer a mathematically sound framework for describing the dependencies between random variables, and have been widely applied in computer vision (Geman and Geman, 1990; Li, 1995) and computational structural biology (Yanover and Weiss, 2002; Kamisetty et al., 2008, 2011; Yanover and Fromer, 2011). In Kamisetty et al. (2008, 2011), an MRF was used to estimate the free energy of protein structures, while in Yanover and Weiss (2002) and Yanover and Fromer (2011), a graphical model similar to MRFs was used to predict side-chain conformations. Although the graphical models in Yanover and Weiss (2002), Kamisetty et al. (2008, 2011), and Yanover and Fromer (2011) provide reasonable models to describe the protein side-chain rotamer interactions, they do not use any experimental data. In addition, the belief propagation approach used in Yanover and Weiss (2002), Kamisetty et al. (2008, 2011), and Yanover and Fromer (2011) to search for the low-energy conformations can be trapped in local minima, whereas our approach computes the global optimum solution.

2. Methods

2.1. Backbone structure determination from residual dipolar couplings

In our high-resolution structure determination protocol, we apply our recently developed algorithms (Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009; Yershova et al., 2011; Donald and Martin, 2009) to compute the protein backbone structures using two RDCs per residue (either NH RDCs measured in two media, or NH and CH RDCs measured in a single medium). Details on backbone structure determination from RDCs are available in Appendix A and elsewhere (Wang and Donald, 2004; Wang et al., 2006; Donald and Martin, 2009; Yershova et al., 2011).

2.2. Using Markov random fields for rotamer assignment

We first use a Markov random field to formulate our side-chain structure determination problem. A Markov random field is a set of random variables defined on an undirected graph, which describes the conditional dependencies among random variables. In our problem, each random variable represents the rotamer state of a residue. Formally, let X_i be a random variable representing the rotamer state at residue i, where 1 ≤ i ≤ n, and n is the total number of residues in the protein sequence. Let t_i be the maximum number of rotamer states at residue i. Then each random variable X_i can take a value from set 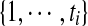. We use x_i to represent a specific value taken by random variable X_i. We also call x_i the rotamer assignment or conformation of residue i. Let 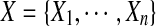be the set of random variables representing the rotamer assignments for all residues 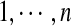in the protein sequence. A joint event 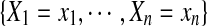, abbreviated as X = x, is called a rotamer assignment or conformation for all residues in the protein sequence, where .

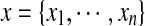In our side-chain structure determination problem, we assume that the backbone is rigid. Based on this assumption, it is generally safe to argue that each residue only interacts with other residues within a certain distance threshold or energy cutoff, when considering the pairwise interactions between side-chains. We use a graph G = (V, E) to represent such residue-residue interactions, where each vertex in V represents a residue, and each edge in E represents a possible interaction between two residues (i.e., the minimum distance between atoms from these two residues is within a distance threshold). Such a graph G = (V, E) is called the residue interaction graph. Given a residue interaction graph G = (V, E), the neighborhood of residue i, denoted by N_i, is defined as 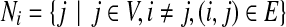. The neighborhood system describes the dependencies between rotamer assignments for all residues in the protein sequence. A Markov random field (MRF), defined based on the neighborhood system of an underlying graph G = (V, E), encodes the following conditional independencies for each variable X_i:

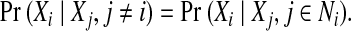(1)

This condition states that each random variable X_i is only dependent on the random variables in its neighborhood.

We use Pr(x) to represent the prior probability for a rotamer assignment 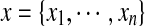of a protein sequence, which is derived from prior information about the protein structures, such as empirical molecular mechanics. Let D be the observation data, which in this case is the unassigned NOESY data. Let σ be the experimental noise in the unassigned NOESY data. The parameter σ is unknown and needs to be estimated. We use Pr(D|x,σ) to represent the likelihood function of a rotamer assignment x and a parameter σ given the observation D. We use Pr(x,σ|D) to represent the a posteriori probability. Our goal is to obtain a combination of rotamer assignment x and parameter σ, denoted by (x,σ), that finds the maximum a posteriori probability (MAP). By Bayes's rule, the posterior probability can be computed by

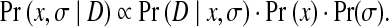(2)

In other words, the MAP solution (x*, σ*) satisfies

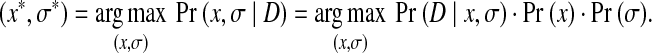(3)

2.3. Deriving the prior probability

According to the Hammersley-Clifford theorem (Besag, 1974) on the Markov-Gibbs equivalence, the distribution of an MRF with respect to an underlying graph G = (V, E) can be written in the following Gibbs form:

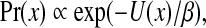(4)

where β is a global control parameter, and U(x) is the prior energy that encodes prior information about the rotamer-rotamer interactions in the protein structure. The prior energy can be defined by 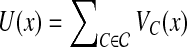, where V_C(·) is a clique potential and 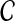is the set of cliques in the neighborhood system of the underlying graph G = (V, E). In our problem, we only focus on one-site and two-site interactions (i.e., with cliques of size 2) in a residue interaction graph G = (V, E). Given an assignment 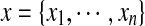for a residue interaction graph G = (V, E), we use the following empirical molecular mechanics energy function to define the prior energy U(x):

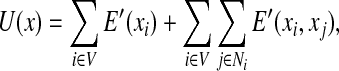(5)

where E′(x_i) is the self energy term for rotamer assignment x_i at residue i, and E′(x_i,x_j) is the pairwise energy term for rotamer assignments x_i and x_j at residues i and j, respectively. We can use the Boltzmann distribution to further specify the prior probability in Eq. (4) by setting β = k_bT, where k_b is the Boltzmann constant, and T is the temperature. In our implementation, the empirical molecular mechanics energy function in Eq. (5) consists of the Amber electrostatic, van der Waals (vdW), and dihedral terms (Weiner et al., 1984; Cornell et al., 1995), and the EEF1 implicit solvation energy term (Lazaridis and Karplus, 1999), combined as in Georgiev et al. (2008b), Chen et al. (2009), and Frey et al. (2010). We also include a rotamer energy term in the prior energy function, which represents the frequency of a rotamer that is estimated from high-quality protein structures (Lovell et al., 2000) and weighted by the term from Krivov et al. (2009).

2.4. Deriving the likelihood function and the scoring function

An accurate likelihood function should effectively interpret the observation data, and incorporate experimental uncertainty into the model. In our framework, the likelihood Pr(D|x, σ) is defined as

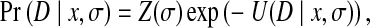(6)

where Z(σ) is the normalizing factor, and U(D|x, σ) is called the likelihood energy, which evaluates the likelihood of observed NOESY data given rotamer assignment x and parameter σ.

The likelihood energy U(D|x, σ) can be measured by matching the back-computed NOE patterns with experimental cross peaks in unassigned NOESY data D. Given a rotamer assignment x_i at residue i, we can back-compute its NOE pattern between backbone and intra-residue atoms. This NOE pattern is called the self back-computed NOE pattern. Similarly, we can back-compute the NOE pattern between a pair of rotamer assignments x_i and x_j at residues i and j respectively. This NOE pattern is called the pairwise back-computed NOE pattern. We use a criterion derived from the Hausdorff distance (Huttenlocher and Kedem, 1992; Huttenlocher et al., 1993), called the Hausdorff fraction, to measure the matching score between a back-computed NOE pattern and unassigned NOESY data. Details of deriving the Hausdorff fraction for a back-computed NOE pattern are found in Appendix B and Zeng et al. (2008, 2009). Let F(x_i) and F(x_i, x_j) be the Hausdorff fractions for the self and pairwise back-computed NOE patterns respectively. Then the likelihood energy U(D|x, σ) is defined as:

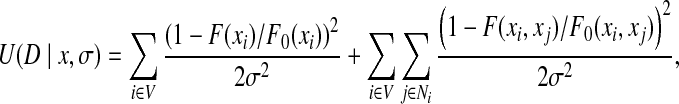(7)

where σ is the experimental noise in unassigned NOESY data, and F₀(x_i) and F₀(x_i, x_j) are the expected values of F(x_i) and F(x_i, x_j) respectively. Here we assume that the experimental noise of unassigned NOESY cross peaks follows an independent Gaussian distribution. Thus, σ represents the standard deviation of the Gaussian noise. Such an independent Gaussian distribution provides a good approximation when the accurate noise model to describe the uncertainty in experimental data is not available (Langmead and Donald, 2004a; Li, 1995). In general, it is difficult to obtain the accurate values of the expected Hausdorff fractions F₀(x_i) and F₀(x_i, x_j). In principle, a rotamer conformation should be closer to the native side-chain conformation if its back-computed NOE pattern has a higher Hausdorff fraction (i.e., with higher data satisfaction score). In practice, we use the maximum value of the Hausdorff fraction among the back-computed NOE patterns of all rotamers as the expected value of F(x_i) and F(x_i, x_j).

The function U(x, σ|D) = −log Pr(x, σ|D) is called the posterior energy for a rotamer assignment x and parameter σ, given the observed data D. Then maximizing the posterior probability is equivalent to minimizing the posterior energy function. Substituting Eqs. (4), (5), and (7) into Eq. (2), and taking the negative logarithm on both sides of the equation, we have the following form of the posterior energy function:

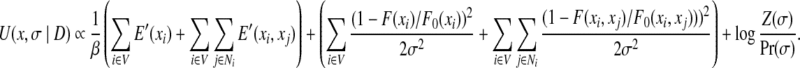(8)

In Section 2.5, we will show how to estimate parameter σ. After σ has been estimated, we have the following form of the posterior energy function:

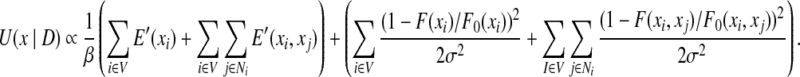(9)

The function U(x|D) is also called the pseudo energy. We rewrite the pseudo energy function in Eq. (9). Let E(x_i) = E′(x_i)/β + (1 − F(x_i)/F₀(x_i))²/ 2σ² and E(x_i, x_j) = E′(x_i, x_j)/β + (1 − F(x_i, x_j)/F₀(x_i, x_j))²/ 2σ². Then we have

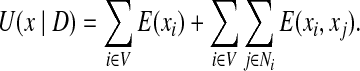(10)

The pseudo energy function defined in Eq. (10) has the same form as in protein side-chain structure prediction (Koehl and Delarue, 1994; Leach and Lemon, 1998; Rohl et al., 2004; Kingsford et al., 2005; Xu and Berger, 2006; Krivov et al., 2009) or protein design (Desmet et al., 1992; Looger and Hellinga, 2001; Goldstein, 1994; Georgiev et al., 2008b; Chen et al., 2009; Frey et al., 2010). Thus, we can apply similar algorithms, including the dead-end elimination (DEE) and A* search algorithms, to solve this problem. A brief overview of the DEE/A* algorithms can be found in Appendix C and elsewhere (Desmet et al., 1992; Looger and Hellinga, 2001; Goldstein, 1994; Georgiev et al., 2008b; Chen et al., 2009). Similar to protein side-chain prediction and protein design, the optimal rotamer assignment x* that minimizes the pseudo energy function in Eq. (10) is called the global minimum energy conformation (GMEC). The DEE/A* algorithms employed in our framework guarantee to find the GMEC with respect to our pseudo energy function. Similar to Georgiev et al. (2008b), Chen et al. (2009), and Frey et al. (2010), we can also extend the original A* search algorithm to compute a gap-free ensemble of conformations such that their energies are all within a user-specified window from the lowest pseudo energy.

2.5. Estimation of experimental noise in the NOESY data

In the likelihood function defined in Eq. (7), parameter σ represents the noise level in the NOESY data, and hence describes the quality of experimental data. On the other hand, σ acts as a weighting factor, denoted by w = 1/σ², between the empirical molecular mechanics energy term and the data term in Eq. (9) in the posterior energy function defined in Eq. (8). A small σ value (i.e., a large weighting factor w) means that the experimental error in the NMR data is small, and hence the data term in the scoring function Eq. (8) should be weighted more. The choice of σ certainly influences the determination of the optimal rotamer assignment. In practice, parameter σ in Eq. (7) is generally unknown, and needs to be estimated for each set of experimental data used in structure calculation. In the likelihood function Eq. (6), the normalizing factor Z(σ) is related to the unknown parameter σ. Based on the independent Gaussian distribution assumption on experimental noise in unassigned NOESY data, we have Z(σ) = (2πσ²)^m / 2, where m is the total number of self and pairwise back-computed NOE patterns. In our problem, m is equal to the size of the residue interaction graph G = (V, E), that is, m = |V|+|E|.

Similar to Rieping et al. (2005) and Habeck et al. (2006), we use the Jeffrey prior (Jeffreys, 1946) to represent the prior probability of parameter σ, that is, Pr(σ) = σ⁻¹. Substituting Z(σ) = (2πσ²)^m / 2 and Pr(σ) = σ⁻¹ into Eq. (8), we have

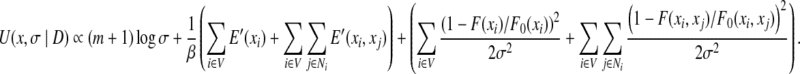(11)

Now our goal is to find a value of (x, σ) that minimizes the posterior energy in Eq. (11). Here we combine a grid search approach with the DEE/A* search algorithms to compute the optimal estimation of w = σ⁻². Once w is determined, parameter σ can be computed using equation 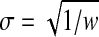. First, our parameter estimation approach systematically searches the grid points of weighting factor w. This devolves to searching a 1-dimensional parameter space. For each grid point of w, it uses the DEE and A* search algorithms to find the GMEC that minimizes the pseudo energy function. Finally, it compares all GMEC solutions over all searched grid points, and chooses the optimal value of parameter w that minimizes the posterior energy function in Eq. (11).

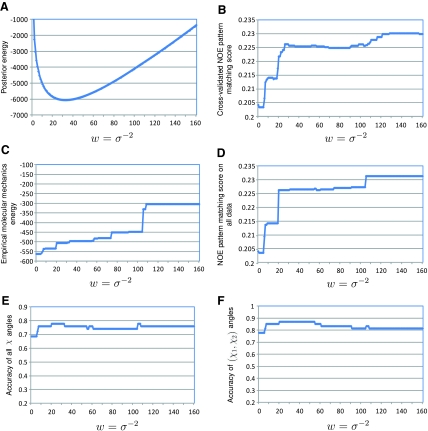
In Eq. (11), as the weighting factor w increases (i.e., the data term is weighted more), the first term (m + 1) log σ in Eq. (11) decreases, while the third term representing the data restraints increases. Figure 1A shows a typical plot of the posterior energy U(x, σ|D) versus the weighting factor w, in which a minimum is usually observed. The performance of our parameter estimation approach is only subject to the resolution used in the grid search. In practice, our approach is sufficient to find the optimal parameter estimation (Fig. 1), as we will show in the Results section.

FIG. 1.

Estimation of the weighting factor parameter w = σ⁻² for the data term in the posterior energy function for GB1. In plots (B) and (D), the Hausdorff fraction was used to measure the matching score between the back-computed NOE pattern of the GMEC and experimental spectra.

2.6. NMR experimental procedures

We tested our Bayesian approach for side-chain structure determination on NMR data of three proteins: the FF Domain 2 of human transcription elongation factor CA150 (FF2), the B1 domain of Protein G (GB1), and human ubiquitin. All NMR data except the RDC data of ubiquitin and GB1 were recorded and collected using Varian 600 and 800 MHz spectrometers at Duke University. The NMR spectra were processed using the program NMRPipe (Delaglio et al., 1995). All NMR peaks were picked by the programs NMRView (Johnson and Blevins, 1994) or Xeasy/Cara (Bartels et al., 1995), followed by manual editing. Backbone assignments, including resonance assignments of atoms N, HN, C^α, H^α, C^β, were obtained from the set of triple resonance NMR experiments HNCA, HN(CO)CA, HN(CA)CB, HN(COCA)CB, and HNCO, combined with the HSQC spectra using the program Paces (Coggins and Zhou, 2003), followed by manual checking. The side-chain resonances were assigned from the HA(CA)NH, HA(CACO), HCCH-TOCSY, and HC(CCO)NH-TOCSY spectra. The NOE cross peaks were picked from three-dimensional ¹⁵N- and ¹³C-edited NOESY-HSQC spectra. In addition, we removed the diagonal cross peaks and water artifacts from the picked NOE peak list. The NH and CH RDC data of FF2 were measured from a 2D ¹H-¹⁵N IPAP experiment (Ottiger et al., 1998) and a modified (HACACO)NH experimental (Ball et al., 2006), respectively. The C^αC′ and NC′ RDC data of FF2 were also measured from a set of HNCO-based experiments (Permi et al., 2000). The CH and NH RDC data of ubiquitin were obtained from the Protein Data Bank (PDB ID of ubiquitin: 1D3Z). For GB1, we computed its global fold using the CH and NH RDC data from a homologous protein, namely the third IgG-binding domain of Protein G (GB3) (PDB ID: 1P7E).

3. Results

We implemented our Bayesian approach for side-chain structure determination and tested it on NMR data of three proteins (the FF Domain 2 of human transcription elongation factor CA150 (FF2), the B1 domain of Protein G (GB1), and human ubiquitin). The numbers of amino acid residues in these three proteins are 62, 56, and 76 for FF2, GB1, and ubiquitin, respectively. The PDB IDs of the NMR reference structures are 2KIQ, 3GB1, and 1D3Z for FF2, GB1, and ubiquitin, respectively. The PDB IDs of the X-ray reference structures are 3HFH, 1PGA, and 1UBQ for FF2, GB1, and ubiquitin, respectively. Since raw NOESY spectra are not deposited in the PDB, the primary experimental data (plus other NMR experiments) must be collected to test our algorithm. We did these experiments (see Section 2.6).

Our algorithm uses the following input data: (1) the protein primary sequence; (2) the protein backbone; (3) the 2D or 3D NOESY peak list from both ¹⁵N- and ¹³C-edited spectra; (4) the resonance assignment list, including both backbone and side-chain resonance assignments; (5) the rotamer library (Lovell et al., 2000). The empirical molecular mechanics energy function that we used in Eq. (5) consists of the Amber electrostatic, van der Waals (vdW), and dihedral terms (Weiner et al., 1984; Cornell et al., 1995), the EEF1 implicit solvation energy term (Lazaridis and Karplus, 1999), and a rotamer energy term, which represents the frequency of the rotamer. All NMR data, except RDCs of GB1 and ubiquitin, were recorded and collected using Varian 600- and 800-MHz spectrometers at Duke University. The NOE cross peaks were picked from 3D ¹⁵N- and ¹³C-edited NOESY-HSQC spectra. Details on the NMR experimental procedures are provided in Section 2.6. Our computational tests were performed on a 2.20-GHz Intel core 2 Duo processor with 4 GB of memory. The total running time of computing the GMEC solution for a typical medium-size protein, such as GB1, is less than an hour after parameter w = σ⁻² has been estimated.

We used the same rules as in Lovell et al. (2000) to classify and identify the rotamer conformations, that is, we used a window of ±30^° to determine most χ angles, except that a few specific values (see Table I in Lovell et al. [2000]) were used in determining the terminal χ angle boundaries for glutamate, glutamine, aspartate, asparagine, leucine, histidine, tryptophan, tyrosine and phenylalanine. Since most rotamer conformations are short, the RMSD is not sufficient to measure the structural dissimilarity between two rotamers. Thus, we did not use the RMSD to compare different rotamers. We used two measurements to evaluate the accuracies of the determined side-chain rotamer conformations. The first one is called the accuracy of all χ angles, measuring the percentage of side-chain rotamer conformations in which all χ angles agree with the NMR or X-ray reference structure. The second measurement is called the accuracy of (χ₁,χ₂) angles, which measures the percentage of side-chain rotamer conformations whose first two χ angles (i.e., both χ₁ and χ₂) agree with the NMR or X-ray reference structure. We say a determined side-chain conformation is correct if all its χ angles agree with the NMR or X-ray reference structure.

Table 1.

Accuracies of the Side-Chain Rotamer Conformations Determined by Our Algorithm Using the Backbones from the NMR Reference Structures

	All residues				Core residues
	Accuracy of all χ angles (%)		Accuracy of (χ1, χ2) angles (%)		Accuracy of all χ angles (%)		Accuracy of (χ1, χ2) angles (%)
Proteins	GMEC	Best 50	GMEC	Best 50	GMEC	Best 50	GMEC	Best 50
GB1	77.8	77.8	87.0	87.0	100.0	100.0	100.0	100.0
Ubiquitin	75.4	78.3	84.1	85.5	84.0	88.0	88.0	92.0
FF2	71.9	71.9	82.5	86.0	100.0	100.0	100.0	100.0

3.1. Parameter estimation

We estimated the weighting factor parameter w = σ⁻² in the posterior energy function using the approach described in Sec. 2.5. Here we use the test on GB1 (Fig. 1) as an example to demonstrate our parameter estimation approach. The parameters for the other two proteins were estimated similarly. For GB1, the optimal weighting factor was 32, where the posterior energy U(x, σ|D) met the minimum (Fig. 1A). This optimal weight value corresponded to the best accuracies 77.8% and 87.0% for all χ angles and (χ₁,χ₂) angles, respectively (Fig. 1E, F).

Figure 1C, D shows the influence of the weight w on the empirical molecular mechanics energy and the NOE pattern matching score of the GMEC. As expected, as the data restraints were weighted more, the empirical molecular mechanics energy declined while the data satisfaction score was improved for the GMEC solution. At the optimal weight value w = 32, the GMEC yielded decent scores for both empirical molecular mechanics energy and NOE pattern matching score. Although the NOE pattern matching score of the GMEC jumped to a higher plateau when w ≥ 110 (Fig. 1C), the accuracies of all χ angles and (χ₁,χ₂) angles did not increase correspondingly (Fig. 1E, F). Probably this high NOE satisfaction score was caused to some extent by overfitting the side-chain rotamer conformations to experimental data. We also demonstrated that our approach performed better than the cross validation approach (Brünger, 1992; Brünger et al., 1993) used in estimating the weighting factor parameter w = σ⁻² (Fig. 1B). Details on the cross validation approach and the comparison results are provided in Appendix D.

3.2. Accuracy of determined side-chain rotamer conformations

We first tested our side-chain structure determination approach on the backbones from the NMR reference structures (Table 1). Next, to check whether our current side-chain structure determination approach can be combined with our previously developed backbone structure determination techniques (Donald and Martin, 2009; Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009; Yershova et al., 2011) for high-resolution structure determination, we also tested our algorithm on the backbones computed mainly using RDC data (Table 2). In all cases, the RDC-defined backbones were computed using our previous structure determination algorithms (Donald and Martin, 2009; Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009; Yershova et al., 2011), thus showing that a pipeline for complete structure determination is feasible. The RMSD between the input RDC-defined backbone and the NMR reference structure is 0.96 Å, 0.87 Å, and 0.97 Å for FF2, GB1, and ubiquitin, respectively. In addition to the GMEC, we also computed the ensemble of the best 50 conformations with the lowest pseudo energies (Tables 1 and 2), using an extended version of the A* algorithm (Georgiev et al., 2008b; Chen et al., 2009; Frey et al., 2010). An ensemble of computed structures is important when multiple models may agree with the experimental data (DePristo et al., 2004). In addition, an ensemble of structures can reflect the conformational variation resulting from different experimental conditions, lack of data, or protein motion in solution (DePristo et al., 2004; Andrec et al., 2007).

Table 2.

Accuracies of the Side-Chain Rotamer Conformations Determined by Our Algorithm Using the RDC-Defined Backbones Computed Using Algorithms from Elsewhere^a

	All residues				Core residues
	Accuracy of all χ angles (%)		Accuracy of (χ1, χ2) angles (%)		Accuracy of all χ angles (%)		Accuracy of (χ1, χ2) angles (%)
Proteins	GMEC	Best 50	GMEC	Best 50	GMEC	Best 50	GMEC	Best 50
GB1	75.9	79.6	81.5	88.9	92.9	100.0	92.9	100.0
Ubiquitin	72.5	76.8	79.7	82.6	80.0	84.0	80.0	84.0
FF2	71.9	75.4	80.7	84.2	100.0	100.0	100.0	100.0

^aDonald and Martin (2009), Wang and Donald (2004), Wang et al. (2006), Zeng et al. (2009), and Yershova et al. (2011).

In addition to examining the accuracies of the determined side-chain conformations in all residues, we also checked the performance of our approach in core residues, which are defined as those residues with solvent accessibility ≤10%. We used the software MOLMOL (Koradi et al., 1996) with a solvent radius of 2.0 Å to compute solvent accessibility for each residue. Note that in the side-chain structure determination problem using experimental data, we were particularly interested in the accuracies of side-chain conformation determination in core residues because: (1) biologically, the side-chains in the interior and buried regions of the protein play more important roles in studying protein dynamics and determining accurate structures, compared to residues on the protein surface; (2) in the X-ray or NMR reference structure, the data for the solvent-exposed side-chains are often missing. Thus, modeling information is often used to compute the side-chain conformations of the residues on the protein surface.

Overall, our approach determined more than 70% correct rotamer conformations, and achieved over 80% accuracy for (χ₁,χ₂) angles for all residues (Tables 1 and 2). Our results also show that computing the ensemble of the best 50 conformations with the lowest pseudo energies can slightly improve the results (Tables 1 and 2), which indicates that it is necessary to compute an ensemble of conformations rather than a single GMEC solution. In core residues, our approach achieved a high percentage of accurate side-chain conformations. Our approach computed all the correct side-chain conformations in core residues for GB1 and FF2, and had accuracies ≥84% for ubiquitin, given the backbone structures from the NMR reference structures (Table 1). The tests on the RDC-defined backbones exhibited similar results (Table 2), which indicates that our current Bayesian approach can be combined with our previously-developed backbone structure determination techniques (Donald and Martin, 2009; Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009; Yershova et al., 2011) to determine high-resolution protein structures mainly using RDC and unassigned NOESY data.

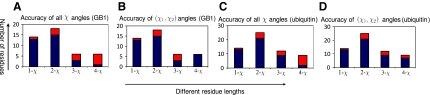
We also examined the accuracies of the determined side-chain conformations for side-chain amino acid residues of different lengths (Fig. 2). In general, more short side-chain conformations (i.e., 1-χ and 2-χ side-chains) were determined correctly than the long side-chain conformations (i.e., 3-χ and 4-χ side-chains). On the other hand, although our program assigned a very low percentage of correct 4-χ rotamers (i.e., arginine and lysine), it was able to compute the first two χ angles correctly for most 4-χ side-chains (Fig. 2). In addition to their side-chain flexibility, arginine and lysine are usually exposed to the solvent and undergo many conformational changes. Also, their NOE data are often missing. Therefore, it is generally difficult to compute all the χ angles correctly for these two long side-chains. We further investigated the accuracies of the determined side-chain rotamer conformations for residues with different numbers of available data restraints. We first define the number of matched NOE peaks for residue i, denoted by d_i, as follows:

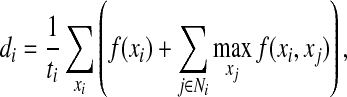(12)

FIG. 2.

Accuracies of the determined side-chain rotamer conformations for residues with different lengths (i.e., with different numbers of rotatable χ angles) for GB1 and ubiquitin. The bars represent the number of residues of the indicated type in the protein. The portions marked in blue represent the percentage of rotamers with all χ angles or (χ₁,χ₂) angles that agree with the NMR or X-ray reference structure.

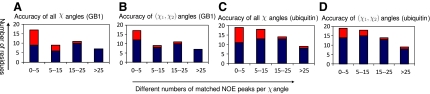
where t_i is the maximum number of rotamer states at residue i, and f (x_i) and f (x_i,x_j) are the numbers of experimental NOE cross peaks that are close to a back-computed NOE peak in the self and pairwise back-computed NOE patterns, respectively. Basically d_i measures the degree of available data restraints for residue i averaged over all possible rotamer conformations. We define the value of d_i divided by the number of rotatable χ angles in the side-chain as the number of matched NOE peaks per χ angle for residue i. As shown in Figure 3, our approach performed much better on those residues with relatively dense data restraints (i.e., with the number of matched NOE peaks per χ angle ≥15) than other residues.

FIG. 3.

Accuracies of the determined side-chain rotamer conformations for residue with different numbers of matched NOE peaks per χ angle for GB1 and ubiquitin. Diagrams are shown in the same format as in Figure 2.

To examine how much empirical molecular mechanics energy and experimental data can influence the side-chain rotamer assignment results individually, we performed a test with GB1 using each term alone, without the other, and compared the results with those from the posterior energy. A comparison of the results shows that the combination of empirical molecular mechanics energy and unassigned NOESY data using the optimal estimated weighting factor allowed the algorithm to determine approximately 10% more accurate side-chain conformations than using only empirical molecular mechanics energy or only experimental data.

3.3. Improvement on our previous approaches hana and Nasca

In our previous approaches, hana (Zeng et al., 2008, 2009) and Nasca (Zeng et al., 2010, 2011), only experimental data were used in determining side-chain conformations. Thus, they did not consider the empirical molecular mechanics energy when packing side-chain conformations. Thus, the side-chain structures computed by hana and Nasca can contain steric clashes. Our new approach solves this problem by taking into account a molecular mechanics potential, which sharply penalizes physically unrealistic conformations. As shown in Table 3, our new approach eliminated all the serious steric clash overlaps (>0.9 Å), which appeared previously in the side-chain conformations computed by hana and Nasca.

3.4. Comparisons with Scwrl4

Scwrl4 (Krivov et al., 2009) is one of the most popular programs for predicting side-chain rotamer conformations given a backbone structure. Note that our algorithm uses unassigned NOESY data, while Scwrl4 does not use any experimental data. We compared the performance of our approach with that of Scwrl4 on GB1 using different input backbone structures (Table 4). The comparison showed that our approach outperformed Scwrl4 for all input backbone structures, especially in the core regions (Table 4). For core residues, our approach achieved accuracies of 92.9–100.0%, while Scwrl4 only achieved accuracies up to 85.7%. As we discussed previously, the correctness of the side-chain conformations in the core regions is crucial for determining the accurate global fold of a protein. Thus, in order to meet the requirement of high-resolution structure determination, the data restraints must be incorporated for packing the side-chain conformations in core residues.

Table 4.

Comparison with the Side-Chain Structure Prediction Program Scwrl4 on GB1 Using Different Input Backbone Structures

	All residues				Core residues
	Accuracy of all χ angles (%)		Accuracy of (χ1,χ2) angles (%)		Accuracy of all χ angles (%)		Accuracy of (χ1,χ2) angles (%)
Backbonesa	Our approach	SCWRL4	Our approach	SCWRL4	Our approach	SCWRL4	Our approach	SCWRL4
3GB1	77.8	72.2	85.2	79.4	100.0	85.7	100.0	85.7
2GB1	72.1	68.5	81.3	74.5	92.9	78.6	92.9	78.6
1GB1	74.1	70.4	83.3	77.8	92.9	78.6	92.9	78.6
1P7E	74.1	70.4	83.3	75.9	92.9	78.6	92.9	78.6
1PGA	70.4	64.8	79.6	70.4	92.9	71.4	92.9	71.4
1PGB	75.9	74.1	83.3	77.8	100.0	85.7	100.0	85.7

The backbone RMSD from 2GB1, 1GB1, 1P7E, 1PGA, and 1PGB to 3GB1 is 1.01 Å, 1.00 Å, 0.44 Å, 0.54 Å, and 0.56 Å, respectively. The program Reduce (Word et al., 1999) was used to add hydrogens to the X-ray backbone structures 1PGA and 1PGB. In our approach, the GMEC was computed for this comparison.

^aPDB ID.

4. Conclusion

In this article, we unified the side-chain structure prediction problem with the side-chain structure determination problem using unassigned NOESY data. We proposed a Bayesian approach to integrate experimental data with modeling information, and used the provable algorithms to find the optimal solution. Tests on real NMR data demonstrated that our approach can determine a high percentage of accurate side-chain conformations. Since our approach does not require any NOE assignment, it can accelerate NMR structure determination.

Although the A* search algorithm guarantees to find the GMEC solution, its worst-case running time can be exponential in the number of residues in the protein sequence. In the future, we can replace it within our Bayesian framework with faster algorithms, which can improve the time complexity of the search process, while still providing the guarantee to provably find the global optimum. We will extend the Nasca module to determine the side-chain conformations without requiring the side-chain resonance assignments from TOCSY experiments, by analogously combining the empirical molecular mechanics energy with unassigned NOESY data. Another possible extension is to exploit more structural flexibility. We can use a finer rotamer library and allow more side-chain flexibility. Currently, we assume that the input backbone structure is rigid. Incorporating backbone flexibility during the search of the GMEC solution, as was done in Georgiev and Donald (2007), Georgiev et al. (2008a), and Chen et al. (2009), will improve the quality of the determined protein structures. Our approach has been tested on NMR data for three proteins. In the future, we plan to test it on more proteins.

5. Appendix

Appendix A briefly reviews the high-resolution protein backbone determination from residual dipolar coupling data. Appendix B derives the Hausdorff-based measure for evaluating the matching score between a back-computed NOE pattern and experimental spectra. Appendix C briefly reviews the DEE and A* search algorithms. Appendix D describes the cross validation approach for estimating the weighting factor parameter in the posterior energy function.

A. Backbone structure determination from residual dipolar couplings

Residual dipolar couplings (RDCs) provide global orientational restraints on the internuclear bond vectors with respect to an external magnetic field (Tolman et al., 1995; Tjandra and Bax, 1997), and have been used to determine protein backbone conformations (Donald and Martin, 2009; Tolman et al., 1995; Fowler et al., 2000; Ruan et al., 2008; Prestegard et al., 2004; Tian et al., 2001; Donald and Martin, 2009; Wang and Donald, 2004; Wang et al., 2006; Rohl and Baker, 2002; Yershova et al., 2011). In our high-resolution structure determination protocol, we applied our recently developed algorithms (Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009; Yershova et al., 2011; Donald and Martin, 2009) to compute the backbone structures using two RDCs per residue (either NH RDCs measured in two media, or NH and CH RDCs measured in a single medium) and sparse NOE distance restraints. In our backbone determination, we first computed conformations and orientations of secondary structure element (SSE) backbones from RDC data using the rdc-analytic algorithm (Wang and Donald, 2004; Wang et al., 2006; Yershova et al., 2011; Donald and Martin, 2009). Instead of randomly sampling the entire conformation space to find solutions consistent with the experimental data, rdc-analytic computes the backbone dihedral angles exactly by solving a system of quartic polynomial equations derived from the RDC equations (Wang and Donald, 2004; Wang et al., 2006; Yershova et al., 2011; Donald and Martin, 2009). A depth-first search strategy is applied to search systematically over all roots of a system of low-degree (quartic) equations, and find a globally optimal solution for each SSE fragment. These RDC-defined SSE backbone fragments are then assembled using a sparse set of inter-SSE NOE distance restraints (Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009; Yershova et al., 2011). These sparse NOE distances can be extracted from unassigned NOESY data using only chemical shift information (Zeng et al., 2009). More details on backbone structure determination using RDCs can be found elsewhere (Donald and Martin, 2009; Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009; Yershova et al., 2011). Alternatively, the global fold (i.e., backbone) could, in principle, be computed by other approaches, such as protein structure prediction (Baker and Sali, 2001), protein threading (Xu et al., 1998), or homology modeling (Langmead and Donald, 2003, 2004b).

B. The NOE pattern matching score

The similarity between a back-computed NOE pattern B and the NOESY spectra Y can be measured by the conventional Hausdorff distance:

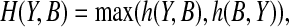where 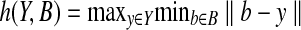and ‖ · ‖ is the normed distance.

This conventional Hausdorff distance is sensitive to a single outlying point in B or Y. To consider outliers and experimental noisy peaks, we can use an extended Hausdorff-based measure, which is derived from the fractional Hausdorff distance (Huttenlocher and Kedem, 1992; Huttenlocher et al., 1993), to compare two sets of peaks. In the fractional Hausdorff distance, the k^th ranked distance is used to measure the discrepancy between two sets of peaks rather than the maximum distance (i.e., the largest ranked one). More formally, in the fractional Hausdorff distance, the original measure h(Y, B) is replaced by the following:

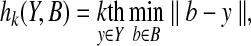where kth is the k^th largest value. We are interested in using the Hausdorff distance to quantify the portion of experimental peaks Y that are close to back-computed NOE peaks B. To implement this goal, we fix a threshold δ, and identify the largest k such that h_k(Y,B) ≤ δ. Here the threshold δ tells how close a non-outlying experimental peak must be to a back-computed NOE peak. We use 0.03 ppm and 0.3 ppm as the threshold δ for protons and the attached heavy atoms ¹³C or ¹⁵N, respectively. Formally, given a set of experimental peaks (i.e., NOESY spectra) Y and a back-computed NOE pattern B, the Hausdorff fraction between Y and B under a threshold distance δ is defined as

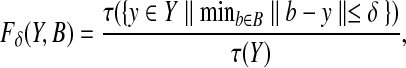(13)

where τ(·) is the size of a set. The Hausdorff fraction represents the percentage of experimental cross peaks that are close to a back-computed NOE peak in B within the threshold distance δ.

In our problem, the coordinates of the protein backbone are known. Given the rotamer state of a residue, the coordinates of side-chain protons in this residue can be also computed. Thus, we can back-compute the self NOE pattern between this side-chain rotamer and the backbone for each rotamer state. Similarly, given rotamer states in two different residues, we can also back-compute the pairwise NOE pattern between these two side-chain rotamer conformations. More details on back-computing an NOE pattern can be found in Zeng et al. (2009, 2010, 2011). Given a rotamer state x_i in residue i, we use F(x_i) to represent the Hausdorff fraction for the self back-computed NOE pattern between the rotamer x_i and the backbone, and use F(x_i, x_j) to represent the Hausdorff fraction for the pairwise back-computed pattern between two rotamers x_i and x_j, where i ≠ j.

C. The DEE/A* search algorithms for computing the optimal rotamer assignment

The major difficulty of computing the optimal solution that minimizes the pseudo energy function in Eq. (10) is due to the pairwise energy terms involving two rotamer assignments x_i and x_j. Since the form of the posterior energy function in Eq. (10) is similar to the energy function in the protein side-chain prediction or protein design, we can apply similar algorithms to solve this problem. Here we first apply the dead-end elimination (DEE) algorithm to prune rotamers when their contribution to the total energy is always less than another competing rotamer in the same residue (Desmet et al., 1992; Looger and Hellinga, 2001; Goldstein, 1994; Georgiev et al., 2008b; Chen et al., 2009). After that, we use an A* algorithm to search over the remaining combinations of side-chain rotamer conformations surviving from DEE and compute the optimal solution that minimizes the pseudo energy function.

The DEE algorithm reduces the complexity of our problem by pruning side-chain rotamers that are provably not part of the optimal solution. Given a residue i, a rotamer assignment 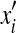in this residue is eliminated if an alternative rotamer assignment x_i satisfies the following Goldstein criterion (Goldstein, 1994):

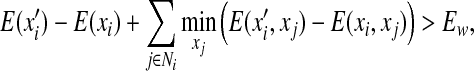(14)

where E_w is the specified energy threshold of the lowest energy rotamer assignment. A rotamer 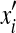in residue i satisfying above criterion in Eq. (14) is provably not part of the optimal solution, and thus can be safely pruned. The time complexity of one round of dead-end elimination at each residue position is O(n³q²), where n is the total number of residues in the protein sequence, and q is the maximum number of rotamer states per residue.

After DEE, we apply an A* search algorithm to compute the optimal solution that minimizes Eq. (10). An A* algorithm provably finds the optimal (i.e., least cost) path from a given starting node to the destination node in a search tree or graph. It uses a heurestic function f = g + h to evaluate the cost of the search path, and determines the order of visiting nodes during the search, where g is the actual cost from the starting node to the current node, and h is the estimated cost from the current node to the goal node. Similar to the protein design (Leach and Lemon, 1998; Georgiev et al., 2008b), we formulate our search configuration space as a tree, in which the root represents an empty rotamer assignment, a leaf node represents a full rotamer assignment, and an internal node represents a partial rotamer assignment (i.e., only rotamers in a partial set of residues are assigned).

Similar to Leach and Lemon (1998) and Georgiev et al. (2008b), we define the following cost functions g and h at the search depth d:

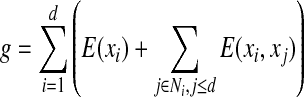and

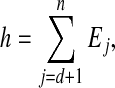where n is the total number of residues in the protein sequence, and E_j is defined as follows:

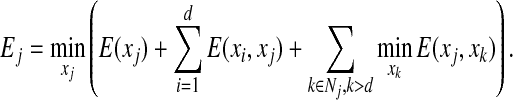The A* algorithm maintains a list of search nodes which are ranked according to f at each iteration, and expands the nodes with the smallest f value. Such an expansion process is repeated until all side-chain rotamers are assigned, that is, when a leaf node with the smallest score in the search tree is reached. This leaf node is returned by the algorithm as a fully assigned conformation. Similar to Georgiev et al. (2008b), Chen et al. (2009), and Frey et al. (2010), we can also extend the original A* search algorithm to compute a gap-free ensemble of conformations such that their energies are all within a user-specified window from the lowest pseudo energy.

D. Details of the cross validation approach for parameter estimation

Both cross validation (Brünger, 1992; Brünger et al., 1993) and sampling-based approaches (Rieping et al., 2005; Habeck et al., 2006) have been used in previous work to estimate the weighting factor between the empirical molecular mechanics energy and the data restraints in NMR protein structure determination. The sampling-based approaches mainly depend on stochastic techniques, such as Monte Carlo or Gibbs sampling, to randomly sample conformation space and joint posterior distribution. These heuristic approaches cannot guarantee to find the global optimum solution. On the other hand, cross validation has been considered as a rigorous approach to estimate unknown parameters. It can also be used to prevent overfitting structures into experimental data. However, the cross validation approach still suffers from several drawbacks. First, fewer data are used to estimate parameter and compute the protein structures, which might influence the accuracy of the parameter estimation result. Second, as observed in Brünger (1992), Brünger et al. (1993), and Habeck et al. (2006), usually there is not a clearly unique choice for the weighting factor parameter, which makes it difficult to objectively find the optimum estimation.

In addition to the approach described in Section 2.5, we also ran a 10-fold cross validation approach to estimate the weighting factor parameter w = σ⁻². In this cross validation approach, we first randomly partitioned all unassigned NOESY data into 10 non-overlapping sets of data. Each set of data had approximately equal size. The cross validation was performed in 10 rounds. In each round, the 9 sets of unassigned NOESY data were used as a working data set to compute the GMEC for each choice of parameter w = σ⁻², and the remaining data set was used as the testing data set to access the choice of w = σ⁻² by measuring the matching score between the back-computed NOE pattern of the GMEC and NOESY spectra. The average result from 10 rounds was used as an estimation of parameter w = σ⁻². In each round, the DEE/A* search algorithms were used to compute the GMEC for each choice of parameter w.

As shown in Figure 1B, the plot of the cross-validated NOE pattern matching score vs. the weighting factor of the data term was nearly flat, and did not exhibit a clearly unique optimum of w that maximized the cross-validated NOE satisfaction score. For GB1, the maximum cross-validated NOE pattern matching score occurred when w was 128–156 (Fig. 1B). Unfortunately, the weighting factor in this interval did not correspond to the best accuracies of all χ angles and (χ₁,χ₂) angles (Fig. 1E, F). Probably this was caused by the fact that fewer data were used to determine side-chain rotamer conformations in the cross validation approach. Thus, our current parameter estimation approach based on the grid search and DEE/A* algorithms outperformed the cross validation approach.

Acknowledgments

We thank Pablo Gainza and Swati Jain for helping us set up the DEE/A* code. We thank all members of the Donald and Zhou Labs for helpful discussions and comments. This work was supported by the National Institutes of Health (R01 GM-65982 and R01 GM-78031 to B.R.D. and R01 GM-079376 to P.Z.).

Disclosure Statement

No competing financial interests exist.