Multiplex De Novo Sequencing of Peptide Antibiotics

Abstract

Proliferation of drug-resistant diseases raises the challenge of searching for new, more efficient antibiotics. Currently, some of the most effective antibiotics (i.e., Vancomycin and Daptomycin) are cyclic peptides produced by non-ribosomal biosynthetic pathways. The isolation and sequencing of cyclic peptide antibiotics, unlike the same activity with linear peptides, is time-consuming and error-prone. The dominant technique for sequencing cyclic peptides is nuclear magnetic resonance (NMR)–based and requires large amounts (milligrams) of purified materials that, for most compounds, are not possible to obtain. Given these facts, there is a need for new tools to sequence cyclic non-ribosomal peptides (NRPs) using picograms of material. Since nearly all cyclic NRPs are produced along with related analogs, we develop a mass spectrometry approach for sequencing all related peptides at once (in contrast to the existing approach that analyzes individual peptides). Our results suggest that instead of attempting to isolate and NMR-sequence the most abundant compound, one should acquire spectra of many related compounds and sequence all of them simultaneously using tandem mass spectrometry. We illustrate applications of this approach by sequencing new variants of cyclic peptide antibiotics from Bacillus brevis, as well as sequencing a previously unknown family of cyclic NRPs produced by marine bacteria. Supplementary Material is available online at www.liebertonline.com/cmb

1. Introduction

In 1939, Renê Dubos discovered that the peptide fraction Tyrothricin, isolated from the soil microbe Bacillus brevis, had an ability to inhibit the growth of Streptococcus pneumoniae, rendering it harmless. Although discovered 10 years after penicillin, it was the first mass produced antibiotic deployed in Soviet hospitals in 1943. Unfortunately, the identification of amino acid sequences of cyclic peptides, once a heroic effort, remains difficult today. The dominant technique for sequencing cyclic peptide antibiotics is two-dimensional (2D) nuclear magnetic resonance (NMR) spectroscopy, which requires large amounts of highly purified materials that, are often nearly impossible to obtain.

Tyrothricin is a classic example of a mixture of related cyclic decapeptides whose sequencing proved to be difficult and took over two decades to complete. By the 1970s, scientists had sequenced five compounds, Tyrocidine A–E, from the original mixture. However, these five are not the only peptides produced by B. brevis, and even today it remains unclear whether all of the antibiotics produced by this bacterium have been documented (see Tang et al. [1992] for a list of 28 known peptides from B. brevis).

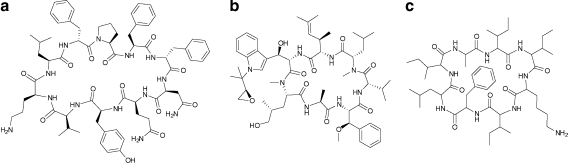
Figure 1a shows structure of Tyrocidine A. Table S1 (all Supplementary Material is available online at www.liebertonline.com/cmb) illustrates that most cyclic decapeptides in the Tyrocidine/Tryptocidine family can be represented as shown (the rounded amino acid masses in daltons are also shown):

FIG. 1.

Structures of Tyrocidine A (a), Cyclomarin A (b), and Reginamide A (c).

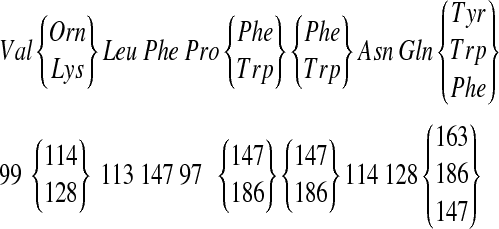It may come as a surprise that there are no genes in B. brevis whose codons encode any of the Tyrocidine peptides! Tyrocidines, similar to many antibiotics such as Vancomycin or Daptomycin, represent cyclic non-ribosomal peptides (NRPs) that do not follow the central dogma “DNA produces RNA produces Protein.” They are assembled by nonribosomal peptide synthetases that represent both the mRNA-free template and building machinery for the peptide biosynthesis (Sieber and Marahiel, 2005). Thus, NRPs are not directly inscribed in genomes and cannot be inferred with traditional DNA sequencing. Cyclic NRPs are of great pharmacological importance as they have been optimized by evolution for chemical defense and communication. Cyclic NRPs include antibiotics, anti-tumor agents, immunosuppressors, toxins, and many peptides with still unknown functions.

Most NRPs are cyclic peptides that contain nonstandard amino acids, increasing the number of possible building blocks from 20 to several hundreds. The now dominant 2D NMR-based methods for NRP characterization are time-consuming, error prone, and requires large amounts of highly purified material. Because NRPs are often produced by difficult to cultivable microorganisms, it may not be possible to get sufficient quantities for 2D structure elucidation therefore it is important to develop a nmol scale structure elucidation approach (Molinski et al. 2009; Molinski, 2010). Such methods promise to greatly accelerate cyclic NRP screening and may illuminate a vast resource for the discovery of pharmaceutical agents (Li and Vederas 2009).

The first automated mass spectrometry (MS)–based approach to sequencing cyclic peptides correctly sequenced two out of six Tyrocidines analyzed by Ng et al. (2009). While the correct sequences for four other Tyrocidines were highly ranked, Ng et al. (2009) came short of identifying them as the highest-scoring candidates. Leao et al. 2010, and Liu et al., (2009b) recently applied the algorithm from Ng et al. (2009) for analyzing new cyclic peptides. In Leao et al. (2010), the authors study peptides produced by the cyanobacterium Oscillatoria sp. that inhibit the growth of green algae and demonstrated that they function in a synergistic fashion (i.e., mixtures of these analogous peptides are needed to inhibit green algal growth). This observation emphasizes the importance of studying various peptide variants and calls for the development of a technology able to simultaneously sequence all peptides produced by a single organism.

Our first attempt to sequence cyclic NRPs from Oscillatoria sp. via MS using the algorithm described by Ng et al. (2009) was inconclusive. We (Leao et al., 2010) resorted to purification of the most abundant peptide with the goal to sequence it via 2D NMR (purification of individual NRPs is often difficult since various NRP variants have similar physiochemical properties). This amounted to a large effort that involved applications of various NMR technologies (including HSQC, HMBC, COSY, and NOESY) but still failed to identify some inter-residue dependencies. Applications of both NMR and MS to finally sequence four compounds using NRP-Dereplication algorithm from Ng et al. (2009) represented a large and time-consuming effort of a multidisciplinary team. A better approach would be to generate MS/MS spectra of all variant NRPs (without the need to purify large amounts of individual peptides) and to multiplex sequence them. By multiplex sequencing we mean simultaneous (and synergistic) sequencing of related peptides from their spectra.

Using this approach, we sequenced many known members of the Tyrocidine family as well as some still unknown Tyrocidine variants. Finding new Tyrocidine variants is surprising since this family has been studied for sixty years now. We further sequenced a previously unknown family of NRPs isolated from a bacterial strain that produces natural products with anti-asthma activities (named Reginamides). To validate these new sequences (obtained from a single mass spectrometry experiment), we analyzed one of them (named Reginamide A) using (rather time consuming) NMR experiments. The mass spectrometry approach revealed the sequence of masses with molecular composition (C₃H₅NO, C₆H₁₁NO, C₆H₁₁NO, C₇H₁₂N₂O₂, C₆H₁₁NO, C₉H₉NO, C₆H₁₁NO, C₆H₁₁NO) that was matched by NMR as the cyclic peptide AIIKIFLI with structure shown in Figure 1c. We emphasize that NMR confirmation of a compound with a known sequence (derived by MS) is much easier than NMR sequencing of a completely unknown compound. The crux of our approach is the analysis of the entire spectral network Bandeira et al. (2007) of multiple Tyrocidines/Reginamides (Fig. 4b, c and Tables 2 and 3) rather than analyzing each Tyrocidine/Reginamide isomer separately. The derived sequences of the Reginamides represent the first automated sequencing of a cyclic peptide family before NMR and highlights the future role that mass spectrometry may play in sequencing cyclic peptides. MS-CyclicPeptide software is available from the NCRR Center for Computational Mass Spectrometry at http://proteomics.ucsd.edu

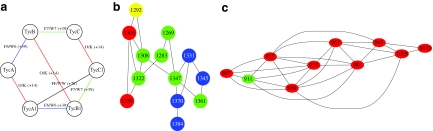
FIG. 4.

(a) The spectral network of six Tyrocidines analyzed in (6) reveals 7 (correct) spectral pairs differing by a single substitution and one (incorrect) spectral pair (Type A1 and Tye-C1) differing by two substitutions. (b) The spectral network of Tyrocidines after clustering similar spectra (see Text S3 for details). The sequences were dereplicated from Tyrocidines A, A1, B, B1, C and C1 in Table 2 (green node) using the multitag algorithm. (c) The spectral network of Reginamides after clustering similar spectra (see Text S4 for details). The sequences were dereplicated from Reginamide A in Table 3 (green node) using the multitag algorithm.

Table 2.

Reconstructed Peptides from the Spectra Corresponding to Vertices in the Spectral Network Shown in Figure 4b

PM	Tag										Score	Comment
1269	99	114	113	147	97	147	147	114	128	163	21	Tyrocidine A
1283	99	128	113	147	97	147	147	114	128	163	26	Tyrocidine A1
1291	99	114	113	147	97	186	147	97	128	163	18	New
1292	99	114	113	147	97	186	131	114	128	163	22	PM matches Tryptocidine A[1]
1306	99	128	113	147	97	186	147	114	112	163	23	New
1308	99	114	113	147	97	186	147	114	128	163	25	Tyrocidine B
1322	99	128	113	147	97	186	147	114	128	163	32	Tyrocidine B1
1331	99	114	113	147	97	186	147	114	128	186	24	Tryptocidine B[1]
1345	99	128	113	147	97	186	147	114	128	186	27	Previously reported[1]
1347	99	114	113	147	97	186	186	114	128	163	24	Tyrocidine C
1361	99	128	113	147	97	186	186	114	128	163	30	Tyrocidine C1
1370	99	114	113	147	97	186	186	114	128	186	26	Tyrocidine D[1]
1384	99	128	113	147	97	186	186	114	128	186	24	Previously reported[1]

The spectra were dereplicated using (known) Tyrocidines A, A1, B, B1, C, and C1 by applying the multitag algorithm described in Figure 3. Four of the sequences are reported previously (see Table S12). For one spectrum with previously reported parent mass, 1292 Da, our reconstruction slightly differs from that of [1].

Table 3.

Dereplication of Reginamide Variants Represented by the Spectral Network in the Figure 4c from the Reginamide A, Using multitag Algorithm

PM	Peptide								Score
897	71	99	113	128	113	147	113	113	31
911	71	113	113	128	113	147	113	113	31
925	71	113	113	142	113	147	113	113	25
939	71	113	113	156	113	147	113	113	31
953	71	113	113	170	113	147	113	113	29
967	71	113	113	184	113	147	113	113	28
981	113	85	113	184	113	147	113	113	28
995	71	113	113	212	113	147	113	113	24
1009	113	113	113	184	113	147	113	113	26
1023	71	113	113	240	113	147	113	113	20

2. Results

Spectral datasets

We analyzed Tyrocidine, Cyclomarin, and Reginamide families of cyclic peptides.

The Cyclomarins represent a family of cyclic heptapeptides with anti-inflammatory activity, isolated from a marine Streptomyces strain (Fenical et al. 1995; Sugiyama et al. 2002; Schultz et al. 2008). The structure of Cyclomarin A is shown in Figure 1b. We sequenced four variants of the Cyclomarins that differ in a single amino acid residue.

The Reginamides represent a newly isolated family of cyclic octapeptides isolated from a marine Streptomyces strain that also produces secondary metabolites with anti-asthma activities (Splenocins). Multiple variants of Reginamide isomers were sequenced using MS. Due to limited quantities of these cyclic peptides and severe separation challenges, it was only possible to purify one of the variants (named Reginamide A) for validating the derived sequences by NMR. Multi-dimensional NMR analysis confirmed the sequence of Reginamide A, derived by our multiplex sequencing algorithm.

Sequencing of individual peptides

Below we describe an algorithm for sequencing individual cyclic peptides. The goal of this algorithm is not improving the method of Ng et al. (2009), but rather proposing the ground for multiplex peptide sequencing, something that the algorithm from Ng et al. (2009) is not suited for.

Consider the cyclic peptide VOLFPFFNQY (Tyrocidine A) with integer masses (99, 114, 113, 147, 97, 147, 147, 114, 128, 163). We will interchangeably use the standard notation 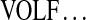and the sequence of rounded masses 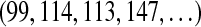to refer to a peptide. One may partition this peptide into three parts as OLF-PFF-NQYV with integer masses 374, 391 and 504 respectively. In general, a k-partition is a decomposition of a peptide P into k subpeptides with integer masses 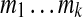(we refer to mass 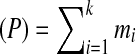as the parent mass of peptide P). A k-tag of a peptide P is an arbitrary partition of mass(P) into k integers. A k-tag of a peptide P is correct if it corresponds to masses of a k-subpartition of P, and incorrect otherwise. For example, (374, 391, 504) is a correct 3-tag, while (100, 1000, 169) is an incorrect 3-tag of Tyrocidine A.

A (linear) subtag of a cyclic k-tag 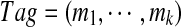is a (continuous) linear substring 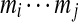of the k-tag (we assume 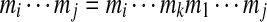in the case j < i). There are k(k − 1) subtags of a k-tag. The mass of a subtag is the sum of all elements of the subtag and the length of a subtag is the number of elements in the subtag. We define Δ(Tag) as the multiset of k(k − 1) subtag masses. For a peptide P, the theoretical spectrum of P is defined as Δ(P). For example, the theoretical spectrum of a cyclic peptide AGPT = (71Da, 57Da, 97Da,101Da) consists of 12 masses (57, 71, 97, 101, 128, 154, 172, 198, 225, 229, 255, and 269).

The problem of sequencing a cyclic peptide from a (complete and noiseless) spectrum corresponds to the Beltway Problem (Skiena et al. 1990) and can be stated as follows:

Cyclic Peptide Sequencing Problem.

• Goal: Given a spectrum, reconstruct the cyclic peptide¹ that generated this spectrum.

• Input: A spectrum S (a set of integers).

• Output: A cyclic peptide P, such that Δ(P) = S.

While the Beltway Problem is similar to the well-studied Turnpike Problem (Skiena and Sundaram, 1994; Cieliebak et al., 2005), the former is more difficult than the latter one (Skiena et al. 1990). Moreover, de novo sequencing of cyclic peptides is much harder than the (already difficult) Beltway Problem. Indeed, the real spectra are incomplete (missing peaks) and noisy (additional peaks). Table S2 represents an experimental spectrum of Tyrocidine A and illustrates that while the experimental spectrum captures many masses from the theoretical spectrum (45 out of 90 masses), it also contains 30 other masses (corresponding to noisy peaks and neutral losses). The limited correlation between the theoretical and experimental spectra makes the spectral interpretation difficult.

Given a tag Tag and an experimental spectrum S (represented as a set of integer masses), we define Score(Tag, S) as the number of elements (masses) shared between Δ(Tag) and S (ignoring multiplicities of elements in Δ(Tag)). For example, for the 3-tag Tag = (374,391,504) of Tyrocidine A, Score(Tag, S) = 5, since the spectrum S contains 5 out of 6 elements in Δ(Tag) = (374,391,504,765,878,895).

The problem of sequencing a cyclic peptide from an incomplete and noisy spectrum can be stated as follows:

Cyclic Peptide Sequencing Problem from Incomplete/Noisy Spectrum.

• Goal: Given an incomplete and noisy spectrum, reconstruct the cyclic peptide that generated this spectrum.

• Input: A spectrum S (a set of integers) and an integer k (peptide length)

• Output: A cyclic peptide P of length k, such that Spectrum and Δ(P) are as similar as possible, i.e., Score(P, S) is maximized among all cyclic peptides of length k.

A tag is valid if all its elements are larger than or equal to 57 (minimal mass of an amino acid). A valid (k + 1)-tag derived from a k-tag Tag by breaking one of its masses into 2 masses is called an extension of Tag. For example, a 4-tag (374, 100, 291, 504) is an extension of a 3-tag (374, 391, 504). All possible tag extensions can be found by exhaustive search since for each 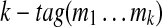there exist at most 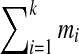extensions.

Our algorithm for sequencing individual peptides starts from scoring all 2-tags and selecting t top-scoring 2-tags, where t is a parameter. It further iteratively generates a set of all extensions of all top-scoring k-tags, combines all the extensions into a single list, and extracts t top scoring extensions from this list. Table 1a shows the reconstructed 7-tags for the Tyrocidine family and illustrates that the highest-scoring tags are incorrect for most Tyrocidines. However, by simultaneously sequencing pairs of spectra of related peptides, one can achieve better results. For the sake of simplicity, we illustrate how our approach works with integer amino acid masses. However, with available high precision mass spectrometry data we are able to derive the elemental composition of each amino acid (see Text S5).

Table 1.

Individual (a), Pairwise (b), and Multiplex (c) De Novo Sequencing of Tyrocidines

a) Individual
Peptide	The highest-scoring correct 7-tag (among all generated tags)										Rank
Tyc A	[99+	114]	[113+	147]	97	147	147	114	[128+	163]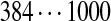
Tyc A1	[99+	128]	[113+	147]	[97+	147]	147	114	128	163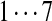
Tyc B	[99+	114]	113	147	97	[147+	186]	114	[128+	163]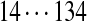
Tyc B1	99	128	[113+	147]	[97+	186]	147	[114+	128]	163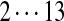
Tyc C	99	114	[113+	147]	[97+	186]	[186+	114]	128	163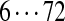
Tyc C1	99	128	[113+	147]	[97+	186]	186	114	[128+	163]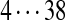

b) Pairwise
Pair	The highest-scoring correct 7-tag (among all generated tags)										Rank
Tyc A/A1	[99+	114/128]	[113+	147]	[97+	147]	147	114	128	163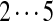
Tyc B/B1	99	114/128	[113+	147]	[97+	186]	147	[114+	128]	163	1
Tyc C/C1	99	114/128	[113+	147]	[97+	186]	186	[114+	128]	163	1
Tyc A/B	99	114	[113+	147]	[97+	147/186]	147	[114+	128]	163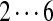
Tyc B/C	99	114	[113+	147]	[97+	186]	147/186	[114+	128]	163	1
Tyc A1/B1	99	128	[113+	147]	[97+	147/186]	147	[114+	128]	163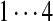
Tyc B1/C1	99	128	[113+	147]	[97+	186+	147/186]	114	128	163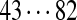

c) Multiplex
Family	Sequences (10-tags)										MS	WMS	Rank
	99	114	113	147	97	147	147	114	128	163	232	29.14	1
	99	114	113	147	97	147	147	69	173	163	228	28.78	2
	99	114	141	119	97	147	147	114	128	163	222	28.14	3
Tyrocidines	99	114	113	147	97	147	147	114	111	180	222	27.85	4

The correct tag is selected from the set of 1000 top-scoring tags (the top scoring correct tag and its rank are shown). Table S3 shows the process of extensions of top scoring tags of Tyrocidine A from 2-tags to 7-tags. Rank 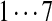for the highest scoring tag of Tyrocidine A1 means that the seven highest scoring tags have equal score, and one of them is the correct tag. Composite masses such as [113 + 147] for Tyrocidine A mean that the sequencing algorithm returned 260Da instead of 113Da and 147Da corresponding to Leu and Phe. [99 + 114/128] for Tyrocidine A/A1 pair means that the mass 99 + 114 = 213 in the first position of Tyrocidine A is substituted by the mass 99 + 128 = 227 in Tyrocidine A1. Part (c) shows 10-tags resulting from multiplex sequencing of six Tyrocidines (projected to Tyrocidine A). Correct masses are shown in bold. MS stands for Multiplex Score, and WMS stands for weighted Multiplex Score (see Text S2 for details).

Furthermore, we describe an algorithm for combining information from all high scoring tags to generate a spectral profile (Fig. 2) that compactly represents all high-scoring tags (similar to sequence logos (Schneider and Stephens, 1990). Eac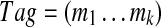h with 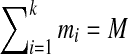defines an M-dimensional boolean vector 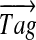with 1s at k positions 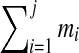for 1 ≤ j ≤ k. For example, a tag (3,2,4) defines a vector 001010001. Given a vector 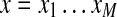, we define its i-shift as the vector 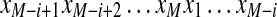and its reversal as the vector 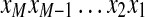. We define the reversed i-shift as the reversal of the i-shift. For example, 2-shift of 001010001 is 010010100, and reversed 2-shift is 001010010. Given vectors x and y, we define alignment(x, y) as a shift or reversed shift of x with maximum dot-product with y. For x = 001010001 and y = 101000000, alignment(x, y) = 101000100.

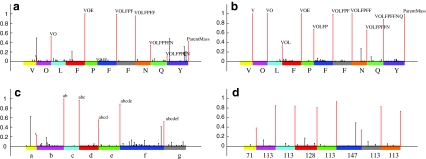
FIG. 2.

(a) Spectral profile of 100 highest scoring 7-tags for Tyrocidine A. Intensities of correct peaks account for 68% of total intensity. (b) Spectral profile of 100 highest scoring 10-tags for Tyrocidine A generated by multiplex sequencing of Tyrocidines. Intensities of correct peaks account for 86% of total intensity. (c) Spectral profile of 100 highest scoring 7-tags generated for Cycolmarin A by multiplex sequencing of four Cyclomarins (Cycolmarin A, Cycolmarin C, Dehydro Cyclomarin A and Dehydro Cyclomarin C). For Cyclomarin A, amino acids a, b, c, d, e, f and g stand for Alanine (71Da), β-methoxyphenylalanine (177Da), Valine (99Da), N-methylleucine (127Da), 2-amino-3,5-dimethylhex-4-enoic acid (139Da), N-(1,1-dimethyl-2,3-epoxyprophyl)-β-hydroxytryptophan (286Da) and N-methyl-δ-hydroxyleucine (143Da). In Cyclomarin C, f is replaced by N-prenyl-β-hydroxytryptophan (270Da). Dehydrations also occur on residue f. Intensities of correct peaks accounts for 59% of total intensitites. (d) Spectral profile of 100 top scoring 8-tags of Reginamide A generated by multiplex sequencing of Reginamides. The top scoring 8-tag of Reginamide A, also verified by NMR, is (71, 113, 113, 128, 113, 147, 113, 113). Intensities of correct peaks account for 81% of total intensity.

Our algorithm for constructing the spectral profile (generated from a spectrum with parent mass M) starts from ordering t high-scoring k-tags 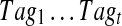in the decreasing order of their scores and defines T₀ as an M-dimensional vector with all zeros. It proceeds in t steps, at each step aligning the tag Tag_i against the vector T_i−1. At step i, it finds 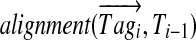between 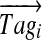and T_i−1 and adds it to T_i−1 to form 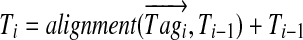. After t steps, the algorithm outputs the vector 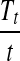as the spectral profile.

For example, for Tyrocidine A, the two 7-tags with the highest scores are Tag₁ = (114, 147, 244, 260, 111, 119, 274) and Tag₂ = (114, 147, 244, 291, 80, 133, 260). After the first step, we form a vector 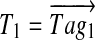with 1s at positions 114, 261, 505, 765, 876, 995 and 1269. At the second step, we align 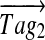and T₁ and form a vector T₂ with 1s at positions 765, 995, 796, 1009 and 2s at positions 114, 261, 505, 876, and 1269. Repeating these steps for 100 high-scoring tags for Tyrocidine A results in the spectral profile shown in Figure 2a. Table S4 provides the annotations of the spectral profiles for Tyrocidine A, B and C.

Sequencing of peptide pairs

We define a spectral pair as spectra S and S′ of peptides P and P′ that differ by a single amino acid. Consider a spectral pair (S, S′) and set δ = Mass(S′) − Mass(S). Given a k-tag 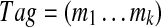of a spectrum S and an offset δ, we define a corresponding k-tag 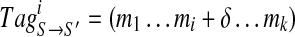of S′ for each 1 ≤ i ≤ k. For example, for Tag = (213, 260, 244, 147, 114, 128, 163) of Tyrocidine A, 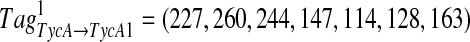is the corresponding tag of Tyrocidine A1. Any k-tag of S corresponds to at most k k-tags of S′, and any correct k-tag of S corresponds to (at least) one correct k-tag of S′. Given a k-tag Tag of a spectrum S, define its PairwiseScore as

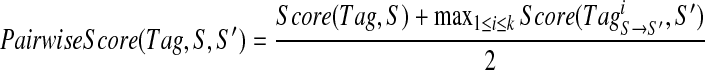The algorithm for pairwise sequencing of the cyclic peptides is exactly the same as the algorithm for sequencing individual cyclic peptide but instead of using Score(Tag, S) for scoring a single tag, it uses PairwiseScore(Tag, S, S′). Table 1b shows that while pairwise sequencing improves on sequencing of individual cyclic peptides, it does not lead to correct reconstructions of all Tyrocidines.

Identifying spectral pairs

While the described algorithm assumed that we know which spectra form spectral pair, i.e., which peptides differ by a single substitution, such an information is not available in de novo sequencing applications. The problem of whether spectra of two linear peptides form a spectral pair was investigated by Bandeira et al., Bandeira et al. (2007). In this section we address a more difficult problem of predicting whether the spectra of two cyclic peptides form a spectral pair based only on their spectra. Our approach extends the dereplication algorithm from Ng et al. (2009) by comparing spectra of mutated peptides (rather than comparing a spectrum against a sequence of a mutated peptide) and is based on the observation that related peptides usually have high-scoring corresponding tags. A simple measure of similarity between spectra is the number of (S, S′)-shared peaks (see Table S6). In the following we introduce Δ(S, S′) distance between spectra, that, in some cases, reveals the similarity between spectra even better than the number of (S, S′)-shared peaks. Given a set of k-tags TagList for a spectrum S, we define:

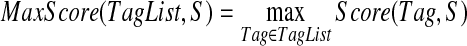Given an additional spectrum S′, we define:

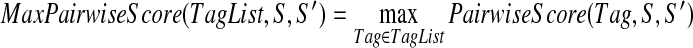Finally, given a set of k-tags TagList for a spectrum S and a set of k-tags TagList′ for a spectrum S′, define Δ(TagList, TagList′, S, S′) (or, simply, Δ(S, S′)) as the differences between the sum of scores of the best-scoring tags for S and S′ and the sum of pairwise scores of the best-scoring tag of S/S′ and S′/S pairs:

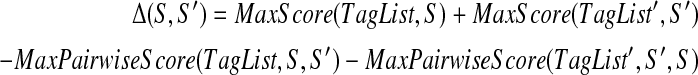It turned out that Δ(S, S′) is a good indicator of whether or not peptides P and P′ that produced S and S′ are only one amino acid apart. Table S6 illustrates that all seven spectral pairs of Tyrocidines have Δ less than or equal to five, while for remaining pairs, Δ is greater than or equal to seven, with exception of Tyrocidine A1/C1 pair representing two substitutions at consecutive amino acids FF → WW. Such substitutions at consecutive (or closely located) positions are difficult to distinguish from single substitutions. For example, the theoretical spectrum for FF → WW substitutions (each with 39 Da difference in the mass of amino acids) is very similar to the theoretical spectrum of a peptide with a single substitution on either of Phe residues with 78-Da difference.

Spectral network construction

Given a set of peptides 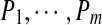, we define their spectral network as a graph with m vertices 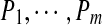and edges connecting two peptides if they differ by a single amino acid substitution. In reality, we are not given peptides 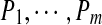but only their spectra 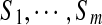. Nevertheless, one can approximate the spectral network by connecting vertices S_i and S_j if the corresponding peptides are predicted to differ by a single amino acid, i.e. if Δ(S, S′) is less than a threshold. Figure 4a show the spectral network of six Tyrocidines analyzed in Ng et al. (2009).

Multiplex sequencing of peptide families

We now move from pairwise sequencing to multiplex sequencing of spectral networks of (more than two) related cyclic peptides. While we use the notion of spectral networks from Bandeira et al. (2007), the algorithm for sequencing linear peptides from spectral networks (Bandeira et al. 2007) is not applicable for sequencing cyclic peptides.

In multiplex sequencing of peptide families, we are given a set of spectra of peptides of the same length n, without knowing their amino acid sequences, and without knowing which ones form spectral pairs. Sequencing of individual cyclic peptides is capable of generating a set of candidate k-tags, that typically contains a correct tag (at least for k smaller than n). However, sequencing of individual spectra typically fails to bring the correct peptide to the top of the list of high-scoring peptides or even, in some cases, fails to place it in this list. To alleviate this problem, we analyze all spectra in the spectral network and introduce a multiplex scoring that utilizes the information from all spectra.

Below we formulate the multiplex sequencing problem. Given a spectral network G of spectra 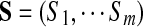, we call a set of peptides 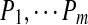G-consistent if for every two spectra S_i and S_j connected by an edge in G, P_i and P_j differ by a single amino acid:

Multiplex Cyclic Peptide Sequencing Problem.

• Goal: Given spectra of related cyclic peptides (of the same length) and their (estimated) spectral network, reconstruct all cyclic peptides that generated this spectra.

• Input: Spectra 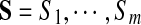, their (estimated) Spectral Network G, and an integer k.

• Output: A G-consistent² set of peptide 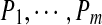(each of length k) that maximizes 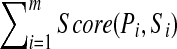among all sets of G-consistent peptides of length k.

Let 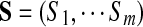be a set of spectra of m peptides forming a spectral network and let 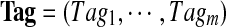be a multitag, which is a set of tags such that Tag_i is a k-tag of spectrum S_i (for 1 ≤ i ≤ m). In Text S1, we describe multiplex scoring of multitags, taking into account dependencies between spectra in the spectral network. This is in contrast to scoring multitags as 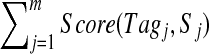that is equivalent to independent optimization of individual scores on all individual k-tags. This approach will not give any payoff in comparison to individual spectral sequencing.

MultiplexScore defined in Text S1 scores a multitag against all spectra in the spectral network. However, generating a correct multitag from m lists of t top-scoring tags in spectra 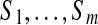is impractical since (i) the number of candidate multitags (t^m) is large, and (ii) some lists may not contain correct individual tags. We therefore generate candidate multitags from individual tags and score them against all spectra using MultiplexScore. Figure 3 describes the algorithm for generating a k-multitag from a single individual k-tag using the spectral network G. Given a candidate individual tag Tag of a spectrum S_u, 1 ≤ u ≤ m, our algorithm generates a candidate multitag 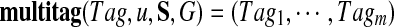satisfying Tag_u = Tag. Note that given a tag 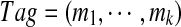, the (i, δ)-modification of Tag is defined as .

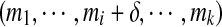FIG. 3.

Algorithm for generating multitags from a candidate Tag of a spectrum S_u in the spectral network formed by spectra 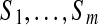corresponding to the spectral network G. Given a k-tag Tag of the spectrum S_u, the algorithm initializes Tag_u = Tag and Tag_j = Null for all other 1 ≤ j ≤ m. We assume that Score(Null, S_i) = −∞ for all 1 ≤ i ≤ m. E(G) stands for the edge set of the spectral network G. Since the sum 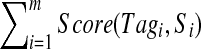is monotonically increasing, the algorithm converges (typically after few iterations).

We now define multiplex score on an individual tag Tag of a spectrum S_u as follows:

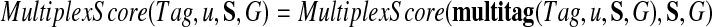The multiplex sequencing algorithm (i) generates lists of individual tags for each spectrum in the spectral network, (ii) constructs the spectral network G, (iii) selects an individual Tag that maximizes MultiplexScore(Tag, u, S, G) among all individual tags, and (iv) outputs multitag(Tag, u, S, G) as the solution of the multiplex sequencing problem.

Multiplex sequencing algorithm is exactly the same as the individual sequencing algorithm, with the only difference that we use MultiplexScore here, instead of Score (individual sequencing). Again we start with high scoring 2-tags (in MultiplexScore sense), and extend them, keeping t highest scoring tags in each step. Table 1c illustrates that the multiplex sequencing algorithm sequences all six Tyrocidines studied in Ng et al. (2009) correctly.

Figure 2b–d shows spectral profiles for t = 100 high scoring tags of multiplex sequencing of Q-TOF spectra of Tyrocidines, Cyclomarins, and Reginamides.

Figure 4b and Table 2 show spectral network and sequences of Tyrocidines, predicted by multiplex sequencing algorithm (using ESI-IT spectra, see Text S3 for details). Figure 4c and Table 3 show similar results for Reginamides (see Text S4 for details).

To analyze Reginamides, the Q-TOF and ESI-IT tandem mass spectrometry data was collected on both ABI QSTAR and ThermoFinnigan LTQ. In both cases, sequencing of Reginamide A resulted in a sequence of integer masses (71, 113, 113, 128, 113, 147, 113, 113). Using accurate FT spectra collected on ThermoFinnigan, we further derived amino acid masses as (71.03729, 113.08406, 113.08405, 128.09500, 113.08404, 147.06849, 113.08397, 113.08402) that pointed to amino acids Ala (71.03711), Ile/Leu (113.08406), Lys (128.09496) and Phe (147.06841) and revealed the elemental composition. These sequences were further confirmed by NMR (see Text S6).

3. Methods

Generating mass spectra

Q-TOF tandem mass spectrometry data for Tyrocidines, Cyclomarines, and Reginamides were collected on ABI-QSTAR. In addition, ESI-IT tandem mass spectrometry data were collected for Tyrocidines and Reginamides on a Finnigan LTQ-MS. All spectra were filtered as described in Ng et al. (2009) and Liu et al. (2009a) by keeping five most intense peaks in each 50 dalton window. All masses were rounded after subtraction of charge mass and multiplication by 0.9995 as described in Kim et al. (2009). High-resolution FT spectra of Reginamides were also collected on a Finnigan. Typical mass accuracy of IT instruments are between 0.1 to 1 Da, while typical accuracy of TOF and FT instruments are between 0.01 to 0.1Da, and 0.001 to 0.01Da, respectively.

Isolation of Reginamide A

CNT357F5F5 sample was obtained from a cultured marine streptomyces in five 2.8-L Fernbach flasks each containing 1 L of a seawater-based medium and shaken at 230 rpm at 27°C. After seven days of cultivation, sterilized XAD-16 resin was added to adsorb the organic products, and the culture and resin were shaken at 215 rpm for 2 hours.

The resin was filtered through cheesecloth, washed with deionized water, and eluted with acetone. Pure Reginamide A eluted at 12.6 min to give 2.0 mg of pure material.

Generating NMR spectra

CD₃OD and C₅D₅N were purchased from Cambridge Isotope. ¹H NMR, ¹³C NMR, ¹H − ¹H COSY, ¹H − ¹H TOCSY (mixing time 90 ms), HMBC (²J or 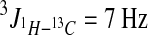), HSQC (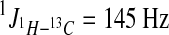), and ROESY (mixing time = 400 ms) spectra were generated on the Bruker (AVANCE III 600) NMR spectrometer with 1.7 mm cryoprobe. All the NMR spectra are provided in the Supplementary Material.

Parameter setting

Text S7 discusses setting of parameters of the algorithm.

Acknowledgments

S.P.G. thanks Fundao para a Cincia e Tecnologia, Portugal, for a postdoctoral fellowship. This work was supported by the U.S. National Institutes of Health (grants 1-P41-RR024851-01 and GM086283).

Disclosure Statement

No competing financial interests exist.