Skip to main content
PMC home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2011 Nov;18(11):1399–1409. doi: 10.1089/cmb.2011.0191

Inferring Mechanisms of Compensation from E-MAP and SGA Data Using Local Search Algorithms for Max Cut

Mark DM Leiserson 1, Diana Tatar 1, Lenore J Cowen 1, Benjamin J Hescott 1,✉
PMCID: PMC3216108  PMID: 21882903

Abstract

A new method based on a mathematically natural local search framework for max cut is developed to uncover functionally coherent module and BPM motifs in high-throughput genetic interaction data. Unlike previous methods, which also consider physical protein-protein interaction data, our method utilizes genetic interaction data only; this becomes increasingly important as high-throughput genetic interaction data is becoming available in settings where less is known about physical interaction data. We compare modules and BPMs obtained to previous methods and across different datasets. Despite needing no physical interaction information, the BPMs produced by our method are competitive with previous methods. Biological findings include a suggested global role for the prefoldin complex and a SWR subcomplex in pathway buffering in the budding yeast interactome.

Key words: algorithms, combinatorics, NP-completeness

1. Introduction

When two genes are mutated together, sometimes a surprising phenotype emerges compared to the phenotype of the individual gene mutants. When studying the yeast genome, often this can be quantified as the growth rate of the double mutant, compared with the expected growth rate of the double deletion mutant based on the growth rate of the single deletion mutants, termed epistasis. One of the most exciting developments in experimental data for large-scale function prediction has been technology, such as SGA from Tong et al. (2004), dSLAM from Pan et al. (2006), and E-MAP from Schuldiner et al. (2005), which can produce high-throughput screens of massive numbers of pairwise mutant combinations. Complete E-MAPs have been published for a set of S. cerevisiae (budding yeast) genes involved in chromosome function (Collins et al., 2007), for a set involved in signaling pathways (Fiedler et al., 2009), as well as a set of genes in S. pombe (fission yeast) (Roguev et al., 2008). The most complete SGA study to date of S. cerevisiae genes was recently done by Costanzo et al. (2010). For computational biologists, pairwise genetic interaction data from E-MAP and other sources can be modeled as a complete, weighted, signed graph, which can be mined by itself, or together with other sources of interaction data, to produce functional predictions.

One of the most well-studied and useful network motifs found in genetic interaction data is the between-pathway model (BPM), introduced first by Kelley and Ideker (2005) and Ulitsky and Shamir (2007). This is a network motif consisting of a particular pattern of genetic and physical interactions that is thought to signify two coherent sets of genes that may be compensatory or adaptive. In particular, each BPM subgraph consists of two subsets of genes, where physical interactions tend to occur between pairs of genes in the same subset, and synthetic lethal interactions tend to occur between pairs of genes in different subsets. The two subsets are called pathways in earlier articles (Kelley and Ideker, 2005; Ulitsky and Shamir, 2007; Ma et al., 2008; Brady et al., 2009), but now the term modules is becoming more standard (to emphasize that it is only a gene set that is being predicted, not directional, or temporal information in a pathway). We will also use the term module in this work to refer to each of the two subsets of genes in a BPM.

It was shown by Kelley and Ideker (2005) and Ulitsky and Shamir (2007), and in subsequent work (Ma et al., 2008; Brady et al., 2009) that BPM modules in the interactome of S. cerevisiae (budding yeast) show significant biological enrichment for functional coherence, based on known ontological annotation. Recently, functional coherence of predicted BPM modules based on gene expression data has also been demonstrated by Hescott et al. (2010). All early methods were based on binary genetic interaction data; that is, a pair of proteins are in a synthetic lethality relationship, or they are not. For example, Brady et al. (2009) showed that a search for maximal graph cuts can be used to help find BPMs based on this binary genetic interaction data.

Recently, Kelley and Kingsford (2011) considered whether the BPM paradigm could be adapted to make use of the more expressive non-binary quantitative genetic interaction data available from an E-MAP or SGA. Their approach interprets the E-MAP weights on the edges as probabilities, and they introduce a new method for clustering E-MAP data they call Expected Graph Compression based on the probabilistic graph that results. They compare the functional coherence of the modules that they found with those found by earlier articles of Bandyopadhyay et al. (2008) and Ulitsky et al. (2008).

In this work, we show that a new method based on local search for maximal cuts can improve the discovery of validated modules and BPMs in E-MAP data. The strength of our approach includes:

  • 1. The method is mathematically natural, algorithmically simple, and fast in practice (though there are some open questions about theoretical convergence times).

  • 2. We achieve improved GO enrichment of BPM modules compared to previous studies.

  • 3. Unlike all previous studies based on E-MAP data, our method makes use of the graph-theoretic structure of the genetic interaction data only when constructing the BPMs, allowing the location of known physical interactions to statistically validate modules. Thus, our method can find novel BPMs in network neighborhoods where less is known about physical interactions between genes.

Finally, there have been enough different studies on finding BPMs in yeast genetic interaction data that in addition to looking at the differences between what these methods can uncover, it becomes interesting to look at which modules are found again and again by all the different algorithms. Looking for these strong signals, we uncover some possible global mechanisms of fault-tolerance within the yeast interactome involving chaperones and chromatin remodeling.

1.1. Related work

As mentioned above, the primary studies on uncovering BPMs in binary yeast interaction data come from Kelley and Ideker (2005), Ulitsky and Shamir (2007), Ma et al. (2008), and Brady et al. (2009). The corresponding computational problem involves finding appropriate subgraphs in an unweighted graph.

Articles by Bandyopadhyay et al. (2008) and Ulitsky et al. (2008) look for modules in yeast E-MAP data; a recent article of Kelley and Kingsford (2010) explicitly tries to generalize the notion of BPMs to E-MAP data. We directly compare our BPMs and modules to all three previous methods that analyzed the Collins et al. (2007) E-MAP data. In addition, we use our LocalCut method to also generate BPMs based on the Boone lab's recent SGA map of budding yeast genetic interactions, one based on an E-MAP for budding yeast genes involved in cell signaling pathways (Fiedler et al., 2009), as well as an E-MAP dataset of S. Pombe (Roguev et al., 2008). We discuss what is similar and different on a systems scale about BPMs across different methods and different datasets.

2. Data

The Collins et al. (2007), Fiedler et al. (2009), and Roguev et al. (2008) scalar genetic interaction datasets were downloaded from The Krogan Lab (http://interactome-cmp.ucsf.edu/). The Boone Lab in Costanzo et al. (2010) reports three variants (lenient, intermediate, stringent) of their SGA data. We report here results from the intermediate set (interaction values with an absolute value greater than 0.08 with a p-value <0.05), though we ran the LocalCut algorithm on all three variants and saw similar results. These genetic interaction datasets span four different sets of genes: the Collins gene sets relate to chromosome function, the Fiedler gene set to signaling, the Roguev gene set to a genetic cross-section of S. Pombe, and the Boone to nearly 75% of the S. cerevisiae genome. To validate the BPMs generated by the LocalCut algorithm on each of the S. cerevisiae datasets, we also obtained a set of physical interactions by considering interactions between genes in these datasets in the BioGRID 3.0.66 release where the experiment type was “physical”, (Stark et al., 2005).

3. Results

Table 1 compares the results of our LocalCut algorithm to those of previous work of Bandyopadhyay et al. (2008), Kelley and Kingsford (2010), and Ulitsky et al. (2008) on the Collins et al. (2007) chromosome function E-MAP data. In order to make the results comparable across methods, we restrict to considering BPMs where each of its two modules contain 3–25 genes. (This removes many BPMs from the Kelley-Kingford set, where 1 module contained only 1 or 2 genes, making it more comparable with other results). Such modules we call “accepted” in Table 1. A module is then declared enriched in Table 1 if, according to the program FuncAssociate (Berriz et al., 2003), it is enriched for any term that describes a set of less than 500 proteins in the GO hierarchy, with a p-value ≤0.01. (Note that all FuncAssociate results are based on GO terms from a version of GO downloaded on 6/28/2010 except for the results of Ulitsky et al. which come from a slightly more recent set of GO terms updated on January 11, 2011.) All methods excel at producing enriched modules, though it is perhaps impressive that we do so looking at genetic interactions only, whereas other methods also use physical interaction information to construct modules. However, the real strength of our method becomes apparent when looking at how the modules are combined into BPMs. A BPM is declared enriched for the same function if at least one enrichment term is in common between both modules. A BPM is declared enriched for related functions using the same definition as Kelley and Kingsford (2010), that is, if both modules are enriched, and each has an enrichment term whose most recent common ancestor describes fewer than 500 proteins. A BPM is declared enriched for different functions if both modules are enriched, but it doesn't meet the criteria above. LocalCut gives a much higher percentage of BPMs enriched for the same function or related functions than previous methods. We remark that LocalCut tends to produce more modules but fewer BPMs than the other methods. That's because the other methods tend to reuse modules several times as part of different BPMs, whereas LocalCut's modules tend to be unique to a particular BPM. Coupled with the enrichment results, it thus seems that other methods are reusing a smaller set of modules, and combining them into BPMs that are not necessarily functionally coherent as a module pair.

Table 1.

Comparison of Our LocalCut Algorithm to Previous Analyses of the Collins et al. (2007) E-MAP Data

 
 Modules
 BPMs
Dataset Accepted Enriched Accepted Enriched for same function Enriched for same or related function Enriched for different functions One mod enriched No mods enriched
Bandyopadhyay et al. 37 35 96 41 (43%) 53 (55%) 36 (38%) 7 (7%) 0 (0%)
Ulitsky et al. 43 43 111 43 (39%) 71 (64%) 40 (36%) 0 (0%) 0 (0%)
EGC (Kelley-Kingsford) 40 40 98 35 (36%) 52 (53%) 45 (46%) 1 (1%) 0 (0%)
Our results (LocalCut) 112 103 58 39 (67%) 43 (74%) 6 (10%) 9 (16%) 0 (0%)
Open in a new tab

We achieve a greater number of enriched modules as well as a higher percentage of BPMs with both modules enriched for either the same or related function.

A notable exception to this rule seems to be two complexes, the SWR-C complex and the prefoldin complex, which seem to appear opposite several different sets of genes, both in our BPMs and in the BPMs of others. (See Section 4 below for a discussion of biological implications.) To quantify this, we ran LocalCut on the Collins et al. (2007) E-MAP data in an ordinary fashion, and again, with the genes from these complexes removed. When we remove these genes, LocalCut produced 18 BPMs, whose enrichment values are 72% enriched for same function; 77% enriched for similar function; 11% with unmatched, but similar BPMs; and 11% with one module enriched. Table 2 gives the average number of BPMs each gene appears in, for each of these experiments, as compared to the same set of other methods as in Table 1. Note that the average number of BPMs per gene is slightly higher for us (7.05) than for the other methods (range, 5.67–6.4). However, when we remove the BPMs involving the SWR-C complex and prefoldin complex, the average number of genes per BPM for LocalCut drops all the way down to 2.7.

Table 2.

Average Number of BPMs in Which Each Fixed Gene is Present, for Each Method for the Collins et al. (2007) Data

Algorithm Average number of BPMs per gene
LocalCut 7.05
LocalCut with SWR and Prefoldin genes removed 2.7
Bandyopadhyay et al. 6.4
Ulitsky et al. 5.67
EGC (Kelley-Kingsford) 5.87
Open in a new tab

In Table 3, we seek to determine how sources of genetic interaction data affects the network of BPMs as discovered by LocalCut on the same gene set. In particular, we looked at LocalCut run on the original Collins et al. (2007) E-MAP data, as compared to the SGA data of Boone et al. (2007) restricted to the same gene set as the Collins et al. (2007) E-MAP data, as well as the full Boone network. On both the original data and on the restricted Boone dataset, the performance of LocalCut seems comparable as approximately the same percentage of modules are enriched, and a similar percentage of BPMs result that are enriched for the same or related functions. However, fewer total modules and BPMs are found in the Boone data restricted to this gene set, which is not surprising because there are many more 0-weight edges due to missing or corrupted data in the Boone data on the restricted set of genes (218,386 nonzero edges in the Collins et al. [2007] E-MAP data versus 15,467 nonzero edges reported by the Boone Lab on the same set of genes; the full Boone dataset has 145,805 nonzero edges). And in fact, the modules found by LocalCut based on the Collins et al. (2007) interaction data are quite different than those generated from the restricted Boone data when measuring the Jaccard index (see Jaccard [1908] and Real and Vargas [1996] for definitions of the Jaccard index). Only 2 modules have a Jaccard index greater than 0.8. However, more than 50% of the modules have Jaccard indices greater than 0.25, meaning the modules uncovered by LocalCut are roughly as similar across datasets (E-MAP and SGA) as the modules uncovered across methods (i.e., LocalCut modules as compared to Kelley-Kingsford, Ulitsky et al., or Bandyopadhyay et al.). Note that the average number of BPMs each gene appears in is lower for LocalCut on these alternative datasets than it was on the Collins et al. (2007) E-MAP data, with an average of 3.70 on the full Boone et al. (2007) dataset, 3.05 on the restricted Boone data, and 1.38 on the Fiedler et al. (2009) data.

Table 3.

Comparison of the Results of Our Algorithm on Different Datasets

 
 Modules
 BPMs
Dataset Accepted Enriched Accepted Enriched for same function Enriched for same or related function Enriched for different functions One mod enriched No mods enriched
Collins et al. 112 103 58 39 (67%) 43 (74%) 6 (10%) 9 (16%) 0 (0%)
Boone (restricted) 55 52 29 18 (62%) 23 (79%) 2 (7%) 4 (14%) 0 (0%)
Boone (full) 285 104 149 8 (5%) 17 (11%) 9 (6%) 56 (38%) 67 (45%)
Open in a new tab

Boone (restricted) refers to the Boone dataset restricted to only contain those genes also in the Collins et al. data. LocalCut finds fewer BPMs on the restricted Boone dataset than on the Collins et al. E-MAP; not surprising since there are more missing or zero-weight edges in the restricted Boone dataset. However, the proportion that are enriched for same or related function is nearly identical across both these data sources. On the full Boone dataset, while many more modules and BPMs are found by LocalCut, many more are not known to be functionally enriched, perhaps because this is a less-understood set of yeast genes with fewer annotations.

In Table 4, we look at how making perturbations in the edge weights can affect the results of the LocalCut algorithm. In Variant 1, we set all positive weights to 0. In Variant 2, every weight whose absolute value is above 2.5 (the threshold for synthetic lethality and synthetic rescue as defined by Collins et al. [2007]) is set to 2.5 or −2.5, consistent with its sign. In Variant 3, we run LocalCut on the binary version of the data, where every edge weight above 2.5 is set to +1, and any weight below −2.5 is set to −1, and all other weights are 0. Variant 4 is the negative half of Variant 3; any weight whose value is below −2.5 is set to −1 and all other weights are 0 (representing synthetic lethality or not). For Variant 5, we use the E-MAP weights augmented with interpolation: that is, we download the E-MAP weights as filled in by Ulitsky et al. (2009) using their method to interpolate for missing data in the original E-MAP. The control variant aims to produce nonsense by exchanging the signs of all the weights on the edges. Of these variants, clearly all of them produce degraded performance, except possibly Variant 1, which produces fewer modules and BPMs, but has nearly the same percentage of the modules enriched for same or related function. This is an interesting result in light of the discussion in the work of Kelley and Kingsford (2010) about whether considering positive edge weights helps or hurts in the construction of BPMs; LocalCut finds more BPMs with no degradation in functional enrichment if positive edge weights are included. The other variants show that, to some extent, the full range of interaction data is helpful in constructing modules and BPMs, and less is discovered if only the binary synthetic lethality or rescue data is used. We are also pleased that the control variant (exchanging the role of positive and negative edge weights in the data) yields only noise—no consistent BPMs with both modules of size between 3 and 25. This proves that the existence of meaningful negative-weight bipartite subgraphs is a true biological property of the yeast genetic interaction network, not a computational artifact; another way to say this is that there are no small bipartite subgraphs in the Collins et al. (2007) E-MAP data with positive weight between the two modules and negative weight within each module.

Table 4.

We Examine How Perturbing Edge Weights Affect the Performance of Our LocalCut Algorithm

 
 Modules
 BPMs
Dataset Accepted Enriched Accepted Enriched for same function Enriched for same or related function Enriched for different functions One mod enriched No mods enriched
LocalCut 112 103 (92%) 58 39 (67%) 43 (74%) 6 (10%) 9 (16%) 0 (0%)
LocalCut – Variant 1 50 46 (92%) 26 17 (65%) 19 (73%) 2 (8%) 5 (19%) 0 (0%)
LocalCut – Variant 2 133 61 (46%) 68 4 (6%) 6 (9%) 9 (13%) 33 (49%) 20 (29%)
LocalCut – Variant 3 54 37 (69%) 30 3 (10%) 7 (23%) 6 (20%) 17 (57%) 0 (0%)
LocalCut – Variant 4 21 14 (67%) 12 1 (8%) 2 (17%) 3 (25%) 7 (58%) 0 (0%)
LocalCut – Variant 5 98 82 (84%) 49 21 (43%) 30 (61%) 5 (10%) 12 (24%) 2 (4%)
LocalCut – Control 0 0 (0%) 0 0 (0%) 0 (0%) 0 (0%) 0 (0%) 0 (0%)
Open in a new tab

The results validate our supposition that the nuances of scalar data are more informative than binary weights, and that positive-weight interaction edges matter as well as negative-weight edges.

Table 5.

Results of Applying LocalCut to Different Datasets

 
 Modules
 BPMs
Dataset Accepted Enriched Accepted Enriched for same function Enriched for same or related function Enriched for different functions One mod enriched No mods enriched
Collins et al. 112 103 58 39 (67%) 43 (74%) 6 (10%) 9 (16%) 0 (0%)
Fiedler et al. 10 8 5 0 (0%) 4 (80%) 0 (0%) 0 (0%) 1 (20%)
Boone (Full) 285 104 149 8 (5%) 17 (11%) 9 (6%) 56 (38%) 67 (45%)
S. pombe 31 18 16 1 (6%) 1 (6%) 4 (25%) 9 (56%) 2 (13%)
Open in a new tab

Notice that the BPM network motif is very rare among the Fiedler et al. cell signaling genes, as compared to the others, implying perhaps that this network is organized at a different level of complexity or with different mechanisms of fault-tolerance. On the other hand, the fact that fewer modules and BPMs are enriched in the full Boone dataset across nearly all S. cerevisiae genes and the S. pombe network is more likely caused by the fact that our knowledge and therefore annotation of basic S. cervisiae cell cycle genes far exceeds our knowledge of the other networks, rather than intrinsic differences in network organization.

While previous work focused on the Collins et al. (2007) E-MAP, in this article we look at the results of LocalCut on other high-throughput genetic interaction datasets. In particular, we look at two other genetic interaction network datasets for Baker's yeast, an E-MAP for cell signaling genes generated by Fiedler et al. (2009) and the full set of genetic interactions generated using SGA by Costanzo et al. (2010). We also ran LocalCut on the first E-MAP dataset generated for S. pombe, fission yeast (Roguev et al., 2008). We find the structure of the negative weight bipartite subgraphs is very different between the chromosome function network and the signaling network. In particular, very few BPMs are found by LocalCut in the signaling dataset. In both the S. pombe and the full Boone network, a much smaller proportion of the BPMs we find are enriched for the same function. We suspect that this is because GO annotation of function is probably weaker for these gene sets than for the well-studied chromosome cell machinery. Thus, LocalCut's BPMs are more likely to discover novel function in these datasets.

Finally, as remarked above, unlike competing methods, LocalCut constructs its modules and BPMs looking at genetic interactions only; thus the location of physical interaction edges can be used to validate the quality of the BPMs produced by LocalCut (whereas other methods take location of physical interaction edges into account when constructing BPMs). We considered 84,785 known physical interactions between pairs of genes in S. cerevisiae. These interactions are from the BioGRID 3.0.66 release of BioGRID where the experiment type was “physical,” excluding physical interaction hubs, that is, genes that have more than 300 physical interactions with other genes. Of these remaining physical interactions, 2235 intersect with gene pairs in Collins et al. (2007), 1900 with Fiedler et al. (2009), 441 with Boone (restricted), and 1274 with Boone (full) from Costanzo et al. (2010).

Not all of these physical interactions participate in BPMs, and some participate multiple times. However, if LocalCut produces meaningful instances of the BPM motif, we would expect that of the physical interaction edges that do appear, many more would appear within BPM modules than between BPM modules. Table 6 shows that this is indeed the case over all of the S. cerevisiae datasets.

Table 6.

Location of Physical Interaction Edges in LocalCut BPMs as Compared to the Number Expected by Chance

Dataset Within modules Expected within Between modules Expected between
Collins et al. 172 (8.6%) 20 18 (0.9%) 20
Fiedler et al. 13 (12.7%) 1 1 (0.9%) 1
Boone (restricted) 138 (14.4%) 27 10 (1.1%) 26
Boone (full) 147 (3.1%) 41 17 (0.3%) 39
Open in a new tab

We see 172 physical interactions appearing within modules across the entire set of BPMs generated from the Collins dataset, representing 8.6% of all possible interactions occuring within modules. There were 13 physical interactions within modules for Fielder (12.7% of all possible interactions within modules), 138 physical interactions within modules for Boone restricted to the Collins gene set (14.4% of all possible interactions within modules), and 147 physical interactions for BPMs generated from the entire Boone dataset (3.1% of all possible interactions within modules.) We then compare these numbers to how many interactions within each dataset we would expect to be physical by random chance. We calculate this by computing the percentage of all possible interactions that are physical and multiplying it by the number of interactions that appear within some module in the dataset. We find far fewer physical interactions appearing between the two modules in a BPM across all datasets: 18 for Collins (0.9%), 1 for Fiedler (0.9%), 10 (1.1%) for Boone restricted to the set of Collins et al. genes, and 17 (0.3%) for the full Boone dataset. We calculate the expected number of physical interactions between modules analogously. We see that LocalCut creates BPMs with more physical interaction swithin modules than is expected by chance and fewer physical interactions between modules than expected by chance. This gives evidence that LocalCut is finding actual motifs in the Between Pathway Model.

All BPMs produced by LocalCut on all datasets are available in full at http://bcb.cs.tufts.edu/localcut.

4. Discussion

We have introduced LocalCut, a method that uses maximal weighted graph cuts to find modules and BPM motifs in high-throughput genetic interaction data. We have shown that it is competitive in functional enrichment measures to other methods despite not needing to consider physical interaction data as other methods do. We ran LocalCut on different high-throughput genetic interaction datasets involving different sets of S. cerevisiae genes, some generated with different technologies (E-MAP or SGA) and one E-MAP dataset for S. pombe, and compared the resulting networks.

A recent article of Jaimovich et al. (2010) tried to add directionality prediction to methods to determine fault tolerance in genetic interaction networks. More specifically, while BPMs are often motivated by discussing two equally important, alternative, compensatory modules (termed bi-directional compensation), an alternative explanation could be that one module is crucial for functions that compensate for the abnormal cellular state resulting from the loss of the other module (termed unidirectional compensation) (Pan et al., 2006; Boone et al., 2007). The work in Jaimovich et al. (2010) used a novel method of exploring phenotype responses to different conditions to attempt to discriminate between unidirectional and bi-directional compensation; we do not duplicate their methods here. However, looking across the set of BPMs produced by our methods and previous methods on the yeast chromosome function genes as a group, we do find several complexes that appear again and again in modules opposite different sets of genes. Could these particular complexes be agents of such unidirectional compensation, (i.e., possible global mechanisms of fault tolerance of the cell)? There are several intriguing clues that suggest that they might be. For example, two of the most popular complexes that shows up in GO enrichment in multiple BPMs, not just for us, but also in the E-MAP BPM sets and modules of Bandyopadhyay et al. (2008), and Kelley and Kingsford (2010) are the Prefoldin complex, and a subunit of the SWR1 complex consisting of genes ARP6, SWC3, SWC5, SWR1, VPS71, VPS72, and YAF9. The Prefoldin complex is particularly intriguing as a global mechanism of fault-tolerance because it is a chaperone; the effects of an alternative chaperone (HSP90) and its ability to buffer difficult conditions in the cell has been recently described (Taipale et al., 2010). The SWR1 complex is also intriguing because it is involved in chromatin remodeling and silencing near telomeres (Krogan et al., 2003), perhaps another way for the cell to compensate when other modules go awry. For the Prefoldin complex, the genes GIM3, GIM4, GIM5, PAC10, PFD1, and YKE2 appear in multiple BPMs for us, Bandyopadhyay et al., and Kelley-Kingsford; an additional gene BUD27 annotated as being part of the Prefoldin complex appears also in the BPMs generated by Bandyopadhyay et al., but not for LocalCut or Kelley-Kingsford. The Prefoldin complex is completely missing from the BPMs when we run LocalCut on the Boone et al. SGA dataset (Costanzo et al., 2010), but this appears to be a missing/corrupted data problem; in particular, they report no genetic interaction data at all on two of the genes in the Prefoldin complex.

We looked at other complexes of size 3 or greater that appear in their entirety in our and in other BPMs; for example the CAF-1 complex consisting of genes CAC2, MSI1, and RLF2 appears in everyone's set of BPMs. Indeed, it has been suggested that CAF-1 participates in one of multiple redundant modules for chromatin assembly (Adams and Kamakaka, 1999; Green et al., 2005). Opposite the module containing CAF-1, we almost always find parts of the HIR complex, where the double mutants missing both CAF-1 and HIR1 result in a synergistic reduction in silencing at telomeres. Another complex that appears in our BPMs as well as the BPMs of Boone et al. and Kelley-Kingsford (but not Bandyopadhyay et al.) is the MRE11 complex, involved in DNA damage repair (D'Amours and Jackson, 2002).

Finally, we consider an interesting example BPM that LocalCut finds in S. pombe. Figure 1 shows the between-pathway interactions between the two modules; where the stronger the edge, the more negative the interaction. In module 1 (on the left), all 14 genes and 6 of the 7 genes in module 2 are enriched for “response to DNA damage stimulus” (GO:0006974). Some of the strongest negative edges come, in module 1, from the 3 genes HUS1, RAD1, RAD9 that make up the checkpoint clamp complex; a conserved heterotrimeric complex involved in DNA damage response (Carr, 2002) and from CRB2, thought to be related to the important BRCAI breast-cancer gene in humans (Callebaut and Mornon, 1997).

FIG. 1.

FIG. 1.

Open in a new tab

A sample BPM generated by LocalCut from E-MAP data in S. pombe. Black lines represent negative weights (aggravating interactions) in the E-MAP data and red lines represent positive weights (alleviating interactions) in the data. The width of the line directly corresponds to how aggravating or alleviating the interaction is between the pair of genes.

5. Methods

5.1. The graph model

We model the E-MAP and SGA interactions as a weighted complete graph G, where vertices represent genes participating in the E-MAP or SGA, and if i and j are vertices in G, the edge eij is assigned a weight as follows:

  • 1. If the E-MAP or SGA value for the genetic interaction of genes i and j is a negative value (i.e., of the form − z, for some positive 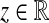Inline graphic), then eij is assigned the weight − z2.

  • 2. If the E-MAP or SGA value for the genetic interaction of genes i and j is a positive value (i.e., of the form z, for some positive 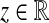Inline graphic), then eij is assigned the weight z2.

  • 3. If the E-MAP or SGA value for the genetic interaction of genes i and j is zero or missing, then eij is assigned the weight 0.

5.2. The algorithm

Consider an arbitrary bipartition (A, B) of the vertex set of G. For such a bipartition, let Same(v) = ∑i evi, for all vertices i that appear in the same subset of the partition as v, and Opposite(v) = ∑j evj, for all vertices j that appear in the opposite partition to v. Call a vertex v unhappy if Same(v) < Opposite(v), otherwise call v happy. Let flip(v) denote the operation that, starting with a bipartition (A, B), creates a bipartition that is identical in all ways, except v switches sides; that is, if v was in A, it is now placed in B, and vice versa.

Consider the following subroutine Weighted-Flip:

foreachvertex udo
 Assign u uniformly at random with equal probability to set A or set B
end
whilethere exists at least one unhappy vertexdo
 Choose v at random from the set of unhappy vertices
 flip (v)
end
output bipartition (A, B)
Open in a new tab

Theorem 5.1

The subroutine terminates, and results in a bipartition (A, B) where all vertices are happy. Furthermore, if E is the set of edges with endpoints either both in A or both in B, and F is the set of edges with one endpoint in each of A and B, then when the subroutine terminates, 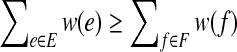Inline graphic.

Proof

It is first shown that there is a minimum positive amount, ε, dependent on the set of edge weights W, by which the weight going across the partition must decrease in any flip of an unhappy vertex. This is because for all partitions of the vertex set into two sets, we can look at the weight going across the partition, and since this is a (albeit large) finite set, there is a positive δ which is the minimum nonzero difference between the weights going across any two of these sets, and ε is clearly bigger than or equal to δ which is greater than 0. As the total sum of the absolute values of all the weights on all the edges is certainly an upper bound on the maximum negative weight that can cross the partition, and any flip decreases the amount of weight crossing the partition by at least a positive amount ε, the algorithm terminates. When the algorithm terminates, if N(v) denotes the edges adjacent to v we have for every vertex v that, 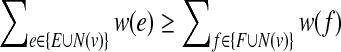Inline graphic; otherwise we could flip v. 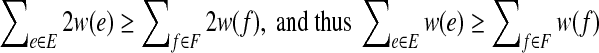Thus summing over each edge twice (once for each endpoint) we get Inline graphic.   ■

We note that this reduces exactly to the procedure Flip in the work of Brady et al. (2009) when the weights are 0 or 1 and the graph is the unweighted graph H instead of the graph G (but all the inequality signs are reversed because all edges are given weight −1 instead of 1). Thus we have replaced a local search for maximal cuts in an unweighted graph with a version for weighted graphs, with both positive and negative edge weights.

While the above theorem proves convergence, it does not show convergence in polynomial time. In fact, the time complexity to convergence time for this algorithm is equivalent to a well-known open problem in combinatorial optimization. In particular, a partition of the vertices of a weighted graph such that all vertices are happy is called a local max cut of the graph. In the special case that the graph is cubic (i.e., all vertices have degree 3), Loebl (1991) showed a local max cut can be found in polynomial time if all weights are nonnegative (using a more complicated algorithm than the one we describe above); a polynomial time algorithm for cubic graphs allowing negative edge weights was later found by Poljak (1995). For general graphs, convergence in the worst case is conjectured to be exponential time, because the problem is PLS-Complete, as shown by Schäffer and Yannakakis (1991).

By squaring the weights in step 1 of our algorithm, however, the absolute values of all nonzero weights greater than 1 are pulled away from 0, while weights with an absolute value less than 1 are pulled closer to zero. In practice, this speeds convergence, because any vertex that changes sides, will result in a larger gain in weight than with many weights close to 0. In practice, we found that this squaring step sufficed to allow us to run on the E-MAP and SGA data and reach convergence in a reasonable amount of time. To generate a bipartition it takes less than 20 minutes per gene. Since this is highly parallelizable to generate the potential modules for an entire dataset is very fast.

Note that the algorithmic procedure Weighted-Flip used to generate the local max cut is randomized, and it will typically generate many different local max cuts. However, if there is a large bipartite subgraph with favorable weights, it will tend to show up as a bipartite subgraph in many if not most of the local cuts, whereas subgraphs that are not naturally weighted bipartite are likely not to be conserved in all the different local cuts. We exploit this to identify such subgraphs and generate candidate BPMs.

Definition 5.2

Given a gene v in G, run Weighted-Flip M times on G. Label each gene with the number of times it appears in the same side as v in one of the M sets (A,B) generated this way, as well as with the number of times it appears on the opposite side from v. If gene w appears consistently (at least C% of the time) in the same partition as v, or consistently in the opposite partition from v, then w is included in the stable bipartite subgraph of v; otherwise w is not included. The stable bipartite subgraph of v in G, then, is the subgraph induced by all included vertices, where v along with the vertices appearing consistently on the same side as v form one partition, and the rest of the included vertices form the other.

For each v, we output v's stable bipartite subgraph as one of our putative between-pathway models. Note, however, that different runs of the Weighted-Flip procedure may generate different sets of results because of the random choices in the initial partition configuration and the choice of the unhappy node that needs to be flipped at each iteration step. However, we set M and C large enough so that the set of BPMs reported will be fairly consistent, regardless of the random choices made by our algorithm. In particular, we determined empirically that setting M = 250 and C = 0.90 gave relatively stable subgraphs of genes. We varied the values of C from 0.70 to 0.95. Not surprisingly, we found that the greater values produced more consistent results. We chose 0.90 to try to maximize stability without deleting potential BPMs. We chose M high enough to ensure consistent results.

Using our algorithm, different genes v may generate the same or highly similar putative BPMs. Thus, we then prune our set in order to report a collection of non-redundant BPMs as follows.

5.3. Removing BPM redundancies

As described in the previous section, each gene's stable bipartite subgraph becomes a putative BPM. If the BPM generated is a true instance of compensatory modules, we would expect our algorithm to produce the same or similar BPM when run on another gene in the BPM. Because of the natural noise in the dataset, these BPMs are not exact matches. To fairly compare our results with alternate studies, we must remove the redundant, highly-overlapping BPMs from our set. We do this as follows. We first sort all the BPMs created by LocalCut according to their interaction weight I, where I is calculated by summing the edge weights of all genetic interactions within the two modules of the BPM, minus the sum of the weights of all interactions appearing between the two modules of the BPM, all divided by the number of genes in the entire BPM.

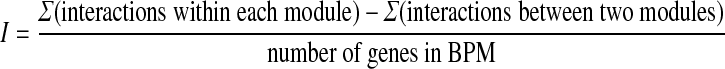graphic file with name M6.gif

Starting with the BPM with the largest interaction weight, we add a BPM to our final output set if its Jaccard index is less than the fixed threshold (set at 0.66 for these results) from every previously added BPM.

Acknowledgments

Thanks go to Tom Zazlabsky for a useful discussion on the theory of signed graphs, to the BCB group at Tufts for helpful feedback, and to David Kelley and Carl Kingsford for access to their BPM data and discussions about its interpretation. This work was supported in part by the NIH (grant R01-GM080330 to L.C.).

Disclosure Statement

No competing financial interests exist.

References

  1. Adams C. Kamakaka R. Chromatin assembly: biochemical identities and genetic redundancy. Curr. Opin. Genet. Dev. 1999;9:185–190. doi: 10.1016/S0959-437X(99)80028-8. [DOI] [PubMed] [Google Scholar]
  2. Bandyopadhyay S. Kelley R. Krogan N. Functional maps of protein complexes from quantitative genetic interaction data. PLoS Comput. Biol. 2008;4:e1000065. doi: 10.1371/journal.pcbi.1000065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Berriz G. King O. Bryant B., et al. Characterizing gene sets with funcassociate. Bioinformatics. 2003;19:2502–2504. doi: 10.1093/bioinformatics/btg363. [DOI] [PubMed] [Google Scholar]
  4. Boone C. Bussey H. Andrews B.J. Exploring genetic interactions and networks with yeast. Nat. Rev. Genet. 2007;8:437–449. doi: 10.1038/nrg2085. [DOI] [PubMed] [Google Scholar]
  5. Brady A. Maxwell K. Daniels N., et al. Fault tolerance in protein interaction networks: stable bipartite subgraphs and redundant pathways. PLoS ONE. 2009;4:e5364. doi: 10.1371/journal.pone.0005364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Callebaut I. Mornon J.-P. From BRCA1 to RAP1: a widespread BRCT module closely associated with DNA repair. FEBS Lett. 1997;400:25–30. doi: 10.1016/s0014-5793(96)01312-9. [DOI] [PubMed] [Google Scholar]
  7. Carr A.M. DNA structure dependent checkpoints as regulators of DNA repair. DNA Repair. 2002;1:983–994. doi: 10.1016/s1568-7864(02)00165-9. [DOI] [PubMed] [Google Scholar]
  8. Collins S. Miller K. Maas N., et al. Functional dissection of protein complexes involved in yeast chromosome biology using a genetic interaction map. Nature. 2007;446:806–810. doi: 10.1038/nature05649. [DOI] [PubMed] [Google Scholar]
  9. Costanzo M. Baryshnikova A. Bellay J., et al. The genetic landscape of a cell. Science. 2010;327:425–431. doi: 10.1126/science.1180823. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. D'Amours D. Jackson S. The MRE11 complex: at the crossroads of DNA repair and checkpoint signalling. Nat. Rev. Mol. Cell Biol. 2002;3:317–327. doi: 10.1038/nrm805. [DOI] [PubMed] [Google Scholar]
  11. Fiedler D. Braberg H. Mehta M., et al. Functional organization of the S. cerevisiae phosphorylation network. Cell. 2009;136:952–963. doi: 10.1016/j.cell.2008.12.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Green E. Antcsak A. Bailey A., et al. Replication-independent histone deposition by the HIR complex and asf1. Curr. Biol. 2005;15:2044–2049. doi: 10.1016/j.cub.2005.10.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hescott B.J. Leiserson M.D.M. Slonim D.K., et al. Evaluating between-pathway models with expression data. J. Comput. Biol. 2010;17:477–487. doi: 10.1089/cmb.2009.0178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Jaccard P. Nouvelles recherches sur la distribution florale. Bull. Soc. Vaudoise Sci. Nat. 1908;44:223–270. [Google Scholar]
  15. Jaimovich A. Rinott R. Schuldiner M., et al. Modularity and directionality in genetic interaction maps. Bioinformatics. 2010;26:i228–i236. doi: 10.1093/bioinformatics/btq197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kelley D. Kingsford C. Extracting between-pathway models from E-MAP interactions using expected graph compression. J. Comput. Biol. 2011;18:379–390. doi: 10.1089/cmb.2010.0268. [DOI] [PubMed] [Google Scholar]
  17. Kelley R. Ideker T. Systematic interpretation of genetic interactions using protein networks. Nat. Biotechnol. 2005;23:561–566. doi: 10.1038/nbt1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Krogan N. Keogh M.-C. Datta N., et al. A Snf2 family ATPase complex required for the recruitment of the histone H2A variant Htz1. Mol. Cell. 2003;12:1565–1576. doi: 10.1016/s1097-2765(03)00497-0. [DOI] [PubMed] [Google Scholar]
  19. Loebl M. Efficient maximal cubic graph cuts. Proc. 18th Int. Colloq. Autom. Lang. Programming (ICALP) 1991;510:351–362. [Google Scholar]
  20. Ma X. Tarone A.M. Li W. Mapping genetically compensatory pathways from synthetic lethal interactions in yeast. PLoS One. 2008;3:e1922. doi: 10.1371/journal.pone.0001922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Pan X. Ye P. Tuan D., et al. A DNA integrity network in the yeast Saccharomyces cerevisiae. Cell. 2006;124:1069–1081. doi: 10.1016/j.cell.2005.12.036. [DOI] [PubMed] [Google Scholar]
  22. Poljak S. Integer linear programs and local search for max-cut. SIAM J. Comput. 1995;24:822–839. [Google Scholar]
  23. Real R. Vargas J. The probabilistic basis of Jaccard's index of similarity. Syst. Biol. 1996;45:380–385. [Google Scholar]
  24. Roguev A. Bandyopadhyay S. Zofall M., et al. Conservation and rewiring of functional modules revealed by an epistasis map in fission yeast. Science. 2008;322:405–410. doi: 10.1126/science.1162609. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Schäffer A. Yannakakis M. Simple local search problems that are hard to solve. SIAM J. Comput. 1991;20:56–87. [Google Scholar]
  26. Schuldiner M. Collins S.R. Thompson N.J., et al. Exploration of the function and organization of the yeast early secretory pathway through an epistatic miniarray profile. Cell. 2005;123:507–519. doi: 10.1016/j.cell.2005.08.031. [DOI] [PubMed] [Google Scholar]
  27. Stark C. Breitkreutz B.-J. Reguly T., et al. BioGRID: a general repository for interaction datasets. Nucleic Acids Res. 2005;34:D535–D539. doi: 10.1093/nar/gkj109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Taipale M. Jarosz D. Lindquist S. HSP90 at the hub of protein homeostasis: emerging mechanistic insights. Nat. Rev. Mol. Cell Biol. 2010;11:515–528. doi: 10.1038/nrm2918. [DOI] [PubMed] [Google Scholar]
  29. Tong A.H.Y. Lesage G. Bader G.D., et al. Global Mapping of the Yeast Genetic Interaction Network. Science. 2004;303:808–813. doi: 10.1126/science.1091317. [DOI] [PubMed] [Google Scholar]
  30. Ulitsky I. Shamir R. Pathway redundancy and protein essentiality revealed in the Saccharomyces cerevisiae interaction networks. Mol. Syst. Biol. 2007;3:104. doi: 10.1038/msb4100144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ulitsky I. Shlomi T. Kupiec M., et al. From E-MAPs to module maps: dissecting quantitative genetic interactions using physical interactions. Mol. Syst. Biol. 2008;4:209. doi: 10.1038/msb.2008.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ulitsky I. Krogan N. Shamir R. Towards accurate imputation of quantitative genetic interactions. Genome Biol. 2009;10:R140. doi: 10.1186/gb-2009-10-12-r140. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES