Abstract
Background:
In spite of extensive research conducted to study how human brain works, little is known about a special function of the brain that stores and manipulates information—the working memory—and how noise influences this special ability. In this study, Functional magnetic resonance imaging (fMRI) was used to investigate brain responses to arithmetic problems solved in noisy and quiet backgrounds.
Methods:
Eighteen healthy young males performed simple arithmetic operations of addition and subtraction with in-quiet and in-noise backgrounds. The MATLAB-based Statistical Parametric Mapping (SPM8) was implemented on the fMRI datasets to generate and analyse the activated brain regions.
Results:
Group results showed that addition and subtraction operations evoked extended activation in the left inferior parietal lobe, left precentral gyrus, left superior parietal lobe, left supramarginal gyrus, and left middle temporal gyrus. This supported the hypothesis that the human brain relatively activates its left hemisphere more compared with the right hemisphere when solving arithmetic problems. The insula, middle cingulate cortex, and middle frontal gyrus, however, showed more extended right hemispheric activation, potentially due to the involvement of attention, executive processes, and working memory. For addition operations, there was extensive left hemispheric activation in the superior temporal gyrus, inferior frontal gyrus, and thalamus. In contrast, subtraction tasks evoked a greater activation of similar brain structures in the right hemisphere. For both addition and subtraction operations, the total number of activated voxels was higher for in-noise than in-quiet conditions.
Conclusion:
These findings suggest that when arithmetic operations were delivered auditorily, the auditory, attention, and working memory functions were required to accomplish the executive processing of the mathematical calculation. The respective brain activation patterns appear to be modulated by the noisy background condition.
Keywords: brain mapping, fMRI, functional laterality, mathematics, memory and cognition, noise
Introduction
Arithmetic is a branch of mathematics involving problem solving and processing of numbers, such as in addition and subtraction (1). Problem solving in mathematics incorporates various cognitive processes and strategies. Three mental operations (i.e., information storage, data organisation, and executive control) are necessary in solving arithmetic problems (2).
Different brain regions are responsible for the different functions executed during arithmetic problem solving. Evidence from brain-imaging studies indicates that parietal lobe areas are central in calculating and processing of numbers (1,3), while frontal lobe areas are involved in recalling numerical knowledge and working memory (3,4).
Working memory is a comprehensive function of the brain normally used in processing and storing information temporarily and is very important for many cognitive actions (5). Several functional imaging studies (6,7) found that the frontal lobe areas are activated in tasks involving executive function and working memory. It has been suggested that frontal lobe areas such as inferior frontal gyrus (IFG), superior frontal gyrus (SFG), and medial frontal gyrus support working memory demand during arithmetic operations (6–10). A previous study on the laterality of brain areas associated with arithmetic calculation (11) revealed greater activation in the right hemisphere IFG than in the left hemisphere. However, different modes of task presentation produce different hemispheric dominance in the frontal region. For example, visually presented tasks tend to produce bilateral frontal region activation (12), whereas tasks presented auditorily trigger a relatively larger activation in the right frontal regions (13). It has also been suggested that the laterality index (LI), which measures the hemispheric dominance of IFG, increases with task difficulty (11). Thus, a complex task is expected to produce a greater number of activated voxels in the left compared with the right hemisphere. Gruber et al. (14) and Fehr et al. (12,13) demonstrated that bilateral frontal regions were differently involved during simple and complex arithmetic tasks in different operations (i.e., addition, subtraction, multiplication, and division), from which complex arithmetic tasks required working memory involvement, whereas simple tasks only required arithmetic facts retrieval (12). In addition to frontal lobe areas, parietal lobe areas are also important in mental calculation, specifically for representing and manipulating quantitative information (4). Number processing and calculation have been shown to activate the inferior parietal lobe regions, including intraparietal sulcus (IPS), angular gyrus (AG), and supramarginal gyrus (SMG) (4). These areas are involved in addition, subtraction, and multiplication tasks (4). The LI of the inferior parietal lobule decreases with increasing task difficulty (11). It is also important to note that the inferior parietal cortex is the region specifically activated in response to increasing arithmetic complexity (10,11). In relation to that, SMG has also been identified as the region that deals with calculation difficulty (4,10), such as listening to spoken words in a noisy background.
However, knowledge of how the human brain processes arithmetic operations in different environments is still lacking, as verbal communication often occurs in the presence of an interfering background, such as noise. The superior temporal gyrus (STG) plays a central role in the perception of speech (15–19) and non-speech stimuli (20). Listening to speech in noisy conditions resulted in the engagement of attention and cognitive networks (18). Other regions involved in attention are the cingulate gyrus, medial frontal gyrus, basal ganglia, and thalamus (19).
In the present study, brain activations involved in arithmetic processing (addition and subtraction) in the human brain for in-quiet and in-noise were explored using a functional magnetic resonance imaging (fMRI) technique and statistical parametric mapping (SPM). The objectives of the study were (1) to identify the areas of activation, and (2) to determine the LI of the areas activated when the participants performed arithmetic working memory tasks for in-quiet and in-noise backgrounds. To achieve a quiet condition, a silent fMRI imaging paradigm (21) with a long silent interval was applied during stimulus presentation; this avoided the effects of scanner sound on the functional images (22).
Subjects and Methods
This study was approved by the Universiti Kebangsaan Malaysia (UKM) Ethics Committee (IEC) (NN-049-2009), and informed consent was obtained from all study subjects prior to testing.
Participants
Eighteen native, Malay-speaking, male adults with an average age of 23.2 (SD 2.5) years (range of 20–28 years) participated in the present study. All participants were screened by means of the Sijil Pelajaran Malaysia (Malaysian Certificate of Education) to obtain a group of participants able to perform simple mathematical operations; only those who passed their mathematics papers were enrolled in this study. Participants’ handedness was determined using the Edinburgh Handedness Inventory (23).
fMRI data acquisition
The fMRI scans were conducted in the Department of Radiology, UKM Medical Centre. Functional images were acquired using a 1.5-T magnetic resonance imaging (MRI) system (Siemens Avanto, Erlangen, Germany) equipped with blood oxygenation level-dependent imaging protocol, echo-planar imaging capabilities, and radiofrequency head coil used for signal transmission and reception. Gradient-echo echo-planar imaging pulse sequence with the following parameters was used: repetition time (TR) = 16 000 ms, acquisition time (TA) = 5000 ms (interscan interval = 16 000 ms − 5000 ms = 11 000 ms), echo time (TE) = 50 ms, field of view (FOV) = 192 × 192 mm, flip angle = 90°, matrix size = 128 × 128, and slice thickness = 3 mm. In addition, high resolution anatomical images of the entire brain were obtained using a T1-weighted multiplanar reconstruction (MPR) spin-echo pulse sequence with the following parameters: TR = 1620 ms, FOV = 250 × 250 mm, flip angle = 90°, matrix size = 128 × 128, and slice thickness = 1 mm.
Tasks
The experimental tasks consisted of simple arithmetic calculations involving addition and subtraction, presented auditorily for in-quiet and in-noise backgrounds. For in-noise conditions, the 83-dB stimuli were embedded in 80-dB white noise. Prior to the scanning, all participants were given detailed instructions on how to respond to the stimuli. The participants were instructed to listen to a series of simple arithmetic operations (e.g., 1 + 2 + 3 + 4) presented binaurally via headphones (transmission of sound through air) and were required to perform the calculations. The participants were also instructed not to move their head during the scan as head movements can cause signal intensity changes over time from any one voxel and present a serious confound in fMRI studies. To minimise head movement, immobilising devices were used together with the head coil. A training session was carried out prior to the scanning session, to ensure that participants understood the task.
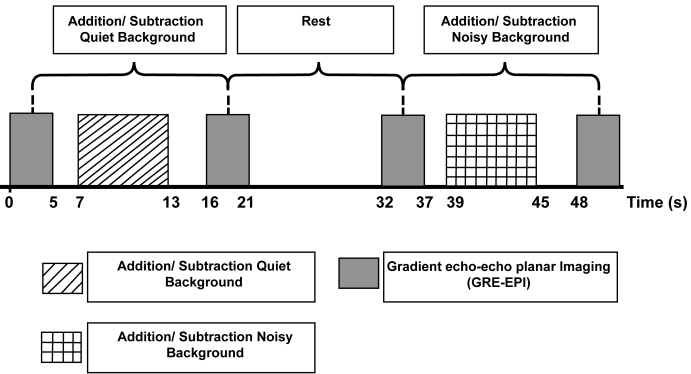
A silent fMRI-imaging paradigm was used to eliminate the effects of the scanner sound on the MRI images. The stimuli were presented during the silent gaps between volume acquisitions so that they did not overlap with the sound arising from the scanner. This paradigm is commonly used in auditory studies using fMRI (21,24). Each participant was subjected to 2 scanning sessions, which were exclusively carried out for addition and subtraction operations. Each session consisted of 2 different conditions, which were scanning in-quiet and in-noise. Thus, the 4 test conditions were addition in-quiet, addition in-noise, subtraction in-quiet, and subtraction in-noise. A schematic representation of the paradigm used in this study is shown in Figure 1. In the first scan, single-digit addition problems were used as stimuli (e.g., 1 + 2 + 3 + 4). Each set of digits that consisted of numbers 1–9 were randomly presented auditorily, without visual presentation, to the participants. In the second scan, single-digit subtractions were used as stimuli (e.g., 9 – 4 – 3 – 1). In this task, the minuend was always larger than the subtrahend, so that the answer to the problem was always positive. The participants were required to provide an answer verbally to each addition and subtraction task in order to evoke responses in the respective brain areas, and to ensure that the participants remained alert and focused throughout the scanning session.
Figure 1:
The study paradigm
Each functional scan consisted of 120 series of trials (or measurements); 30 trials each for both in-quiet conditions (i.e., addition in-quiet and subtraction in-quiet), 30 trials each for both in-noise conditions (i.e., addition in-noise and subtraction in-noise), and 60 trials for baseline (stimulus not given). A long (11 s) inter-measurement interval was used to allow for the haemodynamic response to decline after each given stimulus. The acquisition time was 5 s, with each functional measurement producing 35 axial slices in the 5-s duration (1 image slice per 143 ms). The measurement started with the active state. The imaging time for each session was 32 minutes, which produced 120 × 35 = 4200 images in total.
Post-processing
All the functional (T2*-weighted) and structural (T1-weighted) images were processed in the Functional Image Processing Laboratory, Diagnostic Imaging & Radiotherapy Programme, Faculty of Allied Health Sciences, UKM, Kuala Lumpur. Image analyses were performed using a personal computer using the software MATLAB 7.6 R2008a (Mathworks Inc., Natick, MA, USA) and Statistical Parametric Mapping (SPM8) (Functional Imaging Laboratory, Wellcome Department of Imaging Neuroscience, Institute of Neurology, University College of London). The raw data in DICOM (.dcm) format were transformed into Analyze (.hdr, .img) format using SPM8. Functional images for each measurement were realigned using the 6-parameter affine transformation in translational (x, y, and z) and rotational (pitch, roll, and yaw) directions to reduce artefacts from subject movement and to make within- and between-subject comparisons meaningful (25). After realignment, a mean image of the series was used to estimate some warping parameters that mapped it onto a template that conformed to a standard anatomical space, i.e., EPI template (26) provided by the Montreal Neurological Institute (MNI). The normalisation procedure used a 12-parameter affine transformation, where the parameters constituted a spatial transformation matrix. The images were then smoothed using a 6-mm full-width-at-half-maximum Gaussian kernel. The activated voxels were identified by the general linear model approach by estimating the parameters of the model and deriving the appropriate test statistic (t statistic) for every voxel. Statistical inferences were finally obtained on the basis of the general linear model and Gaussian random field theory (27).
Group analyses
The participants’ activation maps were defined using the WFU Pick Atlas software (28). For group random effects (RFX) analysis, significant statistical inference was made at α = 0.001, uncorrected for multiple comparisons. The laterality of the functional areas was evaluated using LI for each participant for all regions of interest (ROIs). Here, laterality is defined as the hemispheric dominance or preference between left and right hemispheres of functional activation (29). The chosen ROIs for the analysis of LI were based on the activations obtained from single subject analysis, group analysis, and from those reported in previous studies (29,30). The LI for any one ROI was calculated using the formula LI = (VL – VR) / (VL + VR), in which VL is the number of the activated voxels in the left hemisphere, and VR is the number of the activated voxels in the right hemisphere (11). The LI values ranged from −1 to 1, with the range −1 to 0 indicating right-hemisphere dominance and range 0 to 1, left-hemisphere dominance.
Analysis of the main effects and interaction
The two-way repeated measures ANOVA was used to investigate the interaction between tasks (addition and subtraction) and conditions (in-quiet and in-noise) and to make inferences concerning the effects of tasks and conditions. The level of significance was set at uncorrected α = 0.05.
Results
Brain activation
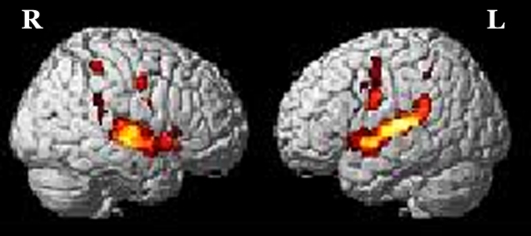
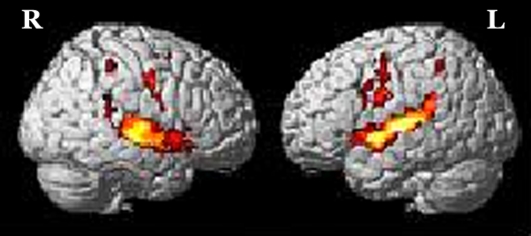
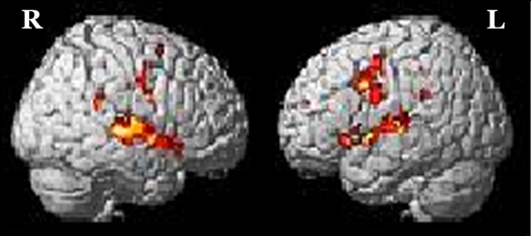
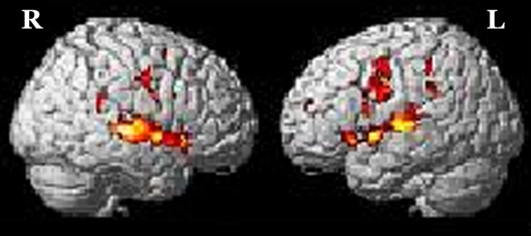
The brain activation obtained from RFX for (a) addition in-quiet, (b) addition in-noise, (c) subtraction in-quiet, and (d) subtraction in-noise, overlaid onto a 3-dimensional MNI-template for brain structure is shown in Figure 1. The corresponding activated regions, together with their number of activated voxels (NOV) at α = 0.001, coordinates of maximum intensity, and the respective t values were tabulated in Tables 1 and 2 . All the addition and subtraction operations in-quiet and in-noise evoked bilateral activation in Heschl’s gyrus (HG), STG, IFG, SMG, precentral gyrus (PCG), superior parietal lobe (SPL), insula lobe, thalamus, and middle temporal gyrus (MTG). However, for MFG and middle cingulate cortex (MCC), there was brain activation only in the right hemisphere in all test conditions. For the inferior parietal lobe (IPL), there was bilateral activation during addition in-quiet and in-noise, whereas during subtraction in-quiet and in-noise, only the left IPL was activated. The total number of activated voxels summed for all ROIs (α = 0.001) were 5516 during addition in-quiet and 5731 during addition in-noise, while for subtraction in-quiet and in-noise, there were 2025 and 3162 activated voxels, respectively (Tables 1 and 2). A greater activation was observed in-noise compared with in-quiet for both addition and subtraction operations. The addition operation activated a relatively larger area of the whole brain than subtraction for both in-quiet and in-noise conditions.
Table 1:
Number of activated voxels (NOV), coordinates of maximum intensity (x,y,z), and the t value obtained from brain activation of group random effects analysis shown in Figures 2 (a) and (b) for addition task
| Condition | AIQ | AIN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | Hemisphere | NOV | x, y, z | t | NOV | x, y, z | t | ||||
| HG | L | 154 | −38, | −28, | 10 | 6.66 | 149 | −42, | −24, | 10 | 7.46 |
| R | 119 | 40, | −26, | 8 | 5.83 | 146 | 48, | −20, | 8 | 7.47 | |
| STG | L | 1608 | −46, | −20, | 4 | 11.69 | 1562 | −52, | −4, | 0 | 10.84 |
| R | 1236 | 46, | −14, | 4 | 7.68 | 1326 | 58, | −24, | −4 | 8.32 | |
| IFG | L | 15 | −48, | 16, | −6 | 5.83 | 23 | −48, | 16, | −6 | 6.09 |
| R | 34 | 52, | 18, | −8 | 7.55 | 40 | 52, | 18, | −8 | 6.81 | |
| IPL | L | 27 | −42, | −48, | 52 | 3.92 | 51 | −42, | −46, | 48 | 4.42 |
| R | 76 | 52, | −40, | 52 | 6.12 | 42 | 50, | −38, | 50 | 5.49 | |
| SG | L | 138 | −64, | −38, | 24 | 4.95 | 127 | −52, | −42, | 28 | 5.17 |
| R | 27 | 68, | −40, | 26 | 5.03 | 10 | 68, | −40, | 24 | 3.19 | |
| Insula | L | 213 | −46, | 8, | −6 | 6.66 | 299 | −46, | 6, | −4 | 7.11 |
| R | 287 | 46, | 2, | −8 | 5.74 | 294 | 50, | 12, | −6 | 6.73 | |
| Thalamus | L | 123 | −2, | −24, | 8 | 7.10 | 121 | −2, | −24, | 8 | 7.44 |
| R | 170 | 8, | −24, | 10 | 7.96 | 144 | 4, | −22, | 8 | 8.22 | |
| MCC | L | - | - | - | - | - | - | ||||
| R | 148 | 6, | −22, | 32 | 7.12 | 71 | 4, | 22, | 32 | ||
| PG | L | 269 | −52, | −4, | 24 | 8.29 | 308 | −48, | −8, | 46 | 7.56 |
| R | 130 | 50, | −6, | 40 | 7.74 | 160 | 50, | −6, | 38 | 7.88 | |
| MTG | L | 432 | −60, | −30, | 6 | 7.03 | 445 | −56, | −20, | 0 | 8.68 |
| R | 298 | 60, | −24, | −4 | 8.59 | 399 | 60, | −24, | −4 | 8.11 | |
| MFG | L | - | - | - | - | - | - | ||||
| R | 2 | 32, | 6, | 60 | 3.71 | 10 | 32, | 6, | 58 | 4.03 | |
| SPL | L | - | - | 4 | −28, | −66, | 50 | 4.15 | |||
| R | 10 | 54, | −38, | 58 | 4.20 | - | - | - | |||
Abbreviations: AIQ = addition in-quiet, AIN = addition in-noise, HG = Heschl’s gyrus, STG = superior temporal gyrus, IFG = inferior frontal gyrus, IPL = inferior parietal lobe, SG = supramarginal gyrus, MCC = middle cingulate cortex, PG = precentral gyrus, MTG = middle temporal gyrus, MFG = middle frontal gyrus, SPL = superior parietal lobe
Table 2:
Number of activated voxels (NOV), coordinates of maximum intensity (x,y,z), and the t value obtained from brain activation from group random effects analysis shown in Figure 2 (c) and (d) for subtraction task
| Condition | SIQ | SIN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | Hemisphere | NOV | x, y, z | t | NOV | x, y, z | t | ||||
| HG | L | 30 | −46, | −14, | 4 | 4.24 | 84 | −40, | −24, | 6 | 5.56 |
| R | 27 | 52, | −16, | 10 | 3.97 | 32 | 48, | −12, | 6 | 4.42 | |
| STG | L | 372 | −52, | 0, | 3 | 6.47 | 602 | −40, | −28, | 6 | 8.38 |
| R | 602 | 60, | −26, | 2 | 5.91 | 795 | 64, | −20, | 0 | 6.66 | |
| IFG | L | 33 | −38, | 22, | −4 | 6.14 | 39 | −38, | 22, | −4 | 6.22 |
| R | 34 | 52, | 18, | −6 | 5.03 | 52 | 52, | 18, | −6 | 5.43 | |
| IPL | L | 9 | −44, | −38, | 44 | 4.04 | 38 | −44, | −36, | 46 | 4.93 |
| R | - | - | - | - | 38, | −44, | 46 | 3.42 | |||
| SG | L | 37 | −50, | −40, | 28 | 4.27 | 72 | −62, | −24, | 16 | 4.85 |
| R | 24 | 62, | −42, | 24 | 4.79 | 21 | 64, | −42, | 24 | 4.38 | |
| Insula | L | 53 | −36, | 22, | −4 | 5.64 | 146 | −38, | 20, | −4 | 6.21 |
| R | 73 | 48, | 4, | −3 | 7.18 | 163 | 48, | 8, | −8 | 8.55 | |
| Thalamus | L | 90 | −4, | −18, | 8 | 5.70 | 364 | −6, | −22, | 8 | 9.41 |
| R | 91 | 6, | −22, | 8 | 4.04 | 3 | 6, | −20, | 6 | 9.06 | |
| MCC | L | - | - | - | - | - | - | ||||
| R | 15 | 6, | 24, | 32 | 3.78 | 103 | 4, | 12, | 44 | 6.50 | |
| PG | L | 332 | −50, | −6, | 22 | 6.90 | 307 | −54, | −4, | 24 | 6.82 |
| R | 116 | 48, | −6, | 28 | 6.30 | 117 | 44, | −10, | 36 | 8.43 | |
| MTG | L | 11 | −58, | −22, | 0 | 4.12 | 56 | −60, | −26, | 2 | 4.63 |
| R | 49 | 58, | −28, | 0 | 5.60 | 135 | 58, | −28, | 0 | 5.86 | |
| MFG | L | 12 | −30, | 50, | 20 | 4.41 | 19 | −32, | 50, | 20 | 4.30 |
| R | 15 | 32, | 6, | 60 | 5.11 | 14 | 36, | 6, | 56 | 4.53 | |
| SPL | L | - | - | - | - | - | - | ||||
| R | - | - | - | - | - | - | |||||
Abbreviations: SIQ = substraction in-quiet, SIN = substraction in-noise, HG = Heschl’s gyrus, STG = superior temporal gyrus, IFG = inferior frontal gyrus, IPL = inferior parietal lobe, SG = supramarginal gyrus, MCC = middle cingulate cortex, PG = precentral gyrus, MTG = middle temporal gyrus, MFG = middle frontal gyrus, SPL = superior parietal lobe.
Laterality
The laterality of the brain regions in relation to addition and subtraction operations was evaluated by LI as previously described (Table 3). Addition and subtraction produced asymmetrical activation in the IPL, PCG, and SPL that favoured the left hemisphere, in both in-quiet and in-noise conditions (i.e., LI > 0). In contrast, the areas of activation for the insula and MCC were more extended in the right hemisphere for all addition and subtraction in-quiet and in-noise (i.e., LI < 0). The STG, IFG, and thalamus indicated a left lateralisation with a small increase in activation for addition (i.e., LI > 0), while subtraction produced reversed lateralization (i.e., LI < 0). For HG, addition and subtraction evoked the right hemisphere region more extensively, except for addition in-quiet, which showed left-hemispheric preference. For MFG, subtraction in-quiet produced a left-hemispheric preference, whereas other tasks increased right-hemisphere activation. For MTG, there was extensive activation in the left hemisphere for all tasks except for subtraction in-noise, which had a right-hemispheric preference. Generally, there was relatively larger activation in the left hemisphere for both arithmetic tasks either for in-quiet or in-noise conditions.
Table 3:
The laterality index for all regions computed from all different tasks and conditions averaged over 18 participants
| Region | AIQ | AIN | SIQ | SIN |
|---|---|---|---|---|
| HG | 0.05 (0.66) | −0.06 (0.65) | −0.01 (0.55) | −0.07 (0.59) |
| STG | 0.13 (0.31) | 0.01 (0.38) | −0.05 (0.38) | −0.10 (0.35) |
| IFG | 0.08 (0.50) | 0.10 (0.50) | −0.08 (0.52) | −0.13 (0.60) |
| IPL | 0.50 (0.52) | 0.30 (0.66) | 0.33 (0.56) | 0.33 (0.49) |
| SG | 0.27 (0.61) | 0.18 (0.61) | −0.09 (0.55) | 0.16 (0.39) |
| Insula | −0.29 (0.40) | −0.19 (0.36) | −0.16 (0.55) | −0.37 (0.49) |
| Thalamus | 0.09 (0.37) | 0.09 (0.39) | −0.18 (0.52) | −0.10 (0.53) |
| MCC | −0.19 (0.52) | −0.26 (0.67) | −0.17 (0.49) | −0.29 (0.43) |
| PG | 0.19 (0.57) | 0.28 (0.45) | 0.26 (0.38) | 0.18 (0.40) |
| MTG | 0.14 (0.43) | 0.10 (0.40) | 0.01 (0.48) | −0.09 (0.43) |
| MFG | − 0.16 (0.45) | −0.25 (0.49) | −0.03 (0.57) | 0.00 (0.61) |
| SPL | 0.08 (0.73) | 0.03 (0.68) | 0.22 (0.59) | 0.05 (0.70) |
Data are expressed in mean (SD).
Abbreviations: AIQ = addition in-quiet, AIN = addition in-noise, SIQ = substraction in-quiet, SIN = substraction in-noise, HG = Heschl’s gyrus, STG = superior temporal gyrus, IFG = inferior frontal gyrus, IPL = inferior parietal lobe, SG = supramarginal gyrus, MCC = middle cingulate cortex, PG = precentral gyrus, MTG = middle temporal gyrus, MFG = middle frontal gyrus, SPL = superior parietal lobe.
Main effects and interaction
The two-way repeated measures ANOVA revealed a significant main effect of arithmetic operations (addition versus subtraction) on brain responses (uncorrected P < 0.05) for bilateral STG, IFG, IPL, MCC, insula lobe, thalamus, PCG, MTG, SFG, and SPL, including left HG and right SMG (Table 4). The comparison between the addition and subtraction operations (addition in-quiet > subtraction in-quiet, and addition in-noise > subtraction in-noise) revealed that the left HG, left STG, left insula lobe, right MCC, bilateral MTG and bilateral MFG were significantly activated according to t values (Table 5). The reverse contrast (subtraction in-quiet > addition in-quiet, and subtraction in-noise > addition in-noise) showed that bilateral hemispheres IPL, SMG, PCG, SPL, and SFG were activated but with a higher number of activated voxels for subtraction compared with addition (Table 6).
Table 4:
Activated brain region during the main effects of arithmetic stimulus type at uncorrected P < 0.05
| Region | Hemisphere | NOV | x, y, z | Fvalue | Pvalue | ||
|---|---|---|---|---|---|---|---|
| HG | L | 35 | −40, | −20, | 2 | 6.90 | 0.005 |
| STG | L | 487 | −58, | −36, | 12 | 15.56 | 0.000 |
| R | 25 | 50, | −10, | −6 | 4.49 | 0.008 | |
| IFG | L | 14 | −28, | 24, | −24 | 9.15 | 0.003 |
| R | 7 | 52, | 26, | −8 | 4.84 | 0.031 | |
| IPL | L | 80 | −44, | −30, | 44 | 9.25 | 0.003 |
| R | 184 | 30, | −44, | 50 | 9.45 | 0.003 | |
| SG | R | 92 | 60, | −16, | 28 | 9.09 | 0.004 |
| Insula | L | 126 | −34, | 18, | 14 | 12.38 | 0.001 |
| R | 10 | 42, | −4, | −8 | 4.52 | 0.036 | |
| Thalamus | L | 23 | −12, | −32, | 0 | 7.63 | 0.007 |
| MCC | L | 27 | −8, | 2, | 40 | 5.68 | 0.020 |
| R | 73 | 0, | 18, | 32 | 7.94 | 0.006 | |
| PG | L | 74 | −20, | −24, | 70 | 11.98 | 0.001 |
| R | 79 | 50, | −14, | 54 | 9.18 | 0.003 | |
| MTG | L | 404 | −58, | −26, | −6 | 11.37 | 0.001 |
| R | 217 | 48, | −76, | 20 | 16.77 | 0.000 | |
| MFG | L | 220 | −24, | 0, | 48 | 17.38 | 0.000 |
| R | 184 | 34, | 54, | 0 | 11.07 | 0.001 | |
| SFG | L | 71 | −22, | 0, | 48 | 18.05 | 0.000 |
| R | 59 | 22, | 0, | 62 | 9.71 | 0.003 | |
| SPL | L | 116 | −16, | −58, | 50 | 6.70 | 0.012 |
| R | 264 | 24, | −66, | 48 | 14.12 | 0.000 | |
Abbreviations: NOV = number of activated voxels, HG = Heschl’s gyrus, STG = superior temporal gyrus, IFG = inferior frontal gyrus, IPL = inferior parietal lobe, SG = supramarginal gyrus, MCC = middle cingulate cortex, PG = precentral gyrus, MTG = middle temporal gyrus, MFG = middle frontal gyrus, SFG = superior frontal gyrus, SPL = superior parietal lobe.
Table 5:
Activated brain regions during addition greater than subtraction in the quiet and noise conditions at uncorrected P < 0.05
| Region | Hemisphere | AIQ > SIQ | AIN > SIN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NOV | x, y, z | t | NOV | x, y, z | t | ||||||
| HG | L | 24 | −40, | −20, | 4 | 1.81 | 5 | −40, | −20, | 2 | 1.96 |
| STG | L | 322 | −58, | −36, | 12 | 3.12 | 251 | −46, | −14, | −10 | 2.64 |
| R | 9 | 50, | −24, | 12 | 1.77 | - | - | - | |||
| MTG | L | 225 | −40, | 6, | −28 | 2.88 | 253 | −58, | −24, | −6 | 2.72 |
| R | 58 | 56, | −14, | −18 | 2.13 | 51 | 58, | −16, | −18 | 2.14 | |
| Insula | L | 40 | −34, | 18, | 14 | 2.44 | 31 | −34, | 18, | 14 | 2.53 |
| MCC | R | 28 | 4, | −24, | 44 | 1.87 | 12 | 4, | −24, | 44 | 1.77 |
| SFG | R | 6 | 18, | 56, | 30 | 2.05 | 11 | −20, | 52, | 32 | 2.30 |
| MFG | L | - | - | - | 6 | - | - | ||||
| R | 14 | 34, | 60, | −2 | 2.20 | 18 | 40, | 12, | 42 | 2.10 | |
Abbreviations: AIQ = addition in-quiet, AIN = addition in-noise, SIQ = substraction in-quiet, SIN = substraction in-noise, NOV = number of activated voxels, HG = Heschl’s gyrus, STG = superior temporal gyrus, MTG = middle temporal gyrus, MCC = middle cingulate cortex, SFG = superior frontal gyrus, MFG = middle frontal gyrus.
Table 6:
Activated brain regions during subtraction greater than addition in the quiet and noise conditions at uncorrected P < 0.05
| Region | Hemisphere | SIQ > AIQ | AIN > SIN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NOV | x, y, z | t | NOV | x, y, z | t | ||||||
| IPL | L | 14 | −58, | −40, | 38 | 1.94 | 70 | −44, | −30, | 44 | 2.58 |
| SPL | R | 121 | 34, | −42, | 54 | 2.44 | 30 | 30, | −44, | 50 | 1.99 |
| L | 6 | −24, | −56, | 58 | 1.74 | 41 | −16, | −58, | 50 | 2.11 | |
| SG | R | 152 | 16, | −56, | 58 | 2.61 | 126 | 24, | −66, | 48 | 2.77 |
| L | 4 | −58, | −40, | 36 | 1.53 | - | |||||
| R | 88 | 60, | −16, | 28 | 2.33 | 16 | 60, | −16, | 28 | 1.95 | |
| SFG | L | 54 | −22, | 0, | 48 | 2.87 | 31 | −22, | 0, | 48 | 3.13 |
| R | 59 | 22, | 24, | 58 | 2.32 | 12 | 20, | 2, | 60 | 1.90 | |
| PG | L | 34 | −20, | −24, | 70 | 2.33 | 27 | −20, | −24, | 70 | 2.56 |
| R | 49 | 18, | −26, | 72 | 2.16 | 47 | 50, | −14, | 54 | 2.37 | |
Abbreviations: AIQ = addition in-quiet, AIN = addition in-noise, SIQ = substraction in-quiet, SIN = substraction in-noise, IPL = inferior parietal lobe, SPL = superior parietal lobe, SG = supramarginal gyrus, SFG = superior frontal gyrus, PG = precentral gyrus.
However, there was no significant main effect of background conditions (i.e., in-quiet and in-noise) and their interaction with operations (i.e., addition and subtraction) in any brain region.
Discussion
This study identified the activated areas in the brain and their laterality during simple addition and subtraction operations for in-quiet and in-noise backgrounds. In addition, it also examined the differential effect of background noise on the task-related activation during the aforementioned operations.
SPM analyses indicated that performing subtraction or addition in-quiet as well as in-noise resulted in a different spatial extent of activation in several brain regions. Group results showed that addition and subtraction operations evoked brain activation in the HG, STG, IFG, IPL, SMG, PCG, MTG, MFG, SPL, MCC, insula, and thalamus. In general, NOV was higher during addition than subtraction, for both in-quiet and in-noise. NOV was also modulated by background condition, where in-noise produced higher NOV in both addition and subtraction operations compared with in-quiet conditions. The differences in NOV for different mathematical operations and background conditions were possibly due to the difference in task demand and participants’ efforts in accomplishing the tasks. These results were similar to those of other studies on speech perception in-noise (19,31) that found increased activation in some regions, especially in superior temporal activation, due to increased effort in extracting the speech signal in-noise.
An extended spread of activation in bilateral HG and STG was observed in-noise compared with in-quiet for both addition and subtraction operations, similar to that found in a study of speech perception, where greater activation was found during speech perception in-noise than in-quiet (19). Bilateral activation of HG and STG was expected due to their respective functions in processing auditory stimuli (18–20,32). The HG, together with the posterior area of STG, is known to be the primary auditory area and is associated to BA41 in Brodmann classification (33). In the present study, HG and parts of STG were assumed to act as the input centre for auditory processing, where auditory signals from sub-cortical areas were received before transmission to other cortical areas involved in processing of arithmetic stimuli. Verbal stimuli (e.g., speech or word numbers) caused an extended activation in the left auditory compared with the right auditory area (34). However, the right auditory area has been shown to be more sensitive to tonality or non-verbal stimuli, such as pure tones and noises. For example, listening to white noise has been found to produce a larger number of activated voxels in the right HG compared with the left HG (32). These findings by Tervaniemia et al. (34) and Yusoff et al. (32) indicate that HG responds differently to verbal and non-verbal stimuli. However, the present study showed that the right HG triggered a relatively wider area of activation (LI < 0) compared with the left HG for all tasks except for addition in-quiet, which evoked a relatively wider extent of activation in the left hemisphere (LI > 0). This right hemispheric dominance is potentially due to the change in the processing strategy for HG when dealing with simple arithmetic operations. For STG, there was an extended activation area in the left hemisphere (LI > 0) for addition in-quiet and in-noise; in contrast, subtraction in-quiet and in-noise showed a wider extent of activation in the right hemisphere (LI < 0). However, the LI values obtained from the analyses were small, reflecting small differences in NOV between the left and right STG during addition and subtraction operation in-quiet and in-noise. These findings suggest that both left and right STG play equal roles in processing mathematical input presented auditorily (19,35).
The present study also found that addition and subtraction operations resulted in extended activation in the frontal and parietal lobes, 2 regions known to be involved in mental calculations (36). In the frontal lobes, there was significant activation in bilateral IFG, SFG, and MFG–regions related to working memory and executive functions (7,8). The present study also revealed that addition and subtraction operations resulted in bilateral activations in the IFG and SFG, suggesting that they may play a role in supporting the processes of arithmetic working memory. The IFG results indicate that the left hemisphere IFG has extended activation compared with the right IFG in addition operations both in-quiet and in-noise (i.e., LI > 0). In contrast, subtraction operations both in-quiet and in-noise resulted in a greater activation in the right hemisphere (LI < 0). In a previous study on simple calculation, complex calculation, and proximity judgement (11), the right IFG exhibited a wider extent of activation than the left IFG, suggesting that the right IFG was associated with the executive function of arithmetic operations. The MFG activation pattern showed a slightly extended activation in the right hemisphere (LI < 0) during addition in-quiet and in-noise, as well as subtraction in-quiet, but not for subtraction in-noise (LI > 0). In addition, a wider spread of bilateral activation in MFG during addition and subtraction tasks may indicate that MFG is the central region in working memory processes dedicated to numerical processing (37). These findings suggest that (1) addition and subtraction operations require working memory for arithmetic facts retrieval, and (2) addition and subtraction in-quiet and in-noise conditions produced different hemispheric laterality patterns in the frontal regions.
The parietal regions are commonly activated in tasks that involve number operations. The activated regions include the IPL (4,10), SPL, and SMG (4,10,11), all regions that play important roles in processing and manipulating numbers. Processing of numbers appears to be important especially in differentiating the arithmetic stimulus type, i.e., addition and subtraction. Furthermore, the IPL, SPL, and SMG seemed to have a wider extent of activation for addition task. For both SMG and IPL, there was LI > 0, and these 2 regions seemed to have a wider extent of activation in the left hemisphere, except for SMG for subtraction in-quiet that was otherwise. Rueckert et al. (38) and Dehaene et al. (39), found bilateral activation in IPL. However, it is well known that the left IPL plays an important role in arithmetic operations as retrieval of arithmetic information involves the left Broca areas (40). Menon et al. (10) identified the IPL region as specifically activated in response to increasing arithmetic complexity. They also suggested that SMG was activated due to increased difficulty of the arithmetic operation. The wider extent of activation in the IPL during addition operations revealed from the present study showed that addition was relatively difficult to solve compared with subtraction.
Interestingly, the right MCC revealed activation during all combinations of operations and conditions. The right MCC also exhibited a wider extent of activation during addition compared with subtraction. In Cowel et al. (40), the activation found in cingulate cortex was associated to cognitive requirements of attention, working memory, and decision making. Based on the results given above, performing addition for in-noise conditions needed higher attention and executive function of working memory compared with subtraction. Thus, the involvement of MCC in this study can be associated with attention when the participants were trying to solve the addition and subtraction operations.
The motor system in the bilateral PCG has also been found to be activated during addition and subtraction in this study. Besides, a wider activation in the left PCG was observed as the LI > 0 during addition and subtraction for both in-noise and in-quiet (43). The motor areas may be activated due to imagery finger movement when the participants were trying to solve numerical processing such as counting (41,42). Both the left and right PCG showed greater activation during subtraction compared with addition. Counting in numerical processing would appear to be most important to differentiate between addition and subtraction (12). Subtraction seemed to promote a relatively larger imagery finger movement in processing numerical quantities to solve problems compared with addition (44).
We also observed other brain areas that were significantly activated (P < 0.001), e.g., the insula lobe and thalamus. The activation in these areas was more extensive in the right compared with the left hemisphere, except for activation in the thalamus for subtraction in-noise that was otherwise. These areas have been suggested to be components of working memory and attention (32).
The results of the present study should be interpreted carefully while considering at least 2 possible limitations: (1) The statistical thresholds used for the whole brain data analyses were rather moderate, and (2) perisylvian activation patterns in relation to arithmetic processing might be over-interpreted due to the underlying contrasts, including a verbal comprehension versus a nonverbal baseline condition. Nevertheless, interaction analyses between modalities and tasks provide valuable information for the presented differential discussion.
Conclusion
The results showed that addition and subtraction tasks evoked extended activation in the left inferior parietal lobe, left precentral gyrus, left superior parietal lobe, left supramarginal gyrus, and left middle temporal gyrus. This was due to the hypothesis that the human brain activates its left hemisphere when working on logical thinking. However, brain areas in the insula, MCC, and MFG showed extended activation in the right hemisphere. For superior temporal gyrus, inferior frontal gyrus, and thalamus, there was extensive left-hemispheric activation for addition tasks but not for subtraction tasks. The bilateral activation in parietal regions promotes arithmetic problem solving, but the involvement of frontal brain regions for mental calculation are for executive processes and working memory in mathematical calculations. The results of the present study suggest that addition (compared with subtraction) and in-noise (compared with in-quiet) conditions promoted higher cognitive processes in working memory and attention. The left hemisphere of the brain showed apparent extended activation in regard to attention, executive processes and working memory.
Figure 2:
Brain activation from group random effect analysis for addition in-quite, (b) addition in-noise, (c) subtraction in-quite, and (d) subtraction in-noise thresholded at α = 0.001 uncorrected for multiple comparisons. R denotes the right side of the brain, while L denotes the left side.
Acknowledgments
The authors would like to thank Sa’adon Samian from the Department of Radiology, UKM Medical Centre for conducting the fMRI scans. This work was supported by the UKM research grant GUP-SUK-SK-07-20-205.
Footnotes
Authors’ Contributions
Conception and design: AIAH, ANY, SZSM, MM
Provision of study materials or patients, collection, assembly, analysis, and interpretation of the data, drafting of the article: AIAH, ANY
Obtaining of funding, statistical expertise, critical revision and final approval of the article, administrative, technical, or logistic support: ANY
References
- 1.Dahaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cogn Neuropsychol. 2003;20(3):487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- 2.Fayol M, Abdi H, Gombert JE. Arithmetic problems formulation and working memory load. Cognition Instruct. 1987;4(3):187–202. [Google Scholar]
- 3.Dehaene S. Varieties of numerical abilities. Cognition. 1992;44(1–2):1–42. doi: 10.1016/0010-0277(92)90049-n. [DOI] [PubMed] [Google Scholar]
- 4.Wu SS, Chang TT, Majid A, Caspers S, Eikhoff SB, Menon V. Functional heterogeneity of inferior parietal cortex during mathematical cognition assessed with cytoarchitectonic probability maps. Cereb Cortex. 2009;19(12):2930–2945. doi: 10.1093/cercor/bhp063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Constantinidis C, Procyk E. The primate working memory networks. Cogn Affect Behav Ne. 2004;4(4):444–465. doi: 10.3758/cabn.4.4.444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kazui H, Kitagi H, Mori E. Cortical activation during retrieval of arithmetical facts and actual calculation: A functional magnetic resonance imaging study. Psychiat Clin Neuros. 2000;54:479–485. doi: 10.1046/j.1440-1819.2000.00739.x. [DOI] [PubMed] [Google Scholar]
- 7.Delazer M, Domahs F, Bartha L, Brenneis, Lochy A, Trieb T, et al. Learning complex arithmetic—An fMRI study. Cognitive Brain Res. 2003;18(1):76–88. doi: 10.1016/j.cogbrainres.2003.09.005. [DOI] [PubMed] [Google Scholar]
- 8.Ranganath C, Johnson MK, D’Esposito M. Prefrontal activity associated with working memory and episodic long-term memory. Neuropsychologia. 2003;41(3):378–389. doi: 10.1016/s0028-3932(02)00169-0. [DOI] [PubMed] [Google Scholar]
- 9.Rickard C, Romero SG, Basso G, Wharton C, Flitman S, Grafman J. The calculating brain: An fMRI study. Neuropsychologia. 2000;38(3):325–335. doi: 10.1016/s0028-3932(99)00068-8. [DOI] [PubMed] [Google Scholar]
- 10.Menon V, Rivera SM, White CD, Glover GH, Reiss AL. Dissociating prefrontal and parietal cortex activation during arithmetic processing. NeuroImage. 2000;12(4):357–365. doi: 10.1006/nimg.2000.0613. [DOI] [PubMed] [Google Scholar]
- 11.Zhang YT, Zhang Q, Zhang J, Wei L. Laterality of brain areas associated with arithmetic calculations revealed by functional magnetic resonance imaging. Chinese Med J-Peking. 2005;118(8):633–638. [PubMed] [Google Scholar]
- 12.Fehr T, Code C, Herrmann M. Common brain regions underlying different arithmetic operations as revealed by conjunct fMRI-BOLD activation. Brain Res. 2007;1172(3):93–102. doi: 10.1016/j.brainres.2007.07.043. [DOI] [PubMed] [Google Scholar]
- 13.Fehr T, Code C, Herrmann M. Auditory task presentation reveals predominantly right hemispheric fMRI activation patterns during mental calculation. Neurosci Lett. 2008;431(1):39–44. doi: 10.1016/j.neulet.2007.11.016. [DOI] [PubMed] [Google Scholar]
- 14.Gruber O, Indefrey P, Steinmetz H, Kleinschmidt A. Dissociating neural correlates of cognitive components in mental calculation. Cereb Cortex. 2001;11(4):350–359. doi: 10.1093/cercor/11.4.350. [DOI] [PubMed] [Google Scholar]
- 15.Liebenthal E, Binder JR, Spritzer SM, Possing ET, Medler DA. Neural substrates of phonemic perception. Cereb Cortex. 2005;15(10):1621–1631. doi: 10.1093/cercor/bhi040. [DOI] [PubMed] [Google Scholar]
- 16.Scoot SK, Wise RJS. The functional neuroanatomy of prelexical processing in speech perception. Cognition. 2004;92(1–2):13–45. doi: 10.1016/j.cognition.2002.12.002. [DOI] [PubMed] [Google Scholar]
- 17.Wong PCM, Nusbaum HC, Small SL. Neural bases of talker normalization. J Cognitive Neurosci. 2004;16(7):1173–1184. doi: 10.1162/0898929041920522. [DOI] [PubMed] [Google Scholar]
- 18.Scott SK, Rosen S, Wickham L, Wise RJ. A positron emission tomography study of the neural basis of informational and energetic masking efforts in speech perception. J Acoust Soc Am. 2004;115(2):813–821. doi: 10.1121/1.1639336. [DOI] [PubMed] [Google Scholar]
- 19.Wong PCM, Uppunda AK, Parish TB, Dhar S. Cortical mechanisms of speech perception in noise. J Speech Lang Hear Res. 2008;51:1026–1041. doi: 10.1044/1092-4388(2008/075). [DOI] [PubMed] [Google Scholar]
- 20.Hall DA, Johnsrude IS, Haggard MP, Palmer AR, Akeroyd MA, Summerfield AQ. Spectral and temporal processing in human auditory cortex. Cereb Cortex. 2002;12(2):140–149. doi: 10.1093/cercor/12.2.140. [DOI] [PubMed] [Google Scholar]
- 21.Hall DA, Haggard MP, Akeroyd MA, Palmer AR, Summerfield AQ, Elliott MP, et al. “Sparse” temporal sampling in auditory fMRI. Hum Brain Mapp. 1999;7(3):213–223. doi: 10.1002/(SICI)1097-0193(1999)7:3<213::AID-HBM5>3.0.CO;2-N. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tomasi D, Caparelli EC, Chang L, Ernst T. fMRI-acoustic noise alters brain activation during working memory tasks. NeuroImage. 2005;27(2):377–386. doi: 10.1016/j.neuroimage.2005.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9(1):97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- 24.Binder JR, Liebenthal E, Possing ET, Medler DA, Ward BD. Neural correlates of sensory and decision processes in auditory object identification. Nat Neuro. 2004;7(3):295–301. doi: 10.1038/nn1198. [DOI] [PubMed] [Google Scholar]
- 25.Ashburner J, Good CD. Spatial registration of images. In: Tofts P, editor. Qualitative MRI of the brain: Measuring changes caused by disease. Chichester, UK: John Wiley & Sons Ltd; 2003. pp. 503–531. [Google Scholar]
- 26.Ashburner J, Friston KJ. Computational neuroanatomy. In: Frackowiak RSJ, Friston KJ, Frith CD, Dolan RJ, Price CJ, Zeki S, et al., editors. Human brain function. Amsterdam: Elsevier; Academic Press; 2004. pp. 655–672. [Google Scholar]
- 27.Friston KJ. Experimental design and statistical parametric mapping. In: Frackowiak RSJ, Friston KJ, Frith CD, Dolan RJ, Price CJ, Zeki S, et al., editors. Human brain function. Amsterdam: Elsevier; Academic Press; 2004. pp. 599–632. [Google Scholar]
- 28.Maldijan JA, Laurienti PJ, Kraft RA, Burdette JH. An automated method for neuroanatomic and cytoarchitectonic atlas-based interrogation of fMRI data sets. NeuroImage. 2003;19(3):1233–1239. doi: 10.1016/s1053-8119(03)00169-1. [DOI] [PubMed] [Google Scholar]
- 29.Seghier ML. Laterality index in functional MRI: Methodological issues. Mag Reson Imaging. 2008;26(5):594–601. doi: 10.1016/j.mri.2007.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pinel P, Dehaene S. Beyond hemispheric dominance: brain regions underlying the joint lateralization of language and arithmetic to the left hemisphere. J Cognitive Neurosci. 2010;22(1):48–66. doi: 10.1162/jocn.2009.21184. [DOI] [PubMed] [Google Scholar]
- 31.Wong PC, Jin JX, Gunasekera GM, Abel R, Lee ER, Dhar S. Aging and cortical mechanisms of speech perception in noise. Neuropsychologia. 2009;47(3):693–703. doi: 10.1016/j.neuropsychologia.2008.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yusoff AN, Abdul Hamid K, Mohamad M, Abd Hamid AI. The acquisition, analyses and interpretation of fMRI data: A study on functional specialization in primary auditory cortex. Med Health. 2008;3(2):131–148. [Google Scholar]
- 33.Upadhyay J, Silver A, Knaus TA, Lindgren KA, Ducros M, Kim DS, et al. Effective and structural connectivity in the human auditory cortex. J Neurosci. 2008;28(13):3341–3349. doi: 10.1523/JNEUROSCI.4434-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tervaniemia M, Hugdahl K. Lateralization of auditory-cortex functions. Brain Res Rev. 2003;43(3):231–246. doi: 10.1016/j.brainresrev.2003.08.004. [DOI] [PubMed] [Google Scholar]
- 35.Munoz-Lopez MM, Mohedano-Mariano A, Insausti R. Anatomical pathways for auditory memory in primates. Front Neuroanat. 2010;4(129):1–13. doi: 10.3389/fnana.2010.00129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Davis N, Cannistraci CJ, Rogers BP, Gatenby JC, Fuchs LS, Anderson AW, et al. The neural correlates of calculation ability in children: An fMRI study. Magn Reson Imaging. 2009;27(9):1187–1197. doi: 10.1016/j.mri.2009.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Burbaud P, Degreze P, Lafon P, Franconi JM, Bouligand B, Bioulac B, et al. Lateralization of prefrontal activation during internal mental calculation. J Neurophysiol. 1995;74(5):2194–2200. doi: 10.1152/jn.1995.74.5.2194. [DOI] [PubMed] [Google Scholar]
- 38.Rueckert L, Lange N, Paetiot A, Appollonio I, Litvan I, Bihan SDL, et al. Visualizing cortical activation during mental calculation with functional MRI. NeuroImage. 1996;3(2):97–103. doi: 10.1006/nimg.1996.0011. [DOI] [PubMed] [Google Scholar]
- 39.Dehaene S, Cohen L. Towards an anatomical and functional model of number processing. Math Cogn. 1995;1(1):83–120. [Google Scholar]
- 40.Cowel SF, Egan GF, Code SC, Harasty J, Watson JDG. The functional neuroanatomy of simple calculation and number repetition: A parametric PET activation study. NeuroImage. 2000;12(5):565–573. doi: 10.1006/nimg.2000.0640. [DOI] [PubMed] [Google Scholar]
- 41.Hanakawa T, Immisch I, Toma K, Dimyan MA, van Gelderen P, Hallet M. Functional properties of brain areas associated with motor execution and imagery. J Neurophysiol. 2003;89(2):989–1002. doi: 10.1152/jn.00132.2002. [DOI] [PubMed] [Google Scholar]
- 42.Lacourse MG, Orr ELR, Cramer SC, Cohen MJ. Brain activation during execution and motor imagery of novel and skilled sequential hand movements. NeuroImage. 2005;27(3):505–519. doi: 10.1016/j.neuroimage.2005.04.025. [DOI] [PubMed] [Google Scholar]
- 43.Yusoff AN, Mohamad M, Ayob MM, Hashim MH. Brain activations evoked by passive and active listening: A preliminary study on multiple subjects. Malaysian J Health Sci. 2008;6(1):35–36. [Google Scholar]
- 44.Cohen L, Dehaene S, Chochon F, Lehericy S, Naccache L. Language and calculation within the parietal lobe: A combined cognitive, anatomical and fMRI study. Neuropsychologia. 2000;38(10):1426–1440. doi: 10.1016/s0028-3932(00)00038-5. [DOI] [PubMed] [Google Scholar]