Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2011 Jun 14;1:11. doi: 10.1038/srep00011

Mechanism of copper(II)-induced misfolding of Parkinson's disease protein

Frisco Rose 1, Miroslav Hodak 1, Jerzy Bernholc 1,a
PMCID: PMC3216499  PMID: 22355530

Abstract

α-synuclein (aS) is a natively unfolded pre-synaptic protein found in all Parkinson's disease patients as the major component of fibrillar plaques. Metal ions, and especially Cu(II), have been demonstrated to accelerate aggregation of aS into fibrillar plaques, the precursors to Lewy bodies. In this work, copper binding to aS is investigated by a combination of quantum and molecular mechanics simulations. Starting from the experimentally observed attachment site, several optimized structures of Cu-binding geometries are examined. The most energetically favorable attachment results in significant allosteric changes, making aS more susceptible to misfolding. Indeed, an inverse kinematics investigation of the configuration space uncovers a dynamically stable β-sheet conformation of Cu-aS that serves as a nucleation point for a second β-strand. Based on these findings, we propose an atomistic mechanism of copper-induced misfolding of aS as an initial event in the formation of Lewy bodies and thus in PD pathogenesis.

Parkinson's disease (PD) is the most prevalent neurodegenerative movement disorder affecting more than 0.1% of the population older than 40 years of age1. At the cellular level, PD is characterized by the accretion of Lewy body plaques in neurons of the substantia nigra2. Lewy bodies are accumulations of amyloid-like fibrils, which are comprised primarily of an oligomerized form of α-synuclein (aS)3, a natively unfolded protein consisting of 140 amino acids4. In addition to being implicated in PD, aS also plays a key role in other neurodegenerative disorders, such as dementia associated with Lewy body disease, diffuse Lewy body disease and multiple system atrophy4. Furthermore, Lewy bodies are found in a significant fraction of Alzheimer's disease (AD) patients5, suggesting that aS is also important in the pathogenesis of AD.

An increasing amount of evidence now points to the significance of metal ions in PD. Elevated levels of iron and zinc were found in PD brains6 and high levels of copper were detected in the cerebrospinal fluid7. Furthermore, aS binds metal ions which accelerate its oligomerization into fibrils6. The link between metals and PD is similar to that in AD, where altered levels of metals in the brain are also observed8. For the case of AD, Bush and Tanzi9 have postulated the metal hypothesis, which argues that neurotoxic effects of proteins are promoted and/or caused by their interactions with metal ions. Based on this hypothesis, metal chelation therapies for AD were developed and are presently being tested in clinical trials10. Similarities between the roles of metals in AD and PD suggest that metals represent a promising therapeutic target for PD.

Copper is one of the most studied metals in neurodegenerative diseases. It appears to have distinctly different biological roles in different diseases: while it is harmful and causes structural damage to proteins in AD and PD11, it is thought to have neuroprotective effects in prion diseases 12,14,15. In fact, our previous investigation12 of copper attachment to prion protein (PrP) showed that copper binding is a part of PrP's normal function and that this protein performs a buffering role, thereby protecting proteins such as aS from damaging effects of free copper ions. However, it appears to have detrimental effects in PD, since it was found to be the most effective metal in causing the in vitro oligomerization of aS16.

In this report, we use a combination of quantum and classical simulations to study Cu(II) attachment to aS. Quantum simulations are employed to determine the local binding geometry of the Cu-aS complex, while classical molecular dynamics is applied to probe the structure of the full-length copper-bound aS. These calculations reveal that copper attachment to aS causes development of secondary structure in the otherwise unstructured protein, which accelerates the misfolding of aS. Based on this finding we propose an atomistic mechanism of copper-induced misfolding of aS.

Results

We consider the attachment of Cu at the experimentally observed site His-50, identified by Rasia et al.17 using a combination of electron paramagnetic resonance (EPR) and nuclear magnetic resonance (NMR) techniques. Their data showed that the neighboring residues (49–52) are also involved in copper binding. A contribution of the N-terminal residues (3–9) was also detected, but a more recent study18 found that the N-terminal residues form an independent binding site not related to the primary binding at His-50. While the NMR data indicate good correlation with Cu(II) attachment to two nitrogen and two oxygen atoms (2N2O), other binding types are not precluded. In particular, a 3N1O type of attachment is plausible, due to the similarity of its nuclear spin interaction coefficients to those of 2N2O19. Therefore, we consider both 2N2O and 3N1O types of attachment in this work.

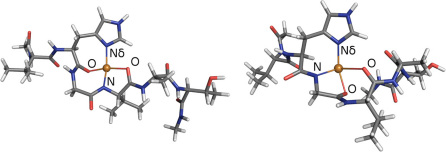
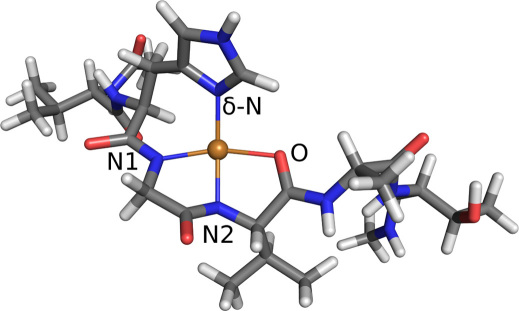
To investigate the properties of the copper-aS complex, we construct multiple binding models of 2N2O and 3N1O attachments. The aS is represented by residues 49–54 (VHGVAT) and the copper ion is assumed to be coordinated by Nδ in the histidine imidazole and by a combination of deprotonated amide nitrogens and carboxyl oxygens in the protein backbone. Several combinations exist for each binding mode, but many can be ruled out because they distort the fragment too severely. Using insight from our previous investigations of Cu-bound proteins12,20,21 and results from Ref.13, where many possible copper attachments modes were investigated, we narrow our search to three plausible candidates: Two 2N2O structures, denoted as NNOO and NONO according to the order of copper ligands in counterclockwise direction starting from the imidazole Nδ (see Fig. 2), and one 3N1O structure. In the calculations, we use neutral ends, i.e., the protein backbone is continued in both directions so that it ends with neutral CH3 groups. Each binding model is geometrically optimized using the hybrid Kohn-Sham/orbital-free density functional theory (KS/OF DFT) method20 and the relaxed geometries are shown in Figs. 1 and 2. For all examined structures, the binding is mostly planar, with the imidazole ring slightly tilted from the coordination plane. Note that for all the binding modes, the attachment of copper causes the protein backbone to deflect at the binding site.

Figure 2. Relaxed 2N2O binding geometries of copper to α-synuclein: NONO (left) and NNOO (right).

Figure 2

Open in a new tab

The bond distances in counterclockwise order are: Cu-Nδ 1.99 Å, Cu-O 2.02 Å, Cu-N 1.92 Å, and Cu-O 2.18 Å (NONO); Cu-Nδ 1.98 Å, Cu-N 1.97 Å, Cu-O 1.93 Å, and Cu-O 2.08 Å (NNOO).

Figure 1. Relaxed 3N1O binding geometry of copper to α-synuclein.

Figure 1

Open in a new tab

The bond distances are: Cu-Nδ 1.95 Å, Cu-N1 2.01 Å, Cu-N2 1.93 Å, and Cu-O 2.08 Å.

Since the 3N1O and 2N2O binding modes differ in the total charges (0 and +1, respectively), we include a hydronium ion in the solvation shell of the 3N1O model to facilitate a direct comparison of energies. The relative energies with respect to the 3N1O mode are listed in Table 1, which shows that the 3N1O type of binding is energetically favorable over the best of the 2N2O structures by 1.77 eV.

Table 1. Relative energies of copper binding modes in aS.

Structure ΔE (eV) ΔE (kJ/mol)
3N1O 0.00 0.00
NNOO +1.77 170.78
NONO +2.51 242.18
Open in a new tab

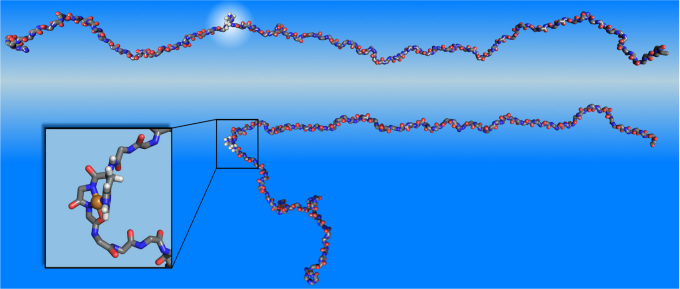
The properties of full-length aS are studied using classical molecular dynamics (MD) via NAMD26. The model of free aS, whose structure has not been determined yet due to its unfolded character27, is built and equilibrated as described in the Methods Section. Extended molecular dynamics simulations show that the free aS is mostly linear and extended. No propensity for forming secondary structure is observed with the exception of several intermittent turns. A snapshot of the equilibrated free aS is shown in Fig. 3 (top). Note that the imidazole group in His-50, which anchors the copper ion in copper-bound aS, is extended away from the backbone and can readily bind metal ions.

Figure 3. Misfolding events in α-synuclein due to copper binding.

Figure 3

Open in a new tab

Top: Snapshot of the free α-synuclein showing the location of His-50 (upper). Bottom: Initial relaxed structure of Cu(II)-bound α-synuclein. The inset shows the details of copper binding.

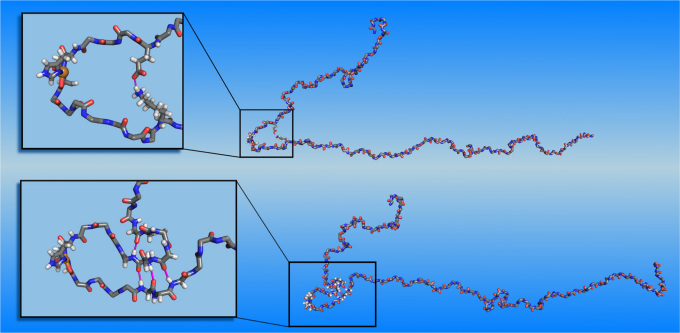
The structural model of the full copper-bound aS is based on the equilibrated free aS, onto which the quantum-mechanically-calculated 3N1O copper binding geometry is imposed. Within classical molecular dynamics we represent the copper binding by a set of harmonic springs. A detailed description of this model is given in the Methods section. The initial structure of copperbound aS is shown in Fig. 3 (bottom). Note that copper binding causes curving of the aS backbone at the binding site, creating a turn-like structure that brings fore and aft portions of the backbone into proximity. These regions stay proximal during the entire simulation (25 ns). This conformation is further stabilized by contacts between side chains, the most stable of which are between Glu-46 and Lys-60. A snapshot exhibiting this contact is displayed in Fig. 4 (top). The simulation also shows that the proximal parts of the protein start to align, indicating the development of a β-sheet around the binding site and the creation of a β-hairpin there. Unfortunately, due to the large time scales involved, the formation of β-sheets in full-length proteins cannot be studied in atomistic simulations at present. Instead, we develop multiple plausible candidates for a β-sheet located in the area where alignment is observed, using inverse kinematics28 and testing their dynamic stabilities in extended MD simulations. Among all the candidate structures, only one turns out to be stable during the MD simulations. The other ones quickly relax to the unstructured form. The dynamically stable β-sheet conformation involves contacts between residues 43–45 and 57–59, see Fig. 4 (bottom). It remains stable for the entire duration of the simulation (23 ns). In addition to the dynamical stability of this β-sheet, an additional structural development at residues 40–42 is also observed during the simulation. These residues align with the already existing β-sheet, indicating the development of a second β-strand parallel to the original β-sheet. The observed onset of the formation of a β-sheet has important implications, since β-sheets are a defining characteristic of aS in Lewy bodies4 and this transformation may constitute the first step in the development of PD.

Figure 4. Top: Snapshot of evolved Cu-bound α-synuclein, showing hydrogen bonds between side chains that stabilize the turn-like conformation.

Figure 4

Open in a new tab

Bottom: Snapshot of Cu-bound α-synuclein with dynamically stable β-sheet. For visual clarity, non-participating side chains are not shown. Insets show close-ups at the β-sheet nucleation point.

Discussion

Our calculations show that 3N1O type of copper attachment is preferred over 2N2O by 1.77 eV. This conclusion seemingly contradicts the work of Rasia et al.17, who proposed that their EPR measurements indicate a 2N2O copper attachment. However, their analysis of EPR data does not include the 3N1O mode; only 4N, 2N2O and 4O were considered. Furthermore, since the values of tensor coefficients A|| and g|| for 2N2O and 3N1O modes are interspersed19, distinction between these modes is difficult. To facilitate comparison with the experimental results, we calculate the EPR tensor coefficients for both 2N2O and 3N1O attachments using ORCA22. Unfortunately, the ORCA EPR calculations do not have sufficient accuracy to distinguish between configurations with similar EPR tensors, because the calculated tensors typically differ by about 10% from the experimental results25. Our ORCA calculations obtain similar results for the 2N2O and 3N1O configurations: |A||| = 473.8 MHz, g|| = 2.20 for 2N2O (NNOO) and |A||| = 467.7 MHz and g|| = 2.17 for the 3N1O structure. These values differ from the experimental data of Rasia et al.17, |A||| = 557.6 MHz and g|| = 2.22, by about 15 %, which is similar to the differences between theory and experiments found in other works25.

The classical molecular dynamics investigation of the full copper-bound aS indicates that the copper attachment in the 3N1O mode leads to the development of β-sheets in aS by bringing the portions of the protein around the binding site into close proximity. Due to the high computational cost, we did not investigate the 2N2O attachments. However, since the NNOO mode, which is preferable over the NONO structure, has a backbone deflection very similar to that of 3N1O, it will likely follow a very similar structural development path. On the other hand, the NONO mode induces a much smaller backbone deflection in the full protein and thus its structural development, if any, will likely be different.

Based on findings in this work, we propose a mechanism for copper-induced misfolding of aS: In the first step, copper attachment causes deflection at the binding site and creates a stable turn-like structure. This feature is crucial for further structural development, since turns play an essential role in the initial steps of protein folding29. Its presence creates favorable conditions for β-sheet nucleation as adjacent parts of the protein are brought into proximity. Hydrogen bond contacts between the proximal side chains are formed and further stabilize this conformation. Subsequently, a β-sheet develops around the binding site, serving as a template for the formation of additional β-sheets. This process continues until the protein is fully misfolded.

In summary, we performed computer simulations to investigate interactions between a copper ion and aS at an atomistic level. Our work, which builds on recent experimental investigations 17, considered 2N2O and 3N1O types of attachment and found that the latter is energetically preferred. Further investigation of the preferred 3N1O mode shows that the copper attachment induces deflection of the protein backbone at the binding site, leading to the creation of a turn-like feature and backbone alignment as a precursor in the development of a β-sheet. This indicates that the role of copper in the fibrillation of aS is both to initiate misfolding via conformational modification and to stabilize the partially folded intermediate once formed. After the formation of the initial β-sheet, the folding process continues by aligning adjacent parts of the protein to the existing β-sheet, leading to a full misfolding.

Methods

The copper binding geometries are investigated at the ab initio level using a hybrid DFT/DFT method20. In this approach, the chemically active parts of the system, including the first solvation shells, are treated at a Kohn-Sham DFT level, while an approximate orbital-free DFT is used for the remaining solvent molecules. The compatibility between the KS and OF DFT methods enables seamless integration between the two. In particular, the flow of solvent molecules across the KS/OF interface is allowed and the total energy is conserved. The implementation of the hybrid KS/OF DFT approach is based on the RMG30,31,32 code, in which Kohn-Sham equations are solved in real-space and the multigrid technique is used to accelerate convergence of the ground state wavefunctions. This method was already successfully used to study the binding of copper to the prion protein12,20,21.

In the KS/OF DFT simulations, aS is represented as a fragment consisting of residues 49–54 (VHGVAT). Neutral ends are applied to the fragment, resulting in a total of 91 atoms. In each calculation, the protein fragment is fully solvated and minimized using classical molecular mechanics prior to performing KS/OF DFT simulations. This is followed by minimization within the KS/OF DFT method, in which the protein fragment, the copper ion and 12 water molecules closest to the binding site are treated by KS DFT, while 1788 waters are enclosed in the orbital-free DFT region. A grid with spacing of 0.32 Bohr is used to represent the wavefunctions, corresponding to a kinetic energy cutoff of 48 Ry. Ultrasoft pseudopotentials31,33 and generalized gradient approximation in the PBE form34 are employed.

An attempt to differentiate conformational binding modes based on EPR data was made using the DFT-based code ORCA22. Due to a high computational cost, only the immediate binding atoms and their nearest neighbors were included. The dangling bonds were passivated by hydrogen. Orbitals were computed via the unrestricted Kohn-Sham (UKS) method using the B3LYP23 exchange-correlation functional with the Ahlrichs-TZV basis set24, which produced the best results in previous investigation of EPR coefficients of copper complexes25. The EPR tensor was calculated for the copper and contributions from the isotropic, dipole and quadrupole hyperfine interactions were all included.

The simulations of the full-length aS protein are performed with the molecular dynamics package NAMD26 with CHARMM2735 force-field parameters. As is well known, copper and other transition metals are difficult to describe with force fields, due to the importance of quantum effects. In this work, the effects of copper were modeled in two ways: In the initial model, the copper ion was not present and its effect is modeled by fixing its ligands, while we later developed a more sophisticated model in which the copper was represented by a set of springs which kept the copper geometry close to that of our quantum investigation. Four springs were used to represent copper-ligands bonds and two additional springs were used to enforce Nδ-Cu-N2 and O-Cu-N1 angles, where the atom labels are from Fig. 1. The angular springs are necessary to preserve the planar character of the copper attachment. A value of 250 was used as a spring constant for all bond and angular springs. The spring constants' units are kcal/(mol Å2) and kcal/(mol Å) for bond and angular springs, respectively. This value reproduced the vibrational amplitudes of the quantum calculations. The springs were implemented using the tclforces framework available in NAMD, and the calculated forces were added to those evaluated from the CHARMM force field. Since the overall charge of the 3N1O copper attachment is 0, no charge was assigned to the copper ion. The differences between the β-sheet formation processes obtained from the models were very minor.

The calculations use periodic boundary conditions and solvent is added to the simulation cell so that the distance between any protein atom and an edge of the water box is at least 7 Å. This results in a total atom count that varies between 275,000 and 350,000. The solvent is ionized with 0.15 mM/L Na+ and Cl− to approximate the human intraneuronal ionic concentration36 and normalize the system to zero net charge. The temperature is maintained at 310 K by means of Langevin dynamics. The Nose-Hoover Langevin Piston algorithm37 is used to keep the pressure constant at 1 atm. The Verlet-I/r-RESPA38 method is employed with the following time steps: 4 fs for the long-range electrostatic forces, 2 fs for short-range nonbonded forces, and 2 fs for bonded forces. Bonds involving hydrogen are constrained using SHAKE39 to enable the use of large time steps.

The initial structural model of aS is built according to its amino acid sequence as a β-strand using PyMol40. The protein is first equilibrated by running molecular dynamics during which the initial structure rapidly degenerates to a conformation with almost no secondary structure, with only random coils and transient turns present. This equilibration is computationally demanding due to the unfolded nature of aS, and requires a large number of solvent molecules. During the 21 ns of simulation time that could be afforded, the root mean square deviation (RMSD) of the protein backbone does not completely flatten out, but other quantities, such as the kinetic and potential energies, solvent accessible surface and radius of gyration achieve stable values, indicating that the structure of the protein is not changing significantly and is sufficiently equilibrated for the study of Cu binding.

The exploration of possible β-sheet registrations is aided by inverse kinematics as implemented within ProteinShop28 and based on the AMBER41 force field. By using inverse kinematics we are able to reduce the sample set to contain only energetically favorable β-sheet conformations.

Author Contributions

FR, MH and JB wrote the main manuscript text and FR prepared figures 1–4. All authors reviewed the manuscript.

Acknowledgments

This work was mainly supported by DOE DE-FG02-98ER45685, with the petascale code development supported by NSF OCI-0749320. The calculations were carried out at the National Center for Computational Sciences at ORNL. Additionally, we would like to thank Robin Chisnell for his efforts in enhancing the CHARMM force modifications.

References

  1. Siderowf A. & Stern M. Update on Parkinson disease. Ann of Intern Med 138, 651–658 (2003). [DOI] [PubMed] [Google Scholar]
  2. Lewy F. H. Paralysis agitans. I. Pathologische anatomie. Handbuch der neurologie 3, 920–933 (1912). [Google Scholar]
  3. Spillantini M. G., Crowther R. A., Jakes R., Hasegawa M. & Goedert M. α-Synuclein in filamentous inclusions of lewy bodies from Parkinson's disease and dementia with lewy bodies. Proc Natl Acad Sci U S A 95, 6469–6473 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Spillantini M. G. & Goedert M. The α-Synucleinopathies: Parkinson's disease, dementia with lewy bodies, and multiple system atrophy. Ann N Y Acad Sci 920, 16–27 (2000). [DOI] [PubMed] [Google Scholar]
  5. Hamilton R. L. Lewy bodies in Alzheimer's disease: A neuropathological review of 145 cases using α-Synuclein immunohistochemistry. Brain Pathol 10, 378–384 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Uversky V. N., Li J. & Fink A. L. Metal-triggered structural transformations, aggregation, and fibrillation of human α-Synuclein. a psossible molecular link between Parkinson's disease and heavy metal exposure. J. Biol. Chem. 276, 44284–44296 (2001). [DOI] [PubMed] [Google Scholar]
  7. Pall H. S. et al. Raised cerebrospinal-fluid copper concentration in Parkinson's disease. Lancet 2, 238–241 (1987). PMID: 2886715. [DOI] [PubMed] [Google Scholar]
  8. Lovell M. A., Robertson J. D., Teesdale W. J., Campbell J. L. & Markesbery W. R. Copper, iron and zinc in Alzheimer's disease senile plaques. J Neurol Sci 158, 47–52 (1998). [DOI] [PubMed] [Google Scholar]
  9. Bush A. I. & Tanzi R. E. Therapeutics for Alzheimer's disease based on the metal hypothesis. Neurotherapeutics 5, 421–432 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Biran Y., Masters C. L., Barnham K. J., Bush A. I. & Adlard P. A. Pharmacotherapeutic targets in Alzheimer's disease. J Cell Mol Med 13, 61–86 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gaggelli E., Kozlowski H., Valensin D. & Valensin G. Copper homeostasis and neurode-generative disorders (Alzheimer's, prion, and Parkinson's diseases and amyotrophic lateral sclerosis). Chem. Rev 106, 1995–2044 (2006). PMID: 16771441. [DOI] [PubMed] [Google Scholar]
  12. Hodak M., Chisnell R., Lu W. & Bernholc J. Functional implications of multistage copper binding to the prion protein. Proc Natl Acad Sci U S A 106, 11576–11581 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Pushie J. M. & Rauk A. Computational studies of Cu (II)[peptide] binding motifs: Cu [HGGG] and Cu [HG] as models for Cu (II) binding to the prion protein octarepeat region. J. Biol. Inorg. Chem. 8, 53–65 (2003). [DOI] [PubMed] [Google Scholar]
  14. Cox D. L., Pan J. & Singh R. R. P. A mechanism for copper inhibition of infectious prion conversion. Biophys. J 91, L11–13 (2006). PMID: 16698781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Bocharova O. V., Breydo L., Salnikov V. V. & Baskakov I. V. Copper(II) inhibits in vitro conversion of prion protein into amyloid fibrils. Biochemistry 44, 6776–6787 (2005). [DOI] [PubMed] [Google Scholar]
  16. Paik S. R., Shin H. J., Lee J. H., Chang C. S. & Kim J. Copper(II)-induced self-oligomerization of alpha-synuclein. Biochem J. 340, 821–828 (1999). PMC1220316. [PMC free article] [PubMed] [Google Scholar]
  17. Rasia R. M. et al. Structural characterization of copper(II) binding to α-synuclein: Insights into the bioinorganic chemistry of Parkinson's disease. Proc Natl Acad Sci U S A 102, 4294–4299 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Sung Y., Rospigliosi C. & Eliezer D. NMR mapping of copper binding sites in alpha-synuclein. Biochim. Biophys. Acta 1764, 5–12 (2006). [DOI] [PubMed] [Google Scholar]
  19. Peisach J. & Blumberg W. E. Structural implications derived from the analysis of electron paramagnetic resonance spectra of natural and artificial copper proteins. Arch. Biochem. Biophys 165, 691–708 (1974). PMID: 4374138. [DOI] [PubMed] [Google Scholar]
  20. Hodak M., Lu W. & Bernholc J. Hybrid ab initio Kohn-Sham density functional theory/frozen-density orbital-free density functional theory simulation method suitable for biological systems. J. Chem. Phys. 128, 014101–9 (2008). [DOI] [PubMed] [Google Scholar]
  21. Hodak M. & Bernholc J. Insights into prion protein function from atomistic simulations. Prion 4, 13–19 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Neese F. ORCA - an ab initio, Density Functional and Semiempirical program package, Vers. 2.7. (2008).
  23. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. Chem. Phys 98, 5648–5652 (1993). [Google Scholar]
  24. Schiafer A. & Horn H. & Ahlrichs R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys 97, 2571 (1992). [Google Scholar]
  25. Ames W. M. & Larsen S. C. Density functional theory investigation of EPR parameters for tetragonal Cu(II) model complexes with oxygen ligands. J Phys Chem 113, 4305–4312 (2009). [DOI] [PubMed] [Google Scholar]
  26. Phillips J. C. et al. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26, 1781–1802 (2005). PMC2486339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Weinreb P. H., Zhen W., Poon A. W., Conway K. A. & Lansbury P. T. NACP, a protein implicated in Alzheimer's disease and learning, is natively unfolded. Biochemistry 35, 13709–13715 (1996). [DOI] [PubMed] [Google Scholar]
  28. Crivelli S., Kreylos O., Hamann B., Max N. & Bethel W. ProteinShop: a tool for interactive protein manipulation and steering. J. Comput. Aided Mol. Des. 18, 271–285 (2004). [DOI] [PubMed] [Google Scholar]
  29. Lewis P. N., Momany F. A. & Scheraga H. A. Folding of polypeptide chains in proteins: A proposed mechanism for folding. Proc Natl Acad Sci U S A 68, 2293–2297 (1971). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Briggs E. L., Sullivan D. J. & Bernholc J. Real-space multigrid-based approach to largescale electronic structure calculations. Phys Rev B 54, 14362–14375 (1996). [DOI] [PubMed] [Google Scholar]
  31. Hodak M., Wang S., Lu W. & Bernholc J. Implementation of ultrasoft pseudopotentials in large-scale grid-based electronic structure calculations. Phys. Rev. B 76, 085108–8 (2007). [Google Scholar]
  32. Bernholc J., Hodak M. & Lu W. Recent developments and applications of the real-space multigrid method. J Phys Condens Matter 20, 294205–294205 (2008). [Google Scholar]
  33. Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys Rev B 41, 7892–7895 (1990). [DOI] [PubMed] [Google Scholar]
  34. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  35. Feller S. E. & MacKerell A. D. An improved empirical potential energy function for molecular simulations of phospholipids. J Phys Chem A 104, 7510–7515 (2000). [Google Scholar]
  36. Purves D. G., Fitzpatrick A. D., Katz L. C., Mantia A. S. L. & McNamara J. O. Neuroscience. Sunderland Mass: Sinauer Assoc (Inc , 1997). [Google Scholar]
  37. Feller S. E., Zhang Y., Pastor R. W. & Brooks B. R. Constant pressure molecular dynamics simulation: the langevin piston method. J Chem Phys 103, 4613 (1995). [Google Scholar]
  38. Tuckerman M., Berne B. J. & Martyna G. J. Reversible multiple time scale molecular dynamics. The Journal of Chemical Physics 97, 1990 (1992). [Google Scholar]
  39. Ryckaert J. P., Ciccotti G. & Berendsen H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. comput. Phys 23, 327–341 (1977). [Google Scholar]
  40. DeLano W. The PyMOL molecular graphics system. http://www.pymol.org/
  41. Weiner S. J. et al. A new force field for molecular mechanical simulation of nucleic acids and proteins. J Am Chem Soc 106, 765–784 (1984). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES