Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2011 Oct 12;1:113. doi: 10.1038/srep00113

An Activation Force-based Affinity Measure for Analyzing Complex Networks

Jun Guo 1,a, Hanliang Guo 2, Zhanyi Wang 1
PMCID: PMC3216595  PMID: 22355630

Abstract

Affinity measure is a key factor that determines the quality of the analysis of a complex network. Here, we introduce a type of statistics, activation forces, to weight the links of a complex network and thereby develop a desired affinity measure. We show that the approach is superior in facilitating the analysis through experiments on a large-scale word network and a protein-protein interaction (PPI) network consisting of ∼5,000 human proteins. The experiment on the word network verifies that the measured word affinities are highly consistent with human knowledge. Further, the experiment on the PPI network verifies the measure and presents a general method for the identification of functionally similar proteins based on PPIs. Most strikingly, we find an affinity network that compactly connects the cancer-associated proteins to each other, which may reveal novel information for cancer study; this includes likely protein interactions and key proteins in cancer-related signal transduction pathways.

Analyzing a complex network usually begins with clustering the network, which is fundamental because it can clarify the structure of the network of interest and reveal previously unknown properties or functions for the members of each community1,2,3,4,5. For example, clustering protein-protein interaction (PPI) networks can promote significant new understanding of protein functions, which is critical for the fields of biology and medicine. However, clustering in complex networks is also challenging because it is difficult to find an effective affinity measure for nodes under conditions that represent complex networks in an information-scattering manner. For example, a PPI network is generally represented as a binary network; the proteins are the nodes, and the interactions are the links, which have a uniform weight of 16,7,8,9. This type of representation equally scatters the information of a node to all its links, which makes the node to be featureless. As a result, these types of representations tend to result in similar affinities between each pair of nodes for a large dataset that contains thousands of nodes.

To detect communities in networks, various network-weighting schemes have been proposed. Two typical schemes are “independent paths” and “betweenness centrality”10,11. Combined with the algorithms that are used to detect community structure in networks12, these schemes have been shown to be effective. However, the performance of the schemes is limited by the richness of the information that is contained in a given network because the schemes are not involved with the establishment of the network. In addition, the community detection that is based on some of the weights, e.g., betweenness centrality, is too time-consuming to process large-scale networks.

To tackle these problems, we first present a novel method for building informative networks from source data (e.g., text corpora and PPI databases) in an efficient manner and then present an affinity measure based on the informative networks to perform network analyses. Our networks are weighted by a new type of statistics, which are called activation forces, from the source data. Different from the traditional methods, our presented affinity measure calculates the similarity of link structures between nodes rather than the distance between them, and it is tightly coupled with our network-building method. To examine the generality of the approach, we adopt it both in a word network and a PPI network, which are two typical types of complex networks; a word network is a map of physically existing neural networks (linguistic neural networks in human brains), whereas a PPI network is a map of the logical interaction relations of proteins. To perform a solid examination, we conduct practical and meaningful large-scale experiments on the two networks. The word network consists of 10,000 of the most frequently used English words, and the PPI network consists of ∼5,000 frequently interacting human proteins. Although the experiment on the word network is only expected to provide the proof of our approach, the experiment on the PPI network is expected to provide proof and a new understanding of protein functions.

We model various complex networks by a unitary type of artificial neural networks with a unique link-weighting scheme, which determines the strength of the links according to the conditions of the node occurrences in the given training data set. Specifically, for a given pair of nodes (neurons) i and j, the strength of the link from node i to node j is defined as (fij / fi) (fij / fj )/dij2, where fi is the occurrence frequency of node i, fij is the co-occurrence frequency of node i and node j, and dij is a distance between the two nodes in their co-occurrences; fij and dij should be accordingly defined in a specific application. By imagining the ratios of fij to fi and fij to fj as masses, we can see that the strength is defined in the same form as universal gravitation. We call the defined strength of the link the activation force from node i to node j; afij originating from that the link conveys an activation from neuron i to neuron j after the former fires. Based on the activation forces, any complex network of interest can be represented by a matrix A = { afij }, where nonzero elements in the ith row provide the out-links of the ith node (from node i to others), while nonzero elements in the ith column provide its in-links (from others to node i). With such a matrix, we present an affinity measure between nodes Aaf, which is defined as the geometric average of the mean overlap rates of the in-links and out-links of the inquired two nodes (see the Methods section for a definition of the affinity measure).

Results

Word networks modeled by the activation forces

Previous studies have suggested that word (neural) networks exist in the human brain, and the networks may be forged by word activation effects, which refer to the idea that the onset of a word in the brain automatically and selectively activates its associates, which facilitates the understanding and generation of language13,14,15. It is commonly believed that the word activation effects and the word networks are trained by individuals' language experiences. However, although many investigations on word activation effects have been performed16,17,18, their modeling remains unclear.

Here, we suppose that word activation effects can be modeled by the proposed activation forces. We also demonstrate that the model makes word networks well-structured and easy to realize and that the affinity measure facilities the identification of word clusters. In the experiment, we approximate an individual's language experience with a large text corpus by using the corpus as the training data set to compute the activation forces. Word occurrence frequencies fi are measured in a literal fashion, the co-occurrence frequencies fij are counted within a predetermined word window19, and dij is defined as the average distance by which word i precedes word j in their co-occurrences (Methods). With the statistics of a vocabulary of 10,000 of the most frequent English words in the British National Corpus (BNC), http://www.natcorp.ox.ac.uk/, we construct a matrix of word activation forces and denote it as W = {wafij}. Obviously, W is squared but asymmetrical because fij and fji are typically different from each other. We find that the distribution of either the in- or out-link strengths of a node in W is heavy tailed, i.e., the words distribute their link strength with high selectivity. For a particular word, the primary fraction of the link strengths is only related to a few words, which are typically its partners with respect to traits, such as compound, phrase, head-modifier, subject-verb, verb-object, synonym, and antonym. This suggests that W highlights the key features of individual words. Meanwhile, the heavy-tailed distributions permit a sparse coding on W, i.e., they eliminate a large amount of the meaningless, weak links at a threshold. In the experiment, the number of links in W was reduced by more than 24-fold by eliminating the weak links at a threshold of 1.0e-6. Fig. 1 shows three ordinary nodes in the sparse W, which demonstrates the properties that were mentioned above. These properties generate significant advantages that effectively facilitate the realization of word networks in computers and human brains because a node typically possesses only a small number of significant links with other nodes. See Supplementary Information for the details on the distributions of the activation forces and the sparse coding.

Figure 1. Three ordinary nodes and their in- and out-links in the sparse W.

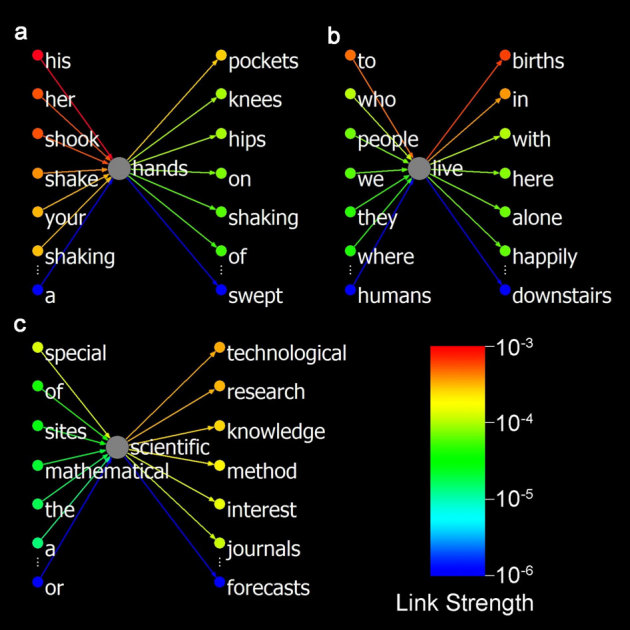
Figure 1

Open in a new tab

For every node (word), the strongest 6 and the weakest 1 in- and out-links are presented, which shows the sharply descending strengths and the most forceful restraints of the meanings of the nodes. (a) “hands” (noun, 164 in-links and 141 out-links in total) is characterized by the forceful links of modifiers (his, her, your), corresponding verbs (shook, shake, shaking), and associates (pockets, knees, hips). (b) “live” (verb, 129, 153) is characterized by the links of subjects (who, people, we, they), syntactic restraints (to, in, with, here, alone, happily, where) and associates (births). (c) “scientific” (adjective, 70, 185) is characterized by the links of the words composing phrases (research, knowledge, method, interest, journals), near-synonyms (technological, mathematical), and syntactic restraints (of, the, a). The unbalanced link strengths can be seen, for example, by the contrasting strong in-links of “hands” and the weak in-links of “scientific”. Note that the coloured strengths are at exponential scales.

Word affinities measured by Aaf

By adopting the affinity measure Aaf to W, we find that the acquired word affinities are highly consistent with human knowledge; nearly every word maintains strong affinities to its relatives but no or weak affinities to the non-relatives. To present the affinities in a visualized way, we group every word and its top 5 neighbours. We find that the affinities are very sensible for the identification of relative words. Across the parts of speech, the granularity of the concepts and the popularity of the words, a large number of the words possess the strongest affinities to their best partners, such as a∼the, abbey∼monastery, aberdeen∼dundee, ability∼capacity, above∼below, abroad∼elsewhere, abruptly∼swiftly, absence∼presence, abundance∼diversity, abuse∼violence, academic∼scientific, academy∼institution, accept∼recognise, acceptable∼reasonable and accommodate∼adapt. Reasonably, nouns and verbs usually maintain strong affinities to their siblings in their altered forms, e.g., arm∼arms, arrive∼arrives, and arriving∼arrive. Fig. 2a shows several examples of the results, and the complete results of the top 5 neighbours for every word are available in Supplementary Data 1. We also compare the top 3 neighbours with those of the human free association in Supplementary Information and Supplementary Data 2, and we show the consistency between the two. The reliable affinities lay advantageous foundations for word clustering. As a benefit, one can discover various word clusters in simple ways. Based on the top-5-neighbour results, for example, meaningful word clusters can be obtained by collecting a word's top 5 neighbours and the neighbours' top 5 neighbours and then excluding those that only have one neighbour in the collection (Fig. 2b).

Figure 2. Top 5 neighbours of words and clusters identified by such types of neighbourhoods.

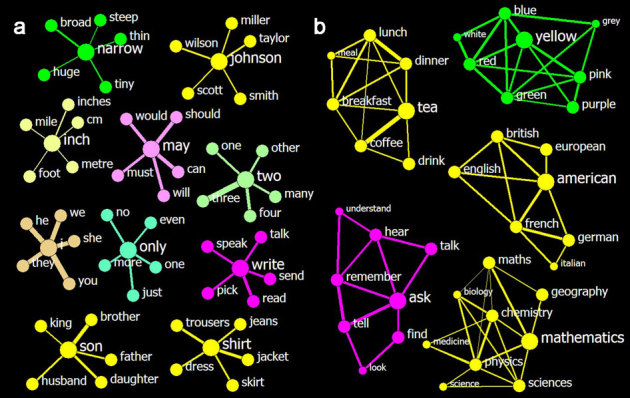
Figure 2

Open in a new tab

The colours are used to label parts of speech, the thickness of a link represents the strength of the affinity between its nodes, but the length means nothing. (a) Ten sample neighbourhoods show that the affinities are reasonably measured across different parts of speech. The central nodes in each neighbourhood are enlarged to promote ease of reading. The affinities range from 0.06 (inch∼mile) to 0.29 (two∼three). (b) Five sample clusters that were identified based on the top-5-neighbourhood show the effectiveness of the clustering. The nodes for the initial words are in the largest size, their neighbours have a medium size, and the neighbours' neighbours are the smallest. The affinities range from 0.05 (math∼chemistry) to 0.23 (tea∼coffee).

A PPI network modeled by the activation forces

Next, we focus our attention on PPI networks to introduce a novel method that can be used to establish a PPI network with weighted links based on the activation forces. The study focuses on human proteins within the Human Protein Reference Database (HPRD)20,21, http://hprd.org/, which currently includes information on ∼39,000 interactions among ∼30,000 proteins. To ensure the reliability of the statistics, we only deal with a subset of the interactions, which are those among the proteins that appear in at least 10 protein interactions. The number of proteins that satisfy this condition is 4,729, and the number of related potential pair-wise interactions is 107,711. Adapting the formula of activation forces, we define protein activation forces (paf) to encode the protein interaction information into a network that contains weighted links. Specifically, pafij, which is the weight of the link from node i to node j represents the extent to which protein i actives (in terms of statistics) protein j to realize an interaction; this is computed with the occurrence and co-occurrence frequencies of proteins i and j in all the interactions that are annotated in the database and a close distance. Having defined a candidate distance between two proteins in an interaction as the quotient of the number of participating proteins divided by 2, we take the smallest candidate distance among all the candidate distances between two proteins as their close distance. Because there is no order information for proteins that participate in the interactions in HPRD, the co-occurrences fij and fji are treated equally. Consequently, we have pafij = pafji. Therefore, the acquired symmetrical matrix P = {pafij} maps an un-directed network with 4,729 nodes. For sparse coding, we eliminate the weak links at a threshold of 1.0e-5. As a result, we acquire a sparse network that contains only ∼30,000 undirected links.

The average number of links per node in P is 13.8, but the distribution nearly follows a power law that is characterized by the fact that most of the nodes possess less than 10 links but a few nodes possess over 100. This is consistent with protein interaction networks that have been previously modeled7,8,9. However, in contrast to the binary networks, the links in P are weighted. The distributions of link weights within individual nodes are sharply skewed, which reflects the highly selective nature of the nodes in the interactions (Fig. 3 and Supplementary Information).

Figure 3. Four typical nodes in P.

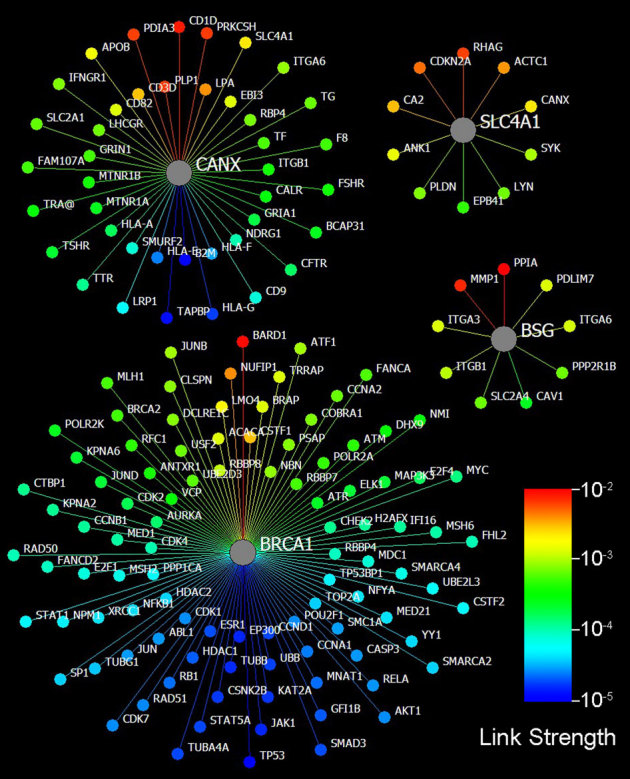
Figure 3

Open in a new tab

For every node (protein), the weighted links are higher than the threshold (1.0e-5), and the corresponding proteins are shown. As examples of link-rich nodes, the proteins BRCA1 and CANX have 99 and 51 links, respectively, while the ordinary proteins SLC4A1 and BSG only have 10 and 9 links, respectively. The sharp decrease at the high end of the link strengths of a node is striking. Note that the coloured strengths are at exponential scales, and the length of a link is not meaningful. *The proteins are named by gene symbols in this study.

Protein affinities measured by Aaf

Having obtained P, we can readily achieve our goal of assessing the affinities between each protein pair in the network by applying the affinity measure Aaf in a simplified form (see the Methods section). After computing the affinities of every pair of proteins in P, we find that Aaf is invaluable for the identification of proteins that are similar in function because our acquired results are often significantly complementary to those of the amino acid sequence aligning algorithms, such as BLAST (basic local alignment search tool)22,23, while the two are generally consistent with each other. Benefited by the link-weighted arithmetic, Aaf frequently identifies the analogous proteins whose amino acid sequences are dissimilar. For example, Aaf can determine that the protein RARS is functionally close to its analogous proteins LARS, MARS and QARS with affinities that are as high as 0.32, 0.27 and 0.19 (as a reference, an affinity higher than 0.05 generally indicates significance, p < 10−3 in random networks), respectively, while BLAST identifies no significant sequence similarity between LARS and every other protein in P because all the E values are larger than 1. In some cases, although BLAST provides valuable matches, Aaf provides more. For example, for MLH1, one of the mismatch repair gene products, BLAST finds only one of its analogs (PMS2) with an E value of 7e-15, while Aaf identifies all three of its analogs (MSH2, MSH6 and PMS2) with affinities as high as 0.14, 0.13 and 0.08.

Meanwhile, we find that our calculated affinity network of proteins is highly consistent with the results from STRING (Search Tool for the Retrieval of Interacting Genes/Proteins), http://string-db.org/, which predicts the functional partners of a given protein by using multiple features that include neighbourhood, gene fusion, co-occurrence, co-expression, experiments, databases and text mining. For example, the top 10 partners of ATM predicted by STRING are TP53, BRCA1, CHEK2, MRE11A, H2AFX, CHEK1, NBN, ABL1, RAD50 and TP53BP1; according to our method, all of these with the exception of TP53 have an affinity to ATM that is higher than 0.03 (p < 10−2) and within the top 30 ones.

A test of the protein clustering performance of the affinity measure

To test the protein clustering performance of the affinity measure that is presented in the study, we randomly selected 50 proteins that form an unbroken network of PPI. We computed the affinities between the 50 proteins based on the pafs between them, and we then clustered the proteins by using the most common method of k-means. We found that the 3-cluster and 4-cluster results are meaningful. Meanwhile, to provide a comparison, we also clustered the proteins with the method that was based on betweenness10,11, which has been considered a benchmark in the literature. Although the 3-cluster result from this method is meaningful as well, the 4-cluster result is meaningless because one of the clusters has only one member. Therefore, the comparison between the 3-cluster results for the two methods is a sensible test of our affinity measure. Table 1 illustrates the comparison with the cluster members and the featured GO (gene ontology) descriptors. The featured GO descriptor of a cluster is the member-shared GO term that has the lowest p-value with the exception of protein binding and nucleus because these two terms are common to all the clusters. From Table 1, we see that while the two methods provide similar results. Our method is superior in terms of the p-values and scores (corresponding to the number of members with the GO terms) of the featured GO descriptors.

Table 1. A comparison of the clustering based on Betweenness and our affinity measure.

  Cluster1 Cluster2 Cluster3
Betweenness based method Members ATM, BARD1, BCCIP, BCL3, BRCA1, CCNA2, CCNB1, CCND1, CCNE1, CDK1, CDK14, CDK2, CDK4, CDKN1A, CSTF1, ESR1, HAP1, LMO4, MAPK14, MDM2, MSH2, MSH6, MYC, NBN, NCL, PARP1, PCNA, PLK1, POLR2A, RAD50, RBBP8, RPA1, RXRA, SREK1, TP53, TRRAP ALK, ARF1, EIF2AK2, NPM1, RPGR, SENP3, TFAP2A GADD45A, GADD45GIP1, HIST1H1A, HIST2H2BE, HIST3H3, HIST4H4, MAP3K4
Featured GO descriptor DNA repairScore = 13, p = 1.00E-16 Protein autophosphorylationScore = 2, p = 2.60E-05 NucleosomeScore = 3, p = 3.01E-08  
Proteins with the descriptor ATM, BARD1, BCCIP, BRCA1, MSH2, MSH6, NBN, PARP1, PCNA, POLR2A, RAD50, RBBP8, RPA1 ALK, EIF2AK2 HIST1H1A, HIST2H2BE, HIST3H3  
Affinity based method Members ATM, BARD1, BCCIP, BCL3, BRCA1, CCNA2, CCNB1, CCND1, CCNE1, CDK1, CDK14, CDK2, CDK4, CDKN1A, CSTF1, ESR1, GADD45A, HAP1, LMO4, MAPK14, MDM2, MSH2, MSH6, MYC, NBN, NPM1, PCNA, POLR2A, RAD50, RBBP8, RPA1, RXRA, TP53, TRRAP ALK, ARF1, EIF2AK2, NCL, PARP1, PLK1, RPGR, SENP3, SREK1, TFAP2A GADD45GIP1, HIST1H1A, HIST2H2BE, HIST3H3, HIST4H4, MAP3K4
Featured GO descriptor DNA repairScore = 14, p = 1.00E-16 Nucleotide bindingScore = 6, p = 1.23E-07 NucleosomeScore = 3, p = 1.72E-08  
Proteins with the descriptor ATM, BARD1, BCCIP, BRCA1, GADD45A, MSH2, MSH6, NBN, NPM1, PCNA, POLR2A, RAD50, RBBP8, RPA1 ALK, ARF1, EIF2AK2, NCL, PLK1, SREK1 HIST1H1A, HIST2H2BE, HIST3H3  
Open in a new tab

*The gene symbols in bold indicate the members which are absent in the corresponding cluster of the compared method. The featured GO descriptors are obtained by using the tool of Set Distiller of GeneDecks. http://www.genecards.org/.

The affinity networks of cancer-associated proteins

This approach to assessing protein similarities initiates a novel study on protein affinity networks. Strikingly, we find that Aaf grasps compact affinity networks that connect cancer-associated proteins (CAPs) that are annotated in HPRD to each other. P includes 60 out of 77 CAPs in HPRD. By setting two thresholds Tp and Ta, we identify a set of proteins for each of which at least Tp CAPs have an affinity that is higher than Ta, and we call them CAP closers (CAPCs). Fig. 4 shows the affinity networks that are constituted by the CAPs and CAPCs at different thresholds of Ta and Tp. The affinity network in Fig. 4a is constructed by the CAPs and CAPCs with 445 affinities (links) higher than 0.03. The detailed data of the network are available in Supplementary Data3. From this affinity network, we understand that the CAPs are functionally close to each other, and we acquire concrete neighbourhoods for them. For example, the neighbourhood of BRCA1 (breast cancer 1), one of the most focused proteins, consists of 6 CAPs RB1, TP53, AR, ATM, EP300 and BARD1, and 12 CAPCs, SP1, PTMA, JUN, ESR1, RELA, E2F1, CEBPB, RFC1, MDM4, CHEK1, NBN and ABL1. Notably, the systematically identified CAPCs in the affinity network have potentially functions in cancer occurrence and remedy. Consistent with this suggestion, some of the CAPCs, e.g., ATR, FANCD2 and BLM, have already been studied in previous cancer studies24,25,26,27.

Figure 4. The affinity networks of cancer-associated proteins.

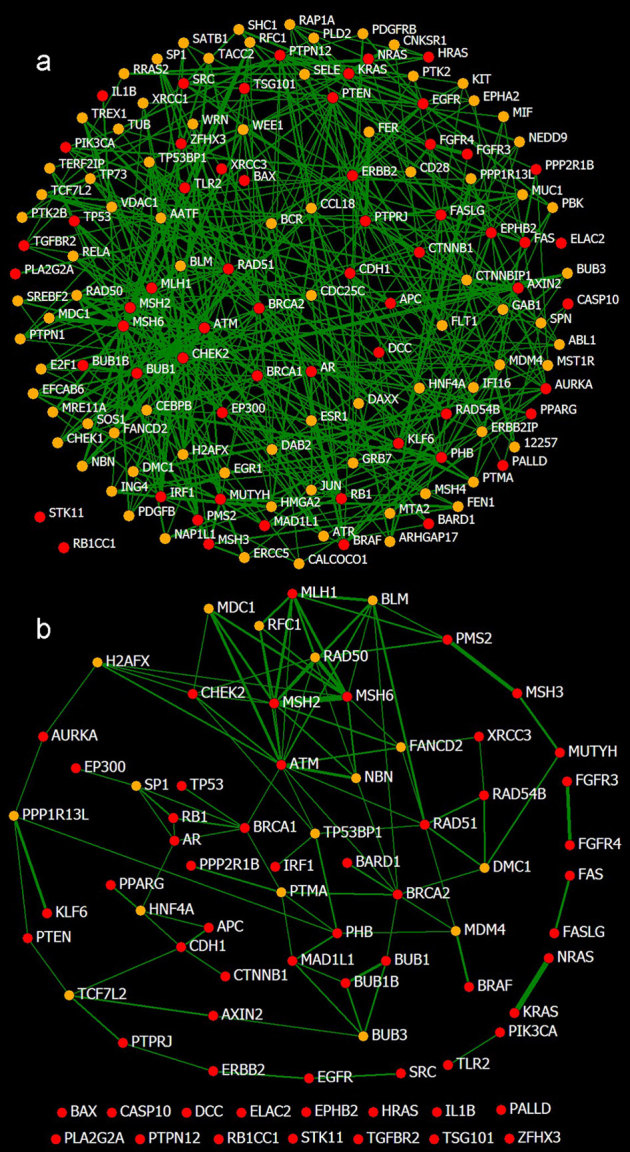
Figure 4

Open in a new tab

The nodes of CAPs (red) and CAPCs (orange) are linked to each other by their affinities that are higher than Ta. The thickness of a link represents the affinity. (a) Eighty-two CAPCs are identified by setting Ta = 0.03 (p < 10−2) and Tp = 4. Incorporating the 82 CAPCs, 58 CAPs form an integral network with 445 links that are stronger than Ta (not including the links between CAPCs), leaving only 2 isolated CAPs. A link-dense portion is located at the bottom left and covers the CAPs of RAD51, MLH1, MSH2, MSH6, BRCA2, ATM, CHEK2, BUB1 and BRAC1. The affinities range from 0.03 (AR∼PTPN1) to 0.31 (MSH6∼MSH2). (b) The core network of the affinities among the CAPs is revealed by enhancing Ta to 0.04 (p < 10−3), which includes 37 CAPs and 16 CAPCs. Eight CAPs are paired and 15 are isolated. The central portion that consists of ATM, MSH2, MSH6, CHEK2 and BRCA1 is crucial, which is consistent with the results of previous studies31,32,33,34,35. The 16 CAPCs may be particularly meaningful for cancer study. The affinities range from 0.04 (MSH6∼CDX2) to 0.31 (MSH6∼MSH2).

Detailed analyses (Supplementary Information) show that the CAPs of MSH6, ATM, RAD51, FASLG, PHB, BRCA1, MSH2, ERBB2 and BRCA2 contain rich links (more than 18 vs. a mean of 8.43) in the affinity network, which reveals their important roles as hubs among those protein affinities. The CAPCs of FLT1, PTMA, RFC1, FANCD2, BLM and TP53BP1 also play significant roles in the connection of the network due to their rich links (more than 7 vs. a mean of 4.68).

Another notable point is that the distribution of the affinities over the links is skewed rather than even (Supplementary Information). The average value of the affinities is 0.05; 200 of the values are lower than 0.04, and 44 are higher than 0.08. This distribution indicates that close attention must be paid to the protein pairs that have the high affinities. Table 2 lists the 44 protein pairs that contain high affinities and the corresponding BLAST E values. The 10 pairs within CAPs are shadowed.

Table 2. Protein pairs with high Aaf.

CAP CAP/CAPC Aaf Blast E value CAP CAP/CAPC Aaf Blast E value
MSH6 MSH2 0.31 4e-059 ATM ATR 0.10 8e-063
KRAS NRAS 0.22 4e-084 BRAF MDM4 0.10 > 10
MSH6 RAD50 0.21 > 10 MSH6 MRE11A 0.10 > 10
PMS2 MSH3 0.18 > 10 FAS FASLG 0.09 > 10
PTPRJ FER 0.17 > 10 RAD51 BLM 0.09 > 10
FGFR3 FGFR4 0.16 0 MSH2 BLM 0.09 > 10
ATM MDC1 0.15 > 10 EGFR SHC1 0.09 > 10
MSH2 MLH1 0.13 > 10 MUTYH MSH3 0.09 > 10
IRF1 HMGA2 0.13 > 10 IRF1 TACC2 0.09 > 10
MLH1 BLM 0.13 > 10 ATM H2AFX 0.09 > 10
BUB1B BUB1 0.13 1e-027 PTPRJ MUC1 0.09 > 10
MLH1 MSH6 0.12 > 10 NRAS CNKSR1 0.09 > 10
KLF6 PPP1R13L 0.12 > 10 RAD54B DMC1 0.09 > 10
ATM NBN 0.11 > 10 MSH6 RFC1 0.08 > 10
IRF1 ING4 0.11 > 10 BUB1 BUB3 0.08 > 10
AR ESR1 0.11 8e-040 MUTYH ERCC5 0.08 > 10
MSH6 MDC1 0.11 > 10 PMS2 MLH1 0.08 8e-015
MLH1 RFC1 0.11 > 10 MUTYH FEN1 0.08 > 10
PHB EFCAB6 0.11 > 10 PMS2 RAD50 0.08 > 10
MSH2 MDC1 0.11 > 10 MSH2 RFC1 0.08 > 10
MLH1 RAD50 0.11 > 10 BUB1B BUB3 0.08 > 10
MSH2 RAD50 0.10 > 10 NRAS RRAS2 0.08 5e-024
Open in a new tab

The reliability of the pairings within CAPs and those with very low E values of the BLAST, 13 out of the 44 pairs, is obvious. The rest 31 pairs are each combined by one CAP and one CAPC. Among them, two pairs, BUB1∼BUB3 and BUB1B∼BUB3, are readily accepted due to the same protein family they belong to. With the common functions of the components of the famous complex BASC28, at least 10 more pairs MSH6∼RAD50, MLH1∼BLM, ATM∼NBN, MLH1∼RFC1, MLH1∼RAD50, MSH2∼RAD50, MSH6∼MRE11A, MSH2∼BLM, MSH6∼RFC1, and MSH2∼RFC1 can also be recognized. Therefore, at least 25 of the 44 pairs show obvious affinities or similarities, which demonstrate the reliability of the outcome. Notably, only 5 out of the 25 obvious affinities can be identified by BLAST (E value < 1). Based on the reliability of our results, we can conclude that the affinity network may provide novel information for cancer studies. For example, a direct link between a CAP and a CAPC may suggest an unknown cancer-related interaction between them, and a hub protein in the affinity network may play a crucial role in cancer-related signal transduction pathways.

Discussion

Generally, our presented statistics of activation forces informatively weight the links of a complex network, which leads to the affinity measure Aaf that sensibly assesses word affinities in a word network and protein affinities in a PPI network.

The experiment that used 10,000 of the most frequently used English words shows that Aaf is superior for the identification of similar word pairs and clusters; this verifies the plausibility of the proposed approach. From a broader viewpoint, our approach may also reveal the learning mechanism that is utilized by linguistic neural networks. The hypothesis that statistical information underlies linguistic neural networks has long been proposed29. However, the specific statistics that are required to develop the neural networks remain unclear. The statistics of activation forces for words efficiently capture the substantial associations between words, and automatically lead to human knowledge-consistent word networks. This suggests that the newly identified statistics are likely to induce a promising change in the understanding of the learning mechanism.

The experiment of the PPI network that contains ∼5,000 human proteins presents a general method for the identification of functionally similar proteins, which may have interactions, the same interaction partners, or both. The method is shown to be significantly complementary to the amino acid sequence-aligning algorithms, which can only identify similarities between homologs; therefore, the proposed method is practically invaluable in biology and medicine. As a more concrete example, we find that CAPs are functionally linked to each other, and their affinity networks contain certain hub proteins. We found that CAPCs are also potentially meaningful for cancer studies, and some of the close affinities that exist between the CAPCs and the CAPs may be revealed for the first time in this study.

Obviously, this type of affinity network can also be useful to identify other functional clusters of proteins. Therefore, our approach provides a generally effective method to study protein functions. Notably, our result is obtained based solely on the current information in HPRD. As biological study progresses and richer information becomes available, our approach will provide more informative outcomes.

Based on the striking results of the two typical complex networks, one can see the effectiveness and generality of our approach to measuring affinities in complex networks. In combination with advanced clustering technologies, the approach is expected to achieve more in the applications of the clustering of various complex networks. Specifically, our link-weighting method presents a distinguished method to encode enriched information with sparse links, which facilitates the structured realization and analysis of complex networks. All of these advantages are derived from the statistics of activation forces, which are defined for the first time in this study.

Methods

Definition of the affinity measure Aaf

The affinity between nodes i and j is defined as

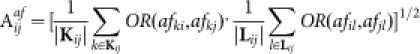graphic file with name srep00113-m1.jpg

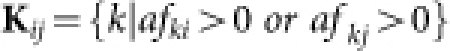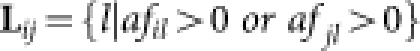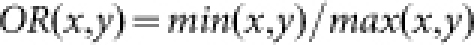where Inline graphic, Inline graphic, and Inline graphic. Readily, Kij is the set of labels of nodes with out-links to node i or node j, while Lij is the set of labels of nodes with in-links from node i or node j. OR(x,y) is an overlap rate function of x and y. Fig. 5 illustrates the computation of the affinity measure with a toy example. Obviously, 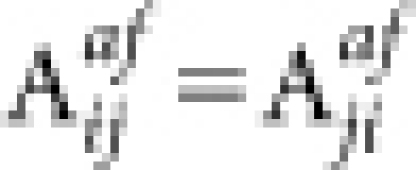Inline graphic. Note that, when the activation matrix is symmetrical, such as P, the affinity measure is simplified as:

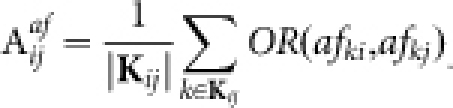graphic file with name srep00113-m6.jpg

Figure 5. Illustration of the computation of the affinity measure.

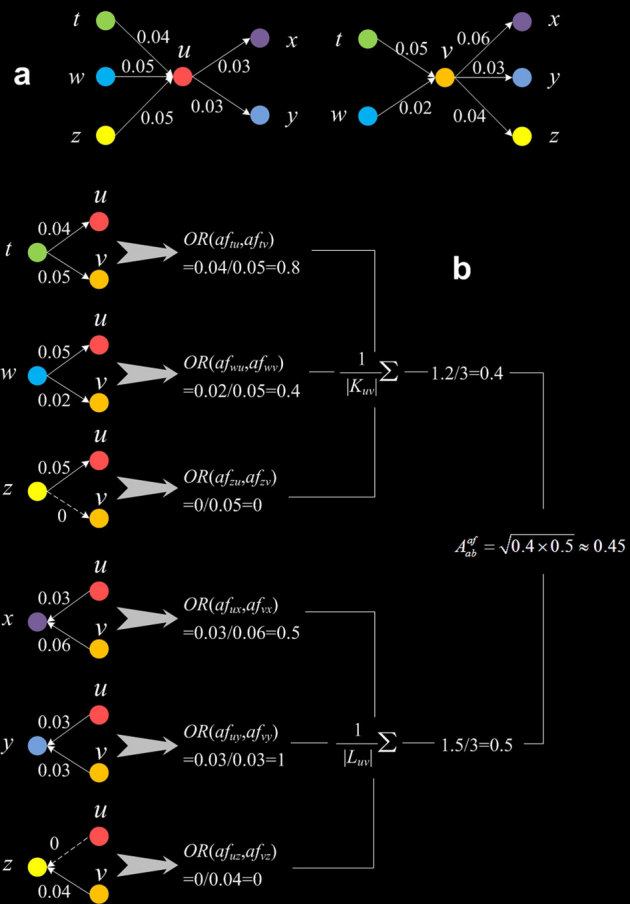
Figure 5

Open in a new tab

(a) The affinity between the central nodes u and v will be computed. The digits on the links are pafs, and the colours of the nodes are simply used for their identification. (b) From the mean in-link overlap rate (upper portion) and the mean out-link overlap rate (lower portion) to the geometric average of the two, i.e., the affinity.

The steps for the main findings

The study is initiated from our statistics of activation forces, which weight the links in complex networks by making the nodes distinct and lead to a superior measure of the affinities between the nodes Aaf. We apply the link-weighting and affinity-measuring scheme to analyze word networks and protein interaction networks, respectively. In word networks, we

  1. Count word frequencies in the BNC and constitute the vocabulary

  2. Count the co-occurrences of the words in the vocabulary

  3. Compute the word activation forces (wafs) that form the directed word network (W)

  4. Compute the word affinities (Aafs)

  5. Identify word clusters with these affinities

In protein interaction networks, we

  1. Count the occurrence frequency of protein interactions for every protein in HPRD, and take the proteins whose frequency is at least 10 as study objects

  2. Count the co-occurrences of the proteins in the protein interactions

  3. Compute the protein activation forces (pafs) that form the un-directed protein interaction networks (P)

  4. Compute the protein affinities (Aafs)

  5. For the cancer-associated proteins (CAPs) in P, identify the CAP closers (CAPCs), such that at least Tp CAPs have an affinity higher than Ta, constituting informative networks of these CAPs and CAPCs by setting proper thresholds of Tp and Ta

Calculation method of word activation forces

The activation force from word i to word j is formulated by (fij / fi) (fij / fj )/dij2, where fi and fj are the occurrence frequencies of word i and word j in the corpus, respectively, fij is their co-occurrence frequency counted within a predetermined word window, and dij is the average distance by which word i precedes word j in their co-occurrences. These basic statistics are counted in the following manner.

Counting basic statistics of words in the BNC

We use the BNC to count the basic statistics of English words. The BNC is a 100 million word collection that is popular in the community of computational linguistics. It is designed to represent a wide cross-section of both spoken and written British English from the latter part of the 20th century, both spoken and written. Both the written part portion (90%) and the spoken part portion (10%) are collected in diverse contexts.

We use the latest BNC XML Edition released in 2007 with an institutional license.

Additional information regarding the corpus can be found at http://www.natcorp.ox.ac.uk/corpus/.

To distinguish the contexts of the different forms of a word, this study counted the occurrences of words in the BNC in a literal fashion, which means that different forms of a word type were treated as different words. However, for simplicity, all upper cases were changed into lower cases. For example, change, changed, changing, term, and terms were treated as 5 different words, but CAT, Cat and cat were treated as the same word cat.

By simply counting the occurrences of each word in the BNC, a frequency is obtained. The most frequent 10,000 words were selected to form the vocabulary. The most frequent word (the) occurs 6,046,442 times, and the 10,000th frequent word (optimum) occurs 612 times. For the preliminary experiments of the prediction of word activation effect and affinity measure validation that were compared with previous studies15,30, an additional set of 44 words were also added into the vocabulary. Therefore the exact number of words in the vocabulary is 10,044.

By simply counting the occurrences of each word in the corpus, the frequency is obtained.

To count the co-occurrence frequency fij, the limit of the furthest position (indicated by word number) where word j appears behind word i, which is referred to as L, should be predetermined. Referring to previous work19, we tested L around 5 in this study. We found that values of wafs are not sensitive to L when it ranges from 4 to 5 and 6. Therefore we only provide the results of L = 5 in the main text.

The counting of the co-occurrences of words within a limit distance L is one point of this work. To ensure the ratios of fij to fi and fij to fj are less than or equal to 1 (actually, with the two ratios the conditional probabilities of p (word i, word j| word i, L) and p (word i, word j| word j, L) are estimated), we only count the co-occurrences of word i and word j where neither word i nor word j appears in the intervening words. The necessary conditions for the identification of a co-occurrence of word i and word j are as follows:

  • There are no punctuates between word i and word j.

  • Neither word i nor word j appears within the intervening word sequence.

To follow these restraints, the traditional moving window-based co-occurrence counting method19 should be modified as below:

  • If there are any punctuates within the window (L+1 sized), decrease the right boundary of the window until all the punctuates are excluded.

  • If there are any appearances of word i within the intervening word sequence, decrease the right boundary of the window to the first appearance of word i. For example, suppose L = 6 and the words in the current window are “care is loss of care with old”; the window must be decreased to only include the first five words “care is loss of care”.

  • Identify the first co-occurrences of the head word (word i) with each of the following words within the window in the order from left to right, i.e., leave out the duplicated co-occurrences of an identical word pair within the same window. For example, suppose the words in the current window are “my care is loss of care with”; the first co-occurrence of my-care in distance 1 will be identified, and the second co-occurrence of my-care in distance 5 will be ignored. Meanwhile, the co-my-is in distance 2, my-loss in distance 3, my-of in distance 4 and my-with in distance 6 will also be identified.

To obtain dij, which is the average distance in the co-occurrences, the distance between word i and word j in every co-occurrence is accumulated.

Calculation method of protein activation forces

The activation force from protein i to protein j is also formulated by (fij / fi) (fij / fj )/dij2; however, the basic statistics are defined in a distinct manner. Specifically, fi (fj) is the occurrence frequency of protein i (protein j) in a PPI database that annotates protein interactions (including those in complexes) that have been verified or suggested in different experiments that are published in the literature. Therefore, two proteins may co-occur in multiple interactions that are annotated in the database, and this co-occurrence frequency (fij) provides information on the tightness between them. dij is the close distance, which is the smallest distance of the candidate distances between the proteins in their interactions. These basic statistics are counted in the following manner.

Counting basic statistics of proteins in HPRD

HPRD currently includes information pertaining to ∼39,000 interactions among ∼30,000 proteins. We downloaded the XML documents that describe these interactions and counted the basic statistics of the proteins locally. One of the available packages (PSIMI_XML) provides the entire information on all the proteins interactions that is annotated by the database producers. Therefore, we simply count the occurrences of a protein in all the annotated interactions as its occurrence frequency, which is equal to the number of all potential pair-wise interactions of the protein with others (including itself), and we count the co-occurrence of a pair of proteins in every single interaction as their co-occurrence frequency.

To ensure the reliability of the statistics, we take only the proteins whose occurrence frequencies are at least 10 as our study objects. The number of proteins that satisfy the condition is 4,729.

A key problem of basic statistics is how to determine the distance of two proteins in the formula of paf. For the binary interaction, the distance between two proteins can reasonably be decided as one. However, for the interaction with multiple participants, the distances of every pair of proteins are unknown without the detailed information from the interaction structure. As a simplified solution, we define the candidate distance for every pair of proteins involved in an interaction as the quotient of the number of participating proteins divided by 2, and we take the smallest value among all the candidate distances between two proteins as their close distance used in the paf formula. For example, if protein a participates in the following three interactions {a,b}, {a,c} and {a,b,c}, then the candidate distances between proteins a and b are 1 and 1.5, and the close distance between them is 1.

To exclude the negative effect that is caused by the uncertainty of a large complex (an interaction involving many participants), we do not count the interactions that contain more than 10 proteins.

Computing protein similarity with BLAST

To compare the protein affinities that are measured by Aaf with the protein similarities that are measured by the amino acid sequence aligning algorithms, we downloaded the BLAST (basic local alignment search tool) software program and created a custom database that contained the amino acid sequences of the 4,729 proteins in our study. Based on this database, BLAST can identify similar proteins within the 4,729 proteins for any target protein.

Author Contributions

J. G. presented the formulae of the activation forces and the affinity measures, computed the activation force networks and the affinity networks, and wrote the manuscript. H. G. prepared materials, compared our results with those of others, and revised the manuscript. Z. W. counted the basic statistics of the words and proteins in the BNC and the HPRD, respectively, and illustrated the word and protein networks.

Supplementary Material

Supplementary Information

supplementary information

srep00113-s1.pdf (898KB, pdf)
Supplementary Information

Dataset 1

srep00113-s2.xls (3.4MB, xls)
Supplementary Information

Dataset 2

srep00113-s3.xls (516KB, xls)
Supplementary Information

Dataset 3

srep00113-s4.xls (49KB, xls)

Acknowledgments

The authors thank Guang Chen for discussions that inspired this study and Yang Luo and Junliang Bai for their assistance in initial data analysis. The research was supported by the Chinese 111 program Advanced Intelligence and Network Service under grant no. B08004 and a key project of the Ministry of Science and Technology of China under grant no. 2011ZX03002-005-01.

References

  1. Frey B. J. & Dueck D. Clustering by Passing Messages between Data Points. Science 315, 972–976 (2007). [DOI] [PubMed] [Google Scholar]
  2. Palla G., Derenyi I., Farkas I. & Vicsek T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 435, 814–818 (2005). [DOI] [PubMed] [Google Scholar]
  3. Ahn Y. Y., Bagrow J. P. & Lehmann S. Link communities reveal multiscale complexity in networks. Nature 466, 761–764 (2010). [DOI] [PubMed] [Google Scholar]
  4. Roweis S. T. & Saul L. K. Nonlinear dimensionality reduction by locally linear embedding. Science 290, 2323–2326 (2000). [DOI] [PubMed] [Google Scholar]
  5. Guimera R., Newman M. E. J. & Moore C. Finding community structure in very large networks. Phys. Rev. E 70, 066111 (2004). [DOI] [PubMed] [Google Scholar]
  6. Wu J. et al.. Integrated network analysis platform for protein-protein interactions. Nat. Methods 6, 75–77 (2009). [DOI] [PubMed] [Google Scholar]
  7. Jansen R. et al.. A Bayesian Networks Approach for Predicting Protein-Protein Interactions from Genomic Data. Science 302, 449–453(2003). [DOI] [PubMed] [Google Scholar]
  8. Stelzl U. et al.. A Human Protein-Protein Interaction Network: A Resource for Annotating the Proteome. Cell 122, 957–968 (2005). [DOI] [PubMed] [Google Scholar]
  9. Rual J. F. et al.. Towards a proteome-scale map of the human protein–protein interaction network. Nature 437, 1173–1178 (2005). [DOI] [PubMed] [Google Scholar]
  10. Girvan M. & Newman M. E. J. Community structure in social and biological networks. Proc. Natl Acad. Sci. USA 99, 7821–7826 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Radicchi F., Castellano C., Cecconi F., Loreto V. & Parisi D. Defining and identifying communities in networks. Proc. Natl Acad. Sci. USA 101, 2658–2663 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Clauset A., Moore C. & Newman M. E. J. Hierarchical structure and the prediction of missing links in networks., Nature, 453, 98–101, 2008 [DOI] [PubMed] [Google Scholar]
  13. Turkeltaub P. E., Gareau L., Flowers D. L., Zeffiro T. A.&, Eden G. F. Development of neural mechanisms for reading. Nature Neurosci. 6, 767–773 (2003). [DOI] [PubMed] [Google Scholar]
  14. Balota D. A. & Lorch R. F. Depth of automatic spreading activation: Mediated priming effects in pronunciation but not in lexical decision. J. Exp. Psychol. Learn. Mem. Cogn. 12, 336–345 (1986). [Google Scholar]
  15. McKoon G. & Ratcliff R. Spreading activation versus compound cue accounts of priming: Mediated priming revisited. J. Exp. Psychol. Learn. Mem. Cogn. 18, 1155–1172 (1992). [DOI] [PubMed] [Google Scholar]
  16. Kutas M. & Hillyard S. A. Brain potentials during reading reflect word expectancy and semantic association. Nature 307, 161–163 (1984). [DOI] [PubMed] [Google Scholar]
  17. Henson R., Shallice T. & Dolan R. Neuroimaging Evidence for Dissociable Forms of Repetition Priming. Science 287, 1269–1272 (2000). [DOI] [PubMed] [Google Scholar]
  18. Crinion J. et al.. Language Control in the Bilingual Brain. Science 312, 1537–1540 (2006). [DOI] [PubMed] [Google Scholar]
  19. Church K. & Hanks P. Word association norms, mutual information, and lexicography. Comput. Linguist. 16, 22–29 (1990). [Google Scholar]
  20. Mathivanan S. et al.. Human Proteinpedia enables sharing of human protein data. Nature Biotech. 26, 164–167 (2008). [DOI] [PubMed] [Google Scholar]
  21. Peri S. et al.. Development of Human Protein Reference Database as an Initial Platform for Approaching Systems Biology in Humans. Genome Res. 13, 2363–2371 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lipman D. J. & Pearson W. R. Rapid and Sensitive Protein Similarity Searches. Science 227, 1435–1441 (1985). [DOI] [PubMed] [Google Scholar]
  23. Altschul S. F. et al.. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 25, 3389–3402 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Ababou M. et al.. ATM-dependent phosphorylation and accumulation of endogenous BLM protein in response to ionizing radiation. Oncogene 19, 5955–5963 (2000). [DOI] [PubMed] [Google Scholar]
  25. Jin S. et al.. Menin associates with FANCD2, a protein involved in repair of DNA damage. Cancer Res. 63, 4204–4210 (2003) [PubMed] [Google Scholar]
  26. Hussain S. et al.. Direct interaction of FANCD2 with BRCA2 in DNA damage response pathways. Hum. Mol. Genet. 13, 1241–1248 (2004). [DOI] [PubMed] [Google Scholar]
  27. Chen J. Ataxia telangiectasia-related protein is involved in the phosphorylation of BRCA1 following deoxyribonucleic acid damage. Cancer Res. 60, 5037–5039 (2000). [PubMed] [Google Scholar]
  28. Wang Y. et al.. BASC, a super complex of BRCA1-associated proteins involved in the recognition and repair of aberrant DNA structures. Genes & Dev. 14, 927–939 (2000). [PMC free article] [PubMed] [Google Scholar]
  29. Seidenberg M. S. Language Acquisition and Use: Learning and Applying Probabilistic Constraints. Science 275, 1599–1603 (1997). [DOI] [PubMed] [Google Scholar]
  30. Rubenstein H. & Goodenough B. Contextual correlates of synonymy. Comm. of the ACM 8, 627(1965). [Google Scholar]
  31. Matsuoka S. et al.. ATM and ATR Substrate Analysis Reveals Extensive Protein Networks Responsive to DNA Damage. Science 316, 1160–1166 (2007). [DOI] [PubMed] [Google Scholar]
  32. Walsh T. et al.. Spectrum of mutations in BRCA1, BRCA2, CHEK2, and TP53 in families at high risk of breast cancer. J. American Med. Asso. 295, 1379–1388 (2006). [DOI] [PubMed] [Google Scholar]
  33. Lee J. H. & Paull T. T. Activation and regulation of ATM kinase activity in response to DNA double-strand breaks. Oncogene 26, 7741–7748 (2007). [DOI] [PubMed] [Google Scholar]
  34. Schmutte C. et al.. The interaction of DNA mismatch repair proteins with human exonuclease I. J. Biol. Chem. 276 (35), 33011–33018 (2001). [DOI] [PubMed] [Google Scholar]
  35. Schmutte C. et al.. Human exonuclease I interacts with the mismatch repair protein hMSH2. Cancer Res. 58, 4537–4542 (1998). [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

supplementary information

srep00113-s1.pdf (898KB, pdf)
Supplementary Information

Dataset 1

srep00113-s2.xls (3.4MB, xls)
Supplementary Information

Dataset 2

srep00113-s3.xls (516KB, xls)
Supplementary Information

Dataset 3

srep00113-s4.xls (49KB, xls)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES