Clustering in Cell Cycle Dynamics with General Response/Signaling Feedback

Abstract

Motivated by experimental and theoretical work on autonomous oscillations in yeast, we analyze ordinary differential equations models of large populations of cells with cell-cycle dependent feedback. We assume a particular type of feedback that we call Responsive/Signaling (RS), but do not specify a functional form of the feedback. We study the dynamics and emergent behaviour of solutions, particularly temporal clustering and stability of clustered solutions. We establish the existence of certain periodic clustered solutions as well as “uniform” solutions and add to the evidence that cell-cycle dependent feedback robustly leads to cell-cycle clustering. We highlight the fundamental differences in dynamics between systems with negative and positive feedback. For positive feedback systems the most important mechanism seems to be the stability of individual isolated clusters. On the other hand we find that in negative feedback systems, clusters must interact with each other to reinforce coherence. We conclude from various details of the mathematical analysis that negative feedback is most consistent with observations in yeast experiments.

1 Introduction

1.1 Background

In this paper we consider simple dynamical models of the cell division cycle. Specifically, consider a culture of n cells, in which the progression of the i-th cell is governed by the equation:

$$\frac{d{x}_i}{dt}=1+a(x_i,\stackrel{‒}{x}).$$ (1.1)

where x_i is the position of the cell within the cycle and $\stackrel{‒}{x}$ denotes the state of all the cells in the culture. We will describe the dependence of a on x_i and $\stackrel{‒}{x}$ below.

Our primary motivation for this model is recent theoretical and experimental work on Yeast Autonomous Oscillations (YAO) ([47], [55], [9], [23], [31]), the periodic oscillations of physiologically relevant variables that have been reported and studied for over 40 years [9, 16, 28, 32, 37, 39, 40, 41, 44, 46, 49, 57, 60, 61] (and many others). Different types of YAO have been called metabolic [55], glycolytic [2] or respiratory [23] oscillations. The control of oscillation and the regulation of yeast metabolism has been an important theme in the chemical engineering literature devoted to the efficient management of bioprocesses [7, 21, 26, 53, 62]. These phenomena are of basic biological interest because they expose questions regarding the coordination of the cell cycle and metabolism, and interconnectedness of various cellular and genetic processes [4, 31]. A correlation between YAO and the bud index was noted as early as [32, 37]. However, it seems that the link between YAO and the Cell Division Cycle (CDC) was obscured by the fact that the periods of YAO always shorter than the CDC times (computed from dilution rate) and a relationship between YAO and the CDC seems to have been largely ignored. However in [31], [55] and elsewhere, the correlation between YAO and CDC was again noted in genetic expression data.

In [3] and [47] the authors proposed cell cycle clustering as a possible explanation of the interaction between YAO and the CDC. Figure 1 roughly illustrates the arrangement of phases of the cell cycle of yeast. We hypothesized that subtle feedback effects on CDC progression could cause populations of cells to segregate into approximately CDC-synchronized subpopulations. Experimental bud index data reported in [47] supported this picture. In [3] the authors studied a few simple forms of (1.1) with the hypothesis that cells in one part of the CDC may influence other cells in Different parts of the CDC in Different ways through various diffusible chemical products. We hypothesized that a large subpopulation of cells in the critical S-phase might e ect metabolism production and the metabolites may in turn inhibit or promote cell growth in the later part of the G1 phase, thus setting up a feedback mechanism in which YAO and CDC clustering are inextricably intertwined. We showed analytically and numerically that differential CDC feedback such as this can robustly cause CDC clustering in the models. By clustering we do not mean spatial clustering (cultures that exhibit YAO occur in well-mixed bioreactors), but groups of cells that are traversing the CDC in near synchrony.

Figure 1.

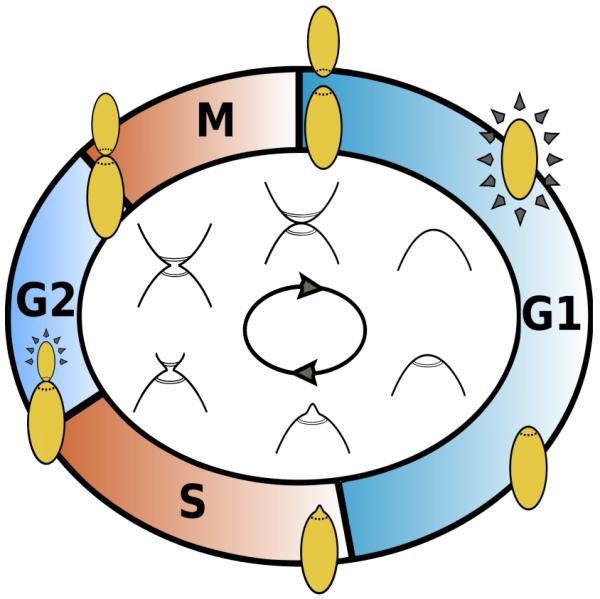
Phases of the yeast cell cycle. The G1 phase begins following cell division. The beginning of the DNA synthesis phase, S, coincides with budding. G2 is a second “gap” phase. The M phase is characterized by narrowing or “necking” between the parent and daughter cell; it ends in cell division. The hypothesized R region is the later portion of G1 and the signaling region S is in the S phase. That is, a large subpopulation of cells in the replicative S phase may promote or inhibit progression of cells approaching the G1-S boundary.

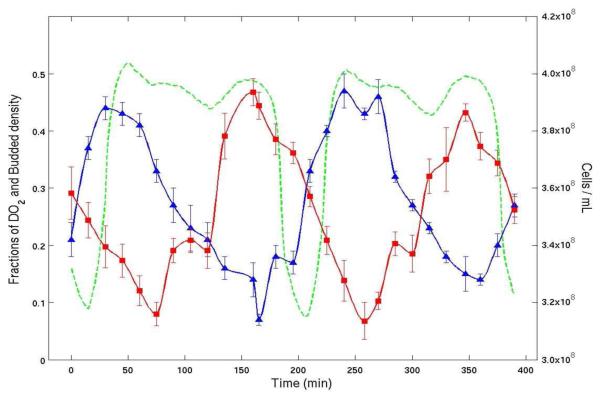
Guided by these mathematical results, we verified the existence of clusters in two types of oscillating yeast [52] using both bud index and cell density data. Some of the measurements from those experiments are shown in Figure 2. First we note that the cell cycle period, as calculated by the dilution rate, is approximately 400 minutes, and two O₂ oscillations occur during this period, suggesting that there may be two clusters. Next, analyzing the figure, we see that approximately half of the cells are budding at times t = 50 and t = 250, while at t = 170 less than 10% of the cells are budded. Each budding event is accompanied by a decrease in density (no cells are dividing) and followed by a sharp increase in cell density as these budded cells proceed through division. Note that at t = 170 since less than 10% of the cells are budded, most of the cells must be in the G1 phase of the cycle. When the bud index hits its next maximum at t = 250, approximately half of the cells must have budded. The other half of the cells must at that time still be in the G1 phase. As the cells that are budded then divide and the cell density increases, the cells that remained in G1 must still be in G1 since the bud index is again low. When the first group of cells has divided, the second group has been in G1 for at least 200 minutes. The next rise in bud index then must be due to these cells, since they have had time to mature, while the first group of recently divided cells clearly has not had time to reach budding again. Thus, these experiments show conclusively the existence of two clusters and that CDC clustering coexists with YAO.

Figure 2.

Experimental time series from a continuous culture of budding yeast. Dissolved O₂ percentage (green), bud index percentage (blue) and cell density (red) are plotted versus elapsed time. The average cell cycle period as calculated from dilution rate was about 400 minutes. The plot shows clearly that the bud index (percentage of cells with buds from microscopy) and cell density (by flow cytometry) are both synchronized with the oscillation in the level of dissolved O₂.

1.2 Modeling of the cell cycle and feedback

In standard modeling the cell volume v_i(t) is a proxy for position in the cell cycle. This has justification for yeast in that milestones in the cell cycle, such as the onset of budding, are closely associated with volume milestones and thought to be causally related. Measurements show that the growth of a single cell is roughly exponential, so a first order approximation is that the volume of the i-th cell satisfies a linear differential equation

$$\frac{d{v}_i}{dt}=c{v}_i.$$ (1.2)

A frequent assumption on the growth rate c is that it does not depend on v_i i.e. it is independent of the cell’s current state within the cycle and on other cells; it depends instead on the nutrients available and other environmental factors. Applying a logarithmic change of variables the growth law becomes dx_i/dt = c, and by further normalizing both the coordinate x and time, the cell cycle can be represented by the unit interval [0, 1], and the equation of motion becomes dx_i/dt = 1. In this simple model each cell reaches division (cytokinesis) at 1 when it returns (perhaps with its descendant cell) to 0 and begins the cycle again. Note that a change to normalized coordinates does not depend essentially on the form of (1.2); if there is no interaction between cells and cells never stop growing, then one can change variables to the form dx_i/dt = 1, with x_i(t) ∈ [0, 1].

A much more general model (again using normalized coordinates) is (1.1). We proposed to consider forms of (1.1) where the cells in one portion of the cell cycle, S for signaling, may influence the growth rate of cells in a preceding portion that we term R for responsive. For example the R region may reside in the later portion of the G1 phase and the signaling region S may be the biological S phase (see Figure 1). This is philosophically justified by the fact that the S phase is the most critical part of the CDC and the link between YAO and CDC may function to protect the integrity of transcription [9]. It is also known that growing yeast store carbohydrates, then liquidate them in the late G1 phase [17]. The actual positions of the signaling and responsive regions within the biological cell cycle play no role in the mathematical analysis. In the rest of the paper we will use S to denote the signaling region and on the few occasions when we refer to the yeast’s S phase we will do so explicitly.

Mathematically, the interval [0, 1], with the endpoints identified is a circle. On this circle, we can specify a positive direction as associated with the increasing direction on [0, 1]. Distance between points x and y on the circle using these coordinates is given by the minimum of |x − y| and 1 − |x − y|.

Definition 1.1

Consider n cells whose coordinates are given by x_i ∈ [0, 1], 1 identified with 0, and governed by an equation of the form (1.1). When a cell reaches 1 it continues at 0. We call such a system a RS-feedback system if:

• (H1)R is an interval that directly precedes another interval S, i.e. the last endpoint of R is the first endpoint of S,
• (H2)$a(x_i,\stackrel{‒}{x})$ vanishes except when x_i ∈ R and there are some x_j in S,
• (H3)$0<v_{min}\le 1+a(x_i,\stackrel{‒}{x})\le v_{max}forall{x}_{i}and\stackrel{‒}{x}$,
• (H4)feedback is monotone, thus adding a cell to S will increase the value $\mid a(x_i,\stackrel{‒}{x})\mid$ for x_i ∈ R, and,
• (H5)$a(x_i,\stackrel{‒}{x})$ is a smooth function for x_i in the interior or R and each x_j in the interior of S, j ≠ i and the one sided derivatives exist at the boundaries of R and S.

By positive feedback we mean a is positive for x_i ∈ R if there are one or more x_j in S. We define negative feedback in the analogous way.

For the sake of definiteness we will specify throughout the rest of the paper:

$$S=[0,s)\text{and}R=[r,1),0<s<r<1.$$

The final endpoint of R is 1, which corresponds to 0, the initial endpoint of S. See Figure 3 below.

Figure 3.

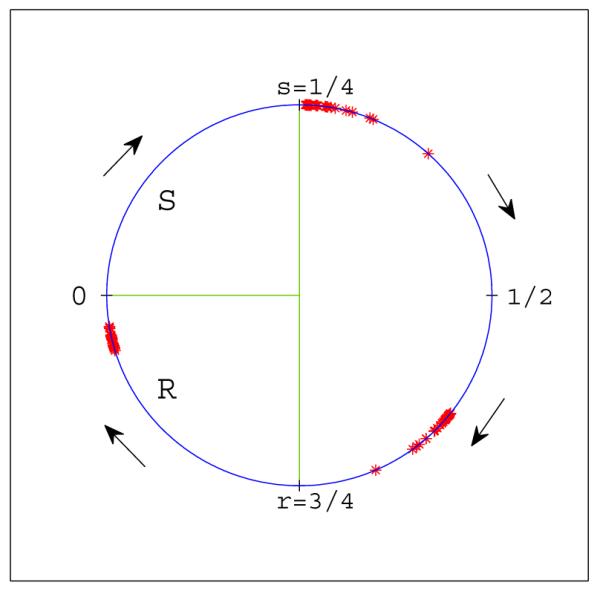
Our coordinate representation of the cell cycle and (weakly clustered) groups of cells from a negative feedback simulation with n = 200 and parameter values s = .25 and r = .75. Positions of individual cells are denoted by red asterisks. In this coordinate system the S region is the interval [0, .25) and the R region is [.75, 1), where 1 is identified with 0.

Note that our restriction that R precedes S, while motivated by biological considerations, is not the only possibility. It is worth noting that in the reverse case, when R follows S, many of our results hold with the roles of positive and negative feedback reversed. In particular, this is true for Propositions 3.1, 3.2, 3.4, 4.1, 4.2, and Corollary 4.3.

In [3] we considered two idealized forms of (1.1) with threshold-triggered feedback and found that with either positive or negative linear feedback, we robustly observe clustering. We also observed that the number of clusters formed is less dependent on the form of the feedback than on the sizes of the signaling and responsive regions, S and R. One aim of the present paper is to demonstrate that clustering typically occurs in a broad class of models (1.1), beyond the idealized situations investigated in [3]. The other aim is to study key differences between positive and negative feedback in the models in order to understand if one or the other is more favorable for clustering and thus more likely to be the process behind experimental observations.

Note in Definition 1.1 that the number of cells in the culture is fixed at n. Thus we will consider neither death, harvesting or proliferation. In the oscillation experiments we are modeling there are in fact proliferation and harvesting (and an insignificant rate of death), but they approximately balance when averaged over a cell cycle. Thus the expected number of cells descended from a single cell at any future cycle is approximately 1. Further, in the model we are considering, there is no distinction between the two cells resulting from a division and to keep track of both trajectories would be redundant.

The differential equation in the general model (1.1) with RS feedback may have discontinuities. Thus we need to consider uniqueness and global existence of solutions. First consider that the equations may be discontinuous only when a variable is at the boundaries of R and S i.e. at the hyper-surfaces given by x_j = 0, s, r for some j. We obtain uniqueness since by (H3) any solution crosses a surface of discontinuity non-tangentially with non-zero speed. Global existence follows from boundedness of the vector field (H3).

A version of the model that we will study in sections 6 and 7 is:

$$\frac{d{x}_i}{dt}=\{\begin{array}{cc}1,\hfill & \text{if}{x}_i\notin R\hfill \\ 1+f\left(I\right),\hfill & \text{if}{x}_i\in R\hfill \end{array}\phantom{\}}$$ (1.3)

where

$$I\left(\stackrel{‒}{x}\right)\equiv \frac{\#\{j:x_j\in S\}}{n}=\frac{\#\{j:x_j\in [0,s)\}}{n},$$ (1.4)

i.e. I is the fraction of cells in the signaling region. The “response function” f(I) in (1.3) must satisfy f(0) = 0 and be monotone, but can be non-linear, for instance sigmoidal (S-shaped). We will see that models of this form, while fairly general, can be studied in some detail. In [15] we studied some cases where f is a linear function.

Understanding the CDC at the genetic and biochemical level is a topic of intense interest and progress has been made in identifying the agents and the nature of relationships between them [5, 10, 17, 50, 51, 56]. Our approach uses a “caricature” of the cell cycle, rather than detailed modeling, and this simplification demands justification. First, we wish to deal with individual cells in a population-wide phenomena. If details within each cell are considered, then the dimensions of the phase space would be extremely large and results would be diffcult to obtain. Second, our understanding of the details of the cell cycle and its relations with other processes is not complete and even if the general nature of relationships were well-understood, the resulting set of differential equations would contain many parameters, e.g. rate constants, that could only be estimated. With our simplified model which is based on biological insight, we hope to obtain general principles that will inform further detailed investigations.

The approach in part of this work is basically that of “phase oscillator” models, e.g. Kuramoto equations, in which details of each individual actor are projected onto a simple phase space and emergent population behaviours are studied. In fact if f(I) is linear then our model can be put into the Kuramoto form by integrating over the cell cycle for each pair of cells and adding the effects (see [33] p. 65-67). This derivation fails in general for RS models (1.1) or (1.3) since the effects of cells in general are not additive.

We note here another modeling simplification that we have implicitly made; namely one might more accurately model the feedback term as a(x_i, z) where z is a vector variable representing all substrate factors that contribute to growth rate and z itself is coupled with $\stackrel{‒}{x}$ [25]. Dropping the z variable can be justified if the time-scale of the dynamics of this variable is significantly shorter than the time-scale of the CDC.

2 Clusters, Gaps and Isolation

In this section we begin to study the existence and stability of periodic “clustered” solutions for both positive and negative RS-feedback systems (1.1) and in later sections we point out crucial differences between these two types of feedback. Reducing to the study of clustered solutions is of practical interest since clusters appear in experiments with YAO. It also limits the dimensions of the problem to a manageable size. This strategy has proven indispensable in many fields; for instance in fluid dynamics, insight is obtained by studying finite dimensional vortex equations rather than the full Navier-Stokes partial differential equations [42].

Definition 2.1

By a cluster, we will formally mean a group of cells that are completely synchronized in the CDC.

Note that RS-feedback systems as defined have the symmetry of globally coupled networks with identical nodes; namely, the vector field is equivariant with respect to the group of permutations of coordinates. This symmetry implies that any cells that initially share the same phase keep the same phase as time evolves. The simplest trajectory consists in taking all cells initially in the same phase. We have a single cluster C (synchrony) that generates a periodic solution that runs at velocity 1 around the circle (i.e. x_i(t) = x_i(0) + t mod 1 for every i and all t > 0).

Definition 2.2

By the gap between two clusters or cells at x_i−1 and x_i we mean the open interval on the circle from x_i−1 to x_i, in the direction of the flow that contains no cells and has width w_i = x_i − x_i−1. (This can be made precise using a lift to the real line.)

Note that if there are only two clusters x₀ and x₁ in the system, then there are two gaps between them and each gap has a width.

It follows from our assumed coordinates that if two clusters are in S and R then the distance between them on the circle is less than |R| + |S| = 1 − r + s. Here |R| denotes the length of the interval R = [r, 1), which is 1 - r and |S| = s denotes the length of the interval S = [0, s). See Figure 3. We say that a cluster of cells is isolated if there are gaps between the cluster and any other cells on either side of length at least |R| + |S| and strictly isolated if the widths of gaps are more than |R| + |S|. This terminology is motivated by the fact that strictly isolated clusters cannot exert feedback on cells outside the cluster, or have feedback exerted upon them from outside. While we consider only clustered solutions in the strictest sense, in real cultures individual cell differences will lead to a weaker form of clustering. For clarity we will refer to such a weakly clustered subset of cells as a group of cells. In Figure 3 the solution in the simulation has formed groups.

The following definition will play a large role in the analysis of the model.

Definition 2.3

Define

$$M\equiv \lfloor {(\mid R\mid +\mid S\mid )}^{-1}\rfloor .$$ (2.1)

M is the maximum number of isolated clusters that can simultaneously exist, given the sizes |R| and |S| of R and S.

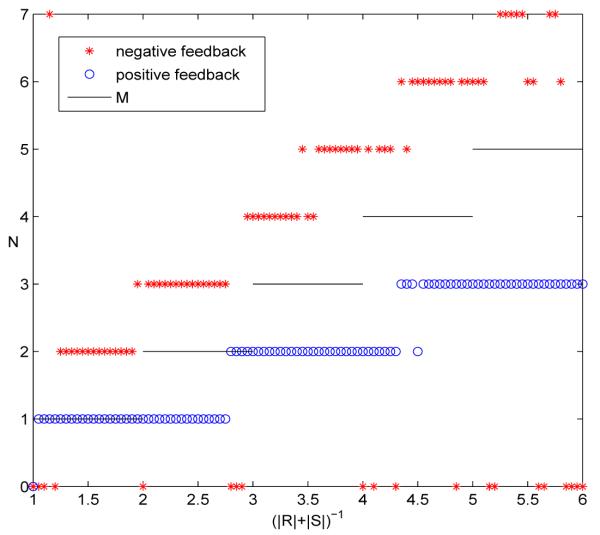
Here ⌊x⌋ denotes the floor function, that is, the greatest integer less than or equal to x (e.g. ⌊2.1⌋ = 2). In Figure 4 when (R| + |S|)⁻¹ is in the range [3, 4), M is 3.

Figure 4.

The number of clusters that form in simulations compared with M = ⌊(|R| + |S|)⁻¹⌋, the maximum number of isolated clusters given R and S.

Proposition 2.4

For any RS feedback model and any positive integer k ≤ M there exist periodic solutions consisting of k isolated clusters that do not interact.

Proof

For k ≤ M consider the solution with initial conditions: $x_0=0,x_1=\frac{1}{k},\dots ,x_k=\frac{k-1}{k}$. We claim that this is such a periodic solution. Notice from the definition of M that

$$M\le {(\mid R\mid +\mid S\mid )}^{-1}$$

and so

$$\frac{1}{k}\ge \frac{1}{M}\ge \mid R\mid +\mid S\mid =1-r+s.$$

Since the distance between any two consecutive clusters x and y is initially d(x, y) = 1/k, no two clusters can be in R ∪ S simultaneously. Thus no feedback will occur and thus the distance between clusters will not change.

By the same reasoning any initial condition of k ≤ M clusters, where all pairs of clusters satisfy d(x, y) ≥ |R| + |S|, will also lead to a periodic solution where all clusters move indefinitely with speed 1.

Conversely, if more than M clusters exist, then at least two of them are within a distance |R| + |S| of each other, and while the first of these clusters lies in the signaling region, it will exert feedback on the second cluster for a non-empty interval of time.

Note that a solution consisting of strictly isolated clusters can be at most neutrally stable (not asymptotically stable) since moving a cluster to the left or right still produces an isolated cluster.

In Figure 4 we plot the results of numerical simulations which compare the number of clusters that formed with the maximum number of possible isolated clusters. The number of cells n was 5000 and the model was taken to be that in equation (1.3) with f linear. Specifically, for the positive feedback simulations f(I) = .6I, and f(I) = −.6I in the negative feedback simulations. There was also stochastic noise added to the equations with level σ = 10⁻⁶ in order to demonstrate robustness. In the plot the x-axis represents (|R| + |S|)⁻¹ which was varied from 1 to 6 in one hundred increments. In the simulations |R| and |S| were taken to be equal. The system was integrated for up to 100 cell cycles (with 50 steps per cycle) to check for the formation of clusters (but clusters usually formed long before the 100th cycle). To test for clustering, we produced histograms with 120 bins and visually inspected these for clustering. If clusters did not clearly form for a given value of (|R| + |S|)⁻¹, then that data point is plotted on the graph as a zero value for N.

The most striking feature of the plots in Figure 4 is that for positive feedback the number of clusters formed is always less than or equal to M, but for negative feedback the number of clusters formed is always greater than M. Notice also that positive feedback always produced clustering, but this was not the case for negative feedback. For negative feedback there are parameter values where no clusters form. Finally, it is worthy of note that for negative feedback, there are no occurrences of one-cluster solutions. Analysis in the next sections will shed light on these observations.

Besides solutions consisting of k ≤ M isolated clusters, RS-feedback systems have other periodic solutions. One of these consists of all n cells spread along the cycle as uniformly as possible. We will define a uniform solution to be a trajectory for which the coordinates satisfy the following relation for some time d > 0:

$$x_i\left(d\right)=x_{i+1}\left(0\right)\text{for all}i=0,\dots ,n-2,\text{and}{x}_{n-1}\left(d\right)=x_0\left(0\right)\text{mod}1.$$ (2.2)

Since the velocity of cells in the complement of R is precisely 1, it follows that for such a solution the cells in R^c will be uniformly distributed with inter-cell distance d. In the process of the construction of uniform solutions we also produce many other periodic k cluster solutions.

Suppose that k divides n and and k sets of n/k cells are initially synchronized. Then we may greatly reduce the dimensions of the differential equations by considering only the positions of the k clusters which we may denote by {x₀(t), x₁(t), …, x_k-1(t)}. In particular we will prove that there always exists a solution of k clusters that satisfy:

$$x_i\left(d\right)=x_{i+1}\left(0\right)\text{for all}i=0,\dots ,k-2,\text{and}{x}_{k-1}\left(d\right)=x_0\left(0\right)\text{mod}1.$$ (2.3)

We will refer to such solutions as cyclic k cluster solutions.

Proposition 2.5

There exists a uniform solution of any RS-feedback system. If k is a divisor of n, then a cyclic k cluster solution exists consisting of n/k cells in each cluster.

We defer the proof of this proposition until Section 5.2. We observe that we do not have uniqueness of the uniform and cyclic clustered solutions.

For n large, as in the application in mind, then we expect k cluster solutions for k << n to exist even if k does not exactly divide n. For example hyperbolicity (linear stability or instability) of the k cyclic solutions when k divides n would imply that such solutions exist for all n^’ ≈ n.

The uniform solution has an analogue in PDE models of the cell cycle which we note in Appendix A.

3 Positive Feedback Systems

In a RS model with positive feedback, first notice that a group of cells that is isolated will remain isolated. Further, positive feedback has a focusing effect on an isolated group.

Proposition 3.1

In a general RS model (1.1) with positive feedback, suppose that a solution has a gap between two adjacent cells x_i-1 and x_i of width greater than or equal to |R| + |S|. Then the width of this gap will never decrease. In particular, an isolated group or isolated cluster will remain isolated indefinitely.

If there are only two clusters in the system, then this proposition applies to either of the two gaps that has width at least |R| + |S|.

Proof

Suppose that two consecutive cells x_i-1 and x_i are separated by a gap of width w_i ≥ |R| + |S|. Since feedback is positive, the cell x_i always moves at a speed of at least 1. The cell speed of x_i-1, being governed by (1.1), will be exactly 1 whenever w_i is greater than or equal to |R| + |S|, since there will be no cells in S when x_i-1 is in R. We then find that the time derivative of w_i is non-negative when w_i ≥ |R| + |S|. Therefore, the gap can never decrease. It follows immediately that a group or cluster of cells that is isolated will remain isolated.

Proposition 3.2

In a general RS model (1.1) with positive feedback, suppose that a group of cells with width w less than |R|+|S| is isolated. Then the width of the group will converge to zero as t → +∞.

Proof

By the previous proposition the group will remain isolated for all future time and we may consider this group of cells as a decoupled sub-system. Without loss of generality we may renumber the cells in the group so that they have coordinates: x₁, x₂, …, x_ℓ, (ordered in the direction of the flow). For i = 1, …, ℓ - 1, denote by w_i = x_ℓ - x_i the width of the interval from x_i to x_ℓ. By assumption w_ℓ-1 ≤ w_i ≤ w₁ < |R| + |S|. Observe that this condition ensures that each x_i, i = 1, …, ℓ - 1 will experience some acceleration every time it passes through R, unless x_i = x_ℓ. This implies that if w_i(t) is non-zero, then w_i(t) will decrease each time the group passes through R and S.

Since the group will remain isolated, the cell x_ℓ will always move with speed 1 and w_i(t) will never increase. Since each w_i(t) is non-increasing and bounded below by 0, it must have a limit $w_i^{\infty }$. Now consider a solution with an initial condition such that $x_i\left(0\right)=x_{\ell }\left(0\right)-w_i^{\infty }$ for 1 ≤ i < ℓ. By a standard argument using continuous dependence of solutions on initial conditions, for this solution each w_i(t) will be identically $w_i^{\infty }$. This implies that $w_i^{\infty }$ must be zero, since, from above, a non-zero w_i(t) < |R| + |S| must decrease during each cycle.

In the next result we discuss stability, for which we need the concept of distance and neighborhoods in phase space, which for the models we are considering is the n-torus, ${\mathbb{T}}^n$, where n is the number of cells. Note that on ${\mathbb{T}}^n$ there is a natural metric (distance) defined by the maximum of the (mod 1) coordinate differences.

Proposition 3.3

In a RS model (1.1) with positive feedback, the set of strictly isolated cluster solutions is locally asymptotically stable. A solution consisting of k ≥ 2 strictly isolated clusters is neutrally stable (stable, but not asymptotically stable) within the set of solutions with k clusters.

Proof

First observe that an ϵ-neighborhood of a configuration consisting of isolated clusters consists of groups of cells within ϵ of the original clusters. If the original clusters are strictly isolated, then we may make ϵ small enough that the groups are also strictly isolated. By Propositions 3.1 and 3.2 each of these groups will remain isolated and converge to a cluster. Thus a solution starting at any initial condition within a neighborhood of the set of strictly isolated clusters will asymptotically approach the set.

The second part of the claim follows since, if a strictly isolated cluster is moved a small distance, then it is still strictly isolated. Thus a small perturbation of a solution consistingof k strictly isolated clusters also will be a solution consisting of k strictly isolated clusters. The distance between the two solutions will remain constant for all future time and thus they are stable, but not asymptotically stable.

Points near the set of isolated cluster solutions will converge to the set, but individual solutions are only neutrally stable with respect to perturbations inside the set.

Since the set of clustered solutions is locally stable, it must have a basin of attraction and it is natural to ask how big the basin is. In simulations for positive feedback systems, the basin seems to include almost all initial conditions. In the next proposition we see that the basin of attraction extends far beyond a small neighborhood of the set.

Proposition 3.4

Suppose that a solution $\stackrel{‒}{x}\left(t\right)$ in a RS model (1.1) with positive feedback has at least one gap of width greater than or equal to |R| + |S|. Then the solution will converge to a periodic solution consisting entirely of isolated clusters.

Proof

We will call a gap large if its width is greater than or equal to |R| + |S|. At time t₀, the cells may be grouped into a minimum number of groups in which there are no large internal gaps. The number of such groups is the same as the number of large gaps. Note that each such group is isolated, and the number of such groups cannot be larger than M = ⌊(|R| + |S|)⁻¹⌋. Consider one such group. Since it contains no large internal gaps and it is isolated, during passage through R the last cell must be accelerated by the presence of at least one cell in S and so its speed is sometimes greater than 1. On the other hand, since the group is isolated it will remain isolated by Proposition 3.1, and the lead cell will travel indefinitely with speed 1 by the same argument that appears in the proof of that proposition.

Thus during one passage through R the distance between the lead cell and the final cell in the group must decrease. If this group continues to have no large internal gaps, then it follows that the width of the group will continue to decrease. By an elementary argument (as for Proposition 3.2), the width will converge to zero; in other words the group will converge to a cluster. Otherwise, if a large internal gap develops then the cells that are separated by the gap will be isolated from each other and thus form two isolated groups. When this occurs the number of isolated groups will increase. Since the number of isolated groups is bounded above, large internal gaps may form only a finite number of times and thus eventually we have a fixed number of groups that never develop large internal gaps and each of these converges to an isolated cluster.

4 Negative Feedback Systems

The key observation is that for negative feedback, isolated clusters are not stable. This is because as a group of cells crosses the R-S boundary all cells of the group are delayed except the lead cell, which moves with unit velocity, causing the group to spread.

Proposition 4.1

In a RS model (1.1) with negative feedback, a solution consisting of strictly isolated clusters is locally unstable.

Proof

Denote by x*(t) a solution consisting of strictly isolated clusters. First observe that under the condition of strict isolation the gaps between clusters are all larger than |R| + |S|, and so any su ciently small perturbation of the clusters consists of groups that are still isolated. In any neighborhood of any configuration with an isolated cluster, there is a configuration where $x_i\ne x_i^{\ast }\left(0\right)$ for any i. Note in fact that a local coordinate system in a neighborhood of x*(0) is $\{x_i-x_i^{\ast }\},0\le <I>i<∕I>\le <I>n<∕I>-1$. Now let x(t) be a solution with initial condition x(0) that differs from x*(0) in only the i-th coordinate. When this cluster passes through the boundary from R to S the separation between x_i and the rest of the cluster to which it belongs will increase. If we further let the perturbation be su ciently small, then the cluster will remain isolated.

Now recall the definition of stability: given any ε > 0, there exists δ > 0 such that any solution x(t) starting within a δ neighborhood of x*(t) will remain indefinitely within an ε neighborhood of x*(t). Let ε₀ be the largest ε so that any x(0) within an ε neighborhood of x*(0) will consist of isolated groups and let ε = ε₀/2. If x(0) is as in the previous paragraph and is arbitrarily close to x*(0) then the distance between x(t) and x*(t) will continue to increase on each unit time interval as long as x(t) continues to consist of isolated groups. Therefore it follows that x(t) will eventually be outside of an ε/2 neighborhood of x*(t). Thus x*(t) is not stable.

Note that we have not proved linear instability (when the derivative of the mapping at the periodic point is greater than one in absolute value which implies that nearby orbit are repelled exponentially). Linear instability can be shown for systems of the form (1.3).

It follows that in order for clusters to remain coherent under small perturbations in negative feedback, they must not be isolated, i.e. the gaps between them must be less than |R|+|S|, and so the number of stable clusters must be at least M + 1. This is clearly confirmed in simulations. Further it seems that sometimes M + 2 is a stable number of clusters. We will show in §7 that a k = M + 1 cluster cyclic solution is stable for negative feedback of the form (1.3) and for some open sets of parameter values.

In the following proposition we see that interacting clusters tend to spread out from each other as far as possible.

Proposition 4.2

In a RS model (1.1) with negative feedback suppose that two clusters are within |R| + |S| of each other, but are isolated from other cells (non-empty). If they remain isolated from other cells, then the gap between the two clusters will increase and converge to |R| + |S|. In the case that the two clusters contain all the cells in the system, if one gap has width less than |R| + |S| and the second gap has width ≥ |R| + |S|, then as long as the width of the second gap remains greater than |R| + |S| the first gap will increase and approach |R| + |S|.

Proof

If the gap width (or smaller gap width in the case of only two clusters) is less than |R| + |S| then each time the second cluster passes through R, the first cluster will be in S for a non-empty interval of time. During this time interval, the cluster in R will experience deceleration, and the width of the gap will increase during the passage through R. If the cluster pair remains isolated, then the distance will be preserved through the rest of the cycle. Thus the distance between clusters will increase during each cycle. The distance is bounded above by |R| + |S| and so, by a standard argument, the sequence of distances thusgenerated will converge to |R| + |S|.

Corollary 4.3

Suppose that there are k ≤ M clusters in a RS system (1.1) with negative feedback. Then the solution will converge to a periodic clustered solution with isolated clusters.

5 Dynamics of clusters via return maps

5.1 The return map for a clustered system

Let us continue to consider the most general model (1.1) with RS feedback. Let a population of n cells be organized into k equal clusters and let the clusters be labeled by a discrete index i ∈ {0, …, k - 1} so that $x={\left\{x_i\right\}}_{i=0}^{k-1}$ represent clusters of n/k cells each. One can assume that all coordinates x_i(0) of the k clusters are initially well-ordered as

$$0=x_0\left(0\right)\le \dots \le x_i\left(0\right)\le \dots \le 1,i=1,\dots ,k-1.$$

This ordering is preserved under the dynamics (this can be well-defined using the orientation of the circle and x₀(t) as a moving reference point). Moreover, the first coordinate x₀ must eventually reach 1, i.e. there exists t_R such that x₀(t_R) = 1. Thus the set x₀ = 0 defines a Poincaré section for the dynamics and the mapping

$$(x_1\left(0\right),x_2\left(0\right),\dots ,x_{k-1}\left(0\right))\mapsto (x_1\left(t_{\mathrm{R}}\right),x_2\left(t_{\mathrm{R}}\right),\dots ,x_{k-1}\left(t_{\mathrm{R}}\right))$$

defines the corresponding return map.

Starting from t = 0, compute the time t₁ that x_k-1 needs to reach 1 and compute the location of the remaining clusters at this time. Define a map F by

$$F:(x_1\left(0\right),x_2\left(0\right),\dots ,x_{k-1}\left(0\right))\mapsto (x_0\left(t_1\right),x_1\left(t_1\right),\dots ,x_{k-2}\left(t_1\right)).$$

Notice that x₀(t₁) = t₁ by assumption on x₀(0). An illustration of F in the case k = 3 is given in Figure 5.

Figure 5.

An illustration of the map F with k = 3; $F(x_1,x_2)=(x_1^{\prime },x_2^{\prime })$.

Now the time t₁ + t₂ that x_k-2 needs to reach 1, together with the population configuration at t = t₁ + t₂, follow by applying F to the configuration (x₀(t₁), x₁(t₁), …, x_k-2(t₁)). By repeating the argument, the desired return time t_R is given by t_R = t₁ + t₂ + + t_k and the desired return map is F^k. Therefore, to study the dynamics one only has to understand the first map F.

Note the Kuramoto derivation (in which one averages over a cell cycle for each pair of cells then adds the effects ([33] p. 65-67)) is a specific way to calculate F^k that is applicable when the feedback is additive.

We will first consider general properties of the map F and then we will compute and analyze it for feedback of the form (1.3) in the simplest case, k = 2. We emphasize that the case k = 2 is also perhaps most important since it is the first to have been directly observed.

5.2 General properties for arbitrary k

We may regard F as a continuous piecewise a ne map of the (k - 1)-dimensional simplex

$$0\le x_1\le x_2\le \cdots \le x_{k-1}\le 1$$

into itself. (Although the boundaries 0 and 1 are identified in the original flow, in the analysis here, we consider them as being distinct points for convenience.)

On the edges of the simplex, F has relatively simple dynamics. Indeed, if initially all coordinates are equal, then they must all reach the boundary 1 simultaneously. In other words, on the diagonal (x_i = x for all i), we have F (x, …, x) = (t₁, 1, …, 1) where t₁ depends on r, s and x (for x = 0, we have t₁ = 1 independently of r and s). Moreover, starting with x_k-1 = 1 implies t₁ = 0 which yields

$$F(x_1,\dots ,x_{k-2},1)=(0,x_1,\dots ,x_{k-2})$$

whatever the remaining coordinates x₁, …, x_k-2 are. As a consequence, the edge

$$\{(x,1,\dots ,1):x\in [0,1]\}$$

is mapped onto

$$\{(0,x,1,\dots ,1):x\in [0,1]\}$$

which is mapped onto {(0, 0, x, 1, …, 1): x ∈ [0, 1]} and so on, until it reaches the edge (0, …, 0, x), which is mapped back onto the diagonal (after k iterations).

A particular orbit on the edges is the k-periodic orbit passing the vertices, and which corresponds to the single cluster of velocity 1 in the original flow, namely

$$(0,\dots ,0)\mapsto (1,\dots ,1)\mapsto (0,1,\dots ,1)\mapsto (0,0,1,\dots ,1)\mapsto \dots \mapsto (0,\dots ,0,1)\mapsto (0,\dots ,0).$$

Geometrically, the corners of the simplex are cyclically permuted by the map F. It follows that the k-2 dimensional simplexes (faces) that make up the boundary of the k-1 simplex are also cyclically permuted by F. This implies that F cannot have a fixed point on the boundary. Propositions 3.2 and 4.1 tell us this orbit (which represents a single isolated cluster) must be asymptotically stable for positive feedback and unstable for negative. Since there are two points of a periodic orbit at each boundary of every edge (which are themselves globally k-periodic 1-dimensional sets), and since these points are either both stable or both unstable, there must be at least one other k-periodic orbit on the edges with coordinates between 0 and 1. Whether this orbit is unique might depend on parameters.

Proof of Proposition 2.1

Since the simplex is a convex and compact invariant set under F, the Brouwer fixed point theorem implies the existence of a fixed point. Since the boundary cannot contain any fixed point, the fixed point is in the interior. Note that the k-cluster cyclic solutions are fixed points of F and vice versa. The uniform solution follows by taking k = n.

6 Dynamics for k = 2

In this section we study the dynamics of 2 cluster systems for the model (1.3). Studying the behavior in the cases of a small number of clusters is not just a matter of convenience, but is important from the perspective of applications since presumably only a small number of clusters can form (for fixed n, more clusters implies that each cluster contains fewer cells and thus can exert less influence) and be observable (smaller clusters would produce smaller oscillation in metabolites and other chemical agents). In the experiment reported in Figure 2 there are 2 clusters.

6.1 The map F

Consider (1.3) where f is a monotone function. In the case k = 2, since only one cluster can exert feedback on the other, RS-feedback (1.3) simplifies to:

$$\frac{d{x}_i}{dt}=\{\begin{array}{cc}1+f\left(\frac{1}{2}\right)\hfill & \text{if}{x}_i\in [r,1)\text{and}{x}_j\in [0,s),j\ne i\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$

Let $\alpha =f\left(\frac{1}{2}\right)$ for notational simplicity.

For k = 2, F is defined on the interval [0, 1] and is determined by x₀(t₁) = t₁ where t₁ is the time at which x₁(t) reaches 1. When regarded as a function of x₁ only, its explicit form depends on the parameters r and s. There are two cases depending on the relative sizes of the signaling and responsive regions, specifically on the size of (1 + α)s with respect to 1 - r. We have put the details of the computation and analysis of F(x₁) in Appendix B.

In the case where r + (1 + α)s < 1, we obtain that F is a continuous decreasing map:

$$F\left(x_1\right)=\{\begin{array}{cc}1-x_1\hfill & \text{if}0\le x_1\le r-s\hfill \\ 1-(1+\alpha )x_1+\alpha (r-s)\hfill & \text{if}r-s<x_1<r\hfill \\ 1-x_1-\alpha s\hfill & \text{if}r\le x_1<1-(1+\alpha s.\hfill \\ \frac{1}{\alpha +1}(1-x_1)\hfill & \text{if}1-(1+\alpha )s<x_1\le 1.\hfill \end{array}\phantom{\}}$$

In the case where r + (1 + α)s ≥ 1, the map F is as follows:

$$F\left(x_1\right)=\{\begin{array}{cc}1-x_1\hfill & \text{if}0\le x_1<r-s\hfill \\ 1-(1+\alpha )x_1+\alpha (r-s)\hfill & \text{if}r-s<x_1\le \frac{1}{\alpha +1}+\frac{\alpha }{\alpha +1}r-s\hfill \\ r-x_1+\frac{1}{\alpha +1}(1-r)\hfill & \text{if}\frac{1}{\alpha +1}+\frac{\alpha }{\alpha +1}r-s<x_1\le r\hfill \\ \frac{1}{\alpha +1}(1-x_1)\hfill & \text{if}r<x_1\le 1.\hfill \end{array}\phantom{\}}$$

Calculating the full return map F² is prohibitively complicated, but in Appendix B we use these two possible forms of F to analyze the dynamics. In the next section we summarize the results.

6.2 Analysis of the dynamics

In Appendix B we find only four distinct types of dynamics; two for positive feedback and two for negative.

• Positive feedback:

  1. There is a unique unstable fixed point for F².
  2. There is an interval of fixed points for F².

  All other orbits are asymptotic to the boundary (merger of the two clusters).
• Negative feedback:

  1. There is a unique stable fixed point for F².
  2. There is an interval of fixed points for F².

  All other orbits, except the boundary points, are asymptotic to the stable fixed point or the interval of fixed points.

These possibilities, for some specific parameter values, are illustrated in Figure 6.

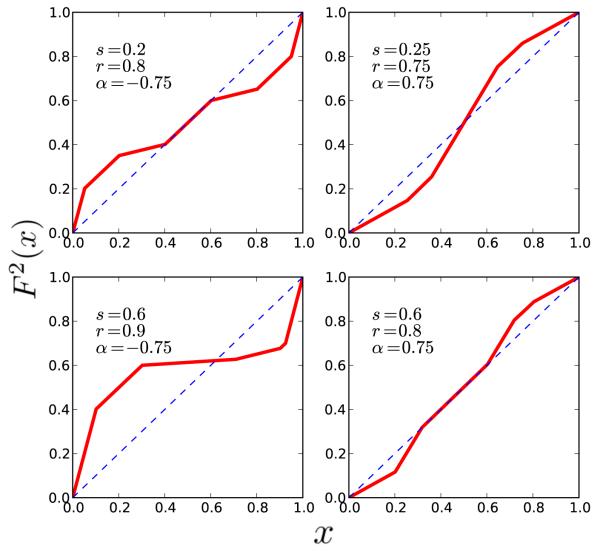
Figure 6.

Plots of the Poincaré map F² in the case k = 2 for various parameter values ($\alpha =f\left(\frac{1}{2}\right)$). Clockwise from top left: interval of fixed points under negative feedback, unstable fixed point under positive feedback, interval of fixed points under positive feedback, stable fixed point under negative feedback.

An interval of fixed points, we observe in the Appendix B, can occur not only because the two clusters may be isolated from each other, but also in certain other situations. Namely if either:

• x₀ is in S for the entire time that x₁ is in R, or,

• x₁ is in R for the entire time that x₀ is in S,

then the unique fixed point of F is neutral and contained in an interval of neutral period 2 points (fixed points of F²).

In [15] we present similar computations for a subset of parameter values with three clusters and positive linear feedback. There we compute F where F³ is the full return map. The results there are similar to those reported here; for all the cases examined the three cluster cyclic solution is either unstable or in the interior of a set of neutral periodic solutions (period 3 points of F). No other periodic orbits were detected and all other initial conditions tend to two cluster or one cluster periodic solutions (on the boundary of the domain of the map F .

A summary of our studies of k = 2 and k = 3 cluster systems is as follows. If the system has positive feedback, then many initial conditions lead to a single cluster, but if the initial condition begins with 2 or 3 clusters, or close to such, then these clusters might persist depending on the parameters and initial conditions (e.g. if the clusters are isolated). If the system has negative feedback, then there may be solutions with 2 or 3 clusters (depending on the parameter values) that are stable within the set of clustered solutions. One cluster is never stable under negative feedback. Biologically, synchrony is likely to appear in systems with positive feedback and clustering in systems that have negative feedback.

7 Cyclic M + 1 Cluster Solutions

Again consider the model (1.3) of RS feedback. Recall that M = ⌊(|R| + |S|)⁻¹⌋ is the maximum number of clusters that can exist without mutual interactions. In this section we consider the cyclic solutions consisting of k = M + 1 clusters, with coordinates x₀, ..., x_k-1, in the dynamics corresponding to (1.3).

We again denote the signaling region S by [0, s) and the responsive region R by [r, 1).

Proposition 7.1

Consider RS feedback of the form (1.3). For any 0 < s < r < 1, there is a cyclic solution consisting of k = M + 1 equal clusters of the form x₀ = 0, x₁ = d, ..., x_k-1 = (k - 1)d, for some d > 0. Denote $\beta =f\left(\frac{1}{k}\right)$. If

$$s<\frac{1}{k}\left(\frac{1+\beta r}{1+\beta }\right)andr>\frac{k-1}{k}(1-s\beta )$$ (7.1)

then the fixed point is unstable for positive β and stable for negative β. Otherwise, the solution is neutrally stable. Both stability results are within the set of k-cluster solutions.

(Note that for k = 2 the first (resp. second) inequality in (7.1) corresponds to the requirement for the second line segment in Figure 8b (resp. 8a) to meet the diagonal, as k = M + 1 = 2 forces $r-s<\frac{1}{2}$)

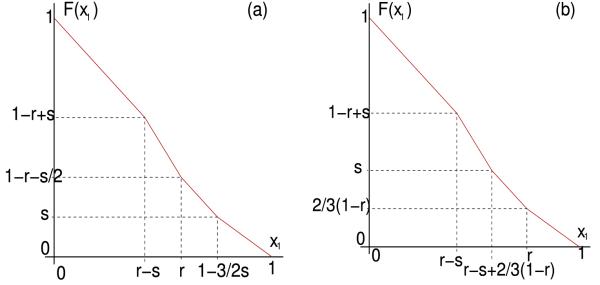
Figure 8.

Plots of the mapping F for k = 2 and $\alpha =f\left(\frac{1}{2}\right)=\frac{1}{2}$. (a) $r+\frac{3}{2}s>1$. (b) $r+\frac{3}{2}s\ge 1$. If r - s > 1/2 (which implies M ≥ 2) then there is a neutral fixed point at 1/2 that represents an isolated 2 cluster cyclic solution. If the second segment intersects the diagonal, then there is an isolated 2 cluster cyclic solutions that is stable for α < 0 and unstable for α > 0. There also may exist neutral fixed points for r - s < 1/2 (M = 1) and certain conditions on the parameters where the third piecewise segment of F intersects the diagonal line. These fixed points represent 2 cluster cyclic solutions that are not isolated, but yet are neutral.

Note that if the solution is neutrally stable, then the fixed point of F must be contained in the interior of a set of period k points that are also neutrally stable, since the return map is piece-wise affine. Note that this is consistent with the results for two and three cluster systems.

The proof of Proposition 7.1 is contained in Appendix C.

8 Discussion

For both positive and negative feedback, the maximum number of non-interacting clusters, M, (see Definition 2.3), plays a large role in the dynamics of the system.

Our main result for positive feedback is that the strictly isolated clustered solutions are neutrally stable (within the set of k clustered solutions, k ≤ M), while the set of strictly isolated clustered solutions is locally asymptotically stable (in the full space). The basin of attraction of this set extends beyond a small neighborhood of the set. For (1.3) with positive feedback and some regions of parameters we have proved that the periodic solution of k = M + 1 equal clusters is completely unstable. In simulations all initial conditions seem to lead to clustered solutions with k ≤ M. Given that these are only neutrally stable within the set of clustered solutions, solutions may quickly approach clustered solutions, but small perturbations of the model may eventually cause the clusters to merge into one cluster (full synchronization).

For negative feedback we observed that isolated clusters are unstable. This implies that clusters need interaction with other clusters to remain coherent. When clusters form, the number of clusters k is at least M + 1. For the model (1.3) and under some restrictions on the parameters, we have proved that the k-cyclic periodic solution of k = M + 1 clusters is stable. In numerical experiments, we observed that clusters sometimes do not form under negative feedback. This perhaps indicates that complicated bifurcations occur in between regions of clustering.

From simulations in the realistic case n >> M the uniform solution seems to be unstable for both positive and negative feedback. Analytic treatment of stability of uniform solutions is a challenge for future work.

Perhaps the key observation from the mathematical models is that positive feedback typically leads to synchrony, while negative feedback systems tend to clustering. In practical terms, if a positive feedback mechanism similar to ours were in effect then one would expect to encounter synchronization, at least some of the time. In yeast experiments a single cluster (fully synchronized behavior) seems to be impossible to sustain in the laboratory [6, 54, 59] and in YAO experiments there is clearly no CDC synchrony. This creates a strong suspicion that the causal mechanism underlying clustering and YAO involves negative feedback rather than positive.

Acetaldehyde [2], ethanol, oxygen and other membrane-permeating metabolites [25] have been conjectured as possible mediators of the YAO. It is natural that these same substances should be considered as signaling agents involved in CDC clustering as well. We have investigated the role of acetaldehyde and ethanol [47], and have shown that we can reset phase and induce autonomous oscillation with pulses of acetaldehyde. Further, we showed that both acetaldehyde and ethanol injections act differentially in different phases of the CDC and YAO and both act as agents of delay, supporting both our model and the role of these substances in processes.

Finally, we note that our analysis is quite general and may find applications outside the realm of the yeast. We note that other micro-organisms can use signaling and coordination of various processes [8, 11, 13, 27, 35]. It is well recognized that feedback can produce synchrony in physical and biological systems and this has been extensively studied [1, 14, 19, 34, 38, 45] (and many others). Clustering is a far less understood phenomenon. As early as 1977 a model of the CDC was introduced with periodic blocking at division [48], and clustering behaviour was also observed there. We note that clustering has been observed in Kuramoto type phase oscillators [43] and in certain all-to-all coupled networks of integrate and fire oscillators [58] and recently a rigorous proof of clustering and the stability of such solutions was obtained [36]. In that work the mechanism that leads to clustering has similarities with the idealized models in [3].

Highlights.

• -We analyze the dynamics of a broad class of cell cycle feedback mechanisms.
• -For positive feedback isolated clusters are stable, but unstable for negative.
• -Non-isolated clusters are unstable for positive feedback, stable for negative.
• -The case of k=2 clusters is studied completely.
• -Positive feedback generally leads to synchronization, negative to clustering.

A Appendix - Relation to PDE models

Consider the hyperbolic conservation law:

$$\frac{\partial u}{\partial t}+\frac{\partial }{\partial x}\left(b(x,\left[u\right])u\right)=0$$ (A.1)

for x on the unit circle, where u(x, t) ≥ 0 represents the density of cells of size x and [u] indicates that b depends functionally on the solution u i.e. b(x, [u]) depends on the values of u at all points x ∈ S¹ at time t. This is a conservation law since ${\int }_{S^1}^{}u(s,t)dx$ is a constant in time. This is the natural PDE version of our model of RS feedback (compare [12, 20, 24, 48]) and we provide it here for comparison with the existing literature.

If b has the form of RS feedback, then given any constant c > 0, there is a solution u(x) such that u(x) ≡ c for x ∈ R^c and u(x) for x ∈ R is determined explicitly by the feedback b(x, [c]), i.e.,

$$u\left(x\right)=\{\begin{array}{cc}c,\hfill & \text{for}x\notin R,\hfill \\ \frac{c}{b(x,\left[c\right])},\hfill & \text{for}x\in R\hfill \end{array}\phantom{\}}$$ (A.2)

This solution is analogous to the uniform solution in Proposition 2.3.

Note that the corresponding version of (1.3) is given by:

$$b(x,\left[u\right])=\{\begin{array}{cc}1,\hfill & \text{if}x\notin R\hfill \\ 1+f\left(I\right),\hfill & \text{if}x\in R,\hfill \end{array}\phantom{\}}$$ (A.3)

where

$$I={\int }_{S}udx,$$

i.e. the fraction of cells in S. For this feedback term, the uniform solution is piecewise constant with value c/(1 + f(c|S|)) in R.

We are not aware of any treatment of PDEs such as (A.1) with b of the form b(x, [u]). When there is no CDC feedback and diffiusion is added to the PDE model (in various ways), then the uniform solution is asymptotically stable [12, 20].

B Appendix - Analysis for k = 2

Recall the notation $\alpha =f\left(\frac{1}{2}\right)$.

We report the details of computations in the case where (1 + α)s < 1 - r. The other case can be treated similarly and we only give below the resulting expression of F. When (1 + α)s < 1 - r, there are 4 situations depending on the location of x₁:

• x₁ ≤ r − s. In this case, x₀ leaves S before x₁ enters R. The point x₁ is not submitted to any feedback and hence x₁(t) = x₁ + t for all t which implies F (x₁) = t₁ = 1 - x₁. (The occurrence of this case is independent of r + (1 + α)s < 1.)

• r − s < x₁ ≤ r. Here x₁ is influenced, but not during the entire responsive region since x₀ gets out of S before x₁ reaches 1. More precisely, we have^*

  $$x_1\left(t\right)=\{\begin{array}{cc}{x}_1\left(t\right)\hfill & \text{if}0<t<r-x_1\hfill \\ r+(1+\alpha )(t-r+x_1)\hfill & \text{if}r-x_1<t<s\hfill \\ r+(1+\alpha )(s-r+x_1)+t-s\hfill & \text{if}s\le t\hfill \end{array}\phantom{\}}$$

  It follows that F (x₁) = 1 - (1 + α)x₁ + α(r − s).
• r < x₁ ≤ 1 - (1 + α)s. Then

  $$x_1\left(t\right)=\{\begin{array}{cc}{x}_1+(1+\alpha )t\hfill & \text{if}0<t<s\hfill \\ x_1+(1+\alpha )s+t-s\hfill & \text{if}s\le t\hfill \end{array}\phantom{\}}$$

  from which we obtain F (x₁) = 1 - x₁ - αs.

• 1 - (1 + α)s < x₁ ≤ 1. In this case, x₁ starts sufficiently close to 1 to have velocity 1 + α when reaching the boundary. We have $F\left(x_1\right)=\frac{1}{\alpha +1}(1-x_1)$.

Recapitulating, in the case where r + (1 + α)s < 1, we obtain the following expression of a continuous decreasing map whose plot is given in Figure 8 (a)

$$F\left(x_1\right)=\{\begin{array}{cc}1-x_1\hfill & \text{if}0\le x_1\le r-s\hfill \\ 1-(1+\alpha )x_1+\alpha (r-s)\hfill & \text{if}r-s<x_1<r\hfill \\ 1-x_1-\alpha s\hfill & \text{if}r\le x_1<1-(1+\alpha )s\hfill \\ \frac{1}{\alpha +1}(1-x_1)\hfill & \text{if}1-(1+\alpha )s<x_1\le 1.\hfill \end{array}\phantom{\}}$$ (B.1)

In the case where r + (1 + α)s ≥ 1, the map F is as follows (see Figure 8 (b)).

$$F\left(x_1\right)=\{\begin{array}{cc}1-x_1\hfill & \text{if}0\le x_1<r-s\hfill \\ 1-(1+\alpha )x_1+\alpha (r-s)\hfill & \text{if}r-s<x_1\le \frac{1}{\alpha +1}+\frac{\alpha }{\alpha +1}r-s\hfill \\ r-x_1+\frac{1}{\alpha +1}(1-r)\hfill & \text{if}\frac{1}{\alpha +1}+\frac{\alpha }{\alpha +1}r-s<x_1\le r\hfill \\ \frac{1}{\alpha +1}(1-x_1)\hfill & \text{if}r<x_1\le 1.\hfill \end{array}\phantom{\}}$$ (B.2)

As argued for arbitrary k, the map F has a k-periodic orbit which, for k = 2, is composed of the boundaries 0 and 1. By the Intermediate Value Theorem, it must also have a fixed point on the diagonal.

The graph of F coincides with the anti-diagonal (1 − x₁) for x₁ ≤ r − s. For $\alpha =f\left(\frac{1}{2}\right)<0$ it is strictly lower than this line if r − s < x₁ < 1; but if α < 0, then it is strictly greater than 1 - x₁ for r − s < x₁ < 1. The dynamics can be characterized completely for arbitrary parameters when k = 2. The following conclusions hold:

• If $r-s>\frac{1}{2}$, each point of the interval [1 - r + s, r − s] is part of a 2-periodic orbit x → 1 - x →x, except for the point $x=\frac{1}{2}$ which is fixed. The return map F² thus has an interval of neutrally stable fixed points centered around $x_1=\frac{1}{2}$.

  • If α > 0, if x₁ is above (resp. below) this neutral interval, we have F²(x₁) > x₁ (resp. F²(x₁) < x₁) and so any initial point converges to 1 (resp. 0).
  • If α < 0, if x₁ is above (resp. below) this neutral interval, we have F²(x₁) < x₁ (resp. F²(x₁) > x₁) and so any initial point converges to the boundary of the neutral interval.

• If $r-s=\frac{1}{2}$, there is a unique fixed point. It is stable for negative α and unstable for positive α.

• If $r-s<\frac{1}{2}$ there are three possibilities depending on where the diagonal line x = y intersects the graph of F (see Figure 8).

  • If the diagonal intersects the second segment then there is a unique fixed point which is stable if α < 0 and unstable if α is positive.
  • If the diagonal intersects the third segment of F, then there is again an interval of neutral period 2 points. The edge of the interval is stable for negative α and unstable for positive α.
  • If the diagonal hits the boundary between segments 2 and 3 of F then there is a unique fixed point which stable for negative α and unstable for positive α.

All of these possibilities are summarized in just four distinct types of behaviour in section 6.2 and Figure 6.

The condition r-s > 1/2 corresponds to M ≥ 2. In such a case the cyclic 2 cluster solution consists of isolated clusters and it is contained in an interval of neutral period two points. This interval is an attractor for negative feedback and a repeller for positive feedback.

Note that the condition r − s < 1/2 corresponds to |R| + |S| > 1/2 which implies that M = ⌊(|R| + |S|)⁻¹⌋ = 1. Thus when the 2 clusters cannot be isolated, there is a cyclic 2 cluster solution which is a fixed point of F. This solution may be unique and stable (negative feedback), unique and unstable (positive feedback), or neutral, depending on the parameters.

One can easily calculate that the diagonal line cannot intersect the fourth segment of the graph of F in either case (B.1) or (B.2).

In (B.1) it is seen that the third segment can be intersected by the diagonal by making r sufficiently small. This corresponds to the x₁ coordinate of the fixed point being greater than r so that the second cluster begins in the responsive region R. From the conditions, it is still in R when x₀ leaves S. There is an interval of fixed points for F² even though the clusters are not isolated.

The diagonal also can intersect the third segment for (B.2) if x₀ is in S when x₁ enters R, and when x₁ reaches 1, x₀ is still in S. Thus we have another case of interacting clusters that still leads to a neutral fixed point.

C Appendix - Proof of Proposition 7.1

Proof

The evolution of the system may be described qualitatively in terms of ‘milestones,’ e.g. x₀ reaching s, or x_k-1 reaching 1. We first consider a system which evolves via the following sequence of events (which we call Case 1):

$$x_{k-1}\mapsto r,x_0\mapsto s,x_{k-1}\mapsto 1$$ (C.1)

at which point after relabeling x_i:= x_i-1 we have the initial condition again. By calculating the time taken in each step and finding the final value of x₀, one can use the relation x_k-1 = (k − 1)d to solve analytically for d, getting:

$$d=\frac{1+\beta (r-s)}{k+\beta (k-1)}.$$ (C.2)

Note that the Case 1 sequence will occur provided that s < x₁ = d and x_k-1 = (k-1)d < r. Using (C.2) in these relations gives (7.1).

Two other sequences of events are possible and occur when we drop each of the constraints in (7.1). Case 2, when we allow r < (k - 1)d, is characterized by:

$$x_0\mapsto s,x_{k-1}\mapsto 1,$$

and Case 3, when we allow s > d, by:

$$x_1\mapsto s,x_{k-1}\mapsto r,x_{k-1}\mapsto 1.$$

Following the same procedure as in Case 1, we obtain for Case 2:

$$d=\frac{1-s\beta }{k}$$

and for Case 3:

$$d=\frac{1+r\beta }{k(1+\beta )}.$$

A simple calculation shows that for a given M, cases 1, 2 and 3 exhaust the parameter set in (r, s). We observe that there is never more than one cluster in the signaling region when the response region is nonempty, and thus the dynamics of the system are determined entirely by $\beta =f\left(\frac{1}{k}\right)$. A graphical representation of the regions of parameter space corresponding to these three cases can be seen in figure (7).

Figure 7.

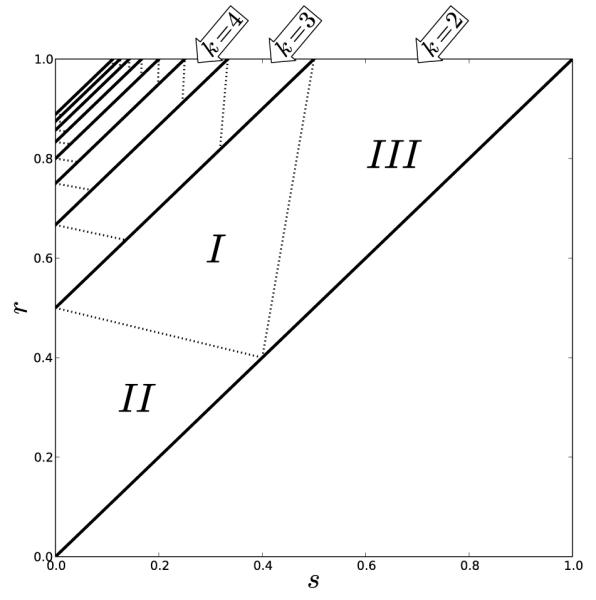
Regions of parameter space for the k cyclic solutions with k = M + 1. Each diagonal band contains the parameters for a specific k and is partitioned into three cases. In case I the k-cyclic solution is unstable for positive feedback and stable for negative. In cases II and III the k-cyclic solution is neutral and is contained in a set of neutral period k solutions. In this plot $\beta =f\left(\frac{1}{k}\right)$ is taken to be 1/k.

The map F is a ne in a neighborhood of the fixed point, i.e. $\overrightarrow{x}\mapsto A\overrightarrow{x}+\overrightarrow{b}$ where $\overrightarrow{x}={(x_0,\dots ,x_{k-1})}^T$ and A is a matrix. We next analyze A in the three cases.

Case 1

$$A=\left[\begin{array}{cccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -(1+\beta )\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -(1+\beta )\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -(1+\beta )\hfill \\ \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -(1+\beta )\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill -(1+\beta )\hfill \end{array}\right]$$

Thus we may determine the stability of the fixed point by studying the eigenvalues A, which has characteristic equation

$$-{\lambda }^{k-1}-(1+\beta )({\lambda }^{k-2}+{\lambda }^{k-3}+\cdots +\lambda +1)=0.$$ (C.3)

Notice that λ = 1 can easily be ruled out as a root. For λ ≠ 1 we can rewrite (C.3) as

$$\frac{1}{1+\beta }{\lambda }^n+\underset{i=0}{\overset{n-1}{\Sigma }}{\lambda }^i=\frac{{\lambda }^n}{1+\beta }+\frac{{\lambda }^n-1}{\lambda -1}=0.$$

After simplification, we see that λ ≠ 1 is a solution of (C.3) if and only if

$$\left(\frac{\lambda +\beta }{1+\beta }\right){\lambda }^n=1.$$ (C.4)

Now, suppose β > 0. If |λ| ≤ 1 (and λ ≠ 1), then |λⁿ| ≤ 1 and |λ + β| < |1 + β|. Thus

$$\mid \frac{\lambda +\beta }{1+\beta }\mid \mid {\lambda }^n\mid <1,$$

i.e. λ cannot satisfy (C.4). Thus for positive feedback all of the eigenvalues lie outside the unit disk and so the map is unstable at the fixed point. Further, it is not only unstable, but is unstable w.r.t. all possible perturbation directions.

For the case β < 0, suppose |λ| > 1. Write λ + β as λ - (-β). Then by the reverse triangle inequality, |λ + β| = |λ - (-β)| ≥ ||λ| - | - β|| = ||λ| + β| = |λ| + β > 1 + β. Thus we have

$$\mid \frac{\lambda +\beta }{1+\beta }\mid \mid {\lambda }^n\mid >1,$$

and (C.4) is not satisfied. Also if |λ| = 1 but λ ≠ 1, then |λ + β| < 1 + β. Therefore if β < 0 then all the eigenvalues of A lie on the interior of the unit disc, and the map is stable.

The stability results for case 1 are illustrated in Figure 9 for k = 2, 4, …, 12 and $\beta =f\left(\frac{1}{k}\right)\in (-.5,.5)$.

Figure 9.

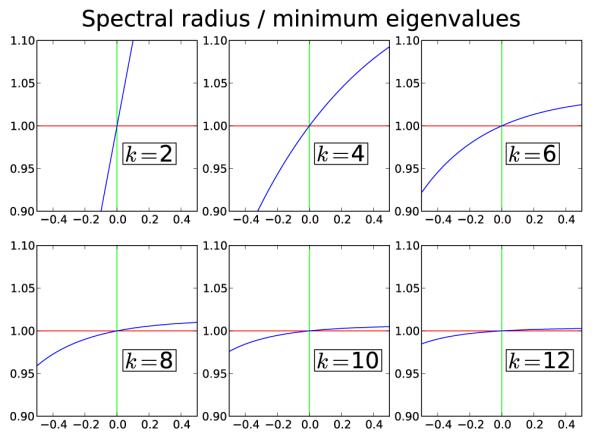
Case 1. The spectral radius / smallest eigenvalue modulus for k = 2, 4, …, 12. The x-axis is the feedback parameter β. For negative β, the y-axis is the spectral radius of A. For positive β, the smallest eigenvalue (w.r.t. modulus) is plotted. The plots show that the k = M + 1 solution is stable for negative feedback and unstable (in all directions) for positive feedback. Notice that as k grows, the stability/instability becomes weaker.

Case 2 and Case 3

In cases 2 and 3, the linear part of the map at the fixed point is represented by the matrix:

$$A=\left[\begin{array}{cccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right].$$

This matrix has characteristic equation λ^k-1 + λ^k-2 + … + λ + 1 = 0 whose roots all have absolute value 1. Thus the map is neutrally stable in both cases 2 and 3.