Abstract
The genetic and environmental origins of individual differences in mathematical self-evaluation over time and its association with later mathematics achievement were investigated in a UK sample of 2138 twin pairs at ages 9 and 12. Self-evaluation indexed how good children think they are at mathematical activities and how much they like those activities. Mathematics achievement was assessed by teachers based on UK National Curriculum standards. At both ages self-evaluation was approximately 40% heritable, with the rest of the variance explained by non-shared environment. The results also suggested moderate reciprocal associations between self-evaluation and mathematics achievement across time, with earlier self-evaluation predicting later performance and earlier performance predicting later self-evaluation. These cross-lagged relationships were genetically rather than environmentally mediated.
Keywords: Self-evaluation, Math achievement, Cross-lagged association, Twins
1 Introduction
In the modern age of digital technology, adequate numeracy cannot be overestimated. The increasing importance of numeracy is reflected in government and commercial initiatives, such as Maths Year 2000 (http://www.mathsyear2000.org/) and Maths@Work Project (http://www.ima.org.uk/), as well as reports on the importance of mathematics and assessments of current levels of numeracy (e.g., Smith, 2004). Unfortunately, despite efforts to date to improve mathematical performance and to reduce mathematical underachievement, the situation remains highly unsatisfactory in many developed countries according to the latest report from the OECD Programme for International Student Assessment (PISA, 2009). For example, a survey from the National Assessment of Educational Progress (2009) reported that 61% of fourth-grade students (age 9 – 10) and 66% of eighth-grade students (age 13 – 14) in the US failed to demonstrate a “proficient” level of required math skills.
For a complex trait like mathematics achievement, many factors are likely to drive variation. In terms of psychological constructs, intelligence, motivation and social context have all been shown to play a role (Winne & Nesbit, 2010). Although a general factor of intelligence has been identified as the best predictor of academic achievement across a wide spectrum of domains and criteria (e.g., Deary, Strand, Smith, & Fernandes, 2007), the correlation between intelligence and mathematics achievement is no more than 0.5 for elementary school children. Individual differences in intelligence therefore only account for one quarter of the variance of mathematics achievement (Helmke, 1992; Spinath, Spinath, Harlaar, and Plomin, 2006), implying that factors other than intelligence are important for mathematics achievement. Moreover, approximately 6% of children of normal intelligence underachieve by at least 2 years below grade level in arithmetic (GrossTsur, Manor, & Shalev, 1996), suggesting the importance of factors other than intelligence. For instance, several studies have demonstrated that self-evaluation of interest and ability explain unique variance in academic achievement unexplained by intelligence (e.g., Gottfried, 1990;Schicke, 1994).
1.1 Self-evaluation
Self-evaluations of interest and ability, also known as self-concepts, are typically examined by self-report questionnaires assessing how good individuals think they are and how interested they are. Specifically for mathematics, self-perceived abilities and interest are substantially correlated (r ≥ .50) (Eccles & Wigfield, 1995; Gottfried, 1985), and both have been shown to contribute incrementally to mathematics achievement beyond intelligence (Wigfield & Eccles, 2000). The present study refers to self-perceived abilities and interest that predict mathematics achievement as mathematical self-evaluation. Specifically for mathematics, self-evaluation has been shown to be moderately correlated with mathematics achievement when assessed at the same age (Spinath, Spinath, Harlaar, & Plomin, 2006). The relationship between actual performance and self-perception of the performance may play an important part in the development of both mathematical self-evaluation and mathematics achievement.
However, the nature of this association remains poorly understood, although evidence suggests that self-evaluation - especially self-perceived abilities - is likely to derive from processes beyond simply internalizing feedback on one’s achievement (Marsh, 1986). Besides external feedback, internal processes, such as the general academic self-concept, possibly moderate the mathematical self-evaluation. Moreover, studies on the directionality of the association between self-evaluation and academic achievement have suggested that although self-evaluation is influenced by prior achievement, it also has independent influences on later achievement, indicating a reciprocal developmental relation between them (Guay, Marsh, & Boivin, 2003; Marsh, Byrne, & Yeung, 1999; Marsh & Yeung, 1997). To improve our understanding of the relationship between mathematics achievement and self-evaluation, we need a cross-lagged design incorporating the two measures at two time points within the same model.
An important aspect of the association between self-evaluation and achievement that has not received sufficient attention is the possible genetic contribution to individual differences in mathematical self-evaluation. The popular view is that self-evaluation is primarily shaped by family and school environment, such as parents’ expectations and teachers’ feedback, which are more likely to be shared by twins (Krapp, 2005; Wigfield & Eccles, 2000). We are aware of only one study that examined the possibility of genetic contributions specifically to mathematical self-evaluation (Spinath, Spinath, & Plomin, 2008). The study, which is a cross-sectional analysis at age 9 of the same sample used in the present study, finds moderate genetic influence on mathematical self-evaluation (≈ 40%), without significant contribution of the shared environment. Moreover, one recent study suggests that self-evaluation of ability predicts general academic achievement even after accounting for intelligence, and that this link is explained by genetic rather than environmental factors (Greven, Harlaar, Kovas, Chamorro-Premuzic, & Plomin, 2009). These results suggest that genetic contributions are not only important for mathematical self-evaluation per se, but also for the association between mathematical self-evaluation and achievement. However, before any general conclusions can be drawn, more research is needed to explore the mechanisms underlying the association between self-evaluation and mathematics achievement, and in particular, longitudinal research is needed to address the origins of the association.
1.2 The present study
To this end, the present study investigates the genetic and environmental origins of mathematical self-evaluation longitudinally from middle childhood to early adolescence. Based on the previous cross-sectional study of 9-year-old twins using the same sample (Spinath et al., 2008), we predicted that the heritability of mathematical self-evaluation would remain moderate at age 12, and environmental influences would be largely due to factors not shared by siblings (e.g., different peer groups). In addition, we examine the etiology of the cross-lagged associations between self-evaluation and mathematics achievement, i.e. the cross-lag from earlier self-evaluation to later achievement (controlling for earlier achievement) and that from earlier achievement to later self-evaluation (controlling for earlier self-evaluation). Given the previous finding that genetic factors explained the association between self-perceptions and general academic achievement at the same age (Greven et al., 2009), we hypothesize that the cross-lagged association between earlier self-evaluation and later mathematics achievement would be largely mediated by genetic effects.
2 Methods
2.1 Participants and Procedure
The participants in this study were sampled from the Twins Early Development Study (TEDS), a study of twins born in England and Wales between 1994 and 1996 (Oliver & Plomin, 2007). TEDS is reasonably representative of the general UK population in terms of ethnicity, parental education and employment status. UK census data for families with children indicate that 93% of children are white and 32% of mothers have at least one A-level (non-compulsory exam taken at age 18), while 49% of mothers and 89% of fathers are employed. For the entire TEDS sample of more than 10,000 twin pairs who completed an initial booklet when the children were two years old, the comparable percentages are 92%, 35%, 43% and 92% respectively. For the sample that participated at age 9, the respective percentages are 94%, 41%, 46% and 93%; and at age 12, the comparable percentages are 93%, 41%, 47% and 93%. Zygosity was assessed through a parent questionnaire of physical similarity, which is over 95% accurate when compared to DNA testing with accuracy over 99.9% (Price et al., 2000). For cases where zygosity was unclear from this questionnaire, DNA testing was conducted. At age 9, TEDS families from the 1994 and 1995 cohorts were invited to participate in the study. At age 12, twins born in 1994, 1995 and 1996 were invited to participate. As described below, self-evaluation was reported by children themselves and mathematics achievement was assessed by their teachers. At age 9, 6770 child booklets were returned complete (83%), and 5836 teacher rating forms were returned complete (76%). At age 12, 11708 child booklets (69%) and 9905 teacher forms were returned complete (78%). For each assessment we obtained informed consent from the parents of the twins.
To conduct the cross-lagged analyses, twin pairs were only included when at least one sibling of the pair had completed both assessments at ages 9 and 12. Twin pairs with specific medical syndromes present in one or both members were excluded. Our analyses indicated some potential differences between same-sex and opposite-sex twin pairs for self-evaluation measures, whereas our previous analyses (e.g., Kovas, Haworth, Dale, & Plomin, 2007) suggest no such difference for mathematics measures. For this reason, and since our sample size provided adequate power, we decided to focus the current analyses on same-sex pairs only. In Table 1 we present the sample sizes for the measures at each age. Numbers of complete twin pairs by zygosity are included in Table 3. At age 9, the mean age of twins was 9.02 (SD = .29); and at age 12, the mean age was 11.76 (SD = .32).
Table 1.
Means (and standard deviations) by zygosity and sex and ANOVA results showing significance and effect size by zygosity and sex
| Zygosity | Sex | ANOVA | ||||||
|---|---|---|---|---|---|---|---|---|
| Measure | All | MZ | DZ | Female | Male | Zygosity | Sex | Zygosity x Sex |
| Age 9 | ||||||||
| Self-evaluation | 3.63 (1.02) | 3.60 (1.01) | 3.67 (1.03) | 3.48 (1.00) | 3.82 (1.00) | p = .148 | p < .001 | p = .783 |
| n = 2008 | n = 1078 | n = 930 | n = 1122 | n = 886 | η2 = .001 | η2 = .028 | η2< .001 | |
| Math achievement | 3.00 (.66) | 2.97 (.66) | 3.03 (.66) | 2.95 (.65) | 3.05 (.67) | p = .053 | p = .006 | p = .368 |
| n = 1568 | n = 821 | n = 747 | n = 874 | n = 694 | η2 = .002 | η2 = .005 | η2= .001 | |
| Age 12 | ||||||||
| Self-evaluation | 3.47 (.89) | 3.46 (.88) | 3.49 (.90) | 3.41 (.89) | 3.55 (.89) | p = .532 | p < .001 | p = .956 |
| n = 1900 | n = 1017 | n = 883 | n = 1069 | n = 831 | η2 < .001 | η2 = .007 | η2< .001 | |
| Math achievement | 4.74 (.98) | 4.71 (.98) | 4.77 (.99) | 4.73 (.97) | 4.75 (.99) | p = .308 | p = .629 | p = .143 |
| n = 916 | n = 501 | n = 415 | n = 511 | n = 405 | η2= .001 | η2< .001 | η2 = .002 | |
Note. Means (and standard deviations) and ANOVA (= analysis of variance) for one randomly selected member of each twin pair. The number of randomly selected individuals (indicated by n) is bigger than expected as compared to Table 3, because there are some twin pairs for whom data were available for only one member. Self-evaluation was reported by children; Mathematics achievement was assessed by teachers according to the National Curriculum; MZ = monozygotic; DZ = dizygotic (only same-sex twins are included); η2 = eta squared (effect size).
Table 3.
Twin intraclass correlations and ACDE estimates from univariate model-fitting analyses
| Measure | rMZ | rDZ | a2 | d2 | c2 | e2 |
|---|---|---|---|---|---|---|
| Age 9 | ||||||
| Self-evaluation | .40 (.35–.45) n = 1040 |
.11 (.04–.17) n = 906 |
.02 (.00– .28) | .38 (.11– .45) | .59 (.55 – .64) | |
| Math achievement | .68 (.64–.72) n = 741 |
.41 (.34–.47) n =658 |
.56 (.43 – .70) | .12 (.00 – .25) | .32 (.28– .35) | |
| Age 12 | ||||||
| Self-evaluation | .42 (.35–.48) n = 703 |
.18 (.10–.26) n = 593 |
.29 (.00 – .47) | .14 (.00 – .46) | .57 (.52 – .64) | |
| Math achievement | .52 (.42–.61) n = 312 |
.39 (.25–.50) n = 263 |
.36 (.07– .61) | .17 (.00 – .42) | .46 (.38 – .56) |
Note. rMZ= monozygotic twin correlation; rDZ = dizygotic (only same-sex twins are included) twin correlation; a2 = the proportion of variance due to additive genetic effects; d2 = the proportion of variance due to non-additive genetic effects; c2 = the proportion of variance due to shared environments; e2 = the proportion of variance due to non-shared environments; n = number of complete twin pairs. Self-evaluation was reported by children; Mathematics achievement was assessed by teachers according to the National Curriculum. 95% confidence intervals are included in parentheses.
2.2 Measures
2.2.1 Mathematical self-evaluation
At both age 9 and 12, children’s self-evaluation was assessed using six items about aspects of mathematics based on UK National Curriculum: (1) “How good do you think you are at solving number and money problems?”; (2) “How good do you think you are at doing math in your head?”; (3) “How good do you think you are at multiplying and dividing?”; (4) “How much do you like solving number and money problems?”; (5) “How much do you like doing maths in your head?”; (6) “How much do you like multiplying and dividing?” (Spinath et al., 2006). Participants were asked to indicate on a 5-point Likert scale how good they think they are at and how much they enjoy those activities. The twins completed the scale independently under the administration of their parents at home.
Factor analysis (at 9: KMO measure = .78, Barlett’s test: p < .001; at 12: KMO measure = .80, Barlett’s test: p < .001) of the six items clearly revealed one factor explaining most of the variance (at 9: 65%; at 12: 69%) and each item loaded heavily on it (.78 ~ .86, see Appendix A for more details) at both ages. Therefore we created two composite self-evaluation scores using the mean of the six items for age 9 and age 12.
Appendix A.
Factor loadings on the first principal component of the items of mathematical self-evaluation.
| Item | Age 9 | Age 12 |
|---|---|---|
| SPA – number | 0.786 | 0.816 |
| SPA – arithmetic | 0.803 | 0.838 |
| SPA – multiplying | 0.776 | 0.815 |
| Liking – number | 0.82 | 0.822 |
| Liking – arithmetic | 0.849 | 0.855 |
| Liking – multiplying | 0.812 | 0.821 |
Note. SPA – number: self-perceived ability of solving numbers; SPA – arithmetic: self –perceived ability of mental arithmetic; SPA – multiplying: self-perceived ability of multiplying and dividing; liking – number: liking of solving numbers; liking – arithmetic: liking of mental arithmetic; liking – multiplying: liking of multiplying and dividing.
2.2.2 Mathematics achievement
The participants’ mathematics achievement at school was assessed using teachers’ ratings based on UK National Curriculum (NC) criteria, which are uniform assessment guidelines followed by all teachers within the UK state school system. Teachers were contacted in the second half of the school year so that they would be familiar with the children’s performance. Both members of a twin pair were rated by a single teacher if they were in the same classroom; co-twins were rated by different teachers if they were in different classrooms. The percentages of twins rated by the same teacher were 59% at 9, and 33% at 12, which is the age when students leave elementary school and move to middle school in the UK. Same-sex DZ twins were in the same class as frequently as MZ twins were (at 9: DZ = 59.0%, MZ = 59.8%; at 12: DZ = 34.3%, MZ = 35.7%). Consistent with previous findings indicating no effect of being taught by the same teacher versus different teachers in terms of the genetic and environmental estimates (Kovas, Haworth, et al., 2007; Kovas, Petrill, & Plomin, 2007), intraclass correlations (twin similarity) were practically identical when the twins were taught by the same vs. different teacher, both for MZ and for DZ pairs at both ages.
At age 9, the NC Teacher Assessments at Key Stage 2, which are designed for children aged 8 to 11, were used. Teachers assessed three broad areas of mathematical performance: using and applying mathematics; numbers and algebra; shape, space and measures. At age 12, the NC Teacher Assessments at Key Stage 3, which are designed for children aged 11 to 14, were used. Teachers assessed the same three broad areas of mathematical activities, with an addition of the fourth area: handling data. Teacher-rated achievement ranges from Levels 1 to 8. By the end of Key Stage 2 (age 11), children are expected to reach level 4; by the end of Key Stage 3 (age 14), children are expected to reach level 5/6. These National Curriculum assessments have been shown to be valid measures of academic achievement (Kovas, Haworth, et al., 2007). Further information about the National Curriculum is available at http://curriculum.qca.org.uk. Factor analyses of the items of the assessment of mathematics achievement showed that these items loaded highly on a single factor: 91% of the variance at age 9 and 96% of the variance at age 12. This justified using the composite to represent the math achievement. Therefore, the mean of the items is used to create composite scores at age 9 and age 12.
2.3 Statistical Analysis
2.3.1 Data Preparation
As both self-evaluation and mathematics achievement are associated with IQ (Ackerman & Wolman, 2007; Chamorro-Premuzic & Furnham, 2005; Furnham & Chamorro-Premuzic, 2004), covariation with IQ would inflate the correlation between self-evaluation and achievement. IQ at age 9 and age 12 were assessed respectively using tests adapted from the multiple-choice version of the WISC-III-UK (Wechsler, 1992) and Raven’s Standard Progressive Matrices (Raven, Court, & Raven, 1996).
Details of the assessment of IQ in TEDS were reported elsewhere (Davis, Arden, & Plomin, 2008; Haworth et al., 2007). Contributions from IQ to self-evaluation and to mathematics achievement were removed by regression separately from the composite scores at each age. Because twins are perfectly correlated for age and same-sex twins are perfectly correlated for sex, variation associated with age or sex would inflate the correlation between twins. For this reason, as is standard in twin analysis, all measures were corrected for age and sex effects using a regression procedure (McGue & Bouchard, 1984).
2.3.2 The Twin Method
The twin method investigates genetic and environmental influences on individual differences (variance) in observed traits (Plomin, DeFries, McCleann, & McGuffin, 2008). By comparing twin intra-class correlations for monozygotic (MZ) and dizygotic (DZ) twin pairs, it is possible to estimate genetic and environmental effects to the variance of a trait. Heritability is the proportion of individual differences in an observed trait explained by genetic variation which can be due to additive (A) or non-additive (D) effects of genes. Shared environmental effects (C) contribute to the similarity of twins growing up in the same family and non-shared environmental effects (E) do not contribute to familial resemblance. MZ twins are 100% genetically similar, whereas DZ twins are on average only 50% similar for additive genetic effects (A) and 25% similar for non-additive genetic effects due to dominance. Any difference between the resemblance of MZ twins and that of DZ twins is attributed to genetic influences. Non-shared environmental influences (E) are the only influences deemed to make MZ twins different. E also includes measurement error.
Narrow-sense heritability is the proportion of variation in the phenotype explained by additive genetic factors, and broad-sense heritability refers to the proportion of variation explained by additive and non-additive genetic effects together. In a classic twin design (i.e. a design including only MZ and DZ twins reared together), it is impossible to assess non-additive genetic effects and shared environmental effects simultaneously (Plomin et al., 2008). Non-additive genetic effects are suggested when the DZ twin correlation is less than half the MZ twin correlation, which is the case for self-evaluation; whereas shared environmental effects are indicated when the DZ twin correlation is more than half the MZ twin correlation, as is the case for mathematics achievement.
A more comprehensive way of estimating these genetic and environmental parameters is maximum-likelihood model-fitting (Rijsdijk & Sham, 2002), which provides estimates of genetic and environmental effect sizes that make the assumptions about the degree of genetic and environmental influences on behavioral variation explicit, tests the fit of the entire model to the data, tests the relative fit of alternative models, and provides confidence intervals for the parameter estimates. Details of the use of maximum-likelihood model-fitting analyses can be found elsewhere (Neale, Boker, Xie, & Maes, 2006). Mx software for structural equation modeling was used to perform model-fitting analyses using raw data (Neale et al., 2006).
2.3.3 Cross-lagged Analysis
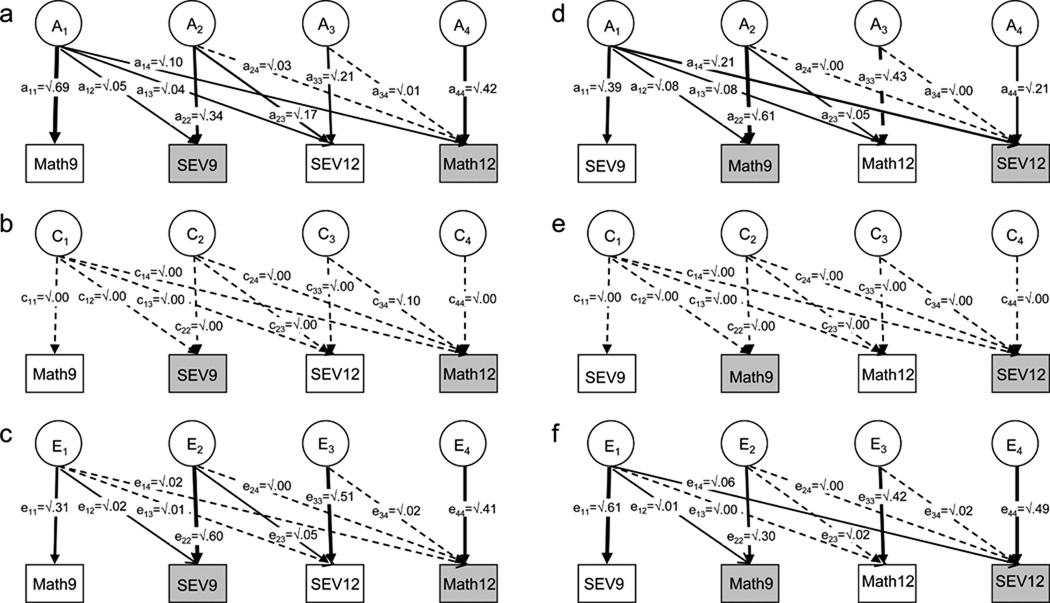
Genetic and environmental influences on cross-lagged associations were examined using multivariate genetic model-fitting methods. The approach, called the genetic cross-lagged model, is an extension of the work of Neiderhiser, Reiss, Hetherington and Plomin (1999). The model is based on a standard Cholesky decomposition, which was fit to raw data to test for common and independent genetic and environmental effects on variance in mathematics and self-evaluation at ages 9 and 12. The Cholesky procedure is similar to hierarchical regression analyses in non-genetic studies, where the independent contribution of a predictor variable is assessed after accounting for its shared variance with other predictor variables (Loehlin, 1996; Neale & Cardon, 1992). The left side of Figure 1 (a, b, c) represents the model that focuses on the cross-lagged association between self-evaluation at 9 and mathematics achievement at 12. The right side of Figure 1 (d, e, f) focuses on the cross-lagged association between mathematics achievement at 9 and self-evaluation at 12.
Figure 1.
The genetic cross-lagged model for self-evaluation (SEV) and mathematics achievement (Math) from 9 to 12 years. The model on the left (a,b,c) tests the cross-lag from SEV9 to Math12. The model on the right (d,e,f) tests the reverse cross-lag from Math9 to SEV12
Note. Measured variables are depicted in rectangles. Latent factors A (genetic factor), C (shared environmental factor), and E (non-shared environmental factor) are presented in the circles. Standardised path estimates (i.e., a11~a44, c11~c44, e11~e44) are also represented in the diagram. The thickness of each arrow indicates the strength of the corresponding path. Nonsignificant paths are depicted by dashed lines. 95% confidence intervals of the estimates are listed in Appendix B. To illustrate the methodology, the full model with all ACE factors is presented here. However, as shared environmental factors were not significant in this study, they were dropped from the full model and an AE model was used to obtain cross-lagged estimates. The models represent only one member of the twin pair. If both siblings are illustrated, all genetic factors should be connected by double-headed arrows with values corresponding to the degree of genetic similarity (1.0 for MZ, 0.5 for DZ). The shared environmental factors are set to be the same for both members of the twin, and the non-shared environmental factors are uncorrelated for both members.
The genetic cross-lagged model has three components: a multivariate analysis between the two variables at each age, a longitudinal analysis between each variable across the two ages, and a cross-lagged analysis between one variable at time 1 and the other variable at time 2. Before assessing the cross-lag, possible confounding influences from the stability of each variable, the contemporaneous association between the two traits at the first time point, and the reverse cross-lag must be removed. This can be done by the Cholesky decomposition, which not only decomposes variance within each variable and covariance between variables into genetic and environmental factors, but also controls confounders by attributing their influences to latent factors before decomposing the target variance or covariance. By appropriately ordering self-evaluation at 9, achievement at 9, self-evaluation at 12 and achievement at 12 in the standard Cholesky decomposition, the cross-lagged influence between self-evaluation at 9 and mathematics achievement at 12 is estimated after controlling for self-evaluation and achievement at 9 and their longitudinal stabilities. The reverse cross-lag between mathematics achievement at 9 and self-evaluation at 12 is assessed similarly by changing the order of variables. In this way, the genetic and environmental analysis of the target cross-lag is independent of the stabilities, the earlier contemporaneous association and the reverse cross-lagged association.
To study the cross-lagged association between self-evaluation at 9 and mathematics achievement at 12, we used the model illustrated in Figure 1 (a, b, c) (each panel represents one part of the same model but are depicted separately to ease presentation), which includes 12 latent factors. A1, C1 and E1 represent genetic, shared environmental and non-shared environmental factors affecting the contemporaneous association between self-evaluation and mathematics achievement at 9 (a11×a12+c11×c12+e11×e12), the correlation between mathematics achievement at 9 and self-evaluation at 12 (a11×a13+c11×c13+e11×e13), and the stability of mathematics achievement (a11×a14+c11×c14+e11×e14). A2, C2 and E2 represent contributions to the stability of self-evaluation (a22×a23+c22×c23+e22×e23), and the cross-lagged association between self-evaluation at 9 and mathematics achievement at 12 (a22×a 24+c22×c24+e22×e24). A3, C3 and E3 represent contributions to the contemporaneous association between self-evaluation and mathematics achievement at 12 (a33×a34+c33×c34+e33×e34). Finally, any genetic and environmental contributions specific to mathematics achievement at 12 are represented by A4, C4 and E4.
The second model, i.e. Figure 1 (d, e, f), examines the cross-lagged association between mathematics achievement at 9 and self-evaluation at 12. The model operates in the same way as above, except the order of the variables in the Cholesky decomposition is changed to control for other measures.
The fit of the genetic cross-lagged model is examined by comparing the −2-log likelihood (−2ll) of the submodel of the Cholesky model, with equality constraints for means of twin 1 and twin 2 across MZ and DZ twins, to a saturated model which estimates variances, covariances and means free of constraints. The differences between the fit of the two models are distributed as a chi-square. The degrees of freedom represent the differences between the number of estimated parameters in the saturated model and that in the cross-lagged model. Akaike’s information criterion (Akaike, 1987) was also computed, with lower values indicating better fit.
3 Results
3.1 Descriptive Statistics
Table 1 shows the means and standard deviations for the measures at ages 9 and 12 along with the results of a 2×2 (Zygosity × Sex) ANOVA. Significant results were observed for main effects of sex on self-evaluation at ages 9 and 12 (boys > girls) and on mathematics achievement at age 9 (boys > girls). Despite the large sample size, these effects accounted for less than 1% of the variances, except for self-evaluation at 9 or which 2.8% of its variance is due to sex differences. The mean mathematical performance at ages 9 and 12 were consistent with the expected levels of achievement for these ages. For further analysis, as mentioned earlier, self-evaluation and achievement were corrected for IQ, age and sex by means of regression (McGue & Bouchard, 1984) and standardized residual scores were created.
3.2 Phenotypic Correlations
As shown in Table 2, after the adjustment for IQ, the phenotypic correlation between self-evaluation at 9 and achievement at 12 was modest (r = .18), as was the correlation between achievement at 9 and self-evaluation at 12 (r = .20). Mathematics achievement at each age could be moderately predicted by self-evaluation at the same age (at 9: r = .26; at 12: r = .29). Both self-evaluation and achievement were relatively stable from 9 to 12 years (self-evaluation: r = .47; achievement: r = .32). Given all the correlations decreased after IQ was controlled, this indicated the importance of IQ for both self-evaluation and achievement and justified our strategy of controlling for IQ in our attempts to understand the developmental relationship between self-evaluation and achievement.
Table 2.
Phenotypic correlations between self-evaluation and mathematics achievement at 9 and 12 years
| Math at 9 | SEV at 9 | SEV at 12 | Math at 12 | |
|---|---|---|---|---|
| Math at 9 | – | .34 n = 1452 |
.38 n = 1393 |
.57 n = 693 |
| SEV at 9 | .26 n = 1410 |
– | .50 n = 1818 |
.26 n = 862 |
| SEV at 12 | .20 n = 932 |
.47 n = 1244 |
– | .35 n = 829 |
| Math at 12 | .32 n = 433 |
.18 n = 571 |
.29 n = 575 |
– |
Note. Correlations for one randomly selected member of each twin pair (indicated by n). All the correlations are significant at p < .01. Correlations before the adjustment of IQ are above the diagonal and correlations after the adjustment of IQ are below the diagonal. SEV = self-evaluation, reported by children; Math = mathematics achievement, assessed by teachers according to the National Curriculum.
3.3 Genetic and Environmental Influences on Mathematical Self-evaluation
The twin intraclass correlations for all measures are shown in Table 3 by zygosity. In every case, the MZ twin correlation exceeded that of DZ twins, indicating genetic influence. For self-evaluation at ages 9 and 12, non-additive genetic effects were indicated as the DZ twin correlations were less than half the MZ twin correlations. However, for math achievement, the influence of shared environments was suggested as the DZ twin correlations were more than half the MZ twin correlations.
Genetic, shared and non-shared environmental influences on each measure were obtained from univariate maximum-likelihood model-fitting (Plomin et al., 2008). The variance of each measure was decomposed into latent factors, i.e. AC(D)E. For math self-evaluation, ADE models were adopted, and fitted the data well as compared to saturated models (age 9: Δχ2 = 4.38, df = 6, p = .63, AIC = −7.62; age 12: Δχ2 = 3.13, df = 6, p = .79, AIC = −8.87); for math achievement, ACE models were used and fitted the data well (age 9: Δχ2 = 4.25, df = 6, p = .64, AIC = −7.75; age 12: Δχ2 = 6.52, df = 6, p = .37, AIC = −5.48). The heritability (A, D), shared environment (C) and non-shared environment (E) estimates from the univariate model-fitting are included in Table 3. Heritability of self-evaluation, estimated as the total of additive and non-additive genetics, was 40% at 9 (a2 = 2%, d2 = 38%). The heritability remained almost the same at 12 (43%), except that the proportions of additive and non-additive genetic effects changed (a2 = 29%, d2 = 14%). Non-shared environmental influences explained the rest of the variance and were substantial for self-evaluation at ages 9 and 12 (age 9: e2 = 59%; age 12: e2 = 57%). Mathematics achievement at age 9 was mainly influenced by additive genetic effects (56%), with moderate environmental influences (c2 = 12%, e2 = 32%). For achievement at age 12, additive genetic effects, shared environment effects and non-shared environment effects each contributed moderately (a2 = 36%, c2 = 17%, e2 = 46%).
3.4 Genetic and Environmental Mediation of Cross-lagged Associations
3.4.1 Results from the genetic cross-lagged models
In addition to the non-shared environment, self-evaluation was influenced by additive and non-additive genetic effects, while achievement was influenced by additive genetic effects and shared environment. Therefore, a comprehensive analysis should incorporate additive and non-additive genetic factors, as well as shared and non-shared environmental factors. However, as mentioned earlier, it is not possible to identify all ACDE factors simultaneously in one model with the classic twin design. On one hand, if non-additive genetic effect is presented but D is not included in the model, most variance due to non-additive genetic effect is likely to be accounted for by A; technically, a2 will be over-estimated comparable to the size of a2+d2 (maybe somewhat conservatively). On the other hand, if shared environment is presented but C is not included in the model, most variance due to shared environment would not be accounted for by non-shared environment given the opposite hypotheses about them in the modelling; this would possibly inflate (a2+d2) largely to the extent of c2 – leading to biased estimates of genetic and environmental contributions to the cross-lags. On the contrary, using A to represent additive and non-additive genetic effects will not bias the etiological pattern, except that the two genetic effects cannot be decoupled. Therefore, we adopted the ACE model to estimate the genetic, shared and non-shared environmental influences on the cross-lags.
The cross-lagged association between self-evaluation at age 9 and mathematics achievement at age 12 was estimated using the model on the left side of Figure 1 (a, b, c). The full model, i.e. the submodel of the Cholesky model with the equality constrains over means of twin 1 and twin 2 across MZ and DZ twins, was compared to the saturated model and fitted the data well (Δχ2 = 55.06, df = 57, p = .55, AIC = −58.94). As most estimates of shared environmental factors were nonsignificant, we dropped C to test the AE model which fitted the data no worse than the full model (Δχ2 = 18.65, df = 10, p = .05, AIC = −1.35).
The genetic and environmental mediation of cross-lagged association between self-evaluation at 9 and mathematics achievement at 12 is presented as the percentage of AE contributions to the model-estimated phenotypic correlations (Neiderhiser et al., 1999). These values were derived from the path estimates shown on the left side of Figure 1. The phenotypic cross-lag controlling for their contemporaneous correlations at age 9, their stabilities from 9 to 12 years, and the reverse cross-lag can be estimated within the model by adding the AE paths that link self-evaluation at 9 and achievement at 12, using the formula a22×a24+e22×e24, i.e. √.34×√.03+√.60×√.00=.11 (95% confidence interval (CI): .05–.16). Genetic and environmental contributions to this phenotypic cross-lag can be estimated by dividing the product of related path estimates by the phenotypic cross-lag. For example, the genetic contribution is a22×a24/(a22×a 24+e22×e24), i.e. (√.34×√.03)/.11. Genetic factors accounted for 98% of the moderate phenotypic cross-lag (CI: .45–.1.00). The non-shared environment accounted for the remainder (2%, CI: .00–.55).
The ‘reverse’ cross-lagged association between achievement at 9 and self-evaluation at 12 was analyzed using the model on the right side of Figure 1 (d, e, f). The goodness-of-fit was examined and an AE model fitted best (Δχ2 = 18.65, df = 10, p = .05, AIC = −1.35). The phenotypic cross-lagged correlation was modest, estimated as .05 (CI: .01–. 10). This cross-lag was also primarily explained by genetics (62%, CI: .00–1.00), with moderate influences from non-shared environment (38%, CI: .00–1.00). It should be noted that these estimates of the AE contributions were based on model-fitting results and may not be exactly equal to values derived from Figure 1 where squared path estimates were rounded up. In addition, the magnitudes of the 95% confidence intervals of these ACE estimates were large because it was difficult to obtain robust estimates given such limited phenotypic correlations.
3.4.2 Results from a different cross-lagged model
The etiology of the cross-lagged associations can also be studied using another, theoretically different, approach which does not directly assess the etiological accounts of the phenotypic cross-lags (Burt, McGue, Krueger, & Iacono, 2005). By assuming that genetic and environmental contributions to cross-lagged associations are transmitted phenotypically, phenotypic cross-lagged correlations are merely weighted by the ACE estimates at the previous age rather than being decomposed into their ACE components of covariance (Burt, et al., 2005; Larsson, Viding, Rijsdijk, & Plomin, 2008). In other words, the cross-lag from self-evaluation at 9 to achievement at 12 is assumed to be affected genetically to the extent that self-evaluation at 9 is heritable. Using this approach, the decomposition of the phenotypic cross-lag from self-evaluation at 9 to achievement at 12 (r = .09) showed almost the same estimates as the univariate model-fitting of self-evaluation at 9: a2 = 38%, c2 = 1% and e2 = 62%. Similarly, for the reverse cross-lag (r = .10) from achievement at 9 to self-evaluation at 12, the decompositions were highly similar to ACE estimates for achievement at 9: a2 = 52%, c2 = 17% and e2 = 32%.
4 Discussion
4.1 The heritability of math self-evaluation
According to the commonly held view (Wigfield & Eccles, 2000; Krapp, 2005), individual differences in mathematical self-evaluation are driven by environments, such as parental or teacher influence, rather than genes. But we found significant genetic effects on mathematical self-evaluation. Self-evaluation of mathematical abilities and interest was moderately heritable at ages 9 and 12 (40% and 43% respectively). Moreover, the rest of the variance was explained by non-shared, rather than family- or school-wide environments. This suggests that any parental or teacher influence on mathematical self-evaluation is individual-specific, potentially interacting with genetically-driven dispositions. In other words, understanding individual differences in mathematical self-evaluation requires acknowledging the role of genes. In addition, as genetic influence on mathematical self-evaluation is largely stable in magnitude from middle childhood to early adolescence, mathematical self-evaluation is likely to stay constant over time, to a large extent for genetic reasons. Thus, genetic effects should be included in theoretical models related to self-concept of mathematics.
We found no significant influence of the shared environment, but considerable non-shared environmental influence on mathematical self-evaluation at both 9 and 12 (59% and 57% respectively). This means that the covariation between siblings' mathematical self-evaluation is a result of genetic similarity, rather than the environmental factors shared by them, such as parents’ beliefs, attitudes and behaviors. In other words, having the same parents, having the same socioeconomic status, and going to the same school did not contribute to the similarity between the two children beyond the similarity in their genetic make-up. On the other hand, our data, at a group level, indicate that differences in self-evaluation between family members largely come from differences in environmental experience. These non-shared experiences or perceptions are, in this case, unknown and require further investigation. Potential candidates include peer pressure, childhood illnesses, and differential expectations and treatment by parents and teachers(Kovas, Harlaar, Petrill, & Plomin, 2005). Another possible source of non-shared environment is that siblings from the same family experience their environment in different ways (Plomin & Daniels, 1987).
4.2 Genetic mediation of the cross-lags
The main findings of this study come from the cross-lagged analyses of the links between self-evaluation and achievement. We found reciprocal influences over time, in that earlier self-evaluation predicted later achievement and earlier achievement also predicted later self-evaluation. The most novel finding was that both cross-lagged relationships were genetically mediated. In this discussion, we focus on the cross-lagged relationship between self-evaluation at age 9 and achievement at age 12 for two reasons. First, this cross-lag is more interesting in that the reverse cross-lag seems obvious: Doing better at mathematics makes children say that they are better at mathematics and like it more. Second, the cross-lag from self-evaluation to achievement is twice as strong as the converse cross-lag even though both are significant.
Although limited in phenotypic magnitude, the cross-lagged contribution of mathematical self-evaluation at age 9 to mathematics achievement at age 12 is almost entirely attributed to genetic effects (98%). In the typical multivariate genetic analysis, finding genetic overlap would imply pleiotropy – the same genes influencing both traits. For example, pleiotropy is likely to explain the results of the only previous multivariate genetic analysis of the association between self-perceived abilities and general school achievement in middle childhood, which found that genetic effects largely mediated the contemporaneous relationship (Greven et al., 2009). However, in the case of cross-lagged analysis, genetic mediation means that genetic influences on self-evaluation at age 9 are associated with genetic influences on mathematics achievement at age 12, independent of genetic influences on mathematics achievement at age 9. In other words, if we were able to identify the genes responsible for the heritability of self-evaluation at age 9, some of these genes would not be associated with mathematics achievement at age 9 but they would be associated with mathematics achievement at age 12. Although there is considerable genetic stability for mathematics achievement from age 9 to age 12, some new genetic effects on mathematics achievement emerges at age 12, and the cross-lagged genetic effects from self-evaluation at age 9 contribute to this new genetic variance. We are far away from understanding the mechanism of such pleiotropic associations, but our results help to clarify at least one important issue: They show that no environmentally determined causal link exists between earlier self-evaluation and later mathematics achievement, at least in the UK.
Nevertheless, we cannot overlook the divergence of results from different methods, which more or less reflect different theories about cross-lagged associations. As described in the results, estimates obtained from a different model (Burt et al., 2005) suggested that genetic factors contribute moderately to the cross-lagged association between self-evaluation at 9 and achievement at 12 (38%), whereas the genetic cross-lagged model suggested predominant genetic contributions (98%). The source of these discrepancies lies with dissimilar approaches to the etiology of a cross-lagged association. The Burt et al. (2005) model assumes that genetic and environmental influences on a cross-lag entirely reflect those on the previous behavior. In other words, there is no genetic analysis of the cross-lag. However, in the genetic cross-lagged model, the focus is on the genetic analysis of the cross-lag itself and no assumption is made except that variables are ordered according to time course (Luo, Haworth, & Plomin, 2010). The ultimate test of direction of effects for cross-lag models will come when these quantitative genetic models are replaced by measured genes that account for the heritability of both variables at both ages. Our genetic cross-lagged analysis predicts that genes can be found that are associated with self-evaluation at age 9 and mathematics achievement at age 12 independent of genetic influences on mathematics achievement at age 9.
In spite of methodological divergence, both methods indicate that genetic influences are essential for the cross-lagged associations between mathematical self-evaluation and achievement. Any attempt at targeting mathematical underachievement through influencing self-evaluation needs to take into account the findings that self-perception of mathematical abilities and interest is shaped by genetic and non-shared environmental influences, and the cross-lagged association between self-perception and actual performance is mostly explained by genetic effects.
It is important to note that the findings of the present study are sample-specific. In other words, the results could be different in a different educational set-up, or with different societal and cultural norms. More research, including conducting genetically-sensitive studies in a cross-cultural context, is needed to identify the exact mechanisms through which mathematical self-evaluation, mathematical achievement, and the links between them develop.
Understanding the genetic and environmental causes can help to direct policy investigations. Instead of thinking about education as a way of countering genetic differences among children, the field of education might profit from accepting that children differ genetically in how and how much they learn (Haworth, Asbury, Dale, & Plomin, 2011). This way of thinking is compatible with the current trend towards personalizing education by optimizing children’s learning (DfES, 2004), which is increasingly possible through the use of interactive information technology.
4.3 Limitations
The current findings must be interpreted in light of several shortcomings. Although it is an interesting finding that the phenotypic cross-lagged correlations were only small, this is also a limitation of the study because this may deflate the reliability of the genetic and environmental estimates and result in large confidence intervals: the cross-lag from self-evaluation at 9 to achievement at 12 and the reverse cross-lag were only 0.11 and 0.05 respectively. However, it should be noted that severe constraints have been placed on those phenotypic cross-lags: They must be controlled for IQ at ages 9 and 12, the contemporaneous correlation at 9 and the stability from 9 to 12.
Another limitation is that the present study could only be conducted from age 9 to age 12 because these are the only ages so far in TEDS in which self-evaluation and mathematics achievement were assessed simultaneously. Incorporating prior performance and self-evaluation in future research will lead to better understanding of causal mechanisms of the observed longitudinal associations among mathematics achievement and self-evaluation. In addition, though a composite score was used to represent the performances of different mathematics areas at each age, mathematics at different ages involves to some extent different cognitive processes and procedures. Further study is necessary to include a more nuanced treatment of similarities and differences in mathematical content across ages. Our previous work indicates that a high degree of genetic and environmental stability exists across the early school years in terms of effects on mathematical performance (Haworth, Kovas, Petrill, & Plomin, 2007).
Limitations specific to the genetic cross-lagged approach are discussed elsewhere in detail (Luo, et al., 2010). Despite the adjustment in the structural equation model adopted in this study, one path (i.e., a22/c22/e22 in Figure 1) remains shared - leading to potential mild inflation of the cross-lagged correlation between self-evaluation at 9 and achievement at 12 due to the stability of self-evaluation.. Similarly, the cross-lagged association between achievement at 9 and self-evaluation at 12 could be inflated by the stability of achievement. To address this problem, we examined several other methods. For instance, to analyse the cross-lag from self-evaluation at 9 to achievement at 12, the contemporaneous covariance between self-evaluation and achievement at 12 was removed from achievement at 12 by regression to prevent influences from any variance related to self-evaluation at 12 including the stability of self-evaluation. Then in a tri-variate model, i.e. a standard Cholesky decomposition of three variables (achievement at 9, self-evaluation at 9 and achievement 12, which are ordered so as to adjust achievement at 9), we decomposed the cross-lag into genetic and environmental factors. Results from this method and others suggested similar results to those presented in this paper: The cross-lagged association between earlier self-evaluation and later achievement, as well as the reverse cross-lag, were largely genetically driven. (Details of these analyses are available from the first author.)
5 Conclusion
For mathematical self-evaluation during middle childhood and early adolescence, individual differences are attributed to moderate genetic influences and considerable non-shared environmental influences, without any significant influence from shared environment. The association between mathematical self-evaluation in middle childhood and mathematics achievement in early adolescence, as well as the reverse association, are primarily genetically driven. Importantly, the cross-lagged analysis indicates that genetic influences on self-evaluation at age 9 predict achievement at age 12 independent of genetic influence on achievement at age 9. A better understanding of the mechanisms underlying these associations will be the first step towards concrete pathways for educational interventions.
Appendix B.
Path estimates (and 95% confidence intervals) of the genetic cross-lagged models in Figure 1
| Genetic cross-lagged model (Figure 1 a, b and c) |
The second genetic cross-lagged model (Figure 1 d, e and f) |
||
|---|---|---|---|
| A | E | A | E |
| a11=.69 (.65–.72) | e11=.31 (.28–.35) | a11=.39 (.34–.43) | e11=.61 (.57–.66) |
| a12=.05 (.03–.07) | e12=.02 (.01–.03) | a12=.08 (.05–.13) | e12=.01 (.01–.02) |
| a13=.04 (.02–.07) | e13=.01 (.00–.02) | a13=.08 (.03–.15) | e13=.00 (.00–.01) |
| a14=.10 (.05–.16) | e14=.02 (.00–.05) | a14=.21 (.16–.28) | e14=.06 (.03–.08) |
| a22=.34 (.29–.39) | e22=.60 (.55–.65) | a22=.61 (.56–.65) | e22=.30 (.28–.34) |
| a23=.17 (.12–.23) | e23=.05 (.03–.08) | a23=.05 (.02–.11) | e23=.02 (.00–.05) |
| a24=.03 (.00–.09) | e24=.00 (.00–.01) | a24=.00 (.00–.01) | e24=.00 (.00–.01) |
| a33=.21 (.16–.27) | e33=.51 (.46–.57) | a33=.43 (.33–.51) | e33=.42 (.35–.51) |
| a34=.01 (.00–.05) | e34=.02 (.00–.04) | a34=.00 (.00–.02) | e34=.02 (.00–.05) |
| a44=.42 (.33–.50) | e44=.41 (.33–.49) | a44=.21 (.16–.27) | e44=.49 (.48–.55) |
Note. All paths estimates are standardized and squared to refer to the percentage of variance explained. A = genetic; E = non-shared environment.
Acknowledgements
We gratefully acknowledge the ongoing contribution of the TEDS families. TEDS is supported by a program grant (G0500079) from the U.K. MRC; our work on school environments and academic achievement is also supported by grants from the US NIH (HD44454 and HD46167). YLLL is supported by Excellent Doctoral Dissertation Fund of Beijing Normal University (BNU, 08049), the National Basic Research Program of China (2010CB833903) and the BNU Innovative Fund (2009SD-3).
Footnotes
This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest: The authors declare no conflict of interest.
References
- Ackerman PL, Wolman SD. Determinants and validity of self-estimates of abilities and self-concept measures. Journal of ExperimentalPsychology-Applied. 2007;13(2):57–78. doi: 10.1037/1076-898X.13.2.57. [DOI] [PubMed] [Google Scholar]
- Akaike H. Factor-Analysis and Aic. Psychometrika. 1987;52(3):317–332. [Google Scholar]
- Burt SA, McGue M, Krueger RF, Iacono WG. How are parent-child conflict and childhood externalizing symptoms related over time? Results, from a genetically informative cross-lagged study. Development and Psychopathology. 2005;17(1):145–165. doi: 10.1017/S095457940505008X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chamorro-Premuzic T, Furnham A. Personality and intellectual competence. Mahwah, N.J.: L. Erlbaum Associates; 2005. [Google Scholar]
- Davis OSP, Arden R, Plomin R. g in middle childhood: Moderate genetic and shared environmental influence using diverse measures of general cognitive ability at 7, 9 and 10 years in a large population sample of twins. Intelligence. 2008;36(1):68–80. [Google Scholar]
- Deary IJ, Strand S, Smith P, Fernandes C. Intelligence and educational achievement. Intelligence. 2007;35(1):13–21. [Google Scholar]
- DfES. Department for Education and Skills: Five year strategy for children and learners. London: Department for Education and Skills; 2004. [Google Scholar]
- Eccles JS, Wigfield A. In the Mind of the Actor - the Structure of Adolescents Achievement Task Values and Expectancy-Related Beliefs. Personality and Social Psychology Bulletin. 1995;21(3):215–225. [Google Scholar]
- Furnham A, Chamorro-Premuzic T. Estimating one’s own personality and intelligence scores. British Journal of Psychology. 2004;95:149–160. doi: 10.1348/000712604773952395. [DOI] [PubMed] [Google Scholar]
- Gottfried AE. Academic Intrinsic Motivation in Elementary and Junior-High-School Students. Journal of Educational Psychology. 1985;77(6):631–645. [Google Scholar]
- Gottfried AE. Academic Intrinsic Motivation in Young Elementary-School-Children. Journal of Educational Psychology. 1990;82(3):525–538. [Google Scholar]
- Greven CU, Harlaar N, Kovas Y, Chamorro-Premuzic T, Plomin R. More Than Just IQ: School Achievement Is Predicted by Self-Perceived Abilities-But for Genetic Rather Than Environmental Reasons. Psychological Science. 2009;20(6):753–762. doi: 10.1111/j.1467-9280.2009.02366.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- GrossTsur V, Manor O, Shalev RS. Developmental dyscalculia: Prevalence and demographic features. Developmental Medicine and Child Neurology. 1996;38(1):25–33. doi: 10.1111/j.1469-8749.1996.tb15029.x. [DOI] [PubMed] [Google Scholar]
- Guay F, Marsh HW, Boivin M. Academic self-concept and academic achievement: Developmental perspectives on their causal ordering. Journal of Educational Psychology. 2003;95(1):124–136. [Google Scholar]
- Haworth CM, Asbury K, Dale PS, Plomin R. Added value measures in education show genetic as well as environmental influence. PLoS One. 2011;6(2):e16006. doi: 10.1371/journal.pone.0016006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haworth CM, Kovas Y, Petrill SA, Plomin R. Developmental origins of low mathematics performance and normal variation in twins from 7 to 9 years. Twin Res Hum Genet. 2007;10(1):106–117. doi: 10.1375/twin.10.1.106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haworth CMA, Harlaar N, Kovas Y, Davis OSP, Oliver BR, Hayiou-Thomas ME, et al. Internet cognitive testing of large samples needed in genetic research. Twin Research and Human Genetics. 2007;10(4):554–563. doi: 10.1375/twin.10.4.554. [DOI] [PubMed] [Google Scholar]
- Helkmke A. Selbstvertrauen und schlische Leistung [Selfconfidence and school management] Gottingen: Hogrefe; 1992. [Google Scholar]
- Kovas Y, Harlaar N, Petrill SA, Plomin R. ‘Generalist genes’ and mathematics in 7-year-old twins. Intelligence. 2005;33(5):473–489. doi: 10.1016/j.intell.2005.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovas Y, Haworth CMA, Dale PS, Plomin R. The genetic and environmental origins of learning abilities and disabilities in the early school years. Monographs of the Society for Research in Child Development. 2007;72(3):1–144. doi: 10.1111/j.1540-5834.2007.00439.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovas Y, Petrill SA, Plomin R. The Origins of Diverse Domains of Mathematics: Generalist Genes but Specialist Environments. J Educ Psychol. 2007;99(1):128–139. doi: 10.1037/0022-0663.99.1.128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krapp A. Basic needs and the development of interest and intrinsic motivational orientations. Learning and Instruction. 2005;15(5):381–395. [Google Scholar]
- Larsson H, Viding E, Rijsdijk FV, Plomin R. Relationships between parental negativity and childhood antisocial behavior over time: A bidirectional effects model in a longitudinal genetically informative design. Journal of Abnormal Child Psychology. 2008;36(5):633–645. doi: 10.1007/s10802-007-9151-2. [DOI] [PubMed] [Google Scholar]
- Loehlin JC. The Cholesky approach: A cautionary note. Behavior Genetics. 1996;26(1):65–69. [Google Scholar]
- Luo LLY, Haworth CMA, Plomin R. A novel approach to genetic and environmental analysis of cross-lagged associations over time: The cross-lagged relationship between self-perceived abilities and school achievement is mediated by genes as well as the environment. Twin Research and Human Genetics. 2010;13(5):426–436. doi: 10.1375/twin.13.5.426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsh HW. Verbal and Math Self-Concepts - an Internal External Frame of Reference Model. American Educational Research Journal. 1986;23(1):129–149. [Google Scholar]
- Marsh HW, Byrne BM, Yeung AS. Causal ordering of academic self-concept and achievement: Reanalysis of a pioneering study and revised recommendations. Educational Psychologist. 1999;34(3):155–167. [Google Scholar]
- Marsh HW, Yeung AS. Causal effects of academic self-concept on academic achievement: Structural equation models of longitudinal data. Journal of Educational Psychology. 1997;89(1):41–54. [Google Scholar]
- McGue M, Bouchard TJ. Adjustment of Twin Data for the Effects of Age and Sex. Behavior Genetics. 1984;14(4):325–343. doi: 10.1007/BF01080045. [DOI] [PubMed] [Google Scholar]
- Neale MC, Boker SM, Xie G, Maes H. Mx:Statistical Modeling. 7th ed. Richmond: Department of Psychiatry, Medical College of Virginia; 2006. [Google Scholar]
- Neale MC, Cardon LR. Methodolgy for genetic studies of twins and families. Dordrecht: Kluwer; 1992. [Google Scholar]
- Neiderhiser JM, Reiss D, Hetherington EM, Plomin R. Relationships between parenting and adolescent over time: Genetic and environmental contributions. Developmental Psychology. 1999;35(3):680–692. doi: 10.1037//0012-1649.35.3.680. [DOI] [PubMed] [Google Scholar]
- Oliver BR, Plomin R. Twins’ Early Development Study (TEDS): A multivariate, longitudinal genetic investigation of language, cognition and behavior problems from childhood through adolescence. Twin Research and Human Genetics. 2007;10(1):96–105. doi: 10.1375/twin.10.1.96. [DOI] [PubMed] [Google Scholar]
- PISA. [Retrieved June, 21, 2010];PISA 2009 results. 2009 from http://www.oecd.org/document/61/0,3746,en_32252351_32235731_46567613_1_1_1_1,00.html.
- Plomin R, Daniels D. Why are children in the same family so different from one another? Behavioral and Brain Sciences. 1987;10:1–16. [Google Scholar]
- Plomin R, DeFries JC, McCleann GE, McGuffin P. Behavioral genetics. 5th ed. New York, NY: Worth Publishers; 2008. [Google Scholar]
- Price TS, Freeman B, Craig I, Petrill SA, Ebersole L, Plomin R. Infant zygosity can be assigned by parental report questionnaire data. Twin Res. 2000;3(3):129–133. doi: 10.1375/136905200320565391. [DOI] [PubMed] [Google Scholar]
- Raven JC, Court JH, Raven J. Manual for Raven’s progressive matrices and vocabulary scales. Oxford: Oxford University Press; 1996. [Google Scholar]
- Rijsdijk FV, Sham PC. Analytic approaches to twin data using structural equation models. Brief Bioinform. 2002;3(2):119–133. doi: 10.1093/bib/3.2.119. [DOI] [PubMed] [Google Scholar]
- Schicke MCF, Thomas K. Contributions of Self-concept and Intelligence to the Prediction . of Academic Achievement Among Grade 4, 6, and 8 Students. Canadian Journal of School Psychology. 1994;10(1):62–69. [Google Scholar]
- Smith A. Making mathematics count: The report of Professor Adrian Smith’s Inquiry into Post-14 Mathematics Education. 2004 [Google Scholar]
- Spinath B, Spinath FM, Harlaar N, Plomin R. Predicting school achievement from general cognitive ability, self-perceived ability, and intrinsic value. Intelligence. 2006;34(4):363–374. [Google Scholar]
- Spinath FM, Spinath B, Plomin R. The nature and nurture of intelligence and motivation in the origins of sex differences in elementary school achievement. European Journal of Personality. 2008;22(3):211–229. [Google Scholar]
- Wechsler D. Wechsler intelligence scale for children — Third Edition UK (WISC-III-UK) Manual. London: The Psychological Corporation; 1992. [Google Scholar]
- Wigfield A, Eccles JS. Expectancy-value theory of achievement motivation. Contemporary Educational Psychology. 2000;25(1):68–81. doi: 10.1006/ceps.1999.1015. [DOI] [PubMed] [Google Scholar]
- Winne PH, Nesbit JC. The Psychology of Academic Achievement. Annual Review of Psychology. 2010;61:653–678. doi: 10.1146/annurev.psych.093008.100348. [DOI] [PubMed] [Google Scholar]