Graph Theoretic Foundations of Multibody Dynamics Part I: Structural Properties

Abstract

This is the first part of two papers that use concepts from graph theory to obtain a deeper understanding of the mathematical foundations of multibody dynamics. The key contribution is the development of a unifying framework that shows that key analytical results and computational algorithms in multibody dynamics are a direct consequence of structural properties and require minimal assumptions about the specific nature of the underlying multibody system. This first part focuses on identifying the abstract graph theoretic structural properties of spatial operator techniques in multibody dynamics. The second part paper exploits these structural properties to develop a broad spectrum of analytical results and computational algorithms.

Towards this, we begin with the notion of graph adjacency matrices and generalize it to define block-weighted adjacency (BWA) matrices and their 1-resolvents. Previously developed spatial operators are shown to be special cases of such BWA matrices and their 1-resolvents. These properties are shown to hold broadly for serial and tree topology multibody systems. Specializations of the BWA and 1-resolvent matrices are referred to as spatial kernel operators (SKO) and spatial propagation operators (SPO). These operators and their special properties provide the foundation for the analytical and algorithmic techniques developed in the companion paper.

We also use the graph theory concepts to study the topology induced sparsity structure of these operators and the system mass matrix. Similarity transformations of these operators are also studied. While the detailed development is done for the case of rigid-link multibody systems, the extension of these techniques to a broader class of systems (e.g. deformable links) are illustrated.

1 Introduction

Graph theory provides concepts that are natural for describing multibody systems and their application to robotic and multibody system dynamics is not new. Wittenburg [36] used the underlying graph associated with a multibody system to organize and formulate the equations of motion. Later it was shown that Wittenburg’s formulation procedure could in fact be completely re-interpreted using linear graph theory ideas from the alternative vector-network technique [24]. The goal of some of these graph theory methods has been to make systematic the process of generating the complex equations of motion for multibody systems [3, 4]. Some of the extensions have led to computer techniques for organizing and automatically generating symbolic representations of the equations of motion [31]. Graph theory techniques have also been used for the kinematic analysis of mechanisms [37].

Motivated by robotics, control and simulation needs, mathematical operator techniques have been developed by researchers to obtain a system-level understanding of the underlying structure of the system kinematics and dynamics. Researchers [5, 7, 8, 30, 32] have used system-level matrices and operators to analyze and exploit the structure and sparsity of the mass matrix. Mass matrix factorization techniques and system-level global transforms to simplify the coupled equations of motion into diagonalized forms have also been explored [1, 2, 10, 20, 22, 33]. One common feature to most of these techniques has been the use of relative, instead of absolute coordinates [25] to parametrized the state of the system. While absolute coordinate models are arguably easier to assemble, relative coordinate models use minimal coordinates (for tree-topology systems) and are more suitable from a control perspective. We adopt the relative coordinates approach throughout this paper.

Spatial operator techniques, developed by Rodriguez and others [16, 27–29], have led to the development of important analytical insights and computational dynamics algorithms. The operator techniques have been inspired by mathematical parallels between the structure of the dynamical equations of motion and the time-domain problem of optimal estimation and smoothing. The covariance factorization and optimal filtering techniques behind the seminal Kalman filtering techniques have been shown to be applicable to the dynamics domain. Spatial operators were initially applied to serial-chain rigid body systems to obtain the following analytical factorization and inversion results for serial-chain, rigid body system mass matrices [27, 28]:

$$\begin{array}{cc}\hfill ℳ=& H\varphi M{\varphi }^{*}{H}^{*}\hfill \\ \hfill ℳ=& [\mathit{I}+H\varphi 𝒦]𝒟{[\mathit{I}+H\varphi 𝒦]}^{*}\hfill \\ \hfill {[\mathit{I}+H\varphi 𝒦]}^{-1}=& [\mathit{I}-H\psi 𝒦]\hfill \\ \hfill {ℳ}^{-1}=& {[\mathit{I}-H\psi 𝒦]}^{*}{𝒟}^{-1}[\mathit{I}-H\psi 𝒦]\hfill \end{array}$$ (1)

In the above ℳ denotes the configuration dependent system mass matrix, and H, ϕ etc. are examples of spatial operators. The results in Eq. 1 have been applied to operational space dynamics [23], under-actuated system dynamics [19], sensitivity analysis [21], dynamics diagonalization [20] etc.

The spatial operator techniques were subsequently extended to dynamics models for systems with rigid and deformable links [18], tree and non-tree topologies [12, 29], geared and flexible hinge systems [17] etc. accompanied by the development of several efficient computational algorithms for robot control and simulation based on these analytical results. While the elements of the H, ϕ and other spatial operators in Eq. 1 varied significantly across these different systems (e.g. rigid versus deformable bodies), remarkably, the mass matrix factorization and inversion relations in Eq. 1 continue to hold across these systems. Despite the convergence of such operator-level mathematical properties, there has been a lack in understanding of the underlying basis for such convergence since each system’s spatial operator formulation was developed independently starting from each system’s specific properties.

In this paper we identify deep connections between graph theory techniques and multibody system dynamics¹. This paper generalizes the notion of adjacency matrices for graphs to introduce the notion of block-weighted adjacency (BWA) matrices and studies their mathematical properties. The primary contribution of this paper is to show that key spatial operators are in fact instances of such BWA matrices for graphs associated with multibody systems. This relationship is quite general and independent of the specific branching structure of the system topology, the rigid/flexible nature of the component bodies, the body indexing schemes etc. The BWA matrices associated with multibody systems are referred to as spatial kernel operators (SKO), and their related 1-resolvents (defined later) as spatial propagation operators (SPO). We show that the system equations of motions described using these SKO and SPO spatial operators have the same form across a broad family of multibody systems. The companion second part of this paper [14] builds upon this foundation to show that important analytical techniques and computational dynamics algorithms follow directly from these abstract, analytical results. As such, these techniques and algorithms are broadly applicable, with minimal restrictions, to a broad range of multibody systems.

The organization of this paper is as follows. We begin by reviewing the properties of directed graphs (digraphs) in Section 2. We examine the properties of adjacency matrices used to describe graph connectivity in Section 3, and review the nilpotency property of such matrices for trees. Section 4 generalizes the notion of adjacency matrices to block weighted adjacency (BWA) matrices with block matrix elements. Section 5 studies the properties of BWA matrices under similarity transformations. In Section 6 we identify the connections between BWA matrices and their 1-resolvents with multibody dynamics by formulating at the dynamics of serial-chain and tree-topology rigid multibody systems. Section 7 shows that these BWA properties extend virtually unchanged to tree-topology systems. It also introduces the SKO and SPO nomenclature. Finally, Section 8 provides a brief overview of how the BWA properties extend beyond rigid body to deformable body multibody systems.

The graph theoretic structural properties developed in this paper provide a unifying perspective for dynamics models across a broad range of multibody systems and lay the groundwork for the examination of analytical and algorithmic properties of multibody systems that are the subject of the companion part II paper [14].

2 Directed graphs and trees

We begin with an overview of terminology and concepts from graph theory. A graph is a collection of nodes, and edges connecting pairs of nodes. A directed graph (also known as a digraph) is a graph where the edges have direction, i.e., an edge from one node to another is not the same as an edge in the reverse direction [34]. Each edge in a digraph defines a parent/child relationship between the node pair of that edge. Nodes defining an edge are said to be adjacent nodes. The node from which the edge emanates is referred to as the parent node, and the destination node is said to be the child node. The set of parent nodes of the k^th node is denoted ℘(k), and the set of its children nodes is ∁(k). When a node has multiple child nodes, each child node represents the start of a branch emanating from the node. Nodes without parent nodes are referred to as root nodes. Digraphs can have zero, one, or multiple root nodes. We assume that there is at most a single edge in the same direction between any pair of nodes, i.e., parallel edges between a pair of nodes are not allowed.

A node, j, is said to be the ancestor of another node, i, if there is a directed path from the node j to the node i. We use the notation i ≺ j (or equivalently j ≻ i) to indicate that node j is an ancestor of node i. The notation i ⊀ j implies that node j is not an ancestor of node i. Node i is said to be the descendant of node j if j is an ancestor of node i. A pair of nodes, i and j, are said to be related if one of them is the ancestor of the other; otherwise they are said to be unrelated.

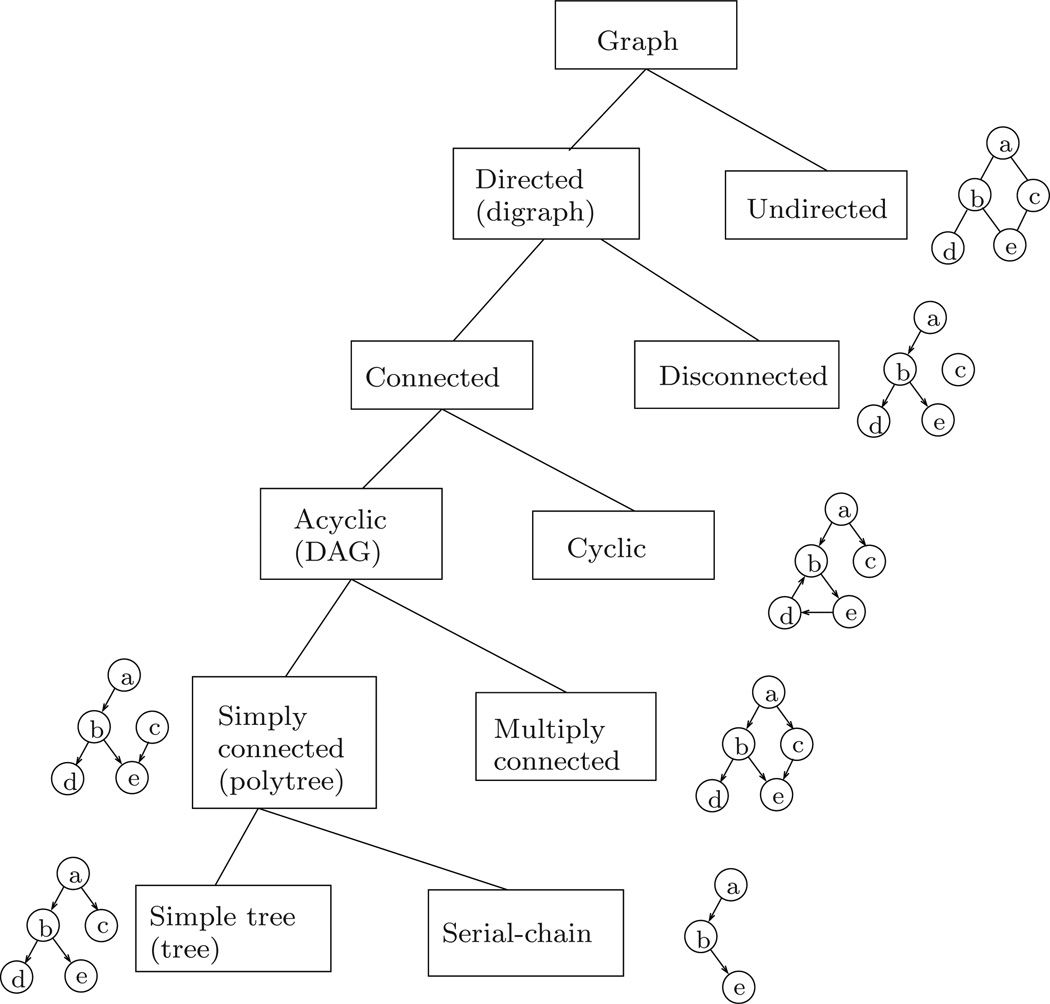
Figure 1 shows a taxonomy for graphs and digraphs adapted from Ramoni [26]. We briefly describe the left branch of this classification hierarchy in increasing order of specialization [6, 35]:

1. A connected digraph is a digraph such that there is an undirected path connecting any pair of nodes, i.e., it is a digraph without disjoint components.

2. A rooted digraph is a connected digraph with a single root node that is the ancestor of every other node in the digraph. All edges connected to the root node are directed away from the root node. Thus, with r denoting the root node, we have r ≽ k for all nodes k in a rooted digraph.

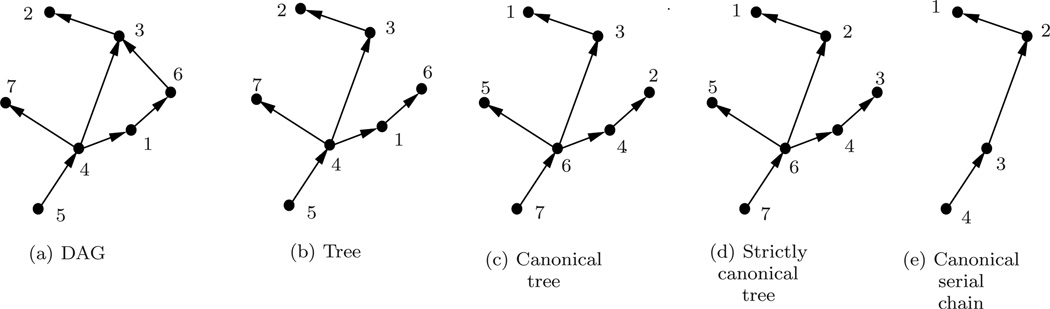
3. A directed acyclic graph (DAG) is a connected digraph without any directed cycles, i.e., there is no directed path from any node back to itself. Thus, a node cannot be its own ancestor in a DAG, i.e., k ⊀ k for any node k in the digraph. Figure 2a illustrates a DAG.

4. A simply connected graph, or a polytree (also known as singly connected networks), is a DAG in which there is at most one directed path between any pair of nodes. For such digraphs, if nodes i and j are both ancestors of node k, then one of the i and j nodes must be an ancestor of the other. Notationally, this condition states that if k ≺ i and k ≺ j, then either i ≼ j or j ≼ i. Removing an edge decomposes a polytree into a pair of polytrees. A node in a polytree can have multiple parent nodes.

5. A simple tree, or tree, illustrated in Figure 2b, is a polytree where a node has at most one parent node, i.e., ℘(k) contains at most one node for any node k. All trees have a unique root node. A tree is a rooted digraph, and is also referred to as a rooted tree or an arborescence. Removing an edge decomposes a tree into a pair of trees.

   While a node in a tree can have at most one parent, there is no restriction on the number of children nodes. The branching structure implies that it is possible for nodes to be on different branches with no directed path connecting them. Thus, trees can have unrelated nodes, i.e., nodes that have no directed paths connecting them. Another noteworthy fact is that, for a pair of nodes, i and j, while j ≻ i ⟹ i ≰ j, the converse is not true in general. For a tree, we use the notation ℘(i, j) for the closest ancestor node of a pair of nodes i and j.

6. A serial-chain is a tree where each node has at most one child. Figure 2e illustrates a serial-chain. Unlike trees, serial-chains have the stronger property that all node pairs are related, i.e., for any pair of nodes in the serial-chain, one of the nodes is necessarily an ancestor of the other.

7. An arborescence forest, or forest, is a collection of disjoint trees. Removing an edge from a tree converts it into a forest. Adding a common root node to the independent trees in a forest converts them into a single tree. Conversely, removing the root node from a tree converts it into a forest.

Fig. 1.

Hierarchical classification of graphs and digraphs

Fig. 2.

Illustrations a digraphs with a DAG, a tree, canonical and strictly canonical trees and a serial-chain.

A tree is said to be canonical² if the index of a parent node is always greater than the index of its child node, i.e., ℘(k) > k for any node k. The digraph in Figure 2c illustrates a canonical tree. Any tree can be converted into a canonical tree with a suitable renumbering of the nodes. The node numbering for a canonical tree is not unique since the canonical tree requirement imposes only a partial ordering on the node indices. The canonical numbering is, however, unique for a serial-chain.

A strictly canonical tree is a canonical tree in which the indices within each of its serial-chain segments are sequential. The digraph in Figure 2d illustrates a strictly canonical tree. The canonical tree in Figure 2c is however not strictly canonical because the (1, 3) and (2, 4) index sets of the nodes in its serial segments are not sequential. Once again, any rooted tree can be converted into a strictly canonical tree with a suitable renumbering of the nodes.

Every rooted digraph has a spanning tree, i.e., a tree that contains all the nodes in the digraph and whose edges belong to the digraph. The edges removed to convert a rooted digraph into its spanning tree are referred to as cut-edges.

3 Adjacency matrices for digraphs

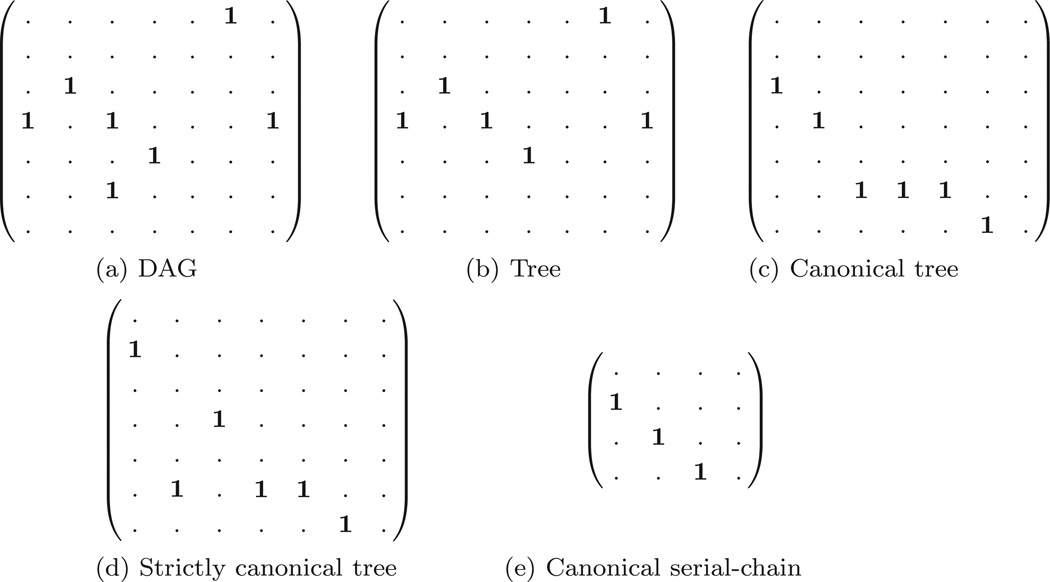
One way of representing the node/edge connectivity of a digraph is through an adjacency matrix for the digraph. For a digraph with n nodes, the adjacency matrix is an n × n square matrix. The only non-zero elements of an adjacency matrix are for adjacent node pairs. Thus, the (i, j)^th element of of an adjacency matrix is 1 if and only if the j^th node is a child of the i^th node, and is 0 otherwise. With the “.” entries indicating 0 entries, adjacency matrices for the digraphs in Figure 2 are shown in Figure 3. Weighted adjacency matrices are generalizations of standard adjacency matrices in allowing arbitrary weight entries, instead of just the 1 value for the edges in a digraph.

Fig. 3.

The adjacency matrices for the digraphs illustrated in Figure 2.

3.1 Properties of digraph adjacency matrices

The adjacency matrix, 𝕊, of a digraph can be expressed as

$$𝕊={\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{k\in \wp (j)}}{e}_k{e}_j^{*}$$ (2)

where e_i denotes a vector of length n, containing all zeros except for the i^th element which has value 1, i.e.,

$$e_i(r)=\{\begin{array}{cc}1\hfill & \text{for }i=r\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}={\mathrm{𝟙}}_{[i=r]}$$ (3)

𝟙_[<cond>] denotes the indicator function, whose value is 1 when the condition specified in its subscript is true, and whose value is 0 otherwise. Observe that

$$e_j^{*}·e_k={\mathrm{𝟙}}_{[j=k]}$$ (4)

The number of $e_k{e}_j^{*}$ terms in Eq. 2 is precisely the number of edges in the digraph. Each $e_k{e}_j^{*}$ edge term is an n × n matrix, with a single non-zero element of value 1 for the associated (k, j) edge. Key structural properties of an adjacency matrix, 𝕊, for a digraph are summarized below:

1. The non-zero entries in the j^th column of 𝕊 are for the ℘(j) parent nodes of the j^th node. Thus, the product of 𝕊 with the i^th unit vector e_i is a vector whose non-zero entries are the parent nodes of the i^th node. In particular, a node p is a root node if and only if

   $$𝕊·e_p=\mathbf{0}$$ (5)

   In other words, root node columns of 𝕊 have all zero elements.

2. The non-zero entries in the i^th row of 𝕊 are for the ∁(i) child nodes of the i^th node. Thus, the product of 𝕊* with the i^th unit vector, e_i, is a vector whose non-zero entries are the child nodes of the i^th node. In particular, a node t is a tip node, i.e., it has no children, if and only if

   $$e_t^{*}·𝕊=\mathbf{0}$$ (6)

   In other words, tip node rows of 𝕊 have all zero elements.

3. Permutation matrices can be used to re-index the nodes in a digraph. Permutation matrices are orthogonal, i.e., the transpose of a permutation matrix is its inverse. With T denoting such a permutation matrix, and 𝕊 the adjacency matrix of the original digraph, the adjacency matrix of the digraph after re-indexing is T𝕊T*.

3.2 Properties of tree adjacency matrices

Since nodes in a tree can have at most one parent node, the adjacency matrix of a tree digraph in Eq. 2 can be expressed in the following simpler form:

$$𝕊={\displaystyle \sum _{k=1}^n}{e}_{\wp (k)}{e}_k^{*}$$ (7)

We now examine the properties of an adjacency matrix, 𝕊, for a tree digraph.

1. Since a node can have at most one parent in a tree, there can be at most one non-zero entry in any column of 𝕊.

2. Only a single column, corresponding to the root node, is all zero in 𝕊.

3. A row can have multiple non-zero elements.

4. For canonical trees, 𝕊 is always strictly lower-triangular.

5. Reversing the direction of the edges in a tree typically destroys the tree character; leaving only a polytree. The reversal process converts multiple children nodes into multiple parent nodes. 𝕊* is the adjacency matrix for the polytree.

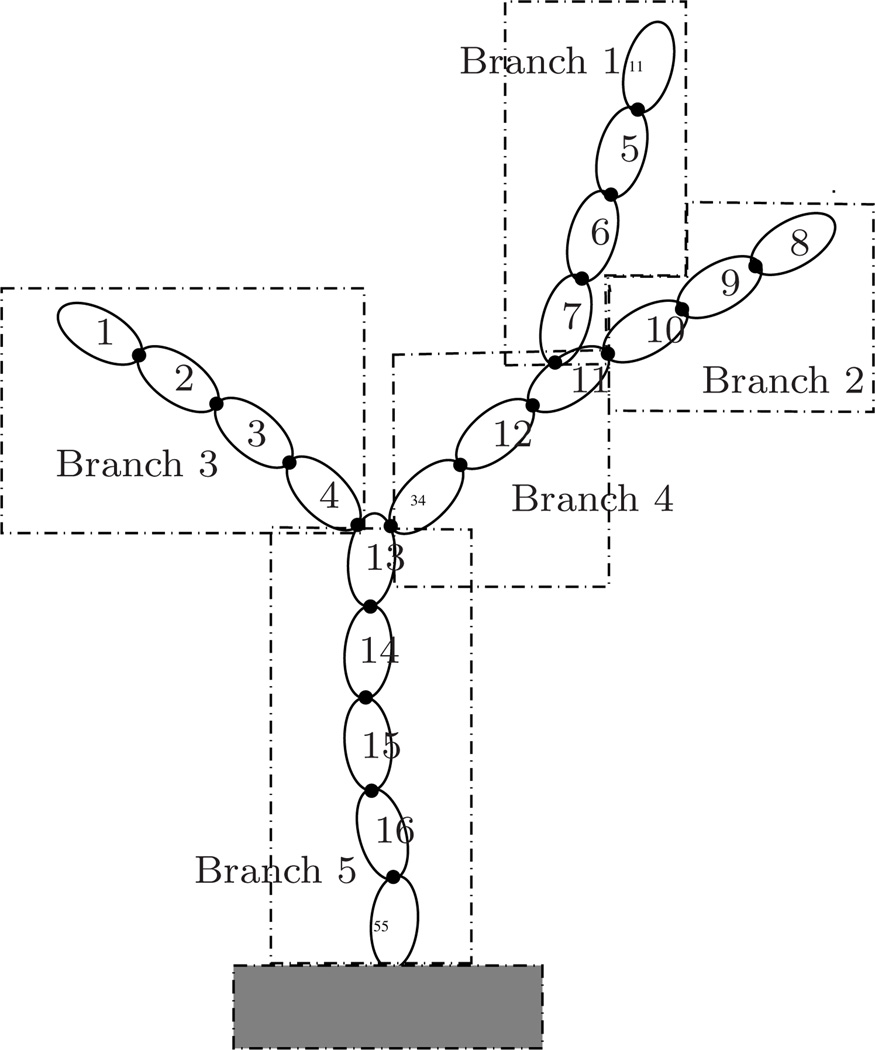
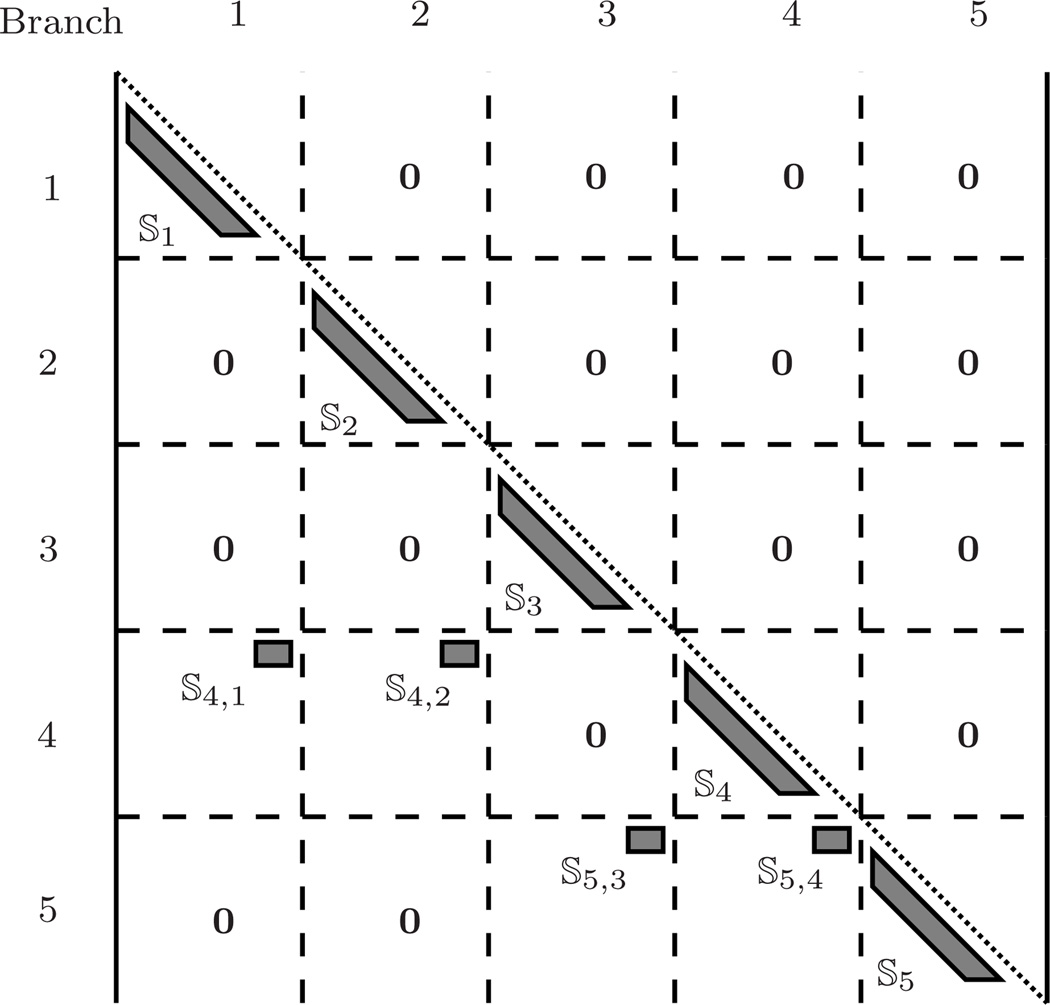
6. 𝕊 has simpler structure for strictly canonical trees. It consists of the adjacency matrix for serial canonical serial-chain segment digraphs, 𝕊_i, along the diagonal, and off-diagonal 𝕊_i,j elements for the edges connecting the serial-chain segments. For the example strictly-canonical tree digraph in Figure 4, 𝕊 has the structure shown in Figure 5.

7. The k^th power of the adjacency matrix, 𝕊^k, contains non-zero elements only for paths of length k connecting the nodes [9]. That is, the (i, j) element of 𝕊^k is non-zero if and only if there is a directed path of length k from node i to node j.

8. With n denoting the number of nodes in the tree, the n^th power of the adjacency matrix, 𝕊ⁿ, is zero. This is because the length of any path in a tree with n nodes is less than n. Thus 𝕊 is a nilpotent matrix³. In other words, the adjacency matrix for a tree digraph is always nilpotent.

Fig. 4.

An example strictly-canonical tree topology system decomposed into serial-chain branch segments.

Fig. 5.

Structure of the 𝕊 adjacency matrix for the strictly-canonical tree topology system in Figure 4

3.3 Properties of serial-chain adjacency matrices

We now review the properties of an adjacency matrix, 𝕊, for a serial-chain digraph.

1. Since a node can have at most one child in a serial-chain, its adjacency matrix can have at most one non-zero element per row.

2. For a canonical serial-chain, only the first sub-diagonal of 𝕊 is non-zero.

3. For a canonical serial-chain, only the k^th sub-diagonal of 𝕊^k contains non-zero elements. Each additional power shifts the sub-diagonal one level lower.

4. A reversed serial chain is once again a serial-chain.

4 Block weighted adjacency matrices

Adjacency matrices have 1 or 0 scalar entries for the node pair of each edge in a digraph, while weighted adjacency matrices allow scalar entries other than 1 for the edges. We now generalize weighted adjacency matrices to define block-weighted adjacency (BWA) matrices. Instead of scalars, BWA matrices are weighted adjacency matrices whose weight entries for the edges are not scalars, but instead matrices. First, each tree node, j, is assigned a weight dimension, m_j, and its parent edge is assigned a weight matrix of dimension m_℘(j) × m_j, denoted w (℘(j), j). The (k, j)^th block-matrix element of a BWA matrix, 𝕊_W, is thus

$${𝕊}_W(k,j)=\{\begin{array}{cc}w(k,j)\hfill & \text{if }k=\wp (j)\hfill \\ \mathbf{0}\hfill & \text{otherwise}\hfill \end{array}\in {ℛ}^{m_k\times m_j}$$ (8)

Other than the dimensionality requirement, there are no additional restrictions on the 𝕊_W (k, j) weight matrices. The standard adjacency matrix, 𝕊, in Eq. 2 is a special case of a BWA matrix, where all the node dimensions are 1, and the edge weights are the scalar 1. 𝕊_W has non-zero block-entries only for node pairs corresponding to edges in the digraph. It is easy to verify from the definition of the block-elements in Eq. 8 that 𝕊_W is a well-defined square matrix of dimension

$$N\triangleq {\displaystyle \sum _{k=1}^n}{m}_k$$ (9)

We extend the notion of the e_k unit vectors in Eq. 3, to the BWA context by assigning them block matrix entries as follows:

$$e_k(i)=\{\begin{array}{cc}{\mathit{I}}_{m_k}\hfill & \text{if }i=k\hfill \\ {\mathbf{0}}_{m_i\times m_k}\hfill & \text{otherwise}\hfill \end{array}$$ (10)

Thus, the e_k unit “vector” is a matrix of dimension N × m_k, with n block matrix elements. The new version of Eq. 4 is

$$e_j^{*}·e_k=\{\begin{array}{cc}{\mathit{I}}_{m_j}\hfill & \text{if }j=k\hfill \\ {\mathbf{0}}_{m_j\times m_k}\hfill & \text{otherwise}\hfill \end{array}$$ (11)

Using the unit vectors, and the component definitions in Eq. 8, 𝕊_W can be expressed as:

$${𝕊}_W={\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{k\in \wp (j)}}{e}_{k}w(k,j)e_j^{*}$$ (12)

Eq. 12 is a generalization of Eq. 2 for BWA matrices.

4.1 BWA matrices for tree digraphs

Analogous to Eq. 7, the BWA matrix expression in Eq. 12 has the following simpler form for tree digraphs:

$${𝕊}_W={\displaystyle \sum _{k=1}^n}{e}_{\wp (k)}w(\wp (k),k)e_k^{*}$$ (13)

The following lemma provides an expression for the block elements of ${𝕊}_W^k$ for tree digraphs.

Lemma 1 Elements of ${𝕊}_W^k$ for a tree digraph

For a tree digraph, ${𝕊}_W^k$ , the k^th power of the 𝕊_W BWA matrix, contains non-zero block-elements only for node pairs connected by directed paths of length k. The value of its block-element is the product of the k weights for the edges along the path, i.e., the non-zero elements are of the form

$${𝕊}_W^k({\wp }^k(i),i)=w({\wp }^k(i),{\wp }^{k-1}(i))*\cdots *w(\wp (i),i)\in {ℛ}^{m_{{\wp }^k(i)}\times m_i}$$ (14)

Here, ℘^k(i) denotes the k^th ancestor of the i^th node.

Proof Let us illustrate the proof for k = 2. ${𝕊}_W^2$ is given by

$$\begin{array}{cc}{𝕊}_W^2\hfill & \stackrel{13}{=}({\displaystyle \sum _{j=1}^n}{e}_{\wp (j)}w(\wp (j),j)e_j^{*})*({\displaystyle \sum _{i=1}^n}{e}_{\wp (i)}w(\wp (i),i)e_i^{*})\hfill \\ \hfill & \stackrel{4}{=}{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^n}{e}_{\wp (j)}w(\wp (j),j){\mathrm{𝟙}}_{[j=\wp (i)]}w(\wp (i),i)e_i^{*}\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^n}{e}_{{\wp }^2(i)}w({\wp }^2(i),\wp (i))*w(\wp (i),i)e_i^{*}\hfill \end{array}$$

The (℘²(i), i) block-element of ${𝕊}_W^2$ is thus,

$${𝕊}_W^2({\wp }^2(i),i)=w({\wp }^2(i),\wp (i))*w(\wp (i),i)$$

which establishes Eq. 14 for ${𝕊}_W^2$ . Continuing in a similar vein, Eq. 14 can be established for arbitrary k.

4.2 The 1-resolvent of tree BWA matrices

The following lemma establishes the nilpotency of 𝕊_W for tree digraphs.

Lemma 2 Nilpotency of tree BWA matrices

The n^th power of a tree BWA matrix, ${𝕊}_W^n$ , is zero, where n denotes the number of nodes in the system. Hence, the BWA matrix for a tree digraph is a nilpotent matrix.

Proof Lemma 1 states that the non-zero entries of ${𝕊}_W^n$ correspond to node pairs connected by paths of length n. Since paths can be of length at most n − 1 in a tree with n nodes, it follows that ${𝕊}_W^n$ is the zero matrix.

In matrix theory, the resolvent of a matrix A, is defined as the (λI − A)⁻¹ matrix for a scalar λ. We use the term, 1-resolvent, to denote the specific resolvent with λ = 1.

Lemma 3 The 1-resolvent of a nilpotent matrix

If U is a nilpotent matrix, such that Uⁿ = 0, then its 1-resolvent, W ≜ = (I − U)⁻¹, is given by

$$W=\mathit{I}+U+U^2+\cdots +U^{n-1}$$ (15)

Proof For W as defined in Eq. 15

$$\mathit{\text{UW}}=\mathit{\text{WU}}=U+U^2+\cdots +U^n=U+U^2+\cdots +U^{n-1}=W-\mathit{I}$$

Rearranging terms, we have

$$\mathit{I}=W-\mathit{\text{UW}}=(\mathit{I}-U)W\Rightarrow {(\mathit{I}-U)}^{-1}=W$$

The following lemma derives an explicit expression for the 1-resolvent of a tree BWA matrix.

Lemma 4 The 1-resolvent of a tree BWA matrix

The 1-resolvent, (I − 𝕊_W)⁻¹, of a tree BWA matrix exists and can be expressed as the following disjoint sum of its powers:

$${(\mathit{I}-{𝕊}_W)}^{-1}=\mathit{I}+{𝕊}_W+{𝕊}_W^2+\cdots +{𝕊}_W^{n-1}$$ (16)

Proof Lemma 2 states that the adjacency matrix of a tree, 𝕊_W, is nilpotent. Eq. 16 follows by applying the expression from Lemma 3 for the 1-resolvent of a nilpotent matrix to 𝕊_W.

Lemma 4 is an important result. It provides an explicit expression for the 1-resolvent of the 𝕊_W BWA matrix for tree systems. For cyclic digraphs, i.e., ones with directed loops, the 1-resolvent is not defined because 𝕊_W is not nilpotent and (I − 𝕊_W) is non-invertible. This topological difference has significant implications for the dynamics properties of tree versus cyclic digraph multibody systems. This is discussed in more detail in [14]

We now introduce notation that better reflects the intimate relationship between a BWA matrix and its 1-resolvent matrix for a tree digraph. With 𝔸 denoting the 1-resolvent matrix for a tree, we will use the notation ℰ_𝔸 to denote its associated BWA matrix. Thus, the relationship between the earlier notation and the new notation is as follows:

$$𝔸\equiv {(\mathit{I}-{𝕊}_W)}^{-1}\text{ and }{ℰ}_{𝔸}\equiv {𝕊}_W=\mathit{I}-{𝔸}^{-1}$$ (17)

The following lemma describes the expression for the block elements of a 1-resolvent matrix.

Lemma 5 Elements of a 1-resolvent matrix 𝔸

The (k, j) element of the 1-resolvent matrix of a tree, 𝔸 = (I − ℰ_𝔸)⁻¹, is given by

$$𝔸(i,j)=\{\begin{array}{cc}{\mathbf{0}}_{m_i\times m_j}\hfill & \mathit{\text{for }}i\nsucc j\hfill \\ {\mathit{I}}_{m_i}\hfill & \mathit{\text{for }}i=j\hfill \\ w(i,j)\hfill & \mathit{\text{for }}i=\wp (j)\hfill \\ w({\wp }^k(j),{\wp }^{k-1}(j))*\cdots *w(\wp (j),j)\hfill & \mathit{\text{for }}i={\wp }^k(j)\hfill \end{array}$$ (18)

Proof Eq. 18 follows from the expression for (I−ℰ_𝔸)⁻¹ in Eq. 16, together with Lemma 1 which describes the elements of the powers of ℰ_𝔸.

Thus, 𝔸 has identity matrices along the diagonal. The non-zero block elements correspond to (i, j) node pairs where node i is an ancestor of node j. For such cases, the block element is the product of the weight matrices associated with each of the edges in the path from i to j. From Eq. 18, it is clear that the 𝔸 1-resolvent is sparse, with its sparsity structure directly reflecting the topological structure of the associated tree.

Remark 4.1 Structure of canonical serial-chain ℰ_𝔸 and 𝔸 matrices

Let us now examine the structure of the 1-resolvent matrix 𝔸 for a canonical serial-chain digraph. We assume for this example that the serial-chain has 4 nodes, and thus ${ℰ}_{𝔸}^4=\mathbf{0}$ . Using Eq. 16, 𝔸 is given by the following disjoint sum:

$$𝔸=\mathit{I}+{ℰ}_{𝔸}+{ℰ}_{𝔸}^2+{ℰ}_{𝔸}^3$$

The non-zero elements of the above matrices are as shown below (with “·” entries indicating zero blocks and the X entries the non-zero ones):

$${ℰ}_{𝔸}=(\begin{array}{cccc}\hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill X\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill X\hfill & \hfill .\hfill \end{array}),{ℰ}_{𝔸}^2=(\begin{array}{cccc}\hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill X\hfill & \hfill .\hfill & \hfill .\hfill \end{array}),{ℰ}_{𝔸}^3=(\begin{array}{cccc}\hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \end{array})$$

ℰ_𝔸 has non-zero block entries only along its first sub-diagonal. Each subsequent power of ℰ_𝔸 shifts the non-zero sub-diagonal lower, until it vanishes entirely for the n^th power.

Thus, 𝔸 has the following structure:

$$𝔸=\left(\begin{array}{cccc}\hfill \mathit{I}\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill \mathit{I}\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill X\hfill & \hfill \mathit{I}\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill \mathit{I}\hfill \end{array}\right)$$

𝔸 is lower-triangular, with all of the diagonal and lower-triangular block-elements being non-zero. All of these terms are non-zero because all nodes in serial-chains are related, i.e., there is a directed path between all node pairs.

This example shows that, for a canonical serial-chain, all of the lower-triangular elements of 𝔸 are non-zero. The following example looks at the structure of a 1-resolvent matrix for a canonical tree.

Remark 4.2 Structure of canonical tree ℰ_𝔸 and 𝔸 matrices

The sparsity structure of the ℰ_𝔸 and 𝔸 matrices for the canonical tree in Figure 2c is shown below. The “·” entries indicate zero block-elements.

$${ℰ}_{𝔸}=(\begin{array}{ccccccc}\hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill X\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill X\hfill & \hfill .\hfill \end{array})\mathit{\text{ and }}𝔸=(\begin{array}{ccccccc}\hfill \mathit{I}\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill \mathit{I}\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill .\hfill & \hfill \mathit{I}\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill X\hfill & \hfill .\hfill & \hfill \mathit{I}\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill \mathit{I}\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill \mathit{I}\hfill & \hfill .\hfill \\ \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill X\hfill & \hfill \mathit{I}\hfill \end{array})$$

These matrices illustrate that, for canonical trees, the ℰ_𝔸 matrix is strictly lower-triangular, and 𝔸 is lower-triangular. However, some of the lower-triangular blocks of 𝔸 are zero, in contrast with the all non-zero case for canonical serial-chains. The zero terms correspond to the unrelated nodes in the tree, i.e., node pairs that are not connected by a path. Jain [14] takes a more detailed look at the sparsity structures of the ℰ_𝔸 and 𝔸 matrices.

This example shows that there is significant sparsity in the lower-triangular blocks of 𝔸 for a tree. The sparsity is a function of the branching topological structure of the tree. Serial-chain systems represent the most dense topological structure since all of their nodes are related. Trees, on the other hand, can have unrelated nodes, i.e., nodes with no directed paths connecting them. This decreased connectivity of the nodes is reflected in the sparsity of 𝔸.

The following lemma highlights the semi-group properties of the block elements of 𝔸.

Lemma 6 Semi-group property of 𝔸 (i, j) elements

For a tree, let i, j, and k denote nodes, where the i^th node is an ancestor of the j^th node, and the k^th node is on the path connecting them. Then, the block-elements of the 𝔸 1-resolvent satisfy the following relationship:

$$𝔸(i,j)=𝔸(i,k)𝔸(k,j)\forall k:i\mathrm{\succcurlyeq }k\mathrm{\succcurlyeq }j$$ (19)

This property is also known as the semi-group property for the elements of a 1-resolvent matrix.

Proof Let i = ℘^m(j) for some m, and k = ℘^r(j) for some r < m. Let l denote the child node of k that is on the path to node j. From the Eq. 18 expression for the block elements of 𝔸, we have

$$\begin{array}{cc}𝔸(i,j)\hfill & \underset{¯}{\underset{¯}{18}}w({\wp }^m(j),{\wp }^{m-1}(j))*\cdots *w(\wp (j),j)\hfill \\ \hfill & =[w({\wp }^m(j),{\wp }^{m-1}(j))*\cdots *w(\wp (k),k)]*[w(k,l)*\cdots *w(\wp (j),j)]\hfill \\ \hfill & \underset{¯}{\underset{¯}{18}}𝔸({\wp }^m(j),k)*𝔸(k,j)=𝔸(i,k)*𝔸(k,j)\hfill \end{array}$$

Define the 𝔸̃ matrix derived from the 𝔸 1-resolvent matrix as follows:

$$\widetilde{𝔸}\triangleq 𝔸-\mathit{I}$$ (20)

𝔸̃ is strictly lower-triangular for canonical trees. The following lemma establishes some basic properties of 𝔸̃.

Lemma 7 The 𝔸̃ spatial operator

For a 1-resolvent 𝔸, the following identities hold:

$$\widetilde{𝔸}=𝔸-\mathit{I}={ℰ}_{𝔸}𝔸=𝔸{ℰ}_{𝔸}$$ (21)

Proof For any matrix X, such that (I −X) is invertible, the following matrix identity holds:

$$X{(\mathit{I}-X)}^{-1}={(\mathit{I}-X)}^{-1}X={(\mathit{I}-X)}^{-1}-\mathit{I}$$

With X = ℰ_𝔸, the above equation, together with Eq. 20, directly lead to Eq. 21.

The following exercise extends the adjacency matrix properties in Eq. 5 and Eq. 6 to BWA matrices and their 1-resolvents.

Corollary 4.1 Root/tip nodes and BWA matrices

1. A node r is a root node of the tree if and only if

   $${ℰ}_{𝔸}·e_r=\mathbf{0},𝔸·e_r=e_r$$ (22)
2. A node t is a tip node of the tree, i.e., it has no children nodes, if and only if

   $${ℰ}_{𝔸}^{*}·e_t=\mathbf{0},{𝔸}^{*}·e_t=e_t$$ (23)

Proof:

1. The first part of Eq. 22 is a generalized restatement of Eq. 5 for BWA matrices. The latter half follows from the following:

   $${𝔸}^{-1}·e_r\underset{¯}{\underset{¯}{17}}(\mathit{I}-{ℰ}_{𝔸})e_r\underset{¯}{\underset{¯}{22}}{e}_r$$

2. The proof here is completely analogous to that of the first part with the use of Eq. 6.

The following remark describes properties of the product of a general matrix, and a diagonal matrix, that we will use in the forthcoming sections.

Remark 4.3 Matrix products

Recall that any block-matrix, Y, can be expressed as

$$Y={\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{k=1}^n}{e}_{j}Y(j,k)e_k^{*}$$

Let $X\triangleq \text{ diag }{\left\{X(i)\right\}}_{i=1}^n\mathit{\text{ and }}Z\triangleq \text{ diag }{\left\{Z(i)\right\}}_{i=1}^n$ denote compatible block-diagonal matrices. Then it is easy to verify that

$$\begin{array}{cc}\hfill \mathit{\text{XY}}& ={\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{k=1}^n}{e}_{j}X(j)Y(j,k)e_k^{*}\hfill \\ \mathit{\text{and YZ}}\hfill & ={\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{k=1}^n}{e}_{j}Y(j,k)Z(k)e_k^{*}\hfill \end{array}$$ (24)

While the discussion in this section has been devoted to BWA matrices and 1-resolvents for tree digraphs, all of the properties and results extend directly to forests, i.e., to digraphs consisting of a set of disjoint trees.

5 Similarity transformations of a tree BWA matrix

We now examine the effect of applying similarity transformations to a BWA matrix.

Lemma 8 Similarity transformation of a BWA matrix

Let T denote an invertible matrix and ℰ_𝔸 a tree BWA matrix. Let Y ≜ = Tℰ_𝔸T⁻¹ denote a similarity transformation of ℰ_𝔸 by the T matrix. Then Y is nilpotent, and its 1-resolvent is given by the following similarity transformation:

$${(\mathit{I}-Y)}^{-1}=T𝔸T^{-1}$$ (25)

Proof Since ℰ_𝔸 is nilpotent, we have

$$Y^n={(T{ℰ}_{𝔸}{T}^{-1})}^n=T{({ℰ}_{𝔸})}^n{T}^{-1}=\mathbf{0}$$

Hence, Y is nilpotent. Also,

$${(\mathit{I}-Y)}^{-1}={(\mathit{I}-T{ℰ}_{𝔸}{T}^{-1})}^{-1}=T{(\mathit{I}-{ℰ}_{𝔸})}^{-1}{T}^{-1}=T𝔸T^{-1}$$

This establishes Eq. 25.

The above lemma provides an expression for the 1-resolvent of the matrix obtained by applying a similarity transformation to a BWA matrix. However, there is no guarantee that the transformed matrix, Y, retains the block partitioned structure of the original BWA matrix. Generally, the transformed Y matrix will not be a BWA matrix for the tree.

5.1 Permutation similarity transformations

A special case, where the BWA property is preserved under similarity transformations, occurs when the transformation matrix is a permutation matrix used to re-index the nodes in the tree. For such a permutation matrix, denoted T, we know that T⁻¹ = T*. The transformed matrix, ℰ_𝔹 ≜ = Tℰ_𝔸T⁻¹ is indeed a BWA matrix for the tree, and its 1-resolvent 𝔹 is given by:

$${ℰ}_{𝔹}=T{ℰ}_{𝔸}{T}^{*}\text{ and }𝔹\triangleq {(\mathit{I}-{ℰ}_{𝔹})}^{-1}\underset{¯}{\underset{¯}{25}}T𝔸T^{*}$$ (26)

In the multibody context, such permutation transformations relate equations of motion obtained using different body numbering schemes. In particular, any tree can be converted into a canonical tree with an appropriate re-labeling of the nodes. This implies that the ℰ_𝔸 and 𝔸 matrices for any tree are related to the lower-triangular versions for the corresponding canonical tree via permutation matrices.

5.2 Similarity-shift transformations

Another type of similarity transformation, referred to as a similarity-shift transformation, that preserves the BWA property is discussed next. Let Δ_ℂ be an invertible, block-diagonal matrix defined as follows:

$$\begin{array}{ccc}{\Delta }_{ℂ}\triangleq \text{ diag }{\left\{{\Delta }_{ℂ}(k)\right\}}_{k=1}^n\hfill & \text{where}\hfill & {\Delta }_{ℂ}(k)\in {ℛ}^{m_k\times m_k}\hfill \end{array}$$ (27)

Let 𝔹 (℘(k), k) denote new weight matrices defined from the original 𝔸 (℘(k), k) weight matrices as follows:

$$𝔹(\wp (k),k)={\Delta }_{ℂ}(\wp (k))𝔸(\wp (k),k){\Delta }_{ℂ}^{-1}(k)$$ (28)

Let ℰ_𝔹 denote the BWA matrix with the 𝔹 (℘(k), k) weight matrices. The following lemma establishes the relationship between the ℰ_𝔸 and ℰ_𝔹 BWA matrices and their 1-resolvents.

Lemma 9 Similarity-shift transformation of a BWA matrix

Let ℰ_𝔸 and ℰ_𝔹 be BWA matrices whose weight matrices satisfy Eq. 28. Then the BWA matrices ℰ_𝔹 and ℰ_𝔸 are related by the following similarity transformation:

$${ℰ}_{𝔹}={\Delta }_{ℂ}{ℰ}_{𝔸}{\Delta }_{ℂ}^{-1}$$ (29)

Also, the 1-resolvent matrices, 𝔸 = (I − ℰ_𝔸)⁻¹ and 𝔹 = (I − ℰ_𝔹)⁻¹, are related by the same similarity transformation:

$$𝔹={\Delta }_{ℂ}𝔸{\Delta }_{ℂ}^{-1}$$ (30)

Proof Now

$$\begin{array}{ccc}{ℰ}_{𝔹}\hfill & \stackrel{28}{=}\hfill & {\displaystyle \sum _{k=1}^n}{e}_{\wp (k)}{\Delta }_{ℂ}(\wp (k))𝔸(\wp (k),k){\Delta }_{ℂ}^{-1}(k)e_k^{*}\hfill \\ \hfill & \stackrel{24}{=}\hfill & {\displaystyle \sum _{k=1}^n}{\Delta }_{ℂ}{e}_{\wp (k)}𝔸(\wp (k),k)e_k^{*}{\Delta }_{ℂ}^{-1}\hfill \\ \hfill & =\hfill & {\Delta }_{ℂ}{\displaystyle \sum _{k=1}^n}{e}_{\wp (k)}𝔸(\wp (k),k)e_k^{*}{\Delta }_{ℂ}^{-1}={\Delta }_{ℂ}{ℰ}_{𝔸}{\Delta }_{ℂ}^{-1}\hfill \end{array}$$

This establishes Eq. 29. Further application of Lemma 8 leads to Eq. 30.

In the multibody context, similarity-shift transformations are used to define the relationship between equations of motion associated with different choices of body frames.

6 Multibody System Graphs

Digraphs provide natural mathematical constructs for describing the topology and connectivity of bodies in a multibody system. They have been used for the systematic formulation of the equations of motion [24, 31, 36], as well as for kinematical analysis [37].

We define the standard digraph associated with a multibody system as one with the inertial frame as the root node, and all the links in the system as the remaining nodes in the digraph. Thus, an n-link multibody system has a digraph with n+1 nodes.

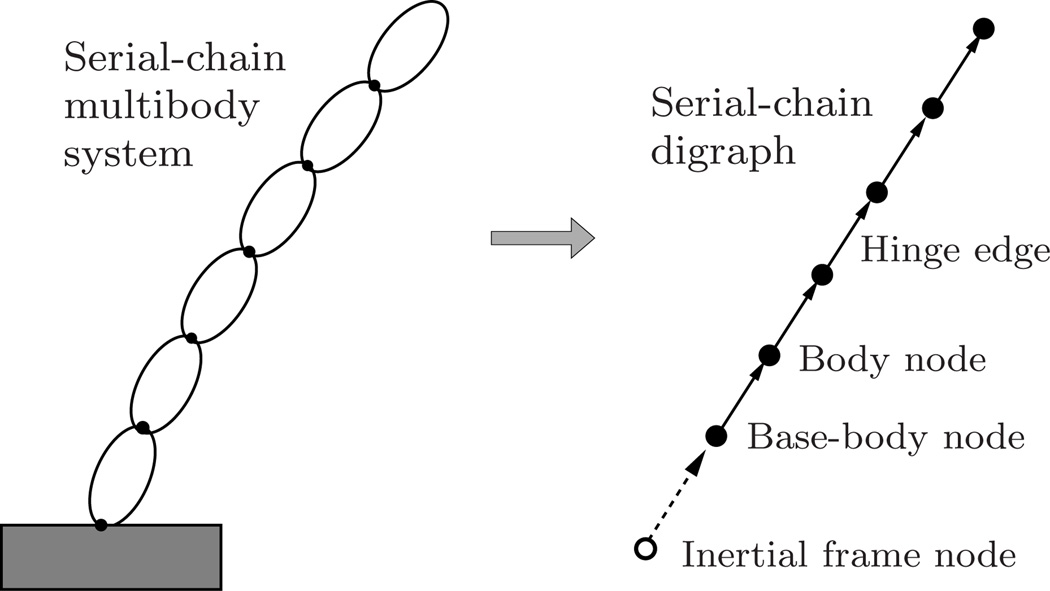
The edges in the digraph are defined by the motion constraints among the bodies, and between the bodies and the inertial frame. Thus, each hinge is represented by an edge, with the edges orientated from the inboard to the outboard body. Additional edges are assigned to other non-hinge motion constraints in the system. All motion constraints with respect to the inertial frame are defined so that edges from the inertial frame node to the link nodes are directed away from the inertial frame root node. These assignments result in a rooted digraph representation for the multibody system. Figure 6 illustrates the correspondence between the bodies and hinges in a serial-chain multibody system and the standard, serial-chain digraph for the system. The convention is to depict the inertial frame node as unfilled, and the edges from the node as dashed lines. Multibody systems are classified as follows, based on the topology of Serial-chain multibody system Serial-chain digraph their standard digraph:

• –systems with tree standard digraphs are referred to as tree-topology systems.
• –systems with serial-chain standard digraphs are referred to as the familiar serial-chain systems. They are special cases of tree-topology systems.
• –systems with non-tree standard digraphs are referred to as closed-chain or constrained systems. These digraphs can have directed cycles and/or multiply-connected nodes. Recall that every rooted digraph can be decomposed (non-uniquely) into a spanning tree together with a set of cut-edges. A decomposition into a spanning tree with n + 1 nodes and a set of cut-edges is often used when working with closed-chain systems.

Fig. 6.

The relationship between a serial-chain multibody system and its standard, serial-chain digraph. The inertial frame nodes are shown as unfilled nodes, while the edges from the node are shown as dashed lines.

Removing the inertial root node converts the spanning tree into a forest. We will refer to this forest as the SKO-forest for the system⁴. The SKO-forest has just n nodes, matching the number of bodies in the system. Nodes corresponding to base-bodies in the multibody system are root nodes in the SKO-forest. We will make extensive use of n-node SKO-forests since they allow us to work with adjacency matrices of dimension n instead of dimension n + 1. There is no information loss because the spanning tree can be fully recovered by adding the inertial frame root node and its edges to the root nodes in the SKO-forest. The inertial frame node is, in reality, redundant in the spanning tree of a multibody system since it is always present as the root node.

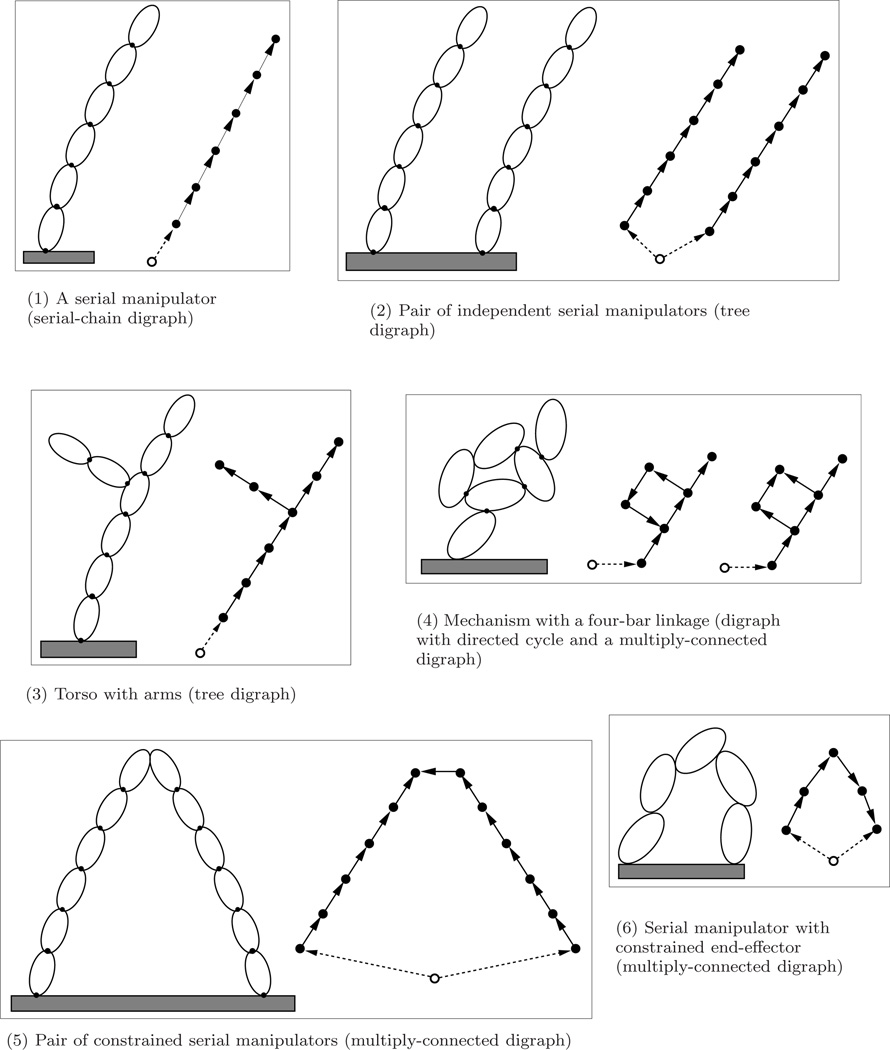
Figure 7 illustrates several examples of multibody systems and their associated standard digraph representations, as described below:

1. A serial-chain system with a serial-chain digraph.

2. A tree-topology system consisting of a pair of independent serial manipulators. The resulting digraph is a tree.

3. A tree-topology system with branching reflected in its tree digraph.

4. A closed-chain four-bar linkage with an internal loop constraint. Based on the directionality of the constraint hinge, the digraph contains a directed cycle or is multiply-connected.

5. A closed-chain pair of serial-manipulators whose end-effectors are constrained. The digraph for this system is a multiply-connected.

6. A closed-chain serial manipulator with constrained end-effector. The digraph is multiply-connected.

Fig. 7.

Examples of general multibody systems and their standard digraph representations.

Non-standard digraphs where the bodies and digraph nodes are not in one-to-one correspondence with each other are permitted - and are used in constraint embedding techniques for modeling closed-chain dynamics [13]

6.1 BWA Matrices and Serial-Chain Rigid Body Systems

In this section we consider serial-chain multibody systems to begin establishing connections between BWA matrices and their 1-resolvents with multibody system dynamics.

6.1.1 Review of serial-chain velocity kinematics

Consider an n-link rigid body serial-chain system. The tip link is denoted link 1 and the base-body link as link n. The associated serial-chain tree associated with this graph is a strictly canonical tree with the parent/child relationship given by ℘(k) = k + 1.

Using spatial coordinate-free notation with 𝒱(k) denoting the spatial velocity (angular+linear, 6-dimensional), θ̇ (k) the hinge generalized velocities, H* (k) the hinge map matrix, and

$${\varphi }^{*}(k+1,k)=\left(\begin{array}{cc}\hfill \mathit{I}\hfill & \hfill \widetilde{𝔩}(k+1,k)\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathit{I}\hfill \end{array}\right)$$ (31)

the rigid body transformation matrix, the link-to-link spatial velocity relationships can be expressed as [7, 11]:

$$𝒱(k)={\varphi }^{*}(k+1,k)𝒱(k+1)+H^{*}(k)\dot{\mathit{\theta }}(k)$$ (32)

The overall velocity degrees of freedom for the system is denoted 𝒩 and is defined as the sum of all the individual hinge degrees of freedom. Now we introduce stacked vectors needed to define system level relationships. The stacked vectors 𝒱 and θ are defined as

$$𝒱\triangleq \text{ col }{\left\{𝒱(k)\right\}}_{k=1}^n=\left[\begin{array}{c}\hfill 𝒱(1)\hfill \\ \hfill 𝒱(2)\hfill \\ \hfill ⋮\hfill \\ \hfill 𝒱(n)\hfill \end{array}\right]\in {ℛ}^{6n},\text{ and }\theta \triangleq \text{ col }{\left\{\theta (k)\right\}}_{k=1}^n=\left[\begin{array}{c}\hfill \theta (1)\hfill \\ \hfill \theta (2)\hfill \\ \hfill ⋮\hfill \\ \hfill \theta (n)\hfill \end{array}\right]\in {ℛ}^{𝒩}$$ (33)

The 𝒱 stacked vector consists of the component body-level 𝒱(k) spatial velocity vectors combined into a single large vector. Correspondingly the θ stacked vector consists of the component body-level θ(k) generalized coordinates combined into a single large vector. The link-level Eq. 32 relationship can now be expressed equivalently at the system level [11] as

$$𝒱={ℰ}_{\varphi }^{*}𝒱+H^{*}\dot{\mathit{\theta }}$$ (34)

where the spatial operator ℰ_ϕ is defined as

$${ℰ}_{\varphi }=\left(\begin{array}{ccccc}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \varphi (2,1)\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \varphi (3,2)\hfill & \hfill \dots \hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill \varphi (n,n-1)\hfill & \hfill \mathbf{0}\hfill \end{array}\right)\in {ℛ}^{6n\times 6n}$$ (35)

and the block-diagonal H ∈ ℛ^𝒩×6n spatial operator as

$$H\triangleq \text{ diag }{\{H(k)\}}_{k=1}^n=\left(\begin{array}{cccc}\hfill H(1)\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill H(2)\hfill & \hfill \dots \hfill & \hfill \mathbf{0}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill H(n)\hfill \end{array}\right)\in {ℛ}^{𝒩\times 6n}$$ (36)

Observe that Eq. 34 is an implicit equation with 𝒱 appearing on the both sides. However, it is explicit at the component-level, i.e. if we look at the k^th row of this matrix equation, we obtain back the Eq. 32 explicit form.

6.1.2 ℰ_ϕ is a BWA matrix

We can re-express Eq. 35 as

$${ℰ}_{\varphi }={\displaystyle \sum _{k=1}^n}{e}_{k+1}\varphi (k+1,k)e_k^{*}={\displaystyle \sum _{k=1}^n}{e}_{\wp (k)}\varphi (\wp (k),k)e_k^{*}$$ (37)

We see that ℰ_ϕ in Eq. 37 has the structure of a BWA matrix in Eq. 13. Indeed, ℰ_ϕ is a BWA matrix for the canonical serial-chain tree with 6 × 6 weight matrices defined by

$$w(\wp (k),k)=w(k+1,k)\triangleq \varphi (k+1,k)=\varphi (\wp (k),k)$$ (38)

Since ℰ_ϕ is a BWA matrix, by Lemma 4, its 1-resolvent ϕ = (I − ℰ_ϕ)⁻¹ is well-defined, and is given by

$$\varphi =\left(\begin{array}{cccc}\hfill I\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill \varphi (2,1)\hfill & \hfill I\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \varphi (n,1)\hfill & \hfill \varphi (n,2)\hfill & \hfill \dots \hfill & \hfill I\hfill \end{array}\right)\in {ℛ}^{6n\times 6n}$$ (39)

The implicit relationship in Eq. 34 can now be converted into an explicit relationship for 𝒱 by rearranging it into the form

$$\begin{array}{ccccc}(\mathit{I}-{ℰ}_{\varphi }^{*})𝒱=H^{*}\dot{\mathit{\theta }}\hfill & \Rightarrow \hfill & {\varphi }^{-*}𝒱=H^{*}\dot{\mathit{\theta }}\hfill & \Rightarrow \hfill & 𝒱={\varphi }^{*}{H}^{*}\dot{\mathit{\theta }}\hfill \end{array}$$ (40)

Thus we have established that the ℰ_ϕ and ϕ spatial operators for serial-chain canonical serial-chain multibody systems are in fact BWA matrices and 1-resolvents respectively for the associated serial-chain graph. Indeed the strictly lower-triangular and lower-triangular structures of ℰ_ϕ and ϕ are consistent with their being associated with canonical serial-chain trees.

6.1.3 Equations of motion for serial-chain systems

From the free-body equations of motion of the k^th link we have:

$$𝔣(k)-\varphi (k,k-1)𝔣(k-1)=M(k)\alpha (k)+𝔟(k)$$ (41)

where 𝔣(k) denotes the inter-link spatial force across the k^th hinge, M(k) denotes the spatial inertia of the k^th link, α(k) its spatial acceleration and 𝔟 (k) the gyroscopic spatial force for the k^th link [11]. Rearranging the above we obtain the following:

$$𝔣(k)=\varphi (k,k-1)𝔣(k-1)+M(k)\alpha (k)+𝔟(k)$$ (42)

Switching to the system-level stacked vector re-expression of Eq. 42, leads to the following relationship:

$$𝔣={ℰ}_{\varphi }𝔣+M\alpha +𝔟$$ (43)

In the above 𝔣, α and 𝔟 are stacked vectors along the lines of Eq. 33, α is a stacked vector of body spatial accelerations, while M is a block-diagonal spatial operator with the M(k) elements along the diagonal. Using Eq. 40 and Eq. 43 it is easy to establish that the overall equations of motion are given by:

$$\begin{array}{c}𝒱={ℰ}_{\varphi }^{*}𝒱+H^{*}\dot{\mathit{\theta }}\hfill \\ \alpha ={ℰ}_{\varphi }^{*}\alpha +H^{*}\ddot{\mathit{\theta }}+𝔞\hfill \\ 𝔣={ℰ}_{\varphi }𝔣+M\alpha +𝔟\hfill \\ 𝒯=H𝔣\hfill \end{array}$$ (44)

In the above 𝒯 is the stacked vector of all the hinge generalized forces, while 𝔞 is the stacked vector of the Coriolis spatial accelerations for all the bodies. Using the 1-resolvent, ϕ, these implicit expressions can be transformed from implicit ones to the following explicit version of the equations of motion:

$$\begin{array}{c}𝒱={\varphi }^{*}{H}^{*}\dot{\mathit{\theta }}\hfill \\ \alpha ={\varphi }^{*}(H^{*}\ddot{\mathit{\theta }}+𝔞)\hfill \\ 𝔣=\varphi (M\alpha +𝔟)\hfill \\ 𝒯=H𝔣\hfill \end{array}$$ (45)

Combining the expressions in Eq. 45 we obtain

$$𝒯=ℳ\ddot{\mathit{\theta }}+𝒞$$ (46)

where

$$ℳ=H\varphi \mathit{M}{\varphi }^{*}{H}^{*}\in {ℛ}^{𝒩\times 𝒩}\text{ and }𝒞\triangleq H\varphi (\mathit{M}{\varphi }^{*}𝔞+𝔟)\in {ℛ}^{𝒩}$$ (47)

ℳ ∈ ℛ^𝒩×𝒩 denotes the mass matrix for the serial-chain system, and 𝒞 ∈ ℛ^𝒩 is the vector of velocity dependent nonlinear Coriolis and velocity dependent terms. The expression for the mass matrix in Eq. 47 is referred to as the Newton-Euler Factorization of the mass matrix [11] and was also shown earlier in Eq. 1. This is our first encounter of the convergence of the new concepts of BWA and 1-resolvent matrices with those of the ℰ_ϕ and ϕ spatial operators that play a key role in spatial operator based dynamics formulations [11].

6.2 Non-canonical serial-chains

For non-canonical serial-chains, the (k + 1)^th link is not necessarily the parent body of the k^th link. So a natural question is whether the ℰ_ϕ and ϕ spatial operators for non-canonical serial-chains continue to be BWA and 1-resolvent matrices? The answer is in the affirmative. We simply need to discard the implicit assumption that the parent body of the k^th link is the (k+1)^th link, and switch to the more general ℘(k) notation for the parent link. The generalization of Eq. 32 for non-canonical serial-chain systems is:

$$𝒱(k)={\varphi }^{*}(\mathrm{\wp }(k),k)𝒱(\mathrm{\wp }(k))+H^{*}(k)\dot{\mathit{\theta }}(k)$$ (48)

The velocity relationship in Eq. 34 continues to hold, with ℰ_ϕ defined by the more general second half of Eq. 37. Thus, ℰ_ϕ is once again a BWA matrix. Indeed, the rest of the development in Section 6.1.3, leading to the equations of motion in Eq. 44 and Eq. 47, continues to apply. However, since the system is non-canonical, neither ℰ_ϕ nor ϕ in Eq. 37 and Eq. 39, respectively, are lower-triangular. Thus, even though the component-level equations and the operator structure depend on the body indexing scheme, the BWA and 1-resolvent properties of the ℰ_ϕ and ϕ spatial operators, and the operator forms of the equations of motion, remain intact! In the next section, we will encounter this theme again for tree-topology systems.

7 BWA matrices and tree-topology, rigid body systems

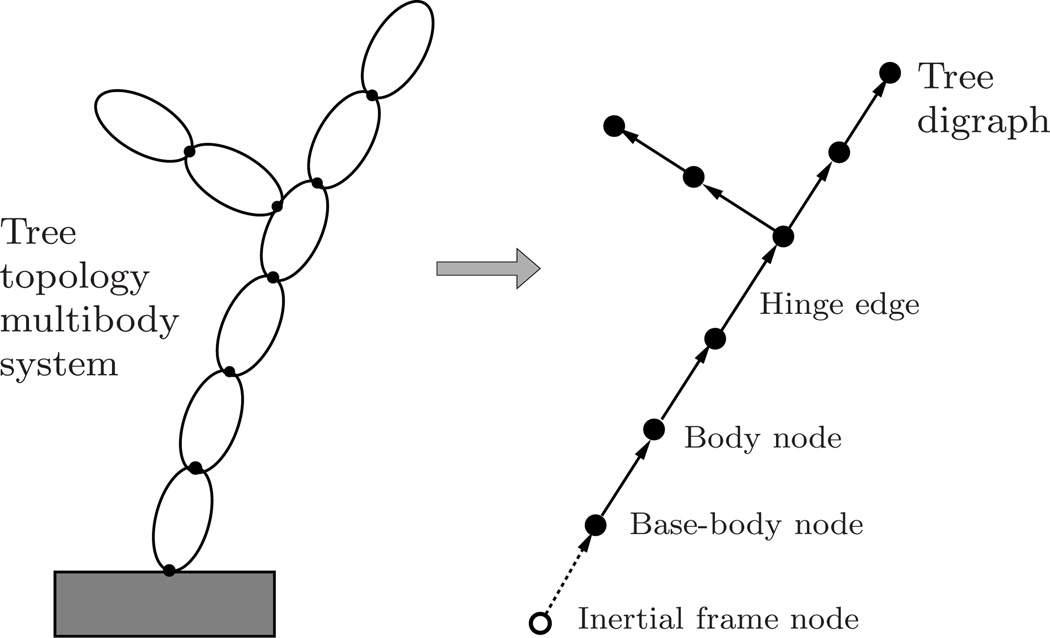
The key difference between serial-chain and tree-topology multibody systems is that, in a tree system, bodies can have multiple children bodies. The standard digraph for an n-links tree-topology multibody system is a tree with (n+1) nodes, as illustrated in Figure 8. We make no specific assumptions about the indexing scheme for the bodies. However, as usual, structural properties are easier to visualize when canonical indexing schemes are used.

Fig. 8.

The correspondence between a tree-topology multibody system and its standard tree digraph.

Examining the kinematic velocity relationships across the links, the inter-link velocity relationship shown in Eq. 48 continues to apply to bodies in a tree-topology system:

$$𝒱(k)={\varphi }^{*}(\mathrm{\wp }(k),k)𝒱(\mathrm{\wp }(k))+H^{*}(k)\dot{\mathit{\theta }}(k)$$ (49)

That is, the spatial velocity of the k^th link can be expressed as the sum of the rigidly propagated spatial velocity of the parent body and the relative spatial velocity, H* (k)θ̇ (k), across the k^th hinge. Defining the 𝒱 and θ̇ stacked vectors and the H spatial operator in the same way as in Section 6.1.1, it is easy to verify that the following operator expression is a system-level rearrangement of the component-level velocity relationship in Eq. 49:

$$𝒱={ℰ}_{\varphi }^{*}𝒱+H^{*}\dot{\mathit{\theta }}$$ (50)

with ℰ_ϕ defined as

$${ℰ}_{\varphi }={\displaystyle \sum _{k=1}^n}{e}_{\mathrm{\wp }(k)}\varphi (\mathrm{\wp }(k),k)e_k^{*}$$ (51)

The ℰ_ϕ spatial operator has the Eq. 13 form of a BWA matrix for the SKO-forest associated with the system. The ϕ(℘(k), k) matrices are the 6 × 6 weight matrices. Since the SKO-forest is a forest, ℰ_ϕ is nilpotent and, from Lemma 4, it has a well defined 1-resolvent, ϕ = (I − ℰ_ϕ)⁻¹. Hence, Eq. 50 can be transformed into

$$(\mathit{I}-{ℰ}_{\varphi }^{*})𝒱=H^{*}\dot{\mathit{\theta }}\text{ and }𝒱={\varphi }^{*}{H}^{*}\dot{\mathit{\theta }}$$ (52)

This operator expression is identical to the one in Eq. 34 for serial-chain systems.

7.1 Equations of motion for tree topology systems

To develop the equations of motion for the tree system, we once again start with the free-body equations of motion of the k^th link, as was done in Eq. 41 for serial-chain systems. The key difference is that we need to take into consideration the 𝔣(.) spatial interaction forces from all the children bodies, instead of from just a single child body, as is the case for serial-chain systems. The following is the generalization of the force balance expression from Eq. 41 extended to tree-topology systems:

$$𝔣(k)-{\displaystyle \sum _{\forall j\in \mathrm{\complement }(k)}}\varphi (k,j)𝔣(j)=M(k)\alpha (k)+𝔟(k)$$ (53)

Rearranging the above leads to the following analog of Eq. 42:

$$𝔣(k)-{\displaystyle \sum _{\forall j\in \mathrm{\complement }(k)}}\varphi (k,j)f(j)=M(k)\alpha (k)+𝔟(k)$$ (54)

Switching to the system-level stacked vector form of Eq. 54, we obtain

$$𝔣={ℰ}_{\varphi }𝔣+\mathit{M}\alpha +𝔟$$ (55)

Continuing in this mode, the following expressions summarize the operator expressions for tree-topology systems:

$$\begin{array}{c}𝒱\underset{¯}{\underset{¯}{50}}{ℰ}_{\varphi }^{*}𝒱+H^{*}\dot{\mathit{\theta }}\hfill \\ \alpha ={ℰ}_{\varphi }^{*}\alpha +H^{*}\ddot{\mathit{\theta }}+𝔞\hfill \\ 𝔣\underset{¯}{\underset{¯}{55}}{ℰ}_{\varphi }𝔣+M\alpha +𝔟\hfill \\ 𝒯=H𝔣\hfill \end{array}$$ (56)

These expressions are identical to the corresponding expressions in Eq. 44 for serial-chain systems. Using ϕ = (I − ℰ_ϕ)⁻¹, these expressions can be transformed from implicit ones into the following explicit operator expressions:

$$\begin{array}{cc}𝒱\hfill & ={\varphi }^{*}{H}^{*}\dot{\mathit{\theta }}\hfill \\ \alpha \hfill & ={\varphi }^{*}(H^{*}\ddot{\mathit{\theta }}+𝔞)\hfill \\ 𝔣\hfill & =\varphi (M\alpha +𝔟)\hfill \\ 𝒯\hfill & =H𝔣\hfill \end{array}$$ (57)

These expressions are identical to the corresponding expressions in Eq. 44 for serial-chain systems. Combining the expressions in Eq. 57 leads to

$$𝒯=ℳ(\theta )\ddot{\mathit{\theta }}+𝒞(\theta ,\dot{\mathit{\theta }})$$ (58)

where

$$ℳ(\theta )=H\varphi \mathit{M}{\varphi }^{*}{H}^{*}\in {ℛ}^{𝒩\times 𝒩}\text{ and }𝒞(\theta ,\dot{\mathit{\theta }})\triangleq H\varphi (\mathit{M}{\varphi }^{*}𝔞+𝔟)\in {ℛ}^{𝒩}$$ (59)

ℳ ∈ ℛ^𝒩×𝒩 denotes the mass matrix for the tree-topology system, and 𝒞 ∈ ℛ^𝒩 is the vector of velocity dependent nonlinear Coriolis and gyroscopic velocity dependent terms. These operator expressions are identical to the ones in Eq. 47 for serial-chain systems. Adopting the terminology from the serial-chain case, we refer to the expression for ℳ in Eq. 59 as the Newton-Euler Factorization of the mass matrix.

We thus conclude that, even though the component-level relationships and the respective operator structures are quite different between canonical and non-canonical serial-chain systems and tree-topology systems, the BWA and 1-resolvent matrix properties of the ℰ_ϕ and ϕ spatial operators persist, and the operator level form of the equations of motion and the mass matrix, remarkably, remain unchanged!

7.1.1 SKO and SPO operators

Now for some change in terminology. BWA matrices and 1-resolvent matrices will start to play a central role in our ongoing study of the dynamics of multibody systems. In the narrower context of multibody systems, we have already encountered spatial operator examples that are in fact BWA and 1-resolvent matrices. In order to conform more closely to the spatial operator terminology, we will henceforth in this multibody context refer to spatial operators that are BWA matrices (such as ℰ_ϕ) as spatial kernel operators (SKO) and their associated 1-resolvent matrices (such as ϕ) as spatial propagation operators (SPO).

8 Illustration of extensions for flexible bodies

The multibody role of SKO and SPO operators has so far focused on rigid body multibody systems. Spatial operator techniques, and analytical results such as Eq. 1, have been developed for systems with deformable bodies [18]. For the purposes of illustration, we now present an overview of the extensions that establish the SKO ans SPO properties of the spatial operators for systems with non-rigid bodies using the notation from reference [18].

1. In addition to the 6-dimensional 𝒱(k) spatial velocity of its body frame, the velocity state of a body is defined by its n_md(k) dimensional η̇ (k) deformation rate coordinates. Thus, the 𝒩̌ (k) = n_md(k) + 6 dimensional free-body generalized velocities vector 𝒱_fl(k) for the k^th body is defined as:

   $${𝒱}_{\mathit{\text{fl}}}(k)=\left[\begin{array}{c}\dot{\mathit{\eta }}(k)\hfill \\ 𝒱(k)\hfill \end{array}\right]\in {ℛ}^{\stackrel{⌣}{𝒩}(k)}$$
2. The appropriate inertia term for the k^th flexible body is defined by the following partitioned matrix

   $$M_{\mathit{\text{fl}}}(k)=\left(\begin{array}{cc}{M}_{\mathit{\text{fl}}}^{\mathit{\text{ff}}}(k)\hfill & M_{\mathit{\text{fl}}}^{\mathit{\text{fr}}}(k)\hfill \\ M_{\mathit{\text{fl}}}^{\mathit{\text{rf}}}(k)\hfill & M_{\mathit{\text{fl}}}^{\mathit{\text{rr}}}(k)\hfill \end{array}\right)\in {ℛ}^{\stackrel{⌣}{𝒩}(k)\times \stackrel{⌣}{𝒩}(k)}$$

   where the sub-blocks define the rigid/rigid,, rigid/flex and flex/flex inertia terms. The kinetic energy of the k^th body, including both the rigid and deformation contributions, is given by:

   $${𝔎}_e(k)=\frac{1}{2}{𝒱}_{\mathit{\text{fl}}}^{*}(k)M_{\mathit{\text{fl}}}(k){𝒱}_{\mathit{\text{fl}}}(k)$$
3. The velocity recursion relating the M_fl(k) velocity of the k^th body to that of its parent is expressed as

   $${𝒱}_{\mathit{\text{fl}}}(k)={\Phi }_{\mathit{\text{fl}}}^{*}(k+1,k){𝒱}_{\mathit{\text{fl}}}(k+1)+H_{\mathit{\text{fl}}}^{*}(k)\dot{\mathit{\vartheta }}(k)$$
   The inter-body transformation operator Φ_fl(k + 1, k), the modal joint map matrix H_fl(k), and the independent ϑ(k) generalized coordinates, for the k^th body are defined as:

   $${\Phi }_{\mathit{\text{fl}}(k+1,k)}\triangleq \left(\begin{array}{cc}\mathbf{0}\hfill & \hfill {\Pi }^{*}({𝕆}_{k+1}^{+})\varphi ({𝕆}_k^{+},k)\hfill \\ \mathbf{0}\hfill & \hfill \varphi (k+1,k)\hfill \end{array}\right)\in {ℛ}^{\stackrel{⌣}{𝒩}(k+1)\times \stackrel{⌣}{𝒩}(k)}{H}_{\mathit{\text{fl}}}(k)\triangleq \left(\begin{array}{cc}\mathit{I}\hfill & \hfill -{\Pi }_{𝔹}^{*}({𝕆}_k)\hfill \\ \mathbf{0}\hfill & \hfill H_{𝔹}(k)\hfill \end{array}\right)\in {ℛ}^{\overline{𝒩}(k)\times \stackrel{⌣}{𝒩}(k),\vartheta (k)\triangleq \left[\begin{array}{c}\eta (k)\hfill \\ \theta (k)\hfill \end{array}\right]\in {ℛ}^{\overline{𝒩}(k)}}$$

   The n_md(k) × 6 dimensional ${\Pi }^{*}({𝕆}_{k+1}^{+})\text{ and }{\displaystyle {\Pi }_{𝔹}^{*}}({𝕆}_k)$ modal influence matrices are obtained from the structural analysis of the body and define the mapping to the deformation of the nodes on either side of the k^th hinge. From this, the SKO weight matrices matrices are identified to be the Φ_fl(k +1, k) terms.

4. The 𝒱_fl and ϑ̇ stacked vectors are assembled as usual. The ℰ_Φfl SKO operator is defined with the Φ_fl(k + 1, k) weight matrices. The SPO operator is defined by Φ_fl = (I − ℰ_Φfl)⁻¹. The block-diagonal H_fl and M_fl operators are defined using the H_fl(k) and M_fl(k) component matrices. These lead to the following operatorlevel equations of motion

   $$\begin{array}{cc}{𝒱}_{\mathit{\text{fl}}}\hfill & ={\Phi }_{\mathit{\text{fl}}}^{*}{H}_{\mathit{\text{fl}}}^{*}\dot{\mathit{\vartheta }}\hfill \\ {\alpha }_{\mathit{\text{fl}}}\hfill & ={\Phi }_{\mathit{\text{fl}}}^{*}(H_{\mathit{\text{fl}}}^{*}\ddot{\mathit{\vartheta }}+{𝔞}_{\mathit{\text{fl}}})\hfill \\ {𝔣}_{\mathit{\text{fl}}}\hfill & ={\Phi }_{\mathit{\text{fl}}}(M_{\mathit{\text{fl}}}{\alpha }_{\mathit{\text{fl}}}+{𝔟}_{\mathit{\text{fl}}}+𝔎\vartheta )\hfill \\ {𝒯}_{\mathit{\text{fl}}}\hfill & =H_{\mathit{\text{fl}}}{𝔣}_{\mathit{\text{fl}}}={ℳ}_{\mathit{\text{fl}}}\ddot{\mathit{\vartheta }}+{𝒞}_{\mathit{\text{fl}}}\hfill \end{array}$$

   with the SKO formulation mass matrix and its Newton-Euler Factorization defined as

   $${ℳ}_{\mathit{\text{fl}}}\triangleq H_{\mathit{\text{fl}}}{\Phi }_{\mathit{\text{fl}}}{M}_{\mathit{\text{fl}}}{\Phi }_{\mathit{\text{fl}}}^{*}{H}_{\mathit{\text{fl}}}^{*}\text{ and }{𝒞}_{\mathit{\text{fl}}}\triangleq H_{\mathit{\text{fl}}}{\Phi }_{\mathit{\text{fl}}}(M_{\mathit{\text{fl}}}{\Phi }_{\mathit{\text{fl}}}^{*}{𝔞}_{\mathit{\text{fl}}}+{𝔟}_{\mathit{\text{fl}}}+𝔎\vartheta )$$

9 Conclusions

This paper develops insights into the graph theory underpinnings of multibody dynamics. We introduce the notion of BWA matrices as weighted matrix generalizations of digraph adjacency matrices. The BWA matrices for trees are shown to be nilpotent, thus making possible explicit expressions for their 1-resolvent. Key connections between BWA matrices, their 1-resolvents and spatial operators used for formulating the dynamics of tree multibody systems are subsequently established. In the dynamics context, the BWA matrices and their 1-resolvents are referred to as SKO and SPO operators respectively. The SKO operators provide a uniform and general way of formulating the system dynamics, with the system-specific details being reflected in the component weight matrices of the operator. The separation between the abstract SKO structure and the specific weight matrices is important because we show in the companion paper Jain [14] that key analytical results are a direct consequence of the SKO properties of the system, and are in fact independent of the specific nature and details of the component weight matrices for the system.