Semiparametric Estimation of Treatment Effect with Time-Lagged Response in the Presence of Informative Censoring

Abstract

In many randomized clinical trials, the primary response variable, for example, the survival time, is not observed directly after the patients enroll in the study but rather observed after some period of time (lag time). It is often the case that such a response variable is missing for some patients due to censoring that occurs when the study ends before the patient’s response is observed or when the patients drop out of the study. It is often assumed that censoring occurs at random which is referred to as noninformative censoring; however, in many cases such an assumption may not be reasonable. If the missing data are not analyzed properly, the estimator or test for the treatment effect may be biased. In this paper, we use semiparametric theory to derive a class of consistent and asymptotically normal estimators for the treatment effect parameter which are applicable when the response variable is right censored. The baseline auxiliary covariates and post-treatment auxiliary covariates, which may be time-dependent, are also considered in our semiparametric model. These auxiliary covariates are used to derive estimators that both account for informative censoring and are more efficient then the estimators which do not consider the auxiliary covariates.

1 Introduction

In many randomized clinical trials, the primary endpoint of interest, denoted by Y, is not observed immediately after patients enroll into a study, but rather is observed after some period of time which may vary among patients. The time from a patient’s entry into the study until the response is observed is referred to as the lag time or time to ascertainment, and the corresponding response variable is referred to as the time-lagged response (Anstrom and Tsiatis 2001) or marked point process (Huang and Louis 1998). The simplest example of a time-lagged response is survival time where the primary endpoint itself is the lag time which varies by individual. Another simple example of a time-lagged response may be a laboratory measurement taken after some fixed period of time in which the lag time is the same for all individuals. Yet another example is when the response variable of interest Y are the total medical costs incurred during the treatment of some disease, in which the time to ascertainment is the length of disease which will vary by individual. The first two examples of the the time-lagged response will be discussed in detail in this paper. Areal data example ACTG 175, which will be introduced shortly in section 1.1, will be used to illustrate the applications of our developed methods on these two cases. The methods can also be applied more generally with other time-lagged response data such as the third example.

Our primary goal is to estimate or test for the treatment effect between two competing treatment groups, e.g., a new treatment versus placebo, which is defined through the statistical model

$$p_{Y\mid Z}(y\mid z;\beta ,\eta )$$ (1)

where Z denotes the treatment assignment with Z = 1 for new treatment and Z = 0 for placebo, pY|Z(y|z) is used to denote the conditional density of Y given Z, β is the treatment effect parameter of interest and η are nuisance parameters used to describe the class of conditional distributions of Y|Z. The lag time that it takes for the response variable Y to be ascertained is denoted by T. For example, if the time-lagged response is survival time then Y = T and a commonly used model for assessing the treatment effect is the proportional hazards model where the conditional density of T given Z is modeled through its hazard function; namely,

$${\lambda }_{T\mid Z}(t\mid z)=\lambda \left(t\right)\text{exp}\left(\beta Z\right),$$ (2)

where λ_T|Z(t|z) denotes the conditional hazard rate of dying at time t for treatment z = 0, 1. Here the parameter β, i.e., the log hazard ratio between the two treatments, is the treatment effect of interest, whereas, the baseline hazard function λ(t), t ≥ 0 is the nuisance parameter η.

For other time-lagged response data where T ≠ Y, if all the patients in a study are followed until their response is ascertained, the lag time itself does not add any useful additional information regarding the estimation of the treatment effect β.

It is very common, however, in such clinical trials that the time-lagged response data are missing because of right censoring of some patients. Depending on the study, censoring occurs for a variety of reasons. Administrative censoring occurs because patients enter the study in a staggered fashion and not all have been observed at the end of the study when the data are analyzed. Often it is assumed that the censoring time is independent of the primary response Y or the slightly weaker assumption that the censoring time is independent of Y given treatment assignment Z. The assumption of independence between censoring time and response Y given Z is also necessary for some commonly used standard methods, for example, the maximum partial likelihood estimator of Cox (Cox 1972) and the logrank test (Mantel 1966; Peto and Peto 1972), to ensure their properties, such as consistency or asymptotic normality, to hold. This assumption is often referred to as noninformative censoring. However, censoring may also occur due to a patient’s drop out of the study before their response data are observed. For example, patients may drop out of the study because of side effects, or prognostically worse or better patients may drop out for reasons that can be attributed to other time-dependent outcomes. Under such situations, the censoring time is likely to be dependent on the response Y given Z and such censoring is usually referred to as the informative censoring. Informative censoring, if not properly accounted for, may bias the results from standard inferential methods and give overly optimistic or pessimistic estimates of treatment effect.

It is also common in clinical trials to collect additional information on auxiliary covariates (for example, age, gender, health conditions, etc.). Some of these auxiliary variables are collected prior to randomization, while others may be collected after treatment assignment. Because of randomization, covariates collected prior to randomization, referred to as baseline auxiliary covariates, are independent of treatment assignment and are not affected by treatment, whereas, covariates measured after randomization, referred to as post-treatment auxiliary covariates, may be time-dependent and affected by treatment assignment. Nonetheless, some of these covariates may be important prognostic factors that are correlated with the primary response variable.

Several researchers in their several recent works (e.g. Zhao and Tsiatis 1999; van der Laan and Hubbard 1999; Wahed and Tsiatis 2006) discussed the estimation methods on the survival distribution when censoring is presented and utilized prognostic covariates to improve the efficiency. More relevant work on the estimation of treatment effect was discussed by Lu and Tsiatis (2008), in which the authors derived an augmented class of consistent and asymptotically normal estimators for the treatment-specific log hazard ratio regression parameter as defined in (2). The auxiliary covariates were used to derive estimators that are more efficient than the maximum partial likelihood estimator and the logrank test. However, the proposed method by Lu and Tsiatis (2008) was based on the assumption of noninformative censoring that the censoring is independentof survival time T given treatment assignment Z. If such an assumption is not satisfied, the corresponding results may be biased.

In the presence of informative censoring, Hubbard et al (1999) and Moor and van der Laan (2009) discussed covariate adjusted estimation methods on the treatment specific survival at a fixed end point for right-censored survival outcomes. In this paper, we focus on estimation of treatment-specific log hazard ratio regression parameter by weakening the assumption of independence between censoring time and the response variable Y given Z to allow for censoring that is informative in a manner that can be explained through the observed auxiliary covariates. The semiparametric theory and the major results in Robins and Rotnitzky (1992) will be used to derive a class of consistent and asymptotically normal estimators for the treatment effect parameter β. The auxiliary covariates here play an important role in deriving a class of augmented semiparametric consistent and asymptotically normal estimators for β when the censoring is informative. The correlations between auxiliary covariates and the primary response variable are also utilized to derive estimators that are more efficient than the estimators without using the auxiliary covariates.

1.1 An illustrative example: ACTG 175

AIDS Clinical Trials Group protocol 175 (ACTG 175) is a double blind study that randomized HIV-infected subjects to four antiretroviral regimes in equal proportions: zidovudine (ZDV) monotherapy, ZDV + didanosine (ddI), ZDV + zalcitabine, and ddI monotherapy Hammer et al (1996). A subset of the data from 2139 HIV subjects are considered in this paper to demonstrate our proposed methods and be compared to the commonly used standard techniques. Among the 2139 subjects, 532 subjects were randomized to ZDV monotherapy, 522 were randomized to ZDV + ddI, 524 were randomized to ZDV + zalcitabine and 561 were randomized to ddI monotherapy. Two primary endpoints, corresponding to the two special cases of time-lagged response mentioned earlier, are taken into account: (1) the survival time that was defined from the time of diagnosis to the first time of a ≥ 50 percent decline in the CD4 cell count, an event indicating progression to the acquired immunodeficiency syndrome (AIDS), or death; (2) the mean CD4 cell counts at 96 ± 5 weeks after diagnosis. Our aim is to compare the treatment effects on the two primary endpoints between each of the treatments ZDV + ddI, ZDV + zalcitabine and ddI monotherapy with the treatment ZDV monotherapy. Roughly 76% of the data were censored.

In addition to the censored survival times, CD4 cell counts at 96 ± 5 weeks and treatment arms, the data also contain several prognostic baseline covariates and post-treatment covariates. The baseline covariates include CD4 cell counts, CD8 cell counts, age (years), weight (kg), gender (0 = female), hemophilia indicator (0 = no), homosexual activity (0 = no), race (0 = white, 1 = non-white), history of IV drug use (0 = no), Karnofsky score (on a scale of 0-100), ZDV in the 30 days prior to 175 (0 = no), antiretroviral history stratification (1 = ’Antiretroviral Naive’, 0 = other), number of days pre-175 antiretroviral therapy and symptomatic status indicator (0 = asymptomatic). The post-treatment covariates include, CD4 at 20 5 weeks, CD8 at 20 ± 5 weeks, indicator of off-trt before 96 ± 5 weeks (0 = no, 1 = yes) and Missing CD4 at 96 ± 5 weeks (0 = missing, 1 = observed). The last two post-treatment covariates as well as CD4 at 96 ± 5 weeks are time dependent covariates that will only be used as covariates for the survival endpoint which extends beyond 96 weeks.

This article is organized as follows: Section 2 describes the notation and model assumptions which will be used throughout this article. Section 3 characterizes the class of regular and asymptotic linear estimators for β using a general time-lagged responses. Section 4 and Section 5 are the specific applications of our method to the two special cases mentioned earlier. For each case, we characterize a subclass of regular and asymptotic linear estimators for β, the treatment effect parameter of interest, when informative censoring exists and perform a series of simulation studies to compare our proposed estimators with the commonly used standard techniques. The proposed estimators are also applied on the real data example ACTG 175.

2 Model framework and notation

2.1 Notation and assumptions

Consider a randomized clinical trial where n subjects are sampled from a population of interest. Let D_i = {U_i, Δ_i, Δ_iY_i, Z_i, X_i(U_i)} denote the observed data that are independent and identically distributed random vectors for i = 1, …, n. For the i-th subject, U_i = min(T_i, C_i), where T_i denotes the underlying lag time, and C_i denotes the potential censoring time, Δ_i = I(T_i ≥ C_i) is an indicator of whether the response data were ascertained (Δ_i = 1) or missing (Δ_i = 0), Y_i denotes the response on which the primary analysis will be based, where Y_i may be continuous or discrete and is only observed if Δ_i = 1, Z_i denotes the treatment indicator with value 1 and 0 denoting experimental treatment and placebo, respectively. Furthermore, we let $X_i\left(U_i\right)=\{X_{1i},X_{2i}^H\left(U_i\right)\}$, where X_1i denotes a vector of baseline auxiliary covariates which are measured prior to randomization, and $X_{2i}^H\left(U_i\right)$ defined by {X_2i(u), 0 ≤ u ≤ U_i} denotes post-treatment auxiliary covariates which may be time-dependent in which case we would observe the history of these values up to time U_i. In addition, we use V_i = {T_i, Y_i, Z_i, X_i(T_i) to denote the full data had there been no censoring or missing data.

Due to randomization, it is reasonable to assume that the treatment indicator Z is independent of the auxiliary baseline covariates X₁ and that the randomization probability of receiving treatment 1 is equal to π with 0 < π < 1 which is known to us; that is,

$$Z\perp X_1\text{and}\text{Pr}(Z=1)=\pi .$$ (3)

It is well known that, instead of using the true value of π, using the estimated π generally leads to further gain in efficiency for estimators for β. Therefore, we recommend estimating π using the sample proportion as it is actually done in all the following computations both for simulations and real data example.

As in any missing data problem it is important to consider assumptions regarding the process in which the data are missing (censored); that is, we need to consider the conditional distribution of the censoring variable C given the full data V which we define through the conditional hazard function λ_C(u|V) at time u given V. Often, in randomized clinical trials, one assumes that the censoring variable C is completely independent of the full-data V. This assumption is similar in spirit to the “missing completely at random” assumption (MCAR) as defined by Rubin (1987) and may be a reasonable assumption if the data were administratively censored. A slightly weaker assumption that is implicitly made when one uses the logrank test to test for differences in the survival distributions for two treatments with right-censored data is that C is conditionally independent of (T, Y ) given Z. When a patient is censored due to drop out or lost to follow-up, one can imagine some scenarios where poorer prognostic patients may be more likely to be censored and other scenarios where the opposite may happen. We therefore consider the weaker assumption that

$${\lambda }_C(u\mid T\ge u,V)={\lambda }_C\{u\mid T\ge u,Z,X\left(u\right)\},$$ (4)

where λ_C(u|·) denotes the conditional hazard rate of C at time u. In words, this assumption means that the probability of being censored at time u, given that one has not been censored or failed by time u, only depends on observed variables measured prior to time u and not additionally on the future data. This last assumption is similar in spirit to what Rubin refers to as missing at random (MAR) and we will refer to this assumption as censoring at random (CAR). This CAR assumption allows greater flexibility than the usual assumptions with censored data.

Without making additional assumptions, other than those given by (1), (3) and (4), we now consider how to derive a class of semiparametric estimators that are consistent and asymptotically normal for β using the results by Robins and Rotnitzky (1992).

2.2 Introduction to semiparametric theory

Robins and Rotnitzky (1992) restricted attention to estimators that are regular and asymptotically linear (RAL). An estimator ${\widehat{\beta }}_n$ for β is asymptotically linear if there exists a random variable φ(D), which, under the truth, β = β₀, has mean zero and finite variance, such that $n^{1∕2}({\widehat{\beta }}_n-{\beta }_0)=n^{-1∕2}{\sum }_{i=1}^n\phi \left(D_i\right)+o_p\left(1\right)$. The function φ(D_i) is referred to as the i-th influence function of the estimator ${\widehat{\beta }}_n$. Regularity is a technical condition that rules out ”pathological” estimators with undesirable local properties (Newey 1990), such as the ”superefficient” estimator of Hodges (e.g. Tsiatis 2006, p. 24). The influence function of an RAL estimator for β is uniquely defined and the asymptotic properties of such an estimator is determined by its influence function. It is clear from the definition of the influence function given above and a simple application of the central limit theorem, that, the asymptotic variance of an RAL estimator ${\widehat{\beta }}_n$ is equal to the variance of its influence function, i.e., E{φ(D)²}.

For a general semiparametric model, Robins and Rotnitzky (1992) provided a series of steps for deducing a class of RAL estimators when data are censored at random: (1) characterize the class of full data influence functions, (2) characterize the class of observed data influence functions by applying the theory of augmented inverse probability complete case estimators and (3) identify the observed data estimators with estimating functions in this class.

3 The class of all semiparametric estimators for β

The class of full data influence functions for β, whose proof was given by Zhang et al (2008), is characterized by

$${\Psi }^F={\Psi }_{YZ}+\mathcal{R},$$ (5)

where Ψ_{Y Z}(Y, Z; β₀) is the class of influence functions for β that only use the information of time-lagged response variable Y and treatment assignment Z derived through model (1),

$$\mathcal{R}=\left\{(Z-\pi )f\left(X_1\right)\text{for}\text{all}\text{functions}f\left(X_1\right)\right\},$$ (6)

and the sum of the two spaces S₁ + S₂ = {s₁ + s₂ : s₁ ∈ S₁ and s₂ ∈ S₂}. In addition, as we will see shortly in Theorem 1, the direct sum ⊕ of the two linear spaces S₁ and S₂ is the same as the regular sum of the two spaces but with an additional property that the two linear spaces only intersect at {0}.

For the time being, assume the hazard function λ_C{u|T ≥ u, Z, X (u)} to be known and let $K_C\{t,Z,X\left(t\right)\}=\exp [-{\int }_0^t{\lambda }_C\{u\mid T\ge u,Z,X\left(u\right)\}du]$ be the conditional survival function for censoring. Under the CAR assumption, we obtain that P(Δ = 1|v) = K_C{T, Z, X(T)}. The theory of Robins and Rotnitzky (1992) tells us that the an observed data influence function for β can be written as an augmented inverse probability weighted complete case (AIPWCC) influence function; namely,

$$\frac{\Delta {\psi }^F(V;{\beta }_0)}{K_C\{U,Z,X\left(U\right)\}}+\int \frac{d{M}_C\{u,Z,X\left(u\right)\}}{K_C\{u,Z,X\left(u\right)\}}L\{u,Z,X\left(u\right)\},$$ (7)

where the full-data influence function ψ^F(V ; β₀) ∈ Ψ^F is given in (5), dM_C{u, Z, X(u)} is the increment of the martingale process dN_C(u) – λ_C{u|T ≥ u, Z, X(u)} Y (u)du, where dN_C(u) is the increment of the counting process for censoring; i.e., N_C(u) = I(U ≤ u, Δ = 0), Y (u) = I(U ≥ u), is the “at-risk” process, and L{u, Z, X(u)} is an function of all the data prior to time u; that is,

Theorem 1 If the hazard function λ_C{u|T ≥ u, Z, X (u)} for censoring is known, the class of all observed data influence functions is given by

$${\Psi }^{obs}=\frac{\Delta {\Psi }_{YZ}}{K_C\{U,Z,X\left(U\right)\}}+\{\mathcal{R}\oplus \mathcal{C}\}$$ (8)

where Ψ_{Y Z} and R are defined in (5) and (6), respectively, and

$$\mathcal{C}=\left[\int d{M}_C\{u,Z,X\left(u\right)\}L\{u,Z,X_u\}:forallfunctionsL(\cdot )\right]$$ (9)

Theorem 1 (see proof in Appendix A) tells that if λ_C{u|T ≥ u, Z, X (u)} is known, then the class of RAL estimators for β be represented as the solution to the following estimating equations

$$\sum _{i=1}^n\left[\frac{{\Delta }_i{\psi }_{YZ}(Y_i,Z_i;\beta )}{K_C\{U_i,Z_i,X_i\left(U_i\right)\}}+(Z_i-\pi )f\left(X_{1i}\right)+\int d{M}_{C_i}\{u,Z_i,X_i\left(u\right)\}L\{u,Z_i,X_i\left(u\right)\}\right]=0,$$ (10)

for arbitrary functions ψ_{Y Z} (Y, Z; β₀) ∈ Ψ_{Y Z}, f (X₁) and L{u, Z, X(u)}.

In practice, however, the hazard function λ_C{u|T ≥ u, Z, X (u)} (also used to derive K_C{u, Z, X (u)}is not known, and must be estimated from the data. Because of its availability and versatility, a proportional hazards regression models with time-dependent covariates will be used to model the hazard relationship for the censoring survival distribution. For maximum flexibility, we will consider separate models for each treatment group. To be specific, we posit a stratified proportional hazards regression model for the censoring time C; that is, λ_C{u|T ≥ u, Z, X (u)} = λ_0C(u, Z) H {Z, X(u); α}, where λ_0C(u, Z) is the baseline hazard function for each treatment group Z = 0.1, and $H\{Z,X\left(u\right);\alpha \}=Z\exp [{\alpha }_{11}{X}_1+{\alpha }_{21g1}\left\{X_2^H\left(u\right)\right\}]+(1-Z)\exp [{\alpha }_{12}{X}_1+{\alpha }_{22g2}\left\{X_2^H\left(u\right)\right\}]$. The vector of parameters α = (α₁₁, …, α₂₂) will be estimated by using the standard partial likelihood estimator (Cox 1975), denoted here by $\widehat{\alpha }$, and λ_0C will be estimated by

$$\sum _{j=1}^n\left\{d{N}_{C_j}\left(u\right)I(Z_j=Z)\right\}∕\sum _{j=1}^n\left[H\{Z_j,X_j\left(u\right);\widehat{\alpha }\}{Y}_j\left(u\right)I(Z_j=Z)\right].$$

Denote the estimated hazard function and corresponding survival function by ${\widehat{\lambda }}_C(\cdot )$ and ${\widehat{K}}_C(\cdot )$, respectively. Placing these estimated functions in (10), after some algebra, we have an equivalent expression of the estimating equation

$$\sum _{i=1}^n\left(\frac{{\Delta }_i{\psi }_{YZ}(Y_i,Z_i;\beta )}{{\widehat{K}}_C\{U_i,Z_i,X_i\left(U_i\right)\}}+(Z_i-\pi )f\left(X_{1i}\right)+\int [L\{u,Z_i,X_i\left(u\right)\}-\stackrel{‒}{L}(u,Z_i)]d{N}_{C_i}\left(u\right)\right)=0,$$ (11)

where

$$\stackrel{‒}{L}(u,Z_i)=\frac{\sum _{j=1}^n\left\{L(u,Z_i,X_i)H\{Z_i,X_j\left(u\right);\widehat{\alpha }\}{Y}_j\left(u\right)I(Z_j=Z_i)\right\}}{\sum _{j=1}^n\left\{H(Z_i,X_j\left(u\right);\widehat{\alpha })Y_j\left(u\right)I(Z_j=Z_i)\right\}}$$ (12)

for arbitrary functions ψ_{Y Z}(Y, Z; β₀) ∈ Ψ_{Y Z}, f(X₁) and L {u, Z, X (u)}.

Clearly, if the proportional hazard regression model is the underlying true model for the censoring time, the estimator derived from equation (11) is a consistent estimator for β. In addition, if we consider the subclass of estimators of (11) by fixing function ψ_{Y Z}(Y, Z; β₀) ∈ Ψ_{Y Z} but varying functions f(X₁) and L{u, Z, X(u)}, following the analogous proof as that for Theorem 3 of Lu and Tsiatis (2008), we have the optimal functions

$$f_0\left(X_1\right)=\frac{1}{\pi (1-\pi )}E\{(Z-\pi ){\psi }_{YZ}(Y,Z;{\beta }_0)\mid X_1\},\text{and}$$ (13)

$$L_0\{u,Z,X_u\}=\frac{E\{{\psi }_{YZ}(Y,Z;{\beta }_0)\mid T\ge u,Z,X\left(u\right)\}}{K_C\{u,Z,X\left(u\right)\}}$$ (14)

for f(·) and L(·), respectively, that lead to the most efficient estimator with the smallest variance in this subclass. However, the conditional expectations in equations (13) and (14) are unknown in practice and they will be estimated by positing parametric regression models. Substituting these estimated functions $\widehat{f}(\cdot )$ and $\widehat{L}(\cdot )$ for f(·) and L(·) in (11) will lead to a more efficient estimator for β than without using auxiliary covariates. This procedure will be explained in details when we discuss the two special applications of our proposed method in sections 4 and 5, respectively.

Remark 1 Although we need the correct model for censoring time to derive the consistent estimators for β, we will see later in the simulation portions of section 4 and 5 that the resulting estimators for β have smaller bias than the standard method even if the true model for censoring does not follow the assumed proportional hazard model.

4 Application to the proportional hazard model

4.1 Class of all semiparametric estimators for β

To illustrate how these estimators are derived, we will focus on the special case where the time-lagged response variable Y is the survival time T and T|Z follows a proportional hazard model (2), where the primary focus is to estimate the treatment effect parameter β. This problem is common in chronic disease clinical trials and is of importance in its own right.

Using standard results for the proportional hazards model (e.g. Andersen et al 1993; van der Laan and Robins 2003; Tsiatis 2006) the class of full data influence functions Ψ_{Y Z} for estimators of β can be described by

$${\Psi }_{YZ}=\left\{C_a^{-1}\int a\left(u\right)\{Z-Z_T^{\ast }(u;{\beta }_0)\}d{M}_T(u,Z;{\beta }_0):\text{for}\text{any}\text{function}a\left(u\right)\right\},$$ (15)

where dM_T(u, Z; β) = dN_T(u)–λ(u) exp(βZ)I(T ≥ u)du, N_T(u) = I(T ≤ u), $Z_T^{\ast }(u,\beta )=E\left\{Z\text{exp}\left(\beta Z\right)I(T\ge u)\right\}∕E\left\{\text{exp}\left(\beta Z\right)I(T\ge u)\right\}$, and the proportionality constant $C_a=E\left[a\left(T\right)\{1-Z_T^{\ast }(T;{\beta }_0)\}{Z}_T^{\ast }(T;{\beta }_0)\right]$.

Applying this class of full data influence functions Ψ_{Y Z} to Theorem 1, we have the following corollary whose proof is given in Appendix B.

Corollary 1 If the hazard function λ_C{u|T ≥ u, Z, X (u)} for censoring is known, and if T|Z follows a proportional hazard model (2), the class of all observed data influence functions is given by

$${\Psi }_{PH}^{obs}=\epsilon +\{\mathcal{R}\oplus \mathcal{C}\}$$ (16)

where

$$\epsilon =\left[C_w^{-1}\int \{Z-Z^{\ast }(u;{\beta }_0)\}\frac{W(u,Z)dM(u,Z;{\beta }_0)}{K_C(u,Z,X\left(u\right))}:forallfunctionW(\cdot )\right],$$ (17)

$$Z^{\ast }(u;\beta )=\frac{E[Z\text{exp}\left(\beta Z\right)Y\left(u\right)W(u,Z)∕K_C\{u,Z,X\left(u\right)\}]}{E[\text{exp}\left(\beta Z\right)Y\left(u\right)W(u,Z)∕K_C\{u,Z,X\left(u\right)\}]},$$ (18)

$$C_W=E[\Delta W(U,Z)∕K_C\{U,Z,X\left(U\right)\}\{1-Z^{\ast }(U;{\beta }_0)\}{Z}^{\ast }(U;{\beta }_0)],$$ (19)

and R and C are defined in (6) and (9), respectively.

Analogous to (11), if we use the estimated functions ${\widehat{\lambda }}_C(\cdot )$ and ${\widehat{K}}_C(\cdot )$, assuming the stratified proportional hazards regression model, the class of all RAL estimators for β can be represented as a solution to the following estimating equation

$$0=\sum _{j=1}^n\left(\int \{Z_i-\stackrel{‒}{Z}(u;\beta )\}\frac{W(u,Z_{i}d{N}_i\left(u\right))}{{\widehat{K}}_C\{u,Z_i,X_i\left(u\right)\}}+(Z_i-\pi )f\left(X_{1i}\right)+\int [L\{u,Z_i,X_i\left(u\right)\}-\stackrel{‒}{L}(u,Z_i)]d{N}_{C_i}\left(u\right)\right),$$ (20)

where

$$\stackrel{‒}{Z}(u;\beta )=\frac{\sum _j^n[Z_j\text{exp}\left(\beta Z_i\right)Y_j\left(u\right)W(u,Z_j)∕{\widehat{K}}_C\{u,Z_j,X_j\left(u\right)\}]}{\sum _j^n[\text{exp}\left(\beta Z_j\right)Y_j\left(u\right)W(u,Z_j)∕{\widehat{K}}_C\{u,Z_j,X_j\left(u\right)\}]},$$ (21)

for arbitrary functions W (u, Z), f(X₁) and L{u, Z, X(u)}. We can also derive a more efficient estimator for β by substituting appropriate estimators $\widehat{f}(\cdot )$ and $\widehat{L}(\cdot )$ for f(·) and L(·) in (20). To be specific, we posit parametric models f(X₁; a) = a^Tq(X₁) that is linear in a and L{u, Z, X (u); b} = b^T s{u, Z, X(u)} that is linear in b, where a and b are r_a-dimensional vector of functions of X₁ and s(·) is and r_b-dimensional vectors of functions of unknown parameters, respectively. q(·) is an r_a-dimensional vector of functions of X₁ and s(·) is an r_b-dimentional vector of {u, Z, X(u)}, and consider the subclass of Ral estimators which solve the estimating equations ${\sum }_{i=1}^n\{\int \{Z_i-\stackrel{‒}{Z}(u;\beta )\}d{N}_i\left(u\right)W(u,Z_i)∕{\widehat{K}}_C\{u,Z,X\left(u\right)\}-(Z_i-\pi )f(X_{1i};a)-\int [L\{u,Z_i,X_i\left(u\right);b\}-L(u,Z_i;b)]dN{C}_i\left(u\right)\}=0$, for all $a\in {\mathbb{R}}^{r_a}$ and $b\in {\mathbb{R}}^{r_b}$. We define a₀ and b₀ to be the values leading to the smallest asymptotic variance of the estimator $\widehat{\beta }$ within this subclass. Using standard regression methods, we obtain the estimators

$$\widehat{a}=\left\{\pi (1-\pi )\sum _{i=1}^{n}q\left(X_{1i}\right)q{\left(X_{1i}\right)}^T\right\}\sum _{i=1}^n\left\{q\left(X_{1i}\right)(Z_i-\pi ){\widehat{m}}_{W(u,Z)}(D_i;{\widehat{\beta }}_{PH})\right\},\text{and}$$ (22)

$$\widehat{b}={\left\{\sum _{i=1}^n{\widehat{G}}_s\{u,Z_i,X_i\left(u\right)\}{\widehat{G}}_s{(u,Z_i,X_i\left(u\right))}^T\right\}}^{-1}\sum _{i=1}^n\left\{{\widehat{G}}_s\{u,Z_i,X_i\left(u\right)\}{\widehat{m}}_{W(u,Z)}(D_i;{\widehat{\beta }}_{PH})\right\},$$ (23)

for a₀ and b₀, respectively, where

$${\widehat{m}}_{W(u,Z)}(D_i;\beta )=\int \{Z_i-\stackrel{‒}{Z}(u;\beta )\}\frac{W(u,Z_i)}{{\widehat{K}}_C\{u,Z,X\left(u\right)\}}\{d{N}_i\left(u\right)-\widehat{\lambda }(u;\beta )du\text{exp}\left(\beta Z_i\right)Y_i\left(u\right)\},$$

$\widehat{\lambda }(u;\beta )du$ is estimated using the increment of the Breslow estimate for the underlying cumulative hazard function, i.e., $\widehat{\lambda }(u;\beta )du={\Sigma }_{i}d{N}_i\left(u\right)∕{\Sigma }_i\left\{\exp \left(\beta Z_i\right)Y_i\left(u\right)\right\}$, ${\widehat{G}}_s\{u,Z_i,X_i\left(u\right)\}=\int [d{N}_{C_i}\left(u\right)-Y_i\left(u\right){\widehat{\lambda }}_{0C}(u,Z_i)H\{u,Z_i,X_i\left(u\right);\widehat{\alpha }\}du][s\{u,Z_i,X_i\left(u\right)\}-\stackrel{‒}{s}(u,Z_i)]$, and ${\widehat{\lambda }}_{0C}(u,Z)du$, for Z = 0, 1 are estimated using the increment of the treatment-specific Nelson-Aalen estimator for the cumulative hazard function of the censoring distribution; that is, ${\widehat{\lambda }}_{0C}(u,Z)du={\Sigma }_{i}d{N}_{C_i}(u,Z)∕{\Sigma }_i{Y}_i(u,Z)$. $\stackrel{‒}{Z}(u;\beta )$ and $\stackrel{‒}{s}(u,Z)$ are calculated the similar manner as in (12) by replacing the function L(·) with s(·). The estimated functions $\widehat{f}(\cdot )$ and $\widehat{L}(\cdot )$ are defined to be $f(X_1;\widehat{\mathbf{a}})$ and $L\{u,Z,X\left(u\right);\widehat{\mathbf{b}}\}$, respectively.

Remark 2 If the censoring time is noninformative, then after some algebra, the class of estimating equations described in (20) will be identical to the class of estimating equations characterized in (9) of Lu and Tsiatis (2008).

Remark 3 Finding the optimal function of W (u, Z) that gives the efficient estimator in the class of all RAL estimators derived from (20) would be very difficult. Therefore our strategy is to choose a function that gives an estimator at least as efficient as the maximum partial likelihood estimator when the censoring time is noninformative. Here, we choose $W(u,Z)={\widehat{K}}_C(u,Z)$, where ${\widehat{K}}_C(u,Z)$ is the treatment specific Kaplan-Meier estimator for the censoring time. Clearly, when censoring is noninformative, the first summand of the estimating equation (20) will reduce to the standard partial likelihood score function that leads to the maximum partial likelihood estimator for β.

4.2 Variance estimator for $\widehat{\beta }$

If the potential censoring time truly follows a stratified proportional hazards regression model, λ_C{u|T ≥ u, Z, X(u)} = λ(u|Z)H{Z, X(u); α}, as described in section 3, then using the estimated function ${\widehat{\lambda }}_C(\cdot )$ and ${\widehat{K}}_C(\cdot )$ in (20) will lead to an estimator with its influence function in $\Pi ({\Psi }_{\mathrm{PH}}^{obs}\mid {\Lambda }_{\phi }^{\perp })$, where ∏(S₁|S₂) denotes the projection of space S₁ onto space S₂, ${\Psi }_{\mathrm{PH}}^{obs}$ is defined in (16) and Λ_φ = Λ_{λ0C(·, Z)} ⊕ Λ_α, in which Λ_{λ(·, Z)} is the nuisance tangent space associated with the nuisance baseline hazard function Λ_λ0C(·, Z) which is given in equation (31) of Appendix C and Λ_α is the nuisance tangent space associated with the nuisance parameters α = (α₁₁, …, α₂₂) given in equation (32) of Appendix C (e.g. van der Laan and Robins 2003; Tsiatis 2006); that is,

Theorem 2 If the hazard function λ_C{u|T ≥ u, Z, X(u)} = λ_0C(u, Z)H{Z, X(u); α}, then the class of all observed data influence functions is given by

$$\Psi =[\Pi \{\psi \left(D\right)\mid {\Lambda }_{{\lambda }_{0C}(.,Z)}^{\perp }\}-\Pi (\psi \left(D\right)\mid {\Lambda }_{\alpha }):\psi \left(D\right)\in {\Psi }_{PH}^{obs}]$$ (24)

where ${\Psi }_{\mathrm{PH}}^{\mathit{obs}}$ is defined in (16), $\Pi \{\psi \left(D\right)\mid {\Lambda }_{{\lambda }_{0C(\cdot ,Z)}}^{\perp }\}$ is given by

$$\begin{array}{cc}\hfill & C_W^{-1}\int \{Z-Z^{\ast }(u;{\beta }_0)\}\frac{W(u,Z)dM(u,Z;{\beta }_0)}{K_C\{u,Z,X\left(u\right)\}}+(Z-\pi )f\left(X_1\right)\hfill \\ \hfill & +\int d{M}_C\{u,Z,X\left(u\right)\}[L\{u,Z,X\left(u\right)\}-L^{\ast }(u,Z)]\hfill \\ \hfill & +\int \frac{E[{\psi }^F(T,Z)∕K_C\{u,Z,X\left(u\right)\}H\{Z,X\left(u\right)\}Y\left(u\right)\mid Z]}{E[H\{Z,X\left(u\right)\}Y\left(u\right)\mid Z]}d{M}_C\{u,Z,X\left(u\right)\}\hfill \\ \hfill & -\int \frac{E[E\{{\psi }^F(T,Z)\mid T\ge u,Z\}∕K_C\{u,Z,X\left(u\right)\}H\{Z,X\left(u\right)\}Y\left(u\right)\mid Z]}{E[H\{Z,X\left(u\right)\}Y\left(u\right)\mid Z]}d{M}_C\{u,Z,X\left(u\right)\},\hfill \end{array}$$ (25)

in which C_W and Z*(u;β) are defined in (19) and (18), respectively,

$${\psi }_F(T,Z)=C_W^{-1}\int \{Z-Z^{\ast }(u;{\beta }_0)\}W(u,Z)d{M}_T(u,Z;{\beta }_0),$$ (26)

$$L^{\ast }(u,Z)=\frac{E[L\{u,Z,X\left(u\right)\}H\{Z,X\left(u\right)\}Y\left(u\right)\mid Z]}{E[H\{Z,X\left(u\right)\}Y\left(u\right)\mid Z]},$$ (27)

and Π(ψ(D)|Λ_α) is given by (35).

Remark 4 The proof of Theorem 2 is given in Appendix C. The expressions for the fourth and fifth summands in (25) are very complicated and difficult to evaluate numerically. Therefore we choose to ignore these terms in our variance estimator of the estimator that solves equation (20). If the censoring time is noninformative, then these two summands will add to zero giving us a consistent variance estimator. In addition, for the posited model L{u, Z, X(u); b} = b^T s{u, Z, X(u)}, if s{u, Z, X(u)} contains Q(u) which is defined by (34), then the projection Π(ψ(D)|Λ_α) is identical to zero, otherwise, our estimator will be slightly conservative. However, in all our simulations studies that will be described later the conservatism in the variance estimator was never noticeable. Thus, the a variance estimator for $\widehat{\beta }$ is computed by the following sandwich estimator

$$\widehat{V}\left(\widehat{\beta }\right)=\frac{\sum _{i=1}^n{\widehat{m}}_2^2(D_i;\widehat{\beta })}{{[\sum _{i=1}^n{\Delta }_{i}W(U_i,Z_i)∕{\widehat{K}}_C\{U_i,Z_i,X_i\left(U\right)\}\{1-\stackrel{‒}{Z}(U_i;{\beta }_0)\}\stackrel{‒}{Z}(U_i;{\beta }_0)]}^2},$$ (28)

where

$$\begin{array}{cc}\hfill {\widehat{m}}_2(D_i;\beta )& =\int \{Z_i-\stackrel{‒}{Z}(u;\beta )\}\frac{W(u,Z_i)}{{\widehat{K}}_C(u,Z,X\left(u\right))}\{d{N}_i\left(u\right)-\widehat{\lambda }(u;\beta )du\text{exp}\left(\beta Z_i\right)Y_i\left(u\right)\}\hfill \\ \hfill & -(Z_i-\pi )f\left(X_{1i}\right)\hfill \\ \hfill & +\int [d{N}_{C_i}\left(u\right)-Y_i\left(u\right){\widehat{\lambda }}_{0C}(u,Z_i)H\{u,Z_i,X_i\left(u\right);\widehat{\alpha }\}du]\left[L(u,Z_i,X_i\left(u\right))-\stackrel{‒}{L}(u,Z_i)\right].\hfill \end{array}$$

4.3 Simulation

We performed a Monte-Carlo simulation study to compare the performance of the maximum partial likelihood estimator ${\widehat{\beta }}_{\mathrm{PH}}$ with our proposed estimators ${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$, and ${\widehat{\beta }}_3$ that are obtained by solving the estimating equation (20) with $W(u,Z)={\widehat{K}}_C(u,Z)$ and {f(·) = 0, L(·) = 0}, $\{f(\cdot )=\widehat{f}(\cdot ),L(\cdot )=0\}$ and $\{f(\cdot )=\widehat{f}(\cdot ),L(\cdot )=\widehat{L}(\cdot )\}$, respectively. It is clear to see that these three estimators have decreasing asymptotic variances as ${\widehat{\beta }}_1$ is obtained without using any auxiliary covariate information except for estimating the survival function for censoring time, and ${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$ are obtained by utilizing the information on baseline covariates and the information on all the covariates, respectively.

For this study, we considered one baseline covariate X₁ and one post-treatment covariate X₂ that can be obtained immediately for all patients. First we generated bivariate data (Y, X) from a bivariate normal density with mean zero, variance 1, and correlation ρ. We then independently generated the treatment indicator Z as a Bernoulli(π). Using inverse transformation, the survival time T was taken to be T = −exp( −βZ) log{1 − Φ(Y)}, where Φ(·) denotes the cumulative distribution function of a standard normal. X₁ = Φ⁻¹(X) follows a uniform (0, 1) distribution. This guarantees that the distribution of T given Z will follow a proportional hazards relationship λ(t|z) = λ(t) exp(βz), with λ(t) = 1, that is, T ~ Exponential exp(βZ)}. The post-treatment covariate was generated using the formula $X_2=rT+\sqrt{1-r^2}∕\sqrt{2}{\chi }_1^2$ which results in the correlation of X₂ and T to be r. Note that this makes X₂ conditionally independent of the treatment Z given T. Censoring time C was generated using the following three scenarios: 1) Exponential distribution with hazard rate λ_C (u|Z) = c exp(βZ) reflecting noninformative censoring given Z; 2) Exponential distribution with hazard rate λ_C(u|X₁, X₂, Z) = c {Z exp (α₁₁ X₁ + α₂₁ X₂) + (1 − Z) exp(α₁₂X₁ + α₂₂ X₂)}, reflecting informative censoring with a stratified proportional hazard regression model; 3) Scaled Lognormal distribution c·LN(μ, σ) with μ = Z(ℓ₁₁X₁ + ℓ₂₁X₂) + (1−Z)(ℓ₁₂X₁ + ℓ₂₂X₂) and σ = 1, in which case the censoring time is correlated with the survival time given Z but does not follow a stratified proportional hazard regression model. To calculate the estimated functions $\widehat{f}(\cdot )$ and $\widehat{L}(\cdot )$, we posited the models $a_0+a_1{X}_1+a_2{X}_1^2$ for f(·), and b₀ + b₁ X₁ + b₂ X₂+ b₃ X₁ Z + b₄ X₂ Z for L(·).

For this demonstration, treatment was assigned with probability π = .5, the correlation between the bivariate normal random variable was taken to be ρ = .5 which resulted in a sample correlation of approximately 0.4 between the survival time T and baseline covariate X₁. The correlation of X₂ and T was taken to be r = 0.7. Two values for the proportional hazards regression coefficient were considered, β = 0 (null hypothesis) and β = .3. For the censoring time, α₁₁ = 1, α₂₁ = 0.1, α₁₂ = 2, α₂₂ = 0.3, ℓ₁₁ = 0.3, ℓ₂₁ = 1, ℓ₁₂ = 1, ℓ₂₂ = 0.3, and the value c was chosen in different scenarios that would result in roughly 36% the data being censored. Sample sizes of 250 and 600 were considered and each scenario used 1000 Monte-Carlo simulations. In Tables 1, 2 and 3, we compare the bias, standard error estimate, Monte-Carlo standard error, relative efficiency (ratio of variance estimate and ratio of Monte-Carlo variance), type I error and the power of the maximum partial likelihood estimator ${\widehat{\beta }}_{\mathrm{PH}}$ with our proposed estimators ${\widehat{\beta }}_k$ k = 1, 2, 3, under the various simulation scenarios.

Table 1.

Simulation Results for the 1st Scenario of Censoring (1000 Monte-Carlo samples, entries in parentheses for SE and Monte-Carlo SE are relative efficiencies with respect to ${\widehat{\beta }}_1$.)

True β0	Statistics	n	${\widehat{\beta }}_{\text{PH}}$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_3$
0	Bias	250	0.004	0.004	0.005	0.005
		600	0.001	0.000	0.001	0.001
	AveSE	250	0.160 (1.00)	0.160 (1.00)	0.145 (1.21)	0.134 (1.42)
		600	0.089 (1.00)	0.089 (1.00)	0.080 (1.24)	0.077 (1.34)
	MCSE	250	0.165 (0.88)	0.155 (1.00)	0.141 (1.21)	0.141 (1.21)
		600	0.091 (0.94)	0.088 (1.00)	0.078 (1.27)	0.078 (1.27)
	Type I Error	250	0.055	0.048	0.041	0.060
		600	0.054	0.043	0.047	0.059
0.3	Bias	250	0.007	0.007	0.008	0.008
		600	0.002	0.003	0.003	0.003
	AveSE	250	0.162 (1.00)	0.161 (1.00)	0.147 (1.21)	0.137 (1.38)
		600	0.103 (1.00)	0.014 (1.00)	0.094 (1.21)	0.088 (1.37)
	MCSE	250	0.165 (0.90)	0.157 (1.00)	0.143 (1.20)	0.143 (1.20)
		600	0.107 (0.91)	0.102 (1.00)	0.091 (1.26)	0.091 (1.26)
	Power	250	0.481	0.474	0.555	0.606
		600	0.826	0.831	0.899	0.923

Table 2.

Simulation Results for the 2nd Scenario of Censoring (1000 Monte-Carlo samples, entries in parentheses for SE and Monte-Carlo SE are relative efficiencies with respect to ${\widehat{\beta }}_1$.)

True β0	Statistics	n	${\widehat{\beta }}_{\text{PH}}$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_3$
0	Bias	250	0.159	0.014	0.015	0.015
		600	0.159	0.008	0.008	0.008
	AveSE	250	0.183 (1.07)	0.189 (1.00)	0.174 (1.18)	0.161 (1.38)
		600	0.117 (1.10)	0.123 (1.00)	0.114 (1.17)	0.105 (1.38)
	MCSE	250	0.185 (1.02)	0.187 (1.00)	0.171 (1.20)	0.171 (1.20)
		600	0.121 (1.02)	0.122 (1.00)	0.110 (1.22)	0.110 (1.22)
	Type I Error	250	0.141	0.053	0.049	0.069
		600	0.289	0.043	0.039	0.064
0.3	Bias	250	0.152	0.019	0.020	0.020
		600	0.149	0.010	0.010	0.010
	AveSE	250	0.185 (1.05)	0.190 (1.00)	0.174 (1.18)	0.163 (1.35)
		600	0.119 (1.08)	0.123 (1.00)	0.113 (1.17)	0.106 (1.34)
	MCSE	250	0.188 (1.01)	0.189 (1.00)	0.173 (1.20)	0.173 (1.20)
		600	0.121 (1.04)	0.123 (1.00)	1.112 (1.21)	1.112 (1.21)
	Power	250	0.684	0.397	0.450	0.493
		600	0.962	0.707	0.769	0.803

Table 3.

Simulation Results for the 3rd Scenario of Censoring (1000 Monte-Carlo samples, entries in parentheses for SE and Monte-Carlo SE are relative efficiencies with respect to ${\widehat{\beta }}_1$.)

True β0	Statistics	n	${\widehat{\beta }}_{\text{PH}}$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_3$
0	Bias	250	−0.245	0.023	0.019	0.019
		600	−0.254	0.051	0.052	0.052
	AveSE	250	0.193 (1.37)	0.225 (1.00)	0.210 (1.15)	0.183 (1.51)
		600	0.123 (1.86)	0.168 (1.00)	0.160 (1.11)	0.133 (1.60)
	MCSE	250	0.191 (1.43)	0.229 (1.00)	0.215 (1.13)	0.215 (1.13)
		600	0.123 (1.89)	0.169 (1.00)	0.164 (1.06)	0.164 (1.06)
	Type I Error	250	0.247	0.045	0.041	0.071
		600	0.527	0.040	0.037	0.088
0.3	Bias	250	−0.230	0.023	0.019	0.019
		600	−0.240	0.046	0.048	0.048
	AveSE	250	0.185 (1.38)	0.218 (1.00)	0.203 (1.15)	0.177 (1.51)
		600	0.118 (1.87)	0.162 (1.00)	0.154 (1.11)	0.128 (1.60)
	MCSE	250	0.182 (1.42)	0.216 (1.00)	0.202 (1.15)	0.202 (1.15)
		600	0.117 (1.83)	0.158 (1.00)	0.154 (1.06)	0.154 (1.06)
	Power	250	0.059	0.297	0.319	0.450
		600	0.067	0.617	0.666	0.781

Table 1 shows the simulation results under scenario 1 where censoring time is noninformative. As we expect, all the estimators are unbiased and control the type I error. Our proposed estimators are more efficient then the traditional maximum partial likelihood estimator and more powerful than the logrank test.

Table 2 shows the simulation results under scenario 2 where censoring time follows a stratified proportional hazards regression model for each treatment group. As we can see the traditional maximum partial likelihood estimator is severely biased whereas all our proposed estimators are unbiased and control the type I error. This is consistent with the theoretical results in this paper.

In addition, from Table 3, we see that when the censoring time is informative, but does not follow a stratified proportional hazard regression model, our proposed estimators are still less biased then the traditional maximum partial likelihood estimator.

4.4 Applying to ACTG 175 data

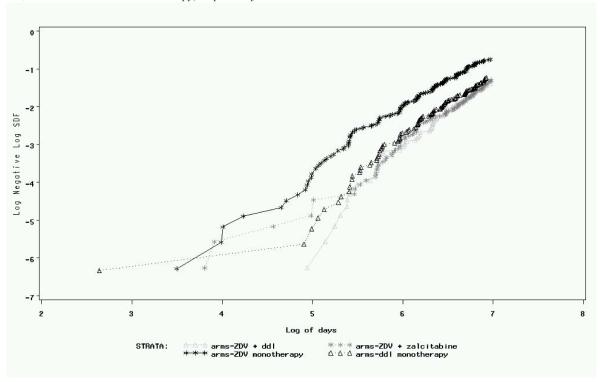
Figure 1 is a plot of the logarithm of the negative logarithm of the survival curve of the survival time for each treatment group. The four lines, except for a few points early in time, are approximately parallel suggesting that a proportional hazards relationship between treatments is reasonable. If the censoring time is noninformative, we know that the maximum partial likelihood estimator is the most efficient estimator and the logrank test is the most powerful nonparametric test without using any additional covariates. The results of applying the standard analysis using Cox’s maximum partial likelihood estimator can be found in Table 4. For example, the estimate of the log hazard ratio between treatments ZDV monotherapy and ZDV + ddI is −0.703 and its standard error is .124, which is highly statistically significant.

Fig. 1.

ACTG 175 data. Log-negative-log survival functions of time to death for treatment ZDV monotherapy, ZDV + ddI, ZDV + zalcitabine and ddI monotherapy, respectively.

Table 4.

Estimates of ${\widehat{\beta }}_{\text{PH}}$ and ${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$ on the ACTG 175 data (RE is the relative efficiencies with respect to ${\widehat{\beta }}_1$.)

		Estimate	Standard Error	RE
ZDV monotherapy and ZDV + ddI	${\widehat{\beta }}_{\text{PH}}$	−0.703	0.124	1.01
	${\widehat{\beta }}_1$	−0.689	0.124	1.00
	${\widehat{\beta }}_2$	−0.724	0.120	1.07
	${\widehat{\beta }}_3$	−0.721	0.117	1.12
ZDV monotherapy and ZDV + zalcitabine	${\widehat{\beta }}_{\text{PH}}$	−0.640	0.121	1.01
	${\widehat{\beta }}_1$	−0.638	0.122	1.00
	${\widehat{\beta }}_2$	−0.617	0.114	1.15
	${\widehat{\beta }}_3$	−0.590	0.111	1.21
ZDV monotherapy and ddI monotherapy	${\widehat{\beta }}_{\text{PH}}$	−0.528	0.116	1.01
	${\widehat{\beta }}_1$	−0.525	0.116	1.00
	${\widehat{\beta }}_2$	−0.536	0.111	1.10
	${\widehat{\beta }}_3$	−0.509	0.109	1.14

Applying a stratified proportional hazard regression model for the censoring time and using Forward selection with selection entry 0.05, we obtained some prognostic covariates for each treatment group. The important prognostic covariates for the censoring time are (AGE, RACE, STRAT, OFFTRT, MisCD4) for ZDV monotherapy, (HOMO, Z30, RACE, CD820, OFFTRT, MisCD4) for ZDV + ddI, (HOMO, RACE, STRAT, SYMP, OFFTRT) for ZDV + zalcitabine, and (Z30, GENDER, CD80, OFFTRT, MisCD4) for ddI monotherapy.

We also applied the similar model for the survival time and found some prognostic covariates for each treatment group, which are (CD40, CD80, GENDER, Z30, CD420, CD496, MisCD4) for ZDV monotherapy, (CD40, PREANTI, STRAT, SYMP, CD420, CD496, MisCD4) for ZDV + ddI, (PREANTI, KARN, SYMP, CD420, CD496, MisCD4) for ZDV + zalcitabine and (CD40, SYMP, CD420, CD496, MisCD4) for ddI monotherapy.

As we can see, for each treatment group, there is only one common covariate that is prognostic for both survival time and censoring time. For example, for treatments ZDV monotherapy, ZDV + ddI and ddI monotherapy, MisCD4 is the only common covariate and for treatment ZDV + zalcitabine, SYMP is the common covariate. Both MisCD4 and SYMP are binary variables, which give us a rough sense that the survival time and censoring time are weakly correlated given treatment assignment. Hence our proposed estimator may be close to the traditional partial likelihood estimator which assumes independence between survival time and censoring time given treatment. This explains why there are no substantial differences between our estimators and the maximum partial likelihood estimator after applying our method to the ACTG 175 data as shown in Table 4. Again, to obtain a more efficient estimator, we incorporated some prognostic covariates into the model that include baseline covariates (CD4, CD8, AGE, WEIGHT, DRUG, KARN, Z30, SYMP, PREANTI) and post-treatment covariates (CD420, CD820, CD496, MisCD4, OFFTRT). The results seem to support that using auxiliary covariates in the model leads to more efficient estimators (${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$) than the estimator $\left({\widehat{\beta }}_1\right)$ that does not consider auxiliary covariates in the model.

5 Application to two-sample treatment comparison

In this section, we discuss another simple yet commonly occurring case where the time-lagged response is to be observed after a fixed time period; that is, the lag time is the same for every response to be observed. The primary endpoint here is to evaluate the population difference in mean responses between two treatment groups. Specifically, the treatment effect parameter β = μ₁ − μ₀, where μ_k denotes the population mean of the response Y for treatment group k; i.e., μ_k = E(Y|Z = k), k = 0, 1.

5.1 Class of all semiparametric estimators for β

Applying Theorem 1, it is straightforward to derive that the influence functions for the RAL estimators for μ_k are

$${\varphi }_{{\mu }_k}(D;f,L)=\frac{\Delta {\psi }_{YZ}(Y,Z;{\mu }_k)}{K_C\{U,Z,X\left(U\right)\}}+(Z-\pi )f\left(X_1\right)+\int d{M}_C\{u,Z,X\left(u\right)\}L\{u,Z,X\left(u\right)\},$$ (29)

for arbitrary functions f(X₁) and L{u, Z, X(u)}, where the full data influence function for estimators of μ_k (Davidian et al 2005) is given by

$${\psi }_{YZ}(Y,Z;{\mu }_k)=k\frac{Z}{\pi }(Y-{\mu }_1)+(1-k)\frac{1-z}{1-\pi }(Y-{\mu }_0).$$

Again, if we use the estimated functions ${\widehat{\lambda }}_C(\cdot )$ and ${\widehat{K}}_C(\cdot )$, assuming the stratified proportional hazards regression model, the class of all RAL estimators ${\widehat{\mu }}_k$ for μ_k can be represented as a solution to the following estimating equation

$$0=\sum _{i=1}^n\left(\frac{{\Delta }_i{\psi }_{YZ}(Y_i,Z_i;{\mu }_k)}{K_C\{U_i,Z_i,X_i\left(U\right)\}}+(Z_i-\pi )f\left(X_{1i}\right)+\int [L\{u,Z_i,X_i\left(u\right)\}-\stackrel{‒}{L}(u,Z_i)]d{N}_{C_i}\left(u\right)\right),$$ (30)

for arbitrary functions f(X₁) and L{u, Z, X(u)}. Consequently, the class of the RAL estimators for β, the difference in mean response Y between treatment groups (Tsiatis et al 2008) is $\widehat{\beta }={\widehat{\mu }}_1-{\widehat{\mu }}_0$ and the corresponding influence function for $\widehat{\beta }$ is ϕ_β (D; f, L) = ϕ_μ1(D; f, L) − ϕ_μ0(D; f, L).

From the results of Lu and Tsiatis (2008), we know that the efficient influence function for μ_k is ${\varphi }_{{\mu }_k}(D;f_k^{\mathrm{opt}},L_k^{\mathrm{opt}})$, where

$$\begin{array}{cc}\hfill f_k^{opt}& =\frac{1}{\pi (1-\pi )}E\{(Z-\pi ){\psi }_{YZ}(Y,Z;{\mu }_k)\mid X_1\}\hfill \\ \hfill & =\frac{{(-1)}^{1-k}}{{\pi }^k(1-\pi )1-k}\{E(Y\mid Z=k,X_1)-{\mu }_k\},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill L_k^{opt}& =\frac{E\{{\psi }_{YZ}(Y,Z;{\mu }_k)\mid T\ge u,Z,X\left(u\right)\}}{K_C\{u,Z,X_u\}}\hfill \\ \hfill & =\frac{Z^k(1-Z)1-k}{{\pi }^k{(1-\pi )}^{1-k}}\frac{[E\{Y\mid T\ge u,Z=k,X\left(u\right)\}-{\mu }_k]}{K_C\{u,Z,X\left(u\right)\}}.\hfill \end{array}$$

Considering that the underlying true model for E(Y|Z = k, X₁) and E(Y|T ≥ u, Z = k, X(u)} are unknown in practice, we posit parametric models $E(Y\mid Z=k,X_1,a_k)=a_k^T{q}_k\left(X_1\right)$ that is linear in a_k and $E\{Y\mid T\ge u,Z=k,X\left(u\right),{\mathbf{b}}_k\}={\mathbf{b}}_k^T{s}_k\{u,Z,X\left(u\right)\}$ that is linear in b_k, where a_k and b_k are r_ak-dimensional and r_bk-dimensional vectors of unknown parameters, respectively, q_k(·) is an r_ak-dimensional vector of functions of X₁ and s_k(·) is an r_bk-dimensional vector of functions of {u, Z, X(u)}. The parameters a_k and b_k are estimated by the commonly used ordinary least squares method. Once we have the estimated functions $\widehat{E}(Y\mid Z=k,X_1)$ and $\widehat{E}\{Y\mid T\ge u,Z=k,X\left(u\right)\}$, the corresponding estimated optimal functions are easily obtained by

$${\widehat{f}}_k^{opt}=\frac{{(-1)}^{1-k}}{{\pi }^k{(1-\pi )}^{1-k}}\{\widehat{E}(Y\mid Z=k,X_1)-{\mu }_k\},$$

and

$${\widehat{L}}_k^{opt}=\frac{Z^k{(1-Z)}^{1-k}}{{\pi }^k{(1-\pi )}^{1-k}}\frac{[\widehat{E}\{Y\mid T\ge u,Z=k,X\left(u\right)\}-{\mu }_k]}{K_C\{u,Z,X\left(u\right)\}}$$

Now, let us consider the following three estimators ${\widehat{\beta }}_j={\widehat{\mu }}_1^j-{\widehat{\mu }}_0^j$, j = 1, 2, 3, for β, where ${\widehat{\mu }}_k^1$ is obtained by solving ∑ϕ_μk (D_i; 0, 0) = 0 without considering auxiliary covariates which results in

$${\widehat{\mu }}_k^1=\frac{\sum _i{\Delta }_{i}Z\frac{i}{k}{(1-Z_i)}^{1-k}{Y}_i∕{\widehat{K}}_C\{U_i,k,X_i\left(U_i\right)\}}{\sum _i{\Delta }_i{z}_i^k{(1-Z_i)}^{1-k}∕{\widehat{K}}_C\{U_i,k,X_i\left(U_i\right)\}};$$

${\widehat{\mu }}_k^2$ is obtained by solving $\Sigma {\varphi }_{\mu k}(D_i;{\widehat{f}}_k^{\mathrm{opt}},0)=0$ which only considers baseline covariates; that is

$${\widehat{\mu }}_k^2=\frac{\sum _i[{\Delta }_i{Z}_i^k{(1-z_i)}^{1-k}{Y}_i∕{\widehat{K}}_C\{U_i,k,X_i\left(U_i\right)\}+{(-1)}^k(Z_i-\widehat{\pi })\widehat{E}(Y\mid X_{1i},Z=k)]}{\sum _i{\Delta }_i{Z}_i^k(1-Z_i)1-k∕{\widehat{K}}_C\{U_i,k,X_i\left(U_i\right)\}};$$

and ${\widehat{\mu }}_k^3$ is obtained by solving $\Sigma {\varphi }_{\mu k}(D_i;{\widehat{f}}_k^{\mathrm{opt}},{\widehat{L}}_k^{\mathrm{opt}})=0$ which considers all covariates; that is,

$$\begin{array}{cc}\hfill {\widehat{\mu }}_k^3& =\sum _i[\frac{{\Delta }_i{Z}_i^k(1-Z_i)1-k{Y}_i}{{\widehat{K}}_C(U_i,k,X_i\left(U_i\right))}+(-1)k(Z_i-\widehat{\pi })\widehat{E}(Y\mid X_{1i},Z=k)\phantom{]}\hfill \\ \hfill & \phantom{[}+Z_i^k{(1-Z_i)}^{1-k}\int \frac{{\widehat{M}}_C\{U_i,k,X_i\left(U_i\right)\}}{{\widehat{K}}_c\{U_i,k,X_i\left(U_i\right)\}}\widehat{E}\{Y\mid T\ge u,Z=k,X_i\left(u\right)\}].\hfill \end{array}$$

The variance of ${\widehat{\beta }}_j$, j = 1, 2, 3, is estimated using the standard sandwich estimator based on the influence function of ${\widehat{\beta }}_j$. According to our theory, the estimators ${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$ using auxiliary covariates should be more efficient than ${\widehat{\beta }}_1$ without using auxiliary covariates and the variance of ${\widehat{\beta }}_j$ should be decreasing as j increases from 1 to 3.

5.2 Simulation

This simulation study is performed to compare our proposed estimators ${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$ with the commonly used t-test. The simulation data were generated from the fit of the data ACTG 175. For each simulated data set, we generated for each of n subjects the continuous baseline covariates logCD40, logCD80, AGE, WEIGHT, KARN and PREANTI from a multivariate normal distribution with the empirical mean and covariance matrix of these variables in the data. We then independently generated the binary indicators of HOMO, RACE, DRUG, and STRAT for each subject from independent Bernoulli distributions using the observed data proportions for each variable. The treatment indicator was generated independently from Bernoulli(π) for each subject. The CD4 cell counts at 8, 20, 32, 44, 56, 68, 80, 92, 96 weeks for each subject was generated using the treatment specific mixed model log{CD4(t)} = α_0k + α_1kt + γX_1k + ∊_k where k is treatment group ZDV monotherapy or ZDV + ddI, α₀, α₁ and ∊ are multivariate normal random effect with empirical means and covariance matrix after fitting this mixed model to the data, and the set of baseline covariates X_1k in the treatment specific mixed model consists of (logCD40, logCD80, STRAT) for ZDV monotherapy; (logCD40, AGE, KARN, PREANTI) for ZDV + ddI. The censoring time for each subject was generated using the treatment specific hazard rate λ_C{u|T ≥ u, Z, X(u)} = λ_0k exp{ζ_1kCD4_k(u)+ζ_2kX_1Ck}, where CD4_k(u) records the last observed CD4 cell counts at or before time u in treatment group k, and the set of baseline covariates taken for each treatment group in this proportional hazard model are (WEIGHT, DRUG, RACE) for ZDV monotherapy and (WEIGHT, KARN) for ZDV + ddI. The coefficients (ζ_1k, ζ_2k) in the proportional hazard model were taken to be the values after fitting this model to the data ACTG 175. If the censoring time is greater than t, t = 8, 12, …, 96, then the CD4 CELL counts at t + 1, …, 96 weeks are set to missing.

The true value of β = 80.13 and the randomization probability to each of the two treatment group is π = 0.5. We considered the sample size n = 250, 600 and 1054 that is the actual sample size of the data from ACTG 175 with treatments ZDV monotherapy and ZDV + ddI.

Similarly, we also performed a simulation study for the comparisons of treatments ZDV + zalcitabine and ddI monotherapy with treatment ZDV monotherapy, respectively. To generate the CD4 cell counts at 8, 20, 32, 44, 56, 68, 80, 92, 96 weeks, we chose the baseline covariates (logCD40, logCD80, PREANTI, STRAT) for ZDV + zalcitabine; (logCD40, logCD80, WEIGHT, KARN) for ddI monotherapy in the treatment specific mixed model. The baseline covariates used in the treatment specific proportional hazard model to generate censoring time were taken to be (HOMO, KARN, PREANTI) for ZDV + zalcitabine and (HOMO, KARN, CD40) for ddI monotherapy. The true values of β for comparing treatments ZDV + zalcitabine and ddI monotherapy with treatment ZDV monotherapy are 63.57 and 46.33, respectively.

Tables 5, 6 and 7 are the simulation results for comparing treatment group ZDV + ddI, ZDV + zalcitabine and ddI monotherapy with treatment ZDV monotherapy, respectively. The results of fitting the models on the data ACTG 175 was shown in table 8. Clearly, under the situations with informative censoring, the standard method of t-test is severely biased while the biases of our proposed estimators ${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$ are negligible. In addition, the estimators ${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$ using auxiliary covariates seem to have smaller estimated variances than ${\widehat{\beta }}_1$ without using the auxiliary covariates, which is consistent with our theoretical results mentioned earlier.

Table 5.

Simulation Results for comparing treatment ZDV monotherapy and ZDV + ddI (5000 Monte-Carlo samples, true β = 80:13, entries in parentheses for SE and Monte-Carlo SE are relative efficiencies with respect to ${\widehat{\beta }}_1$

Statistics	n	t-test	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_3$
Bias	250	−21.050	−5.953	−5.564	−3.871
	600	−21.120	−5.258	−4.980	−3.533
	1054	−21.310	−5.267	−5.027	−3.664
AveSE	250	62.645 (0.71)	52.961 (1.00)	51.637 (1.05)	47.126 (1.26)
	600	40.858 (0.70)	34.246 (1.00)	33.572 (1.04)	30.815 (1.24)
	1054	30.949 (0.70)	25.859 (1.00)	25.395 (1.04)	23.357 (1.23)
MCSE	250	64.104 (0.60)	49.756 (1.00)	50.074 (0.99)	49.070 (1.03)
	600	41.377 (0.59)	31.891 (1.00)	31.490 (1.03)	30.952 (1.06)
	1054	31.492 (0.59)	24.150 (1.00)	23.866 (1.02)	23.530 (1.05)
95% CI	250	94.3	96.9	96.2	94.9
	600	91.9	96.4	96.1	94.9
	1054	89.2	95.7	96.0	94.5

Table 6.

Simulation Results for comparing treatment ZDV monotherapy and ZDV + zalcitabine (5000 Monte-Carlo samples, true β = 63:57, entries in parentheses for SE and Monte-Carlo SE are relative efficiencies with respect to ${\widehat{\beta }}_1$.)

Statistics	n	t-test	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_3$
Bias	250	−19.130	−2.664	−2.323	−1.478
	600	−18.980	−2.213	−1.871	−1.075
	1056	−19.040	−2.308	−2.105	−1.320
AveSE	250	57.639 (0.71)	48.548 (1.00)	47.068 (1.06)	43.102 (1.27)
	600	37.648 (0.70)	31.417 (1.00)	30.595 (1.05)	28.172 (1.24)
	1056	28.497 (0.69)	23.715 (1.00)	23.132 (1.05)	21.337 (1.24)
MCSE	250	58.415 (0.62)	45.859 (1.00)	45.678 (1.01)	44.740 (1.05)
	600	37.895 (0.61)	29.479 (1.00)	28.753 (1.05)	28.170 (1.10)
	1056	28.685 (0.61)	22.415 (1.00)	21.794 (1.06)	21.421 (1.09)
95% CI	250	95.4	96.7	96.2	94.4
	600	93.4	96.9	96.5	94.7
	1056	91.6	96.5	96.3	95.3

Table 7.

Simulation Results for comparing treatment ZDV monotherapy and ddI monotherapy (5000 Monte-Carlo samples, true β = 46:33, entries in parentheses for SE and Monte-Carlo SE are relative efficiencies with respect to ${\widehat{\beta }}_1$.)

Statistics	n	t-test	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_3$
Bias	250	−10.970	−1.748	−1.325	0.081
	600	−11.040	−1.893	−1.622	−0.333
	1093	−10.970	−2.478	−2.338	−1.034
AveSE	250	60.028 (0.69)	49.787 (1.00)	48.521 (1.05)	44.447 (1.25)
	600	39.159 (0.67)	32.165 (1.00)	31.493 (1.04)	29.015 (1.23)
	1093	29.126 (0.67)	23.826 (1.00)	23.368 (1.04)	21.581 (1.22)
MCSE	250	61.090 (0.59)	46.897 (1.00)	46.771 (1.01)	45.881 (1.04)
	600	39.473 (0.58)	29.981 (1.00)	29.444 (1.04)	28.958 (1.07)
	1093	29.254 (0.58)	22.233 (1.00)	21.714 (1.05)	21.408 (1.08)
95% CI	250	95.4	96.9	96.5	95.0
	600	94.7	96.8	96.6	95.0
	1093	93.7	96.7	96.9	95.5

Table 8.

Estimates of t-test and ${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$ on the ACTG 175 data (RE is the relative efficiencies with respect to ${\widehat{\beta }}_1$.)

		Estimates	Standard Errors	RE
ZDV monotherapy and ZDV + ddI	t-test	53.485	13.216	1.05
	${\widehat{\beta }}_1$	66.092	13.532	1.00
	${\widehat{\beta }}_2$	70.219	12.242	1.22
	${\widehat{\beta }}_3$	69.850	10.426	1.68
ZDV monotherapy and ZDV + zalcitabine	t-test	68.566	13.286	1.03
	${\widehat{\beta }}_1$	76.215	13.483	1.00
	${\widehat{\beta }}_2$	77.115	12.143	1.23
	${\widehat{\beta }}_3$	74.750	10.308	1.71
ZDV monotherapy and ddI monotherapy	t-test	41.881	13.294	1.04
	${\widehat{\beta }}_1$	48.367	13.537	1.00
	${\widehat{\beta }}_2$	53.300	12.065	1.26
	${\widehat{\beta }}_3$	53.852	9.857	1.89

6 Conclusion

Our interest in this paper is estimating the unconditional treatment effect β as defined in (1), where the primary outcome is the time-lagged response whose values are often missing in practice due to censoring of some patients. Under the assumption of censoring at random (CAR) given in (4) and the assumption of independence between baseline covariates and treatment assignments given in (3), we developed a class of regular and asymptotically linear (RAL) estimators for β by using the theory of semiparametrics and the major results of Robins and Rotnitzky (1992). The prognostic covariates were utilized by the model to improve the efficiency of the estimators.

We have discussed in detail the applications of our method to two special cases of time-lagged responses. Nevertheless, our proposed method has wider applicability to more general time-lagged response problems. In the first case, the time-lagged response itself is the survival time and the parameter of interest is the treatment-specific log hazard ratio. A class of RAL estimators for β characterized by (20) were derived that took advantage of auxiliary covariates to gain efficiency while allowing us to weaken the usual assumption of noninformative censoring to the more reasonable assumption of censoring at random. In the second case, we are interested in estimating the population difference in mean response between two treatment groups where the time-lagged response is observed after a fixed period of time; i.e., the lag time is the same for each individual in the study. A class of RAL estimators was derived and compared with the commonly used standard method, t-test.

Deriving the RAL estimators for β requires the correct model for the censoring time, which is impossible to know in practice. A stratified proportional hazard regression model was hereby proposed to estimate the survival function of the censoring time. As we demonstrated numerically in the above two applications, even if the underlying true model for censoring time did not follow the proportional hazard model, our proposed estimators had much less bias than the standard estimation methods. As expected, when the censoring time truly followed a stratified proportional hazard model, the standard estimation techniques were biased while our proposed estimators were unbiased. In addition, both the results of the simulation study and the analysis on the data from ACTG 175 seemed to indicate that the estimators using prognostic covariates were more efficient than that without using covariates in the model.

Appendix A

Proof of Theorem 1

Using the equality

$$\frac{\Delta }{K_C\{U,Z,X\left(U\right)\}}+\int \frac{d{M}_C\{u,Z,X_u\}}{K_C\{u,Z,X\left(u\right)\}}=1,$$

the influence function (7) can be written as

$$\frac{\Delta {\psi }_{YZ}(Y,Z;{\beta }_0)}{K_C(U,Z,X\left(U\right))}+(Z-\pi )f\left(X_1\right)+\int \frac{d{M}_C(u,Z,X\left(u\right))}{K_C(u,Z,X\left(u\right))}[L(u,Z,X\left(u\right))-(Z-\pi )f\left(X_1\right)].$$

Since L(·) is an arbitrary fuction of $\{Z,X_1,X_2^H\left(u\right)\}$, we have the class of all observed data influence functions as described in theorem 1.

APPENDIX B. Proof of corollary 1

We first prove the following Lemmas.

Lemma 1 For any function b(u, Z), we have the following equality

$$\int \frac{b(v,Z)}{K_C\left(\right\{v,Z,X\left(u\right)\left\}\right)}dM(v,Z)=\frac{\Delta \int b(u,Z)d{M}_T(u,z)}{K_C\{U,Z,X\left(U\right)\}}+\int \frac{d{M}_C(u,z,X\left(u\right))}{K_C(u,Z,X\left(u\right))}E\left\{\int b(u,Z)d{M}_T(u,Z)\mid T\ge u,Z\right\},$$

where dM_T (u, Z) = I(T = u) − λ₀(u) exp(β₀Z)I(T ≥ u)du.

Proof: Since E{I(T = v)|T ≥ u, Z} = I(v ≥ u)e^β₀Zλ₀(v)dv P(T≥v, Z)=P(T≥u, Z) and E{I(T ≥ v)|T ≥ u, Z} = I(v < u) + I(v ≥ u)P(T ≥ v, Z)=P(T ≥ u, Z), we have that

$$E\{d{M}_T(v,Z)\mid \ge u,Z\}=-I(v<u)e^{{\beta }_{0}Z}{\lambda }_0\left(v\right)dv.$$

This implies

$$\begin{array}{cc}\hfill & \int \frac{d{M}_C\{u,Z,X\left(u\right)\}}{K_C(u,Z,X\left(i\right))}E\{\int b(u,z)d{M}_T(u,Z)\mid T\ge u,Z\}\hfill \\ \hfill & =\frac{\Delta -1}{K_C(U,Z,X\left(U\right))}{\int }_0^{U}b(v,Z)e^{{\beta }_{0}Z}{\lambda }_0\left(v\right)dv+{\int }_0^U\frac{{\lambda }_C\{u,z,X\left(u\right)\}}{K_C\{u,Z,X\left(u\right)\}}du{\int }_0^{u}b(v,Z)e^{{\beta }_{0}Z}{\lambda }_0\left(v\right)dv\hfill \\ \hfill & =\frac{\Delta }{K_C\{U,Z,X\left(U\right)\}}\int b(v,Z)I(v\le U)e^{{\beta }_{0}Z}{\lambda }_0\left(v\right)dv-\int \frac{b(v,Z)}{K_C(v,Z,X\left(v\right))}I(v\le U)e^{{\beta }_{0}Z}{\lambda }_0\left(v\right)dv\hfill \end{array}$$

The last equality is because that

$${\int }_v^U\frac{{\lambda }_C\{u\mid T\ge u,Z,X\left(u\right)\}}{K_C\{u,Z,X\left(u\right)\}}du=\frac{1}{K_C\{U,Z,X\left(U\right)\}}-\frac{1}{K_C(v,Z,X\left(v\right))}.$$

Hence, we have

$$\begin{array}{cc}\hfill & \frac{\Delta \int b(u,,Z)d{M}_T(u,Z)}{K_C\{U,Z,X\left(U\right)\}}+\int \frac{dMC(u,Z,X\left(u\right))}{K_C\{u,Z,X\left(u\right)\}}E\left\{\int b(u,Z)d{M}_T(u,Z)\mid T\ge u,Z\right\}\hfill \\ \hfill & =\frac{\Delta b(U,Z)}{K_C(U,Z,X\left(U\right))}-\int \frac{b(u,Z)}{K_C(u,Z,X\left(u\right))}I(u\le U)e^{{\beta }^{0}Z}{\lambda }_0\left(u\right)du\hfill \\ \hfill & =\int \frac{b(u,Z)}{K_C(u,Z,X\left(u\right))}dM(u,Z),\text{for}\text{all}\text{functions}b(u,Z).\hfill \end{array}$$

Applying ψ_{Y Z} in (15) to Theorem 1 and using Lemma 1, we have the class of all influence function written as

$${\Psi }_{PH}^{obs}={\epsilon }_1+\{\mathcal{r}\oplus \mathcal{C}\}$$

where

$${\epsilon }_1=\left[C_a^{-1}\int \frac{a\left(u\right)\{Z-Z_T^{\ast }(u;{\beta }_0)\}}{K\left(C\right)\{u,Z,X\left(u\right)\}}dM(u,Z;{\beta }_0):\text{for}\text{all}\text{functions}a\left(u\right)\right],$$

$\mathcal{R}$ and $\mathcal{C}$ are defined in (6) and (9), respectively.

Now for any function W(u,Z), if we let the function a(u) = W(u, 1) − {W(u, 1) − W(u, 0)} Z*(u;β₀), where Z*(u; β) is given in (18), after some simple algebra, we can easily get that $a\left(u\right)\{Z-Z_T^{\ast }(u;{\beta }_0)\}=W(u,Z)\{Z-Z^{\ast }(u;{\beta }_0)\}$. Recalculate the proportionality, according to the theory of semiparametrics (Tsiatis 2006, chap. 4), is equal to the expectation of the partial derivative of

$$e_{W(u,Z)}(D;{\beta }_0)=\int W(u,Z)\{Z-Z^{\ast }(u;{\beta }_0)\}∕K_C\{u,Z,X\left(u\right)\}dM(u,Z;{\beta }_0)$$

with respect to β evaluated at the true value β₀, that is, C_W = [E{∂e_{W(u, Z)}(D; β₀)/∂β}]⁻¹. After some algebra, we derive the proportionality constant C_W is the same as (19) and hence, the space ε₁ is the same as ε as described in (17).

APPENDIX C. Proof of theorem 2

Using standard results for the proportional hazards model (e.g. van der Laan and Robins 2003; Tsiatis 2006) the nuisance tangent space associated with the nuisance baseline hazard function λ_0C(·, Z) is given by

$${\Lambda }_{\lambda (.,Z)}=\left[\int a(u,Z)d{M}_C\{u,Z,X\left(u\right)\}\text{for}\text{all}a(u,Z)\right],$$ (31)

and the nuisance tangent space associated with the nuisance parameters α = (α₁₁, …, α₂₂) is given by

$${\Lambda }_{\alpha }=\left(B\int {[Z{X}_1,Z_{g1}\left\{X_2^H\left(u\right)\right\},(1-Z)X_1,{(1-Z)}_{g2}\left(X_2^H\left(u\right)\right)]}^{T}d{M}_C\{u,Z,X\left(u\right)\}:B\in {\mathbb{R}}^{1\times 4}\right)$$ (32)

Find the projection $\Pi \{\psi \left(D\right)\mid {\Lambda }_{\lambda 0C(\cdot ,Z)}^{\perp }\}$ in (25) is equivalent to find the function a₀(u, Z) such that $\psi \left(D\right)-\int a_0(u,Z)d{M}_C\{u,Z,X\left(u\right)\}$ is perpendicular to the nuisance tangent space Λ_{λ(·, Z)}, that is

$$E\left(\left[\psi \left(D\right)-\int a_0(u,Z)d{M}_C\{u,Z,X\left(u\right)\}\right]\int a(u,Z)d{M}_C(u,Z,X\left(u\right))\right)=0$$ (33)

for all functions a(u, Z). Using the result of Lemma 1, we have the influence function $\psi \left(D\right)\in {\Psi }_{\mathrm{PH}}^{\mathit{obs}}$ be written as

$$\psi \left(D\right)=\frac{\Delta {\psi }^F(T,Z)}{K_C(T,Z,X\left(T\right))}+\int \frac{d{M}_C(u,Z,X\left(u\right))}{K_C\{u,Z,X\left(u\right)\}}E\{{\psi }^F(T,Z)\mid T\ge u,Z\},$$

where ψ^F(T, Z) is defined in (26). Following the standard results of Fleming and Harrington (1991) for the covariance of two martingale processes, we have (33) equivalent to

$$0=E\left(\int \left[-\frac{\Delta {\psi }^F(T,Z)}{K_C\{T,Z,X\left(T\right)\}}+\frac{E\{{\psi }^F(T,Z)\mid T\ge u,Z\}}{K_C(u,Z,X\left(u\right))}+L\{u,Z,X\left(u\right)\}-a_0(u,Z)\right]\times a(u,Z){\lambda }_{C0}(u,Z)H\{u,Z,X\left(u\right)\}Y\left(u\right)du\right),$$

for all functions a(u, Z). After a little algebra, we have that

$$\begin{array}{cc}\hfill a_0(u,Z)& =-\frac{E[{\psi }^F(T,Z)∕K_C\{u,Z,X\left(u\right)\}H\{u,Z,X\left(u\right)\}Y\left(u\right)\mid Z]}{E[H\{u,Z,X\left(u\right)\}Y\left(u\right)\mid Z]}\hfill \\ \hfill & +\frac{E[E\{{\psi }^F(T,Z)\mid T\ge u,Z\}∕K_C\{u,Z,X\left(u\right)\}H\{u,Z,X\left(u\right)\}Y\left(u\right)\mid Z]}{E[H\{u,Z,X\left(u\right)\}Y\left(u\right)\mid Z]}\hfill \\ \hfill & +\frac{E[L\{u,Z,X\left(u\right)\}H\{u,Z,X\left(u\right)\}Y\left(u\right)\mid Z]}{E[H\{u,Z,X\left(u\right)\}Y\left(u\right)\mid Z]}.\hfill \end{array}$$

Therefore, $\Pi \{\psi \left(D\right)\mid {\Lambda }_{{\lambda }_{0C(\cdot ,Z)}}^{\perp }\}=\psi \left(D\right)-\int a_0(u,Z)d{M}_C\{u,Z,X\left(u\right)\}$ is identical to (25).

Similarly, obtain the projection Π(ψ(D)|Λ_α) is equivalent to find the function B₀ such that $\psi \left(D\right)-{\mathrm{B}}_0\int \mathrm{Q}\left(\mathrm{u}\right)d{M}_C\{u,Z,X\left(u\right)\}$ is perpendicular to the nuisance tangent space $\mathrm{B}\int \mathrm{Q}\left(\mathrm{u}\right)d{M}_C\{u,Z,X\left(u\right)\}$, where

$$Q\left(u\right)={[Z{X}_1,Z_{g1}\left\{X_2^H\left(u\right)\right\},(1-Z)X_1,{(1-Z)}_{g2}\left(X_2^H\right)\left(u\right)]}^T.$$ (34)

After some algebra, we have that

$$\begin{array}{cc}\hfill B_0& =-\frac{E[Q\left(u\right){\psi }^F(T,Z)∕K_C\{u,Z,X\left(u\right)\}H\{u,Z,X\left(u\right)\}Y\left(u\right){\lambda }_{C0}(u,Z)]}{E\left[Q\left(u\right)Q{\left(u\right)}^{T}H\{u,Z,X\left(u\right)\}Y\left(u\right){\lambda }_{C0}(u,Z)\right]}\hfill \\ \hfill & +\frac{E[E\{Q\left(u\right){\psi }^F(T,Z)\mid T\ge u,Z\}∕K_C\{u,Z,X\left(u\right)\}H(u,Z,X\left(u\right))Y\left(u\right)]}{E\left[Q\left(u\right)q{\left(u\right)}^{T}H\{u,Z,X\left(u\right)\}Y\left(u\right){\lambda }_{C0}(u,Z)\right]}\hfill \\ \hfill & +\frac{E\left[Q\left(u\right)L\{u,Z,X\left(u\right)\}H(u,Z,X\left(u\right))Y\left(u\right)\right]}{E\left[Q\left(u\right)Q{\left(u\right)}^{T}H\{u,Z,X\left(u\right)\}Y\left(u\right){\lambda }_{C0}(u,Z)\right]},\hfill \end{array}$$

and

$$\Pi (\psi \left(D\right)\mid {\Lambda }_{\alpha })=B_0\int Q\left(u\right)d{M}_C\{u,Z,X\left(u\right)\}.$$ (35)