Synchronizing Self and Object Movement: How Child and Adult Cyclists Intercept Moving Gaps in a Virtual Environment

Abstract

Two experiments examined how 10- and 12-year-old children and adults intercept moving gaps while bicycling in an immersive virtual environment. Participants rode an actual bicycle along a virtual roadway. At 12 test intersections, participants attempted to pass through a gap between 2 moving, car-sized blocks without stopping. The blocks were timed such that it was sometimes necessary for participants to adjust their speed in order to pass through the gap. We manipulated available visual information by presenting the target blocks in isolation in Experiment 1 and in streams of blocks in Experiment 2. In both experiments, adults had more time to spare than did children. Both groups had more time to spare when they were required to slow down than when they were required to speed up. Participants’ behavior revealed a multistage interception strategy that cannot be explained by the use of a monotonic control law such as the constant bearing angle strategy. The General Discussion section focuses on possible sources of changes in perception-action coupling over development and on task-specific constraints that could underlie the observed interception strategy.

Moving the self in relation to other objects is a central problem faced by children and adults alike. We cross traffic-filled roads, walk through crowded malls, and catch fast-moving balls. On the perceptual side, this requires learning to perceive information specifying relevant properties of the environment (e.g., speed, distance, and angle). On the motor side, this requires learning to control relevant aspects of the movement (e.g., posture, balance, and force). But adaptive movement within the environment (e.g., avoiding collisions with people and cars) involves more than just perceiving the relevant information or controlling physical movement: One must also synchronize motor movements with perceptual information. When crossing busy intersections, for example, motor movements must be closely timed to perceptual information that specifies the potential for colliding with oncoming traffic. In this article, we focus on how children and adults synchronize self and object movement in the context of bicycling through moving gaps in a virtual environment.

Children’s Road-Crossing Behavior

One everyday locomotor task that has received a great deal of attention is crossing traffic-filled roads. To successfully navigate through gaps in moving traffic, children and adults alike must coordinate their actions with the movements of vehicles on the roadway. Although most past work has focused on child pedestrians (Barton, Schwebel, & Morrongiello, 2007; Lee, Young, & McLaughlin, 1984; Simpson, Johnson, & Richardson, 2003; te Velde, van der Kamp, Barela, & Savelsbergh, 2005; Young & Lee, 1987), more recent work has examined how child cyclists cross intersections with continuous cross-traffic (Plumert, Kearney, & Cremer, 2004, 2007). Understanding how child cyclists and pedestrians negotiate traffic-filled roads is important because collisions with cars pose a serious health risk to bicyclists and pedestrians (Mehan, Gardner, Smith, & McKenzie, 2008; Rivara & Aitken, 1998). A critical first step in developing programs to prevent such collisions between bicycles and motor vehicles is understanding why such collisions occur.

Studies of pedestrian behavior have examined two broad classes of factors that may lead to errors in children’s road crossing. One of these focuses on cognitive factors such as children’s knowledge of the dangers associated with crossing traffic-filled roads (Rosenbloom, Nemrodov, Ben-Eliyahu, & Eldror, 2008) and children’s understanding of the rules for crossing roads safely (Barton et al., 2007). The second class of factors focuses on the perceptual–motor skills involved in road crossing. These perceptual–motor skills are generally framed in terms of perception of time to contact and timing of gap interception. The standard paradigm for examining children’s road-crossing skills is the “pretend road” task developed by Lee et al. (1984). Studies using this paradigm have generally found that children are less effective at navigating gaps in traffic than are adults (Barton et al., 2007; Lee et al., 1984; Young & Lee, 1987). Moreover, there are clear developmental changes in children’s ability to negotiate traffic-filled roadways, with younger children more likely than older children to make road-crossing errors (Lee et al., 1984).

The role of perceptual–motor skills in road-crossing behavior has also been examined in the context of bicycling across traffic-filled roads. Plumert et al. (2004) developed an immersive, interactive bicycling simulator to examine the gaps that 10- and 12-year-olds and adults accept when bicycling across traffic-filled intersections. In relation to adults, children’s gap choices and road-crossing behavior were less well matched. Children and adults chose the same-size gaps, and yet children ended up with less time to spare between themselves and the approaching car when they cleared the path of the approaching car. Further analyses revealed that in relation to adults, children delayed in getting started, leading to pronounced age differences in the time left to spare between the bicyclist and the approaching car.

An important question these findings raise is, why do children delay initiation of movement in comparison with adults? One possibility is that children have immature movement preparation strategies and do not position their feet on the pedals in such a way that provides maximal acceleration. A second possibility is that children take longer to arrive at “go–no go” decisions than do adults. This may leave them with less time to translate their decision into action. A third possibility is that children have less precise control over the synchronization of self and object movement. As a result, they may delay in initiating movement to allow a greater margin of safety between themselves and the lead vehicle in the gap.

The road-crossing paradigm used by Plumert et al. (2004) required participants to cross through traffic from a full stop. Thus, this paradigm cannot distinguish the degree to which children’s delay in initiation of crossing is due to immature movement preparation strategies, difficulties with go–no go decision making, or allowing for a greater margin of safety. However, if the task is modified such that participants are already in motion when attempting to intercept a preselected gap, the influence of movement preparation capabilities and go–no-go decision making is removed from the equation. Furthermore, by investigating children’s ability to intercept a moving gap when they themselves are already in motion, more basic questions regarding the control of locomotion in performing interceptive actions can be explored.

Controlling Interceptive Actions

Past work on controlling interceptive actions has focused on several kinds of everyday interception problems. These include ball catching, object grasping, and even kissing (Chapman, 1968; Lee, 1998; Sugar, McBeath, & Wang, 2006; Wann, Edgar, & Blair, 1993). Not all interception tasks are alike, however. Interceptive actions can be categorized on the basis of the desired objective of the action. People use different control strategies depending on whether the goal of their movement is to avoid or to make contact with an object (Tresilian, 2005). Road crossing can be conceptualized as a horizontally constrained (people cannot fly) interception task, the objective of which is to intercept the open space between two objects—a space that is defined by the rear bumper of the lead vehicle and the front bumper of the trailing vehicle. Crossing through a moving gap can also be thought of as a coupled avoidance task, in which the objective of the action is to avoid contact with the two vehicles composing the target gap. We prefer the former description of the road-crossing task for two reasons. First, the underlying motive of road crossing is to pass through a region of space on the way to a destination, not to simply avoid two cars in traffic. Second, thinking of road crossing as two coupled avoidance tasks effectively doubles the amount of perceptual processing required to perform the action. Hence, considering the task as a single interceptive action is more parsimonious.

What kinds of strategies might be used to successfully intercept moving gaps? Several compelling theories pertaining to the control of locomotion, such as Lee’s (1976, 1998) tau hypothesis, have shown how individuals could successfully intercept objects in the environment by using optic flow information directly perceivable on the retina. One such established strategy for successfully intercepting an object is to maintain a constant bearing angle with that object. An individual in motion will intercept an object on a convergent trajectory so long as the exocentric bearing angle between the object and the individual’s current heading is held constant. Note that when an individual is constrained to a linear trajectory, the instantaneous heading can be optically specified by the focus of expansion. This technique has long been used by sailors to guide navigation on open seas, but more recently, researchers have investigated whether individuals appear to use their bearing angle in relation to another object as a source of information in guiding other horizontally constrained interceptive actions.

The instantaneous motion of a human in the terrestrial plane can be described by that individual’s velocity and heading, or direction of movement. Individuals can dynamically change both their speed and heading in order to intercept a moving object in an obstacle-free environment. Fajen and Warren (2004, 2007) used a virtual environment to explore the effects of optic flow and other visual variables on how people walk to intercept moving targets in an obstacle-free environment. From this work they have developed a model of steering dynamics, which incorporates the constant bearing angle strategy, in attempting to explain how humans coordinate goal-directed movement. They found that people appear to lead moving targets, walking not to the current position of the target but to a point ahead of the target’s current position. This behavior is consistent with an interception strategy, but not a pursuit strategy, in which people would be expected to walk toward the current position of a target. At this point, however, it is unclear how well the model can account for interception behavior when the direction in which an individual can travel is highly constrained (as in road-crossing situations).

How do people perform interceptive actions in situations in which their heading is tightly constrained? Lenoir, Musch, Janssens, Thiery, and Uyttenhove (1999) used a rail-mounted tricycle to investigate whether participants maintained a constant bearing angle between themselves and a moving target when attempting to intercept (hit) the target. In this study, the target had to be intercepted with an effector. They found that participants appeared to be using a constant bearing angle strategy. Moreover, participants maintained a constant bearing angle for the effector, not for their visual egocenter. In a follow-up study, Lenoir, Musch, Thiery, and Savelsbergh (2002) concluded that people were actually using the first-order derivative (change) of the bearing angle as a control variable to guide their actions. That is, when a participant’s instantaneous trajectory was moving away from what was required to maintain the constant bearing angle, the participant adjusted speed in the direction that would facilitate maintenance of a constant bearing angle. This control strategy is similar to what Yilmaz and Warren (1995) found when investigating whether people could use optically specified information about the rate of change of time to contact (i.e., τ̇; see Lee, 1976) to control braking behavior.

Another possible interception control strategy that could be applicable to the road-crossing scenario is the required velocity model (Bootsma, Fayt, Zaal, & Laurent, 1997). This model proposes that as an individual approaches a target, optically specified information about the discrepancy between the current and required states of the environment–actor system (e.g., approach speed in relation to target movement) is used to modulate the individual’s movement, yielding a successful interception. Chardenon, Montagne, Buekers, and Laurent (2002) tested this theory with a ball interception task in a virtual environment. Participants adjusted their speed as they walked on a treadmill in order to intercept a virtual target ball. The authors concluded that the constant bearing angle theory better fit the observed data than did the required velocity model. Interestingly, the results also suggested that the constant bearing angle strategy only matched the participants’ behavior up until 2 s from contact with the target, at which time a shift in the bearing angle occurred.

Subsequent research using the same apparatus investigated how the initial bearing angle and temporal displacement (±2 s) of the target impacted approach behavior (Chardenon, Montagne, Laurent, & Bootsma, 2005). Changing the point on the participant’s path at which the target was set to converge required participants to adjust their speed in order to successfully intercept the target. Again, they found that participants appeared to use a constant bearing angle strategy up until 2 s from interception. The most interesting results came from the condition in which the initial bearing angle was 75°. When no speed adjustment was required, participants sped up significantly in the first 3 s of the trial, only to have to slow down again in order to successfully intercept the target. When participants were required to speed up to intercept the target, they accelerated rapidly in the first 4 s of the trial, then maintained roughly the same speed until the last 2 s of the trial, at which time they steeply accelerated again. Neither a required velocity nor a constant bearing angle model of control can account for these systematic variations in behavior, particularly at the end of the trial.

In a related line of work, Montagne and colleagues (see Buekers, Montagne, de Rugy, & Laurent, 1999; Camachon, Jacobs, Huet, Buekers, & Montagne, 2007; Montagne, Buekers, Camachon, de Rugy, & Laurent, 2003) have found that when performing a highly constrained interceptive action, participants appear to walk at their preferred speed for the majority of the approach, adjusting their gait within the last few meters of the approach. Montagne et al. (2003) categorized this as a “funnel-like type of control” in which participants make adjustments to their rate of travel only when the constraints of the task warrant, and not earlier on the approach as is implicitly suggested in the constant bearing angle model of control.

Children’s Interception Behavior

Although a good deal of research has examined children’s road-crossing behavior, comparatively little attention has been given to the question of what specific control variables, such as bearing angle, children may be using to guide this kind of interceptive action. Recently, Chohan, Verheul, Van Kampen, Wind, and Savelsbergh (2008) investigated whether 5- to 7-year-old children and 10- to 12-year-old children used a constant bearing angle strategy when intercepting a moving ball with their hands. When the target began moving toward the interception point, participants initiated walking, aiming to arrive at the interception point at the same time as the target. The speed of the moving target was varied between trials, and approach times ranged between 3.5 and 7.5 s. Both the younger and older children deviated significantly from a constant bearing angle while approaching the target, although this deviation was more pronounced for the younger children. The authors suggested that the overall pattern of behavior indicated that both groups of children were attempting to maintain a constant bearing angle, but that immature movement-control skills prevented adherence to this strategy.

The specific nature of these movement-control deficits have only recently been explored in greater detail. Te Velde, van der Kamp, and Savelsbergh (2008) recorded children’s movement while performing a small-scale interception task that was qualitatively similar to a road-crossing task. Children were asked to move a doll across a small-scale “roadway” in between two approaching model cars. Their results indicated that younger children (5- to 7-year-olds) were not able to maneuver the doll as successfully as were older children (10- to 12-year-olds) or adults. This suggests that younger children have more difficulty modulating their velocity in coordination with the velocity of other objects in the environment than do adults. However, because the experimental task was of a different scale from an actual road-crossing task and did not require participants to actually move themselves through traffic, the applicability of these findings to the current research question is unclear.

The Present Investigation

The goal of the present investigation was to further investigate how children and adults time their interceptive actions in the context of a road-crossing task. Ten- and twelve-year-old children and adults rode an actual bicycle through an immersive, interactive virtual environment. The environment consisted of a series of right-angle intersections through which participants were asked to ride. The participants’ task at each intersection was to pass without stopping through a gap between two fast-moving objects (i.e., rectangular blocks the size of a typical car that moved at 35 miles per hour). For each intersection, we also manipulated the initial state of the environment–actor system. Depending on the trial, participants needed to speed up or slow down to successfully intercept the gap. We measured participants’ movement and position in relation to the leading and trailing blocks in the target gap along their approach to the intersection.

Three questions were of interest. First, we wanted to determine whether children’s time to spare (in relation to the rear car of the gap) upon arriving at the point of interception was less than that for adults. This would suggest that time-to-spare deficiencies observed in previous studies were not solely due to issues with poor movement preparation strategies or difficulties in go–no-go decision making. Second, we wanted to see whether participants’ time to spare was dependent on the initial state of the environment–actor system—that is, whether participants needed to speed up or slow down to successfully intercept the gap. Finally, we wanted to examine the behavior of participants along the approach to the intersection to determine whether specific patterns in speed and timing emerged. In particular, we were interested in whether participants were attempting to maintain a constant bearing angle with the gap.

Experiment 1

Method

Participants

Fifty 10- and 12-year-olds and adults participated. There were 9 boys and 6 girls in the 10-year-old group (M = 10 years, 9 months, SD = .14), 10 boys and 6 girls in the 12-year-old group (M = 12 years, 6 months, SD = .10), and 8 men and 11 women in the adult group (M = 19 years, 3 months, SD = 1.27). The children were recruited from a child research participant database maintained by the Department of Psychology at the University of Iowa, and were paid $10 for their participation. Adult participants were recruited from an introductory-level psychology course, and received course credit for their participation.

Apparatus and materials

The study was conducted using a high-fidelity, real-time bicycling simulator (Figure 1). An actual bicycle mounted on a stationary frame was positioned in the middle of three 10-ft-wide by 8-ft-high screens placed at right angles relative to one another, forming a three-walled room. Three Projection Design F1+ projectors were used to rear-project high-resolution graphics onto the screens, providing participants with 270° of nonstereoscopic, immersive visual imagery. The viewpoint of the scene was adjusted for each participant’s eye height. The virtual environment was populated with residential buildings, trees, and other roadside features typical of a small town. Participants rode through the town on a 2.25-km-long, two-lane residential roadway. There were 15 cross-streets that intersected the primary roadway at 150-m intervals. All roadways were 12-m wide, and at a level grade. There was no ambient traffic on the roadway with the participant, and the intersections did not have stop signs or other traffic control devices.

Figure 1.

The bicycling simulator.

The pedals, handlebars, and right-hand brake on the bicycle were all functional, but participants were not required to balance the bicycle because the bicycle mount was rigid. The bicycle was fitted with instruments to record the steering angle of the front wheel and the speed of the rear wheel. These two measures (steering angle and wheel speed) were combined with virtual terrain information to render the graphics corresponding to the bicyclist’s real-time trajectory through the virtual environment. The rear wheel was mated to a friction-drive flywheel. This flywheel was connected to a torque motor, which generated an appropriate dynamic force that took into account rider and bicycle mass and inertia, ground friction, and other physical factors. The computing platform for the simulation environment was a network of six PCs. The underlying software system was a sophisticated real-time ground vehicle simulator developed in-house by the co-investigators. This system supported complex scenarios involving ambient and programmatically controlled traffic (Cremer, Kearney, & Willemsen, 1997; Willemsen, Kearney, & Wang, 2003).

Design and procedure

The experimenter first helped participants don a bicycling helmet and adjust the bike seat height. The experimenter then measured participants’ eye height while they were seated on the bike. The experimenter informed participants that they would be riding through a virtual neighborhood, and instructed them to ride as though they were riding in a similar, real-world neighborhood.

The experiment began with a brief warm-up session designed to familiarize participants with the characteristics of the bicycle and the virtual environment. During the familiarization session, participants were instructed to notify the experimenter if they experienced any simulator sickness. The familiarization session provided participants with the opportunity to learn how to steer, pedal, and stop the bicycle.

Following the warm-up session, children and adults participated in an approximately 10-min test session in which they crossed 13 intersections. Prior to reaching the first test intersection, the experimenter asked participants to stop. The experimenter then explained that their task was to ride through the gap between two moving red-colored, car-sized blocks at each of the intersections. (We used blocks rather than cars to make the task somewhat more abstract, attempting to avoid teaching children about intercepting tight gaps in real-world traffic.) Participants were told not to stop at the intersections. When the experimenter was satisfied that participants understood the task, they were asked to begin riding toward the first intersection with moving blocks.

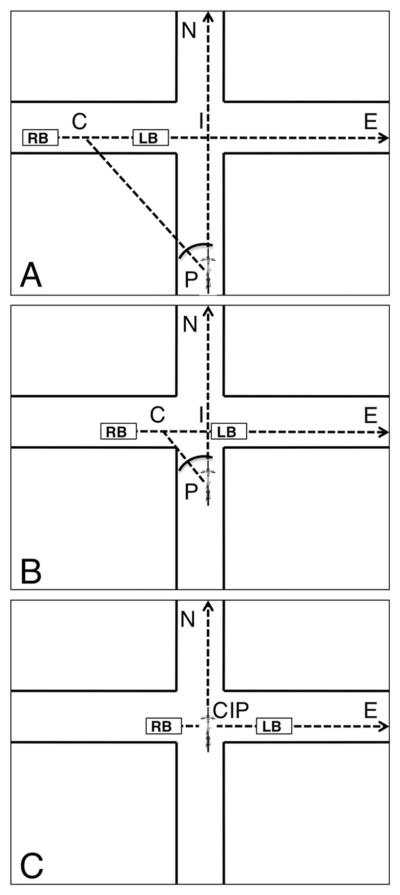
At each intersection, there were two red blocks placed in the near lane of the cross-street on the participant’s left-hand side. The blocks were 7.8 m long, 2 m wide, and 2 m high—roughly the size of a typical sedan. The front of the lead block was positioned 180 m from the intersection, and the gap between the two blocks was approximately 55 m. The projected time the cyclist would arrive at the intersection was used to trigger the blocks to begin moving. The blocks traveled toward the intersection at 15.646 m/s (35 miles per hour [mph]). In temporal terms, this meant that once the blocks were triggered, it would take 12 s for the rear of the lead block to arrive at the intersection (i.e., the crossing line), and another 3.5 s for the front of the trailing block to arrive. The participants’ task was to adjust their speed such that they would arrive at the intersection in time to safely pass through the 3.5-s gap between the two blocks (i.e., intercept the gap). A visual representation of the task can be seen in Figure 2.

Figure 2.

This diagram of the task explains how holding the bearing angle with the gap at a constant value can yield a successful interception. The lead and rear blocks (LB, RB) move toward point E at a constant speed, while the participant (P) rides at a variable speed toward point N. The paths of the blocks and the participant intersect at point I, which is the spatial point of interception. Point C represents the point of constant bearing in the gap, which is also the projected point of interception in relation to the blocks. By holding angle CPI at a constant value, the participant will successfully pass though the gap at the point of constant bearing.

The timing of the trigger was based on an estimate of the participant’s time to arrival at that intersection. On a given trial, the participant’s average speed was measured over a 20-m segment starting 120 m away from the intersection. The simulation then calculated the participant’s likely time to arrival, assuming that the participant maintained this speed. In a given trial, the blocks were timed to begin moving so that if participants maintained their constant speed, they would arrive at the intersection either early in the target gap or late in the target gap. This meant that it was sometimes necessary for participants to speed up or slow down in order to safely pass through the gap. Because of individual variation in riding speed, the overall distribution of projected arrivals was centered on the middle of the gap (1.75 s after the lead block cleared the intersection).

The first intersection served as a practice intersection for the interception task. After the practice intersection, participants rode through six test intersections, after which the experimenter asked participants to come to stop. Participants were given a 2-min rest period before the next set of intersections. After the break, participants rode through an empty intersection (with no moving blocks) before riding through the next set of six test intersections. After participants finished riding through all of the intersections, the experimenter stopped the scenario. The participant was then debriefed about the experiment and thanked for participating.

Results

Two aspects of the bicyclists’ interception behavior were analyzed. The first was the participants’ time to spare when arriving at the point of interception between the path of the bicyclist and the center of the path of the moving blocks. In these analyses, we examined both the mean time to spare as well as the variability of an individual’s time to spare. These measures provide information about performance and consistency. The second aspect of interception performance was participants’ behavior along the approach to the intersection. To this end, we generated plots of each participant’s speed and instantaneous projected time to spare as a function of the participant’s actual time until arrival at the intersection.

There were two independent variables in the analyses below. The first variable, participant age, was a between-subjects variable, and the second variable, trial type, was a within-subjects variable. Each trial was classified as either projected early arrival or projected late arrival. Trials were assigned to these categories on the basis of the participant’s projected time to spare at the moment when the blocks began to move toward the intersection. The computation of the projected time to spare was based on the participant’s speed and distance from the intersection and is explained in greater detail later in this section. If in a given trial the participant was expected to arrive at the intersection prior to the middle of the gap, the trial was categorized as projected early arrival. If the participant was expected to arrive after the middle of the gap, the trial was categorized as projected late arrival. Because the trial classification metric was based in part on the speed of the participants, there was not always an equal number of each type of trial for each participant. However, the overall impact of this variability was negligible: The mean number of projected late-arrival trials for each participant was 7 (SD = 2.43), and the mean number of projected early-arrival trials was 5 (SD = 2.43).

In extreme cases in which the participant missed the gap by more than 1.75 s (half the size of the gap) in either direction, the trial was excluded from all analyses. For 10- and 12-year-olds, 8 of 372 individual trials were excluded, and for adults, 1 out of 228 trials was excluded.

Time-to-spare at the point of interception

Although it is possible to pass through at any point in the gap, there are some ways to cross that are safer than others. If the bicyclist crosses early in the gap (closer to the lead block), this results in a larger safety margin than if the bicyclist crosses late in the gap (closer to the trailing block.) Time to spare was defined as the temporal difference between the time at which the bicyclist crossed the interception point and the time at which the rear block of the target gap arrived at the interception point (i.e., the gap closed). Higher values of time to spare are generally preferable, because they provide participants with a greater safety margin within which a correction can be made should participants miscalculate their passage through the gap. However, if a participant’s time to spare on a given trial is too large, the participant risks colliding with the lead vehicle. We also looked at the variability of participants’ time to spare as a measure of the consistency with which they performed the task. Given that children have relatively less experience than do adults in performing interceptive actions in traffic, they are less likely to have developed a consistent strategy that can be reliably used in a gap-interception scenario.

Hits

If a participant failed to intercept the gap (collided with one of the blocks), the trial was categorized as a hit. In the 591 trials that were not excluded because of the participant missing the gap by more than 1.75 s, 10- and 12-year-olds were collectively hit 22 times, whereas no adults were hit.

Mean time-to-spare

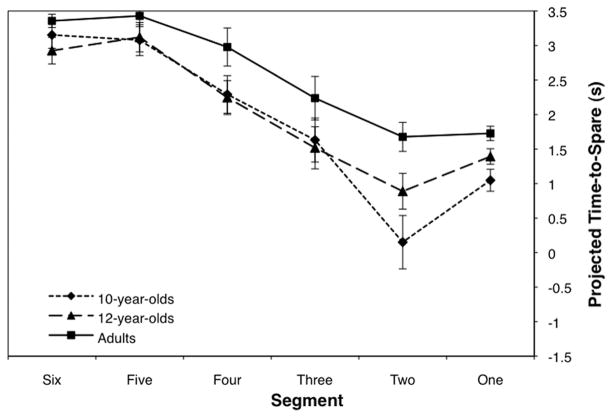
For each participant, mean time-to-spare scores were calculated for projected early-arrival and projected late-arrival trials. Mean time-to-spare scores were entered into an Age (10 years vs. 12 years vs. adults) × Trial Type (projected early vs. late arrival) repeated-measures analysis of variance (ANOVA). This analysis revealed significant main effects of age, F(2, 47) = 3.38, p < .05, ${\eta }_{\text{p}}^2=0.13$, and of trial type, F(1, 47) = 181.29, p < .001, ${\eta }_{\text{p}}^2=0.79$. There were no significant interactions. Post hoc analyses using Fisher’s Protected Least Significant Distance indicated that 10-year-olds (M = 1.9 s, SD = .74) and 12-year-olds (M = 1.8 s, SD = .71) had significantly less time to spare than did adults (M = 2.2 s, SD = .50). In addition, participants had more time to spare in projected early-arrival trials (M = 2.4 s, SD = .57) than in projected late-arrival trials (M = 1.5 s, SD = .44), indicating that they did not completely make up for lost time in the projected late-arrival trials.

Variability of time-to-spare

To examine variability, we calculated each participant’s standard deviation of time to spare for the projected early-arrival and projected late-arrival trials. Variability scores were entered into an Age (3) × Trial Type (2) repeated-measures ANOVA. This analysis revealed significant main effects of age, F(2, 47) = 4.03, p < .05, ${\eta }_{\text{p}}^2=0.15$, and of trial type, F(2, 47) = 20.58, p < .001, ${\eta }_{\text{p}}^2=0.30$. There were no significant interactions. Both 10-year-olds (M = .49, SD =.31) and 12-year-olds (M =.46, SD =.30) had higher variability scores than did adults (M =.31, SD =.15). In addition, there was more variability in projected late-arrival trials (M =.50, SD =.29) than in projected early- arrival trials (M =.33, SD =.21).

Approach profiles—mean speed

According to the constant bearing angle theory, if an individual in motion maintains a constant visual angle between the focus of expansion and another object in the environment, the individual will intercept that object. When the object (or gap) to be intercepted is moving at a constant speed and the object and individual are moving in straight lines, then the individual must move at a constant speed in order to maintain a constant bearing angle. In the current study, the two blocks moved toward the intersection at a constant speed on a straight road as the rider cycled on an intersecting straight road. Under these conditions, there is a single speed at which an individual must travel so that a particular point on or between the two blocks will remain at a constant bearing. As the observer’s speed increases or decreases, the point of constant bearing shifts in a predictable way—moving closer to the point of interception on the observer’s path as speed increases and further away as speed decreases. This regular relationship is the basis for a control strategy that adjusts speed to shift the point of constant bearing to the desired location (i.e., the desired point of interception) and then maintains a constant speed while approaching the intersection. If riders in our experiment were using such a strategy, then their speed profiles should indicate a period of speed adjustment followed by a period of relatively constant speed. This was evaluated by plotting participants’ mean speed over their actual (not projected) temporal distance from the point of interception.

The analysis of mean speed focused on the participants’ approach to each intersection between the time at which the blocks began moving toward the intersection and the time at which the participant arrived at the interception point (i.e., a roughly 12-s period). For each individual and trial, the speed data were segmented into 1-s intervals, counting backward from the point at which the participant arrived at the interception point. The mean speed in each of these intervals was calculated. This procedure was similar to the “binning” procedure used by Chardenon et al. (2005) to reduce noise in their data. Once the mean speeds for each trial and interval had been calculated, the participant’s approaches were grouped into the two trial types (projected early and projected late arrival). Then for each interval, the participant’s mean speed for all the approaches in each trial type was calculated.

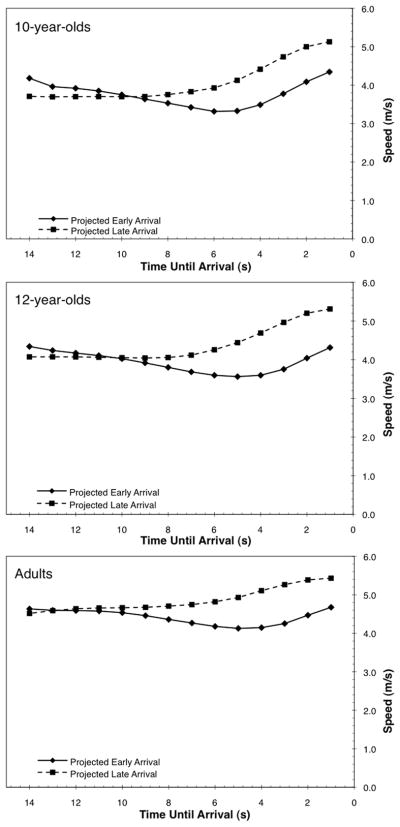
For each trial type and age group, these individual segmented mean speed data were then averaged across all participants. This produced a total of six profiles of overall mean speed for each 1-s segment on the approach—one for each trial type and age group. These aggregate profiles were then plotted and can be seen in Figure 3. The overall pattern of results was very similar for all three age groups. Not surprisingly, the main difference between the age groups was the overall mean speed—on average, adults traveled faster than did children. In trials in which participants were projected to arrive late at the intersection, the mean approach profiles indicate a gradual acceleration as participants closed on the intersection. The slope of this acceleration increased slightly around 5 s prior to arrival. When they were projected to arrive early at the intersection, participants on average slowed down for a period as they approached. Then, at around 5 s prior to arrival, the mean approach profiles for each age group showed a strong acceleration that continued through the intersection.

Figure 3.

Speed profiles on the approach to the intersection by projected arrival time for 10-year-olds, 12-year-olds, and adults.

To analyze how speeds changed during the approach to the intersection, we divided the mean speed data for each participant into four 4-s segments, starting from the point of interception and working backward. We chose this interval because it provided for reasonably fine-grained analyses of changes occurring during the approach to the intersection. The mean speed within each segment was then calculated for each participant. These segmented data were entered into two repeated-measures ANOVAs—one for each trial type—with age as the between-subjects variable and segment as the within-subjects variable. The projected early-arrival trials were examined separately from the projected late-arrival trials, because the nature of the task (need to slow down vs. need to speed up) was different for each trial type.

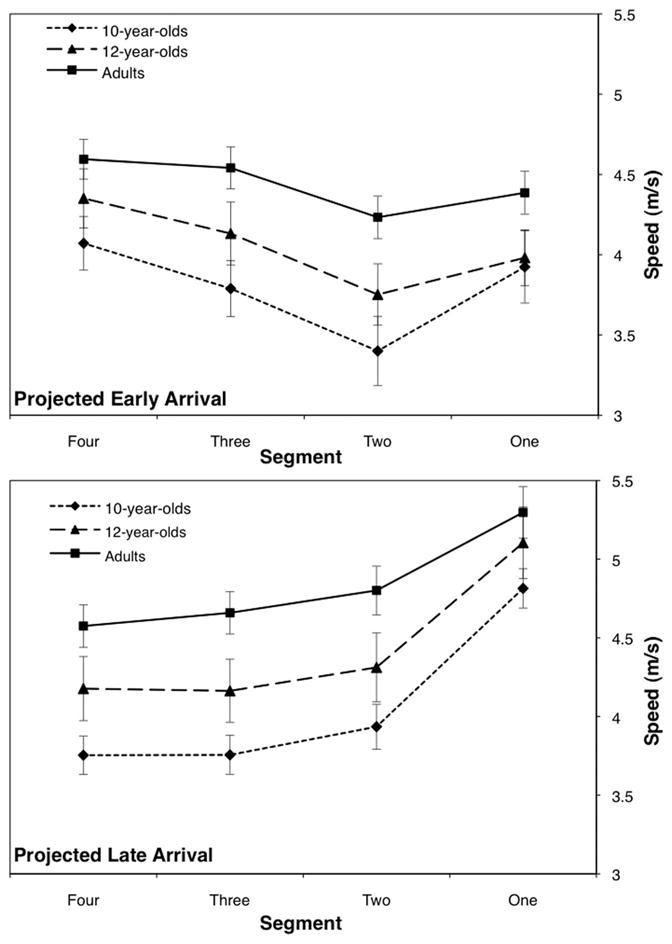
The analysis of the projected early-arrival trials revealed a significant main effect of age, F(2, 47) = 4.08, p < .05, ${\eta }_{\text{p}}^2=0.15$. Over the entire approach, 10-year-olds (M = 3.80 m/s, SD =.79) were significantly slower than were adults (M = 4.44 m/s, SD =.58), but 12-year-olds (M = 4.05 m/s, SD =.76) did not differ significantly from either of the other age groups. More important, there was significant effect of segment, F(3, 141) = 50.76, p <.001, ${\eta }_{\text{p}}^2=0.52$, and a significant Age × Segment interaction, F(6, 141) = 3.34, p < .01, ${\eta }_{\text{p}}^2=0.12$. Follow-up tests of the segment effect indicated that overall the mean speed in Segment 2 was slower than that in all the other segments and that the mean speed in Segment 4 was faster than that in any of the other segments. As is seen in the top half of Figure 4, all the age groups showed this general pattern of decelerating up until the second segment (5–8 s from the intersection), at which point they began accelerating (10-year-olds accelerated more than did 12-year-olds or adults).

Figure 4.

Profiles of mean speed in each segment for projected early-arrival trials and projected late-arrival trials by age group.

The analysis of the projected late-arrival trials revealed a significant main effect of age, F(2, 47) = 5.84, p <.01, ${\eta }_{\text{p}}^2=0.20$. Again, 10-year-olds (M = 4.07 m/s, SD =.66) were significantly slower than were adults (M = 4.83 m/s, SD = 0.69). The mean speed for 12-year-olds (M = 4.44 m/s, SD =.92) was not significantly different from that of either of the other age groups. There was also a significant effect of segment, F(3, 141) = 175.66, p < .001, ${\eta }_{\text{p}}^2=0.79$, as well as an Age × Segment interaction, F(6, 141) = 3.45, p < .01, ${\eta }_{\text{p}}^2=0.13$. Follow-up tests of the segment effect revealed no significant difference between the mean speeds in Segment 3 and Segment 4. However, for Segments 1–3, the mean speed in each segment was significantly faster than that in the segment that preceded it. As can be seen in the bottom half of Figure 4, all age groups showed a sharp increase in speed during the final segment of the approach, but adults also exhibited a significant increase in speed just prior to this final segment.

Approach profiles—mean projected time-to-spare

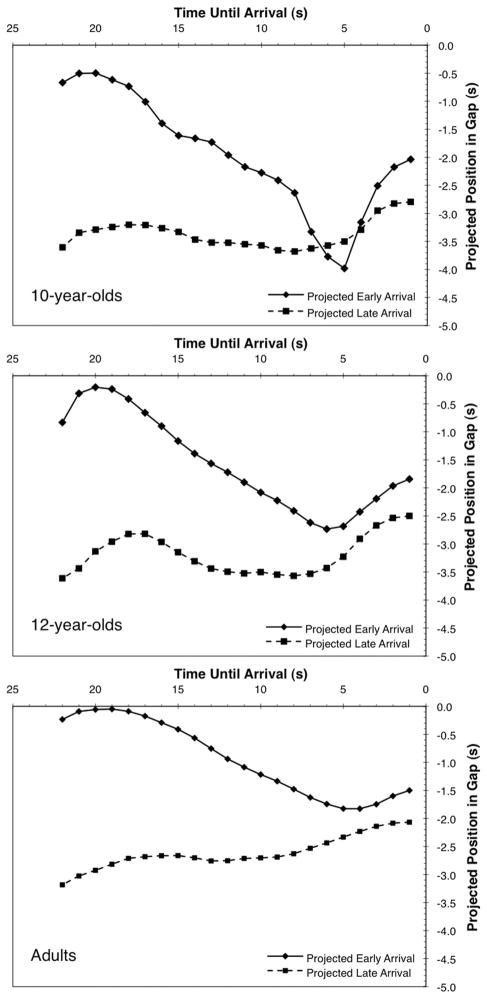
Participants could cross anywhere within the 3.5-s target gap and achieve a successful outcome. Because there was a range of potential crossing positions within the gap, that meant that there was a range of values for any given control variable (such as bearing angle) that would allow for successful completion of the action. The present study was designed such that on the majority of trials, participants would need to make some adjustment to their speed in order to successfully intercept the gap. From the perspective of the constant bearing angle strategy, the objective would be to adjust speed to place the point of constant bearing at the desired position on the target, then maintain this speed for the rest of the approach, thereby maintaining a constant bearing angle to the moving target. We cannot directly measure the control strategy used by riders. However, we can examine how the point of constant bearing shifted during the riders’ approach to the intersection. This point is also the projected point of interception in the gap, which is coincident with the projected time to spare at arrival, based on the assumption that cyclists maintain that particular speed through the rest of their ride to the intersection.

To compute the projected time to spare (temporal point of interception in the gap), we first calculated the participants’ projected time to arrival (TTA_p) at the intersection for each data point along the approach by dividing the participant’s current distance from the intersection (D_p) by the participant’s current speed (V_p):

$${\mathit{TTA}}_p=\frac{D_p}{V_p}.$$

This projected time-to-arrival value was then subtracted from the time to arrival of the rear block in the target gap (TTA_b). The difference between these two times to arrival gives the projected time to spare (i.e., how many seconds ahead of the rear block the participant would arrive at the intersection if the participant were to maintain a constant speed for the remainder of the approach):

$$\text{Projected}\text{Time}-\text{to}-\text{Spare}(\text{s})=({\mathit{TTA}}_b-{\mathit{TTA}}_p).$$

This instantaneous projected time to spare was calculated for each trial between the time at which the blocks began moving and the time the participant arrived at the intersection—the same portion of the approach for which the mean speed data were analyzed. This measure was similar to the current arrival condition variable described by Montagne et al. (2003). The projected time-to-spare data for each participant were averaged and divided into 1-s intervals by using the same procedure as was used to calculate the speed data. Recall that the projected time to spare is the temporal equivalent of the projected position in the gap at the time of interception, which is also equivalent to the instantaneous point of constant bearing (the point that will remain at a constant bearing angle if the rider maintains constant speed).

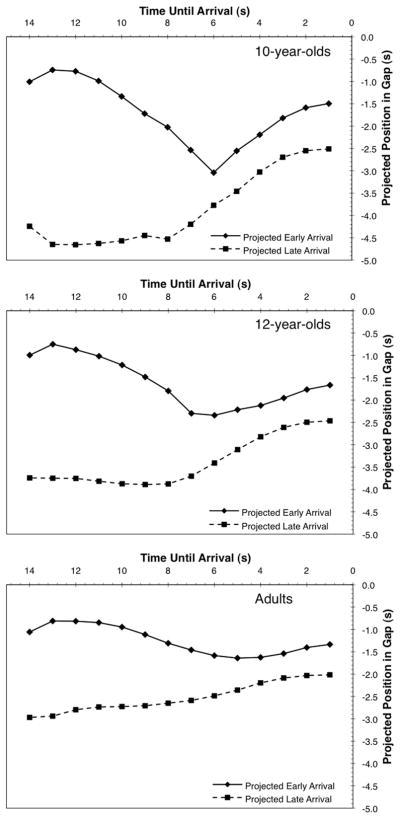
For each trial type and age group, these individual segmented mean projected time-to-spare data were then averaged across all participants. This produced a total of six profiles of overall mean projected times to spare for each 1-s segment on the approach—one for each trial type and age group. These aggregate profiles were then plotted, and can be seen in Figure 5. For all age groups, there appear to be distinct differences in the pattern of behavior along the approach depending on the initial projected time to spare. In trials during which participants were expected to arrive early in the gap, they initially (and appropriately) reduced their speed such that their projected time to spare was also reduced. This reduction in projected time to spare continued until around 5–6 s away from the intersection, at which time, participants initiated a pronounced acceleration that increased their projected time to spare, shifting their point of interception toward the front of the gap. In trials in which participants were expected to arrive late, they initially (and appropriately) gradually increased their speed, increasing their projected time to spare. However, as was seen in the projected early-arrival trials, at 5–6 s away from the intersection, participants’ acceleration again increased, thereby further increasing their projected time to spare. The same overall pattern of behavior for both trial types was observed across all the age groups. The most notable difference between age groups was the magnitude of the adjustments in arrival position. The adjustments of the 12-year-olds were more dramatic than were those of the adults, whereas the 10-year-olds’ shifts in arrival position were even more dramatic than were those of the 12-year-olds.

Figure 5.

Mean projected time to spare on the approach to the intersection by trial type for 10-year-olds, 12-year-olds, and adults.

The projected-time-to spare data were segmented and analyzed in the same manner as were the speed data above. The analysis of the projected early-arrival trials revealed a significant main effect of segment, F(3, 141) = 46.37, p < .001, ${\eta }_{\text{p}}^2=0.50$, as well as a significant Age × Segment interaction, F(6, 141) = 3.11, p < .01, ${\eta }_{\text{p}}^2=0.12$. While approaching the intersection, participants progressively decreased their projected time to spare, shifting their projected point of interception in the gap toward the rear of the gap as they moved toward the intersection, and then increased their projected time to spare in the final segment (in the last 5 s of the approach). As is seen in Figure 6, all the age groups showed this general pattern, although the shifts between segments were more pronounced for the children than for the adults.

Figure 6.

Profiles of mean projected time to spare in each segment for projected early arrival trials by age.

The analysis of the projected late-arrival trials revealed significant main effects of age, F(2, 47) = 8.88, p < .001, ${\eta }_{\text{p}}^2=0.27$, and of segment, F(3, 141) = 27.60, p < .001, ${\eta }_{\text{p}}^2=0.37$. Over the entire approach, both 10-year-olds (M = −.32 s, SD = 1.85) and 12-year-olds (M =.23 s, SD =.86) were expected to arrive at the intersection later in the gap than were the adults (M =.93 s, SD =.55). Post hoc tests of the segment effect showed that in the projected late-arrival trials, participants progressively increased their projected time to spare as they approached the intersection.

Discussion

The results of this experiment clearly show that children timed their interceptive actions less well than did adults. As in previous work (Plumert et al., 2004), both 10- and 12-year-olds had less time to spare when they intercepted the blocks than did adults. The amount of time to spare across intersections was also more variable for children than for adults. These results show that children’s difficulty with timing their interceptive actions extends beyond situations in which they must synchronize self and object movement from a dead stop, to situations in which they must do so while remaining in motion.

The overall patterns of speed along the approach in the two projected arrival trial types provide a more fine-grained picture of the age differences in time to spare outlined above. In the projected early-arrival trials, children slowed down more than was necessary to successfully cross the gap, and then accelerated in the last 5 s of the approach. Adults did this as well, although their overall fluctuation in speed was smaller. In the projected late-arrival trials, both children and adults increased their speed over the course of the approach, but children were not able to catch up to the gap as effectively as adults were. Together, these results suggest that the ability to finely tune motor movements with visual information in complex interception tasks is undergoing developmental change between late childhood and adulthood.

The pattern of participant behavior along the approach indicates that rather than making immediate initial corrections and then maintaining a projected time to spare, participants make pronounced corrections to their projected time to spare along the entire approach. Of particular interest was the tendency for participants in early-arrival trials to overcorrect for their initial speed, requiring them to accelerate sharply in the last few seconds of the approach. Because the projected time to spare can be mapped to the point of constant bearing angle, this pattern of behavior is not consistent with what would be expected if participants were attempting to maintain a constant bearing angle over the duration of the approach. It is, however, reminiscent of the funnel-like pattern of behavior described by Buekers et al. (1999), in which participants did not correct for discrepancies in the environment–actor system until the last few seconds of the approach.

It is also important to note that in the projected late-arrival trials, even adults arrived later in the gap than in the projected early-arrival trials. Nonetheless, adults still crossed with a safe tolerance in time to spare in the projected late-arrival trials. However, the systematic delay raises the question of why adults did not adjust their position in the gap to fully compensate for the initial difference in projected time to spare. Other studies have shown that adults are quite good at adjusting their actions to intercept moving objects (e.g., Chardenon et al., 2005; Fajen & Warren, 2004). In our task the lead block was positioned 180 m from the intersection. This meant that participants had to track the movement of the blocks over a long distance. Gauging the velocity of objects at long distances is notoriously difficult (Connelly, Conaglen, Parsonson, & Isler, 1998). Thus, even adults may have had difficulty perceiving that the gap would arrive ahead of them until they were relatively late into the approach. The two blocks also presented a relatively small target for judging the change in bearing angle over time. This may have made it difficult to determine how to adjust speed such that the bearing angle of the gap remained constant.

In Experiment 2, we examined whether performance was improved by embedding the gap in a longer stream of traffic. The target gap was defined by two red blocks surrounded by a series of yellow blocks traveling at the same speed as the red blocks. The yellow blocks were designed to provide additional sources of optic-flow information about the movement of the target blocks, and an enhanced context for judging the point of constant bearing across the train of blocks. Because the train of blocks would arrive at the point of interception (closer to the cyclist) before the target gap, we thought that they might provide more salient visual cues about the arrival time of the target gap. This additional information could simplify the task of maintaining a speed that would keep the point of constant bearing at the desired interception point.

Experiment 2

Method

Participants

Sixty-five 10- and 12-year-olds and adults participated. There were 10 boys and 11 girls in the 10-year-old group (M = 10 years, 8 months, SD =.47), 8 boys and 14 girls in the 12-year-old group (M = 12 years, 7 months, SD =.23), and 11 men and 11 women in the adult group (M = 19 years, 9 months, SD = 1.38). Participants were recruited in the same manner as in Experiment 1, and received the same compensation for their participation.

Design and procedure

The same apparatus and experimental procedure were used for Experiment 2, with the exception of the number and location of the moving blocks. At each test intersection, there was a train of 14 blocks placed in the near lane of the cross-street on the participant’s left-hand side. The front of the lead block was positioned 165 m from the intersection. The blocks were the same size as those in Experiment 1. The sequence of blocks consisted of nine yellow blocks, two red blocks, and then three yellow blocks. The red blocks were used to define the target gap, and were spaced 55 m (3.5 s) apart. All of the other blocks were spaced 7.8 m (0.5 s) apart.

When participants bicycled past a trigger point on the roadway, the blocks began moving toward the intersection in unison at 15.646 m/s (35 mph.) In temporal terms, this meant that once the blocks were triggered, it would take 20 s for the rear of the lead block of the target gap to arrive at the intersection, and another 3.5 s for the front of the trailing block of the target gap to arrive (i.e., for the gap to close). Again, the participants’ task was to adjust their speed such that they would arrive at the intersection in time to safely pass through the 3.5-s target gap within the train of blocks. As in Experiment 1, the blocks were programmed to begin moving at a point on the road so that if participants maintained a constant speed, they would either arrive before the center of the target gap (which was 1.75 s after the first block cleared the intersection), or after the center of the target gap.

Results

Time-to-spare at the point of interception

The bicyclists’ mean and variable time to spare were analyzed in the same manner as in Experiment 1. The mean number of projected late-arrival trials for each participant was 5 (SD = 1.58), and the mean number of projected early-arrival trials was 7 (SD = 1.58). As in Experiment 1, we excluded trials in which participants missed the gap by more than 1.75 s. We excluded 12 of 516 individual trials for 10-and 12-year-olds and 2 out of 264 trials for adults. Out of the remaining trials included in the analyses, 10- and 12-year-olds were collectively hit 24 times, whereas there was only one trial in which an adult was hit.

Mean time to spare

This analysis revealed significant main effects of age, F(2, 62) = 3.97, p < .05, ${\eta }_{\text{p}}^2=0.11$, and of trial type, F(1, 62) = 161.38, p < .001, ${\eta }_{\text{p}}^2=0.72$. Ten-year-olds (M = 1.5 s, SD = 0.68) had significantly less time to spare than did adults (M = 1.9 s, SD =.57). There were no significant differences between the 12-year-olds (M = 1.7 s, SD =.55) and the other age groups. As in Experiment 1, participants had more time to spare in projected early-arrival trials (M = 2.1 s, SD =.47) than in projected late-arrival trials (M = 1.4 s, SD =.54).

Variability of time to spare

There were again significant main effects of age, F(2, 62) = 13.76, p < .001, ${\eta }_{\text{p}}^2=0.31$, and of trial type, F(1, 62) = 15.59, p < .01, ${\eta }_{\text{p}}^2=0.20$. Ten-year-olds (M = 0.66, SD =.31) had significantly higher standard deviation scores than did 12-year-olds (M =.51, SD =.25). Both groups of children had significantly higher standard deviation scores than did adults (M =.36, SD =.14). Additionally, there was more variability in projected late-arrival trials (M =.58, SD =.28) than in projected early-arrival trials (M =.44, SD =.24).

Approach profiles—mean speed

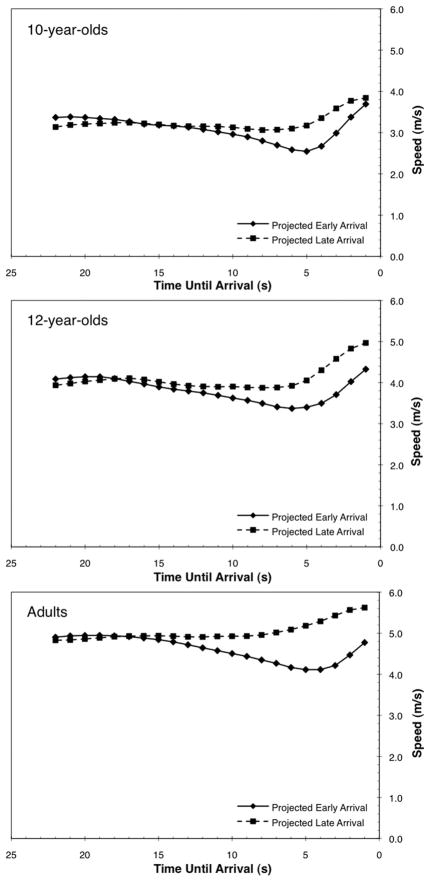
For each trial type and age group, the mean segmented speed data were calculated using the same procedures as in Experiment 1. The plots of these aggregate approach profiles are provided in Figure 7. Again, the overall mean speed for adults was higher than that for the other age groups. In trials in which participants were projected to arrive at the intersection late, participants maintained a relatively constant speed up until around 4–6 s away from the intersection. At this point there was a significant acceleration, which continued for the duration of the approach. In the projected early-arrival trials, participants in all age groups decelerated gradually until around 4–6 s away from the intersection, at which point there was a sharp acceleration that continued for the duration of the approach.

Figure 7.

Speed profiles on the approach to the intersection by trial type for 10-year-olds, 12-year-olds, and adults.

The data were processed the same way as in the first experiment, except this time there were six 4-s segments to allow for the longer time that the blocks were in motion. These segmented data were entered into separate repeated-measures ANOVAs for each trial type with age as the between-subjects variable, and segment as the within-subjects variable.

For the projected early-arrival trials, there were significant main effects of age, F(2, 62) = 19.07, p <.001, ${\eta }_{\text{p}}^2=0.38$, and of segment, F(5, 310) = 57.96, p < .001, ${\eta }_{\text{p}}^2=0.48$. Ten-year-olds (M = 3.7 m/s, SD =.63) and 12-year-olds (M = 3.8 m/s, SD =.63) rode more slowly than did adults (M = 4.6 m/s, SD =.62) over the course of the approach. In addition, the mean speeds in each segment were significantly different from one another. Participants progressively slowed down in each segment as they approached the intersection until around 5 s from arrival, at which time they accelerated.

For the projected late-arrival trials, there were significant main effects of age, F(2, 62) = 23.54, p <.001, ${\eta }_{\text{p}}^2=0.43$, and of segment, F(5, 310) = 86.90, p < .001, ${\eta }_{\text{p}}^2=0.58$. As was the case in the projected early-arrival trials, 10-year-olds (M = 4.02 m/s, SD = .54) and 12-year-olds (M = 4.08 m/s, SD =.62) were slower than were adults (M = 4.94 m/s, SD =.57) over the course of the approach. Additionally, for all age groups, the mean speed in the final segment was significantly faster than they were in the other segments.

Approach profiles—mean projected time-to-spare

For each trial type and age group, the mean projected time-to-spare data were calculated using the same procedures as in Experiment 1. The plots of these aggregate approach profiles are provided in Figure 8. Again, in projected early-arrival trials, participants slowed down more than was necessary, then accelerated sharply at 4–6 s away from the intersection, increasing their projected time to spare. In projected late-arrival trials, participants accelerated early on, increasing their projected time to spare. Then, their projected time to spare held steady (or even decreased slightly) until around 4–6 s away from the intersection, at which time they accelerated again, shifting their projected point of interception forward in the gap. As was seen in Experiment 1, children’s adjustments in temporal position were again of a greater magnitude than those of adults.

Figure 8.

Mean projected time to spare on the approach to the intersection by trial type for 10-year-olds, 12-year-olds, and adults.

The analysis of the projected early-arrival trials revealed a significant main effect of age, F(2, 62) = 4.53, p <.05, ${\eta }_{\text{p}}^2=0.13$. Ten-year-olds (M = 1.89 s, SD = 1.63) and 12-year-olds (M = 2.01 s, SD = 1.34) were expected to arrive at the intersection later than were adults (M = 2.57 s, SD = 1.21). There was also a significant main effect of segment, F(5, 310) = 81.63, p < .001, ${\eta }_{\text{p}}^2=0.57$, as well as an Age × Segment interaction, F(10, 310) = 1.93, p < .05, ${\eta }_{\text{p}}^2=0.06$. Post hoc tests of the segment effect indicated that the projected time to spare in each segment was significantly different from the projected time to spare in every other segment, with the exception of Segments 5 and 6. However, as is shown in Figure 9, adults’ projected time to spare leveled off toward the end of the approach.

Figure 9.

Profiles of mean projected time to spare in each segment for projected early arrival trials by age.

The analysis of the projected late-arrival trials revealed significant main effects of age, F(2, 62) = 3.28, p < .05, ${\eta }_{\text{p}}^2=0.10$, and segment, F(5, 310) = 17.17, p < .001, ${\eta }_{\text{p}}^2=0.22$. Ten-year-olds (M =.16 s, SD = 1.03) were projected to arrive later in the gap than were adults (M =.70 s, SD =.80), but the mean projected time to spare for 12-year-olds (M =.29 s, SD =.91) was not significantly different from either of the other age groups. Post hoc tests of the segment effect indicated that participants progressively increased their projected time to spare across the segments. Thus, the mean projected time to spare in Segment 6 was later in the gap than that in Segments 4 and 5. In addition, the mean projected time to spare in Segment 5 was later than that in Segments 2 and 3. Finally, in Segment 1, participants were projected to arrive earlier in the gap than in any of the other segments.

Discussion

The results of this experiment largely replicated the findings of Experiment 1. Even with the supplemental optic flow information provided by the stream of blocks, and more time available for viewing the target gap, 10-year-olds (though not 12-year-olds) had less time to spare at the point of interception than did adults, and both groups of children exhibited more variability in their performance than did adults. An examination of the approach profiles also reveals a pattern of behavior that was similar to that observed in the first experiment. Most notably, in trials during which participants were initially projected to arrive early to the intersection, all age groups showed a pattern of slowing down until approximately 4–6 s from the intersection, at which point there was a significant increase in their speed.

The results of this experiment again showed that, rather than making an immediate correction to compensate for being ahead of or behind the gap, participants were making continuous adjustments to their projected time to spare over the entirety of the approach. This pattern of behavior—in particular the marked acceleration in the last 4–6 s of the approach—is inconsistent with an attempt to maintain a constant bearing angle for the entirety of the approach. The implications of this are further addressed below.

General Discussion

The current investigation set out to answer three primary questions about how children and adults coordinate interceptive actions in the context of a road-crossing task. The first was whether children had less time to spare than did adults when gap selection and movement initiation were not factors. We found that children did in fact have less time to spare than did adults when they intercepted the gap between the moving blocks. Children also exhibited significantly more variability in the amount of time they had to spare than did adults. These findings parallel those obtained by Plumert et al. (2004), even though the interception task in the current investigation did not involve initiating movement from a stop. Additionally, we found that children’s approach profiles were more volatile than were those of the adults, with more pronounced corrections in speed and projected time to spare. In summary, although the patterns of interceptive actions were similar in children and adults, children’s interceptive actions were less finely tuned than were those of adults.

The fact that children had less time to spare than did adults even though they were not required to come to a stop suggests that children’s problems with road crossing are not solely the product of issues with poor movement preparation strategies or difficulties in go–no-go decision making. Rather, these results indicate that 10- and 12-year-old children are not as skilled as are adults at synchronizing self and object movement. This conclusion is further supported by the fact that children exhibited more variability in time to spare across intersections and a greater tendency to overcorrect during the approach than did adults. This tendency to overcorrect suggests that although children appear to be aware of the need to either accelerate or decelerate at a given moment, they have a diminished ability to produce the amount of correction that is necessary.

What might underlie these differences between children and adults? One factor might be differences between children and adults in their ability to perceive distance and velocity, particularly the higher velocities used in the present investigation (i.e., 35 mph). Other work has shown that the judgments of safe vehicle distances dropped in accuracy quite dramatically for car speeds of 35 mph and above, particularly for children (Connelly et al., 1998). Although adults also have difficulty judging speed when vehicles are moving at high speeds, their experience with judging vehicle speeds in the context of driving may have helped them in our interception task. A second factor might be differences between children and adults in their ability to steer the bike at the same time that they are watching the target blocks. Dividing one’s attention between the task of steering the bike and the task of regulating speed to pass through the oncoming gap might be challenging for children, particularly over long distances (Dunbar, Hill, & Lewis, 2001). Anecdotally, we often observe that child participants veer toward the right as they watch cars on the left, suggesting that they have more difficulty than do adults with attending to two tasks at the same time. A third factor may be a difference in the perception of what is a safe clearance with the lead vehicle in the gap. Children may aim to pass through a point further behind the lead vehicle to reduce the likelihood of a collision with the lead vehicle. This may reflect a sense of greater cautiousness to account for their lower ability to control the precise timing of their actions with respect to other events in the environment.

More generally, these findings provide further evidence of significant developmental change in perception–action coupling at least into late childhood and early adolescence (Plumert et al., 2007). Much of the work to date on perceptual–motor development has focused on infancy and toddlerhood because this is when visual perception and motor skills are undergoing dramatic change (Adolph & Berger, 2006). However, perception–action coupling continues to undergo change even in late childhood and early adolescence. This is particularly obvious when children and adolescents are faced with the problem of coordinating the movement of a complicated mechanical device (e.g., a bike or car) in relation to other fast-moving objects in the environment. One question that our results raise is how to characterize the nature of this developmental change (Adolph, Robinson, Young, & Gill-Alvarez, 2008). Although no longitudinal data on the development of children’s interceptive skills currently exist, our cross-sectional work suggests that children’s ability to bring their actions tightly in line with perceptual information improves through childhood and early adolescence, likely resulting from the bidirectional influences of repeated practice with interception tasks and the tuning of relevant neurological substrates. Further research is needed to track changes in children’s interception skills over both the short term and the long term.

The second objective of this investigation was to examine how the initial state of the environment–actor system (i.e., projected early or late arrival in the gap) affected time-to-spare and approach strategies. In both experiments, time to spare at the moment of interception was greater than that in trials for which participants were initially projected to arrive early rather than late (±0.9 s in Experiment 1, ±0.7 s in Experiment 2). This pattern of results could reflect an inability of the participants to fully compensate for being behind at the beginning of the approach in the projected late-arrival trials—particularly given that in the projected early arrival trials, participants exhibited a tendency to slow down more than was necessary, then accelerate again near the end of the approach. Alternatively, it could be the case that this difference in time to spare is not due to a shortcoming in participant performance, but rather is a byproduct of the task itself. In both conditions, the overwhelming majority of participants were able to successfully complete the task. Unlike other interception tasks, such as ball catching, which have a relatively narrow window for success, our road-crossing task presented a relatively large window of time (3.5 s) in which participants could arrive and successfully complete the task. Although greater time to spare is generally considered indicative of safer road-crossing, the smaller time to spare in the projected late-arrival conditions was well within the range of acceptable outcomes for the task, and not necessarily unsafe. Additional research is needed to distinguish between these alternative explanations.

The final objective of the study was to describe how participants’ behavior as they approached the intersection was affected by the initial state of the environment–actor system. It appears that participants’ approach profiles conformed to a two-stage interception strategy that was not consistent with what would be expected if participants were using a constant bearing angle strategy to guide their entire approach. In the constant bearing angle strategy, the observer adjusts speed to eliminate variations in the bearing angle of the desired point of interception. When the object to be intercepted is traveling at constant speed on a linear trajectory, then the observer is expected to modify speed to shift the point of constant bearing to the desired point of interception and then maintain constant speed through the rest of the approach. In contrast to this prediction, the approach profiles in both experiments showed an increased acceleration beginning somewhere between 4 and 6 s away from the end of the trial, regardless of the age of the participants. This late acceleration might reasonably be expected in projected late-arrival trials. However, it is curious that in projected early-arrival trials, in which participants must slow down to intercept the gap, they first decelerate more than is necessary and then accelerate through the gap. Regardless of what visual information participants may have been using to guide their movement up to that point, there appears to be a shift in strategy at this temporal distance from the intersection. This late shift in speed is consistent with the findings of Chardenon et al. (2005), whose participants demonstrated a similar shift in speed in the last few seconds of their approach. It is also consistent with the recurring funnel-like pattern of behavior observed by Buekers et al. (1999), by Montagne et al. (2003), and more recently by Camachon et al. (2007). The notion of a shift in strategy while performing other visually guided actions such as effector-based interception (Lenoir et al., 1999, 2002) and stopping a car (Treffner, Barrett, & Petersen, 2002) has precedent in the literature.

What might be motivating this shift in behavior, manifested as a two-stage approach? We propose that the observed pattern of behavior in both projected early-arrival trials and projected late-arrival trials is due to participants attempting to create and maintain a “window of adjustment” that allows them to accomplish the goal of crossing the road, while satisfying potentially competing constraints. As is stated in the introduction, the basic goal of road crossing is to pass through a gap between two moving vehicles without getting hit. This sets up several potentially competing constraints that the rider must negotiate. One is to intercept the gap at the right time, while traveling at a speed that allows for control over the bicycle. For example, if an early-arriving cyclist is traveling at an excessively high rate of speed, the deceleration necessary for a safe interception could exceed the braking capabilities of the bicycle. Likewise, if a late-arriving cyclist is traveling too slowly, then the amount of acceleration necessary for the cyclist to hit the gap could exceed the acceleration that the cyclist is capable of producing. In general, it is desirable to avoid operating near the limits of controllability because this restricts the degrees of freedom under control. Thus, a bicyclist pedaling as fast as possible cannot accelerate and is therefore less able to adjust to changing circumstances, or correct for errors in perception. Another constraint is to maximize the time within striking distance of road crossing. Because of the potential for errors in both perception and control, it is desirable to have as large a temporal window of opportunity as possible to enter the gap. The faster the bicyclist is traveling during the final approach to the intersection, the finer the tolerance for hitting the temporal gap. Thus, from the perspective of timing the entry into the gap, it is desirable to be traveling slowly while approaching the intersection. The final constraint is to minimize the amount of time spent in the path of the cross traffic—this can be accomplished by riding through the intersection at a high rate of speed. Note that satisfying all of these constraints can be challenging, particularly when the approach distance is long and the car speeds are high.

The constraints on action listed above are specifically related to the motor capabilities of the cyclist at different points along the approach to the intersection. The existence of these high-level performance-based constraints does not preclude the possibility that cyclists are also behaving in such a way so as to maximize the availability of the visual cues used for timing their road crossing. As the cyclist moves toward the interception point, the number of potential sources of visual information—as well as the saliency of these sources—increases (Cutting & Vishton, 1995). So, in the context of the gap-crossing task, the cyclist can exercise additional discretion within the speed range that affords both acceleration and braking in order to maximize the amount of time spent closest to the intersection, where the most useful perceptual information about the movement of the cross-traffic is available. A cyclist implementing this strategy would speed up to get within close range of the intersection, then slow down to maximize the amount of time that could be used to acquire the most optic flow information available. Recent work by Fajen (2008) has indicated that people appear to utilize the most reliable sources of information available when performing visually guided actions.

How might the cyclist satisfy the competing constraints of the need for speed late in the approach and the need for controllability (lower speeds) earlier in the approach? It is reasonable to assume that cyclists would attempt to approach the intersection at a speed that affords both braking and acceleration—braking if the cyclist decides that the gap cannot be safely crossed (thereby bailing out before it is too late) and acceleration to enable the cyclist to speed through the intersection (thereby minimizing exposure to the path of cross-traffic). When these goals and constraints are considered together, we would expect to see cyclists approach the intersection at the maximum rate of speed that would enable both additional acceleration and safe braking. Once the cyclist reaches a closer distance from the point of interception at which more and better visual information becomes available, the cyclist will attempt to maximize the amount of time spent within this window—slowing down if possible. In the final phase of the interception, the cyclist will accelerate as much as possible to minimize the overall exposure to the danger zone that is the path of the cross traffic. In the current study, participants in both projected early-arrival trials and projected late-arrival trials appeared to be using a strategy that is consistent with this pattern of behavior.

The model of control that we propose here relies on the supposition that cyclists are seeking to maximize the affordances available to them at any given moment along the approach, as is defined by the boundaries for action imposed by their motor capabilities in relation to the demands of the situation. Fajen (2007) has recently proposed an affordances-based model for the control of visually guided actions that is based on the action boundaries of the actor within the environment. That is, actors produce the movements necessary to maintain the possibility of successful action. The pattern of behavior observed in the present study initially appears to be consistent with an affordances-based model of control. However, until the predictive power of our model of control for gap interception can be evaluated, care must be taken when drawing conclusions about the viability of the model. In the future, we intend to modify the constraints that define the road-crossing/gap interception task to see whether we can produce predictable shifts in participants’ behavior.

Although many potential manipulations of the present road-crossing task exist, another promising method for beginning to evaluate and refine our model would be to explore the effects of learning on participants’ performance of the task (see also Montagne et al., 2003). As participants become familiar with the task over a number of trials, their perceptual systems will zero in on which visual cues are most reliable at any given distance from the intersection. This being the case, it may become easier for them to recognize discrepancies between the desired state of the environment–actor system (i.e., the one leading to a successful interception) and the current state of the environment–actor system. With added practice, it is likely that participants could also identify these discrepancies at a greater distance from the intersection. If this is the case, we would expect to see corrections of a higher magnitude occurring earlier in the approach, diminishing the need for large adjustments in speed, such as an exaggerated deceleration, closer to the intersection. We might also expect to see children’s approach profiles more closely resemble those of the adults after extended practice.

In summary, this study revealed that the performance differences on road-crossing tasks between child and adult bicyclists are not solely the product of deficiencies in children’s movement initiation. Children appear to have more difficulty coordinating their actions with the movement of other objects in the environment. Additionally, the two-staged approach behavior observed in this study cannot be explained by the use of a monotonic control law such as the constant bearing angle strategy. Instead, the results suggest that participants were maximizing the potential for action on the approach, while using the most reliable visual sources of information in coordinating their movements with the movements of the target blocks. Further research is needed to better understand how learning the constraints of the task leads to shifts in behavior as individuals attempt to intercept moving gaps.