Abstract
The aims of this study were to compare the responses of human maxilla and frontal bones under 30°-oriented impacts. Maxilla and frontal bones of the same subject were impacted by a guided horizontal steel cylinder. Linear acceleration time histories and force time histories were plotted and corridors were proposed for maxilla bone response. Sensitivity of head dynamics in regard to impact energy level and localization showed the protection of the intracranial contents by the facial bones crushing. Injury risk curves were established for impact on frontal bone, showing a 50% risk injury for impact energy of 265 J or impact force of 7500 N.
For the past 80 years, improvement in design and increased usage of seat belt systems have led to increased frequency of face injury in roadway accidents [Ramet, Vallet, 1987]. The development of the air bag resulted in decreased severity of injuries of the head and face [Krafft et al., 1998]. Using the AIS scale, fractures of facial bones are often coded as minor or moderate. Yet, the personal consequences of faces injuries are considerable because of the long-term cosmetic repercussions.
Based on research on the prevention of severe injuries to the head, injury criteria have been established. The National Highway Traffic Safety Administration (NHTSA) proposed the Head Injury Criterion: it uses time duration of impact and linear acceleration of the center of gravity of the head. The Gambit has been proposed for brain injuries induced by rotational accelerations of the head.
Past research has proposed fracture tolerances for major facial bones using different impactor sizes. These reference data was summarized in a SAE report in 1980 [SAE, 1980]. Later, this data was completed [Allsop et al., 1988] and overall facial response analyzed. Since contact on the face with the steering wheel is still most frequent [Thomas et al., 1991], several studies analyzed facial bone fractures following dynamic contact with the steering wheel or substitute [Nyquist et al., 1986] [Allsop et al., 1988] [Yoganandan et al., 1988] [Bermond et al., 1999].
Energy absorbed during the crush of facial bones has an influence on both facial injuries and overall head dynamics. Thus, the global dynamic behavior of the face and its injury mechanisms must be considered to define injury criteria for head impacts. Moreover, the knowledge of mechanical response of face is essential to evaluate and improve the biofidelity of mechanical and numerical models of the head. Recent works performed as part of the European project called Advanced Crash Dummy Research for Injury Assessment in frontal test conditions (ADRIA) brought new data concerning dynamic response of malar bone in comparison with frontal bone under impact with a steel cylinder [Bermond et al., 1999].
This paper compares impacts on the maxilla bone with the frontal bone. The aims of the analysis were firstly to propose corridors of the dynamic behavior of head during impact on maxilla bone, and secondly to analyze the sensitivity of the head dynamics with regard to the impact energy level and localization.
MATERIAL AND METHODS
Fifteen impact tests were realized on 9 Post Mortem Human Subjects aged between 58 and 77, with a mean of 68 years. Eleven tests were realized on maxilla bone and 4 on frontal bone (Figure 1). These last tests on frontal bone completed a first series of 26 tests previously performed (see Appendix) [Bermond et al., 1999].
Figure 1.
Impact locations
PMHS PREPARATION
A set of anthropometric data was collected to characterize the whole corpse (height, weight) and the head (circumference, height and weight). The Frankfurt plane was materialized by four small lead balls, placed at infraorbital notches and auditory meati. The anatomical frame was then defined as shown on Figure 2 with frame origin located at the middle of auditory meati segment. The center of gravity of the head (G) was defined according to the results of Beier et al. (1980) with x = 8.3mm, y = 0 and z = −31.2 mm in the anatomical frame.
Figure 2.
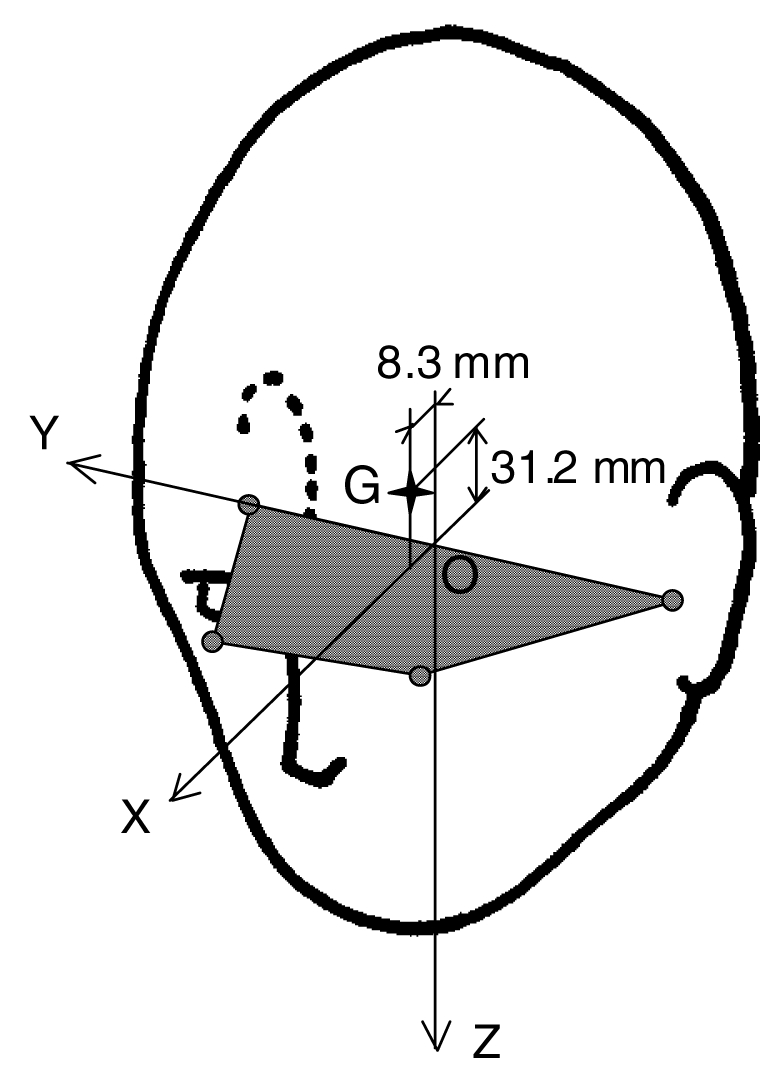
Anatomical frame of the head (G = center of gravity of the head)
IMPACT CONDITIONS
A horizontal guided impactor was used. To simulate steering wheel rim, the extremity of the impactor was equipped with a horizontal steel cylinder with a diameter equal to 2.25 cm. This rigid portion directly contacted the face of the subject during tests. The weight of impacting mass was 17 kg as used since 1989 at INRETS [Welbourne et al., 1989] [Césari et al., 1989] [Bermond et al., 1999].
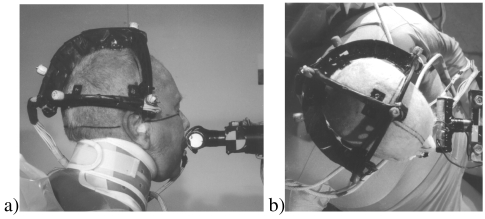
During tests, subjects were seated, linked to the armchair by a strap and a cervical collar was used in order to hold the head in good position (Frankfurt plane in the horizontal) and to reduce the neck’s flexibility as decided by the ADRIA project consortium [TNO, 1998]. The direction of impact on maxilla or frontal bones was chosen as 30°-angled from the mid-sagittal section plane in order to obtain impact conditions closer to real impact conditions, where the seat belt leads to the rotation of the upper torso and the head (Figure 3).
Figure 3.
Configuration of impact on maxilla bone a) Lateral view, b) Top view
The impact energy taken from the mass and the velocity of the impactor was chosen on the basis of results from previous tests [Césari, 1989][TNO, 1998] and in a way to observe either facial bone fractures or not. For impact on maxilla bone, two levels of impact energy were chosen: – a low level with energy ranged between 106 J and 189 J, the mean was close to 140 J, – a high level with energy ranged between 248 J and 298 J, the mean was close to 280 J. In order to make a comparison of the response of frontal and facial bones, the impact energy for the impacts on frontal bone ranged between 22 J and 283 J, the mean was equal to 114 J.
Some subjects have been submitted to both right and left impacts on maxilla. In these cases, the low energy impacts were performed first and it has been verified that they were sub-injury impacts. Some subjects have been submitted to both impacts on frontal bone and maxilla. In this case, it was verified that the impact on frontal bone would not affect the integrity of the maxilla region.
Table 1 summarizes conditions for all tests performed on these 9 subjects.
Table 1.
Impact conditions, measured parameters and observed injuries
| Impact location | Test Number | Subject Number/Age (Years) | Head Weight (g) | Impact Energy (E(J)) | Max. Impact Force (N) | Peak linear acceleration of the center of gravity of the head (m/s2) | HIC | AIS | Injuries |
|---|---|---|---|---|---|---|---|---|---|
| Maxilla |
Low level (E = 140 J) |
||||||||
| FCA 54 | #1/71 | 3820 | L : 152 | 2085 | 989 | 176 | 3 | Caving in of the maxilla body | |
| FCA 55 | #2/70 | 3750 | R : 106 | 1572 | 651 | 67 | 1 | Localized wound | |
| FCA 57 | #2/70 | 3750 | L : 189 | 1462 | 616 | 62 | 3 | Caving in of the maxilla body | |
| Rupture of the suture between malar and frontal bones | |||||||||
| FCA 58 | #3/77 | 4200 | R : 130 | 1394 | 809 | 64 | 1 | Localized wound | |
| Mean (SD) | 1628 (313) | 766 (170) | 92 (56) | ||||||
|
High level (E = 280 J) |
|||||||||
| FCA 59 | #3/77 | 4200 | L : 287 | 1802 | 561 | 87 | 4 | System of fractures of the zygomatic process of the maxilla running to the lower orbital cavity | |
| Fracture and displacement on the right of nasal bones | |||||||||
| Transversal fracture of the palatine bone | |||||||||
| FCA 61 | #4/unknown | 4280 | R : 286 | 1972 | 1081 | 161 | 4 | Caving in of the maxilla body | |
| Transversal fracture of the palatine bone | |||||||||
| FCA 63 | #5/76 | 3620 | R : 248 | 1842 | 1355 | 275 | 1 | Localized wound | |
| FCA 64 | #6/66 | 3410 | R : 282 | 2615 | 1300 | 265 | 1 | Localized wound | |
| FCA 66 | #7/72 | 3380 | R : 289 | 3116 | 1810 | 479 | 3 | Caving in of the maxilla body | |
| FCA 68 | #8/58 | 3880 | R : 298 | 2187 | 1283 | 294 | 1 | Localized wound | |
| FCA 70 | #9/70 | 3500 | R : 291 | 3331 | 1644 | 455 | 1 | Localized wound and dental wrench | |
| Mean (SD) | 2409 (622) | 1291 (403) | 288 (142) | ||||||
| Frontal bone | FCA 52 | #1/71 | 3820 | R : 157 | 6387 | 2577 | 1257 | 1 | Localized wound |
| FCA 53 | #1/71 | 3820 | L : 270 | 6932 | 3542 | 2716 | 3 | Y-shaped fracture of the frontal bone running to the orbital surface of the frontal bone | |
| FCA 56 | #2/70 | 3750 | R : 270 | 7849 | 3282 | 1559 | 1 | Localized wound | |
| FCA 60 | #3/77 | 4200 | L : 289 | 7988 | 3260 | 1819 | 3 | 3cm-long fracture of the frontal bone running to the orbital surface of the frontal bone | |
| Mean (SD) | 7289 (762) | 3165 (413) | 1838 (629) | ||||||
INSTRUMENTATION
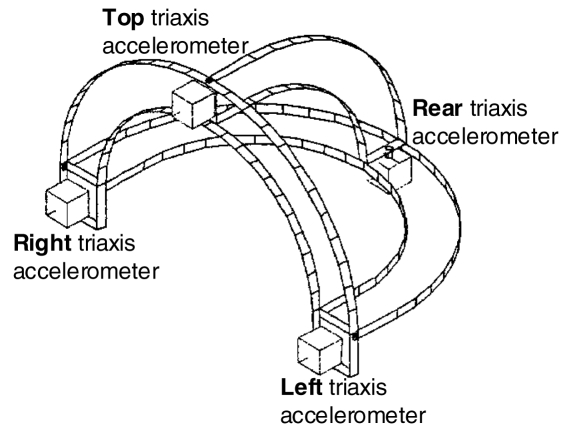
The head was equipped with a light helmet comprising 4 blocks of triaxis accelerometers located on the top, rear, left and right of the helmet (Figure 4). This helmet was screwed onto the head and weighed 0.34 kg, which was generally lower than 10% of the head mass. The location of the center of gravity of the head was adjusted by considering this additional weight. The impact force and the speed and acceleration of the impactor were also measured.
Figure 4.
Scheme of helmet equipped with 4 triaxis accelerometers
The data was prefiltered at 2.5kHz and digitized at a sampling rate of 10kHz. Then, data was filtered according to the ISO normalization: accelerations of the head were filtered with a FIR1000 filter and data from the impactor was filtered at 180Hz.
ANALYSIS
In terms of mechanical response of the face, the studied parameters are the linear acceleration of the center of gravity of the head, the HIC criterion and the impact force.
Linear acceleration of the center of gravity of the head
The 4 triaxis accelerometers were used to calculate the linear acceleration at the center of gravity of the head during the impact. The method used was the N×1 method, developed by APR [Oudenard et al., 1991]. Computing is based on equations for the head motion, considering it as a rigid body. These equations contain 6 unknown parameters, which are the linear and angular accelerations of the center of gravity of the head along X, Y and Z axis ( AccX , AccY , AccZ and ω̇X , ω̇Y , ω̇Z ). Using information supplied by N accelerometers with N ≥ 6 leads to a set of N equations. The redundancy of equations is treated using the least square method and these are resolved by an explicit integrating method.
The N×1 method requires the orientation and position of each accelerometric sensors relative to the center of gravity in the head anatomical frame. This information was provided by X-Ray photographs of the head and helmet system, taken in frontal and sagittal planes before the test. The use of a helmet made the orientations and positions of the accelerometric sensors easier to obtain from X-Ray photographs.
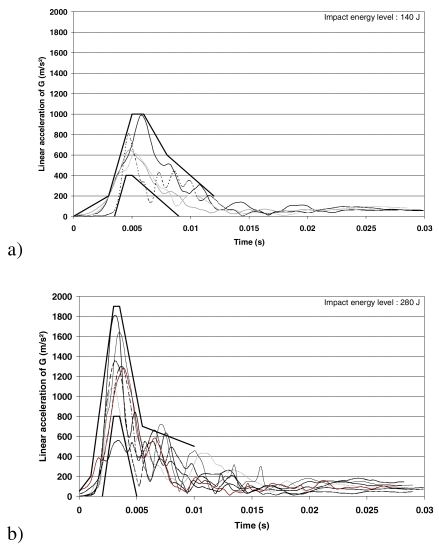
The linear acceleration of the center of gravity of the head was plotted as a function of time. For maxilla bone, response corridors were proposed for the two energy levels since responses were quite different. The maximum value of the linear acceleration was also considered.
HIC criterion
The HIC criterion was computed according to the NHTSA definition (NHTSA, 1997):
where a(t) is the linear acceleration of the center of gravity of the head and t1 and t2 are two points in time which are separated by not more than a 36 ms time interval.
Impact force
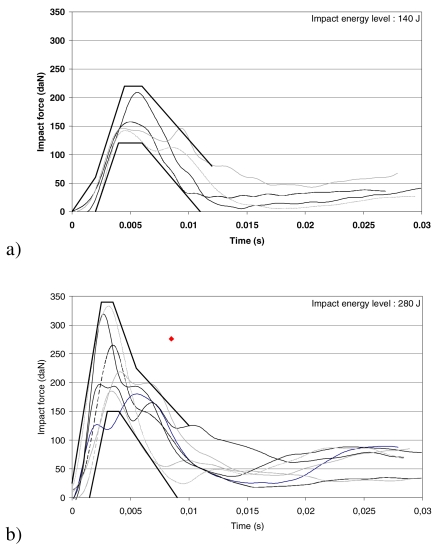
The impact force was computed from the measured force of impactor, considering the mass of the impacting cylinder. Response corridors were established for impact force time-histories during impact on maxilla. The maximum value of the impact force was also considered.
KINEMATICS
The impacts were documented by a high-speed camera (1000 frames/second) in the lateral view. Photographs documented pre-test and post-test situations of the subject.
MEDICAL INVESTIGATION
Autopsy of head included an inspection of the soft tissue injuries of the face, and of the skull and facial bones after the soft tissues were removed. Injuries were coded according to the AIS90 scale [AIS, 1990].
STATISTICS
Statistical analysis was performed using the SAS® Software. The relationship between the injury risk and the measured parameters was evaluated by the test of maximum likelihood. Logistic regressions were also evaluated by test of maximum likelihood. Likelihood is considered as significant for a probability p ≤ 0.05.
RESULTS
MECHANICAL RESPONSE
Time histories of linear acceleration of the center of gravity of the head and of the impact force are given for the maxilla bone in Figures 5a,b and Figures 6a,b. Findings in terms of maximum linear acceleration, HIC and maximum impact force are given in Table 1.
Figure 5.
Maxilla bone impact : linear acceleration of the center of gravity of the head versus time plots and proposed response corridors
Figure 6.
Maxilla bone impact : impact force versus time plots and proposed response corridor (Isolated point on figure b defined from Nyquist et al, 1986)
SENSITIVITY OF THE MECHANICAL RESPONSE
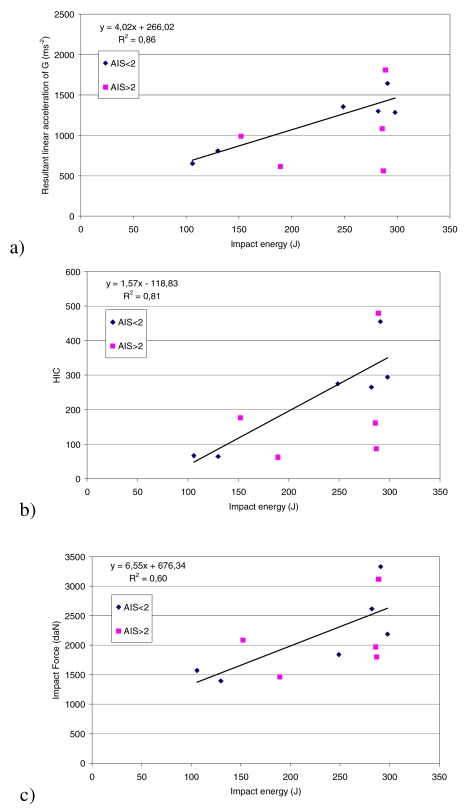
The maximum value of the linear acceleration, the HIC and the maximum impact force are plotted against impact energy for maxilla bone with AIS level indicated (Figures 7a,b,c). For all the parameters, linear trends are observed in case of sub-injury level (AIS < 2) (see R2). For cases with AIS ≥ 2, trends are not evident. For the maximum linear acceleration of the center of gravity of the head and the maximum impact force, relations seem to be the same as sub-injury cases (without considering 1 far point on Figure 7a). For HIC values, no tendency seems to appear since a large range of HIC is obtained for impact energy close to 300 J.
Figure 7.
Maxilla bone impact : maximum linear acceleration, HIC and maximum impact force versus impact energy (Linear regression given for AIS < 2)
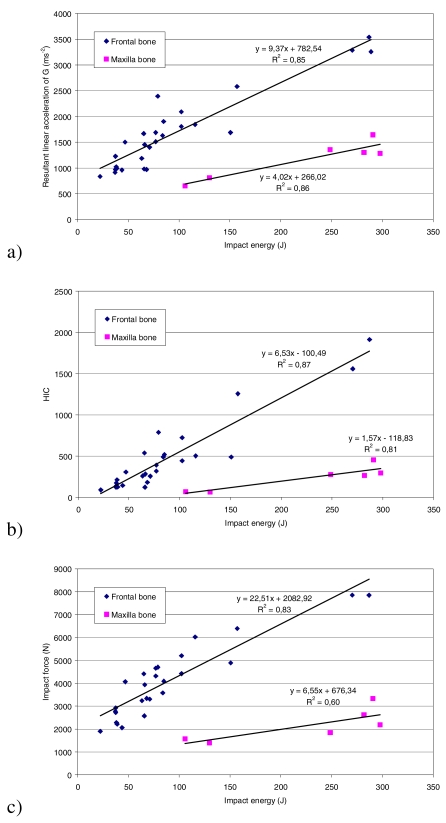
Comparisons with similar data for frontal bone impact in the case of AIS ≤ 2 are given in Figures 8a,b,c. For both frontal bone and maxilla, linear trends are observed (see R2). Lower levels of values for impact on maxilla are observed, showing the lower stiffness of this facial bone compared to the frontal bone. Moreover, lines obtained for maxilla are less steep.
Figure 8.
Maxilla and frontal bone impacts : maximum linear acceleration, HIC and maximum impact force versus impact energy (AIS < 2)
OBSERVED INJURIES (Table 1)
Localized abrasions or wounds of the skin were always observed and coded as AIS 1. In case of severe impact on frontal bone, fractures of this bone and of the orbital cavity were observed. Impacts on maxilla bone conducted to a caving in of the maxilla body and more severe impact also conducted to complete fracture of the palatine bone and/or displacement of the face with rupture of the suture between frontal and zygomatic bones.
INJURY RISK CRITERIA
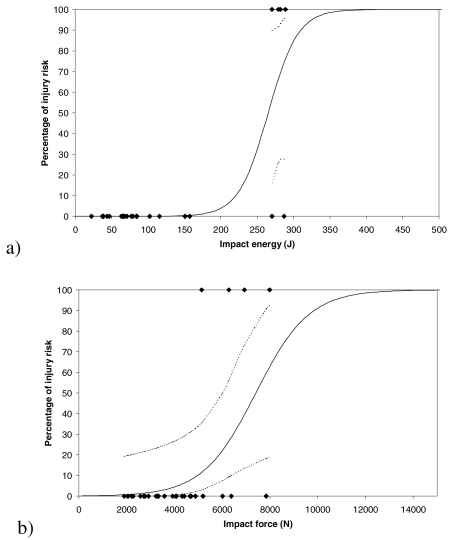
In order to evaluate the studied parameters or impact energy as injury risk criteria, their values have been compared to the risk of injury, considering it equal to 100% for AIS ≥ 2. For impacts on maxilla, risk distributions obtained did not allow the interpolation of the injury risk function by logistic curves since the probability of dependence was not significant (Table 2). For frontal bone impact, the probability of dependence was significant for the impact energy and the impact force. Logistic regressions are illustrated by Figures 9a & b. Considering the impact energy as injury criterion, a 50% injury risk is obtained for a value of 265 J. For the impact force, it corresponds to a value of 7500 N.
Table 2.
Significance of relationship between injury risk and the studied parameters
| Parameters | Impact on maxilla | Impact on frontal bone |
|---|---|---|
| Impact energy | Not significant | p < 0.01 |
| Impact force | Not significant | p < 0.01 |
| Linear acceleration | Not significant | Not significant |
| HIC | Not significant | Not significant |
Figure 9.
Frontal bone impact : injury risk obtained in function of impact energy and impact force (95% confidence intervals in dotted line)
DISCUSSION AND CONCLUSION
Comparison of the presented results with the literature data needs to take into account the conditions of impacts and measurements. In this study, impacts test were performed on seated cadavers: the torso was fixed and a cervical collar was used in order to give stiffness to the neck since there is no muscle tone. This collar certainly has an influence on the head kinetics but it enables the reproduction of the same boundary conditions for each subject. The mechanical response of the head during impact on the frontal bone or the facial bone was analyzed in terms of linear acceleration of the center of gravity of the head, which was computed using a center of gravity location based on the study by Beier et al. (1983) and adjusted by considering the presence of the helmet. The helmet modified the head inertia and center of gravity location but this influence was the same in all tests. Moreover, considering the location of the center of gravity of the head proposed by Beier et al., without consideration of anatomical variations, is an approximation.
Time-histories of linear acceleration of the center of gravity of the head and of the impact force obtained for impact on maxilla showed expected phenomena, i.e. higher amplitude and shorter impact duration for the higher impact energy (Figures 5 & 6). For impact on nose and upper part of the maxilla using similar impact conditions except a weightier impacted mass (34 kg to 64 kg), Nyquist et al. published peak location for force time histories (1986): considering the 6 impacts with lowest energy level (from 241 J to 320 J, mean 257 J), the point 2760 N at 8.5 ms defines the mean location of the force peak. The force level of this point located on Figure 6b is close to the mean peak force that we obtained but the rise time is longer. This difference could be explained by the deformation of the nose, which leads to lower slopes of the linear part of the curves and longer impact duration, and by the lower impact speed. In our case of direct 30°-angled impact on maxilla, the rise time depends on the thickness of skin. The maximum impact forces we measured can also be compared to the fracture forces obtained by Allsop et al. (1988) on frontal bone and maxilla, using similar impact characteristics. In our study, all maxilla impacts with AIS < 2 showed impact forces (comprised between 1394 N and 3331 N) upper to the mean fracture force proposed by Allsop et al. (1350 N). For impact on frontal bone, the same observation is made.
In the comparison of the sensitivity of the measured parameters with regard to impact energy, the less steep slopes observed for impact on maxilla bone showed a lower sensitivity of the head behavior in case of facial bone impact. Linear trend were observed in case of sub-injury impact, between mechanical parameters quantifying the head behavior and the impact energy, but no real trend has been showed for impact on maxilla bone with AIS ≥ 2.
Concerning injuries, some of those observed in case of impact on maxilla bone are similar to those shown by Yoganangan et al. in case of steering wheel impact on zygoma (1991) such as the displaced fracture of orbit located at the frontal/malar suture.
For impact on maxilla, in our range of impact energy [106 J – 298 J] and generated impact force [1585 – 2929 N], injury risk distribution with regard to impact energy and the measured parameters did not allow us to establish logistic regressions. For impact on frontal bone, it has been possible to define logistic regression with impact energy and impact force as injury criteria. Logically, the impact force level obtained for 50% injury risk on frontal bone (7500 N) is higher than the one obtained by Yoganandan et al. for 50% injury risk in case of steering wheel impact on zygoma (1500 N). Yet, the great difference between these two values is also due to the differences of impact conditions since the study of Yoganandan et al. involves drop tests of isolated heads on steering wheel.
At the beginning of the work performed at INRETS, one objective was to compare the head behavior during impact on the facial bone and frontal bone for the same impact energy level. Since AIS ≥ 2 was obtained for zygoma at impact energy level close to 100 J (Bermond et al., 1999), many tests were carried out with quite low impact energy level. So, results for impact with impact energy higher than 300 J will be necessary: 1) to confirm the logistic regressions obtained for the risk distribution versus impact energy and impact force in the case of impact on frontal bone, 2) to complete the risk distribution in case of impact on maxilla and to define injury risk criteria.
The variability of PMHS response has been observed but the use of PMHS implies variations in anthropometry and in the biological tissue properties, which directly influences the mechanical behavior. The bone strength, which depends on many parameters (such as age, sex, living conditions, bone geometry), directly influences the mechanical behavior and strength of the face. Moreover, differences in the mechanical behavior of PMHS and living persons exist, namely due to the lack of muscle tone in PMHS.
In conclusion, despite the variations in the mechanical responses of PMHS and the necessary caution in applying the results to living persons, trends in the mechanical response of the human face have been shown. Moreover, the comparison of the head behavior when maxilla or frontal bone is impacted showed the protection of the intracranial contents by the facial bones crushing.
(Presenter: Karine Bruyere)
Stefan Duma: The energy for your injury criteria, how did you actually calculate that energy?
K. Bruyere: That energy is calculated from the speed and the mass of the impacting mass.
S. Duma: The speed and the mass. Because the head will leave with some energy so that energy may not necessarily go into the bone or into the failure, you may want to account for some of that.
K. Bruyere: Yes, I see what you mean.
ACKNOWLEDGEMENT
We would like to thank Pierre LAPELLERIE, Michel MARAIS and Gérard GOUTELLE for their work in collecting data, photos and measurements during the tests and Sabine COMPIGNE for her work in statistical analysis.
Appendix: Impact conditions, measured parameters and observed injuries for previous tests on frontal bone (from Bermond et al., 1999)
| Test N° | Impacted area | Impact Energy [J] | Impact force (N) | Res.acc. head c. g. [g] | HIC | Medical findings |
|---|---|---|---|---|---|---|
| FCA02 | right forehead | 22 | 1900 | 85 | 89 | skin laceration AIS 1 |
| FCA04 | left forehead | 65 | 4410 | 170 | 536 | skin laceration AIS 1 |
| FCA06 | right forehead | 37 | 2280 | 104 | 211 | skin laceration AIS 1 |
| FCA08 | left forehead | 82 | 3580 | 166 | 490 | frontal bone fracture AIS 1 |
| FCA10 | right forehead | 37 | 2920 | 125 | 174 | skin laceration AIS 1 |
| FCA11 | left forehead | 77 | 4320 | 172 | 391 | skin laceration AIS 1 |
| FCA14 | right forehead | 37 | 2770 | 93 | 121 | skin laceration AIS 1 |
| FCA16 | left forehead | 77 | 4650 | 154 | 318 | skin laceration AIS 1 |
| FCA18 | right forehead | 37 | 2720 | 99 | 140 | skin laceration AIS 1 |
| FCA20 | left forehead | 63 | 3240 | 121 | 259 | skin laceration AIS 1 |
| FCA22 | right forehead | 39 | 2210 | 101 | 126 | skin laceration AIS 1 |
| FCA24 | left forehead | 79 | 4700 | 244 | 788 | skin laceration AIS 1 |
| FCA26 | right forehead | 44 | 2060 | 98 | 144 | skin laceration AIS 1 |
| FCA28 | left forehead | 85 | 4090 | 194 | 520 | frontal bone fracture AIS 1 |
| FCA30 | right forehead | 47 | 4070 | 153 | 307 | skin laceration AIS 1 |
| FCA32 | left forehead | 102 | 4420 | 184 | 443 | skin laceration AIS 1 |
| FCA34 | right forehead | 66 | 2576 | 100 | 122 | skin laceration AIS 1 |
| FCA35 | left forehead | 116 | 6031 | 188 | 502 | skin laceration AIS 1 |
| FCA36 | right forehead | 66 | 3944 | 148 | 283 | skin laceration AIS 1 |
| FCA38 | left forehead | 151 | 4503 | 172 | 489 | bone fracture AIS 1 |
| FCA41 | right forehead | 68 | 3352 | 89 | 181 | skin laceration AIS 1 |
| FCA42 | left forehead | 282 | 5149 | 201 | 548 | frontal bone fracture AIS 3 |
| FCA45 | right forehead | 71 | 3317 | 143 | 256 | skin laceration AIS 1 |
| FCA46 | left forehead | 287 | 7866 | 361 | 1914 | skin laceration AIS 1 |
| FCA49 | right forehead | 102 | 5210 | 213 | 724 | skin laceration AIS 1 |
| FCA50 | left forehead | 279 | 6293 | 245 | 1048 | frontal bone fracture AIS 3 |
REFERENCES
- The Abbreviated Injury Scale 1990 Revision, Association for the Advancement of Automotive Medicine, Des Plaines, IL, 1990
- Allsop DL, Warner CY, Wille MG, Schneider DC, Nahum AM. Facial Impact Response. A Comparison Of The Hybrid III Dummy And Human Cadaver. 32nd Stapp Car Crash Conference, Society of Automotive Engineers, Paper N°881719; 1988. [Google Scholar]
- Beier G, Schuller ES, Schuck M, Ewing CL, Becker ED, Thomas DJ. Center of gravity and moments of inertia of human heads. 5th International IRCOBI Conference; 1980. pp. 218–228. [Google Scholar]
- Bermond F, Kallieris D, Mattern R, Ramet M, Bouquet R, Caire Y, Voiglio E. Human Face Response at an Angle to the Fore-aft Vertical Plane Impact. 1999 International IRCOBI Conference; 1999. pp. 121–132. [Google Scholar]
- Césari D, Ramet M, Welbourne E. Experimental evaluation of human facial tolerance to injuries. 1989 International IRCOBI Conference; 1989. pp. 55–63. [Google Scholar]
- Krafft M, Kullgren A, Lie A, Tingvall C. The risk of skull/brain injuries in modern cars. 16th International Technical Conference on Experimental Safety Vehicles, Paper N° 98-S6-O-14; 1998. [Google Scholar]
- Nyquist GW, Cavanaugh JM, Goldberg SJ, King AI. Facial impact tolerances and response. 30th Stapp Car Crash Conference, California, Society of Automotive Engineers, Paper N° 861896; 1986. [Google Scholar]
- National Highway Traffic Safety Administration, Code of federal regulation, 49CFR Part571.208, Published by the Office of the Federal Register National Archives and Records Administration
- Oudenard L, Bendjellal F, Bellini A, Uriot J. The use of a multi-accelerometric method in automotive safety tests. 13th International Technical Conference on Experimental Safety Vehicles, Paper N° 91-S8-O-04; 1991. [Google Scholar]
- Ramet, M. Vallet, G. Typologie des accidentés du trafic routier, à partir de 5459 Dossiers : Rapport INRETS, 41; Août 1987, 106 p.
- Society of Automotive Engineers, Inc., Human Tolerance To Impact Conditions As Related To Motor Vehicle Design, SAE J885 APR80 ; 1980
- Thomas P, Bradford M, Ward E. The cause of head injuries in real world car crashes. 13th International Technical Conference On Experimental Safety Vehicles, Paper N° 91-S1-O-08; 1991. [Google Scholar]
- TNO Crash Safety Research Centre, Eindhoven University of Technology, National Institute of Transport Safety Research, Polytechnical University of Madrid, Transport Research Laboratory, University of Heidelberg, Advanced crash Dummy Research for Injury Assessment in frontal test conditions, Deliverable D7 : Impact Human Specimen, Transport RTD Programme of the 4th Framework Programme, 1998
- Welbourne E, Ramet M, Zarebski M. A comparison of human facial fracture tolerance with the performance of a surrogate test device. 12th International Technical Conference On Experimental Safety Vehicles; 1989. [Google Scholar]
- Yoganandan N, Pintar F, Sances A, et al. Steering Wheel Induced Facial Trauma. 32nd Stapp Car Crash Conference, Society of Automotive Engineers, Paper N°88171; 1988. [Google Scholar]
- Yoganandan N, Pintar F, Reinnartz J, Sances A. Human Facial Tolerance to Steering Wheel Impact : A Biomechanical Study. Journal of Safety Research. 1993;24:77–85. [Google Scholar]
- Yoganandan N, Sances A, Pintar F, et al. Traumatic facial injuries with steering wheel loading. Journal of Trauma. 1991;31:699–708. doi: 10.1097/00005373-199105000-00015. N°5. [DOI] [PubMed] [Google Scholar]