Dynamic Bending Tolerance and Elastic-Plastic Material Properties of the Human Femur

Abstract

The objective of this study was to provide data on the structural tolerance and material properties of the human femur in dynamic bending. Fifteen (15) isolated femurs from eight (8) males were tested in either posterior-to-anterior or lateral-to-medial three-point bending. The failure moment was 458 ± 95 Nm and did not differ significantly with loading direction. A method was developed to estimate the elastic-plastic material properties of the bone using both force-deflection data and strain gauge measurements. The bone material appeared to yield at about one third of the ultimate strain level prior to fracture. It is hoped that these data will aid in the development of injury criteria and finite element models for predicting injuries to pedestrians and vehicle occupants.

Femur fractures are serious injuries to which pedestrians are especially vulnerable. In 2002, 4808 pedestrians were killed and 71,000 pedestrians were injured in the U.S. (NHTSA, 2004). According to the National Highway Traffic Safety Administration’s Pedestrian Crash Data Study (PCDS), the lower extremity is the most commonly injured body region among pedestrians, comprising 33% of all injuries (Chidester and Isenberg, 2001). Femur fractures account for approximately 10% of all lower extremity fractures for adult pedestrians, and 30% for children under 15 (Edwards and Green, 1999). The typical injury mechanism for midshaft femur fracture in a pedestrian impact is bending due to lateral impact. Less commonly, lateral-to-medial (L-M) bending may also fracture the femur of a vehicle occupant in a side impact (Banglmaier et al., 2003).

In order to better protect pedestrians and vehicle occupants, it is important to define the biomechanical parameters that relate to femur fracture. Femur fracture is generally predicted by applying data from cadaver experiments to physical or computational models. Physical models, such as the Hybrid III anthropomorphic test device (ATD) or the European Enhanced Vehicle-Safety Committee (EEVC) legform impactor, are used in compliance testing and predict injury based on structural criteria such as force or moment. Finite element models are currently used primarily for research purposes and predict injury based on material parameters, such as stress or strain. It is therefore desirable to obtain biomechanical data for both structural and material properties of the femur.

Numerous studies have been conducted to determine the structural bending tolerance of the human femur (Table 1). Most of these studies report results from tests conducted at quasistatic loading rates, which may significantly underestimate the bending tolerance of the femur under impact loading (Carter and Hayes, 1977). Kress et al. (1993) conducted dynamic bending tests on 94 femurs. However, their tolerance data are limited because they used primarily embalmed specimens, which were 44% weaker than fresh specimens, and did not report failure moments. Kerrigan et al. (2003) tested 4 matched pairs of femurs in dynamic L-M bending, but varied the loading conditions between each test as a way of running several pilot studies. The sample size for any one loading condition was no more than three. The most useful source of dynamic bending tolerance data for the femur is probably Martens et al. (1986), who conducted dynamic four-point bending tests on 33 femurs in the posterior-to-anterior (P-A) direction. They reported a high moment tolerance (373 Nm for midshaft fractures) compared to the quasistatic studies (Table 1). It is unknown whether these data apply to the L-M direction as well. Kress et al. (1993) reported that the breaking strength of the femur is greater in the A-P direction than the L-M direction. On the other hand, Yamada (1970) asserted that the bending tolerance of the femur in these two directions is the same.

Table 1.

Summary of isolated femur bending studies.

Study	Sample size	Failure Moment	Test conditions
Weber, 1859 (in Nyquist, 1986)	9	233 Nm (males)	Quasistatic 3-pt bending
		182 Nm (females)
Messerer, 1880 (in Nyquist, 1986)	12	310 Nm (males)	Quasistatic 3-pt L-M bending
		180 Nm (females)
Mather, 1968	145	318 Nm (males)	Quasistatic 3-pt A-P bending
		202 Nm (females)
Motoshima, 1960 (in Yamada, 1970)	35	211 Nm	Quasistatic 3-pt A-P bending
Martens et al., 1986	33	373 Nm (mid fx)	Dynamic 4-pt P-A bending
		275 Nm (distal fx)
Kress et al., 1993	94	3053 N breaking force	Dynamic 3-pt L-M and A-P bending
Stromsoe et al., 1995	14	185 Nm (males)	Quasistatic 3-pt L-M bending
		125 Nm (females)
Kerrigan et al., 2003	8	412 Nm	Dynamic 3-pt L-M bending

Many of the above studies have also attempted to calculate bone material properties by applying linear beam theory to the force-deflection data from their whole bone bending tests (Mather, 1968; Yamada, 1970; Kress et al., 1993). The problem with this approach is that it ignores plastic behavior in the bone. Although some researchers believe bone to be brittle (Cordey and Gautier, 1999), the consensus in the bone biomechanics literature is that bone exhibits significant yielding behavior (Burstein et al., 1972; Reilly et al., 1974; Carter and Hayes, 1977; Wright et al., 1981; Fischer et al., 1986; McCalden et al., 1993; Currey et al., 1999). Burstein et al. (1972) estimated that linear beam theory would overpredict the ultimate tensile stress in a three-point bending test by a factor of 1.56 for a square cross-section, and by a factor of 2.1 for a circular cross-section.

In general, the stress-strain behavior of human femoral bone has been studied primarily by uniaxial tension and compression testing of small machined specimens. In a uniaxial test of a small specimen, it is easy to determine the yield point because the entire cross-section yields at about the same time. However, the yield point is difficult to determine in a whole bone three-point bending test because the geometry is complex and only the outermost tensile fibers yield initially. For that reason, some researchers have concluded that it is not possible to determine bone material properties from a whole bone three-point bending test (Martens et al., 1986; Currey et al., 1999). However, there is concern that machining the surface of a small bone specimen may remove small stress concentrations and work-harden the fracture surface, thereby altering its failure properties. Therefore, it would be valuable if elastic-plastic bone material properties could be derived from whole bone three-point bending tests.

METHODS

THREE-POINT BENDING TESTS

Fifteen (15) fresh-frozen human lower extremities were obtained from medical cadavers in accordance with ethical guidelines and research protocol approved by a University of Virginia institutional review board. Prior to testing, all specimens were screened for HIV and hepatitis, and x-rays and CT scans were checked for signs of pre-existing bone and joint pathology. All specimens used in this study were from middle-aged and older male donors (Table 2). Dynamic three-point bending tests were performed on both femurs from each donor, except for cadaver 8, in which only the left femur was tested. For each donor, one femur was tested in P-A bending and the other femur was tested in L-M bending. The direction of loading was alternated between left and right legs. Bone mineral density (BMD) was available for the ipsilateral tibias of most specimens as a result of other studies that required the removal of the middle 10 cm of the tibial shaft. Dual-energy x-ray absorbtiometry (DEXA) was used to determine the bone mineral content of each tibial shaft. This value was divided by the cross-sectional area of the tibial specimen to obtain bone mineral density.

Table 2.

Cadaver information.

Cadaver #	Age (yrs)	Height (cm)	Mass (kg)	Ave. femur length (mm)	Tibia BMD (g/cm2)
1	67	188	64	481	1.13
2	59	183	108	476	1.30
3	40	180	70	486	1.27
4	55	168	64	477	0.92
5	70	168	73	445	1.08
6	69	163	92	467	1.03
7	51	188	124	499	N/A
8	66	183	95	446	1.10
Mean	59	177	86	474	1.12
SD	10	10	22	18	0.13

Specimens were allowed to thaw at least 24 hours before testing. The femur was dissected out of each leg with the periosteum left intact. The bone ends were potted in bone cups to a depth of approximately 8 cm using a quick-curing two-part polyurethane foam (U.S. Composites, West Palm Beach, FL). Specimens were instrumented with a strain gauge rosette (CAE-06-062UR-350, Measurement Group, Inc., Raleigh, NC) and an acoustic sensor (Nano 30, Physical Acoustics, Princeton, NJ). Both sensors were mounted to the bone surface by scraping off a small area of the periosteum, drying out the underlying bone surface with ether, and adhering the instruments using a cyanoacrylate adhesive. The acoustic sensor was mounted near the distal bone cup, and the strain gauge was affixed to the tensile surface of the bone approximately 2.5 cm distal to the center of the bone. Care was taken not to disturb the periosteum in the center of the bone where fracture was expected to initiate.

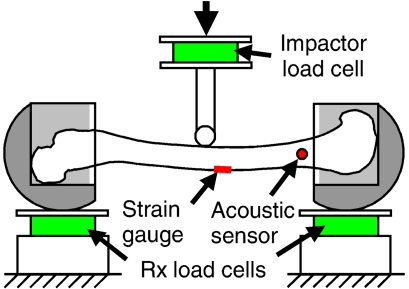
Specimens were placed in the test apparatus by attaching the bone cups to rolling supports in the configuration appropriate to the desired direction of bending (Figure 1). The bone ends were mounted such that the center of rotation of the rollers coincided as closely as possible with the joint center of rotation. The specimens were mounted in a universal test machine (Instron 8874, Canton, MA) with the rollers placed on supports instrumented with triaxial load cells (Hybrid III lumbar load cells, 1842, Denton ATD). The contact surfaces of the rolling supports were greased to reduce shear and moment. A cylindrical impactor (12 mm diameter) attached to the crosshead of the test machine was lowered until it touched the specimen precisely at its mid-length with a nominal resistive force (2 N). The test machine then applied a step displacement input at a constant velocity of approximately 1.2 m/s, fracturing the specimen in about 10–20 ms. All electronic data except for the acoustic sensors were sampled at 10,000 Hz using a DSP TRAQ-P data analysis system. The data were subsequently debiased and filtered to CFC1000. Acoustic emission (AE) data were sampled at 2.5 MHz using a digital storage oscilloscope (Lecroy 9350AM – 500 MHz, Chestnut Ridge, NY) and bandpass filtered from 50–400 kHz. After testing, an orthopaedic surgeon classified the fractures according to the AO/OTA (Arbeitsgemeinschaft für Osteosynthesefragen – Association for the Study of Internal Fixation/Orthopaedic Trauma Association) classification.

Figure 1.

Test apparatus.

DATA PROCESSING

The midshaft moment (M) was determined by averaging the value of each reaction load multiplied by the distance to the center of the bone. Linear beam theory was used to calculate the elastic modulus of the bone material using only the linear portion of the data (M less than half the peak value). Cross-sectional geometric properties, including the distance from the centroid to the outermost tensile fiber (c) and the moment of inertia (I) were obtained from pre-test CT scans (3 mm slices, 0.9375 mm/pixel) using an in-house computer program (Table 3). Elastic modulus was calculated using two methods, one based on moment-deflection data and one based on moment-strain data. The elastic modulus calculated from deflection (E_δ) was obtained from the slope of a line fit through the linear part of the moment-deflection curve:

Table 3.

Summary of geometric information.

Specimen#	L (mm)	2a/L	Area (mm2)	c (mm)	IM-L axis (mm4)	IA-P axis (mm4)
1-L	425	0.79	464	16.5	66518	35917
2-R	429	0.87	501	14.7	70771	44321
3-L	444	0.89	449	15.4	49508	45490
4-R	411	0.88	411	14.0	21297	26095
5-L	393	0.92	448	13.2	33845	24343
6-R	409	0.86	469	13.7	38264	27131
7-L	452	0.88	576	17.1	45506	39743
8-L	392	0.85	459	14.5	22908	30377
1-R	424	0.89	440	14.0	65697	35242
2-L	418	0.90	499	16.7	71038	42940
3-R	427	0.87	444	15.2	44613	26634
4-L	427	0.88	412	14.0	19973	27008
5-R	385	0.96	463	14.3	37156	23189
6-L	417	0.91	447	10.5	49706	32075
7-R	444	0.86	579	14.4	43899	39568
Mean	420	0.88	471	14.5	45380	33338
SD	20	0.04	50	1.6	17286	7657

$$M=\frac{12E_{\delta }I}{L^2}\delta$$ (1)

where L was the distance between the reaction loads and δ was the displacement of the crosshead. The elastic modulus calculated from the strain gauge data (E_g) was obtained from the slope of a line fitted through the linear part of the moment-strain curve:

$$M=\frac{E_{g}I}{c}\left(\frac{L}{2a}\right){\epsilon }_g$$ (2)

where a was the distance from the point of application of the distal reaction load to the strain gauge and ɛ_g was the principal longitudinal strain calculated from the rosette.

Ultimate stress and strain were calculated by assuming an elastic-perfectly plastic (EPP) material model. The parameters defined by Burstein et al. (1972) were used in the present study. The amount of post-yield strain was characterized by the strain ratio (γ), defined as the yield strain (ɛ_y) divided by the maximum strain (ɛ_max):

$$\gamma =\frac{{\epsilon }_y}{{\epsilon }_{max}}$$ (3)

The value of γ is equal to 1 for a brittle material and less than one after yield in an EPP material. The yield stress (σ_y) was assumed to be equal to the ultimate stress (σ_ult). However, this value could be different in tension and compression according to the yield ratio (η):

$$\eta =\frac{{\sigma }_{yC}}{{\sigma }_{yT}}$$ (4)

If the material yields only in tension, η is large (∞). In cases of asymmetric yielding (η ≠ 1), an additional parameter is necessary to express the post-yield shift in the location of the neutral axis (C):

$$C=\frac{c}{h}$$ (5)

where the distance from the neutral axis to the outer fiber is given by h in the linear region and c in the plastic region.

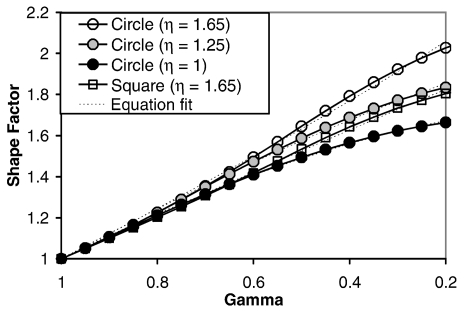
After yield, an EPP beam is able to withstand additional moment before failure. This phenomenon is characterized by the shape factor, which is the ratio of the plastic moment (M_p) to the yield moment (M_y) (Beer and Johnston, 1992). Calculating the shape factor as a function of γ (for a given η) involves integrating the stress multiplied by the fiber distance to the neutral axis over the shape of the cross-section. Burstein et al. (1972) derived equations expressing the shape factor of a solid square and solid circular cross-section as a function of γ and η. Unfortunately, these equations are complicated and have no closed-form solution in many cases. Therefore, an approximate equation form for the shape factor function was employed in the present study:

$$\frac{M_p}{M_y}=A-(A-1){\gamma }^B$$ (6)

where A is ostensibly the shape factor (for a fully plastic hinge) and B is obtained from a least-squares fit to the actual solution. The accuracy of this approximation can be improved slightly if A is not constrained and the least-squares fit is only performed over the region of interest, which in this case was chosen to be 0.2 < γ < 1. Several equation fits were performed to derive coefficients for various types of beams (Table 4). In all cases, the fits were extremely close to the original solution over the region of interest (R² > 0.99, max error ≤ 2%) (Figure 2).

Table 4.

Shape factor function coefficients for eq. (6) and eq. (9).

Shape	η	A	B	A′	B′
Hollow Circle (di/do = 0.5)	1	1.596	2.042
Circle	1	1.727	1.603
Circle	1.25	1.977	1.280	1.983	1.314
Circle	1.65	2.422	0.848	2.489	0.843
Circle	∞	3.808	0.378	4.872	0.281
Hollow square (di/do = 0.5)	1	1.393	2.690
Square	1	1.500	2.000
Square	1.25	1.682	1.603	1.682	1.703
Square	1.65	2.005	1.066	2.035	1.119
Square	∞	2.666	0.563	3.000	0.500

Figure 2.

Shape factor function for selected shapes.

One objective of this study was to characterize the post-yield deflection of a beam. For a linear elastic material subjected to bending, it can be shown that the curvature of the beam is given by:

$$\frac{d^{2}y}{d{x}^2}=\frac{1}{\rho }=\frac{M}{E_{\delta }I}$$ (7)

where ρ is the radius of curvature. The curvature of the beam in the plastic region can be shown to be dependent on the yield moment (M_y), the strain ratio (γ), and the location of the neutral axis (C):

$$\frac{d^{2}y}{d{x}^2}=\frac{1}{{\rho }_p}=\frac{M_y}{E_{\delta }I}·\frac{1}{\gamma C}$$ (8)

In materials with asymmetric yielding (η ≠ 1), the dependence of curvature on the product γC requires an additional equation approximation to account for the shift of the neutral axis after yield:

$$\frac{M_p}{M_y}=A^{\prime }-(A^{\prime }-1){(\gamma C)}^{B^{\prime }}$$ (9)

For materials that yield symmetrically in tension and compression (η = 1), A′ and B′ are equal to A and B, respectively.

Deflection of a beam is calculated by double-integrating its curvature along the length of the beam and applying the appropriate boundary conditions. The deflection of the center of a linear elastic beam subjected to three-point bending is given by:

$$\delta =\frac{M{L}^2}{12E_{\delta }I}$$ (10)

After yield, it can be shown that the deflection equation becomes:

$$\delta =\frac{M_y{L}^2}{12E_{\delta }I}\left\{\frac{C_1{(\gamma C)}^{2B^{\prime }-1}+C_2{(\gamma C)}^{B^{\prime }-1}+C_3}{{\left[A^{\prime }-(A^{\prime }-1){(\gamma C)}^{B^{\prime }}\right]}^2}\right\}$$ (11)

where

$$\begin{array}{l}{C}_1=\frac{3B^{\prime }{(A^{\prime }-1)}^2}{2B^{\prime }-1}\\ C_2=\frac{-3A^{\prime }{B}^{\prime }(A^{\prime }-1)}{B^{\prime }-1}\\ C_3=\frac{1-3A^{\prime }{B}^{\prime }+3{A^{\prime }}^2{B^{\prime }}^2-{B^{\prime }}^2}{(B^{\prime }-1)(2B^{\prime }-1)}\end{array}$$

The post-yield moment-deflection equation form is obtained by combining eq. (11) with eq. (9):

$$M_p=\frac{12E_{\delta }I}{L^2}\left\{\frac{{\left[A^{\prime }-(A^{\prime }-1){(\gamma C)}^{B^{\prime }}\right]}^3}{C_1{(\gamma C)}^{2B^{\prime }-1}+C_2{(\gamma C)}^{B-1}+C_3}\right\}\delta$$ (12)

The equation relating the post-yield moment to the strain measured at the gauge is obtained by combining eq. (2), eq. (3), and eq. (6):

$$M_p=\frac{E_{g}I}{c}\left(\frac{L}{2a}\right)\left[A-(A-1){\gamma }_g^B\right]{\gamma }_g{\epsilon }_g$$ (13)

where γ_g represents the strain ratio at the location of the strain gauge, as opposed to the strain ratio at center of the bone, designated by γ.

Post-yield bone material properties were calculated by performing least-squares fits of the theoretical equations to the experimental data using the Solver tool in Microsoft Excel. Four different shapes were studied to characterize a wide range of possible cross-sections, including solid circles with three different η values (1.65, 1.25, and 1) and a solid square with η = 1.65. For each shape, eq. (1) and eq. (12) were fit to the moment-deflection data, solving for γC for each specimen. When necessary, the equations of Burstein et al. (1972) were used to obtain γ from γC. Eq. (2) and eq. (13) were fit to the moment-strain data for each shape to obtain γ_g for each specimen. The value of γ at the center of the bone was determined from γ_g using the following relationship:

$$\gamma ={\left[\frac{A}{A-1}-\left(\frac{L}{2a}\right)\left(\frac{A}{A-1}-{\gamma }_g^B\right)\right]}^{\frac{1}{B}}$$ (14)

Results between matched pairs of femurs tested in P-A and L-M bending were statistically compared using a one-tailed paired t-test. Linear regressions were performed to examine the effect of various specimen parameters on the failure moment.

RESULTS

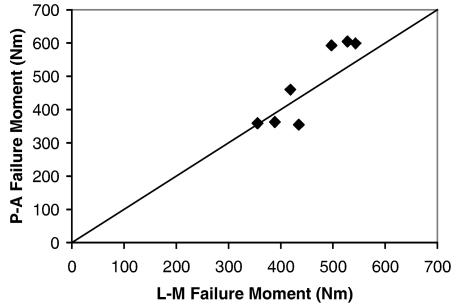
The mean failure moment for all specimens was 458 ± 95 Nm, which corresponded to a summed support load of 4349 ± 746 N (Table 5). In femurs from the same individual, the mean failure moment was 4% ± 13% higher in P-A bending than L-M bending, but this difference was not statistically significant (p = 0.172) (Figure 3). The mean deflection of the center of the bone at failure was 17.6 ± 3.8 mm and was slightly higher in the P-A group (18.4 ± 4.2 mm) compared to the M-L group (16.7 ± 3.4 mm) (p = 0.096). The most common fracture pattern was a tension wedge, which occurred in 67% of the specimens. Transverse fractures were also common, occurring in 27% of the specimens. One specimen sustained both a tension and a compression wedge, with the tension wedge occurring beneath the point of impact.

Table 5.

Summary of test results. Fracture patterns are transverse (T), tension wedge (TW), and tension/compression wedge (T/CW).

Spec#	Load direction	Moment (Nm)	Rx Force (N)	Defl (mm)	Fx pattern	AO code
1-L	P-A	355	3339	12.3	T	32A3.2
2-R	P-A	593	5529	22.8	TW	32B2.2
3-L	P-A	605	5445	23.9	TW	32B2.2
4-R	P-A	363	3599	19.6	TW	32B3.2
5-L	P-A	359	3651	14.5	TW	32B2.2
6-R	P-A	460	4499	14.9	T/CW	32C3.1
7-L	P-A	599	5301	20.5	T	32A3.2
8-L	P-A	373	3809	19.0	TW	32B2.2
1-R	L-M	435	4104	13.0	T	32A3.2
2-L	L-M	497	4759	16.1	TW	32B2.2
3-R	L-M	528	4943	23.3	T	32A3.2
4-L	L-M	389	3646	18.0	TW	32B2.2
5-R	L-M	356	3695	13.8	TW	32B2.2
6-L	L-M	419	4018	16.6	TW	32B2.2
7-R	L-M	543	4890	15.8	TW	32B3.2
Mean		458	4349	17.6
SD		95	746	3.8

Figure 3.

Comparison of bending tolerance by loading direction.

Different results for bone material properties were obtained depending on whether moment-deflection data or moment-strain data were analyzed (Tables 6 and 7). The elastic modulus of the bone was 40% ± 20% higher when calculated from strain gauge data compared to deflection data (p < 0.001). The estimated degree of yielding was similar regardless of whether deflection data (γ = 0.34 ± 0.07) or strain gauge data (γ = 0.39 ± 0.10) were analyzed. The estimated yield stress was also similar for both data processing methods (100 ± 28 MPa vs. 101 ± 24 MPa). However, the moment-deflection curves produced higher estimates for the yield strain (0.78% ± 0.15%) and ultimate strain (2.41% ± 0.63%) of the bone than did the moment-strain curves (0.57% ± 0.06% and 1.60% ± 0.71%, respectively). Compared to the EPP material model, linear beam theory overpredicted the ultimate stress by a factor of approximately 1.6–1.9 and underpredicted the ultimate strain by approximately 30%–40%.

Table 6.

Material properties derived from moment-deflection data assuming a circular cross-section (η = 1.65).

Spec #	Eδ (GPa)	γ	σy (MPa)	ɛy	ɛult
1-L	7.1	0.47	53	0.74%	1.57%
2-R	11.5	0.30	64	0.55%	1.85%
3-L	11.7	0.20	89	0.76%	3.82%
4-R	14.2	0.34	127	0.90%	2.64%
5-L	11.5	0.21	67	0.58%	2.76%
6-R	12.1	0.37	90	0.74%	2.01%
7-L	12.5	0.37	123	0.98%	2.68%
8-L	12.5	0.34	126	1.01%	2.96%
1-R	14.9	0.40	97	0.65%	1.63%
2-L	11.8	0.36	105	0.89%	2.46%
3-R	16.1	0.31	156	0.97%	3.17%
4-L	13.0	0.34	107	0.83%	2.41%
5-R	14.0	0.36	119	0.85%	2.34%
6-L	12.2	0.34	73	0.60%	1.78%
7-R	15.9	0.32	104	0.65%	2.02%
Mean	12.7	0.34	100	0.78%	2.41%
SD	2.2	0.07	28	0.15%	0.63%

Table 7.

Material properties derived from moment-strain data assuming a circular cross-section (η = 1.65).

Spec #	Eg (GPa)	γg	γ	σy (MPa)	ɛy	ɛult
1-L	11.0	0.75	0.50	57	0.52%	1.04%
2-R	16.3	0.55	0.39	111	0.68%	1.75%
3-L	N/A	N/A	N/A	N/A	N/A	N/A
4-R	18.9	0.57	0.42	121	0.64%	1.51%
5-L	17.7	0.60	0.51	89	0.50%	0.98%
6-R	16.7	0.51	0.34	90	0.54%	1.58%
7-L	20.4	0.61	0.47	95	0.47%	0.99%
8-L	20.6	0.52	0.27	121	0.59%	2.18%
1-R	17.5	0.63	0.50	94	0.54%	1.07%
2-L	17.5	0.50	0.39	100	0.57%	1.48%
3-R	23.7	0.42	0.18	154	0.65%	3.70%
4-L	18.9	0.50	0.35	107	0.57%	1.62%
5-R	21.4	0.58	0.53	118	0.55%	1.05%
6-L	11.1	0.48	0.37	63	0.57%	1.55%
7-R	16.8	0.47	0.29	97	0.58%	1.97%
Mean	17.7	0.55	0.39	101	0.57%	1.60%
SD	3.5	0.08	0.10	24	0.06%	0.71%

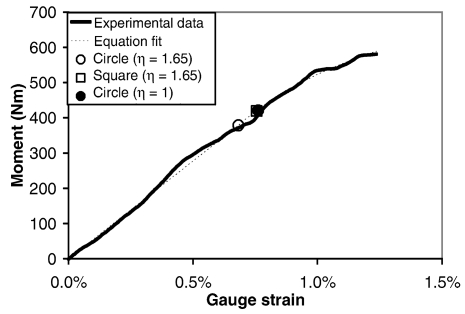
Parameter estimation for the EPP material model was not highly dependent on the assumed shape factor function. Estimated values for the strain ratio (γ) and ultimate strain were similar for all four shape factor functions investigated. Estimated values for yield stress and yield strain increased as the value of the shape factor decreased. Relative to the reported values for an assumed circular cross-section with η = 1.65, estimated values for yield stress and yield strain were about 10% higher for the assumption of a square cross-section with η = 1.65, and about 15% higher for the assumption of a circular cross-section with η = 1 (Figure 4). No significant directional dependence was observed with respect to the strain ratio, yield stress, yield strain, or ultimate strain.

Figure 4.

Equation fits showing estimated yield points (2-R).

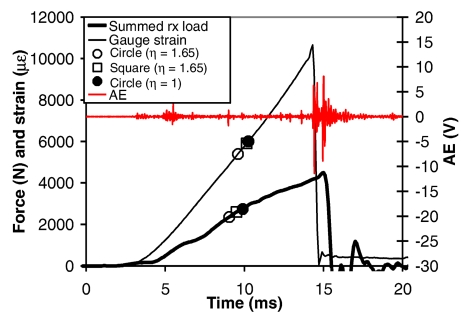
In all tests, the summed support load and gauge strain rose monotonically until failure (Figure 5). The gauge strain typically peaked about 1 ms before the reaction load. The timing of the peak strain always coincided with a high amplitude burst of acoustic emission. In seven of the tests, one or two low amplitude AE bursts occurred prior to fracture, but the timing of these bursts generally did not correspond to the estimated time of yielding.

Figure 5.

Typical timing of summed support load, gauge strain, acoustic emission, and estimated yield points (6-L).

Although the sample size of the present study was too small for a detailed statistical analysis, several statistically significant trends were observed in the data. Linear regression analyses showed that failure moment was positively related to the body mass, femur length, and BMD of the donor, and negatively related to donor age (Table 8). Increasing donor age was also associated with a decrease in the elastic modulus (p = 0.071) and the degree of yielding (increase in γ) (p = 0.029). There was no relationship between the calculated material properties of the bone material (σ_y, ɛ_y, ɛ_ult, γ) and the structural strength (M) of the whole bone.

Table 8.

Linear regression fits to failure moment data (M = mx + b).

	Age (yrs)	Body mass (kg)	Femur length (mm)	BMD (g/cm2)
m	−6.31	2.52	3.28	144
b	831	243	−1100	521
R2	0.47	0.34	0.50	0.58
p-value	0.005	0.024	0.003	0.003

DISCUSSION

The present data demonstrate that the dynamic bending tolerance of the femur for mid-sized males is dramatically higher than results from many previous studies suggest (Table 1). This is probably due to the fact that the present study used only femurs from male donors and tested them at dynamic loading rates. The average height (177 cm) and femur length (47.4 cm) of the donors in this study compared very well to a 50^th percentile male, although the average weight was somewhat greater (86 kg). Even within this relatively homogeneous donor group, the influence of age, body size, and BMD was significant (Table 8). Equally important was the finding that the bending tolerance of the femur did not differ significantly with loading direction in this study. The implication is that a much larger pool of biomechanical data encompassing different loading directions may be combined to derive injury criteria for predicting femur fractures in pedestrians and vehicle occupants.

The most common fracture pattern observed in this study was the tension wedge, which occurred in two thirds of the specimens tested. The tension wedge accurately indicated loading direction in both P-A and L-M bending tests. This observation is at odds with the results of Martens et al. (1986), who reported that all 28 of their midshaft fractures generated by P-A bending were compressive wedges. No true compression wedge fractures were observed in this study. Other femur bending studies have reported compression wedge fractures only very rarely (Kress et al., 1993), or not at all (Stromsoe et al., 1995; Kerrigan et al., 2003; Matsui et al., 2004).

A method was developed to estimate elastic-plastic material properties from three-point bending tests. This method addresses the complaint of previous investigators that it is not possible to determine the yield strain of bending specimens because the onset of yield is too gentle (Currey, 1999). However, it must be acknowledged that a three-point bending test is not nearly as sensitive as a uniaxial tension test for determining the onset of yield. The method developed in this study relies on a least-squares fit of a rather subtle curve in the experimental data. The difficulty is exacerbated by noisy data, which are common in dynamic tests. In addition, a simplified shape factor function must be assumed to represent a complicated cross-sectional geometry. Fortunately, the results reported here were relatively insensitive to the choice of shape factor function. The advantage of the present approach is that both structural and material properties can be derived using the same data from a realistic whole bone bending test. This method could also be applied to a three-point bending test of a small machined specimen.

In the present study, the strain gauge was not affixed to the bone at the expected fracture site out of concern that the mounting process would alter the material properties of the bone. The mounting process involves drying the bone with ether, which may reduce the amount of plastic deformation prior to fracture (Burstein et al., 1972). In addition, the cyanoacrylate adhesive and the strain gauge itself may affect the local properties of the bone. Therefore, the strain gauges were placed a short distance away from the center of the bone and the strain at the center of the bone was calculated using eq. (14).

An interesting result from this study was that the strain gauge measurements always predicted less strain at the center of the bone than the deflection measurements, in spite of the fact that these two measurements are theoretically redundant. Consequently, the elastic modulus was 40% greater on average when it was derived from strain gauge data compared to deflection data. The strain gauge data are presumed to be more accurate because they are a direct measurement. Deflection at the center of the bone may have been greater than expected due to the effect of shear stresses or a varying bending rigidity (EI) along the length of the bone. Regardless of the reason, the data demonstrate a systematic error in the estimation of strain-related material properties based on deflection data from whole bone three-point bending tests.

Despite the discrepancy in predicted strain values, the deflection and strain gauge data were in agreement with regard to the post-yield strain ratio (γ). Less yielding was observed at the location of the strain gauge compared to the center of the bone as calculated from the deflection data (γ_g > γ). However, when the strain ratio at the gauge was scaled to the center of the bone (eq. 14), the two methods were generally in good agreement. The EPP material model accurately predicted not only the deflection behavior at the center of the bone, but also the tensile strain a short distance away (~5% of the bone length). This validates the use of an EPP material model to describe the tensile strain field due to yielding in a three-point bending test. Furthermore, the values for bone material properties derived here are in good agreement with uniaxial tension experiments involving small machined specimens, although the small machined specimens appear to yield to a somewhat higher ultimate strain before failure (Reilly et al., 1974; Burstein et al., 1976; Wright et al., 1981; Fischer et al., 1986; McCalden et al., 1993). This finding suggests that the yielding properties of whole bones in bending are similar to small machined specimens in tension, although the failure properties may be somewhat different.

Recent pedestrian lower extremity finite element models incorporate elastic-plastic bone material properties obtained from the bone biomechanics literature and validated against structural tests of whole bones (Takahashi et al., 2000; Schuster et al., 2000). Findings from the present study support that approach. It is understood that an elastic-plastic material model of bone is only meant to be a phenomenological description of macroscopic behavior, and is not meant to imply that the microstructural mechanisms of yielding in bone are the similar to those seen in metals and other elastic-plastic engineering materials. This study did not the address microstructural aspects of bone failure, other than to note that little or no AE occurred prior to fracture. AE would not be expected at the onset of yield in a three-point bending test, because only a small portion of the bone yields initially.

CONCLUSIONS

1. The mean dynamic bending tolerance of the 15 femurs tested in this study was 458 ± 95 Nm. This value approximates the dynamic femur bending tolerance of a 50^th percentile male.

2. The bending tolerance of the femur did not differ significantly with loading direction (p = 0.172).

3. Elastic-plastic bone material properties were estimated using strain gauge data from whole bone three-point bending tests. For an assumed circular cross-section with a yield stress ratio (η) of 1.65, the mean elastic modulus was 17.7 ± 3.5 GPa, the mean yield stress was 101 ± 24 MPa, the mean yield strain was 0.57% ± 0.06%, and the mean ultimate strain was 1.60% ± 0.71%.

4. Deflection measurements in whole bone three-point bending tests underpredicted the elastic modulus, yield strain, and ultimate strain of bone when compared to direct strain gauge measurements by approximately 40%.

5. Compared to an elastic-perfectly plastic material model, linear beam theory overpredicted the ultimate stress in the bone by a factor of approximately 1.6–1.9 and underpredicted the ultimate strain in the bone by approximately 30%–40%.