Prediction of Severe Eye Injuries in Automobile Accidents: Static and Dynamic Rupture Pressure of the Eye

Abstract

The purpose of this paper is to determine the static and dynamic rupture pressures of 20 human and 20 porcine eyes. This study found the static test results show an average rupture pressure for porcine eyes of 1.00 ± 0.18 MPa while the average rupture pressure for human eyes was 0.36 ± 0.20 MPa. For dynamic loading, the average porcine rupture pressure was 1.64 ± 0.32 MPa, and the average rupture pressure for human eyes was 0.91 ± 0.29 MPa. Significant differences are found between average rupture pressures from all four groups of tests (p = 0.01). A risk function has been developed and predicts a 50% risk of globe rupture at 1.02 MPa, 1.66 MPa, 0.35 MPa, and 0.90 MPa internal pressure for porcine static, porcine dynamic, human static, and human dynamic loading conditions, respectively.

The improvement of automobile safety systems has reduced the number of life threatening injuries sustained by crash victims (Libertiny 1995; Malliaris et al. 1995). Whereas in most cases, these improved safety systems lower the overall incidence of injuries in crashes, certain types of injuries have become more prevalent with the advanced restraint systems. Eye injuries sustained during automobile crashes occur at a higher rate (3.1%) when the occupant is exposed to a deploying airbag than when the occupant is not (2.0%) (Duma et al. 2002). During airbag deployment, foam particles are released that have been linked to eye injury (Duma and Crandall 2000; Fukagawa et al. 1993; Hansen et al. 2003). Blunt impact of the eye with an airbag, night vision goggles, or other objects can result in severe eye injury such as hyphema or globe rupture (Bass et al. 2002; Chisholm 1969; Duma et al. 1996; Ghafouri et al. 1997; Lueder 2000; Power et al. 2002; Stein et al. 1999; Vichnin et al. 1995) (Figure 1). Of vehicle occupants sustaining an eye injury during a crash as many as 15% to 25% sustain severe eye injuries (Duma et al. 2002). Tools such as finite element models of the eye have been developed to study the risk of eye injury in impact situations (Stitzel et al. 2002) (Figure 2); however, the usefulness of such models is limited by the relative paucity of data on material properties and dynamic structural response of the eye. With accurate material properties and validation to the structural response of actual tissue, computational models allow the researcher to observe and characterize the response of tissues that are impossible or difficult to observe in laboratory experiments. However, accurate experimental data is, of course, required before computational models can be built and validated for this purpose.

Figure 1.

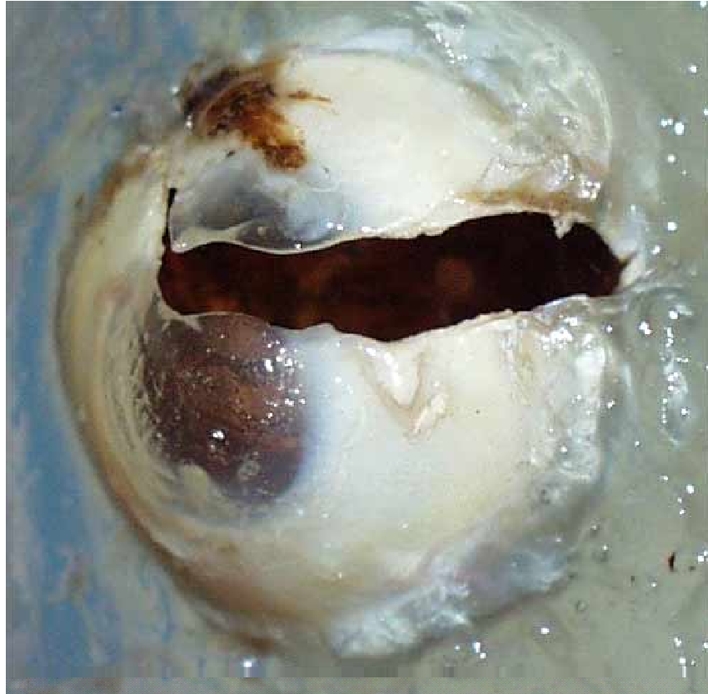
Globe rupture due to blunt force trauma.

Figure 2.

Computational model of the eye (Stitzel et al. 2002).

To determine the material properties of the eye, dynamic uniaxial strip tests were conducted on the sclera and cornea by Kisielewicz et al. (1998) and Uchio et al. (1999). However, no work was performed to identify the dynamic rupture pressure of the eye. For in situ testing, the presence of other anatomical ocular components will affect the overall response of the eye to impact loading; therefore, it is desirable that material properties and structural response of the eye are obtained in a more lifelike manner. Currently, computer models are unable to show rupture; instead the user must infer rupture based on other related outputs of the model such as intraocular pressure. Without experimentally verified data, computer models are unable to predict globe rupture.

Additionally, safe intraocular pressures are of particular interest to the clinical ophthalmologist, who may not be aware of the upper range for intraocular pressures before the eye would rupture. To determine the effect of ocular surgery on the strength of eyes, Burnstein et al. (1995) and Pinheiro et al. (1995) performed static rupture tests on human and porcine eyes. Burnstein et al. found the rupture pressure of human eyes subjected to photorefractive keratectomy to be 0.46 ± 0.12 MPa. Porcine eyes subjected to photorefractive keratectomy were observed to rupture at 0.53 ± 0.10 MPa. Pinheiro et al. (1995) studied the anterior chamber of the eye and found rupture pressures for unoperated human eyes to be 1.27 ± 0.06 MPa. No experiments have been found where globe rupture was studied for the intent of learning the structural failure properties of healthy postmortem eyes.

Due to the lack of data on dynamic rupture pressure of the eye, the purpose of this study is to determine the static and dynamic rupture pressure of human and porcine eyes. Furthermore, this rupture pressure data was used to develop injury risk functions to predict the likelihood of severe eye injuries due to increased internal pressure. Although the scope of this study does not provide new material properties also needed for computational models, it will allow for much needed risk assessment for globe rupture due to increasing internal pressure. This will be valuable not only for computer models but physical experimental models as well.

METHODS

A pressure system that utilizes physiological fluid to internally pressurize the eye was built to examine the static and dynamic rupture pressures for human and porcine eyes (Figure 3). Porcine eyes were included in the test matrix due to their frequent use in previous automotive ocular research. Static testing was accomplished by increasing the internal pressure of the eye by approximately 0.02 MPa/second, using 10 human and 10 porcine eyes until the eyes ruptured at their maximum static pressure. In addition, the dynamic testing of 10 human and 10 porcine eyes was accomplished by setting the initial pressure to release at 2.8 MPa, resulting in a loading rate of approximately 2.77 MPa/second, and measuring the pressure at which the eyes ruptured. The eye was connected to the pressure system via tubing and a 16 gauge intravenous (IV) needle inserted through the optic nerve. The optic nerve was clinched to the needle to form a water-tight seal and secure the eye during pressurization. The eye was mounted in the test apparatus and a holding tank was pressurized with nitrogen to a pressure set by a pressure regulator. The release of a solenoid valve would release the nitrogen to a saline holding area forcing saline to pressurize the eye.

Figure 3.

Schematic of eye pressurization system.

The exact time and pressure at rupture was determined by high-speed video (Phantom 4, Vision Research, Wayne, NJ) that was synchronized with a pressure transducer (HKM-375-500G, Kulite Semiconductor, Leonia, NJ). Static test data was recorded at 50 Hz, while the dynamic test data was recorded at 6 kHz. High-speed video was taken at 50 frames/second for static tests and 6000 frames/second for dynamic tests.

Postmortem human and porcine eyes were used for this experiment. Twenty human eyes were procured from the Roanoke Eye Bank (Roanoke, VA). All eyes used were completely intact, meaning no eyes were tested that had undergone corneal transplantation or other donor procedures. To prevent the tissue from breaking down prior to test, the eyes were packaged in gauze and saline solution and refrigerated in glass jars until testing. Age of donors ranged from 55 to 87 years of age, and the eyes were tested at a range of 21 to 115 days after death (Table 1). Twenty porcine eyes were procured from Animal Technologies (Tyler, TX) and were shipped to the testing location in saline with tissue attached. Porcine eyes used were tested within 48 hours of slaughter and the donor pigs were between six and nine months of age. All test procedures were reviewed and approved by the Virginia Tech Institutional Review Board.

Table 1.

Age and days after death information for human eyes.

Human Static			Human Dynamic
Test	Donor Age (Years)	Days to Test	Test	Donor Age (Years)	Days to Test
SH1	85	81	DH1	75	93
SH2	65	29	DH2	55	78
SH3	71	88	DH3	72	21
SH4	65	24	DH4	85	80
SH5	72	25	DH5	70	86
SH6	87	76	DH6	67	87
SH7	67	36	DH7	60	39
SH8	67	36	DH8	71	115
SH9	71	57	DH9	72	96
SH10	75	35	DH10	63	112
Average	73	49	Average	69	81
Standard Deviation	8	25	Standard Deviation	8	30

Risk functions were developed for eye rupture in a similar methodology used in previous biomechanics research (Funk et al. 2002). In order to develop risk functions for each of the different scenarios, survival analysis methodology was utilized. Parametric survival analysis (Collett 1999) was performed on rupture pressure data for all four testing scenarios and was used to develop the risk functions using a Weibull distribution. These risk functions were then plotted to create a chart for the risk of eye rupture, determined by the intraocular pressure of the eye, for all four types of tests.

RESULTS

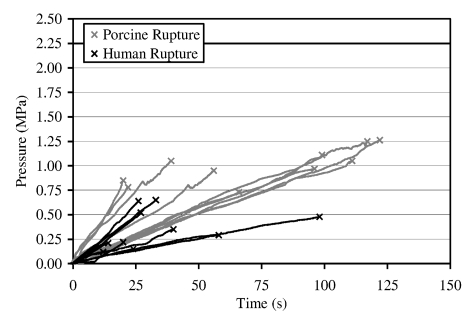
Globe rupture occurred primarily at the equator for both static and dynamic tests (Figure 4). The average loading rate under static loading was 0.02 ± 0.01 MPa/second while the average loading rate for dynamic tests was 2.77 ± 0.58 MPa/second. Static test results displayed an average rupture pressure for porcine eyes of 1.00 ± 0.18 MPa while the average rupture pressure for human eyes was 0.36 ± 0.20 MPa (Table 2) (Figure 5). Porcine eyes under static loading were found to be significantly stronger than human eyes (p = 0.01). For dynamic loading, the average porcine rupture pressure was 1.64 ± 0.32 MPa, and the average rupture pressure for human eyes was 0.91 ± 0.29 MPa (Table 3) (Figure 6). Again, the porcine eyes were found to be significantly stronger than the human eyes (p = 0.01). Additionally, the dynamic rupture pressures for both porcine and human eyes were significantly higher (p = 0.01) than the static rupture pressures.

Figure 4.

a) Pre-test picture of the human eye mounted to pressurization needle, b) post-test picture with rupture site seen at equator of eye.

Table 2.

Data for static rupture testing.

Porcine Static			Human Static
Test	Time to Rupture (s)	Rupture Pressure (MPa)	Test	Time to Rupture (s)	Rupture Pressure (MPa)
SP1	117	1.25	SH1	40	0.35
SP2	111	1.05	SH2	12	0.12
SP3	66	0.73	SH3	98	0.48
SP4	96	0.97	SH4	24	0.15
SP5	122	1.26	SH5	58	0.29
SP6	99	1.11	SH6	20	0.22
SP7	56	0.95	SH7	26	0.64
SP8	39	1.05	SH8	27	0.52
SP9	22	0.78	SH9	33	0.65
SP10	20	0.85	SH10	14	0.21
Average	75	1.00	Average	35	0.36
Standard Deviation	39	0.18	Standard Deviation	26	0.20

Figure 5.

Pressure vs. time plot for static pressurization of both porcine and human eyes.

Table 3.

Data for dynamic rupture testing.

Porcine Dynamic			Human Dynamic
Test	Time to Rupture (s)	Rupture Pressure (MPa)	Test	Time to Rupture (s)	Rupture Pressure (MPa)
DP1	0.47	1.06	DH1	0.38	0.85
DP2	0.68	1.75	DH2	0.44	0.84
DP3	0.77	1.61	DH3	0.41	0.81
DP4	0.61	1.51	DH4	0.41	0.79
DP5	0.58	1.78	DH5	0.53	0.94
DP6	0.41	1.34	DH6	0.59	0.88
DP7	1.18	1.91	DH7	0.30	0.79
DP8	1.18	2.18	DH8	0.21	0.82
DP9	0.47	1.81	DH9	0.23	0.68
DP10	0.57	1.46	DH10	0.53	1.70
Average	0.69	1.64	Average	0.40	0.91
Standard Deviation	0.28	0.32	Standard Deviation	0.13	0.29

Figure 6.

Pressure vs. time plot for dynamic pressurization of both porcine and human eyes.

For human eyes, rupture pressure was found to be independent of both age and time from death before testing. Maximum pressure sustained did not correlate to the age of the donor either under static (R² = 0.02), or dynamic loading rates (R² = 0.08). Rupture pressure also did not correlate to the number of days from death prior to testing for static (R² = 0.06), or dynamic testing (R² = 0.14).

Using parametric survival analysis, the general formula for the risk function based on the Weibull distribution using a linear predictor is given in Equation 1. In this equation, the internal pressure of the eye is specified in MPa and the units of the coefficients β₀ and σ are also specified in MPa. Values for the coefficients for static and dynamic porcine, and static and dynamic human analyses are given (Table 4).

Table 4.

Model parameters for single variable risk function to predict globe rupture due to internal pressure. (Values listed are in units of MPa)

	Static		Dynamic
	Porcine	Human	Porcine	Human
Intercept (β0)	0.0702	−0.8872	0.5680	0.0098
Scale (σ)	0.1517	0.4806	0.1610	0.3161

$$\begin{array}{l}\text{Risk}\hspace{0.17em}\text{of}\hspace{0.17em}\text{Globe}\hspace{0.17em}\text{Rupture}\hspace{0.17em}(pressure,linear\hspace{0.17em}predictor)=\\ 1-e^{-e^{\left[\frac{1}{\sigma }ln(pressue)-\frac{{\beta }_0}{\sigma }\right]}}\end{array}$$ (1)

Utilizing the developed risk function to predict globe rupture, injury risk curves are presented for porcine and human eyes, under both static and dynamic loading rates (Figure 7). The injury risk function predicts a 50% risk of rupture at 1.02 MPa, 1.66 MPa, 0.35 MPa, and 0.90 MPa internal pressure for porcine static, porcine dynamic, human static, and human dynamic loading conditions, respectively.

Figure 7.

Eye rupture risk curves for porcine and human eyes, both static and dynamic loading rates.

DISCUSSION

Static human rupture pressures of 0.36 ± 0.20 MPa compare favorably with the results observed by Burnstein et al. (1995) at 0.46 ± 0.12 MPa. Static porcine rupture pressures do not compare as well, with the observed rupture pressure of 1.00 ± 0.18 MPa being nearly twice as high as that observed by Burnstein et al. (0.53 ± 0.10 MPa). It is unknown how the ages and breed of the pigs used in this and Burnstein et al.’s study compare; therefore, it is possible that either age or breed differences between pigs could contribute to differences observed between these two studies.

In this study, the age of the specimens used differs greatly between the human and porcine eyes. It is therefore also possible that some of the differences observed between human and porcine eyes can be attributed to age. However, porcine eyes typically used in biomechanics research are obtained from young, recently sacrificed pigs, while human eyes are generally obtained from the elderly segment of the population. For this reason, it is of interest to compare results of testing of these different types of eyes, as both are commonly used in an attempt to predict injuries in humans.

Although the age range of donors was between 55 and 87 years, rupture pressure and age are shown to be completely independent, both for static and dynamic tests (R² = 0.02 and R² = 0.08, respectively). This suggests that at least for the integrity of the globe, little structural changes occur in the latter stages of life. Similarly, all eyes were stored in saline and refrigerated prior to testing, and the rupture pressure and the number of days after death before testing are also shown to be completely independent, both for static and dynamic tests (R² = 0.06 and R² = 0.14, respectively). This is likely because the cornea and sclera are acellular and their strength comes from collagen fibers similar to those found in ligaments. These tissues break down very slowly and are sensitive to freeze-thaw cycles. Since the tissue was never frozen and was stored in refrigerated saline, the integrity of the globe was maintained prior to testing.

Both human and porcine eyes exhibit large viscoelastic effects when loaded dynamically. The viscoelastic behavior of the eye under dynamic loading is consistent with that seen in other biological tissue (Yamada and Evans 1970). Under dynamic loading the human eye can withstand approximately 150% more pressure before rupture than under static loading, while under the same circumstances the porcine eye can withstand approximately 64% more pressure before rupture. This behavior proves that previously determined material characteristics of the eye from static tests will lead to inaccurate predictions of the rupture pressure of the eye, both human and porcine.

The primary site of rupture is reported to occur at the equator. This is consistent with other research that has shown equatorial globe rupture to occur due to blunt object impact with very large objects, such as a baseball (Stitzel et al. 2002). Assuming blunt object impact with no sharp edges, such as an airbag, the eye is expected to fail at its weakest point. Therefore, since failures occur primarily at the equator of the eye, this study suggests that the equator is the weakest portion of the eye.

Given their anatomical similarities and availability, porcine eyes have been used for automotive safety design (Duma et al. 2000). However, testing results indicated that the porcine eye is significantly stronger (p = 0.01) than human eyes in both static and dynamic testing. With their common use as surrogates for human eyes, this research proves that researchers must exercise caution when evaluating the risk of injury to human occupants based on tests performed on porcine eyes. If the risk of globe rupture is being evaluated, this study indicates that separate criterion must be used to evaluate the injury potential to human occupants depending on which surrogate eye or eye model is used.

While it is possible to obtain material properties, such as failure stress and strain of the eye, there are several limitations to this approach. Failure stress of the eye can be calculated using the assumption of a thin-walled sphere (Equation 2).

$$\text{Stress}\hspace{0.17em}\text{of}\hspace{0.17em}\text{corneo}-\text{scleral}\hspace{0.17em}\text{shell}=\sigma =\frac{Pr}{2t}$$ (2)

In this equation, the pressure at failure, P, is used along with the radius of the eye, r, and the thickness, t, of the corneo-scleral membrane. The pressure at failure is known, and the radius of the eye can be measured from the high-speed video data of the test; however, the accuracy of the measurement is limited by the resolution of the video. In order to determine the thickness of the eye, histological sections must be taken from the post-test eyes. Still, the thickness of the eye varies across the eye and this thickness can only be approximated. It is especially difficult to obtain the thickness directly at the rupture site as the local tissue deforms, curls, or is missing post-test. Measurement error is also possible in computing lagrangian strain, based again upon measurements from the high-speed video.

Measurement error will be included in the calculation of both stress and strain of the corneo-scleral shell. While material properties such as failure stress and failure strain are certainly useful, especially for computer models, it is not felt that these measures offer a significant improvement for rupture prediction over the direct measure of internal pressure itself. Given the measurement uncertainty involved in determining failure stress and failure strain, the survival analysis was performed on the measurement of the internal pressure of the eye at rupture.

Currently there are no injury predictors that are measured in Anthropomorphic Test Devices (ATDs) to determine the likelihood of an occupant sustaining an eye injury. ATD designs currently being developed utilize state of the art sensors to improve their ability to measure potential injury mechanisms. One such improvement would be the incorporation of a synthetic eye, which would combine the geometric profile of the eye with an internal pressure transducer, to interact appropriately with the impacting object and measure the change in internal pressure of the eye. Additionally, computer models of the eye are being developed to offer the response of eye tissue from an impact by a foreign object (Stitzel et al. 2002). As a necessity for biofidelic response, accurate response characteristics of the eye must be known in order for it to behave realistically and to predict when failure of local tissues would occur. For experimental tests using either porcine or human eyes, it is possible to utilize a pressure transducer in the eye that would measure the intraocular response of the eye for use in calculating injury risk. The rupture pressures presented in this study can be used in conjunction with computational, synthetic, and other experimental models to predict globe ruptures in automobile accidents.

These surrogate models can then be used to evaluate unlimited scenarios of foreign object impacts to the eye without the complexities of obtaining human tissue for testing. With new tools to study potential interactions with the eye, whether it is a baseball, foam particles from an airbag deployment, or night vision goggles forced into the orbit, improved counter-measures and safety devices, such as redesigned airbag covers can help to reduce the total number of eye injuries, including blindness, sustained each year.

CONCLUSION

This is the first known study to gauge the structural integrity of healthy postmortem eyes, both under static and dynamic loading. Human and porcine eyes were each used in 10 static and 10 dynamic tests to determine the maximum internal pressure at globe rupture. The rupture pressure of porcine eyes has been shown to be significantly higher (p = 0.01) than human eyes in both static and dynamic loading rates. Also, the dynamic rupture pressure is shown to be significantly higher (p = 0.01) than static rupture pressure for both porcine and human eyes. Static rupture pressures were found to be 1.00 ± 0.18 MPa for porcine eyes and 0.36 ± 0.20 MPa for human eyes. Dynamic rupture pressures were found to be 1.64 ± 0.32 MPa and 0.91 ± 0.29 MPa for porcine and human eyes, respectively. Risk functions are presented to predict the risk of globe rupture and a 50% risk of injury exists at 1.02 MPa, 1.66 MPa, 0.35 MPa, and 0.90 MPa internal pressure for porcine static, porcine dynamic, human static, and human dynamic loading conditions, respectively. These risk functions can be used in the laboratory for both experimental and computational work, and by the clinician to determine the risk of severe eye injury due to increased pressurization of the eye.