Feasibility of Transdermal Ethanol Sensing for the Detection of Intoxicated Drivers

Abstract

Transdermal ethanol detection is a promising method that could prevent drunk driving if integrated into an ignition interlock system. However, experimental data from previous research has shown significant time delays between alcohol ingestion and detection at the skin which makes real time estimation of blood alcohol concentration via skin measurement difficult. Using a validated model we studied the effects that body weight, metabolic rate and ethanol dose had on the time lag between the blood alcohol concentration and transdermal alcohol concentration. The dose of alcohol ingested was found to have the most significant effect on the skin alcohol lag time; a dose of 15 ml of ethanol resulted in a peak lag time of approximately 33 minutes, while a dose of 60 ml of ethanol resulted in a peak time lag of 53 minutes. The time lag was found to be insensitive to body mass and only moderately sensitive to changes in metabolic rates.

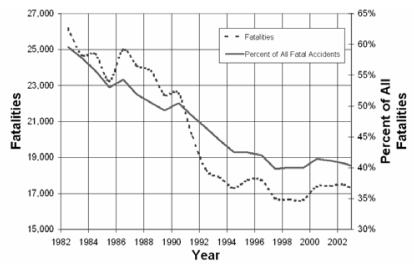
Over 16,000 people were killed in alcohol related traffic crashes in 2005. This toll comprised 39% of all traffic fatalities in 2005 [NHTSA, 2006]. Efforts to curb drunk driving have included an increase in the presence of law enforcement personnel on the roads, stiff criminal and financial consequences if caught driving under the influence of alcohol and increased media coverage of the problem. These social solutions to the drunk driving problem have significantly reduced the percentage of alcohol related traffic fatalities. As shown in Figure 1, between 1982 and 1992 alcohol related traffic fatalities dropped from 60% to 40% of all traffic fatalities. However since the early 1990’s the influence of alcohol in traffic deaths has reached a plateau, constituting 40% of all traffic fatalities. This stagnation suggests that social efforts to prevent drinking and driving may have reached the limit of their effectiveness.

Figure 1.

Alcohol Related Traffic Fatalities per Year

The best way to reduce the number of alcohol related traffic fatalities is to prevent people from driving drunk to begin with. One aggressive method to eliminate drunk driving would be to fit every highway vehicle with an ignition interlock [MADD, 2006]. Current ignition interlock systems use a breath alcohol detector to sample the driver’s breath alcohol concentration prior to starting the car. If the detector senses a high enough concentration the ignition interlock system will act like a switch, preventing the engine from starting. Current breath testing interlock systems are cumbersome, expensive and carry the stigma of being a convicted ‘drunk driver.’ As a result, installation of ignition interlocks, as described previously, in every vehicle would most likely not be tolerated by the public.

The installation of ignition interlocks in every vehicle would be better accepted by the public if the detection was performed non-invasively. One method to accomplish this is to measure the driver’s Blood Alcohol Concentration (BAC) by analyzing the ethanol emitted from their skin. It has been observed that 0.7% of the ethanol consumed is excreted through the breath, constituting what is measured by a breath alcohol detector. However, and additional 0.1% of the ethanol consumed is lost through sweat [Ramchandani, 2001], which can be detected at the surface of the skin. In addition to sweat, ethanol is also absorbed by the skin from the blood and transported to the surface of the skin where it exits the body. The integration of ethanol sensors into the steering wheel of a vehicle could allow an interlock system to continuously monitor the concentration of alcohol emitted from the driver’s hands.

Ethanol circulating in the blood stream will readily diffuse into the surrounding tissues of the body, including the skin. This phenomenon allows the concentration of ethanol in the skin to be used as an indicator of the ethanol in the blood. The largest issue with using skin measurements to detect BAC is that the alcohol does not diffuse through the skin instantly. Because of this, there can be a significant time delay between the equivalent blood and skin concentration values.

Despite this time delay, transdermal sensing of ethanol alcohol has been explored in several experimental studies (Giles, 1987; Swift, 1992; Phillips, 1995). This detection method has been shown to very accurately shadow the concentration profile of the ethanol in the blood via proportionally smaller concentrations of ethanol emitted at the surface of the skin.

OBJECTIVE

The goal of this study is to assess the feasibility of transdermal alcohol sensing using a computational model that predicts the lag time between peak blood and skin alcohol concentrations. In particular, our objective is to determine how the lag time varies with ethanol dose, body weight and metabolic rate. We used the model as a tool to determine if transdermal alcohol sensing is appropriate for detecting driver BAC for different segments of the population and levels of intoxication.

METHODS

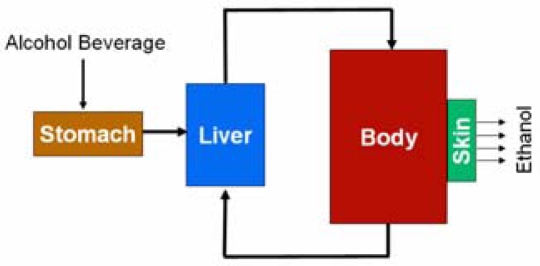
To model the transport of alcohol from ingestion to excretion through the skin, models of ethanol metabolism and ethanol transport were developed and linked. The ethanol metabolism model consists of three well mixed compartments: the liver, the body fluids, and the stomach compartment. The second model describes ethanol diffusion through the skin. The skin is modeled as a two layer system that is exposed to the concentration of alcohol in the blood on one side and atmospheric air on the other. Since only minute amounts of ethanol are actually lost through the skin, the complete model does not reduce the total ethanol mass by the mass of ethanol excreted through the skin. Figure 2 shows a diagram of the system.

Figure 2.

Model Diagram

ETHANOL METABOLISM AND BLOOD TRANSPORT

The metabolism of ethanol has been rigorously studied both experimentally and computationally. Dose dependent BAC profiles have been well documented for specific body weight and ethnic groups [Widmark, 1932; Wilkinson, 1977] and mathematically modeled by several authors [Levitt, 1998; Umulis, 2005]. After the consumption of an alcoholic drink, the ethanol in the drink is metabolized by the body via several biochemical reactions, mostly occurring in the liver. Although studies have shown that other organs can metabolize alcohol to a lesser degree [Ramchandani, 2001] we chose to restrict ethanol elimination to only the liver compartment.

We modeled ethanol elimination in the liver using classical Michaelis - Menten kinetics for enzymatic reactions. The ethanol elimination rate is given in Equation 1.

$$\text{Ethanol\hspace{0.17em}Elimination\hspace{0.17em}Rate}=\frac{V_{max}{C}_{Liver}}{C_{Liver}+K_m}$$ (1)

V_max represents the maximum rate the liver can metabolize ethanol given in mol/min, K_m is the concentration of ethanol necessary for the liver to metabolize ethanol at half of its maximum elimination rate, given in mol/liter and C_Liver is the concentration of ethanol in the liver, also given in mol/liter. The rate of ethanol elimination is proportional to the concentration of ethanol in the liver, so that ethanol is eliminated faster when higher concentrations are present, but reaches its maximum elimination rate of V_max when C_Liver overwhelms K_m.

The stomach compartment was added to the model to gradually add ethanol to the body, mimicking the actual behavior of the stomach. This is representative of how alcoholic beverages are absorbed into the blood stream. Figure 2 shows that the stomach compartment empties into the liver simulating the transport of ethanol from the stomach to the liver via the Portal vein which connects the small intestines to the liver. In this manner the liver may eliminate some of the ethanol entering the system before it enters the body compartment. The rate at which the stomach empties is controlled by the constant k_s. Equation 2 describes the volumetric rate of change of the stomach contents as a function of k_s and the current fluid volume in the stomach.

$$\frac{d{V}_s}{dt}=-k_s{V}_s$$ (2)

Many values, developed both experimentally and computationally, have been suggested for k_s (Levitt, 1994, Wilkinson, 1977, Umulis, 2005). k_s was calculated based on k_smax, the maximum rate of emptying in min⁻¹, x, the dose of ethanol given in moles and a, a constant with units mol⁻² as shown in Equation 3.

$$k_s=\frac{k_{S\text{max}}}{(1+a{(x)}^2)}$$ (3)

Using Equations 2 and 3 the rate of stomach emptying, and thus the rate of ethanol addition to the body, is controlled by the amount of ethanol in the stomach, in moles, and the volume of the stomach, in liters. The rate at which ethanol is added to the body is dependent largely upon the initial dose of ethanol in the stomach and the current volume of the stomach.

Mass balance equations were developed to describe the change in concentration between the liver compartment and the body compartment. Equation 4 describes the change in concentration of ethanol in the body compartment, where V_Body is the volume of the body fluids given in liters, and Q is the blood flow rate into and out of the liver, given in liters/min. It should be noted that V_Body represents both the blood volume and the volume of tissue fluids combined, which we took to be 60% of the total body mass. In this model both blood and water are considered to be well mixed since we are only concerned with the concentration of ethanol. Equation 5 describes the rate of concentration change in the liver. V_Liver is the volume of the liver, which we chose to be 0.61 liters. All concentrations are given in mol/min. The stomach emptying rate appears in the middle of this equation serving as the addition of ethanol to the liver compartment, multiplied by the concentration of ethanol in the stomach to give units of mol/min. Finally, ethanol is eliminated from the liver by the last term, as described previously, at a rate proportional to the liver ethanol concentration.

$$V_{Body}\frac{d{C}_{Body}}{dt}=Q(C_{Liver}-C_{Body})$$ (4)

$$V_{Liver}\frac{d{C}_{Liver}}{dt}=Q(C_{Body}-C_{Liver})+(k_s{V}_{Stomach}{C}_{Stomach})-\frac{V_{max}{C}_{Liver}}{K_m+C_{Liver}}$$ (5)

Equations 2, 4 and 5 were solved using a stiff ordinary differential equation solver from the commercial computing package MATLAB.

SKIN MODEL

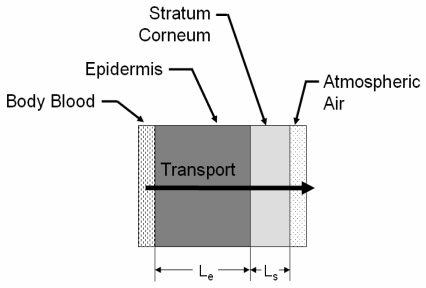
Several models exist to describe the transport of substances across the skin both from the skin’s surface to the blood and vice versa [Anderson, 2006]. Based on these models we modeled the skin as a two-layer system consisting of the epidermis and the stratum corneum, which have drastically different transport properties. A diagram is given in Figure 3. The concentration of ethanol in the blood, as calculated from the metabolism model, serves as the time dependent boundary condition imposed at the blood-epidermis boundary. Driven by the concentration gradient, ethanol diffuses through the epidermis and the stratum corneum to the atmospheric air boundary where a constant concentration devoid of ethanol is imposed.

Figure 3.

Skin Diagram

Equations 5 and 6 describe the transport of ethanol, in terms of partial pressures, across the epidermis and stratum corneum respectively. β represents ethanol solubility, D represents molecular diffusivity, A is the cross sectional area for transport and L is the linear distance for this transport; all for the medium indicated by the subscript.

$${\beta }_{e}A{L}_e\frac{\partial P_e}{\partial t}=D_e{\beta }_{e}A{L}_e\frac{{\partial }^2{P}_e}{\partial x^2}\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }0\le x<L_e$$ (6)

$${\beta }_{s}A{L}_s\frac{\partial P_s}{\partial t}=D_s{\beta }_{s}A{L}_s\frac{{\partial }^2{P}_s}{\partial x^2}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{L}_e<x\le L_e+L_s$$ (7)

At x = 0, the partial pressure of ethanol in the blood is imposed at the epidermis. Similarly, at x = L_e + L_s a partial pressure of zero is imposed which represents the clearing of the surface of the skin of ethanol vapor which would have accumulated there due to the diffusion process. A forward-difference approximation was implemented using MATLAB to solve Equations 6 and 7 simultaneously.

Table 1 summarizes the constants used in the simulation of this model.

Table 1.

Summary of Constants

Variable	Value	Description	Unit
Vmax	2.75	Maximum Liver Metabolism Rate	mmol/minute
Km	0.1	Concentration for 50% Vmax	mM
Ksmax	0.1	Maximum Stomach Emptying Rate	min−1
a	1.22	Stomach Emptying Constant	mol−2
Q	1.5	Liver Blood Flow	liter/minute
βe	232	Solubility in Epidermis	ml ethanol*100 ml medium−1*Torr−1
βs	211	Solubility in Stratum Corneum	ml ethanol*100 ml medium−1*Torr−1
De	5.00E-06	Molecular Diffusivity in Epidermis	cm2/second
Ds	5.00E-10	Molecular Diffusivity in Stratum Corneum	cm2/second
Le	0.02	Thickness of Epidermis	cm
Ls	0.0015	Thickness of Stratum Corneum	cm
A	7.50E-02	Capillary Surface Area	cm2
R	62360	Universal Gas Constant	Torr*cm3*mol−1*K−1

RESULTS

METABOLISM MODEL VALIDATION

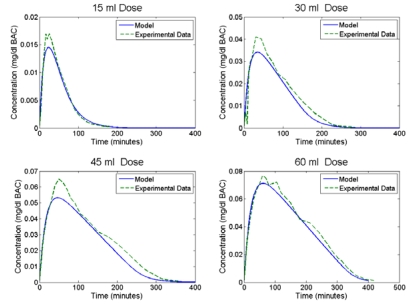
Validation of the model was performed using available experimental data published from several sources. Figure 4 presents the BAC predicted by the model overlaid with experimental data taken from Wilkinson [1977] under the same experimental conditions. Simulations were conducted for 95% ethanol doses of 15, 30, 45 and 60 ml diluted in 150 ml of fluid and compared to the average BAC curve generated from eight adult males averaging 74.6 kg in weight. Figure 4 shows good agreement between the model and the experimental data. Comparison of the model and experimental data using root means square (RMS) differences gave R² values of 0.94, 0.95, 0.94 and 0.99 for each of the doses previously mentioned. The concentration curves generated by the metabolism model were then used to drive the skin diffusion model.

Figure 4.

Metabolism Model Validation using Wilkinson data [1977]

COMPLETE MODEL VALIDATION

The combined metabolism-diffusion model was validated using data published by Swift [1998] in a paper describing a transdermal ethanol sensor system. The subject in the Swift study was given 0.75 ml ethanol per kg of body weight diluted 4:1 in cold orange juice. The weight of the subject was not specified in the study. We assumed a 50^th percentile male (78 kg). Our model input parameters were adjusted to reflect this dosage of 1.028 moles of ethanol and an initial stomach volume of 240 ml.

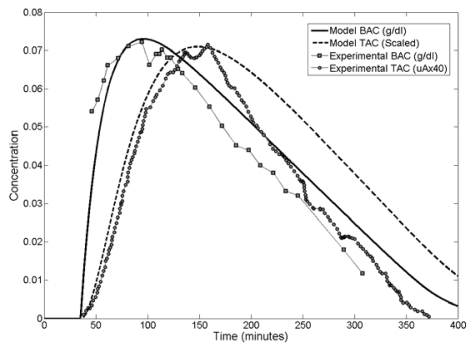
In the Swift study, blood alcohol concentration was carefully measured using a breath alcohol detector. The subject also wore a wrist watch style data logger/ethanol sensor that measured and recorded the concentration of ethanol at the surface of the skin during the experiment. The data logger reported the concentration as an electrical current proportional to the actual ethanol concentration present. Data was reported in microamperes, rather than in concentration. The correlation between the electrical current and actual concentration was not given. The ethanol concentration time-course behavior of the skin relative to the blood is of interest in this study; for validation purposes, model predicted transdermal alcohol concentration values were scaled to match the peak magnitude of the Swift data. Some time shifting was also required as the time zero in the Swift study was different from the time zero in our model. The results are shown in Figure 5.

Figure 5.

Complete Model Validation against Swift Data [1992]

The model accurately predicts when the BAC and Transdermal Alcohol Concentration (TAC) curves will peak, which we will use a registration mark to study time lag effects. The model is also able to replicate the shape of the experimentally determined BAC and TAC curves up to the point of peak TAC. Beyond peak TAC the model over predicts TAC. Comparison of the model and experimental BAC curves RMS differences gave an R² value of 0.75 over the full range of data. The model and experimental TAC curves have an R² value of 0.66 over the full range of values and an R² value of 0.96 if only the first 180 minutes are considered.

LAG TIME EFFECTS

Using the validated model we studied the effects that body weight, metabolic rate and ethanol dose had on the peak lag time between the BAC and TAC curves.

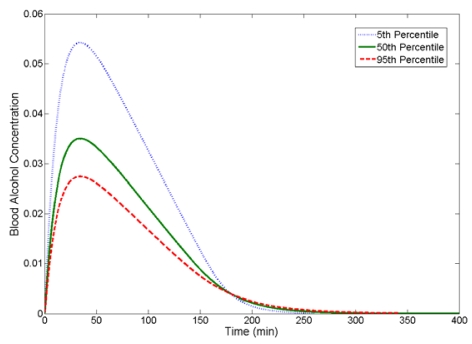
To give the reader some perspective as to how BAC varies with body weight Figure 6 shows BAC vs. time curves for 5^th (50 kg), 50^th (78 kg) and 95^th (100 kg) percentile body weights given the same dose of ethanol. Hereafter, a subject with a 5^th, 50^th or 95^th percentile body weight will be referred to as a 5^th, 50^th or 95^th percentile driver, respectively.

Figure 6.

BAC curves as a Function of Body Weight 30 ml of 95% Ethanol in 150 ml Solution

For a given dose, peak BAC increases as body weight decreases. Body fluid volume is proportional to body weight. When compared to 50^th and 95^th percentile drivers, a 5^th percentile driver has a lower body fluid volume and is not able to dilute the ethanol to the same extent as the two larger drivers; this results in a higher predicted peak BAC. Additionally, all three drivers are assumed to have the same liver size and metabolize ethanol at the same maximum rate.

Our model shows that the dose of ethanol given to a driver affects the maximum BAC and time of max BAC. To show this, we held the body weight constant and varied the dose. Table 2 shows the peak BAC values as well as the time it takes for the BAC to reach its maximum for a 50^th percentile driver given 15, 30, 45 and 60 ml doses of 95% ethanol in 150 ml of solution. As dose size increases the maximum BAC increases and the time to reach peak BAC increases.

Table 2.

Dose Effects on Peak Value and Time for 50th Percentile Driver

Dose (ml)	Peak BAC (g/dl)	Peak Time (min)
15	0.01	23.3
30	0.04	34.4
45	0.05	46.5
60	0.07	60.9

LAG TIME VS BODY WEIGHT AND DOSE

With the knowledge of how our model predicted the BAC response to different doses for different body weights, we examined how body weight affects the time lag between peak BAC and peak TAC. Skin diffusion coefficients and thickness were maintained constant for all simulations.

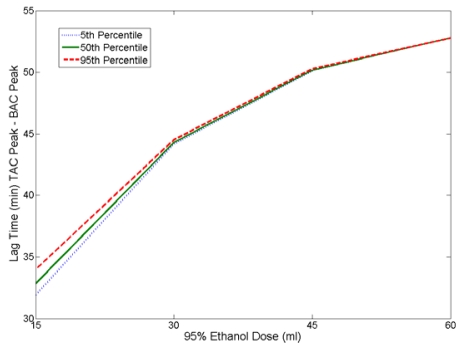
We first examined how the dose of ethanol given would affect the lag between the peak BAC and peak TAC. We chose dosages of 15, 30, 45 and 60 ml of 95% ethanol given in 150 ml of solution. We applied these doses to the model for 5^th, 50^th and 95^th percentile driver body weights. The results are reported in Figure 7.

Figure 7.

Time Lag Between peak BAC and peak TAC as a Function of Dose

As dose size increases, the lag time between peak BAC and peak TAC also increases. From this plot we also see that lag time is insensitive to body weight.

LAG TIME VS METABOLIC RATE

There is also variance in the rate at which individuals metabolize ethanol. This variance comes from a variety of sources including the individual’s developed tolerance to alcohol and ethnicity.

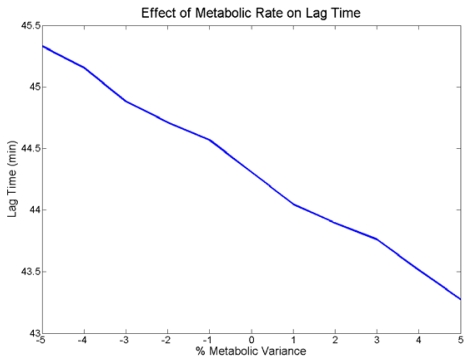
We simulated the effect of different metabolic rates on a 50^th percentile body consuming 30 ml of 95% ethanol diluted in 150 ml of fluid. We varied the maximum rate which the liver can metabolize ethanol, V_max, by +/− 5%. The results are plotted in Figure 8. We see that as V_max is varied from below nominal to above nominal the lag time decreases. Over the entire +/− 5% variance on V_max the time lag varied approximately 2 minutes, which equates to a total variance of 5% of the nominal lag time.

Figure 8.

Metabolic Effects on Lag Time

DISCUSSION

The model presented here is capable of predicting the blood alcohol concentration in a person given a single dose of ethanol in beverage form. It also predicts the concentration of ethanol at the surface of the skin as a result of diffusion from the blood stream. Validation of the model was performed using experimental data taken from a study performed by Swift [1992]. The model was used to estimate the time lag between peak BAC and TAC values to assess the feasibility of transdermal ethanol sensing as a method to measure real time BAC.

BODY WEIGHT

Our model shows that body weight has little effect on the time lag between peak BAC and TAC. Using four different doses we showed that the lag time was approximately the same for 5^th, 50^th and 95^th percentile drivers. This assumes that the metabolic rate and liver size is the same for all three body weights.

DOSE

The amount of ethanol ingested had a significant effect on the lag time; as the dose increased so did the lag time. We varied the dose of ethanol given to 5^th, 50^th and 95^th percentile drivers and calculated the lag time between peak BAC and TAC. In our study, increasing the dose from 15 ml to 60 ml of 95% ethanol increased the lag time by approximately half an hour. As we showed previously, increasing the dose increases the peak BAC and increases the time to max BAC. However, this relationship is not linear which becomes apparent when the BAC curves are applied to the skin model. Different BAC values are imposed on the skin model’s blood boundary during the same periods of time for the different doses. Since ethanol diffusion through the skin is concentration driven this affects the time it takes for each of the dose curves to cross the skin. The time differences experienced at the skin for each curve combined with the delay in peak BAC time results in an increase in the lag time as the dose is increased.

METABOLIC RATE

We modeled differences in metabolic abilities among individuals by varying the V_max variable in the ethanol elimination expression by +/− 5%. This changed the rate at which ethanol was eliminated from the body. We noted that decreasing the metabolic rate increased lag time. These results are consistent with the values gathered from the dose-dependant study because decreasing the metabolic ability is similar to ingesting a larger dose of ethanol, which both result in a higher concentration of ethanol present in the body and a greater peak lag time. Similar to decreasing the ethanol dose, increasing the metabolic rate decreased the lag time. Changes in metabolic rate did not affect the lag time as significantly as changes in the dose amount. Regardless, by decreasing the metabolic rate by 5% the lag time was changed by approximately 5%.

IMPLICATIONS

The time lag between the blood and skin ethanol concentrations is not constant for all situations, making it difficult to develop a reliable algorithm to calculate BAC based on a TAC measurement. An ethanol measurement made at the surface of the skin could be mapped to a range of BAC values depending on the amount of alcohol consumed, as shown in the dose effect studies presented previously. Therefore, an ethanol concentration measurement made at the surface of the skin under quiescent conditions can not be equated to a real-time BAC value without additional information about how much the subject had to drink. Transdermal measurements made in this manner cannot accurately measure BAC in real-time. However, this detection method could prove useful as a dichotomous test to sense if the driver has been drinking.

Additionally, an easy way to circumvent a transdermal measurement would be to block direct skin contact with the sensor. An intoxicated driver wearing gloves could potentially prevent the sensors for detecting any ethanol on their skin at all. A secondary sensor system would be required to ensure that the measurement is being made at the surface of the skin.

LIMITATIONS

The model used for these simulations is a simple ethanol metabolism and skin diffusion model, which has several limitations. The model was developed using metabolic rate and transport coefficients developed from a limited number of experiments performed on subjects who fall into the 50^th percentile driver weight class. Because of this, it is unknown how accurate our results are for the 5^th and 95^th percentile weight groups. Additionally, the model does not account for human variability in ethanol metabolism and transport; in particular, differences in gender or ethnicity. Our model also assumes that the stomach is empty when the dose of ethanol is given, which ignores the effects of a full stomach on ethanol absorption. Finally, our model uses a rudimentary mass scaling approach to generate the differences between the weight groups which will be improved in future projects to more accurately describe how liver size and metabolic abilities vary with body weight.

CONCLUSION

Transdermal sensing of the alcohol in a driver’s blood is one possible way to non-invasively detect intoxicated drivers. However, the feasibility of this method suffers from the time delay required for the alcohol in the driver’s blood to diffuse to the surface of the skin where it can be easily and non-invasively measured. To explore the feasibility of transdermal sensing, we developed and validated a model capable of predicting the time difference between the peak blood alcohol concentration and peak skin alcohol concentration in human subjects given a single dose of ethanol. The model and our findings are limited to the study of a single dose of ethanol; therefore our findings may not be applicable to drivers who ingest multiple drinks. We used this model to study the effects that body weight, amount of alcohol consumed and differences in ethanol metabolic rates have on the lag time between peak BAC and TAC values. We found that, for a given dose of alcohol, lag time is insensitive to body weight. However, the dose size has a significant impact on the blood-skin concentration lag. A larger dose of alcohol causes an increase in the lag time. A 15 ml dose of 95% ethanol given to all percentile drivers was found to have a lag time of approximately 33 minutes. Quadrupling the dose to 60 ml of ethanol increases the lag time to approximately 53 minutes. Finally, we examined the effect of minor variances in a person’s ability to metabolize alcohol, which is representative of the differences between individuals. A 5% decrease in metabolic rate corresponds approximately to a 5% increase in time lag. Our model suggest that, due to the highly variable relationship between the BAC and TAC curves, transdermal sensing of real-time BAC using only skin surface measurements may prove to be very challenging.