The costs and benefits of library site licenses to academic journals

Abstract

Scientific publishing is rapidly shifting from a paper-based system to one of predominantly electronic distribution, in which universities purchase site licenses for online access to journal contents. Will these changes necessarily benefit the scientific community? By using basic microeconomics and elementary statistical theory, we address this question and find a surprising answer. If a journal is priced to maximize the publisher's profits, scholars on average are likely to be worse off when universities purchase site licenses than they would be if access were by individual subscriptions only. However, site licenses are not always disadvantageous. Journals issued by professional societies and university presses are often priced so as to maximize subscriptions while recovering average costs. When such journals are sustained by institutional site licenses, the net benefits to the scientific community are larger than if these journals are sold only by individual subscriptions.

When academic journals were distributed only as paper editions, the obvious way for scholars to share a journal was to borrow a copy from the shelves of their university library. With the arrival of electronic access, the logistics of journal sharing has changed. Physical proximity and storage constraints, which once made libraries the natural venue for shared access, are no longer important. Despite this change, university libraries continue to act as publishers' revenue collectors and gatekeepers, by purchasing site licenses that entitle their faculty and students to access journals electronically.

Because there is no compelling logistic reason for university libraries to participate in the journal distribution process, we ask whether university wide site licenses perform a fiscal function that benefits the academic community. We find a surprising answer. If a journal is priced to maximize the publisher's profits, scholars on average are likely to be worse off when universities purchase site licenses than they would be if access were by individual subscriptions only. However, site licenses are not always disadvantageous. We show that institutional site licenses for nonprofit journals such as those published by professional societies and university presses are broadly beneficial to the scientific community.

The Market for Paper Journals

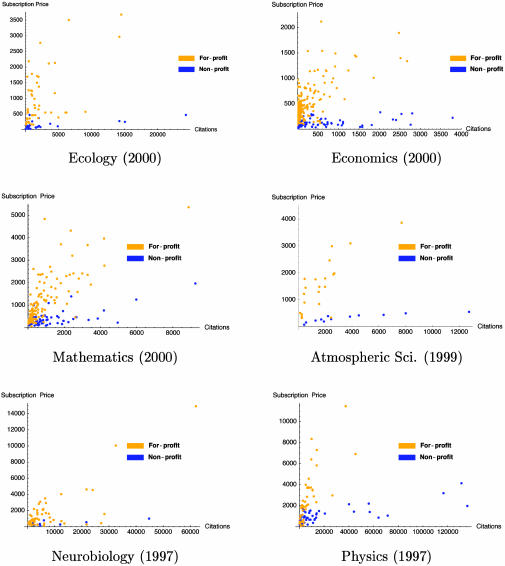
There is a remarkable difference between institutional subscription prices for print copies of those academic journals owned by commercial publishers and those owned by nonprofit publishers, professional societies, and university presses. Surveys of journal pricing for institutional subscriptions in several academic disciplines show that the average price per page charged by commercial publishers is several times higher than that which is charged by professional societies and university presses (Table 1). These price differences do not reflect differences in quality. If we use citation counts as a measure of journal quality (useful for within-field comparison, although less useful for between-field comparisons), we see that the prices charged per citation differ by an even greater margin (Table 1). The magnitude of this discrepancy is illustrated in Fig. 1, which shows library subscription price versus the number of citations for academic journals in six scientific fields.

Table 1. Mean institutional price per page and per citation for journals in six scientific fields.

	Cost per page (U.S. $)		Cost per citation (U.S. $)
Field	For profit	Nonprofit	For profit	Nonprofit	Year
Ecology	1.01	0.19	0.73	0.05	2000
Economics	0.83	0.17	2.33	0.15	2000
Atmosph. Sci.	0.95	0.15	0.88	0.07	1999
Mathematics	0.70	0.27	1.32	0.28	2000
Neuroscience	0.89	0.10	0.23	0.04	1997
Physics	0.63	0.19	0.38	0.05	1997

Data for atmospheric sciences (Atmosph. Sci.) are from a September 2000 University of Washington Libraries report prepared by Patty Carey, which can be accessed at www.lib.washington.edu/subject/atmosphericsci/scholcom. Data for mathematics are from the American Mathematical Society's Journal Price Survey, which can be accessed at www.ams.org/membership/journalsurvey.html. Data for neurosciences and for physics are from a 1998 University of Wisconsin Libraries report by George Soete and Athena Salaba, which can be accessed at www.library.wisc.edu/projects/glsdo/cost.html. Data for economics and ecology were collected by the authors and are available by request. Citation rates are from the Institute for Scientific Information's Journal Citation Reports, which can be accessed at www.isinet.com.

Fig. 1.

Annual price (U.S. dollars) and yearly citations to the journal, for journals in six scientific disciplines. Data sources are as in Table 1.

These price differences have grown rapidly over the past 15 years. In economics, for example, the average inflation-adjusted price per page charged by commercial publishers has increased by 300% since 1985, whereas that of nonprofit economics journals has increased by “only” 50%. Studies of journal production costs indicate that the price differences over time and among journal types do not reflect differences in production and distribution costs (1–3).

Markets for information goods such as computer software or journal access are quite different from those for ordinary commodities such as shoes or houses. If you sell a house to one buyer, you cannot sell the same house to others. For each buyer, you must bear the full cost of producing an additional house. In contrast, once an information good is produced, access to this information can be sold to many different buyers with a negligible cost of extending access to an additional user. The information vendor can also sell collective access to groups of individuals in firms or universities by means of site licenses. This marketing device has no direct parallel in markets for ordinary commodities. Varian (4) presents a particularly stimulating discussion of the distinctive nature of information goods and their marketing.

Another curious feature of the market for academic journals is that publishers of major commercial journals appear to enjoy substantial monopoly power despite the absence of obvious legal barriers to entry by new competing journals. Bergstrom (1) argues that journals achieve monopoly power as the outcome of a “coordination game” in which the most capable authors and referees are attracted to journals with established reputations. This market power is sustained by copyright law, which restricts competitors from selling “perfect substitutes” for existing journals by publishing exactly the same articles. In contrast, sellers of shoes or houses are not restrained from producing nearly identical copies of their competitors' products.

The Emerging Electronic Journal Market

Whereas electronic distribution can dramatically reduce the costs of producing and disseminating scholarly work (5), it is not clear that the scientific community will reap any of the benefits. Because electronic distribution is relatively new, pricing structures for electronic access are still evolving, but some consistent patterns seem to have emerged. Commercial publishers commonly include electronic site licenses with print for a surcharge of 10–25% and they offer electronic subscriptions without print for about the same price as print alone. The electronic subscription prices of nonprofit journals vary widely. For example, Science, which can be accessed at www.sciencemag.org, charged $1,500 to $5,500 for an electronic site license in 2001, which is many times the institutional print price of $370. In the same year, PNAS offered electronic access at no additional charge to institutions that purchased the $970 print subscription. There is method to this apparent madness. Science has traditionally relied heavily on individual subscription and advertising revenue, both of which are undercut by university wide electronic access. PNAS, by contrast, has featured no advertising and received little in the way of individual subscription revenue. As a consequence, its publisher loses little by offering online access to universities with print subscriptions.

Along with electronic distribution, several commercial and nonprofit publishers have introduced tiered pricing structures, whereby large research universities pay substantially more for electronic journal access than their smaller, less wealthy counterparts. Commercial publishers are well aware that the use of price discrimination allows them to increase their profits. In a recent speech, Dirk Haank, CEO of Elsevier Science, explained Elsevier's pricing plans for electronic site licenses: “And, basically the price then depends on a rough estimate of how useful is that product for you; and we can adjust it over time. We want to distinguish between big universities versus small universities, corporate versus universities, and maybe rich countries versus developing countries” (6). Apparently, Haank understands full well that Elsevier's prices are determined not by its production costs but by the amount that buyers are willing to pay.

Along with electronic access, publishers have also introduced the policy of selling “bundled” collections of journals. University libraries are offered all-or-nothing packages in which they can purchase a publisher's entire portfolio of journals at a significant discount from the cost of buying journals one by one. (Economists are familiar with the idea that a monopoly seller can increase its profits by bundling. This possibility was discussed by W.J. Adams and Janet Yellen (7) and by Richard Schmalensee (8). Hal Varian (4) noted that academic journals are particularly well suited for this kind of bundling. Mark Armstrong (9) and Yannis Bakos and Erik Brynjolfsson (10) demonstrated that bundling large collections of information goods such as scholarly articles will not only increase a monopolist's profits, but will also decrease net benefits to consumers.)

Whereas many libraries have chosen to purchase the bundles offered by commercial publishers, not all are convinced that this arrangement is in their interest. Ken Frazier, head librarian at the University of Wisconsin, maintains that university libraries will not benefit from purchasing bundled site licenses from commercial publishers: “Academic library directors should not sign on to the Big Deal or any comprehensive licensing agreement with commercial publishers... the Big Deal serves only the Big Publishers... increasing our dependence on publishers who have already shown their determination to monopolize the marketplace” (11).

The Future of Electronic Distribution

Given what we know about the aims of publishers and the economics of the academic journal market, what should we expect to happen to journal prices in the future? Here, we explore the way that profit-maximizing publishers and nonprofit societies are likely to manage the sale of site licenses for academic journals, and the impact of these policies on the welfare of the scientific community.

We begin with an example that shows the way that a monopolist can increase its profits by selling university site licenses instead of selling individual electronic subscriptions. As noted by Bakos and Brynjolfsson (12) and Bakos et al. (13), there is a formal similarity between site licenses and bundling of journals. Bundling clusters commodities for a single buyer, whereas site licensing groups consumers for a single product. Both devices serve to increase monopoly profits by reducing the amount of variation in willingness to pay among buyers. In our example, the use of site licenses expands access to a monopolist's journals, but it also enables the monopolist to set prices so high that the university community is worse off than it would be if the only available subscriptions were to individuals.

Our example shows a very different outcome when the publishers are nonprofit organizations. In this case, the introduction of site licenses increases both the amount of access and the net benefits to subscribers.

An Example. A scientific journal is of interest to three types of scientists, A, B, and C. There are 100 scientists of each type. The buyer value for type A scientists, which is the largest amount of money that each would be willing to pay to have the journal, is $300. The buyer values for type B and type C individuals are $200 and $100, respectively. The cost of editing the journal and putting it online is $32,000. Once the journal is produced, there is no additional cost to adding another subscriber.

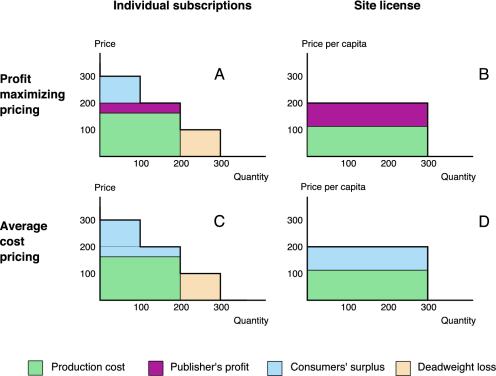
A Profit-Maximizing Publisher. Suppose that the journal's publisher is a profit maximizer who must charge the same price to all buyers. At a price of $300, only type As buy the journal and 100 subscriptions are sold. At a price of $200, the type As and type Bs buy, and 200 subscriptions are sold. At a price of $100, the publisher sells 300 subscriptions. Profit is maximized by selling 200 subscriptions at $200 each. Revenue is then $40,000, and, because production costs are $32,000, profit is $8,000. This situation is depicted in Fig. 2A. For each quantity, the demand curve (i.e., the upper boundary of the colored region) gives the price necessary to sell at least that many subscriptions.

Fig. 2.

Demand curves, profits, costs, consumers' surplus, and deadweight loss for individual subscriptions and site licenses.

A buyer's consumer's surplus is defined as the difference between her buyer value and the price that she actually pays. At a price of $200, type A scientists each get a consumer's surplus of $100. Type Bs get zero consumer's surplus, because the price is as high as their buyer values. Type Cs get zero consumer's surplus, because they pay nothing and get nothing. Scientists therefore gain a total consumers' surplus of $100 × 100 = $10,000. Deadweight loss is a measure of the inefficiency caused by excluding some interested scientists from access to the journal, and is defined as the expected total of the buyer values of all individuals who are unwilling to pay the full subscription price to obtain access. In our present example, the deadweight loss is equal to the total buyer values of type C individuals, $100 × 100 = $10,000.

Now, imagine that these scientists are used at 100 universities, each of which employs one scientist of each type. The publisher chooses not to sell individual subscriptions but any university can buy a site license that provides free access to all of its employees. Acting in the best interests of its scientists, a university library will buy a site license so long as the site license price does not exceed the sum of its resident scientists' buyer values. Because each university has one scientist of each type, the sum of buyer values at each university is $600. The publisher can set a price of $600 and sell one site license to each university. The 100 sales yield a revenue of $60,000 and a profit of $60,000 – $32,000 = $28,000 (Fig. 2B).

With university site licenses, deadweight loss is eliminated. All three types of scientists have access to the journal, whereas with individual subscriptions, only type A and B scientists have access. Because there is no real cost to extending access to everyone, site licenses offer superior efficiency (as publishers are quick to point out). But these efficiency benefits are all absorbed as extra profits for the publisher, and paradoxically, total consumer surplus of the scientific community is reduced by the use of site licenses. In our example, the site license price of $600 is equal to the sum of all scientists' buyer values at each university. Thus, the scientific community receives zero consumer surplus; it is worse off than it would be if subscriptions were sold only to individuals, and no better off than if the journal did not exist.

An Average-Cost-Pricing Publisher. What happens if this journal is produced by a professional society that seeks the largest possible circulation consistent with recovering its total costs from subscription revenue? Such a society will choose the (lower of the two prices such that) price equal to average cost. In our present example, there is no single price at which the society could recover its costs and sell to all 300 scientists. The type Cs will buy only if the price is $100 or less, at which price total revenue would be only $30,000, whereas total costs are $32,000. However, the society could recover its total costs by setting a price of $160 and selling 200 subscriptions (to type A and B scientists). At this price, type A and B scientists have consumer's surpluses of $140 and $40, respectively. The scientists' total consumers' surplus is $18,000 (Fig. 2C).

In this case, the scientists will get greater total consumer surplus if universities buy site licenses. The society can cover its costs by selling a site license to each of the 100 universities at a price of $320. Because the sum of buyer values at each university exceeds $320, all 100 libraries will subscribe. Deadweight loss is eliminated, and scientists at each university get a consumers' surplus of $600 – $320 = $280. The sum of consumers' surpluses is $28,000 (Fig. 2D). Thus, for nonprofit journals, the scientific community benefits when universities purchase electronic site licenses rather than leaving individuals to purchase their own subscriptions.

More Realistic Markets. Our example assumed that all universities employ the same number of scientists of each type, and that, as a consequence, all universities place the same value on a site license. In this case, a publisher can expropriate all of the benefits resulting from the journal's existence by setting a price equal to the total willingness to pay of a university's faculty.

The same qualitative results are found when universities are less uniformly constituted. Consider a model in which there are several universities, each of which employs n scientists. (Variation in size also produces variation in willingness to pay across universities, but publishers are able to overcome this effect by setting prices that depend on the size of the institution.) The buyer values of the n scientists at each institution are drawn from a specified distribution function, F. If journal access is sold by individual subscriptions at price p, then only those scientists with buyer values of at least p will subscribe and the seller's revenue will be proportional to p[1 – F(p)]. If access is sold by university site licenses at a price np, then assuming that libraries purchase a journal when the sum of buyer values exceeds the price, a university will purchase the journal only if the mean buyer value of its faculty exceeds the per capita price p of a site license. In this case, the seller's revenue will be proportional to p[1 – F_n(p)] where F_n is the distribution of the sample mean for a group of size n. A profit-maximizing publisher will choose a per capita price p that maximizes its total revenue. For a specified distribution and any given size of university groups, we can calculate the profit-maximizing price, the publishers' expected profits, the expected deadweight loss, and the scientists' expected per capita consumers' surplus.

Thus, we can explore the effect of group size on profits, consumers' surplus, and deadweight loss. As group size increases, the variance of mean buyer values across groups decreases. For sufficiently large groups of equal size, this variance becomes arbitrarily small and a profit-maximizing seller can sell site licenses to almost all groups at a per capita price that is arbitrarily close to the population mean buyer value. Therefore, for large group size, a profit-maximizing publisher captures almost the entire value of net benefits and the academic community is left with almost no consumers' surplus.

The results for small groups are less straightforward. We have considered three different probability distributions of buyer values for which the distribution of sample means for small samples is manageable: the normal distribution, the uniform distribution, and the exponential distribution. In each case, the group demand function can be expressed in closed form as a convolution of individual distributions. [Bakos and Brynjolfsson (10) apply a similar method to determine a demand for bundled commodities.]

Here, we discuss the case of the exponential distribution. Results for the normal and uniform distribution are qualitatively similar, with a few interesting differences. Our code can be accessed at http://octavia.zoology.washington.edu/publishing/suppl.html, along with a similar analysis for the normal and uniform distributions.

Suppose that buyer values are distributed according to the exponential distribution function F(x) = 1 – e^–x (a convenient choice, in that the sample means of independent draws from this distribution have gamma distributions). Although we leave the choice of currency units unspecified, the reader may want to think of x as measured in hundreds of dollars. With this distribution, the mean buyer value is 1. We assume that the total cost of producing the journal is 0.2 times the total number of scientists.

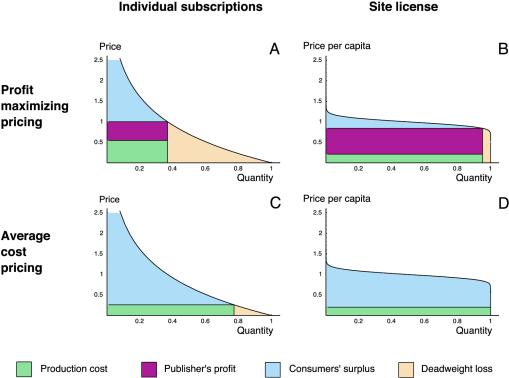
Fig. 3 shows the demand curves for this model, in a manner analogous to that of Fig. 2. As before, the shaded areas represent total costs, profits, consumers' surplus, and deadweight loss for each case. Fig. 3A shows the outcome when the publisher is a profit maximizer, and Fig. 3C shows the outcome when the seller prices at average cost. Simple calculus shows that a profit-maximizing seller selling individual subscriptions would set the price P = 1 and sell subscriptions to the fraction 1/e of all scientists (Fig. 3A). An average-cost pricing publisher could recover its costs by charging 0.26 per individual subscription and selling subscriptions to a fraction 0.77 of all scientists (Fig. 3C).

Fig. 3.

Demand curves, profits, costs, consumers' surplus, and deadweight loss for individual subscriptions and site licenses. Calculations were performed numerically by using the program mathematica.

The graphs in the right column of Fig. 3 show the demand curve for site licenses when scientists are randomly clustered into “universities” with 100 members. Here, the demand curve gives the fraction of universities that would subscribe at each per capita price. The profit-maximizing price is 0.84, and, at this price, 95% of all universities would subscribe. An average-cost pricing publisher will almost certainly recover its costs at a price of 0.20, at which virtually all universities will subscribe.

Some academic societies rely on journal publishing revenues to support other society programs which are, in effect, public goods provided to the scientific community. Relative to individual subscriptions, site-licensing systems allow societies to collect the necessary revenue to provide these public goods with reduced deadweight loss. When academic societies price above-average cost to fund other scholarly activities, site-licensing plans will generally increase the efficiency with which these public goods can be provided and thus benefit the scientific community on the whole.

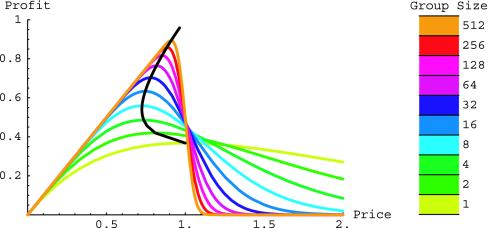
The single-peaked curves in Fig. 4 show the relationship between the per capita price and the publisher's per capita profit when buyer values are exponentially distributed. Different colors correspond to different group sizes. For each group size, the profit-maximizing price is the value at which the price-profit-curve peaks. The black curve connects the locus of these profit-maximal price-profit combinations. Moving along the black curve from the peak of the yellow curve (individual sales) to the orange curve (groups of 512), the profits of the seller rise monotonically, whereas the per capita price decreases with group size for group sizes up to seven and increases with group size beyond that. Indeed, numerical analysis (data not shown) reveals that every increase in group size leads to an increase in the profits enjoyed by a commercial seller, a decrease in consumers' surplus, and a decrease in deadweight loss. Although the sale of site licenses to larger groups increases efficiency, in the sense of increasing the sum of profits and consumers' surplus, the gains in efficiency are more than absorbed by the sellers, so that the scientists are actually worse off as group size increases.

Fig. 4.

Per capita profit as a function of price for various site license group sizes. The black arc traces the profit-maximizing price.

Discussion

Our models suggest that university libraries, acting in their collective interest, should agree to purchase a journal site license only if the subscription price is close to the publisher's average cost. Commercial publishers seeking to maximum their profits would then be faced with a choice between selling site licenses at prices close to average cost or of selling subscriptions only to individuals. Although the former arrangement is more efficient than the latter, either of these two outcomes would result in greater net benefits for the scientific community than would a policy of purchasing electronic site licenses at prices set by profit-maximizing publishers.

If universities act independently, the situation is more problematic. Publishers have an incentive to set higher prices for individual subscriptions than they would if site licenses were not sold, so as not to spoil the market for site licenses. Given these inflated individual subscription prices, scientists at a single university may benefit if their own library purchases site licenses that are priced far above average cost. Thus, university libraries face a collective action problem. If all were to refuse to buy site licenses to the expensive commercial journals, publishers would have to cut prices and all would benefit. However, each individual library would better serve its patrons by purchasing a site license despite the cost. Some sort of coordinating mechanism among libraries could facilitate a collective response to this problem.

For nonprofit journals, the problem disappears: the incentives to the academic community at large, and those of individual university libraries, operate in the same direction. The scientific community benefits, and individual universities benefit, if libraries purchase site licenses and make access freely available to their faculty and students.