Bayesian Adaptive Trial Design for a Newly Validated Surrogate Endpoint

Summary

The evaluation of surrogate endpoints for primary use in future clinical trials is an increasingly important research area, due to demands for more efficient trials coupled with recent regulatory acceptance of some surrogates as ‘valid.’ However, little consideration has been given to how a trial which utilizes a newly-validated surrogate endpoint as its primary endpoint might be appropriately designed. We propose a novel Bayesian adaptive trial design that allows the new surrogate endpoint to play a dominant role in assessing the effect of an intervention, while remaining realistically cautious about its use. By incorporating multi-trial historical information on the validated relationship between the surrogate and clinical endpoints, then subsequently evaluating accumulating data against this relationship as the new trial progresses, we adaptively guard against an erroneous assessment of treatment based upon a truly invalid surrogate. When the joint outcomes in the new trial seem plausible given similar historical trials, we proceed with the surrogate endpoint as the primary endpoint, and do so adaptively–perhaps stopping the trial for early success or inferiority of the experimental treatment, or for futility. Otherwise, we discard the surrogate and switch adaptive determinations to the original primary endpoint. We use simulation to test the operating characteristics of this new design compared to a standard O’Brien-Fleming approach, as well as the ability of our design to discriminate trustworthy from untrustworthy surrogates in hypothetical future trials. Furthermore, we investigate possible benefits using patient-level data from 18 adjuvant therapy trials in colon cancer, where disease-free survival is considered a newly-validated surrogate endpoint for overall survival.

1. Introduction

While no single approach to surrogate endpoint evaluation is universally accepted across all endpoint and disease types, a number of endpoints demonstrating consistently good surrogacy in particular settings have recently been identified and approved for primary use in future trials by regulatory authorities. Within the setting of adjuvant therapy in colon cancer, Sargent et al. (2005) demonstrated that disease-free survival (DFS) with 3 years median follow-up is a valid surrogate for 5 years median follow-up on overall survival (OS). In the setting of advanced colorectal cancer, progression-free survival was similarly validated as a surrogate for overall survival (Buyse et al., 2007).

Even after a surrogate endpoint has been deemed “valid“ for primary use in a future trial, however, a healthy skepticism should remain regarding the surrogate’s ability to reflect the true treatment effect that would be observed given full follow-up on the clinical endpoint; however, few (if any) efforts have been made to formalize existing knowledge and uncertainty in the design of a future clinical trial where a validated surrogate takes on its intended role. This new trial should use the surrogate endpoint (which may be observed earlier or more often among patients) as the primary endpoint to establish efficacy, so that the benefits of having validated the endpoint may be realized. At the same time, the fact that the new primary endpoint is really a surrogate, and perhaps only a recently-validated one, should not be ignored.

We propose a trial design which adaptively checks accumulating data for consistency with relationships expected from the surrogacy validation process based on similar trials. At prospectively-defined checkpoints, we assess the performance of the surrogate and decide whether it should continue to be used to measure the effect of treatment. If the surrogate is behaving in the expected manner, we continue to use it as the primary endpoint as the trial progresses to the next checkpoint; otherwise, we adaptively switch consideration back to the original clinical endpoint for the duration of the trial. Furthermore, at each checkpoint, we also test for early efficacy, inferiority, or futility of the experimental treatment arm compared to control, based on the primary endpoint at that time. If any of these conditions are met with adequate precision, we stop accrual, and thus avoid continuing a trial that is unnecessarily long, unnecessarily large, probably futile, or needlessly exposing many of its patients to a regimen which is likely to be inferior to a standard-of-care control. When faced with insufficiently precise information to establish early efficacy, inferiority, or futility, we continue accrual to the next prospectively-designed checkpoint. If a maximum number of patients are allowed to accrue and given reasonable follow-up, we compute a final measure of clinical benefit based on either a trusted surrogate or the original clinical endpoint.

The remainder of the paper evolves as follows. In Section 2, we describe a Bayesian model for summarizing the relationship between treatment effects on the surrogate and clinical endpoints from multiple historical trials – the same relationship which previously validated the surrogate, and which we will reference during the new trial. We describe the design of this trial in Section 3, including its adaptive handling of efficacy, inferiority, futility, and expected surrogacy. Section 4 presents simulations for Type I error, power, and surrogacy discrimination compared to a standard O’Brien-Fleming approach (O’Brien and Fleming, 1979), while Section 5 demonstrates the new trial design using patient-level data from actual trials and a historically-validated endpoint in colon cancer (Sargent et al., 2005). We conclude with a discussion in Section 6.

2. Bayesian Model for Historical Trials

Assume that a surrogate endpoint S has been validated to replace a primary clinical endpoint T based on a collection of historical trials indexed by i ∈ {1, …, N}. We further assume that S and T are time-to-event endpoints, as is often the case when a surrogate endpoint is desired, but the ensuing development is similar for endpoints of other types. Denote by Z the treatment assignment, where Z = 1 for experimental and Z = 0 for control. For historical trials containing more than one experimental arm, pairwise comparisons to the control arm may be required.

Many parametric and semiparametric survival models exist, and for a given endpoint, only one such model may be appropriate. For ease of exposition, here we assume both S and T follow Weibull(r, μ) distributions parameterized according to

$$f(x\mid r,\mu )=\mu r{x}^{r-1}exp(-\mu x^r),$$

where x > 0 and μ r > 0. Further assuming unique baseline hazard functions for each trial and endpoint, the surrogate and clinical endpoints for patient j ∈ {1,…,n_i} from trial i are modeled as

$$S_{ij}\sim \text{Weibull}(r_i^S,{\mu }_{ij}^S)$$ (1)

and

$$T_{ij}\sim \text{Weibull}(r_i^T,{\mu }_{ij}^T),$$ (2)

where $r_i^S$ and $r_i^T$ are trial-specific shape parameters, and regressors z_ij and corresponding coeffcients α_i and β_i are introduced through trial and patient-specific scale parameters ${\mu }_{ij}^S=exp({\gamma }_i^S+{\alpha }_i{z}_{ij})$ and ${\mu }_{ij}^T=exp({\gamma }_i^T+{\beta }_i{z}_{ij})$. Under this parameterization, median times until S and T for treatment arm Z in trial i are given by

$$m_{i,z}^S={\{log(2)exp[-({\gamma }_i^S+{\alpha }_i{z}_{ij})]\}}^{1/r_i^S}$$

and

$$m_{i,z}^T={\{log(2)exp[-({\gamma }_i^T+{\beta }_i{z}_{ij})]\}}^{1/r_i^T}.$$

While joint modeling of S and T by copulas may be ideal for purposes such as surrogacy evaluation (Burzykowski et al., 2001), we choose marginal models to prevent unwanted learning between the endpoints and treatment effects within each trial. Parameter estimates for each trial and endpoint may be obtained by maximum likelihood estimation, or alternatively, through Markov chain Monte Carlo (MCMC) estimation within a Bayesian framework (see Carlin and Louis (2009), Sec. 3.4).

Given that a linear theoretical relationship between α_i and β_i is reasonable, we assume

$$\left(\begin{array}{c}{\alpha }_i\\ {\beta }_i\end{array}\right)\sim N_2\left(\left(\begin{array}{c}\alpha \\ \beta \end{array}\right),\mathrm{\sum }=\left(\begin{array}{cc}{\sigma }_{aa}& {\sigma }_{ab}\\ {\sigma }_{ab}& {\sigma }_{bb}\end{array}\right)\right),$$ (3)

as in Burzykowski et al. (2001). We further note that the above relationship induces a regression line for α_i given β_i with intercept δ₀ = α – βσ_ab/σ_bb and slope δ₁ = σ_ab/σ_bb. Using vague prior distributions on (α, β) and Σ, we obtain posterior distributions summarizing what is known about the relationship of treatment effects across the historical trials, quite possibly the same relationship that led to the validation of S as a surrogate endpoint for T.

3. Bayesian Adaptive Design

Given the model presented in Section 2 relating treatment effects on S and T across similar historical trials, we now describe the design of a future trial, indexed by i = N + 1, which uses the newly-validated surrogate endpoint S as the primary endpoint. In the context of a Phase III trial, we expect S to be the endpoint used to establish efficacy of the experimental treatment for regulatory purposes. This new trial will monitor the effect of treatment on both S and T, though in general, more events may be expected to occur (and occur earlier) for S than for T, hence the desirability of S as a surrogate for T. Any information accumulating for T will be used adaptively to assess the performance of the surrogate endpoint S throughout the trial, but will not influence the assessment of treatment effect on S.

At various prospectively-defined interim checkpoints in our trial, we check accumulating information regarding the current trial’s treatment effects, (α_N+1, β_N+1), for consistency with their expected relationship based on (3). Given that the observed relationship between α_N+1 and β_N+1 at any time point is consistent with past experience, we proceed to check α_N+1 for early efficacy and inferiority based on pre-specified posterior thresholds. If either reason for early stopping of the trial cannot be established, we check for futility of the trial based on the predictive probability of trial success (an efficacious treatment), before continuing accrual to the next interim checkpoint. If, on the other hand, the relationship between α_N+1 and β_N+1 is inconsistent with that given by (3), we adaptively switch to consideration of T (and β_N+1) for establishing early efficacy, inferiority, or futility. We assume up to K interim checks during the trial, which we index by k = 1, …, K. The timing of checkpoints is generally associated with specific levels of accrual or percentages of observed (uncensored) events, so that stopping the trial early at any point may have the effect of decreasing overall sample size and/or shortening total trial length.

Though adaptive randomization could be considered (see Berry et al. (2010), Section 4.4), we maintain equal allocation to each of two treatment arms, and collectively denote the historical trials’ data by D_h and the new trial’s currently accrued patient data by D_k. We continue to assume that S_N+1,j and T_N+1,j, j = 1, …, n_N+1 follow Weibull distributions as in (1)-(2), but the same design may be easily implemented using other endpoint models. Enrolled patients not experiencing an event S or T by time k will be right-censored at their present length of follow-up for that endpoint. At a given checkpoint k, using vague priors and MCMC sampling to estimate the parameters of (1)-(2) for trial i = N + 1, we may obtain posterior distributions on the treatment effects α_N+1 and β_N+1 given current data D_k. In particular, for independent priors ${\alpha }_{N+1}\sim N({\mu }_{0,\alpha },{\sigma }_{0,\alpha }^2),{\gamma }_{N+1}^S\sim N({\mu }_{0,{\gamma }_S},{\sigma }_{0,{\gamma }_S}^2)$, and $r_{N+1}^S\sim \text{Exp}({\lambda }_0^S)$, the joint posterior for (α_{N + 1}, ${\gamma }_{N+1}^S,r_{N+1}^S$) given data D_k on currently enrolled patients $j\in \{1,\dots ,n_{N+1}^k\}$ is proportional to the data likelihood times the joint prior,

$$\begin{array}{l}\pi ({\alpha }_{N+1},{\gamma }_{N+1}^S,{\gamma }_{N+1}^S\mid D_k)\propto L({\alpha }_{N+1},{\gamma }_{N+1}^S,r_{N+1}^S\mid D_k)p({\alpha }_{N+1})p({\gamma }_{N+1}^S)p(r_{N+1}^S)\\ \propto \prod _{j=1}^{n_{N+1}^k}\left\{{\left[{\mu }_{N+1,j}^S{r}_{N+1}^S{(s_{N+1,j})}^{r_{N+1}^S-1}\right]}^{{\nu }_j}exp\left[-{\mu }_{N+1,j}^S{(s_{N+1,j})}^{r_{N+1}^S}\right]\right\}\\ \times exp\left\{-{\lambda }_0^S{r}_{N+1}^S-\frac{1}{2}\left[{\left(\frac{{\alpha }_{N+1}-{\mu }_{0,\alpha }}{{\sigma }_{0,\alpha }}\right)}^2+{\left(\frac{{\gamma }_{N+1}^S-{\mu }_{0,{\gamma }_S}}{{\sigma }_{0,{\gamma }_S}}\right)}^2\right]\right\}.\end{array}$$

Here, ${\mu }_{N+1,j}^S$ is defined as in (1), and ν_j is a censoring indicator equal to 1 if the jth individual has experienced event S prior to checkpoint k, and equal to 0 otherwise. The joint posterior $\pi ({\beta }_{N+1},{\gamma }_{N+1}^T,r_{N+1}^T\mid D_k)$ associated with endpoint T may be derived similarly. For early interim checks, the variability in one or both of these posteriors may be large, and this uncertainty will be formally incorporated in any adaptive decisions.

3.1 Trial Algorithm for Checkpoint k

At a given checkpoint k, we adaptively assess the progress of trial i = N + 1 according to the following algorithm:

Algorithm 3.1 (Adaptive Design for a Surrogate Endpoint)

• Step 1Surrogacy: Assess the consistency of (α_N+1; β_N+1) with the historical relationship given by (3). Denote by π(α_N+1|D_k) the current posterior for the treatment effect on S in the new trial, and denote by π(E(α_N+1|β_N+1)|D_h, D_k) the current posterior for the expected treatment effect on S, given both the effect on T in the new trial and historical uncertainty from (3). If these posteriors overlap in probability to a degree less than P_surr, discontinue consideration of the surrogate endpoint for the remainder of the trial, and perform Steps 2 through 4 using the treatment effect β_N+1 for the endpoint T (skipping Step 1 at subsequent checkpoints). Otherwise, if π(α_N+1|D_k) and π(E(α_N+1|β_N+1)jD_h, D_k) overlap to a degree greater than or equal to P_surr, continue with S as the primary endpoint, and perform Steps 2 through 4 using α_N+1. See Section 3.2 for more details.
• Step 2Efficacy: Check for early efficacy by computing the posterior probability that α_N+1 (or β_N+1) is less than 0, assuming an efficacious treatment extends the time-to-event endpoint. If P(α_N+1 < 0|D_k) > P_eff (good surrogacy) or P (β_N+1 < 0|D_k) > P_eff (rejected surrogacy), where P_eff is some chosen threshold, stop the trial for early efficacy. Otherwise, continue to Step 3.
• Step 3Inferiority: Check for early inferiority by computing P(α_N+1 > 0|D_k) (or P(β_N+1 > 0|D_k) under rejected surrogacy), assuming an inferior treatment reduces the time to an event. If the posterior probability of inferiority of the experimental arm is greater than some threshold P_inf, stop the trial for early inferiority. Otherwise, continue to Step 4.
• Step 4Futility: Check for early futility by computing the empirical probability of trial success (the experimental treatment is efficacious) given full accrual to n_N+1 and sufficient follow-up. In this case, eventual success is determined using a posterior predictive method: random samples from the joint posterior $\pi ({\alpha }_{N+1},{\beta }_{N+1},{\gamma }_{N+1}^S,{\gamma }_{N+1}^T,r_{N+1}^S,r_{N+1}^T\mid D_k)$ at the current checkpoint k are used to simulate event times for patients that would be observed if the trial were to continue to a pre-determined maximum length. If the updated posterior probability of efficacy after some minimum follow-up for the last hypothetical patient enrolled is greater than P_eff, the trial is considered a success. The empirical probability of trial success, computed over the random draws from π(·|D_k), is compared to P_fut. The trial only continues to the next checkpoint k if this probability is greater than P_fut.

If the final interim checkpoint K is reached and the decision is made to continue enrollment, the trial proceeds to full accrual at the pre-set maximum sample size n_N+1 determined by the sponsor. Generally, a final analysis of treatment benefit is performed after some minimum follow-up period on the last patient enrolled, so that some scientific contribution to the trial exists for every patient (Berry et al. (2010), p. 223). This final analysis consists of Steps 1–3 if the surrogate endpoint is still in use, or Steps 2–3 if the surrogate endpoint has been previously rejected. The conclusions made with respect to the effect of the experimental treatment on final active outcome (S or T) will be those presented to regulatory authorities, assuming a Phase III confirmatory trial is being conducted. If the endpoint S is indeed a good surrogate for T, we might expect the information on the effect of treatment to be more precise for S than for T, as more observations on S were likely possible.

3.2 Checking Surrogacy Concordance

We now describe implementation of Step 1 from Algorithm 3.1 in more detail, for a given interim checkpoint k. Having obtained posterior distributions π(δ₁|D_h) and π(δ₀|D_h) for the slope and intercept, respectively, summarizing the historical relationship between treatment effects on S and T (as described in Section 2), we compute the conditional posterior we expect for the current trial’s treatment effect on S given the current trial’s treatment effect on T, denoted π(E(α_N+1|β_N+1)|D_h, D_k). This may be constructed using posterior samples from each of π(δ₁|D_h), π(δ₀|D_h), and π(β_N+1|D_k), according to the historical fixed relationship E(α_i|β_i) = δ₀ + δ₁β_i. The posterior π(E(α_N+1|β_N+1)|D_h, D_k) combines historical uncertainty regarding (α, β) and Σ with current uncertainty on β_N+1 to give a plausible (expected posterior) distribution for α_N+1. When symmetric, this distribution is centered at E[E(α_N+1|β_N+1)|D_h, D_k], the point along the historical regression line corresponding to the present value of E(β_N+1|D_k). Also of interest is π(α_N+1|D_k), which independently summarizes the current location and uncertainty for the treatment effect on the surrogate endpoint at checkpoint k. The surrogate is only performing in the historically expected way in the current trial if π(α_N+1|D_k) is “close“ to π(E(α_N+1|β_N+1)|D_h, D_k). To measure this closeness, we approximate the amount of posterior overlap by computing:

$$2min\{P({\alpha }_{N+1}<{\delta }_0+{\delta }_1{\beta }_{N+1}\mid D_h,D_k),P({\alpha }_{N+1}>{\delta }_0+{\delta }_1{\beta }_{N+1}\mid D_h,D_k)\}.$$ (4)

Assuming π(α_N+1|D_k) and π(E(α_N+1|β_N+1)|D_h, D_k) are approximately symmetrically distributed, the multiplier 2 in (4) is required as roughly half of posterior samples within the region of overlap will be detected for a given inequality direction. Perfect surrogacy exists in those situations where the posterior means of α_N+1 and E(α_N+1|β_N+1) coincide; that is, when symmetry is present and E(α_N+1|D_k) = E[E(α_N+1|β_N+1)|D_h, D_k]. If the empirical amount of overlap is at least P_surr, we conclude based on available information that there is no reason to believe the surrogate is performing poorly; in other words, the current posterior distribution for α_N+1 is centered near the historical regression line evaluated where posterior mass for β_N+1 is currently located (surrogacy concordance). Otherwise, if π(α_N+1|D_k) and π(E(α_N+1|β_N+1)|D_h, D_k) overlap very little, we learn that the surrogate and former clinical endpoints are not relating in the historically-expected way in the current trial, and thus the surrogate endpoint should not be trusted (surrogacy discordance).

Although this design combines past and present sources of uncertainty in order to evaluate surrogacy, it is important to note that it also explicitly (and correctly) prohibits Bayesian learning between the collection of historical trials indexed by i ∈ {1, …, N} and the current trial, indexed by i = N + 1. Prior to the new trial, information is shared across similar historical trials in estimating parameters of (3), or equivalently, in confirming the trial-level surrogacy which previously validated S for T. This historical snapshot of the surrogacy relationship across trials, as well as posterior uncertainty for the slope δ₁ and the intercept δ₀ that summarize this relationship, are considered fixed prior to and during the new trial that uses S as a primary endpoint. In other words, data accumulated during the new trial do not inform or update the posteriors obtained from the historical model (3), as this would undermine interim checks for surrogacy. Likewise, posterior information from fitting (3) to historical treatment effects is not used to inform estimation of the treatment effects α_N+1 and β_N+1 in the new trial. Thus, while we adaptively monitor the surrogacy of S for T in the new trial for consistency with historical trials, any conclusions made with respect to the intervention (efficacy, inferiority, or futility) may still be regarded as independent from historical information for regulatory purposes.

In general, we choose P_surr to be quite small (say, 0.10 or less), relying on the fact that the surrogate has been previously validated and changing the primary endpoint mid-trial should be difficult. Throughout this paper, we do not reassess surrogacy concordance at later checkpoints after the surrogate is rejected, as we are not interested in regaining trust in surrogate endpoints that only work well “some of the time“ during a trial. Furthermore, any decision to switch from a surrogate to a true endpoint mid-trial is based on posterior probabilities that combine all available (historical and current) uncertainty regarding the surrogacy relationship, rather than the outcome of some Bernoulli draw with a probability derived from this relationship.

4. Simulation Study

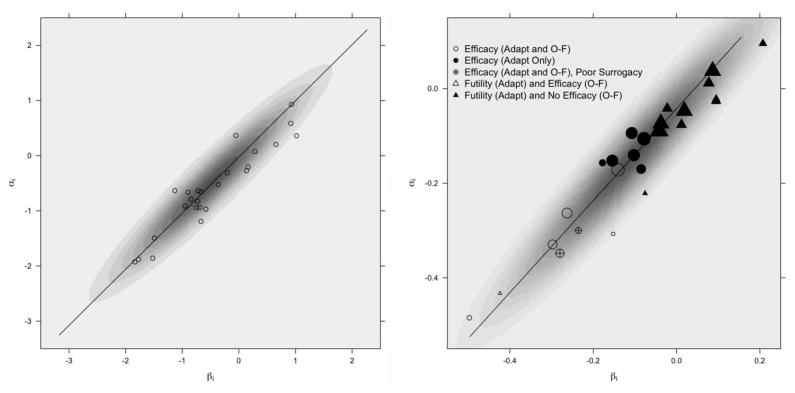
As is generally the case for trials designed with Bayesian adaptive stopping rules, frequentist operating characteristics such as Type I error and power are most conveniently assessed through simulation studies. We note that our simulation settings were intentionally chosen to reflect characteristics of actual trials presented in the data analysis of Section 5. Throughout, we assume fixed historical validation data in the form of treatment effects (αi, β_i), i = 1, …, 25 arising from model (3) with mean (α, β) = (−0.5, −0.5), variances σ_aa = σ_bb = 1, and covariance σ_ab = 0.95. These specifications correspond to δ₀ = 0, δ₁ = 1, and correlation 0.95 across the historical treatment effects, which are superimposed on a contour plot of their underlying bivariate Normal distribution in the left window of Figure 1. We assume this strong relationship previously played a role in validating S as a surrogate for T.

Figure 1.

Scatterplots of historical treatment effect pairs (α_i, β_i), i ∈ {1, …, 25}, for the simulated historical trials (left) and the ACCENT trials (right). The simulated effects are superimposed on an image plot of the bivariate normal density from which they were sampled, while the ACCENT effects are superimposed on an image plot of the bivariate normal distribution estimated from model (3) and weighted by the square root of trial size. Regression lines based on E(δ₀|D_h) and E(δ₁|D_h) from model (3) fits are included for each case, where D_h collectively denotes data from the historical trials. The position of each ACCENT treatment effect pair is based on the original trials with all available patient follow-up, while the symbol for each treatment effect pair denotes the conclusions that would have been reached had the trial been performed according to our adaptive design or an O’Brien-Fleming design. Trials with efficacious experimental arms according to a frequentist O’Brien-Fleming design are further denoted with unfilled symbols, while filled symbols denote O’Brien-Fleming trials which would have required full follow-up to determine no treatment effect.

After generating (α_i, β_i) from (3) as specified above, we estimate the parameters of the same model – which we now assume to be unknown – using MCMC with vague prior distributions. In particular, we place N(0, τ = 0.0001) priors on each of the mean parameters (where τ is the reciprocal variance), and we choose a Wishart(2, M) prior for the precision matrix Σ⁻¹, where M is a diagonal matrix with diag(M) = (10⁻⁶, 10⁻⁶). Based on rapid mixing, we acquire posterior sample chains of length 10,000 for each parameter, after a burn-in of 1,000 iterations. With these samples, we derive posteriors for the slope δ₁ and intercept δ₀ of the regression line induced by model (3), which remain fixed throughout our simulations and will be referenced as we assess surrogacy in the new trial.

4.1 Data Generation and Settings

While the posterior uncertainty for δ₀ and δ₁ derived from fitting model (3) remains fixed throughout our simulations, we vary some characteristics of the new trial in order to assess the operating characteristics of its design. We continue to assume that S and T follow Weibull distributions parameterized as in (1)-(2), and consider a maximum sample size of n = 2000 patients with equal allocation to two treatment arms. Throughout, we fix $r_{N+1}^S=r_{N+1}^T=2$, but common shape parameters need not be assumed; indeed, we relax this assumption in the data analysis of Section 5. At the top level of the simulation, we specify true median event times $m_{N+1,0}^S$ and $m_{N+1,0}^T$ associated with the control group (Z = 0) for each endpoint in the new trial, as well as true improvement ratios of the experimental over control groups (in terms of median event times) for each endpoint. We denote these true improvement ratios by Δ_S and Δ_T. Together, the specified shape parameters, baseline median event times, and improvement ratios determine the true underlying Weibull regression parameters according to the following equations:

$$\begin{array}{ll}{\gamma }_{N+1}^S=-log[{(m_{N+1,0}^S)}^{r_{N+1}^S}/log(2)]\hfill & {\alpha }_{N+1}=-log[{({\mathrm{\Delta }}_S)}^{r_{N+1}^S}]\hfill \\ {\gamma }_{N+1}^T=-log[{(m_{N+1,0}^T)}^{r_{N+1}^T}/log(2)]\hfill & {\beta }_{N+1}=-log[{({\mathrm{\Delta }}_T)}^{r_{N+1}^T}].\hfill \end{array}$$

These in turn determine the true scale parameters given by ${\mu }_{N+1,j}^S=exp({\gamma }_{N+1}^S+{\alpha }_{N+1}{z}_{N+1,j})$ and ${\mu }_{N+1,j}^T=exp({\gamma }_{N+1}^T+{\beta }_{N+1}{z}_{N+1,j})$ for j = 1, …, n_N+1.

For each scenario and endpoint, we generate random event times for patient j in trial i = N + 1 by $S_{N+1,j}\sim \text{Weibull}(r_{N+1}^S,{\mu }_{N+1,j}^S)$ and $T_{N+1,j}\sim \text{Weibull}(r_{N+1}^T,{\mu }_{N+1,j}^T)$, with shape and scale parameters fixed at their true values. Motivated by the prior validation of S as a surrogate for T, we consider the situation where S is known to have an earlier median event time than T in the control arm, setting $m_{N+1,0}^S=350\text{days}$ and $m_{N+1,0}^T=700\text{days}$.

At this stage, we also generate random accrual dates for each patient according to a discrete uniform(1, b) distribution, where b is chosen to be twice the true median event time for T in the control group. While this choice of b may seem arbitrary, it ensures that both early stopping rules and the use of a surrogate remain useful. Accrual dates are assumed unrelated to treatment assignment, so at any interim checkpoint k, we expect approximately equal enrollment in each treatment arm. Throughout the simulation studies, we define 3 interim checkpoints to be the dates on which 25%, 50%, and 75% of patients have experienced events. Trials which continue beyond the third checkpoint have final analyses after 100% of patients have experienced events. In the data analysis of Section 5, timing of checkpoints and final analyses will be adapted for trials with a high level of censoring throughout.

With the Weibull shape parameters and true median event times fixed in each simulation, we focus primarily on the effect of varying the improvement ratios Δ_S and Δ_T. When Δ_S = Δ_T = Δ, the treatment effect pair in the new trial is concordant with the validating trials, falling on the historical regression line representing perfect surrogacy. Given concordance of the new and historical trials, we investigate scenarios where Δ = 1, indicating no improvement in the experimental arm over the control arm (Type I error case), and scenarios with Δ ≠ 1, where the experimental treatment is either efficacious or inferior (power cases). We also consider poor surrogacy scenarios with Δ_S ≠ Δ_T, where the treatment effects α_N+1 and β_N+1 become discordant and no longer fall along the regression line induced by model (3).

We perform R = 100 replications (hypothetical trials) for each of 12 scenarios, described in Table 1. At each checkpoint k reached within a simulated trial, we follow Algorithm 3.1 using available data on currently accrued patients and posterior thresholds given by P_surr = 0.01, P_eff = 0.99, P_inf = 0.99, and P_fut = 0.05, assuming rejection of the surrogate or early stopping should be difficult. Diffuse normal priors on the treatment effects and more informative priors for ${\gamma }_{N+1}^S$ and ${\gamma }_{N+1}^T$ (centered at true values) are used to obtain posterior samples of length 10,000 after 1,000 burn-in iterations, apparently suficient given the MCMC algorithm’s good convergence properties.

Table 1.

Scenarios explored in the simulation study.

Surrogacy Concordance	Surrogacy Discordance
No effect on S or T:	Positive effect on T, no effect on S:
Δ = 1.0	ΔS = 1, ΔT = 1.1
	ΔS = 1, ΔT = 1.2
Negative effects on Sand T:	ΔS = 1, ΔT = 1.4
Δ = 0.8
Δ = 0.9
Positive effects on S and T:	Positive effect on S, no effect on T:
Δ = 1.1	ΔS = 1.1, ΔT = 1
Δ = 1.2	ΔS = 1.2, ΔT = 1
Δ = 1.4	ΔS = 1.4, ΔT = 1

To facilitate comparison with a commonly-used frequentist interim design, we perform parallel O’Brien-Fleming analyses for early efficacy based on log-rank tests, using the same set of checkpoints and an overall α = 0.05 for each trial. We note that our choice of Bayesian efficacy threshold, P_eff = 0.99 (corresponding to a one-tailed test with α = 0.01 at each checkpoint), is more conservative than an overall α = 0.05 threshold when considered across four potential checkpoints per trial.

4.2 Simulation Results

In Tables 2 and 3, we present simulation results where concordance and discordance with the historical surrogacy relationship are assumed, respectively.

Table 2.

Simulation results for scenarios with surrogacy concordance (Δ_S = Δ_T = Δ). Mean(SS) is the mean sample size across hypothetical trials (to be compared with n = 2000). P(1), P(2), P(3), and P(Full) are the proportions of trials at interim checkpoints 1, 2, 3, or full follow-up, respectively, that switched endpoints and/or stopped early due to efficacy, inferiority, or futility, presented by endpoint used. The final column reports total percentages of observed discordance (switching) and each stopping reason across time points, by endpoint. Switching results are italicized for clarity, as they do not affect early stopping or average sample size.

Δ	Mean(SS)	Reason	Endpoint	P(1)	P(2)	P(3)	P(Full)	Total
0.8	975	Switch S to T		-	-	-	-	0.00
		Efficacy	S	-	-	-	-	-
			T	-	-	-	-	-
		Inferiority	S	1.00	-	-	-	1.00
			T	-	-	-	-	-
		Futility	S	-	-	-	-	-
			T	-	-	-	-	-
	2000	Efficacy (O-F)	S	-	-	-	-	0.00
0.9	999	Switch S to T		-	-	-	-	0.00
		Efficacy	S	-	-	-	-	-
			T	-	-	-	-	-
		Inferiority	S	0.61	-	-	-	0.61
			T	-	-	-	-	-
		Futility	S	0.39	-	-	-	0.39
			T	-	-	-	-	-
	2000	Efficacy (O-F)	S	-	-	-	-	0.00
1.0	1259	Switch S to T		0.02	-	-	-	0.02
		Efficacy	S	-	0.01	-	-	0.01
			T	0.01	-	-	-	0.01
		Inferiority	S	-	-	-	-	-
			T	-	-	-	-	-
		Futility	S	0.61	0.28	0.07	0.01	0.97
			T	0.01	-	-	-	0.01
	2000	Efficacy (O-F)	S	-	-	-	0.02	0.02
1.1	1380	Switch S to T		-	-	-	-	0.00
		Efficacy	S	0.48	0.33	0.11	0.05	0.97
			T	-	-	-	-	-
		Inferiority	S	-	-	-	-	-
			T	-	-	-	-	-
		Futility	S	0.02	-	-	0.01	0.03
			T	-	-	-	-	-
	1759	Efficacy (O-F)	S	-	0.55	0.36	0.09	1.00
1.2	1073	Switch S to T		0.01	-	-	-	0.01
		Efficacy	S	0.99	-	-	-	0.99
			T	0.01	-	-	-	0.01
		Inferiority	S	-	-	-	-	-
			T	-	-	-	-	-
		Futility	S	-	-	-	-	-
			T	-	-	-	-	-
	1316	Efficacy (O-F)	S	0.52	0.48	-	-	1.00
1.4	1110	Switch S to T		-	-	-	-	0.00
		Efficacy	S	1.00	-	-	-	1.00
			T	-	-	-	-	-
		Inferiority	S	-	-	-	-	-
			T	-	-	-	-	-
		Futility	S	-	-	-	-	-
			T	-	-	-	-	-
	1110	Efficacy (O-F)	S	1.00	-	-	-	1.00

Table 3.

Simulation results for scenarios with surrogacy discordance (Δ_S ≠ Δ_T). Mean(SS) is the mean sample size across hypothetical trials (to be compared with n = 2000). P(1), P(2), P(3), and P(Full) are the proportions of trials at interim checkpoints 1, 2, 3, or full follow-up, respectively, that switched endpoints and/or stopped early due to efficacy, inferiority, or futility, presented by endpoint used. The final column reports total percentages of observed discordance (switching) and each stopping reason across time points, by endpoint. Switching results are italicized for clarity, as they do not affect early stopping or average sample size.

ΔS	ΔT	Mean(SS)	Reason	Endpoint	P(1)	P(2)	P(3)	P(Full)	Total
1	1.1	1299	Switch S to T		0.06	0.03	-	-	0.09
			Efficacy	S	0.01	-	0.02	0.01	0.04
				T	0.06	0.03	-	-	0.09
			Inferiority	S	-	-	-	-	-
				T	-	-	-	-	-
			Futility	S	0.51	0.26	0.10	-	0.87
				T	-	-	-	-	-
		2000	Efficacy (O-F)	S	-	-	0.02	0.01	0.03
1	1.2	1284	Switch S to T		0.25	0.10	0.02	-	0.37
			Efficacy	S	0.01	-	-	-	0.01
				T	0.25	0.10	0.02	-	0.37
			Inferiority	S	-	-	-	-	-
				T	-	-	-	-	-
			Futility	S	0.34	0.18	0.10	-	0.62
				T	-	-	-	-	-
		2000	Efficacy (O-F)	S	-	-	0.01	0.02	0.03
1	1.4	1073	Switch S to T		0.86	0.10	-	-	0.96
			Efficacy	S	-	-	-	-	-
				T	0.86	0.10	-	-	0.96
			Inferiority	S	-	-	-	-	-
				T	-	-	-	-	-
			Futility	S	0.04	-	-	-	0.04
				T	-	-	-	-	-
		2000	Efficacy (O-F)	S	-	-	0.01	0.02	0.03
1.1	1	1377	Switch S to T		0.08	0.02	-	-	0.10
			Efficacy	S	0.44	0.27	0.16	0.03	0.90
				T	-	-	-	-	-
			Inferiority	S	-	-	-	-	-
				T	0.01	0.01	-	-	0.02
			Futility	S	-	-	-	-	-
				T	0.07	0.01	-	-	0.08
		1752	Efficacy (O-F)	S	-	0.57	0.36	0.06	0.99
1.2	1	1091	Switch S to T		0.31	-	-	-	0.31
			Efficacy	S	0.66	0.03	-	-	0.69
				T	-	-	-	-	-
			Inferiority	S	-	-	-	-	-
				T	-	-	-	-	-
			Futility	S	-	-	-	-	-
				T	0.30	0.01	-	-	0.31
		1336	Efficacy (O-F)	S	0.48	0.52	-	-	1.00
1.4	1	1382	Switch S to T		0.97	-	-	-	0.97
			Efficacy	S	0.03	-	-	-	0.03
				T	0.01	0.02	0.02	0.01	0.06
			Inferiority	S	-	-	-	-	-
				T	-	-	-	-	-
			Futility	S	-	-	-	-	-
				T	0.58	0.18	0.12	0.03	0.91
		1119	Efficacy (O-F)	S	1.00	-	-	-	1.00

Simulation results for scenarios with surrogacy concordance are presented in Table 2, where we consider hypothetical trials with treatment worse than control (Δ = 0.8, 0.9), equal to control (Δ = 1), and better than control (Δ = 1.1, 1.2, 1.4) in terms of improved median S and T. Bearing in mind the order in which the steps of Algorithm 3.1 are performed at each checkpoint, we find that most simulated trials stop early for the correct decision. When the treatment arm has no benefit (Δ = 1), 98% of trials stop early for futility based on either endpoint (usually S), with most stopping at the first checkpoint. In this case, the trials that incorrectly stop for efficacy or inferiority together yield an estimated Type I error rate of 2%, the same error rate observed for the O’Brien-Fleming approach (though O’Brien-Fleming does not allow for inferiority stopping). When Δ = 0.80, the median event times for S and T in the treatment group are 80% of the median times in the control group, and all 100 simulated trials correctly stop at the first interim checkpoint for treatment inferiority. Once median event times in the treatment group increase to 90% of the median event times in the control group, power decreases as fewer trials stop for inferiority and more stop for futility. In each inferiority case, no trials demonstrate efficacy according to the O’Brien-Fleming approach. Once we set Δ to be greater than 1, yielding improved median event times for the experimental treatment relative to control, the vast majority of trials correctly stop early for treatment efficacy under each approach. However, our adaptive design tends to stop a larger percentage of trials for efficacy at earlier checkpoints compared to the O’Brien-Fleming design, thus offering significant savings in time and cost. Across all concordant cases, we obtain an average reduction in sample size of more than 43.3%, while many O’Brien-Fleming cases show no savings in sample size.

Scenarios with surrogacy discordance (Δ_S ≠ Δ_T ) also show promising results, which we present in Table 3. The first three sections of this table represent trials where a beneficial effect on the former endpoint T is not reflected in a beneficial treatment effect on the surrogate endpoint S. These may be the scenarios of greatest interest (or concern) in practice, as we usually anticipate improved experimental outcomes over control when designing a trial, corresponding to values of Δ_T greater than 1. It may be feared that the surrogate endpoint may fail to detect a truly beneficial treatment, indicated by concurrently setting Δ_S = 1. However, poor surrogacy in the new trial is often detected among these cases using our design, and is detected earlier as the treatment effects on S and T become more discordant. This is indeed comforting, as we would like to avoid trusting an invalid surrogate well into an expensive and lengthy trial. It is interesting to note that many trials stop for futility of S in less discordant cases Δ_S = 1 and Δ_T = 1.1 or 1.2; this is due to the fact that futility is determined through S using predictive probabilities based on π(α_N+1|D_k). With Δ_S = 1, we would expect to reach a futility decision, given that the surrogate’s performance is not so poor in Step 1 as to preempt Step 4 of Algorithm 3.1. The O’Brien-Fleming approach with S as its primary endpoint is unable to detect surrogacy discordance, and continues to trust S throughout the trial. In most cases, this design determines that the experimental treatment is ineffective. In reality, S is unable to measure the true positive effect on T, and thus the O’Brien-Fleming trials here may prevent regulatory acceptance of truly beneficial treatments.

For symmetry, we also consider cases where a positive effect on S (Δ_S > 1) is not supported by a positive effect on T (Δ_T = 1), with results presented in the last three sections of Table 3. Although simulated trials stop more frequently for early efficacy based on S than for futility based on T in the cases of Δ_S = 1.1 or 1.2 with Δ_T = 1, this is not entirely surprising, as determinations of efficacy are based on S through π(α_N+1|D_k) when the surrogate’s performance is not so discordant as to switch consideration to T. Once the differences in treatment effect on S and T become more pronounced, trials correctly stop early for futility based on T at a greater rate. The O’Brien-Fleming approach based on S incorrectly stops for efficacy in nearly all cases where S shows a positive effect and T does not, representing situations where regulatory acceptance might be awarded to a truly ineffective treatment. Across all discordant cases, we obtain an average reduction in total sample size of more than 37.4%, while many O’Brien-Fleming cases show no savings in sample size.

5. Example: Adaptive Monitoring of ACCENT Trials

In this section, we illustrate our new design with an example from colorectal cancer, the third most common cancer in the United States with approximately 145,000 new cases diagnosed every year (Sargent et al., 2005). When no interventions are administered to patients with node-positive disease after primary resection, approximately half will experience relapse and eventually die as a result of their disease. Sargent et al. (2005) demonstrated that disease-free survival (DFS) with a median of 3 years follow-up is a valid surrogate for overall survival (OS) with a median of 5 years follow-up in the adjuvant setting. The trials used in the validation process were provided by the Adjuvant Colon Cancer End Points (ACCENT) Group, and contain individual patient data from 18 randomized phase II and phase III trials for adjuvant therapy in colon cancer. These trials were conducted from 1977 to 1999, and collectively include 20,898 patients assigned to 43 treatment arms, composed of 34 active treatment arms (with at least one fluorouracil (FU)-based chemotherapy arm per trial) and 9 surgery-only arms. Using patient-level data from the ACCENT trials and maintaining the natural ordering of the treatment arms in the original trial designs, we consider pairwise comparisons of experimental to control arms for a total of N = 25 trial units.

The ACCENT trials are ideally suited for re-evaluation in our adaptive design framework for a number of reasons, in addition to the well-established good surrogacy of DFS for OS in this setting. First, the median observed DFS time across trials and treatment groups is 643 days, compared to a median OS time of 1093 days, a difference of well over 1 year. As long as the effect of treatment on DFS is a good predictor of the effect of treatment on OS, the amount of follow-up required to observe an adequate number of events will be substantially less for the surrogate endpoint. Second, accrual is relatively slow, ranging from 17 patients to 126 patients per month to fully enroll trials ranging in size from 200 to over 2000 individuals. Third, the maximum follow-up within trials is usually well over 10 years, implying substantial ongoing effort and operational expense.

5.1 ACCENT Analysis Settings

Considering all available patient data without imposing additional censoring to construct specific median follow-up times (as in Sargent et al. (2005)), we use the 25 trial-level units as historical trials in our design, which collectively indicate that DFS is a valid endpoint to use as a surrogate for OS in a future adjuvant colon cancer trial. While we verified that DFS and OS may be reasonably assumed to follow Weibull distributions for these trials, other parametric or semiparametric models such as Cox proportional hazards (Cox, 1972) may be substituted when necessary. A scatterplot of estimated treatment effects (α̂_i, β̂_i) from models (1)-(2) is shown in the right panel of Figure 1, superimposed on an image plot of the bivariate Normal distribution estimated from model (3). The treatment effects on OS and DFS are highly linearly related, with Pearson correlation 0.9541.

To demonstrate how our design performs for realistic “future“ trials, we will imagine that each of the ACCENT trials in turn has yet to be conducted until now. We first fit models (1)-(2) to the full data from each trial, and then fit model (3) to the estimated treatment effects, using diffuse priors for all parameters. This in turn yields posteriors π(δ₁|D_h) and π(δ₀|D_h) for the historical slope and intercept, respectively, summarizing historical knowledge and uncertainty for the ACCENT trials’ relationship in the right panel of Figure 1.

Now, with this historical picture fixed, we effectively re-run each ACCENT trial under our new adaptive design. We use the actual dates of enrollment and event times for each patient, and assume trial sizes were chosen to observe uncensored outcomes for a total of 25% of patients by the end of each trial. Thus, we perform interim checks on those dates where 25%, 50%, and 75% of the total desired number of events have occurred. For each trial and checkpoint, we choose P_surr = 0.10, P_fut = 0.05, and P_eff = P_inf = 0.95. If the decision is made at the final interim checkpoint to continue, we follow all patients until a 25% event rate is observed before performing a final analysis. Estimation of models (1) and (2) at each checkpoint is based only on those patients actually enrolled and is implemented using vague priors on all parameters. MCMC chains of length 100,000 after 10,000 burn-in samples were required to achieve adequate accuracy given the algorithm’s slower mixing, apparently the result of fewer observed (uncensored) event times. We present the endpoint switching and stopping frequencies across the 25 trials at each interim point, by reason, in Table 4.

Table 4.

Frequencies at which surrogacy discordance (based on DFS for OS), efficacy, inferiority, or futility were determined at each time point (percentages of the maximum number of desired events for final analysis) for the 25 ACCENT trial comparisons, by endpoint. The total number of trials stopped at each time point are also given for each design (adaptive and O’Brien-Fleming). Trials with futility results at the final checkpoint had insufficient evidence to reject the null hypothesis of no treatment effect after the desired number of events had been observed.

	Endpoint	25% Max Events	50% Max Events	75% Max Events	100% Max Events	Total
Switch S to T		2	0	0	0	2 (8%)
Efficacy	S	5	4	2	0	11 (44%)
	T	2	0	0	0	2 (8%)
Inferiority	S	0	0	0	0	0 (0%)
	T	0	0	0	0	0 (0%)
Futility	S	4	1	0	7	12 (48%)
	T	0	0	0	0	0 (0%)
Adaptive Design Totals	S; T	11 (44%)	5 (20%)	2 (8%)	7 (28%)	25 (100%)
O’Brien-Fleming Totals	S	0	4 (16%)	3 (12%)	1 (4%)	8 (32%)

5.2 ACCENT Analysis Results

Among the 25 ACCENT trial units considered in our new adaptive framework, a total of 13 trials stopped early for efficacy, based either on S with surrogacy concordance or T with surrogacy discordance. Of these, 7 trials stopped after the first interim check. Given the original treatment effect estimates based on all available follow-up in Figure 1, this is not surprising, as most plotted estimates α̂_i are less than 0. Those ACCENT trials demonstrating efficacy at any time point within our adaptive design have original treatment effect pairs denoted by a circle in Figure 1. Filled circles denote trials where the O’Brien-Fleming design was not able to determine the positive treatment effect, while unfilled circles represent trials where both approaches measured a treatment benefit. A special case of these trials, where efficacy was established by both approaches but through T for the adaptive approach, is given by an unfilled circle containing a +. It may seem surprising that the original treatment effect pairs for the two trials showing poor surrogate performance fall close to the line indicating perfect historical surrogacy, but the high precision of π(α_N+1|D_k) in each large trial may have prevented substantial overlap with π(E(α_N+1|β_N+1)|D_h, D_k). However, neither case is costly in terms of wrong conclusions or additional resources, as the correct treatment benefit was observed (only in terms of T) at the same time the surrogate endpoint was rejected.

ACCENT trials demonstrating futility at any time according to the adaptive design have original treatment effect pairs denoted by a triangle in Figure 1. It is interesting to note that most of the original treatment effects for these trials are located near the null treatment effect point (α_i, β_i) = (0, 0); the conclusions reached in the adaptive setting are similar to those reached in the non-adaptive historical setting, but with less follow-up required. Of the 12 futile trials identified by the adaptive approach, only one very small trial showed a treatment benefit under O’Brien-Fleming approach, which is represented by an unfilled triangle. The other O’Brien-Fleming trials failed to detect efficacy, thus agreeing with the adaptive approach, and are shown as filled triangles.

We find that none of the adaptively-designed ACCENT trials reach a decision of treatment inferiority compared to control. Overall, the average percent reduction in total sample size from the original trials was 11.8% (range: 0% to 69%) for the adaptive approach and 0.08% (range: 0% to 2%) for the O’Brien-Fleming approach, indicating that substantial time and resources could have been saved in most trials under our design.

6. Discussion

In this paper, we proposed a novel trial design that allows a newly-validated surrogate endpoint to play its intended role as the primary endpoint for determining the effect of an experimental treatment, while adaptively checking its performance for consistency with historical data used for its validation. Understanding that practical concerns are likely to remain even after a surrogate has been deemed ‘valid’ for future use, our design quantifies knowledge and uncertainty from the validation stage and uses this information to assess the surrogate’s performance during a new trial, while retaining other advantages of Bayesian adaptivity. While we focused on time-to-event endpoints, other types of endpoints and treatment effect measures could easily be used, with only minor modifications.

In both our simulation studies and application to adjuvant therapy trials in colon cancer, substantial savings in trial length and sample size were observed, while incorrect conclusions regarding surrogacy and effect of treatment were generally avoided (and avoided early). With patients, clinicians, and sponsors alike hoping to see beneficial new therapies approved and available for use as quickly as is reasonably possible, this design offers promise for those diseases where validated surrogate endpoints already exist or will exist in the future.