Integration of diffusion weighted MRI data and a simple mathematical model to predict breast tumor cellularity during neoadjuvant chemotherapy

Abstract

Diffusion-weighted magnetic resonance imaging (DW-MRI) data obtained early in the course of therapy can be used to estimate tumor proliferation rates, and the estimated rates can be used to predict tumor cellularity at the conclusion of therapy. Six patients underwent DW-MRI immediately before, after one cycle, and after all cycles of neoadjuvant chemotherapy. Apparent diffusion coefficient (ADC) values were calculated for each voxel and for a whole tumor region of interest (ROI). Proliferation rates were estimated using the ADC data from the first two time points, and then used with the logistic model of tumor growth to predict cellularity after therapy. The predicted number of tumor cells was then correlated to the corresponding experimental data. Pearson’s correlation coefficient for the ROI analysis yielded 0.95 (p = 0.004), and, after applying a 3×3 mean filter to the ADC data, the voxel-by-voxel analysis yielded a Pearson correlation coefficient of 0.70±0.10 (p < 0.05).

Introduction

Neoadjuvant chemotherapy improves the likelihood of successful breast conservation surgery in patients with locally advanced breast cancer by potentially reducing tumor size at the time of surgery (1). Predicting the outcome of neoadjuvant chemotherapy early during the course of therapy may provide clinicians the ability to adjust treatment on an individual patient basis. One way to achieve this may be through the use of mathematical models. Mathematical models of tumor growth often require knowledge of parameters that may be difficult to measure noninvasively and spatially for individual patients, but in principle this limitation may be overcome through the use of noninvasive imaging. Here we focus on using measurements made with diffusion weighted magnetic resonance imaging (DW-MRI) to provide initial conditions for the logistic model of tumor growth.

The microscopic thermally-induced behavior of molecules moving in a random pattern is referred to as self-diffusion or Brownian motion. The rate of diffusion in cellular tissues is described by the apparent diffusion coefficient (ADC), which largely depends on the number and separation of barriers that a diffusing water molecule encounters. MRI methods have been developed to map the ADC, and in well-controlled situations the ADC has been shown to correlate inversely with tissue cellularity (2–6). Several clinical studies have confirmed the ability of ADC to report on changes in tumor cellularity in the breast after neoadjuvant chemotherapy (7–9). Investigators have used DW-MRI and its extension, diffusion tensor imaging (DTI), to model how brain tumors grow or respond to treatment. For example, Ellingson et al. used ADC values obtained at three time points for patients with glioblastoma to estimate parameters of the diffusion growth model, including the proliferation rate and the rate of diffusion of tumor cells (10). Other groups (11–14) have used DTI to calculate some of the parameters of the diffusion growth model or extensions thereof for patients with brain tumors. However, these studies have not made explicit use of the biophysical relationships between ADC and cellular variations. Here we build on previous work (15,16) to show how serial DW-MRI data can be used to calculate the proliferation rate of tumors for patients with localized invasive breast cancer. The calculated proliferation rates were used to simulate the tumor cell density at the time of a later DW-MRI exam allowing a direct comparison of the estimated and simulated tumor density at the latter time point.

Materials and Methods

Data were acquired from six patients with locally advanced breast cancer who were enrolled in an ongoing clinical trial (9). The patients provided informed consent, and the study was approved by our Institutional Review Board. The patients were enrolled on a study that involved neoadjuvant chemotherapy which consisted of 12 weekly cycles of Cisplatin, Paclitaxel, with or without RAD001. Dynamic contrast enhanced MRI (DCE-MRI) and DW-MRI of the patients were obtained before (t₁), after one cycle (t₂), and at the completion of neoadjuvant chemotherapy (t₃).

Imaging Protocol

DW-MRI and DCE-MRI were performed using a Philips 3T Achieva MR scanner (Philips Healthcare, Best, The Netherlands) equipped with a 4-channel receive double-breast coil (Invivo Inc., Gainesville, FL).

DW-MRIs were acquired with a single-shot spin echo (SE) echo planar imaging (EPI) sequence in three orthogonal diffusion encoding directions (x, y, and z), with two b-values (50 and 600 s/mm² (500 s/mm² for one subject)), in-plane field of view (FOV) = 192 mm × 192 mm (unilateral), an acquisition matrix of 96×96 reconstructed to 144×144, and 10 signal acquisitions. SENSE parallel imaging (acceleration factor = 2) and spectrally-selective adiabatic inversion recovery (SPAIR) fat saturation were implemented to reduce image artifacts. Subjects were breathing freely with no gating applied. The patient DWIs consisted of 12 sagittal slices with slice thickness = 5 mm (no slice gap), TR = 3080 ms, TE = 43 ms, diffusion time (Δ) = 20.7 ms, and diffusion gradient duration (δ) = 11.6 ms for a total scan time of 4 m and 40 s.

DCE-MRI data were acquired with a 3D RF-spoiled gradient echo sequence with TR\TE = 7.9 ms\1.3 ms. The acquisition matrix was 192×192×20 over a sagittal FOV (25.6 cm)² with slice thickness of 5 mm, one signal acquisition, and a SENSE factor of 2. This scan was repeated for 10 flip angles (ranging from of 2° to 20° in 2° increments) thereby generating data to estimate the pre-contrast T₁. The same protocol (with the flip angle fixed at 10°) was used for the dynamic study in which each 20-slice set was collected in 16 seconds at 25 time points. A catheter placed within an antecubital vein delivered 0.1 mmol/kg of Gd-DTPA (Magnevist, Berlex, Wayne NJ) at a rate of 2 mL/s (followed by a saline flush) after the acquisition of the first three (baseline) dynamic scans.

Image Analysis

ADC maps were calculated from the DW-MRI data using Eq. [1]:

$$\mathit{ADC}=\frac{{\sum }_{i=x,y,z}ln(S_0/S_i)/b_i}{3},$$ [1]

where i is the diffusion-weighting direction, b_i represents the amount of diffusion-weighting imparted to the sample, S_i is the measured signal in each voxel, and S₀ is the signal at the minimum b value (17). This analysis was performed for each patient and for each time point. In order to perform the modeling described below, it is imperative that the ADC maps be spatially co-registered across time points. The DCE-MRI data, which was also collected at the three time points, provided this capability. These data were registered to each other non-rigidly using an adaptive basis algorithm (ABA) with a tumor volume preserving constraint (18, 19). The DCE-MR and DW-MR images were collected at the same time with minimal patient motion so, the images were inherently registered to each other. Thus, by registering the DCE data and applying the corresponding transformation to the DW-MRI data, the DW-MRI data are registered as well.

Once registered, the tumor region of interest (ROI) was manually drawn on the difference image between the averaged post-contrast and the averaged pre-contrast baseline images. The ROIs were drawn on multiple slices to cover the entire visible lesion. The enhanced voxels in the manually drawn ROI was used as the tumor voxels. A voxel was considered “enhanced” if its signal in the post contrast image was greater than the signal in the baseline image by at least 40%. (The 40% cut-off was selected empirically; values of 30 or 50% did not significantly affect the results below.) The tumor ROI from the pre-treatment scan (time point t₁) was then copied onto the images obtained at subsequent time points (t₂ and t₃).

Mathematical Modeling

For early times, the logistic model allows exponential growth of the tumor cells, while for later times the tumor asymptotically approaches the limiting cellular carrying capacity for a given region of space (here, an imaging voxel). The logistic model is explained in detail in (20), and the relevant equation is

$$N(r,t)=\frac{\theta N(r,0)}{N(r,0)+(\theta -N(r,0)){\text{e}}^{-k(r)t}},$$ [2]

where N(r,t) is the number of cells per voxel at position r and time t, N(r,0) is the number of cells present at t = 0 (first time point) and position r, k(r) is the cell proliferative rate at position r, and θ is the cell carrying capacity of the population. Note that k(r) can be negative or positive to describe cell death or proliferation, respectively, and therefore implicitly includes the effects of the treatment. To estimate the number of cells in each voxel at each time point, we used the ADC values of the voxels obtained from Eq. [1]. Several studies have shown a strong negative correlation between ADC and cellularity (2–6). We therefore used this relationship to convert ADC values to tumor cell number. To do this conversion, we assumed that the voxels with an ADC value of free water will have no tumor cells and the voxel with the minimum ADC value will contain the maximum number of cells, θ. This allows us to define the following mapping between ADC and cell number as shown in Eq. [3]:

$$\mathit{ADC}(r,t)={\mathit{ADC}}_w-\lambda N(r,t),$$ [3]

where ADC_w is the ADC of free water, and λ is a proportionality constant. To obtain λ we assume that the minimum ADC, ADC_min, within the tumor occurs at the voxel that has reached the carrying capacity θ. The minimum ADC in the tumor ROI from t₁ and t₂ was used as the ADC_min. The carrying capacity is assumed to be the maximum number of cells that can be contained in a voxel. This was calculated by dividing the voxel volume by the average cell volume of a (spherical) breast tumor cell. We assumed a nominal radius of 10 μm leading to a tumor cell volume of 4189 μm³.

Combing the above assumptions with Eq. [3] results in Eq. [4]:

$${\mathit{ADC}}_{min}={\mathit{ADC}}_w-\lambda \theta .$$ [4]

Combining Eqs. [2]–[4] gives Eq. [5] as previously described (16):

$$\left(\frac{\mathit{ADC}(r,t)-{\mathit{ADC}}_{min}}{\mathit{ADC}(r,t)-{\mathit{ADC}}_w}\right)=\left(\frac{\mathit{ADC}(r,0)-{\mathit{ADC}}_{\mathit{min}}}{\mathit{ADC}(r,0)-{\mathit{ADC}}_w}\right)e^{-k(r)t}.$$ [5]

The ADC data from t₁ and t₂, were used with Eq. [5] to calculate the proliferation rate k(r) of the tumor cells in each voxel. The ADC values from t₂ and t₃ were then converted to tumor cell number N_estimated(r,t₂) and N_estimated(r,t₃), respectively, using Eqs. [3] and [4]. The number of cells within the tumor at t₃, was then calculated via Eq. [2] using the calculated proliferation rate and N_estimated(r,t₂) to yield N_simulated(r,t₃). As the treatment was given weekly, the logistic model was run in a pulsed fashion whereby the model was switched “on” for the day of treatment, and switched “off” for all other times. At each iteration of the model (i.e., after each weekly cycle), a new number of cells for the end of the cycle was calculated. More specifically, for the first model update, N_estimated(r,t₂) and k(r) were used in conjunction with Eq. [2] to calculate the number of cells at the end of the second cycle. The newly calculated number of cells was then used in conjunction with k(r) to calculate the number of cells at the end of the third cycle. We allowed the tumor cells to proliferate according to the calculated proliferation rate only during the day of treatment; a point we return to in the Discussion section. This was repeated until the number of cells at the end of all cycles of treatment N_simulated(r,t₃) was calculated. The estimated and simulated values were then compared as described in the statistical analysis section.

In addition to the voxel-by-voxel comparisons between the estimated and simulated values, we also compared regions of interest (ROI). To do this, the mean ADC values for each tumor ROI for each patient and for each time point were calculated. The mean ADC values for t₁ and t₂ were then used to calculate the mean proliferation rate, k_mean, using Eq. [5]. The mean number of cells on t₂ and t₃, N_{estimated_mean}(t₂) and N_{estimated_mean}(t₃), respectively, were then calculated using Eqs. [3] and [4]. N_{estimated_mean}(t₂) in conjunction with k_mean via Eq. [2] was used to calculate the simulated mean number of cells at t_3, N_{simulated_mean}(t₃). This was then compared to N_{estimated_mean}(t₃) as described below in the statistical analysis section.

Effects of smoothing on voxel level analysis

In order to explore the effects of the signal-to-noise ratio (SNR) and potential registration errors on the results of the modeling, we convolved the voxel level ADC values with a mean filter of varying kernel sizes. Convolving the ADC values with a mean filter removes spurious ADC values that are not representative of their surroundings. We used three different kernel sizes: [3×3], [6×6], and [9×9] with the degree of smoothing increasing with increasing kernel size. The ADC values obtained after smoothing were used to calculate new k(r), N_estimated(r,t₃), and N_simulated(r,t₃) values for all patient data sets as described in the mathematical modeling section.

Statistical Analysis

Four different statistical analyses were performed on the data sets: the 1) Pearson correlation coefficient was used to compare voxel based N_simulated(r,t₃) and N_estimated(r,t₃) values for each patient; 2) concordance correlation coefficient (21) was used to compare voxel based N_simulated(r,t₃) and N_estimated(r,t₃) values for each patient; 3) Pearson correlation coefficient was calculated for the ROI based N_{simulated_mean}(t₃) and N_{estimated_mean}(t₃) values for all the patients grouped together; 4) concordance correlation coefficient was calculated for the ROI based N_{simulated_mean}(t₃) and N_{estimated_mean}(t₃) values for all the patients grouped together. Tests 1 and 2 were then repeated for the smoothed data.

Results

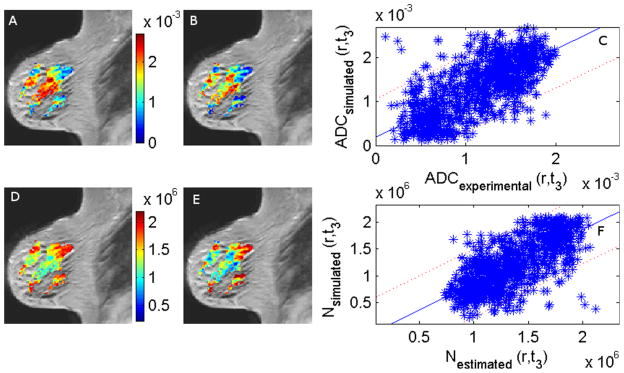
Figure 1 shows the ADC maps, the estimated and simulated number of tumor cells, and the difference image between the averaged post-contrast and averaged pre-contrast image from which the tumor ROI was drawn for one of the patients. The minimum ADC value (ADC_min) used to calculate the carrying capacity of the tumor was slightly different for each patient. The values ranged from 0.1 × 10⁻³ to 0.5 × 10⁻³ mm²/s with a mean value of 0.2 × 10⁻³ mm²/s. Figure 2 shows the experimental and simulated ADC maps and the estimated and simulated number of cells at t₃ superimposed on the corresponding T₁-weighted MR image for a representative patient. Panels A and B show the experimental and the simulated ADC values at t₃, respectively. Panel C is a scatter plot of the data in panels A and B with the 95% confidence interval. Panels D and E are the estimated and simulated number of cells at t₃, N_estimated(r,t₃) and N_simulated(r,t₃), respectively, and panel F is a scatter plot of N_estimated(r,t₃) versus N_simulated(r,t₃) again with the 95% confidence interval. Panels A and B, and panels D and E show that there is a general agreement in the spatial distribution and the relative values of the tumor cells in each voxel. The Pearson’s and concordance correlation coefficients for the voxels in the slice are 0.71 and 0.63, respectively. The Pearson and concordance correlation coefficients for all the voxels within the tumor for this patient are 0.70 and 0.65, respectively.

Figure 1.

Panels A, B and C show the ADC maps (mm²/s) of a cross section of the tumor for a representative patient before therapy (t₁), after one cycle of therapy (t₂), and at the conclusion of therapy (t₃), respectively. Panels D, E and F show the estimated number of tumor cells at t_1, t₂, and t₃, respectively. Panel G is the difference image between the averaged post-contrast and the averaged pre-contrast baseline images from which the tumor ROI was drawn, and Panel H is the simulated number of tumor cells as t₃.

Figure 2.

Panels A and B show an overlay of the experimental and the simulated ADC (mm²/s) values at day t₃, respectively, on a saggital, T₁-weighted image. Panel C compares the experimental and the simulated ADC values at t₃ with the 95% confidence interval indicated by the dotted lines. Panels D and E are the estimated number of cells at t₃, N_estimated(r,t₃) and the simulated number of cells at t₃, N_simulated(r,t₃), respectively. Panel F compares the simulated and the estimated number of cells at t₃ with the 95% confidence interval indicated by the dotted lines. The Pearson’s and concordance correlation coefficients for the voxels in the slice are 0.71 and 0.63, respectively. The Pearson and concordance correlation coefficients for all the voxels within the tumor for this patient are 0.70 and 0.65, respectively.

The Pearson’s correlation coefficient between the N_simulated(r,t₃) and N_estimated(r,t₃) for all the tumor voxels for each patient range from 0.38 to 0.70, and the concordance correlation coefficient range from 0.32 to 0.65. All the Pearson’s correlation coefficients were highly statistically significant (p ≪ 0.0001). These results are summarized in Table 1.

Table 1.

Summary statistics for the six patients

Patient	Mean k × 10−3 (1/day)	Mean ADC (t1) × 10−3 (mm2/s) ± SD	Mean Nestimated (t3) × 106	Mean Nsimulated (t3) × 106	No Filtering		3 × 3		6 × 6		9 × 9
					PCC	CCC	PCC	CCC	PCC	CCC	PCC	CCC
P1	−0.96	1.62±0.36	1.59	1.37	0.64	0.63	0.77	0.77	0.86	0.85	0.90	0.90
P2	0	1.44±0.32	1.20	1.21	0.38	0.32	0.55	0.47	0.69	0.59	0.76	0.65
P3	−0.95	1.21±0.33	1.76	1.55	0.44	0.32	0.61	0.46	0.72	0.55	0.78	0.60
P4	−19.9	0.99±0.24	1.50	1.41	0.50	0.44	0.62	0.58	0.73	0.72	0.82	0.80
P5	−1.86	1.04±0.33	1.64	1.51	0.70	0.65	0.81	0.76	0.89	0.84	0.92	0.87
P6	−30.3	1.39±0.23	1.06	0.88	0.57	0.57	0.85	0.85	0.96	0.95	0.98	0.98
Mean ±1.96.SE	−9±10.3	1.28±0.20	1.46±0.22	1.32±0.20	0.54 ±0.10	0.49 ±0.12	0.70 ±0.10	0.65 ±0.13	0.81 ±0.09	0.75 ±0.13	0.86 ±0.07	0.80 ±0.12

For the ROI analysis, the mean number of cells at t₃ for both the simulated, N_{simulated_mean}(t₃), and the estimated, N_{estimated_mean}(t₃), number of cells with the 95% confidence interval are shown in Figure 3. The Pearson’s correlation coefficient between N_{simulated_mean}(t₃) and N_{estimated_mean}(t₃) is 0.95 (p = 0.004) with a 95% confidence interval of (0.58, 1.0). The range of the confidence interval is enlarged because the number of patients used is relatively small; however, the Pearson’s correlation is statistically significant and this indicates that there is a strong correlation between the simulated and the estimated number of cells on the last time point. The concordance correlation coefficient between N_{simulated_mean}(t₃) and N_{estimated_mean}(t₃) for all the patients is 0.83. This indicates that there is a strong agreement along the line of unity between N_{simulated_mean}(t₃) and N_{estimated_mean}(t₃).

Figure 3.

The ROI average N_{estimated_mean}(t₃) is plotted versus N_{simulated_mean}(t₃) for all six patients with the 95% confidence interval displayed as dotted curves. Each point in the figure represents a single patient. The Pearson’s correlation coefficient between N_{simulated_mean}(t₃) and N_{estimated_mean}(t₃) for all the patients is 0.95 (p = 0.004), and the concordance correlation coefficient for all the patients is 0.83.

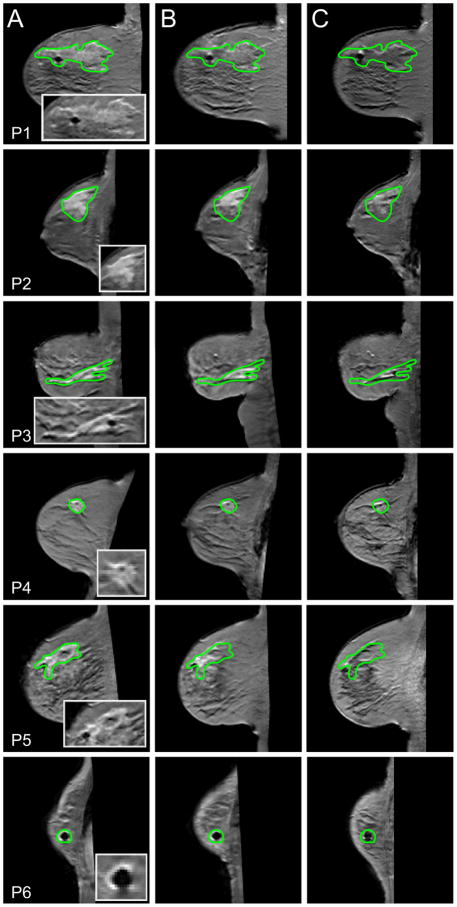
Given the promising results in the ROI analysis, we hypothesized that the relatively weak correlation for the voxel level data may be due to SNR limitations and registration errors. Figure 4 shows cross sections through the tumors of the six patients at the three time points. Columns A, B and C show a single representative slice through the tumor of each patient at t₁, t₂ and t₃ respectively. There are slight misalignments in the tumors at the three time points and this may contribute to the relatively low voxel level correlations found in some of the patients.

Figure 4.

Columns A (time point t₁), B (t₂) and C (t₃) display the registered post-contrast T₁-weighted images through the tumor for each patient for each imaging time point. A magnification of the tumor at t₁ is also shown in the first column. There is some misalignment in the tumor at the three time points for the patients and this may contribute to the relatively low correlations in the voxel level analysis found in some of the patients (see Table 1).

By smoothing the data, we reduce the effect of the registration errors and also increase the SNR, and an example is shown in figure 5. Column A is the estimated number of cells at t₃, column B is the simulated number of cells at t₃, and column C is a scatter plot of these data with the 95% confidence interval. Each row increases the kernel size and therefore the degree of smoothing. The Pearson’s and concordance correlation coefficients between the estimated and the simulated number of cells increase as the kernel size increases and this is summarized in Table 1. The Pearson’s correlation ranged from (0.38, 0.70) for no filtering, and then (0.55, 0.85), (0.69, 0.96), and (0.76, 0.98) for kernel sizes of 3×3, 6×6, and 9×9, respectively. The concordance correlation ranged from (0.32, 0.65) for no filtering, and then (0.46, 0.85) (0.55, 0.95), and (0.60, 0.98) for kernel sizes of 3×3, 6×6, and 9×9, respectively. All the Pearson’s correlation coefficients were highly statistically significant (p ≪ 0.0001). As the kernel size increases the Pearson’s correlation increases from weak to strong. This indicates that an increase in the SNR in the acquired DW-MRI data and/or improved accuracy in image registration may lead to an increase in both the Pearson’s and the concordance correlation coefficients between the estimated and the simulated number of cells at the last time point.

Figure 5.

Columns A and B displays an overlay of the estimated and simulated number of cell at t₃ respectively, on a saggital, T₁-weighted image slice through the tumor of a single patient. Column C displays the corresponding plots of the estimated and the simulated number of cells at t₃ with the 95% confidence interval displayed (red dashed lines). The rows (from top to bottom) correspond to different degrees of smoothing. Row 1 corresponds to the original image with no smoothing (Pearson’s correlation (r = 0.51 and p ≪ 0.0001 between the estimated and the simulated number of cell at t₃ for the slice shown); row 2 corresponds to a convolution with a 3×3 averaging filter (r = 0.65, p ≪ 0.0001); row 3 corresponds to a convolution with a 6×6 averaging filter (r = 0.75, p ≪ 0.0001); and the last row corresponds to a convolution with a 9×9 averaging filter (r = 0.81, p ≪ 0.0001).

The salient features of the pathology reports for the patients are summarized in Table 2. The patients that had a complete response to the therapy appear to have a higher correlation between the simulated and the estimated number of cells at t₃ than patients with a partial response to the therapy, though the small patient number precludes a definitive conclusion.

Table 2.

Summary of the key histology findings for each patient in the study

Patients	Response	Histology grade	Proliferative rate	Estrogen	Progesterone	Her2
P1	Complete	High	High	−	−	+
P2	Incomplete	Intermediate	Intermediate	−	−	−
P3	Incomplete	High	Intermediate	−	−	−
P4	Incomplete	Intermediate	Low	−	−	−
P5	Complete	Low	Low	+	+	−
P6	Incomplete	High	Intermediate	−	−	−

Discussion

We have shown how ADC values computed from DW-MRI data from breast cancer patients undergoing neoadjuvant chemotherapy can be used to estimate tumor cell proliferation values via the logistic model of tumor growth. The estimated proliferation rates were then used to predict tumor cellularity at the conclusion of therapy on both the voxel and ROI levels. The correlations between the simulated and the estimated number of cells on the last time point for the voxel based analysis performed on individual patients showed weak to a moderately strong correlation. However, using the mean value of the ADC in the tumor ROI for the modelling resulted in a strong and significant relationship between the simulated and estimated data. We hypothesized that the strong relationship at the ROI level may be due to the inherent difficulties with acquiring high SNR DW-MRI data of the breast, as well as performing longitudinal registration of a deformable tissue like the breast. To test this hypothesis we smoothed the ADC values with a mean filter which resulted in a substantial increase in the strength of the correlation between simulated and estimated data as the size of the mean filter increases. This increase in the correlation, however, comes at the expense of losing some characterization of the spatial heterogeneity of ADC values within the tumors. Analysis with the mean ADC and the filtered ADC shows a much greater correlation between the estimated and simulated number of cells at the last time point. This shows the possibility of using sequential ADC data as a way to model tumor growth and treatment response if sufficient SNR and minimal registration error can be achieved.

Some of the limitations in the work include the small number of patients that were included in the study, and a number of simplifying assumptions. For example, we assumed that the proliferation rate can be predicted from the first two time points and that this rate remains constant over the course of treatment. Also, proliferation was modeled only on discrete days (days of treatment) in the cycle. We assumed that the change in ADC from the pre-treatment image to the first post-treatment image was due entirely to the reduction in cellularity. We assumed that the voxels are comprised only of tumor cells and as such we ignored the fact that each voxel most likely contains healthy breast and other supportive cells, as well as vascular spaces. We further assumed that the tumor cells can completely occupy a voxel, thereby ignoring the maximum packing fraction of the voxel which may undermine future efforts to correlate the modeling results with histology. Furthermore, we did not consider the size changes of the tumor during the course of therapy.

There are differences in the absolute values of the simulated and the estimated number of cells at the conclusion of therapy. Some of these differences may be due to slight misregistration between the tumors at the different time points, changes in the tumor proliferation rate during therapy and the possible growth of healthy cells. Also, there may be distortions in the DW-MRI that are not present in the DCE–MRI and this may impact the accuracy of the tumor ROI transfer from DCE-MRI to DW-MRI.

Future improvements to the model will involve the incorporation of more biologically relevant tumor characteristics including the tissue volume fractions available from the DCE-MRI data, improvement in the registration between the tumors, and the comparison of the tumor cell count to histology.

Conclusion

Sequential ADC data can be used to predict tumor cell values at later time points. Improvement in the image quality and the image coregistration will lead to a better agreement between the estimated and the predicted tumor cells numbers at a later time point. To the best of our knowledge, this represents the first attempt to use imaging data to parameterize a mathematical model in order to predict changes in the cellularity of breast tumors during neaodjuvant chemotherapy.