Summary
We consider the problem of high-dimensional regression under non-constant error variances. Despite being a common phenomenon in biological applications, heteroscedasticity has, so far, been largely ignored in high-dimensional analysis of genomic data sets. We propose a new methodology that allows non-constant error variances for high-dimensional estimation and model selection. Our method incorporates heteroscedasticity by simultaneously modeling both the mean and variance components via a novel doubly regularized approach. Extensive Monte Carlo simulations indicate that our proposed procedure can result in better estimation and variable selection than existing methods when heteroscedasticity arises from the presence of predictors explaining error variances and outliers. Further, we demonstrate the presence of heteroscedasticity in and apply our method to an expression quantitative trait loci (eQTLs) study of 112 yeast segregants. The new procedure can automatically account for heteroscedasticity in identifying the eQTLs that are associated with gene expression variations and lead to smaller prediction errors. These results demonstrate the importance of considering heteroscedasticity in eQTL data analysis.
Keywords: Generalized least squares, Heteroscedasticity, Large p small n, Model selection, Sparse regression, Variance estimation
1. Introduction
Heteroscedasticity, or the state of having non-constant error variances, is frequently encountered in the analysis of genomic data sets. For example, in genetical-genomics experiments, genetic variants can effect not only the mean gene expression levels, but also the gene expression variances. Such expression quantitative loci (eQTLs) can hold important biological interpretations. Moreover, genomic data sets are often subject to numerous sources of experimental and data pre-processing errors, which can result in non-constant error variances due to the presence of outlying observations. In Section 4, we examine the gene expression data set of 112 yeast segregants from Brem and Kruglyak (2005) and find more than 40% out of 5,428 gene expression levels that exhibit heteroscedasticity at the 1e-6 p-value level. We also observe that genetic variants can explain some of the heteroscedasticity and the presence of clear outliers in this data set. Furthermore, in statistical genomics, as well as numerous modern applications, data sets are often high-dimensional, where the number of predictors p is much larger than the number of observations n. In these applications, it is essential to incorporate heteroscedasticity in order to efficiently utilize the limited number of observations available for statistical modeling and analysis.
The complications in eQTL data analysis from such heteroscedasticity and outlying observations motivate the development of the method that we present in this paper. We consider the high-dimensional heteroscedastic regression (HHR) model,
| (1) |
where yi are responses, xij are predictors, are true coefficients on the mean, and ∊i are independent and identically distributed (i.i.d.) normal random errors. In this setting, an underlying model is assumed across observations for the expected mean, i.e. and observations are perturbed by random errors having possibly different variances. The non-constant error variances may depend upon a q-dimensional vector of true coefficients α and predictors zi, where g is a pre-defined function to ensure that the variances are positive. Particularly, we assume . Modeling the logarithm of variances as linear in predictors is a common choice (Carroll, 1988). Other than guaranteeing positivity, the log-transformation is relevant in modeling multiplicative and higher-order quantities, such as the variance, whose values can otherwise vary over several orders of magnitudes (Cleveland, 1993). In the HHR model, both p and q can be of high-dimensions. For example, in eQTL analysis, yi is the expression level of a gene in the ith sample, and xij = zij can be the genotype for the ith sample at the jth genetic marker, where both p – 1 and q – 1 are numbers of genetic markers considered which can be very large.
The HHR model (1) is very general and encompasses common situations of heteroscedasticity encountered in statistical genomics. For example, when variability is suspected to come from predictors explaining error variances, the variance design matrix can be constructed as,
| (2) |
where . When outliers are suspected to be present, we may set
| (3) |
where In is an n × n identity matrix and .
Substantial progress has been made recently in the regression analysis of high-dimensional data under the assumption of constant error variances. In these applications, model selection, in addition to estimation, is often required in order to establish statistical models with good prediction accuracy and interpretation. The Lasso (Tibshirani, 1996) presents as an important procedure for variable selection and estimation in high-dimensions. It can be computed efficiently even when p is very large (Efron et al., 2004; Friedman et al., 2007) and has been shown to be successful in various applications. Other methods of sparse estimation for high-dimensional regression include the smoothly clipped absolute deviation (SCAD) (Fan and Li, 2001) and Dantzig selector (Candes and Tao, 2007). However, these methods do not consider heteroscedasticity, a common situation that occurs in statistical genomics. Jia, Rohe, and Yu (2009) provide asymptotic results for Lasso under the special setting when error variances are Poisson-like. Their paper presents insightful theoretical studies that illustrate the limitation of the Lasso under non-constant variance assumption. However, no new methodology was provided to account for non-constant error variances.
Several recent works have considered robust procedures for high-dimensional sparse regressions. The LAD-Lasso has been proposed in Wang et al. (2007) that utilizes the least absolute deviations (LAD) instead of the least squares loss for the purpose of robust estimation. It has also been extensively studied in Wang et al. (2006), Li and Zhu (2008), Wu and Liu (2009), and Xu and Ying (2010), which have shown it to be advantageous over the Lasso under many situations. The LAD-Lasso can be computed relatively efficiently using the interior point method (Koenker, 2005). However, as the LAD-Lasso does not model heteroscedasticity explicitly, observations with large or moderately large error variances may still have considerable impact on its performances. She and Owen (2010) considered the problem of outlier detection using sparse regression, where they assume a mean-shift model, in which observations may have different intercept terms while error variances are homogeneous. This is quite different from the HHR model (1), where we assume a consistent underlying mean model and observations arising from random errors with heterogenous variances. An advantage of the HHR model is that it can handle different scenarios when the heteroscedasticity arises in statistical genomics, including both predictors explaining error variances and the presence of outliers.
In order to simultaneously select the variables that are associated with means and also the variances in the HHR model (1), we propose a doubly regularized likelihood estimation with L1-norm penalties to attain sparse estimates for the mean and variance parameters. By incorporating heteroscedasticity, the HHR allows more robust estimation and improved selection of predictors explanatory of the response. Furthermore, it can identify important factors contributing to heteroscedasticity, such as predictors explaining variability or observations having outliers. We develop an efficient coordinate descent algorithm to solve the penalized optimization problem.
The rest of the paper is organized as follows. In Section 2, we first introduce the penalized estimation procedure for the HHR model, including methods for tuning parameter selection and efficient algorithms for the HHR. Section 3 compares finite-sample performances of our method with those of the Lasso and the LAD-Lasso using Monte Carlo studies. In Section 4, we apply our procedure to the eQTL dataset of 112 yeast segregants from Brem and Kruglyak (2005). Section 5 concludes with further discussions.
2. Penalized Estimation for High-Dimensional Heteroscedastic Regression
In typical eQTL experiments, both p and q can be large. In order to estimate the parameters β and α in model (1), we propose the following high-dimensional heteroscedastic regression estimator,
| (4) |
where λ1 and λ2 are tuning parameters on the variance α and mean β coefficients, respectively, and
| (5) |
is the negative log-likelihood of the model (1), assuming the logarithm of error variances to be linear in predictors and ignoring a constant. Intercept terms are included by setting zi1 = 1 and xi1 = 1 for i = 1, … , n, and non-intercept predictors xj = (x1j, … , xnj)T are assumed to be centered and standardized to have mean 0 and variance 1. Further, for numerical stability, we assume y = (y1, … , yn) to be standardized to have variance 1. The second term in the negative log-likelihood (5) efficiently utilizes the data by down-weighting observations with relatively large error variances, whereas the first term provides regularization on variances, that has the effect of retaining information on mean estimation by preventing the second term from going towards 0. These properties allow the estimation to be effective even when the underlying error distribution is non-normal. Note that the HHR is related to the generalized least squares (Box and Hill, 1974; Carroll and Ruppert, 1982; Carroll et al., 1988) in the classical setting when p < n. The L1-norm regularization is applied to both the mean β and variance α coefficients in the HHR to achieve sparsity for high-dimensional regression. Sparsity assumption is expected in our application since we expect only a few genetic factors to contribute to mean or variance of gene expressions.
2.1 An Efficient Coordinate Descent Algorithm
Optimization in (4) for the HHR involves computing for an objective function that is jointly non-convex in coefficients (α, β). Common approaches to non-convex optimization rely on convex optimization as basic components (Boyd and Vandenberghe, 2004). The HHR objective function is, however, convex in β for α fixed and convex in α for β fixed. In other words, the HHR objective function is bi-convex. In the following, we describe efficient algorithms for computing HHR estimates when α is fixed and when β is fixed. Finally, we discuss an iterative strategy to obtain HHR estimates (α,β) altogether.
Let for α fixed and for β fixed. We have the following objective functions
| (6) |
| (7) |
where fα,λ2(β) is the HHR objective function with respect to β for α fixed and fβ,λ1(α) with respect to α for β fixed. We employ the coordinate descent strategy (Tseng, 1988, 2001; Friedman et al., 2008) to minimize fα,λ2(β) and fβ,λ1(α) individually for a given λ2 and λ1, respectively. In the coordinate descent, each element βj (or αj) is updated one at a time for j = 1, … , p (or q), and this is iterated till the minimizer of fα,λ2(β) (or fβ,λ1(α)) converges. The procedure is further sped up by iterating only through the active set till convergence before updating all coordinates. For conciseness of presentation, we obtain unpenalized estimates for the intercept terms by setting xi1 and zi1 to 1/δ for δ very small and dividing the resulted estimates by δ.
First, consider the optimization, minβ fα,λ2(β), defined as in equation (6). This problem can be reformulated as that of an ordinary Lasso by using and as the new response and design matrix, respectively. For completeness, we state the coordinate descent updating equation for each j as the following,
where . Maximum value for λ2 is , where x1 is an intercept term.
Next, we consider the minimization problem, minα fβ,λ1(α), defined as in equation (7). For αj to be 0, we must have for some and ∊ > 0 such that ∊ → 0+. Let η = 1/∊. We obtain,
Hence, we have
| (8) |
and the maximum value for λ1 is for z1 an intercept term. When condition (8) fails to hold, αj is nonzero. In this case, we compute for the minimization of fβ,λ1(α) with respect to αj using the Newton-Raphson algorithm. Let τ be a pre-specified maximum step size. Then, αj is updated iteratively till convergence with where
The Newton-Raphson algorithm is very fast in the univariate setting, attaining at least quadratic convergence rate (Nocedal and Wright, 1999). For numerical stability, we control to be smaller than 10300. (Maximum value representable by a double precision number is about 1.798 × 10308.)
Finally, we propose the following algorithm for obtaining HHR estimates for a given pair of tuning parameters (λ1, λ2):
Step 1. Initialize . Then, obtain ;
Step 2. Update ;
Step 3. Update ;
Step 4 Repeat. Steps 2 and 3 until practical convergence of is obtained.
The algorithm iteratively optimizes the HHR objective function (4). At each step, coefficient estimates on the mean or the variance are updated. The algorithm usually reaches a convergent point in a few iterations. Due to the bi-convex nature of the objective function, it is easy to check that the algorithm satisfied the conditions of Tseng (2001), Theorem 4.1 (c), and therefore converges to a stationary point of the objective function. Median numbers of iterations in our simulations in Section 3 is usually between 2 to 6 using a tolerance level of 10−6. While the iterative algorithm reaches a stationary point of the HHR objective function (4), it is not guarantee to reach the global minimum. Since the objective function is not always convex in (α, β), it is convex in either α or β with the other fixed. We also note a few straightforward properties of the iterative procedure, namely that each iteration monotonically decreases the penalized negative log-likelihood and the order of minimization is unimportant.
2.2 Selection of Tuning Parameters
We select tuning parameters for the penalized estimation for the HHR using the Akaike (AIC) and Bayesian (BIC) information criteria defined as the following,
| (9) |
| (10) |
where is the negative log-likelihood (5) and is the number of nonzero coefficients for estimates . Estimates minimizing the AIC or BIC are obtained by computing over a grid of candidate values of λ1 and λ2 and selecting the estimate with the smallest AIC or BIC. Tuning parameters λ1, λ2 with estimates that minimize the AIC or the BIC are selected in order to obtain models that best explain the data with minimal complexity. Similar formulations for the AIC and BIC using numbers of nonzero coefficients have been applied for the Lasso in Zou et al. (2007). Re-sampling techniques, such as the cross-validation, are not applied in this paper for tuning parameter selection, as performances of re-sampling techniques can be undermined under heteroscedasticity by outlying observations appearing randomly in the training or validation set. Moreover, it is commonly noted that the BIC often selects models conservatively compared to the AIC in finite samples (Hastie et al., 2001, p. 208). We compare the AIC and the BIC for HHR in Section 3 using Monte Carlo simulations, where we find that the AIC can sometimes be preferred for prediction accuracy and inclusion of relevant variables when the sample size n is small relative to the number of predictors p.
3. Simulation Studies
In this section, we examine finite-sample performances of the penalized estimation procedure for the HHR via simulation studies. We consider situations where error variances depend on predictors, outliers are present, and the distribution of the error is non-normal. We compare our procedure with the ridge, Lasso, and the LAD-Lasso. When n < p, initial weights in the LAD-Lasso are obtained by an unweighted LAD-Lasso with the number of variables selected less than n instead of the usual LAD (Wang et al., 2007). We present results where models are estimated using the AIC and BIC for the Lasso (Zou et al., 2007), LAD-Lasso (Wang et al., 2007), and the HHR. Tuning parameters for the non-sparse ridge regression are estimated using the generalized cross-validation (Golub et al., 1979).
We measure prediction accuracy using the mean-squared error (ME), , where ∑ is the population covariance matrix of X. Further, variable selection based upon the identification of nonzero mean β and variance α coefficients are examined using sensitivity, specificity, and g-measure. Let p0 (or q0) be the number of the underlying relevant predictors with nonzero coefficients for β0 (or α0). We define sensitivity as (no. of true positives)/(p0 (or q0)) and specificity as 1–(no. of false positives)/(p–p0 (or q–q0)). Sensitivity and specificity, respectively, describe the marginal proportions of selecting relevant variables and discarding irrelevant variables correctly. We measure overall variable selection performances using g-measure, or the geometric mean between sensitivity and specificity, . A g-measure close to 1 indicates accurate selection, and a g-measure close to 0 implies that few relevant variables or too many irrelevant variables are selected, or both. Intercept terms are not included in these measurements.
In each example, we generate the true model (1) repeatedly 100 times. We assume that the model has an intercept term such that X = (1n, X1), where X1 ~ N(0, ∑) and ∑ij = 0.5∣i–j∣. Further, for simplicity of presentation, we use the same coefficients
with p–1 = 600 non-intercept predictors throughout the examples. Note that configurations on the mean are not crucial for examining the effects of heteroscedasticity on regression models. We report medians and bootstrapped standard deviations of medians out of 500 re-samplings, in parentheses, in Tables 1-3. Further, we boldface, as top measurements, the 2 smallest MEs and largest g-measures for the selection of mean predictors in each case.
Table 1.
Simulation example 3.1: presence of predictors that explain the error variance variability. p – 1 = 600, q – 1 = 600 and n = 100, 200 and 400.
| Methods | ME |
β
|
α
|
||||
|---|---|---|---|---|---|---|---|
| g-measure | sens | spec | g-measure | sens | spec | ||
| n=100 | |||||||
| Ridge | 82.167 (1.891) | ||||||
| Lasso (AIC) | 85.807 (12.044) | 0.761 (0.023) | 0.667 | 0.868 | |||
| Lasso (BIC) | 60.699 (4.837) | 0.577 (0.037) | 0.333 | 0.998 | |||
| LAD-Lasso (AIC) | 42.554 (4.609) | 0.780 (0.025) | 0.667 | 0.948 | |||
| LAD-Lasso (BIC) | 45.588 (2.919) | 0.577 (0.022) | 0.333 | 0.997 | |||
| HHR (AIC) | 11.065 (0.736) | 0.955 (0.003) | 1.000 | 0.934 | 0.570 (0.017) | 0.333 | 0.970 |
| HHR (BIC) | 34.683 (3.741) | 0.846 (0.034) | 0.722 | 0.997 | 0.332 (0.037) | 0.111 | 0.991 |
| n=200 | |||||||
| Ridge | 72.024 (1.268) | ||||||
| Lasso (AIC) | 111.277 (10.877) | 0.768 (0.013) | .778 | 0.751 | |||
| Lasso (BIC) | 34.555 (3.265) | 0.745 (0.039) | 0.556 | 0.999 | |||
| LAD-Lasso (AIC) | 26.122 (3.038) | 0.822 (0.009) | 0.778 | 0.876 | |||
| LAD-Lasso (BIC) | 19.912 (1.574) | 0.745 (0.021) | 0.556 | 0.990 | |||
| HHR (AIC) | 3.667 (0.736) | 0.977 (0.003) | 1.000 | 0.961 | 0.724 (0.014) | 0.556 | 0.909 |
| HHR (BIC) | 5.013 (0.635) | 0.992 (0.001) | 1.000 | 0.990 | 0.611 (0.040) | 0.389 | 0.992 |
| n=400 | |||||||
| Ridge | 59.694 (2.423) | ||||||
| Lasso (AIC) | 209.264 (18.311) | 0.682 (0.009) | 0.889 | 0.517 | |||
| Lasso (BIC) | 24.875 (2.047) | 0.880 (0.029) | 0.778 | 1.000 | |||
| LAD-Lasso (AIC) | 6.506 (1.246) | 0.852 (0.009) | 1.000 | 0.788 | |||
| LAD-Lasso (BIC) | 8.699 (1.423) | 0.878 (0.006) | 0.778 | 0.992 | |||
| HHR (AIC) | 1.627 (0.243) | 0.969 (0.006) | 1.000 | 0.941 | 0.746 (0.024) | 0.667 | 0.995 |
| HHR (BIC) | 2.419 (0.446) | 0.997 (0.001) | 1.000 | 0.996 | 0.743 (0.021) | 0.556 | 0.997 |
Table 3.
Simulation example 3.3: non-normal errors. n = 100, p – 1 = 600, q – 1 = 100. Errors are sampled with the t(df)-distribution with df = 3, 5 and ∞.
| Method | ME |
β
|
α
|
||||
|---|---|---|---|---|---|---|---|
| g-measure | sens | spec | g-measure | sens | spec | ||
| df = 3 | |||||||
| Ridge | 66.040 (0.557) | ||||||
| Lasso (AIC) | 18.884 (0.949) | 0.936 (0.014) | 1.000 | 0.885 | |||
| Lasso (BIC) | 18.755 (1.237) | 0.935 (0.015) | 0.889 | 0.995 | |||
| LAD-Lasso (AIC) | 10.192 (0.731) | 0.925 (0.010) | 0.889 | 0.970 | |||
| LAD-Lasso (BIC) | 22.503 (1.397) | 0.745 (0.021) | 0.556 | 1.000 | |||
| HHR (AIC) | 5.284 (0.357) | 0.969 (0.002) | 1.000 | 0.942 | 0.622 (0.016) | 0.400 | 0.967 |
| HHR (BIC) | 8.486 (0.715) | 0.979 (0.008) | 1.000 | 0.986 | 0.316 (0.076) | 0.100 | 1.000 |
| df = 5 | |||||||
| Ridge | 69.142 (0.612) | ||||||
| Lasso (AIC) | 27.834 (1.846) | 0.888 (0.002) | 0.889 | 0.883 | |||
| Lasso (BIC) | 23.708 (2.052) | 0.879 (0.001) | 0.778 | 0.995 | |||
| LAD-Lasso (AIC) | 15.788 (1.291) | 0.868 (0.004) | 0.778 | 0.966 | |||
| LAD-Lasso (BIC) | 26.699 (0.865) | 0.741 (0.035) | 0.556 | 1.000 | |||
| HHR (AIC) | 7.036 (0.428) | 0.967 (0.001) | 1.000 | 0.942 | 0.735 (0.019) | 0.600 | 0.967 |
| HHR (BIC) | 13.436 (1.721) | 0.943 (0.013) | 0.889 | 0.990 | 0.447 (0.090) | 0.200 | 1.000 |
| df = ∞ | |||||||
| Ridge | 68.312 (0.730) | ||||||
| Lasso (AIC) | 24.088 (1.298) | 0.890 (0.014) | 0.889 | 0.882 | |||
| Lasso (BIC) | 21.324 (1.710) | 0.885 (0.022) | 0.889 | 0.995 | |||
| LAD-Lasso (AIC) | 14.564 (1.059) | 0.873 (0.017) | 0.778 | 0.970 | |||
| LAD-Lasso (BIC) | 28.557 (1.336) | 0.745 (0.026) | 0.556 | 1.000 | |||
| HHR (AIC) | 6.456 (0.246) | 0.966 (0.001) | 1.000 | 0.939 | 0.748 (0.026) | 0.600 | 0.978 |
| HHR (BIC) | 15.608 (2.216) | 0.937 (0.007) | 0.889 | 0.992 | 0.316 (0.117) | 0.100 | 1.000 |
3.1 Presence of Predictors Explaining Error Variances
In this example, we demonstrate situations where heteroscedasticity arises from the presence of predictors explaining error variances. We generate error variances with where α = {1, 1, 1, 1, 0, 0, 0, 0.5, 0.5, 0.5, 0, 0, 0, .75, .75, .75, 0, … , 0} with q – 1 = p – 1 = 600. The variance design matrix Z = (1n, x2, … , xp) is employed in (5). Furthermore, we vary n over {100, 200, 400} to illustrate the effect of sample size on performances.
In Table 1, we present results on both prediction accuracy and variable selection. We observe that the performances of the LAD-Lasso tend to dominate those of the Lasso. This suggests that the LAD-Lasso, by utilizing the least absolute deviations, can sometimes be more robust towards heteroscedasticity than the Lasso. Nonetheless, the HHR out-performs both the Lasso and the LAD-Lasso with the smallest ME’s and the largest g-measures for the selection of nonzero mean coefficients β. Improvements in performances for the HHR over the Lasso and LAD-Lasso are most pronounced when the sample size n is relatively small. Further, when n is small, HHR using the AIC tends to dominate HHR with the BIC in terms of prediction accuracy and the selection of nonzero variance coefficients α. As noted in Section 2.2, the BIC often selects models too conservatively in finite samples. Thus, for the purpose of prediction accuracy and the inclusion of important variables, the AIC is preferred when n is small relative to p.
3.2 Presence of Outliers
In this example, we present results when outliers are present. We use n = 100 number of observations, in which noutlier = 10 are outliers, and σi = σ = 6. We employ Z = (1n, In). Since errors generated from the normal distribution may contain a few extreme values by random, in order to examine the performances of our method for outlier detection, we generate errors for outliers from a truncated normal, such that and , and errors for non-outlying observations with σ∊i ~ N(0, σ2) and ∣σ∊i∣ <= σ. We vary τ over {1, 3, 5} in order to examine situations when outliers are beyond the first, third, and fifth standard deviations.
Table 2 presents the results for this example. When τ = 1, the outlying observations are moderate with their distribution concentrated around the first standard deviation. In this case, the performances of the Lasso, LAD-Lasso, and HHR are similar. In particular, prediction accuracy are not significantly different for these methods considering the large bootstrapped standard errors, except for the LAD-Lasso (BIC). Moreover, the median proportions of non-intercept variance coefficients α selected are 0.1 and 0 for the HHR using AIC and BIC, respectively. This suggests that the HHR tends to be reduced to the Lasso when the level of heteroscedasticity is small. When τ increases, the performances of both the Lasso and the LAD-Lasso tends to deteriorate in terms of prediction accuracy and the selection of mean predictors, whereas those of the HHR remain relatively stable. Detection of outliers, as indicated by the selection of nonzero αi+1 coefficients, also improves with increasing n. Again, the BIC selects variables too conservatively in this example, leading to lower sensitivities and g-measures.
Table 2.
Simulation example 3.2: presence of outliers. n = 100, p – 1 = 600, q – 1 = 100. The noutlier = 10 outliers have distribution and , for τ = 1, 3 and 5.
| Method | ME |
β
|
α
|
||||
|---|---|---|---|---|---|---|---|
| g-measure | sens | spec | g-measure | sens | spec | ||
| τ = 1 | |||||||
| Ridge | 63.551 (0.532) | ||||||
| Lasso (AIC) | 13.461 (0.462) | 0.943 (0.001) | 1.000 | 0.893 | |||
| Lasso (BIC) | 13.514 (0.871) | 0.941 (0.008) | 1.000 | 0.993 | |||
| LAD-Lasso (AIC) | 10.603 (0.559) | 0.929 (0.013) | 0.889 | 0.982 | |||
| LAD-Lasso (BIC) | 24.233 (0.862) | 0.745 (0.000) | 0.556 | 1.000 | |||
| HHR (AIC) | 8.491 (0.474) | 0.964 (0.001) | 1.000 | 0.938 | 0.316 (0.161) | 0.100 | 1.000 |
| HHR (BIC) | 11.109 (0.644) | 0.983 (0.016) | 1.000 | 0.988 | 0.000 (0.000) | 0.000 | 1.000 |
| τ = 3 | |||||||
| Ridge | 71.544 (0.653) | ||||||
| Lasso (AIC) | 34.396 (0.716) | 0.884 (0.001) | 0.889 | 0.880 | |||
| Lasso (BIC) | 30.037 (1.363) | 0.870 (0.027) | 0.778 | 0.995 | |||
| LAD-Lasso (AIC) | 21.198 (1.274) | 0.864 (0.016) | 0.778 | 0.967 | |||
| LAD-Lasso (BIC) | 34.996 (1.627) | 0.667 (0.000) | 0.444 | 1.000 | |||
| HHR (AIC) | 10.747 (1.156) | 0.961 (0.001) | 1.000 | 0.931 | 0.937 (0.006) | 1.000 | 0.967 |
| HHR (BIC) | 28.142 (2.202) | 0.845 (0.030) | 0.722 | 0.997 | 0.000 (0.000) | 0.000 | 1.000 |
| τ = 5 | |||||||
| Ridge | 80.111 (0.671) | ||||||
| Lasso (AIC) | 70.466 (2.053) | 0.816 (0.025) | 0.778 | 0.871 | |||
| Lasso (BIC) | 53.384 (3.191) | 0.666 (0.022) | 0.444 | 0.998 | |||
| LAD-Lasso (AIC) | 40.352 (3.182) | 0.732 (0.009) | 0.556 | 0.959 | |||
| LAD-Lasso (BIC) | 45.314 (1.442) | 0.577 (0.015) | 0.333 | 1.000 | |||
| HHR (AIC) | 7.215 (0.317) | 0.966 (0.001) | 1.000 | 0.939 | 0.972 (0.005) | 1.000 | 0.944 |
| HHR (BIC) | 17.832 (6.225) | 0.934 (0.040) | 0.889 | 0.996 | 0.943 (0.017) | 1.000 | 0.994 |
3.3 Non-Normal Errors
In this example, we demonstrate situations when errors have non-normal distributions. We use n = 100 observations, in which 10 have larger error variances. We sample ∊i from the t-distribution t(df) with degrees of freedoms df varying over {3, 5, ∞}. The multiplier σi is set equal to to induce equal variances across different degrees of freedoms. We set for the 10 observations with large variances and , otherwise. We use Z = (1n, In) as in (3), and the selection of α refers to the identification of the 10 observations with larger variances.
The t-distribution is often utilized in robust modeling, where it has been shown to be useful in applications of small sample sizes (Lange, Little, and Taylor, 1989). It has finite variance for df > 2 and approaches the normal distribution as df goes towards ∞. In Table 3, we see that performances for the HHR methods remain excellent even when df = 3. This suggests the applicability of our procedure when the error is non-normal.
4. Application to yeast eQTL Dataset
We illustrate our method in an application to eQTL data analysis. We consider the gene expression data set from Brem and Kruglyak (2005). In this experiment, gene expression levels, as measured using cDNA microarrays, are treated as quantitative traits, and 2,957 markers genotyped on n = 112 yeast segregants are used to identify expression quantitative trait loci (eQTLs). Originally, 6,216 yeast gene are assayed. We remove 788 genes which contain missing values and use the remaining 5,428 gene expression levels as responses. Due to linkage disequilibrium, markers located on adjacent loci tend to be very similar. Following Li et al. (2004), in our analysis, a few missing markers are first imputed based on data from 10-nearest neighbors and adjacent markers differing by at most one sample are combined into blocks. For each block, we then choose a representative marker with the smallest number of missing values across the samples as the marker for the block. Note that including identical or nearly identical markers individually will not increase the amount of information used but, instead, can introduce unnecessary multicollinearity and inflate estimation errors in regression models. Statistical analysis is performed by regressing the 5,428 individual gene expression levels on these p – 1 = 585 representative markers.
We first test for the presence of heteroscedasticity in this data set and find more than 40% out of 5,428 regressions showing some degree of heteroscedasticity at the 1e-6 significance level using the Breusch-Pagan/Cook-Weisberg test. We then illustrate the performance of our method in several examples where presence of predictors explaining error variances and outliers are suspected.
4.1 Presence of Heteroscedasticity
We test for the presence of heteroscedasticity in this data set for each of the 5,428 genes using the Breusch-Pagan/Cook-Weisberg test, developed independently by Breusch and Pagan (1979) and Cook and Weisberg (1983). The Breusch-Pagan/Cook-Weisberg is one of the most widely-used test for heteroscedasticity. It assumes a linear model for the log variance and utilizes the score statistics to test for the significance of coefficients. The Breusch-Pagan/Cook-Weisberg test is not directly applicable when p > n. To reduce dimensions, we apply the HHR to select markers that are predictive of gene expression levels and markers that are explanatory of variability. These variables are then applied in the Breusch-Pagan/Cook-Weisberg test to specify predictors on the response and log variance, accordingly. We use the AIC to select tuning parameters for this purpose. The BIC can sometimes select too few variables when the sample size is small, as shown in Section 3 with simulation studies.
Table 4 presents the numbers and proportions of genes when regressions of markers on gene expression levels demonstrate heteroscedasticity at various p-value levels. Out of 5,428 regressions, 2,244 (41.3%) and 776 (14.3%) demonstrate heteroscedasticity at the 1e-6 and 1e-16 significance levels, respectively. The prevalence of heteroscedasticity in this eQTL data set suggests the need to incorporate non-constant error variances in high-dimensional regressions and potential applicability of our method for identifying the genetic variants that are associated with gene expression variations.
Table 4.
Analysis of eQTL data set from Brem and Kruglyak (2005). Numbers and proportions of cases out of 5,428 genes with significant heteroscedasticity using the Breusch-Pagan/Cook-Weisberg test.
| p-value | No. | Proportion |
|---|---|---|
| 1e-32 > p-value | 239 | 4.4% |
| 1e-16 > p-value ≥ 1e-32 | 537 | 9.9% |
| 1e-10 > p-value ≥ 1e-16 | 626 | 11.5% |
| 1e-6 > p-value ≥ 1e-10 | 842 | 15.5% |
| Total | 2,244 | 41.3% |
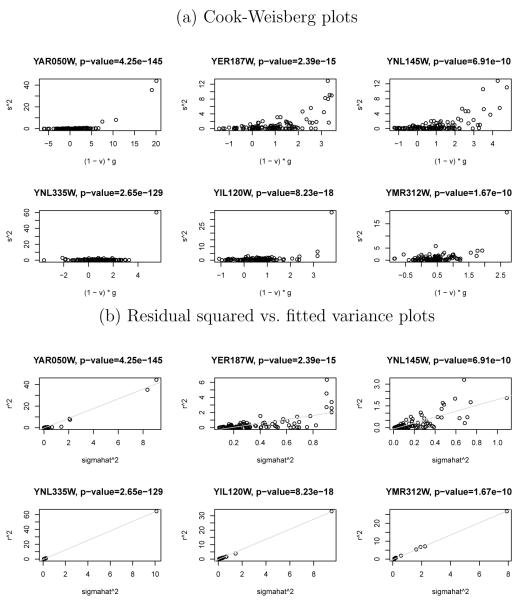
As further evidence for the existence of heteroscedasticity, we apply the graphical method of Cook and Weisberg (1983), where the squared studentized residuals are plotted against (1 – vii)gi. The quantities vii are diagonal elements of the hat matrix for an OLS regression of markers on the response, whereas gi are the fitted values from an ordinary least square (OLS) regression of markers on the standardized squared residuals. Again, the HHR with AIC is applied beforehand to reduce dimensions. Figure 1(a) presents Cook-Weisberg plots of individual gene expression levels at varying p-values from the Breusch-Pagan/Cook-Weisberg test. Plots for genes YAR050W, YER187W, and YNL145W at p-values of 4.25e-145, 2.39e-15, and 6.91e-10, respectively, display wedge shapes and are indicative of predictors explaining variability; plots for genes YNL335W, YIL120W, and YMR312W at p-values of 2.65e-129, 8.23e-18, and 1.67e-10, respectively, display the presence of outliers.
Figure 1.
Analysis of eQTL data set of Brem and Kruglyak (2005). (a) Cook-Weisberg plots and (b) residual squared vs. fitted variance plots with HHR (AIC) estimates for six genes at various Breusch-Pagan/Cook-Weisberg p-values.
4.2 Results from eQTL Data Analysis
We apply the HHR to the six genes discussed in the previous section and demonstrated in Figure 1(a) and compare its performances with those of the ridge, Lasso, and LAD-Lasso. For the three genes (YAR050W, YER187W, YNL145W) where predictors explaining error variances are suspected in Figure 1(a), our goal is to select the genetic variants from the 585 markers that can explain gene expression levels in both the mean and variance by fitting the following model,
where yi is the expression level of the gene in the ith segregant, xij is the 0/1 genotype indicator for segregant i at the jth marker, β1 (or α1) is an intercept term, and βj+1 (or αj+1) measures the effect of marker j on the mean (or variance) of gene expressions. For the three genes (YNL335W, YIL120W, YMR312W) where presence of outliers are suspected in Figure 1(a), we seek to robustly select markers explanatory of gene expression levels and discover segregants that are outliers using the following model,
where nonzero αj+1 indicates deviation of segregant j from homogeneity.
We evaluate the performance of the different procedures based on random training/testing sample partitions. To avoid possible inconsistency of results due to randomization (Bøvelstad et al., 2007), we use 25 different partitions of the training and testing sets. In each partition, regression coefficients are estimated using n = 90 randomly selected training observations. The AIC and BIC are applied for the Lasso, LAD-Lasso, and HHR; whereas ridge regression is estimated using the generalized cross-validation as in Section 3. The remaining 22 observations are further trimmed by removing those with studentized residuals significant at the 0.1 level using a conservative t-test with Bonferroni correction for outliers. This prevents the test error from being strongly influenced by a few outlying observations. The ≤ 22 trimmed observations are, then, used to robustly estimate the test error, .
Table 5 reports median test errors and numbers of variables selected, with the standard errors based on 500 bootstrapped re-samplings in parentheses. The two smallest test errors are boldfaced in each case. We observe that the HHR dominates the ridge in terms of prediction accuracy by using more parsimonious models with typically only a few nonzero coefficients. Furthermore, the HHR tends to dominate both the Lasso and LAD-Lasso in terms of prediction accuracy when heteroscedasticity is strong and performs comparably at low heteroscedasticity. The results suggest that the HHR can fit the data more adequately by incorporating non-constant error variances, especially at significant levels of heteroscedasticity. In addition, the HHR model also selects genetic variants that can explain the error variances and discover segregants that are outliers.
Table 5.
eQTL analysis of three genes (YAR050W, YER187W, YNL145W) where genetic variants led to differences in error variances and three genes (YNL335W, YIL120W, YMR312W) where outliers were detected. Results are based on 25 training/testing partitions with n = 90 number of training observations and ntest ≤ 22 number of testing observations trimmed for outliers at the 0.1 level. p – 1 = 585. q – 1 = 585 for YAR050W, YER187W, YNL145W; and q – 1 = 90 for YNL335W, YIL120W, YMR312W.
| Method | Test error | β no. selected | α no. selected | |
|---|---|---|---|---|
| YAR050W (p-value = 4.25e-145) |
Ridge | 0.387 (0.073) | ||
| Lasso (AIC) | 0.944 (0.082) | 79.0 (0.6) | ||
| Lasso (BIC) | 0.368 (0.046) | 1.0 (0.0) | ||
| LAD-Lasso (AIC) | 0.524 (0.111) | 43.0 (11.6) | ||
| LAD-Lasso (BIC) | 0.388 (0.105) | 15.0 (14.8) | ||
| HHR (AIC) | 0.164 (0.033) | 11.0 (1.7) | 28.0 (2.2) | |
| HHR (BIC) | 0.269 (0.046) | 2.0 (0.1) | 13.0 (2.8) | |
| YER187W (p-value = 2.39e-15) |
Ridge | 0.796 (0.043) | ||
| Lasso (AIC) | 0.838 (0.066) | 64.0 (1.1) | ||
| Lasso (BIC) | 0.817 (0.059) | 64.0 (1.1) | ||
| LAD-Lasso (AIC) | 0.824 (0.060) | 81.0 (19.5) | ||
| LAD-Lasso (BIC) | 0.735 (0.058) | 75.0 (30.9) | ||
| HHR (AIC) | 0.393 (0.064) | 16.0 (1.3) | 15.0 (2.1) | |
| HHR (BIC) | 0.480 (0.053) | 6.0 (0.8) | 6.0 (1.9) | |
| YNL145W (p-value = 6.91e-10) |
Ridge | 0.665 (0.033) | ||
| Lasso (AIC) | 0.267 (0.029) | 51.0 (1.6) | ||
| Lasso (BIC) | 0.225 (0.036) | 2.0 (0.0) | ||
| LAD-Lasso (AIC) | 0.293 (0.060) | 19.0 (5.8) | ||
| LAD-Lasso (BIC) | 0.262 (0.050) | 2.0 (5.5) | ||
| HHR (AIC) | 0.224 (0.037) | 2.0 (0.6) | 9.0 (0.5) | |
| HHR (BIC) | 0.224 (0.037) | 2.0 (0.4) | 7.0 (1.9) | |
| YNL335W (p-value = 2.65e-129) |
Ridge | 0.423 (0.028) | ||
| Lasso (AIC) | 0.725 (0.074) | 77.0 (1.4) | ||
| Lasso (BIC) | 0.435 (0.032) | 1.0 (0.6) | ||
| LAD-Lasso (AIC) | 0.526 (0.048) | 83.0 (3.6) | ||
| LAD-Lasso (BIC) | 0.473 (0.035) | 77.0 (6.4) | ||
| HHR (AIC) | 0.305 (0.015) | 39.0 (1.1) | 12.0 (2.4) | |
| HHR (BIC) | 0.321 (0.020) | 5.0 (0.8) | 2.0 (0.4) | |
| YIL120W (p-value = 8.23e-18) |
Ridge | 0.551 (0.034) | ||
| Lasso (AIC) | 0.788 (0.058) | 74.0 (0.6) | ||
| Lasso (BIC) | 0.549 (0.021) | 2.0 (0.7) | ||
| LAD-Lasso (AIC) | 0.680 (0.074) | 53.0 (4.6) | ||
| LAD-Lasso (BIC) | 0.582 (0.047) | 15.0 (4.8) | ||
| HHR (AIC) | 0.454 (0.034) | 33.0 (1.8) | 16.0 (2.7) | |
| HHR (BIC) | 0.443 (0.029) | 8.0 (1.2) | 2.0 (0.5) | |
| YMR312W (p-value = 1.67e-10) |
Ridge | 0.872 (0.061) | ||
| Lasso (AIC) | 1.603 (0.093) | 74.0 (1.2) | ||
| Lasso (BIC) | 0.778 (0.053) | 2.0 (0.4) | ||
| LAD-Lasso (AIC) | 1.614 (0.135) | 41.0 (1.8) | ||
| LAD-Lasso (BIC) | 0.867 (0.066) | 5.0 (1.0) | ||
| HHR (AIC) | 0.792 (0.053) | 46.0 (1.6) | 7.0 (0.9) | |
| HHR (BIC) | 0.812 (0.045) | 2.0 (0.4) | 4.0 (0.3) | |
Finally, we examine residual squared versus fitted variance plots in Figure 1(b). The HHR with the AIC estimated using the full n = 112 observations are used for these plots. Fitted variances are computed with for the three genes (YAR050W, YER187W, YNL145W) where predictors explaining variability are suspected and for the three genes (YNL335W, YIL120W, YMR312W) where the presence of outliers are suspected. We see that the fitted variances describe the squared residuals well by increasing linearly with increasing , even though are estimated with only a few selected genetic variants when predictors explain variability and a small number of non-zero coefficients when outliers are present. Moreover, by modeling both large and moderate variabilities, the HHR efficiently utilizes the entire data set by down-weighting observations according to their relative quality.
5. Discussions
Motivated by identifying the genetic variants that are associated with gene expression levels in eQTL analysis, we have proposed and developed high-dimensional heteroscedastic regression models in order to account for variance heterogeneity. We have provided evidence of the presence of heteroscedasticity in eQTL data analysis and demonstrated the importance of incorporating heteroscedasticity in estimation and variable selection. Results from both simulation and real-data analysis have demonstrated the advantages of incorporating heteroscedasticity in high-dimensional data analysis in parameter estimation and variable selection. In typical eQTL analysis, since tens of thousands of regression models are often fitted, it is important to have an automated procedure that are robust to outliers and can handle error variance heterogeneity. In addition, the genetic variants identified that explain the error variances may provide additional insights into how genetics regulate gene expression, not only at the mean levels, but also at the level of the variances.
In our proposed penalized estimation for the HHR models, we used the L1-norm penalty functions for selecting the variables in both the mean and the variance. This particular penalization is selected for its simplicity, computational ease, and successes in various statistical applications. The L1-norm penalized regression has been demonstrated to perform well in large-scale genome-wide association (Wu et al., 2008) and eQTL studies (Lee et al., 2009). However, other sparse regularization methods can be applied, such as the SCAD (Fan and Li, 2001), adaptive Lasso (Zou, 2006), and Dantzig selector (Candes and Tao, 2007), with additional computational cost. Although a global minimizer is usually not guaranteed in non-convex optimization (Nocedal and Wright, 1999), both simulated and real-data comparisons in Sections 3 and 4, respectively, demonstrate that our procedure often improves over existing methods in both estimation and variable selection.
Acknowledgments
We thank the associate editor and two anonymous referees, whose comments led to sub-stantial improvements in the paper. This research is supported by the National Institutes of Health (ES009911, CA127334).
References
- Bøvelstad HM, Nygård S, Størvold HL, Aldrin M, Borgan Ø, Frigessi A, Lingjærde OC. Predicting survival from microarray data-a comparative study. Bioinformatics. 2007;23:2080–2087. doi: 10.1093/bioinformatics/btm305. [DOI] [PubMed] [Google Scholar]
- Box GEP, Hill WJ. Correcting inhomogeneity of variance with power transformation in weighting. Technometrics. 1974;16:385–389. [Google Scholar]
- Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; 2004. [Google Scholar]
- Brem RB, Kruglyak L. The landscape of genetic complexity across 5,700 gene expression traits in yeast. Proceedings of National Academy of Sciences USA. 2005;102:1572–1577. doi: 10.1073/pnas.0408709102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breusch TS, Pagan AR. Simple test for heteroscedasticity and random coefficient variation. Econometrica. 1979;47:1287–1294. [Google Scholar]
- Candes E, Tao T. The dantzig selector: Statistical estimation when p is much larger than n. Ann. Statist. 2007;35:2313–2351. [Google Scholar]
- Carroll R. Transformation and weighting in regression. Chapman and Hall; New York: 1988. [Google Scholar]
- Carroll RJ, Ruppert D. Robust estimation in heteroscedastic linear models. Ann. Statist. 1982;10:429–441. [Google Scholar]
- Carroll RJ, Wu CFJ, Ruppert D. The effect of estimating weights in weighted least squares. J. Am. Statist. Ass. 1988;83:1045–1054. [Google Scholar]
- Cleveland WS. Visualizing Data. Hobart Press; 1993. [Google Scholar]
- Cook RD, Weisberg S. Diagnostics for heteroscedasticity in regression. Biometrika. 1983;70:1–10. [Google Scholar]
- Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Ann. Statist. 2004;32:407–499. [Google Scholar]
- Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Statist. Ass. 2001;96:1348–1360. [Google Scholar]
- Friedman J, Hastie T, Hoefling H, Tibshirani R. Pathwise coordinate optimization. Technical report. 2007.
- Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. Technical report. 2008. [PMC free article] [PubMed]
- Golub GH, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics. 1979;21:215–223. [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. Springer; 2001. [Google Scholar]
- Jia J, Rohe K, Yu B. Technical Report 783. Dept. of Statistics; UC Berkeley: 2009. Lasso under heteroscedasticity. [Google Scholar]
- Koenker R. Econometric Society Monograph Series. Cambridge University Press; 2005. Quantile Regression. [Google Scholar]
- Lange KL, Little RJA, Taylor JMG. Robust statistical modeling using the t distribution. J. Am. Statist. Ass. 1989;84:881–896. [Google Scholar]
- Lee S, Dudley A, Drubin D, Silver P, Krogan N, Pe’er D, Koller D. Learning a prior on regulatory potential from eqtl data. PLoS Genet. 2009;5(1):e1000358. doi: 10.1371/journal.pgen.1000358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K, Liu C, Sun W, Yuan S, Yu T. A system for enhancing genome-wide co-expression dynamics study. Proceedings of National Academy of Sciences. 2004;101:15561–15566. doi: 10.1073/pnas.0402962101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Zhu J. l1-norm quantile regressions. Journal of Computational and Graphical Statistics. 2008;17:163–185. [Google Scholar]
- Nocedal J, Wright S. Numerical Optimization. Springer; 1999. [Google Scholar]
- She Y, Owen AB. Outlier detection using nonconvex penalized regression. Technical report. 2010.
- Tibshirani R. Regression shrinkage and selection via the lasso. J. R. Statist. Soc. B. 1996;58:267–288. [Google Scholar]
- Tseng P. Technical Report LIDS-P 1840. Massachusetts Institute of Technology, Laboratory for Information and Decision Systems; 1988. Coordinate ascent for maximizing nondifferentiable concave functions. [Google Scholar]
- Tseng P. Convergence of block coordinate descent method for nondifferentiable maximation. J. Opt. Theory Appl. 2001;109:474–494. [Google Scholar]
- Wang H, Li G, Jiang G. Robust regression shrinkage and consistent variable selection via the lad-lasso. Journal of Business & Economic Statistics. 2007;25:347–355. [Google Scholar]
- Wang L, Gordon MD, Zhu J. Regularized least absolute deviations regression and an efficient algorithm for parameter tuning. Proceedings of the Sixth International Conference on Data Mining (ICDM06); IEEE Computer Society; 2006. pp. 690–700. [Google Scholar]
- Wu TT, Chen YF, Hastie T, Sobel E, Lange K. Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics. 2008;25:714–721. doi: 10.1093/bioinformatics/btp041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y, Liu Y. Variable selection in quantile regression. Statistica Sinica. 2009;19:801–817. [Google Scholar]
- Xu J, Ying Z. Simultaneous estimation and variable selection in median regression using lasso-type penalty. Annals of the Institute of Statistical Mathematics. 2010;62:487–514. doi: 10.1007/s10463-008-0184-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H. The adaptive lasso and its oracle properties. J. Am. Statist. Ass. 2006;101:1418–1429. [Google Scholar]
- Zou H, Hastie T, Tibshirani R. On the “degrees of freedom” of the lasso. Ann. Statist. 2007;35:2173–2192. [Google Scholar]