Abstract
The reminiscence bump is the tendency to recall relatively many personal events from the period in which the individual was between 10 and 30 years old. This effect has only been found in autobiographical memory studies that used participants who were older than 40 years of age. The increased recall of recent events possibly obscures the reminiscence bump in the results of younger participants. In this study, a model was proposed that removes the increase for recent events from the temporal distribution. The model basically estimates a retention function based on the 10 most recent years from the observed distributions and divides the observed distributions by predictions derived from the estimated retention function. The model was examined with three simulated data sets and one experimental data set. The results of the experiment offered two practical examples of how the model could be used to investigate the temporal distribution of autobiographical memories.
Keywords: Autobiographical memory, Reminiscence bump, Retention function, Adolescence, Aging
When people speak of autobiographical memory, they are referring to the memories a person has of his or her own life experiences (Robinson, 1986). If no personal event were ever forgotten and people experienced the same number of events every year, the temporal distribution of autobiographical memory would be completely constant. However, when looking at this temporal distribution, one can distinguish three components. First, people hardly recall any personal events from early childhood, which is called childhood amnesia. They only start to remember events from the age of 3 or 4 years (Nelson & Fivush, 2004; Rubin, 2000). Second, people usually recall many personal events from the most recent years, because older memories are more likely to be forgotten. Third, people tend to recall relatively many personal events from the period in which they were between 10 and 30 years old (Rubin, Rahhal, & Poon, 1998; Rubin, Wetzler, & Nebes, 1986). This last effect is called the reminiscence bump.
The reminiscence bump has been found in studies that have looked at the most important events of people’s lives, as well as in studies that have looked at memories sampled with the help of cue words. The location of the peak of the reminiscence bump depends on how the personal events are elicited (Rubin & Schulkind, 1997b). The peak in the distribution of the most important events tends to be located in the third decade of people’s lives (20–30 years), whereas it is often located in the second decade in the distribution of word-cued memories (10–20 years). The difference between these two distributions can be explained by life scripts, which are culturally shared knowledge about the prevalence and timing of important personal events (Berntsen & Rubin, 2002, 2004; Bohn, 2010; Bohn & Berntsen, 2011; Janssen & Rubin, 2011; Rubin & Berntsen, 2003; Rubin, Berntsen, & Hutson, 2009). When people are asked to report the most important events that have occurred in their personal lives, they will use these cultural life scripts to tell their life story. However, when their memories are cued with words, people tend to report the personal events that come to mind first.
In the present study, the temporal distribution of word-cued memories and how it is affected by the increased recall of recent events is investigated. This increase is not present in every temporal distribution of autobiographical memory. The temporal distribution of the most important events from people’s lives generally does not have an increase of recent events (Rubin & Schulkind, 1997b). Past studies (cf. Rubin et al., 1986), which used age bins of 10 years to display the temporal distribution of word-cued memories, found a reminiscence bump only in the results of participants who were 40 years of age or older, possibly because in the results of younger participants the reminiscence bump was obscured by the increased recall of recent events (Janssen, Chessa, & Murre, 2005).
One needs at least four data points to establish the reminiscence bump with age bins of 10 years. First, people have few memories from the first decade. The lack of memories from the first 3 or 4 years, due to childhood amnesia, affects the proportion of memories of the entire decade. Second, more memories are retrieved from the second decade (i.e., the reminiscence bump). Third, most personal events come from the most recent decade (i.e., the increased recall of recent events). To distinguish the reminiscence bump from a constantly increasing function, one would need a fourth data point (between the reminiscence bump and the increased recall of recent events) from which people recall fewer memories. To identify the reminiscence bump in the temporal distribution of autobiographical memory of participants younger than 40 years, one therefore has to use smaller age bins or remove the increased recall of recent events from the distribution.
The model
In the present study, a method is proposed that can be used to examine the temporal distribution of autobiographical memory (Janssen et al., 2005; Janssen & Murre, 2008). This model, which is technically an algorithm, corrects the distributions for the increased recall of recent events. The influence of this effect could also be minimized by simply asking participants not to recall recent events (e.g., Conway, Wang, Hanyu, & Haque, 2005; Jansari & Parkin, 1996), but this approach can possibly cause participants to apply a retrieval strategy in which they focus on certain lifetime periods in favor of other periods, rather than to simply report the personal event that comes to mind first.
The model basically estimates a power function (Rubin & Wenzel, 1996) based on the 10 most recent years (i.e., the increased recall of recent events) from the observed distributions and subsequently divides the observed distributions with predictions derived from the estimated retention function. The resulting functions then highlight the ages from which participants recalled more or fewer personal events than would be expected on the basis of the retention function. Values of exactly 1 represent ages from which participants recalled the same proportion of personal events as expected. Values higher than 1 represent ages from which the participants recalled more events (e.g., the reminiscence bump), and values lower than 1 represent ages from which participants recalled fewer events (e.g., childhood amnesia) than expected on the basis of the retention function.
If the retention function perfectly predicted the observed distribution (i.e., when there is no childhood amnesia or reminiscence bump), the observed and predicted values would then be identical, and the resulting function would be constant because, if one divides a number by the same number, the result is always 1. Since personal events that happened 40 years ago have a larger likelihood to be forgotten than events that took place 20 years ago, it is less likely for a 50-year-old person to recall events from the age period in which he or she was 10 years old than to recall events from the age period in which he or she was 30 years old. The model corrects the recall of remote events more than it corrects the recall of recent events, because the predicted values of remote events would be lower.
The resulting functions give researchers a way of comparing different distributions of autobiographical memories. It can also help shed light on issues such as whether the reminiscence bump is affected by age, gender, education, or culture (Janssen et al., 2005; Kawasaki, Janssen, & Inoue, 2011) or whether there are more important or more emotional memories in the teenage period than in adjacent lifetime periods (Janssen & Murre, 2008).
The present study
We first investigated the model with three simulated data sets. With these simulations, we show how the model works and examine whether there is any bias in the model for displaying the reminiscence bump. The first simulated data set did not contain childhood amnesia, a reminiscence bump, or an increased recall of recent events. The participants in this data set recalled the same number of events from every year, and the observed distributions were therefore constant. Since events were not forgotten, the retention function that was estimated on the basis of the observed distributions was also constant. Dividing a constant function by another constant function always results in a third constant function. There was also no childhood amnesia or reminiscence bump in the observed distributions of the second simulated data set, but it did include the increased recall of recent events. The estimated retention function, however, mirrored the observed distributions, and the resulting function was therefore constant too. The third simulated data set contained the increased recall of recent events and a reminiscence bump, but no childhood amnesia. The resulting function of this data set displayed a reminiscence bump in the period in which we simulated the effect in the data set, but it did not display any other effects.
The model was then applied to an experimental data set of autobiographical memories provided by Polish young and middle-aged adults, who took the Galton–Crovitz test (Crovitz & Schiffman, 1974; Galton, 1879; Robinson, 1976). In this questionnaire, participants were presented 10 cue words. For each cue word, they were asked to describe the specific memory that came to mind first. After the participants had given 10 descriptions, they were asked to date each personal event. The participants were also asked to rate the events on pleasantness. These ratings were used to examine whether memories from the teenage period are more pleasant than memories from other lifetime periods.
The results from this experimental data set were used to answer two methodological questions about the model. We investigated whether the length of the period that is used to estimate the retention function influences the resulting functions, and whether the resulting functions are affected when one subtracts the predicted proportions from the observed distributions (rather than dividing the observed proportions by the predicted proportions).
Subsequently, two examples for the practical use of the model are given. The model is used to examine whether the reminiscence bump is obscured by the increased recall of recent events in the results of participants who are younger than 40 years old and whether the reminiscence bump is caused by an increase of positive events in the teenage period.
Simulation 1
Data set
To show how the model works and to examine whether the model has a bias for displaying the reminiscence bump, we first simulated a data set in which participants had experienced the same number of events for every year (i.e., no childhood amnesia or reminiscence bump) and no event was forgotten (i.e., no increased recall of recent events).
In this simulated data set, there were 50 participants, who were between 16 and 65 years old. There was only 1 participant for each age (1 participant was 16 years old, 1 was 17 years old, etc.), and each participant recalled five events from every year of his or her life. Since a participant who is n years old is in the (n + 1)th year of his or her life, the youngest participant, who was 16 years old, recalled 85 events (17 years × 5 events = 85 events), while the oldest participant, who was 65 years old, recalled 330 events (66 years × 5 events = 330 events). The 50 participants recalled in total 10,375 events.
We chose to use 5 events for every year in Simulation 1 because we wanted to have similar numbers of data points in the three simulations and the experiment. Simulation 1 could have been conducted with only 1 event (2,075 events) or with 10 events (20,750 events) per year and would have yielded the same results. No additional transformations or randomizations were done (e.g., Monte Carlo simulations) on this data set or the data sets generated for Simulations 2 and 3.
The model
The model, or algorithm, consists of six steps (see Table 1). In the first three steps of the model, we look at the age of the event, while in the last three steps we look at the age at the event. If a person is currently 50 years old and remembers an event from 10 years ago, then the age of the event is 10 years, but the person was 40 years old when the event happened (i.e., the age at the event).
Table 1.
Description of the six steps of the model
| Step | Description |
|---|---|
| 1 | Calculate the proportion of events per year for each participant |
| 2 | Estimate one power function for all participants on the basis of the proportions of the 10 most recent years of each participant (Step 1) |
| 3 | Calculate a predicted value per year for each participant with a power function that uses the exponent of the estimated retention function as the exponent (Step 2) and the proportion of the most recent year as the constant (Step 1) |
| 4 | Divide the observed values (Step 1) by the predicted values (Step 3) |
| 5 | Normalize the resulting values (Step 4) to the maximum age of the participants +1 |
| 6 | Average the normalized values (Step 5) across all participants and normalize the averaged values to the maximum age of all participants +1 |
In the first step of the model, one observed distribution is calculated for each participant by comparing the number of recalled events per year to the total number of recalled events. The 16-year-old participant in this simulation recalled from the most recent year 5 of the total of 85 events (proportion = .059). He or she also recalled 5 events from each previous year. The 65-year-old participant also recalled 5 events (proportion = .015) from each year. Thus, although the participants recalled the same number of events from each year, the proportion of events per year was different.
In the second step of the model, a single retention function is estimated. From each of the 50 observed distributions, the proportions of the 10 most recent years were taken, and one power function (Rubin & Wenzel, 1996) was fitted through the results of these sections of the distributions. Since no event was forgotten in this simulated data set (i.e., no increased recall of recent events), the proportion of recalled events did not change across time. Because we attempted to fit a constant data set with a power function (when a constant function would have been more appropriate), the estimated function had an exponent of 0. The retention function, which had a constant of 0.026, fitted the data set extremely poorly (R 2 = .000).
In the next step of the model, the exponent of the estimated retention function (i.e., 0) is used to predict the proportion of recalled events. For each participant here, a different constant was used, because, although the numbers of recalled events per year were identical, the proportions were different for each participant. The proportion of the most recent year was therefore taken as the constant for the power functions. For the youngest and the oldest participants, these constants were 0.059 and 0.015, respectively, and, because there was no forgetting in this data set (as reflected by the exponent of 0), the predicted proportions for these 2 participants were held constant at .059 and .015.
Because there was no forgetting in this simulation, the power function could not fit the 10 most recent years of the observed distributions well. In more realistic simulations and in experimental data sets there is forgetting, and the power function is then the most appropriate function to estimate the retention function (Rubin & Wenzel, 1996). The model is, however, not committed to using a power function. One could use other types of functions, such as an exponential function, as long as one then uses the same type for the estimation of the retention function (Step 2) and the predictions (Step 3).
In the model’s fourth step, the observed proportions are compared to the predicted proportions by dividing the former by the latter. If a participant recalled more events than predicted from a certain year, the resulting value would then be higher than 1 for that particular year (Oi,j/Ei,j > 1 if Oi,j > Ei,j). If a participant recalled fewer events than expected, the resulting value would be lower than 1 (Oi,j/Ei,j < 1 if Oi j < Ei,j). Since there were no periods from which participants recalled more or fewer events and no event was forgotten in this data set, the predicted values were identical to the observed values, and the resulting values were therefore constant at the value of 1 (Oi,j/Ei,j = 1 if Oi,j = Ei,j).
In the fifth step of the model, the resulting values are first normalized (i.e., the sum of the results is made equal) to the maximum age of the participant +1, because a participant who is currently n years old is in the (n + 1)th year of his or her life. The resulting values in this data set were constant at 1, and their sum was already equal to the maximum age of the participant +1. The resulting values therefore did not have to be corrected for this data set.
In the final step of the model, the normalized values are averaged across the participants. The values of this function are also normalized, but this time they are adjusted to the maximum age of the entire population +1 (i.e., 66 years). The averaged values of this data set were again consistently 1, so their sum was again already equal to the maximum age of the population +1.
The resulting values were normalized in Step 5 to the maximum age of the participant +1, so the weight of each participant’s contribution to the averaged function that was calculated in Step 6 corresponded to the relation between their age and the maximum age of the population. If the sum of the resulting values had been made equal to 1 in Step 5, then the youngest participant would have had a resulting value of 0.059, and the oldest participant would have had a resulting value of 0.015. The averaged function of this data set would then have shown a peak for the period in which the participants were between 0 and 16 years old, because the participant with the highest resulting values (i.e., the youngest participant) only contributed to this period. The lowest point of the averaged function would then have been at the age of 65, because the oldest participant (who had the lowest resulting values) was the only participant who contributed to this point.
Discussion
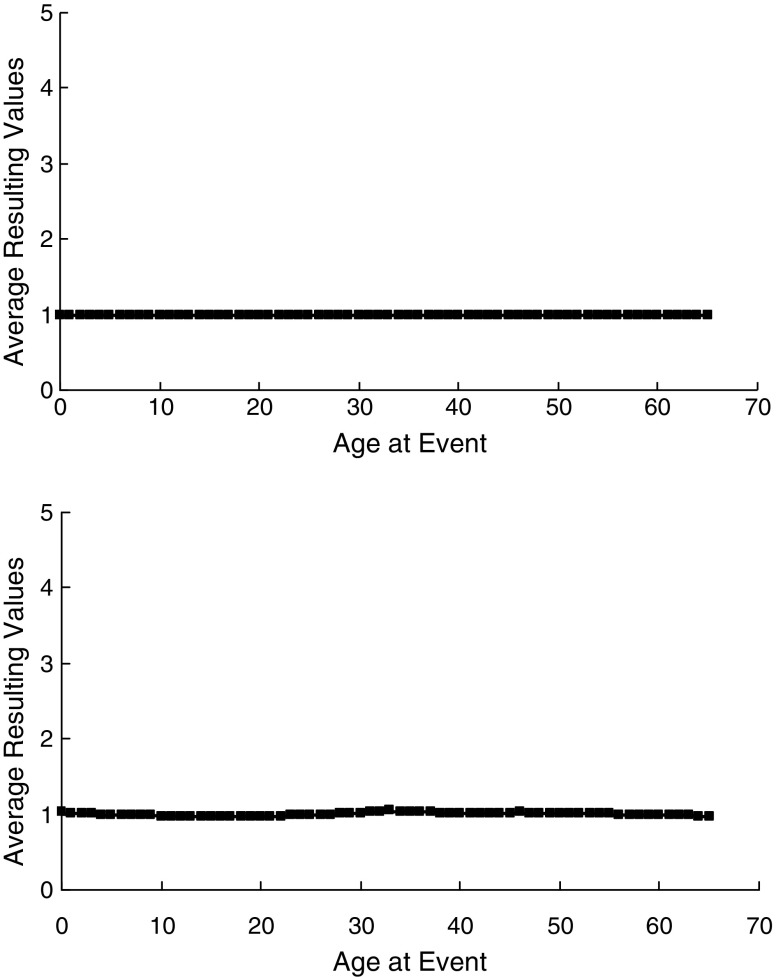
To show how the model works and to examine whether the model has a bias for displaying the reminiscence bump, we simulated a data set in which participants had experienced the same number of events for every year (i.e., no childhood amnesia or reminiscence bump) and no event was forgotten (i.e., no increased recall of recent events). Because the estimated retention function could perfectly predict the observed distributions, the final averaged function was constantly 1, suggesting that the model does not have a bias for showing the reminiscence bump.
Simulation 2
Data set
In the second simulation, we generated a data set in which participants experienced the same number of events every year (i.e., no childhood amnesia or reminiscence bump), but there was an increased recall of recent events. In this simulated data set, there were also 50 participants, who were between 16 and 65 years old. There was again only 1 participant for every age, but each participant recalled 50 events from the most recent year of his or her life. Forgetting was based on a power function with the exponent −1.000, but the data set could only contain whole numbers (50, 25, 17, 13, 10, 8, 7, 6, 6, 5, etc.). Participants, for example, recalled 17 events and not 16.7 events from 2 years ago. We used 50 events for the most recent year, so the total number of events in this simulation (10,683) was similar to the numbers of events in the other simulations and in the experiment.
The model
In the first step of the model, one observed distribution is calculated for each participant. The youngest participant, who was 16 years old, recalled 173 events, 50 of which (proportion = .289) came from the most recent year. The participant recalled, respectively 25, 17, and 13 events (proportions = .145, .098, and .075) from the three previous years. The oldest participant, who was 65 years old, recalled 241 events. Fifty events (proportion = .207) came from the most recent year, and the participant recalled, respectively 25, 17, and 13 events (proportions = .104, .071, and .054) from 1, 2, and 3 years ago.
In the second step of the model, one retention function is estimated for all participants. In comparison to the previous data set, events in this simulation could be forgotten. The power function that was fitted (R 2 = .982) through the 10 most recent years of the observed distributions had an exponent (−1.001) that was similar to the one used to establish the data set. The reason that they are not identical is that the data set could only contain whole numbers. The constant of the retention function was 0.236.
The exponent of the retention function (−1.001) was then used to predict the proportion of recalled events. For the youngest and oldest participants, the constants for the power functions were 0.289 and 0.207. In the data set from Simulation 1, the predicted proportion did not change across time, because there was no forgetting. In this data set, there was forgetting, so the predicted proportions decreased as the age of the events increased.
In the model’s fourth step, the predicted proportions are compared to the observed proportions. The predicted values were similar but not identical to the observed values, because the observed distributions were based on a set of whole numbers. The resulting values therefore did not deviate much from 1 (range: 0.682–1.324).
In the final two steps of the model, the resulting values are first normalized to the maximum age of the participant +1 and then averaged across the participants. As a result, the averaged values deviated less from 1 (range: 0.974–1.052) than the resulting values. The averaged function is subsequently normalized to the maximum age of the population +1. This final function was also constantly about 1 (range: 0.972–1.050).
The problem of the model in its above-described form is that it requires many data points to estimate the retention function. In the two simulations, participants recalled between 85 and 330 events. Although this is not entirely impossible (see, e.g., Rubin & Schulkind, 1997a), it would be difficult to find many participants who were willing to recall so many events. To decrease the number of observations that would be required, one could group the results of participants of exactly the same age. Each group of participants with exactly the same age would then still need to recall at least one event from each year of the 10 most recent years, because a power function cannot be estimated from a data set with values of 0. One could, however, replace these values with values that approach 0, such as 0.001. To decrease the required number of observations even further, one could divide the participants into small age groups when estimating the retention function (Step 2). For each age group, the same retention function would then be used to predict the proportions (Step 3), but one would group the participants with exactly the same age for the other steps in the model, such as comparing the predicted values to the observed values (Step 4).
When we applied these changes to the model, it did not affect the retention or the final function in the two simulated data sets. In Fig. 1, we have given normalized averaged function of the first (top panel) and second (bottom panel) simulations as a function of the age at the events.
Fig. 1.
Normalized averaged resulting values of the first simulation (top panel) and the second simulation (bottom panel) as a function of the ages at the events
Discussion
In the second simulation, we generated a data set with an increased recall of recent events, but without periods in which participants had experienced more or fewer events. There was no reminiscence bump and no childhood amnesia in this simulated data set, because we did not add or remove events. Because the estimated retention function could predict the observed proportions very well, the averaged resulting function was constantly about 1, again suggesting that the model does not have a bias for showing the reminiscence bump.
Simulation 3
Data set
In the third simulation, we generated a data set that contained an increased recall of recent events and a reminiscence bump. In this simulated data set, there were also 50 participants, who were between 16 and 65 years old. There was again only 1 participant for every age and, as in Simulation 2, each participant recalled 50 events from the most recent year of his or her life. Forgetting was again based on a power function with the exponent −1.000, and the data set could only contain whole numbers (50, 25, 17, 13, 10, 8, 7, 6, 6, 5, etc.).
The reminiscence bump was simulated by adding events to the observed distributions. The peak of this simulated reminiscence bump was located at the age of 15. Six events were added at this age. Another five events were added at the ages of 14 and 16, and four events were added at the ages of 13 and 17. For the ages of 12 and 18, three events were added, and two events were added at the ages of 11 and 19. Finally, one event was added to the ages of 10 and 20.
The additions for the reminiscence bump meant that all observed distributions, except those of participants who were younger than 20 years of age, consisted of 36 extra events. For the youngest participants, the reminiscence bump and the increased recall of recent events coincided (cf. Janssen et al., 2005). The participant who was 16 years old therefore recalled 55 events (50 + 5 = 55 events) from the most recent year. The 50 participants recalled in total 12,462 events.
The model
The youngest participants, who were between 16 and 20 years old, recalled 1,053 events, and 265 of these events (proportion = .252) came from the most recent year. They recalled, respectively, 145, 108, and 89 events (proportions = .138, .103, and .085) from the three previous years. The oldest participants, who were between 61 and 65 years old, recalled 1,375 events. A total of 250 events (proportion = .182) came from the most recent year, and the oldest participants recalled, respectively, 125, 85, and 65 events (proportions = .091, .062, and .047) from 1, 2, and 3 years ago.
The power function (R 2 = .916) that was fitted through the 10 most recent years of the observed proportions had a constant of 0.200 and an exponent of −0.953. The exponent was used to predict the proportion of recalled events per year. For each age group, the proportion of recalled events of the most recent year was used as the constant for these power functions.
The observed proportions were then divided by the predicted proportions. The predicted values were not similar to the observed values, because the reminiscence bump was added to the observed distributions. The range of averaged values of this simulation was much larger than the range of averaged values of the earlier simulations. The resulting values at the peak of the reminiscence bump (age 15) ranged between 1.199 and 5.900. The 16-year-old participant recalled in total 199 events, and 31 events came from the year that he or she was 15 years old (proportion = .156), which was slightly more than the value predicted by the retention function for that year (proportion = .130). The retention function predicted that the 65-year-old participant would recall .004 from the year that he or she was 15 years old, but he or she recalled 7 of the 277 events from that year (proportion = .025), which is almost six times as much. The resulting values at the ages outside the reminiscence bump (younger than 10 years or older than 21 years) did not deviate much from 1 (range: 0.572–1.130).
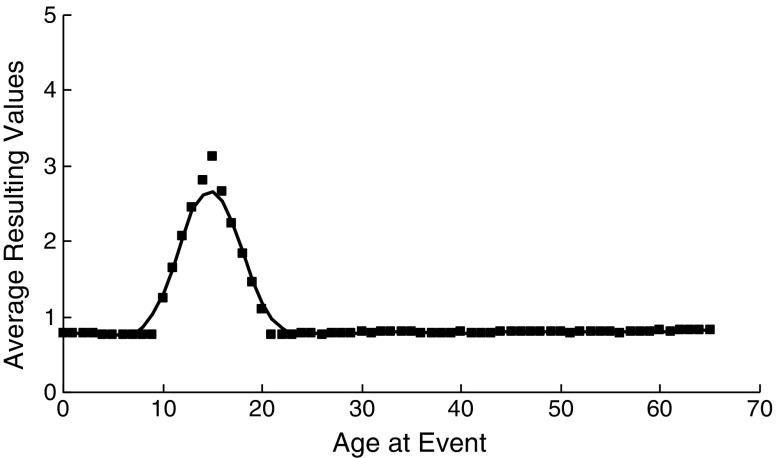
In the final steps of the model, the resulting values were first normalized, then averaged, and finally normalized again. We have given the normalized averaged values as a function of the age at the events in Fig. 2 (black squares). We have also added a moving average of 5 years, which will make this figure easier to read. This function is represented by the solid line. The results show a clear reminiscence bump. The peak of the averaged resulting function is located at the age of 15 (3.128). The values are higher than 1.5 in the period in which the participants had been between 11 and 18 years old and higher than 2.0 in the period in which the participants had been between 12 and 17 years old.
Fig. 2.
Normalized averaged resulting values of the third simulation as a function of the ages at the events
Discussion
In the third simulation, we generated a data set with an increased recall of recent events and additional events at the ages between 10 and 20 to simulate the reminiscence bump. The peak of these extra events was at age 15. Because the retention function was estimated on the sections of the observed distributions that included the reminiscence bump for younger participants (cf. Janssen et al., 2005), the estimated function had an exponent that was smaller than the exponent used to generate the data set.
The averaged resulting function showed a clear reminiscence bump. The location of this effect was exactly where we had simulated it. Whereas the first two simulations showed that the model did not have a bias to display the reminiscence bump when there was no such effect in the data set, the third simulation showed that the model did not change the location of the reminiscence bump when the data set included such an effect.
Experiment
In the three simulations, one could see that the model has no bias to display the reminiscence bump and that it does not alter the location of the effect when the reminiscence bump was simulated. We will now examine how the model performs with a real data set that contains childhood amnesia, a reminiscence bump, and an increased recall of recent events. The model is first applied to autobiographical memories collected from 1,089 Polish participants who were between 16 and 65 years old.
The autobiographical memories are then used to answer two methodological questions about the model. We investigate whether the length of the period that is used to estimate the retention function influences the resulting functions and whether the resulting functions are affected when one subtracts the predicted proportions from the observed distributions rather than dividing the observed proportions by the predicted proportions.
The reason for conducting the latter analyses is that the resulting values are more sensitive for minor changes in the predicted proportions when one divides the observed proportions by the predicted proportions than when one subtracts the predicted proportions from the observed proportions. If 5 of a participant’s 250 events (proportion = .020) came from a year for which the model initially predicted a proportion of .006, the resulting value according to the subtraction method would be .014. The resulting value according to the division method would be 3.33. If the predicted proportion changed to .008, the resulting value according to the subtraction method would be 0.012 (a change of 0.002). The resulting value according to the division method would be 2.50 (a change of 0.83). The problem with the subtraction method is, however, that functions cannot be normalized to 0. The contribution of each age group to the averaged resulting function is therefore unclear when one uses the subtraction method.
The model is also used to give two practical examples. We examined whether the reminiscence bump in the temporal distribution of autobiographical memories of participants who are younger than 40 years old is obscured by the increased recall of recent events and whether the reminiscence bump is caused by an increase of positive memories. The latter analysis is done by comparing the averaged resulting functions of pleasant and unpleasant events.
The experiment was conducted via the Internet, which allowed us to collect data from a large and diverse participant population (Gosling, Vazire, Srivastava, & John, 2004; Reips, 2000, 2002; Schmidt, 1997; Skitka & Sargis, 2006). The size of the population (N = 1,089) gave us the opportunity to display the results in age bins of 1 year.
Method
Participants
The study was conducted over the Internet. Participants could come into contact with the website, on which the Galton–Crovitz test (Crovitz & Schiffman, 1974; Galton, 1879; Robinson, 1976) was presented, in at least five ways: We submitted the website to search engines; we asked other websites with psychological tests to include a link to our site; Polish participants who had completed other tests on the website, such as the Daily News Memory Test (Meeter, Murre, & Janssen, 2005; Meeter, Ochtman, Janssen, & Murre, 2010), were sent invitations for the Galton–Crovitz test; advertisements were placed at various places in the Warsaw School of Social Sciences and Humanities; and participants could invite other people, such as relatives, friends, and colleagues, to take the questionnaire as well by sending them standardized e-mails that were provided by us.
A total of 1,089 participants completed the questionnaire. The average completion time was 28 min 11 s. To ensure the quality of the data, several measures were taken: Results from incomplete questionnaires or from questionnaires that took longer than 1 h to complete were not included in the analyses; results from participants who did not live in Poland or who were younger than 16 or older than 65 years were also excluded from the analyses; and participants could take the questionnaire as many times as they wanted, but only their first contribution was included in the analyses.
The majority of participants were female (87.1%), and the population contained more young adults (16–40 years, N = 961) than middle-aged adults (41–65 years, N = 128). These unequal distributions did not affect the results, because participants with exactly the same age were treated as 1 participant by the model. To estimate the retention functions, the participants were divided into 10 age groups of 5 years (16–20 years, 21–25 years, etc.). The distribution of the participants over these age groups is given in Table 2.
Table 2.
Number of participants; number of recalled events from the most recent year; number of recalled events from 1, 2, and 3 years ago; and total number of recalled events per age group
| Age Group | N | Most recent year | 1 year ago | 2 years ago | 3 years ago | Total |
|---|---|---|---|---|---|---|
| 16–20 years | 159 | 569 | 288 | 141 | 75 | 1,587 |
| 21–25 years | 489 | 1,529 | 830 | 323 | 261 | 4,890 |
| 26–30 years | 131 | 351 | 195 | 70 | 41 | 1,307 |
| 31–35 years | 116 | 332 | 139 | 39 | 32 | 1,156 |
| 36–40 years | 66 | 133 | 75 | 27 | 19 | 660 |
| 41–45 years | 29 | 66 | 25 | 10 | 5 | 289 |
| 46–50 years | 20 | 41 | 19 | 5 | 6 | 199 |
| 51–55 years | 25 | 53 | 17 | 7 | 8 | 249 |
| 56–60 years | 32 | 44 | 15 | 8 | 10 | 319 |
| 61–65 years | 22 | 26 | 10 | 3 | 4 | 220 |
| Total | 1,089 | 3,144 | 1,613 | 633 | 461 | 10,876 |
Materials
We selected 64 words with values of 6.00 or more for imagery, concreteness, and meaningfulness from Paivio, Yuille, and Madigan (1968) and translated them into Polish. The words and their translations are given in Table 3. Each participant received a semirandom selection of 10 cue words from the list. The cue words were divided into 10 categories, such as places, objects, people, and food, and participants received one cue word from each category.
Table 3.
The 64 cue words in the experiment and their English translations
| Polish | English | Polish | English | Polish | English |
|---|---|---|---|---|---|
| Bar | Bar | Fajka | Pipe | Mięso | Meat |
| Kościół | Church | Statek | Ship | Ziemniak | Potato |
| Miasto | City | Buty | Shoes | Cukier | Sugar |
| Fabryka | Factory | Bilet | Ticket | Wino | Wine |
| Sala | Hall | Okno | Window | Niemowlę | Baby |
| Szpital | Hospital | Ptak | Bird | Lekarz | Doctor |
| Biblioteka | Library | Kot | Cat | Sędzia | Judge |
| Targowisko | Market | Kwiat | Flower | Król | King |
| Więzienie | Prison | Koń | Horse | Uczeń | Pupil |
| Ulica | Street | Ogród | Garden | Kobieta | Woman |
| Wieża | Tower | Las | Woods | Wybrzeże | Coast |
| Deska | Board | Bawełna | Cotton | Góra | Mountain |
| Książka | Book | Kurz | Dust | Rzeka | River |
| Butelka | Bottle | Ogień | Fire | Niebo | Sky |
| Miska | Bowl | Futro | Fur | Burza | Storm |
| Krzesło | Chair | Złoto | Gold | Ręka | Arm |
| Zegar | Clock | Para Wodna | Steam | Wojsko | Army |
| Moneta | Coin | Kamień | Stone | Pocałunek | Kiss |
| Gazeta | Newspaper | Jabłko | Apple | Tory | Railroad |
| Flaga | Flag | Masło | Butter | Gwiazda | Star |
| Paznokieć | Nail | Kawa | Coffee | ||
| Silnik | Engine | Kukurydza | Corn |
Procedure
Before participants could start the Galton–Crovitz test, they were first asked to register with the website (http://memory.uva.nl) on which the questionnaire was presented. The participants were asked to indicate their age, gender, level of education, country of residence, and how often they read a newspaper and watched the news on television. They also had to supply their e-mail address, a user name, and a password. If participants wanted to take the questionnaire a second time, they could use the user name and password to log in directly.
After the participants had registered themselves or had logged in and had read the instructions, they were given one cue word. They were asked to think about the word and describe the personal event that came to mind first. They were informed that the event did not have to be important, but that it had to be personal and specific. The events should have occurred in their own lives and in a certain place at a certain time.
When participants had given a short description, they were asked to date a public event. The answers to the news events were not analyzed in this study (cf. Janssen, Chessa, & Murre, 2006), but the news events were included, among other reasons, to discourage participants from recalling personal events from only a single lifetime period (Sato, 2002). After the public event, the participants were given another cue word, which was followed by another news question. This continued until the participants had given 10 descriptions of personal events and had answered 10 news questions.
The participants were then given their descriptions back to date the personal events one by one. For each event, they could indicate how long ago the event had happened (e.g., “5 weeks ago”) or when the event had happened (e.g., “May 2010”). When participants wanted to indicate how long ago the event had happened, they selected the number of time units and the appropriate time unit (i.e., days, weeks, months, or years) from two drop-down menus. When they wanted to indicate the exact date of the event, they selected the day of the month, the month, and the year from three other drop-down menus. The participants were, however, also allowed to indicate only the month and the year or only the year in which the event had taken place. After the participants had dated the event, they were required to indicate the pleasantness of the event on a seven-point scale, which ranged from −3 (very unpleasant) to 3 (very pleasant).
When the participants had completed the questionnaire, they were thanked for their participation and briefly informed about the purposes of the study. They also had the opportunity to invite friends, family, or colleagues by entering their e-mail addresses into the system, which sent the potential new participants a standardized e-mail.
Results
The youngest participants, who were between 16 and 20 years old, recalled 1,587 events, and 569 of these events (proportion = .359) came from the most recent year. They recalled, respectively, 288, 141, and 75 events (proportions = .181, .089, and .047) from the three previous years. The oldest participants, who were between 61 and 65 years old, recalled 220 events. Of these events, 26 (proportion = .118) came from the most recent year, and the participants recalled, respectively, 10, 3, and 4 events (proportions = .045, .014, and .018) from 1, 2, and 3 years ago. The results of the other eight age groups are given in Table 2. The 1,089 participants recalled in total 10,876 events.
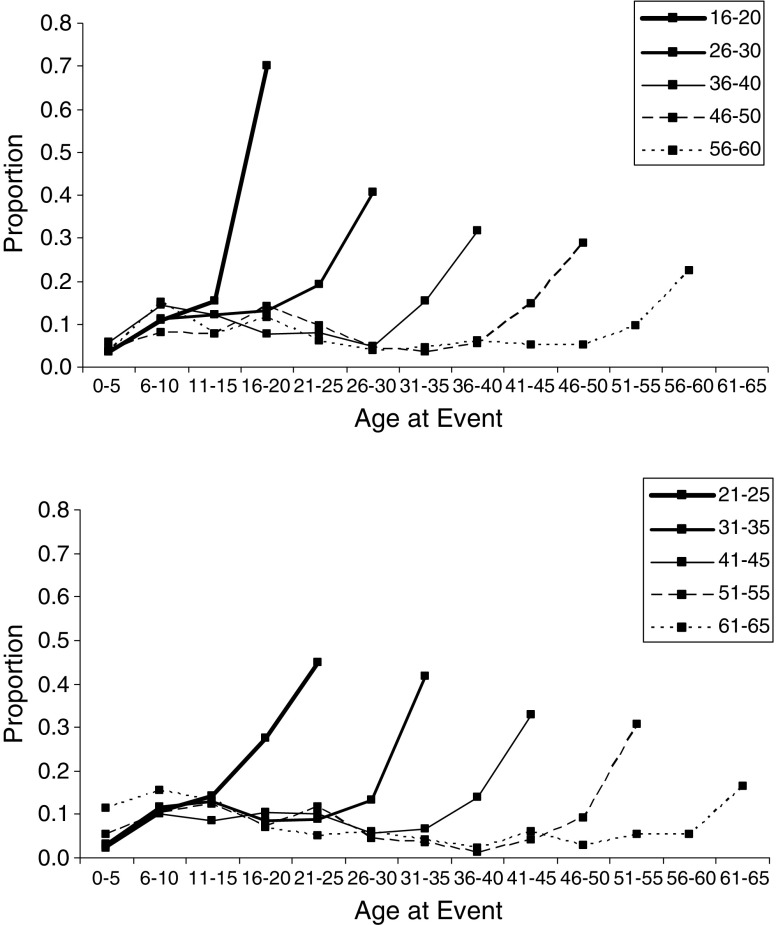
In Fig. 3, we have given the observed distributions of the ten 5-year age groups. We have divided the ten age groups over two panels to improve the readability of the figure. In the observed distributions of age groups that were older than 30 years of age, reminiscence bumps are visible. The peak of the reminiscence bump is located in different periods for different age groups. Participants who were between 31 and 35 years old had a reminiscence bump in the period in which they were between 6 and 15 years old. They recalled more memories from this period (M = 2.49) than from comparable periods that consisted of the 5 years directly before and after (M = 1.17), t(115) = 5.95, p < .001, or from the 10 years directly after (M = 1.74), t(115) = 3.11, p < .001. Although they recalled more events from the period in which they were between 11 and 15 years old (M = 1.30) than from the period in which they were between 6 and 10 years old (M = 1.19), this difference was not significant, p = .54.
Fig. 3.
Observed distributions per 5-year age group
For participants who were between 36 and 40 years old, the reminiscence bump was located in the same period. They recalled more memories from the period in which they were between 6 and 15 years old (M = 2.71) than from the 5 years directly before and after (M = 1.37), t(65) = 4.10, p < .001, or from the 10 years directly after (M = 1.58), t(65) = 3.01, p < .01. Although they recalled more events from the period in which they were between 6 and 10 years old (M = 1.48) than from the period in which they were between 11 and 15 years old (M = 1.23), this difference was not significant, p = .19.
The reminiscence bump in the temporal distribution of participants who were between 41 and 45 years old was located later. They recalled more events from the period in which they were between 11 and 20 years old (M = 1.90) than from the periods in which they were between 0 and 10 years old (M = 1.21) and in which they were between 21 and 30 years old (M = 1.55), but neither difference was significant (p = .06, p = .38).
For the participants who were between 46 and 50 years old, the reminiscence bump was also located in the second decade. They recalled more events from the period in which they were between 11 and 20 years old (M = 2.15) than from the periods in which they were between 0 and 10 years old (M = 1.20) and in which they were between 21 and 30 years old (M = 1.40), but, again, neither difference was significant (p = .18, p = .12).
Participants who were between 51 and 55 years old had a reminiscence bump in the period in which they were between 6 and 15 years old. They recalled more memories from this period (M = 2.28) than either from the 5 years directly before and after (M = 1.24), t(24) = 2.28, p < .05, or from the 10 years directly after (M = 1.88). The latter difference, however, was not significant, p = .50.
The results of the participants who were between 56 and 60 years old were similar to those of the participants who were 5 years younger. They also recalled more memories from this period (M = 2.28) than either from the 5 years directly before and after (M = 1.50) or from the 10 years directly after (M = 1.75). Neither difference, however, was significant (p = .09, p = .28).
Finally, the participants who were between 61 and 65 years old recalled more events from the period in which they were between 6 and 15 years old (M = 2.86) than either from the 5 years directly before and after (M = 1.82) or from the 10 years directly after (M = 1.18). The first difference was not significant (p = .10), but the second difference was, t(21) = 3.50, p < .01.
The power function (R 2 = .669) that was fitted through the 10 most recent years of the observed proportions had a constant of 0.216 and an exponent of −1.359. The exponent was used to predict the proportion of recalled events per year. For each age group, the proportion of recalled events of the most recent year was used as the constant for these power functions. The observed proportions were then divided by the predicted proportions. Subsequently, the resulting values were first normalized, then averaged, and finally normalized again.
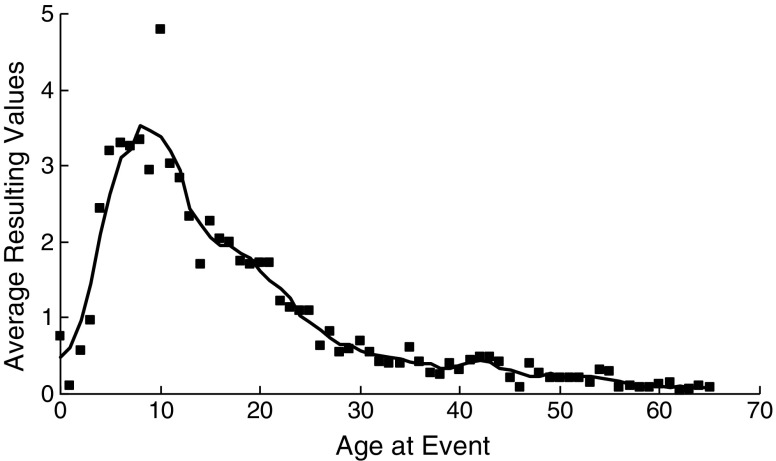
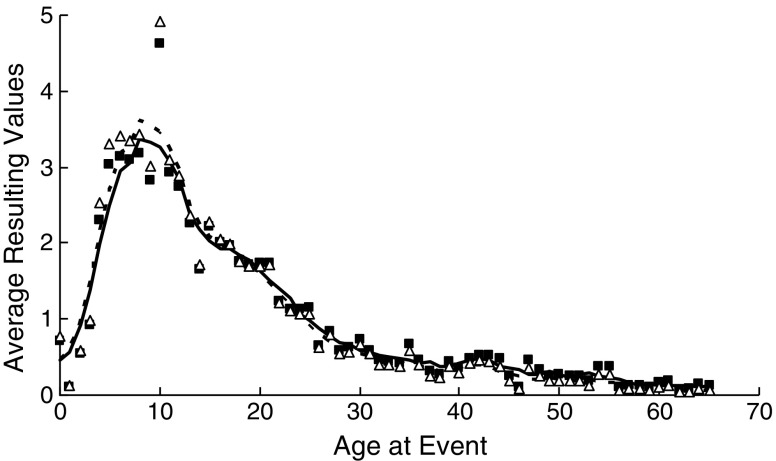
The range of the averaged values of the experiment was much larger than the ranges of averaged values of the simulations. We have given the averaged resulting values as a function of the ages at the events in Fig. 4. To make the figure more readable, we have added a moving average of 5 years to the figure. Moving averages are also added to the subsequent figures for the same reason. This function is represented by the solid line. For some ages, participants recalled hardly any personal events (min = 0.044, age 62), while for other ages they recalled relatively many personal events (max = 4.800, age 10). The function shows a clear reminiscence bump. The values are higher than 1.5 in the period in which the participants were between 4 and 21 years old and higher than 2.0 in the periods in which the participants were between 4 and 13 and between 15 and 16 years old.
Fig. 4.
Normalized averaged resulting values as a function of the ages at the events when using the observed proportions of the 10 most recent years for estimating the retention function
Length of period for estimating retention function
In the next two sections, we will address two methodological issues. We will later examine whether subtracting the predicted values from the observed values gives a different averaged function than dividing the predicted values from the observed values, but we will first investigate whether the averaged function would be affected if one used bins of 5, 10, or 15 years to estimate the retention function.
If one used the observed proportions of the 5 most recent years, the power function (R 2 = .772) that was fitted through them had a constant of 0.223 and an exponent of −1.427. The retention function based on the 10 most recent years had a constant of 0.216 and an exponent of −1.359 (R 2 = .669), and the retention function based on the 15 most recent years had a constant of 0.199 and an exponent of −1.265 (R 2 = .564). As the period for estimating the retention function becomes longer, the exponent becomes smaller.
A smaller exponent leads to lower resulting values at younger ages and higher resulting values at older ages (because the predicted values were higher at younger ages and lower at older ages), but it had no influence on the overall shape of the distribution. The averaged values when the participants were 10 years old (which were the highest values of each function) were 4.918, 4.800, and 4.619 when the retention function was based on the observed proportions of the 5, 10, and 15 most recent years. The averaged values when the participants were 62 years old (which were the lowest ones) were 0.035, 0.044, and 0.060, when the retention function was based on the 5, 10, and 15 most recent years.
The averaged resulting values are given as a function of the age at the time of the events in Figs. 4 and 5. The averaged resulting function when the observed proportions of the 10 most recent years were used has already been given in Fig. 4. The averaged resulting functions when the observed proportions of the 5 and 15 most recent years were used are represented by white triangles and black squares in Fig. 5. All three functions showed a clear reminiscence bump in the same time period. The averaged resulting values were higher than 1.5 in the period in which the participants were between 4 and 21 years old, and higher than 2.0 in the periods in which the participants were between 4 and 13 and between 15 and 16 years old.
Fig. 5.
Normalized averaged resulting values as a function of the ages at the events when using the observed proportions of the 5 most recent years (white triangles, dashed line) and the 15 most recent years (black squares, solid line) for estimating the retention function
Dividing versus subtracting
We subsequently examined whether subtracting the predicted values from the observed values gives a different averaged resulting function than dividing the observed values by the predicted values. When one subtracts the predicted values from the observed values, the estimated retention function is the same as when one divides the observed values by the predicted values. However, one should not normalize the resulting values of the subtractions to the maximum age of the participants, because these values are supposed to be 0 when the predicted value is identical to the observed value.
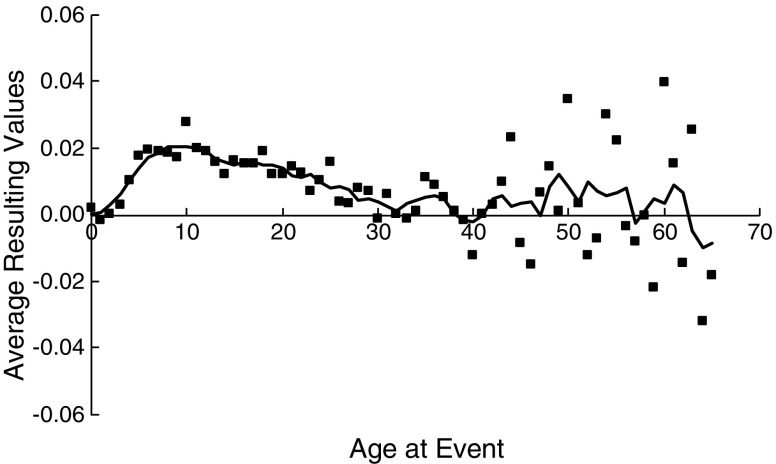
The averaged resulting function when one subtracts the predicted values from the observed values is given in Fig. 6. The function is relatively smooth until the age of 40 (range: –.002 to .028). After this period, the averaged values deviate more from 0 (range: –.032 to .040). If one ignores the averaged resulting values at later ages and focuses on the first 40 years of the function, then one can see a reminiscence bump, which is located in the same period as the function when one divides the observed values by the predicted values (Fig. 4). The averaged resulting values are higher than .015 in the periods in which the participants were between 5 and 13 and between 15 and 18 years old. The averaged resulting values were also higher than .015 at ages 21 and 25. These periods correspond reasonably well to the period that was found when one divided the observed values by the predicted values (i.e., between 4 and 21). The averaged resulting values were higher than .020 at ages 6, 10, and 11. The locations of these peaks also correspond well with the periods that were found when one divided the observed values by the predicted values (i.e., between 4 and 13 and between 15 and 16).
Fig. 6.
Normalized averaged resulting values as a function of the ages at the events when the predicted values were subtracted from the observed values
Young adults versus middle-aged adults
In the following two sections, we will give two examples for the practical use of the model. We will first use the model to compare the temporal distributions of young and middle-aged adults, and we will then use the model to compare the temporal distributions of pleasant and unpleasant memories. There were more young adults than middle-aged adults in the sample, but this does not affect the model, because for each age only one observed distribution will be calculated. The chance of outliers is, however, smaller when the distribution is based on more observations.
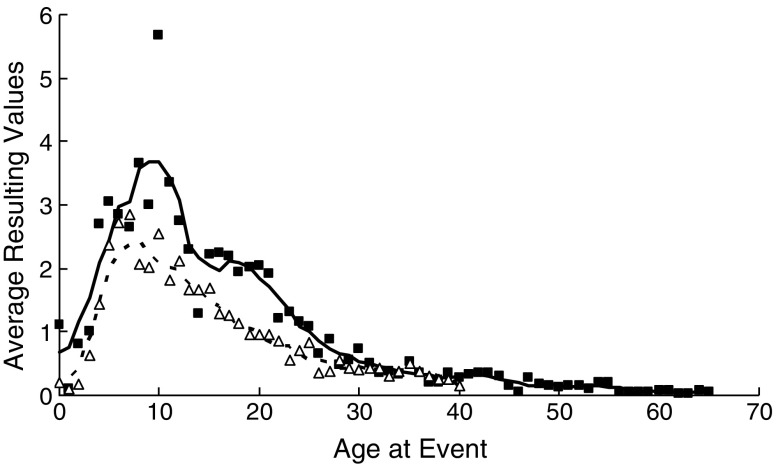
If one uses the same retention function (exponent: −1.359) for young and middle-aged adults to predict the observed values, one finds that the averaged resulting values of the young adults were higher than 1.5 in the period in which they were between 4 and 15 years old. The values were higher than 2.0 in the period in which the young adults were between 5 and 10 years old and at the age of 12. The averaged resulting values of the middle-aged adults were higher than 1.5 in the periods in which they were between 4 and 13 and between 15 and 21 years old. The values were also higher than 1.5 when the middle-aged adults were 24 years old. The averaged values of the middle-aged adults were higher than 2.0 in the periods in which they were between 4 and 13 and between 15 and 17 years old. The values were also higher than 2.0 when the middle-aged adults were between 19 and 20 years old.
When one estimates separate retention functions for the young (y = 0.264 x −1.242, R 2 = .847) and middle-aged (y = 0.176 x −1.477, R 2 = .701) adults, one finds that the averaged resulting values of the young adults were higher than 1.5 in the period in which they were between 5 and 15 years old. The values were higher than 2.0 in the period that the young adults were between 5 and 10 years old and at the age of 12. The averaged resulting values of the middle-aged adults were higher than 1.5 in the periods in which they were between 4 and 13 and between 15 and 21 years old. The values of the middle-aged adults were higher than 2.0 in the periods in which they were between 4 and 13 and between 15 and 17 years old. The values were also higher than 2.0 when the middle-aged adults were between 19 and 20 years old.
In Fig. 7, we have given the averaged resulting values as a function of the age at the events when separate retention functions were estimated for young and middle-aged adults. The results of the young adults are represented by white triangles, while the results of the older adults are represented by black squares.
Fig. 7.
Normalized averaged resulting values for the young adults (white triangles, dashed line) and the middle-aged adults (black squares, solid line) as a function of the ages at the events
Pleasant versus unpleasant memories
Participants were asked to rate the pleasantness of the personal events on a seven-point scale that ranged from −3 (very unpleasant) to 3 (very pleasant). Participants recalled more pleasant (M = 5.32, SD = 1.93) than unpleasant (M = 3.05, SD = 1.82) events, t(1087) = 22.67, p < .001. The remaining events (i.e., rating value = 0) were rated as neither pleasant nor unpleasant and were not used in the following analyses.
The unpleasant memories were forgotten at the same rate as the pleasant memories. The retention function that was used to predict the proportions of pleasant memories had a constant of 0.202 and an exponent of −1.341 (R 2 = .576), while the retention function that was used to predict the proportions of unpleasant memories had a constant of 0.169 and an exponent of −1.358 (R 2 = .358).
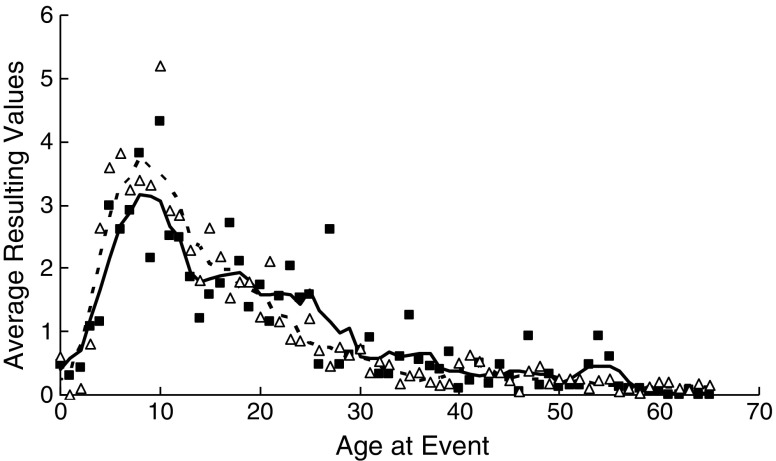
Pleasant memories were often recalled from the period in which the participants were between 4 and 19 years of age and at the age of 21 (higher than 1.5), and especially from the periods in which the participants were between 4 and 13 and between 15 and 16 years old and at the age of 21 (higher than 2.0). Many unpleasant memories came from the same period. They were often recalled from the periods in which the participants were between 5 and 13, 15 and 18, and 22 and 25 years old, and at the ages of 20 and 27 (higher than 1.5), and especially from the periods in which the participants were between 5 and 12 and between 17 and 18 years old and at the ages of 23 and 27 (higher than 2.0).
In Fig. 8, the averaged resulting values are given as a function of the age at the events. The black squares represent the unpleasant memories, while the pleasant memories are represented by the white triangles. Using a Kolmogorov–Smirnov two-sample test, it was determined that the distributions of the pleasant and unpleasant memories were not equal (D = .116, α < .001). Despite the similar shapes of the distributions, relatively more pleasant memories were remembered from the period in which the participants were between 2 and 17 years old, and relatively more unpleasant memories were remembered from the period in which the participants were between 18 and 39 years old.
Fig. 8.
Normalized averaged resulting values of pleasant memories (white triangles, dashed line) and unpleasant memories (black squares, solid line) as a function of the ages at the events
Discussion
With the results of the experiment, we examined how the model performed with a real data set that contained childhood amnesia, a reminiscence bump, and an increased recall of recent events. When we applied the model to the observed distribution of the autobiographical memories, we found a reminiscence bump in the period in which the participants were between 4 and 21 years old, which is earlier than most studies that have used cue words have found, although several studies have also found such an early peak (e.g., Cohen & Faulkner, 1988; Conway et al., 2005; Jansari & Parkin, 1996; Rybash & Monaghan, 1999). The location of the reminiscence bump was not an artifact caused by the model. The uncorrected observed distributions (Fig. 3) also showed peaks between the ages of 5 and 20.
Studies often report their results in 10-year age bins. If we too reported the results using such large age bins, we would also find a peak in the second decade of participants’ lives (cf. Janssen, Rubin, & St. Jacques, 2011). If, for example, one were to take the uncorrected results from participants older than 30 years of age and present them in 5-year age bins, one would find that most memories come from the period in which the participants were between 6 and 10 years old (12.5%), but if the same results were to be presented in 10-year age bins, more memories would come from the second decade (11.4% + 9.0% = 20.4%) than from the first (4.5% + 12.5% = 17.0%) or the third (8.4% + 7.9% = 16.3%) decade.
The autobiographical memories were used to answer two methodological questions about the model. We investigated whether the length of the period that is used to estimate the retention function influences the resulting functions and whether the resulting functions are affected when one subtracts the predicted proportions from the observed distributions. We found that the exponent of the retention function became smaller as the period for estimating became longer and that a smaller exponent led to lower values at younger ages and higher values at older ages. The change of the period length did not change the location of the reminiscence bump.
The averaged resulting function when one subtracted the predicted values from the observed values was relatively smooth until the age of 40. After this period, the averaged resulting values deviated more from 0. If one ignored the averaged resulting values at later ages and focused on the first 40 years of the function, then one could see a reminiscence bump, which was located in the same period as the average function when one divided the observed values by the predicted values. The use of subtraction did not influence the location of the reminiscence bump, but this method resulted in difficulties for predicting the observed values at later ages.
Two examples for the practical use of the model were also provided. We examined whether the reminiscence bump in the temporal distribution of autobiographical memories of participants younger than 40 years was obscured by the increased recall of recent events and whether the reminiscence bump was caused by an increase of positive memories.
When we corrected the observed distributions of young adults, it was found that the corrected distribution also showed a reminiscence bump that was located in the same period as the reminiscence bump in the distribution of middle-aged adults. The reminiscence bump therefore is also present in the temporal distribution of autobiographical memories in participants who are younger than 40 years, but it is obscured by the increased recall of recent events (cf. Janssen et al., 2005). The model could also be used to show that public events can influence the temporal distribution of autobiographical memory (see, e.g., Berntsen & Rubin, 2006; Conway & Haque, 1999; Maki & Naka, 2006), by comparing different age groups and identifying a shift in the location of the reminiscence bump.
When the distributions of pleasant and unpleasant memories were compared, we found that both distributions showed a reminiscence bump, but the participants recalled relatively more positive events from childhood and adolescence, while they recalled relatively more negative events from young adulthood.
General discussion
The reminiscence bump is the tendency to recall more memories from adolescence and early adulthood than from adjacent lifetime periods (Rubin et al., 1986, 1998). Past studies, which used age bins of 10 years to display the temporal distribution of word-cued memories, found a reminiscence bump only in the results of participants who were 40 years of age or older, possibly because the reminiscence bump is obscured by the increased recall of recent events in the results of younger participants (Janssen et al., 2005).
In this study, a model was proposed that removes the increased recall of recent events from the temporal distribution of autobiographical memory. The model, which is technically an algorithm, estimates a retention function based on the 10 most recent years from the observed distributions and divides the observed distributions by predictions derived from the estimated retention function.
The three simulations showed that the model has no bias to display the reminiscence bump when the data set does not contain one (Simulations 1 and 2), and that it does not alter the location of the reminiscence bump when the data set does contain one (Simulation 3). The results of the experiment showed that the reminiscence bump could be found in the results of young adults, provided that one corrects for the increased recall of recent events.
The model was designed without making many assumptions about the nature of the reminiscence bump. As a result, it cannot distinguish the causes of the decreased recall of the earliest memories (childhood amnesia), the increased recall of memories from adolescence and early adulthood (the reminiscence bump) and the decreased recall of memories from middle and late adulthood. It is possible that these three components have one single underlying cause or that they have different causes.
The model has one clear limitation. It needs relatively many observations to ensure that the retention function can be estimated. To decrease the number of observations required, one could group the participants into age groups of 5 years and replace the values for years from which the participants did not recall any events with values that approach 0. We recommend that, as a rule of thumb, the number of observations be about 10 times larger than the maximum age of the age group. To use the model for participants who are between 61 and 65 years old, one needs between 610 and 650 observations. If participants are asked to recall 20 personal events, then one would require 30–35 participants. For younger age groups, fewer observations are needed. If the participants are between 26 and 30 years old and if they have to recall 20 personal events, then one would require only 15 participants to use the model.
In the experiment, there were relatively few middle-aged adults (N = 128), but we could apply the model to the data set with only half of the recommended number of observations (n = 2,750) when we grouped these middle-aged adults into five age groups of 5 years and replaced the values of the years from which they recalled no events during the estimation of the retention function (Step 2). With the relatively small data set (n = 1,276), we had to replace a value only twice. Both of these instances were in the results of the participants who were between 61 and 65 years old. These 22 participants had recalled no events from either 8 or 10 years ago. In the other steps of the model, these two values were not replaced. Although the model could be applied to a data set with fewer observations than recommended, we would still advise researchers to follow the rule of thumb that 10 times the maximum age of the age group is required for the number of observations.
Conclusions
The reminiscence bump is the effect according to which people tend to recall relatively many personal events from the period in which they were between 10 and 30 years old. This effect has only been found in autobiographical memory studies that used participants who were older than 40 years of age. The increased recall of recent events possibly obscures the reminiscence bump in the results of younger participants. In this study, a model was proposed that removes this increase from the temporal distribution. The model basically estimates a retention function based on the 10 most recent years from the observed distributions and divides the observed distributions by predictions derived from the estimated retention function. Using the model, it was shown that the temporal distribution of autobiographical memories of participants who were younger than 40 did contain a reminiscence bump.
Author Note
This research was supported by a grant from the Japanese Society for the Promotion of Science (JSPS) to S.M.J.J. We thank Makiko Naka and Tomasz Maruszewski for their helpful suggestions and support.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- Berntsen D, Rubin DC. Emotionally charged autobiographical memories across the life span: The recall of happy, sad, traumatic, and involuntary memories. Psychology and Aging. 2002;17:636–652. doi: 10.1037/0882-7974.17.4.636. [DOI] [PubMed] [Google Scholar]
- Berntsen D, Rubin DC. Cultural life scripts structure recall from autobiographical memory. Memory & Cognition. 2004;32:427–442. doi: 10.3758/BF03195836. [DOI] [PubMed] [Google Scholar]
- Berntsen D, Rubin DC. Flashbulb memories and posttraumatic stress reactions across the life span: Age-related effects of the German occupation of Denmark during World War II. Psychology and Aging. 2006;21:127–139. doi: 10.1037/0882-7974.21.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bohn A. Generational differences in cultural life scripts and life story memories of younger and older adults. Applied Cognitive Psychology. 2010;24:1324–1345. doi: 10.1002/acp.1641. [DOI] [Google Scholar]
- Bohn A, Berntsen D. The reminiscence bump reconsidered: Children’s prospective life stories show a bump in young adulthood. Psychological Science. 2011;22:197–202. doi: 10.1177/0956797610395394. [DOI] [PubMed] [Google Scholar]
- Cohen G, Faulkner D. Life span changes in autobiographical memory. In: Gruneberg MM, Morris PE, Sykes RN, editors. Practical aspects of memory: Current research and issues. New York: Wiley; 1988. pp. 277–282. [Google Scholar]
- Conway MA, Haque S. Overshadowing the reminiscence bump: Memories of a struggle for independence. Journal of Adult Development. 1999;6:35–44. doi: 10.1023/A:1021672208155. [DOI] [Google Scholar]
- Conway MA, Wang Q, Hanyu K, Haque S. A cross-cultural investigation of autobiographical memory: On the universality and cultural variation of the reminiscence bump. Journal of Cross Cultural Psychology. 2005;36:739–749. doi: 10.1177/0022022105280512. [DOI] [Google Scholar]
- Crovitz HF, Schiffman H. Frequency of episodic memories as a function of their age. Bulletin of the Psychonomic Society. 1974;4:517–518. [Google Scholar]
- Galton F. Psychometric experiments. Brain. 1879;2:149–162. doi: 10.1093/brain/2.2.149. [DOI] [Google Scholar]
- Gosling SD, Vazire S, Srivastava S, John OP. Should we trust Web-based studies? A comparative analysis of six preconceptions about Internet questionnaires. American Psychologist. 2004;59:93–104. doi: 10.1037/0003-066X.59.2.93. [DOI] [PubMed] [Google Scholar]
- Jansari A, Parkin AJ. Things that go bump in your life: Explaining the reminiscence bump in autobiographical memory. Psychology and Aging. 1996;11:85–91. doi: 10.1037/0882-7974.11.1.85. [DOI] [PubMed] [Google Scholar]
- Janssen SMJ, Chessa AG, Murre JMJ. The reminiscence bump in autobiographical memory: Effects of age, gender, education and culture. Memory. 2005;13:658–668. doi: 10.1080/09658210444000322. [DOI] [PubMed] [Google Scholar]
- Janssen SMJ, Chessa AG, Murre JMJ. Memory for time: How people date events. Memory & Cognition. 2006;34:137–148. doi: 10.3758/BF03193393. [DOI] [PubMed] [Google Scholar]
- Janssen SMJ, Murre JMJ. Reminiscence bump in autobiographical memory: Unexplained by novelty, emotionality, valence and importance. Quarterly Journal of Experimental Psychology. 2008;61:1847–1860. doi: 10.1080/17470210701774242. [DOI] [PubMed] [Google Scholar]
- Janssen SMJ, Rubin DC. Age effects in cultural life scripts. Applied Cognitive Psychology. 2011;25:291–298. doi: 10.1002/acp.1690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssen SMJ, Rubin DC, St. Jacques PL. The temporal distribution of autobiographical memory: Changes in reliving and vividness over the life span do not explain the reminiscence bump. Memory & Cognition. 2011;39:1–11. doi: 10.3758/s13421-010-0003-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawasaki Y, Janssen SMJ, Inoue T. Temporal distribution of autobiographical memory: Uncovering the reminiscence bump in Japanese young and middle-aged adults. Japanese Psychological Research. 2011;53:86–96. doi: 10.1111/j.1468-5884.2010.00451.x. [DOI] [Google Scholar]
- Maki Y, Naka M. Reminiscence bump and contents of autobiographical memory in Japanese elders. Japanese Journal of Psychology. 2006;77:333–341. doi: 10.4992/jjpsy.77.333. [DOI] [PubMed] [Google Scholar]
- Meeter M, Murre JMJ, Janssen SMJ. Remembering the news: Modeling retention data from a study with 14,000 participants. Memory & Cognition. 2005;33:793–810. doi: 10.3758/BF03193075. [DOI] [PubMed] [Google Scholar]
- Meeter M, Ochtman DJC, Janssen SMJ, Murre JMJ. Of sports and politics: Predicting category-specific retention of news events from demographic variables. European Journal of Cognitive Psychology. 2010;22:117–129. doi: 10.1080/09541440802708037. [DOI] [Google Scholar]
- Nelson K, Fivush R. The emergence of autobiographical memory: A social cultural development theory. Psychological Review. 2004;111:486–511. doi: 10.1037/0033-295X.111.2.486. [DOI] [PubMed] [Google Scholar]
- Paivio A, Yuille JC, Madigan SA. Concreteness, imagery, and meaningfulness values for 925 nouns. Journal of Experimental Psychology. 1968;76(1, Pt. 2):1–25. doi: 10.1037/h0025327. [DOI] [PubMed] [Google Scholar]
- Reips U-D. The Web experiment method: Advantages, disadvantages, and solutions. In: Birnbaum MH, editor. Psychological experiments on the Internet. San Diego, CA: Academic; 2000. pp. 89–114. [Google Scholar]
- Reips U-D. Standards for Internet-based experimenting. Experimental Psychology. 2002;49:243–256. doi: 10.1026//1618-3169.49.4.243. [DOI] [PubMed] [Google Scholar]
- Robinson JA. Sampling autobiographical memory. Cognitive Psychology. 1976;8:578–595. doi: 10.1016/0010-0285(76)90020-7. [DOI] [Google Scholar]
- Robinson JA. Autobiographical memory: A historical prologue. In: Rubin DC, editor. Autobiographical memory. Cambridge: Cambridge University Press; 1986. pp. 19–24. [Google Scholar]
- Rubin DC. The distribution of early childhood memories. Memory. 2000;8:265–269. doi: 10.1080/096582100406810. [DOI] [PubMed] [Google Scholar]
- Rubin DC, Berntsen D. Life scripts help to maintain autobiographical memories of highly positive, but not highly negative, events. Memory & Cognition. 2003;31:1–14. doi: 10.3758/BF03196077. [DOI] [PubMed] [Google Scholar]
- Rubin DC, Berntsen D, Hutson M. The normative and the personal life: Individual differences in life scripts and life stories among U.S.A. and Danish undergraduates. Memory. 2009;17:54–68. doi: 10.1080/09658210802541442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DC, Rahhal TA, Poon LW. Things learned in early adulthood are remembered best. Memory & Cognition. 1998;26:3–19. doi: 10.3758/BF03211366. [DOI] [PubMed] [Google Scholar]
- Rubin DC, Schulkind MD. The distribution of autobiographical memories across the lifespan. Memory & Cognition. 1997;25:859–866. doi: 10.3758/BF03211330. [DOI] [PubMed] [Google Scholar]
- Rubin DC, Schulkind MD. Distribution of important and word-cued autobiographical memories in 20-, 35-, and 70-year-old adults. Psychology and Aging. 1997;12:524–535. doi: 10.1037/0882-7974.12.3.524. [DOI] [PubMed] [Google Scholar]
- Rubin DC, Wenzel AE. One hundred years of forgetting: A quantitative description of retention. Psychological Review. 1996;103:734–760. doi: 10.1037/0033-295X.103.4.734. [DOI] [Google Scholar]
- Rubin DC, Wetzler SE, Nebes RD. Autobiographical memory across the adult life span. In: Rubin DC, editor. Autobiographical memory. Cambridge: Cambridge University Press; 1986. pp. 202–221. [Google Scholar]
- Rybash JM, Monaghan BE. Episodic and semantic contributions to older adults’ autobiographical recall. Journal of General Psychology. 1999;126:85–96. doi: 10.1080/00221309909595353. [DOI] [PubMed] [Google Scholar]
- Sato K. Changes in the temporal organization of autobiographical memories. Psychological Reports. 2002;91:1074–1078. doi: 10.2466/pr0.2002.91.3f.1074. [DOI] [PubMed] [Google Scholar]
- Schmidt WC. World-Wide Web survey research: Benefits, potential problems, and solutions. Behavior Research Methods, Instruments, & Computers. 1997;29:274–279. doi: 10.3758/BF03204826. [DOI] [Google Scholar]
- Skitka LJ, Sargis EG. The Internet as psychological laboratory. Annual Review of Psychology. 2006;57:529–555. doi: 10.1146/annurev.psych.57.102904.190048. [DOI] [PubMed] [Google Scholar]