Coding Design of Positional Information for Robust Morphogenesis

Abstract

Robust positioning of cells in a tissue against unavoidable noises is important for achieving normal and reproducible morphogenesis. The position in a tissue is represented by morphogen concentrations, and cells read them to recognize their spatial coordinates. From the engineering viewpoint, these positioning processes can be regarded as an information coding. Organisms are conjectured to adopt good coding designs with high reliability for a given number of available morphogen species and their chemical properties. To answer, quantitatively, the questions of how good coding is adopted, and subsequently when, where, and to what extent each morphogen contributes to positioning, we need a way to evaluate the goodness of coding. In this article, by introducing basic concepts of computer science, we mathematically formulate coding processes in morphogen-dependent positioning, and define some key concepts such as encoding, decoding, and positional information and its precision. We demonstrate the best designs for pairs of encoding and decoding rules, and show how those designs can be biologically implemented by using some examples. We also propose a possible procedure of data analysis to validate the coding optimality formulated here.

Introduction

Providing cells with precise information on their position is an important step in morphogenesis, and it is followed by cell differentiation and formation of morphological structures, both of which depend on the position. The positional information is provided in the form of concentrations of diffusive chemicals called morphogens. Perturbation of the spatial profiles of morphogen concentrations often causes critical morphological anomalies (1, 2).

A main focus of studies on positioning in tissues is the formation and read-out of morphogen gradients. The molecular mechanisms have been revealed by experiments, and mathematical models describing them have been proposed to reproduce and predict outcomes of experiments. Moreover, recent advances in imaging techniques have enabled us to visualize the spatial profiles of morphogens and to quantitatively measure their variability among embryos (3, 4, 5, 6, 7, 8, 9, 10). The design of robust positioning by morphogens in the face of this variability or noise has been explored by a systems approach, and possible noise-reducing mechanisms in the formation and interpretation of gradients have been discussed in specific systems (11, 12, 13, 14, 15, 16, 17).

We recently asked a new question, one about robustness (18, 19): What are the best spatial profiles of morphogen concentrations for achieving the most efficient and reliable transfer of positional information to cells in the presence of noise? Fig. 1 illustrates the problem. Let us consider the following in silico experiment. In a two-dimensional tissue, cells in a region with an arbitrary shape (labeled T) need to differentiate from the rest of the tissue according to the concentrations of three morphogens. For given spatial profiles of these morphogens, the correspondence between position and a set of concentrations of the three morphogens is determined. It maps region T in real space to region T′ in chemical space where the coordinates are given by morphogen concentrations (see T₁′ and T₂′). If each cell on the plane can recognize its own position only through the morphogen concentrations (i.e., concentration coordinates) that it detects, and if the cell differentiates in accordance with those concentrations in an appropriate manner, then the target differentiation pattern T is realized in the tissue.

Figure 1.

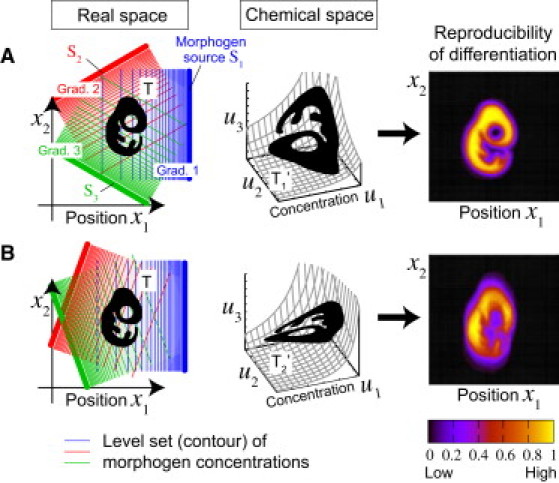
Coding problem of positional information. (Left panels) (Blue, red, and green lines) Morphogen gradients (contours of concentrations). (Black images, represented by T) The regions that need to differentiate from the rest of tissue based on the morphogen concentrations. The spatial profiles of the morphogens determine the way the shape T in real space is mapped into T′ in chemical space where the coordinates are given by the morphogen concentrations (middle panels). In the presence of noise in the morphogen concentrations, the reproducibility of differentiation (right panels) depends on the spatial profiles of the morphogens, suggesting that the spatial profile determines the reliability of positional information. In this example, profile A provides more precise information than profile B, even though the noise has the same magnitude in both cases. Finding the best spatial profile for achieving maximal reliability is thus a coding problem (specifically, encoding problem). (See Model in the main text, and see subsection SA in the Supporting Material for additional details.)

Our interest here is in the reproducibility of the differentiation pattern T when the spatial profiles of the morphogens are perturbed by noise. The right panels in Fig. 1 illustrate the reproducibility of the produced pattern when different spatial profiles are adopted in the presence of noise of the same magnitude (see subsection SA in the Supporting Material for a mathematical description of the problem). For spatial profile A, focal shape T is reproduced with reasonably high accuracy, whereas for profile B, it is not reproduced well. Note that although the magnitude of the noise is exactly the same in these two cases, the directions of the three morphogen gradients are different. This implies that the spatial profile of morphogen concentrations strongly affects the reliability of positioning based on those concentrations. It also suggests that there might exist a best spatial profile of morphogens that achieves the highest reliability.

From an engineering viewpoint, the above question about robustness is interpreted as an information coding problem: spatial coordinates in a tissue, that is, original information that should be transferred to cells, are converted into morphogen concentrations, and then the cells read-out the coordinates from the concentrations that they detect. In previous works, we discussed coding designs in a few simple situations. In the case without informational redundancy where two-dimensional positioning is achieved by two morphogens, we proved mathematically that orthogonal morphogen gradient vectors provide the highest precision of positional information at a focal region (orthogonality principle) (18). In the case with informational redundancy where one-dimensional positioning is achieved by two morphogens, we showed that the precision depends strongly on the relative directions of their gradients (i.e., opposite or identical), and that which is better is determined by the sign of the correlation of the noise associated with the two morphogens (19). Using these theoretical results, we identified the optimality of the mode of encoding adopted and evaluated the relative contribution of each morphogen to cell positioning in vertebrate limb bud development and in early patterning of the Drosophila embryo. However, the above coding designs were discussed under different mathematical formalisms restricted to specific situations.

In this article, we construct a general mathematical framework for the coding processes in multidimensional positioning by multiple morphogens. This framework includes our previous results as special cases. We clearly define some key concepts such as encoding, decoding, and positional information and its precision in terms of information and statistical theories. Based on this framework, we mathematically derive optimal coding designs that achieve the most reliable positioning during morphogenesis. We also show how those optimal designs can be biologically implemented by using some examples. We expect this study to provide important criteria in analyzing quantitative data on the spatial profiles of morphogens, which is becoming increasingly available as a result of recent advances in optical systems and imaging techniques.

Model

Information coding in computer science and developmental biology

The concept of information coding originates from the field of computer science (Fig. 2 A). The coding process consists of two steps: encoding and decoding. Original information (e.g., texts, images, movies) that a sender would like to transfer is converted into binary sequences by the sender's computer based on a rule. This conversion process is called encoding. The binary sequences are transferred to the receiver's computer through a channel, which is followed by their conversion into the information that the sender transferred (i.e., texts, images, or movies) based on another rule. The latter process is called decoding. By designing appropriate rules for encoding and decoding, the information transfer becomes efficient and reliable against noise, such as stochastic flips between 0 and 1, which may arise when information is transferred through channels (20).

Figure 2.

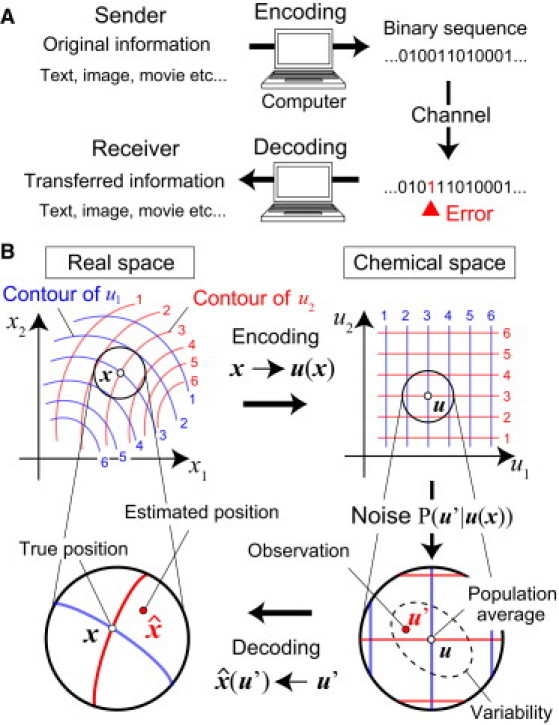
Information coding processes. (A) In information transfer between computers, the original message is converted into a binary sequence by an encoding rule. The sequence is transferred to the receiver's computer through an information channel. Finally, it is converted into the message that the sender transferred by a decoding rule. (B) In morphogenesis, a set of spatial coordinates in a tissue is converted into a set of concentrations of multiple morphogens by an encoding rule, i.e., the spatial profiles of the morphogens, u(x). Cells in the tissue read-out their spatial coordinates from the morphogen concentrations they detect through intracellular dynamics corresponding to a decoding rule. Each contour in real space corresponds to one in chemical space with the same number and color. (See Information Coding in Computer Science and Developmental Biology, and Mathematical Formulation of Positional Information Coding, for details.)

Using the concept of coding in computer science, we can interpret in a similar manner the positioning by morphogens in developmental biology (Fig. 2 B). The original information to be transferred here is the spatial coordinates in a tissue (denoted by a vector x = (x₁, …, x_N) (N = 1, 2, or 3)), and it is converted into a set of morphogen concentrations (u = (u₁, …, u_M) (N ≤ M)) by an encoding rule u(x) (i.e., spatial profiles of morphogens). Biologically, the encoding rule is determined by various factors such as the configuration of morphogen sources, morphogen diffusivity, and organ geometry that specifies the boundary condition (21, 22, 23, 24, 25).

Decoding is the process to read-out morphogen gradients, which is to determine the correspondence between an observed set of morphogen concentrations u′ (the prime symbol indicates the concentration observed by cells) and position $\hat{\mathit{x}}$ or its function $F\left(\hat{\mathit{x}}\right)$ (the caret symbol is used to distinguish from the original information x). If all developmental processes occurred in a deterministic manner without any noises, each cell would detect a unique set of morphogen concentrations depending on the position. The inverse map of the encoding rule u⁻¹(x) is the natural decoding rule, by which each cell would exactly recognize its true position from the observed concentrations regardless of the encoding rule u(x) used.

In the presence of noise, however, the situation is not so simple, because the morphogen concentrations detected by a cell are not unique but fuzzy (see subsection SB in the Supporting Material for assumed origins of the noise). For a fuzzy input, a cell must decide its response. In other words, it must choose a decoding rule, the correspondence between u′ and $\hat{\mathit{x}}$. In terms of statistics, this is an estimation problem, and $\hat{\mathit{x}}$ is the estimated position. We can regard $\hat{\mathit{x}}$ as the mathematical definition of positional information. Because $\hat{\mathit{x}}$ is a random variable, we can measure its precision or ambiguity by its variance or other statistics. Biologically, each decoding rule or an equivalent response is realized by appropriately choosing the structures of signaling networks and parameters for biochemical reactions. We will discuss the biochemical implementation of the decoding rule later.

The reliability of the information transfer depends strongly on the encoding and decoding rules adopted (Fig. 1). In the following section, we mathematically formulate the coding processes for the positioning by morphogens, and derive the best coding rules to achieve the maximum precision of positional information.

Mathematical formulation of positional information coding

Static variability in morphogen spatial profiles is one noise source. The probability that a cell located at x detects morphogen concentration u′ is modeled by a multivariate Gaussian probability distribution P(u′; u(x)), where u(x) is the population average over all embryos. We assume that the variance of the noise is not very large, and that u(x) is time-invariant. The latter is plausible because chemical reactions and diffusion processes are generally much faster than organ growth, and also because changes in morphogen source levels are slow (see subsection SB in the Supporting Material for a more general treatment of noise).

The goodness of coding, which is equivalent to the goodness of estimation or the precision of positional information, is measured in terms of the inverse of the generalized variance of $\hat{\mathit{x}}$, $1/\det \left[\text{Var}\left(\hat{\mathit{x}}\right)\right]$, where $\text{Var}\left(\hat{\mathit{x}}\right)$ is the variance-covariance matrix of $\hat{\mathit{x}}$. Intuitively speaking, $1/\det \left[\text{Var}\left(\hat{\mathit{x}}\right)\right]$ represents how the estimated position concentrates around the true position (see Fig. 3 A). Under plausible statistical assumptions (see subsection SB in the Supporting Material), Cramer-Rao's inequality gives us the upper limit of the precision of positional information for a given encoding rule u(x), as

$$\frac{1}{\det [\text{Var}\left(\hat{\mathit{x}}\right)]}\le \det \left[I\left(\mathit{x}\right)\right],$$ (1)

where I(x) is Fisher information matrix in which component (i,j) is defined as

$$I_{ij}\left(\mathit{x}\right)=\text{E}\left[\left(\frac{\partial \text{log}P}{\partial x_i}\right)\left(\frac{\partial \text{log}P}{\partial x_j}\right)\right].$$ (2)

The upper limit in Eq. 1 is realized when the maximum likelihood (ML) estimate (${\hat{\mathit{x}}}_{ML}$) is adopted as $\hat{\mathit{x}}$ (i.e., ML decoding); thus, ML decoding is the best decoding rule. In the following analysis, we assume ML decoding, and then det[I (x)] indicates the precision of the positional information at position x. When the noise is not large, the precision is approximately given by

$$\det \left[I\left(\mathit{x}\right)\right]=\det \left[D^T{\Sigma }^{-1}D\right],$$ (3)

where D is a M × N morphogen gradient matrix (i.e., D_ij = ∂u_i/∂x_j) and ∑ is the variance-covariance matrix of noises added to u(x). This value strongly depends on the choice of encoding rules, that is, on the spatial profiles of morphogens u(x). Thus, our main purpose in the following analysis is to identify the best encoding rule that maximizes the precision of positional information (det[I (x)]) when the best decoding rule (ML decoding) is adopted (see subsection SC in the Supporting Material for a geometrical interpretation of det[I (x)] maximization).

Figure 3.

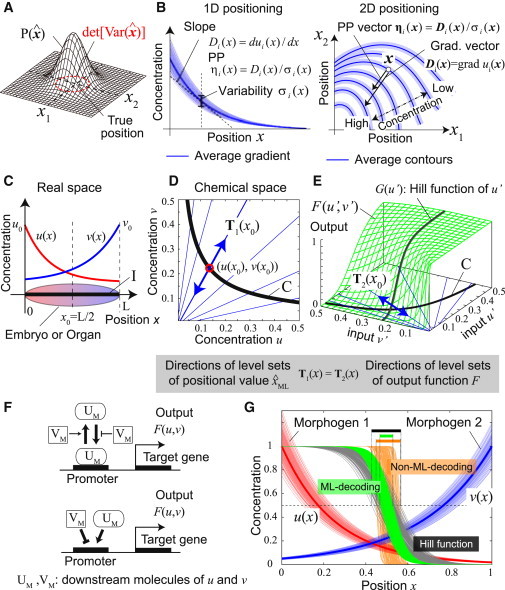
Definitions of some statistics and biochemical implementation of ML decoding. (A) Precision of positional information is defined as the inverse of the generalized variance of the position estimated ($1/\det \left[\text{Var}\left(\hat{\mathit{x}}\right)\right]$) from the morphogen concentrations that each cell detects. $P\left(\hat{\mathit{x}}\right)$ is the probability distribution of $\hat{\mathit{x}}$. (B) PP vector of morphogen i at position x, η_i (x), is defined as the gradient vector divided by the magnitude of noise, i.e., η_i (x) = (grad u_i(x))/σ_i(x). In one-dimensional positioning (left), it is just a scalar whose sign indicates the direction of the gradient. (C) One-dimensional-positioning by two morphogens with exponential gradients, u(x) = u₀ exp(−αx) and v(x) = v₀ exp(β(x− L)). The values u₀, v₀, and L are the source levels of two morphogens and embryo size. Parameters: (u₀, v₀, L, α, β) = (1,1,1,4,3). (D) Interval I in the real space is mapped into curve C in the chemical space by map (u(x), v(x)). (Blue lines) Directions of the contours of positional values in the chemical space, T₁(x) (see the text for the definition of T₁(x)). (E) A cellular response F(u′,v′). (Blue lines) Directions of dF = 0, T₂(x) = (−∂F/∂v, ∂F/∂u), at each point on curve C. ML decoding can be approximately achieved when T₁(x) ∝ T₂(x). Functions and parameters: F(u′,v′) = u′^h/(u′^h + (Kv′^1/S)^h), G(u′) = u′^h/(u′^h + K₀^h), (h, K, S, K₀) = (4,exp(−0.7/1.1), 1.1, exp (−2)). (F) Biochemical interpretation of Eqs. 8a and 8b. (Top) Promoter regulation of a target gene by a downstream molecule of u (U_M) in which the binding (or unbinding) between U_M and the promoter is repressed (or enhanced) by a downstream molecule of v (V_M). (Bottom) Competitive regulation of a promoter in which U_M and V_M work as an activator and a repressor, respectively. (G) An example of cellular responses. (Thin red and blue curves) Embryo-to-embryo variability of the gradients of two morphogens over 150 embryos. As a noise source, we assumed the variability of morphogen source levels among embryos that obeys two-variable Gaussian distribution with σ₁ = σ₂ = 0.1 and ρ₁₂ = 0.5 (see (4, 19) for the magnitude of noise in real biological systems). (Green and gray curves) Outputs of different embryos when ML-response (F(u′,v′)) and ordinary Hill equation (G(u′)) are adopted, respectively. Parameters for F(u′,v′) and G(u′) are the same as Fig. 3E. Note that the values of both output functions are 0.5 at the center (x = L/2). (Orange curves) An example of the outputs when a non-ML decoding is adopted (where the output function is the same as for the case of green curves but the parameter S(= 0.1) is different from it). ML decoding achieves the minimum variation of the output.

Positioning performance vector

To aid in our understanding of the coding designs discussed in the following sections, we introduce a quantity that we call the positioning performance (PP) vector. The PP vector of morphogen i (denoted by η_i (x)) is defined as the morphogen's gradient vector divided by the magnitude of the noise at a focal location x (see Fig. 3 B):

$${\mathit{\eta }}_{\text{i}}\left(\mathit{x}\right)=\frac{\text{grad}{u}_i\left(\mathit{x}\right)}{{\sigma }_i\left(\mathit{x}\right)}.$$ (4)

In one-dimensional positioning, the PP vector becomes a scalar whose sign indicates the gradient direction (we called this scalar “directional-PP” in the previous study (19)). We call the magnitude of PP vector ‖η_i (x)‖ the PP of the morphogen i. The PP of a morphogen is interpreted as the precision of positioning along direction η_i (x) provided by morphogen i. This can be understood easily by considering the one-dimensional positioning by a single morphogen. In that case, det[I(x)] = I(x) ≅ (du/dx)²/σ² = η(x)² holds, and thus PP is a natural measure of the precision of positioning along a single axis as has been adopted by some studies (4, 19). The PP (and the PP vector) is the generalized quantity necessary for evaluating multidimensional positioning. Note that the PP becomes larger as the morphogen gradient becomes steeper and the noise smaller.

Using PP vectors, the Fisher information matrix is rewritten as I(x) ≅ E^T C⁻¹ E and thus the precision of positional information is given by

$$\det \left[I\left(\mathit{x}\right)\right]=\det \left[E^T{C}^{-1}E\right],$$ (5)

where C is the correlation coefficient matrix for the concentration noises ∑ (i.e., C_ii = 1 and C_ij = ρ_ij (i ≠ j)), and E is a matrix whose component is η_ij ≡ (∂u_i/∂x_j)/σ_i.

PP may, in general, depend on the position, but the dependence may not be very large. For example, PP of Bicoid, a major morphogen in Drosophila development, is almost constant within the spatial range in which Bicoid effectively works (see (4, 19) and see subsection SD in the Supporting Material).

Biochemical implementation of ML decoding

We here explain how to implement ML decoding biochemically. As an example, let us think of one-dimensional positioning by two morphogens (Fig. 3 C). Let us suppose that the spatial profiles of morphogens vary among embryos due to the variability of the morphogen source levels. Then the observed concentrations (u′,v′) by the cell located at x₀ is distributed around its average (u(x₀), v(x₀)). When the variability of the source levels is not very large, the ML decoding (i.e., a correspondence between (u′,v′) and estimated position ${\hat{x}}_{ML}$) for cells located around x₀ is approximately given by

$${\hat{x}}_{ML}\left(u^{\prime },v^{\prime }\right)-x_0=\frac{w_1}{du/dx}\left(u^{\prime }-u\left(x_0\right)\right)+\frac{w_2}{dv/dx}\left(v^{\prime }-v\left(x_0\right)\right),$$ (6)

where w_i = (η_i² – ρη₁η₂)/(η₁² + η₂² – 2ρη₁η₂) (19). The values η_i and ρ are PP vectors (or directional-PP) and the correlation coefficient of the variability of the two morphogen source levels, respectively. In the following analysis, we assume that those values are spatially invariant constants (see subsection SD in the Supporting Material).

Equation 6 indicates that any sets of observed concentrations (u′,v′) satisfying ${\hat{x}}_{ML}\left(u^{\prime },v^{\prime }\right)-x_0=0$ define the contour of the positional value equivalent to x₀ in the chemical space. Its direction at (u(x₀), v(x₀)) is given by T₁ = (−w₂/(dv/dx), w₁/(du/dx)) (Fig. 3 D).

On the other hand, cellular responses such as the expression levels of target genes are given as functions of (u′,v′). For simplicity, we here consider a scalar function, F(u′,v′). Along the direction T₂ = (−∂F/∂v, ∂F/∂u), which is perpendicular to gradF = (∂F/∂u, ∂F/∂v), there is no change of F (i.e., dF = 0). Therefore, if T₂ is parallel to T₁, F(u′,v′) can be regarded as an ML response:

$${\mathbf{T}}_2\propto {\mathbf{T}}_1\iff \frac{\partial F}{\partial u}u+\frac{w_1\beta }{w_2\alpha }\frac{\partial F}{\partial v}v=0.$$ (7)

A class of functions, F(u,v) = F(v^1/S/u) with S = w₂β/w₁α, satisfies Eq. 7. For example, the following generalized-Hill equation is one of the functions included in that class (Fig. 3 E),

$$F\left(u,v\right)=\frac{1}{{\left(\frac{K{v}^{1/S}}{u}\right)}^h+1}=\frac{u^h}{u^h+{\left(K{v}^{1/S}\right)}^h},$$ (8a)

where h and K are a Hill coefficient and a constant, respectively. Compared with the ordinary Hill equation, G(u) = u^h/(u^h + K₀^h), the dissociation constant in Eq. 8a, Kv^1/S, depends on v. Because Eq. 8a is not defined at (u,v) = (0,0), we may consider the following function instead of Eq. 8a:

$$F\left(u,v\right)=\frac{u^h}{\left(u^h+{\left(K{v}^{1/S}\right)}^h+\epsilon \right)}\left(\epsilon <<1\right).$$ (8b)

A biochemical interpretation of Eq. 8a is the promoter regulation of a target gene by the signal of u, in which the binding (or unbinding) between the signal and the promoter is repressed (or enhanced) by the signal of v (Fig. 3 F). An interpretation of Eq. 8b is the competitive regulation of a promoter in which the signals of u and v work as an activator and a repressor, respectively.

Fig. 3G shows an example of cellular responses. In this example, the purpose is the precise recognition of position around the center of an embryo. The thin red and blue curves show embryo-to-embryo variability of the gradients of two morphogens. The green curves are the outputs over embryos calculated by using Eq. 8a. The variability of the output is clearly smaller than that of the output calculated by the ordinary Hill equation G(u), shown by the gray curves. The orange curves with larger variability shows the output calculated by Eq. 8a but with parameter S ≠ w₂β/w₁α, which gives an example of non-ML decoding. This shows that the precision of spatial recognition is not improved even though multiple information sources are available if appropriate response functions and parameters are not chosen.

Similar discussions are possible for multidimensional positioning by multiple morphogens by replacing Eq. 6 with the following Eq. 9:

$${\hat{\mathit{x}}}_{ML}-\mathit{x}={\left[D^T{\Sigma }^{-1}D\right]}^{-1}{D}^T{\Sigma }^{-1}\left({\mathit{u}}^{\prime }-\mathit{u}\left(\mathit{x}\right)\right).$$ (9)

Local and global precision of positional information

Our goal is to elucidate the optimal encoding rule (i.e., the optimal spatial profile of morphogen concentrations u(x) to maximize the precision of positioning). The precision is measured by det[I (x)] at each location x. Its value depends on x for a given u(x), and thus det[I (x)] is a local quantity. Eq. 5 indicates that det[I (x)] is determined by the relative orientation of different morphogen gradient vectors at a focal location for a given set of PPs (‖η_i (x)‖) and noise correlation (C) (see also Results, below). Because the curvature radius of contours of morphogen concentrations is generally much larger than the scale of each cell size, the relative orientation of the gradient vectors hardly changes around the location. Therefore, the local optimum for a location is also approximately optimum for its neighboring locations.

On the other hand, when we consider more-global situations (i.e., the scale much larger than the curvature radius of contours of morphogen concentrations), we need a global quantity to evaluate the precision of positional information in the whole region of a target tissue. The weighted average of det I[(x)] over a focal region Ω (denoted by Ψ_Ω) is a candidate of such a quantity:

$${\Psi }_{\Omega }=\frac{1}{|\Omega |}{\int }_{\Omega }W\left(\mathit{x}\right)\det \left[I\left(\mathit{x}\right)\right]d\mathit{x},$$ (10)

where |Ω| is the volume of the focal region, and W(x) is a weighting function. To achieve normal development, higher precision may be required in some parts (e.g., an undifferentiated region) than in other parts (e.g., an already differentiated region) of the tissue. As an example of the weighing function, we may set the weight as W(x) = 1 for the undifferentiated region and W(x) = 0 for the already differentiated region (see Morishita and Iwasa (18) as a biological application).

In the following analysis, we mainly focus on encoding rules that maximize the local precision det[I (x)]. But the local rules provide a basis for the calculation of global precision Ψ_Ω. We will discuss how the local rules relate to conditions for maximizing Ψ_Ω. Especially, in one-dimensional positioning, we will see that optimal encoding for a local region is consistent with that in a global sense if the spatial dependences of η_i (x) and ρ_ij are not large. On the other hand, in two-dimensional or three-dimensional positioning, to derive general rules for maximizing the global precision is much more difficult because we need much information about geometries to calculate Ψ_Ω such as organ morphologies, shapes and spatial arrangement of morphogen sources. But once we fix the information we will be able to evaluate the global optimality of encoding by calculating the spatial dependence of det I[(x)]. We will illustrate this procedure by a biological example later (see Orthogonal Morphogen Gradient Vectors is the Best Encoding in the Absence of Informational Redundancy, below, and Fig. 6).

Figure 6.

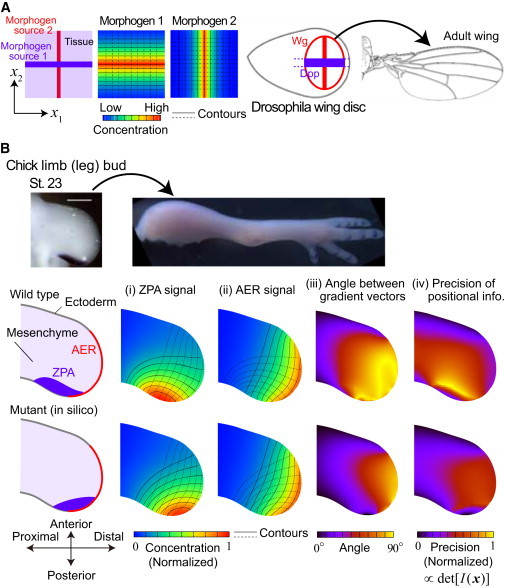
Spatial dependence of local precision and global optimality of encoding in two-dimensional positioning by two morphogens. (A) (Left) When the two morphogens have linear sources crossing orthogonally with each other, their gradient vectors also cross orthogonally everywhere in a tissue. (Right) This idea appears to be adopted in the case of Dpp and Wg in the wing disk during the development of Drosophila embryo. (B) When the shapes of morphogen sources and tissue boundaries have curvature, the contours of morphogen concentrations also become curved. The spatial pattern of the angle between gradient vectors strongly depends on those shapes and the arrangement of locations of morphogen sources. In the vertebrate limb development (Top, chick limb bud), the angle between the gradient vectors of two signals from typical information sources, ZPA and AER, is nearly orthogonal in a wide range of the tissue for the wild-type (middle), whereas the orthogonality is lost remarkably if an information source is perturbed (bottom). This implies that the encoding is optimized to improve the global precision Ψ_Ω (see Eq. 10). (Middle and bottom panels) In panels (i) and (ii), we calculated the spatial patterns of ZPA and AER signals by assuming diffusion and linear degradation, ∂u_i/∂t = DΔu_i − γu_i with zero-flux boundary condition except for the proximal end for which the signal level is assumed to be zero. We also assumed constant influx from ZPA and AER. The shapes of contours do not depend on parameters (i.e., diffusion constant (D), degradation rate (γ), and the levels of signal influx). Real organ geometry was used by tracing the picture shown in the top panels. In panel (iv), σ_i (x) ∝ u_i (x) was assumed, where the proportionality constant is independent of x.

Results

Optimal encoding in one-dimensional positioning (N = 1)

We first consider encoding rules for one-dimensional positioning by multiple morphogens. We here assume that morphogen sources are located at either end of a line segment, representing a one-dimensional organ (or embryo, egg, etc.). Then, each encoding rule is defined by the combination of the source locations. For M morphogen species, there are 2^M possible source location combinations in total.

If the noises associated with the different morphogens are uncorrelated with each other, the situation is quite simple: all of the encoding rules have the same performance, because the precision is just the sum of the squared PP of each morphogen ($I\left(x\right)={\sum }_i{\eta }_i^2$). If the different morphogens have the same PP, then the precision is proportional to the number of morphogen species, I(x) ∝ M (see subsection SE in the Supporting Material).

In contrast, when morphogens share signaling pathways relating to, for example, their synthesis, degradation, or modification, the noise associated with different morphogens are likely to be correlated (19). Then, the precision can be improved by choosing appropriate source arrangements for a given set of correlation coefficients. In the following analysis, we summarize the results on the best encoding for given correlations ρ_ij and PPs |η_i| for M species of morphogens.

Two morphogens

In the case of two morphogens, I(x) = (η₁² + η₂² – 2ρη₁η₂)/(1 − ρ₁₂²). Thus, the better source arrangement to improve the precision at x in an embryo is determined only by the sign of the noise correlation ρ₁₂ (x). For positive correlation (ρ₁₂ > 0), oppositely directed gradients (i.e., η₁η₂ < 0) are better than the alternative, and vice versa for negative correlated noise (Fig. 4 A). The probability distribution of the estimated position, $P\left(\hat{x}\right)$, becomes sharper (i.e., a more reliable information transfer is achieved) when the relative directions of the gradients is appropriately chosen.

Figure 4.

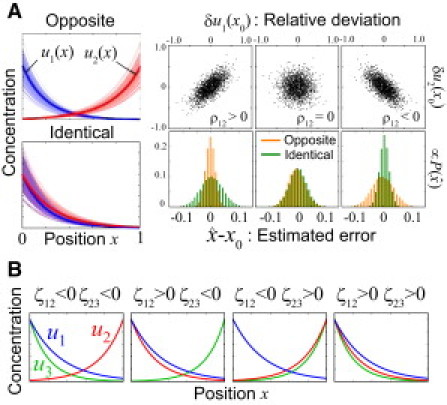
Optimal encoding design for one-dimensional positioning. (A) Optimal encoding for two morphogens (M = 2). For positively correlated noises, the oppositely directed gradients are better than identically directed gradients, and vice versa for negatively correlated noises. (Left) (Blue and red curves) Variability of morphogen gradients over 150 embryos. (Bold curves) Average profiles are u₁(x) = exp(−5x), u₂(x) = exp(4(x − 1)) (upper left), and u₂ (x) = exp(−4x) u₂ (x) = exp(−4x) (lower leftt). As a noise source, we assumed the variability of the morphogen source levels that obeys two-variable Gaussian distribution, where the SD was set as σ₁ = σ₂ = 0.2. (Upper right) When the variability of the morphogen source levels are correlated with each other, the concentrations of the two morphogens (u₁′, u₂′) observed at any position x₀ are also correlated with each other, where the correlation coefficient is denoted by ρ₁₂. The upper right panels show the distributions of the relative deviations of concentrations from their averages at x₀, δu_i(x₀) ≡ u′_i/u_i (x₀) −1. ρ₁₂ = 0.7 (left) and ρ₁₂ = −0.7 (right). (Lower right) The histograms (∝$P\left(\hat{x}\right)$) of the estimated error relative to the organ size. It becomes sharper when the appropriate choice of relative directions of gradients is made in the presence of correlation (ρ ≠ 0). (B) Optimal encoding for three morphogens when inequality |ζ₁₂| > |ζ₂₃| > |ζ₃₁| holds (see the text for the definition of ζ_ij). The direction of a morphogen gradient is fixed as u₁ (x) = exp(−5x). The directions for the rest two are u₂ (x) = exp(−4x) or u₂ (x) = exp(4(x − 1)) for the second morphogen, and u₃ (x) = exp(−3x) or u₃ (x) = exp(3(x − 1)) for the third morphogen. Parameters: (|η₁|, |η₂|, |η₃|) = (50, 40, 30) for PP values and (σ₁, σ₂, σ₃, ρ₁₂, ρ₂₃, ρ₃₁) = (0.1, 0.1, 0.1, ±0.5, ±0.5, 0) for the variability of morphogen source levels.

We note that this encoding rule is for maximizing the precision of positional information at a focal location x. But it is also the best for maximizing the precision at any locations (thus, for maximizing global precision, Ψ_Ω (see Eq. 10)) if ρ₁₂ does not depend on x (see subsection SD in the Supporting Material and (19)).

Three or more morphogens

The best source arrangement in the case of three or more morphogens depends not only on the signs of the noise correlations but also on the PP of each morphogen. For each morphogen pair (i, j), we can calculate the impact of the relative directions of the gradients of morphogens i and j on the precision (denoted by |ζ_ij|). For example, in the case of three morphogens (M = 3), ζ_ij = (ρ_jkρ_ki −ρ_ij)|η_iη_j| (k ≠ i, j) hold (see subsection SF in the Supporting Material). The best encoding to maximize the precision of positional information at a location is uniquely determined by the combination of the signs (sgn) of ζ for the two pairs with large impact at the location (e.g., sgn(ζ₁₂) and sgn(ζ₂₃); Fig. 4 B). We should note again that this encoding design is also the best for maximizing global precision if the impact |ζ_ij| (i.e., ρ and |η|) can be regarded as constant. Similarly, better encoding for M > 3 is realized by considering the relative source locations of morphogen pairs with larger impact (see subsection SF in the Supporting Material).

Optimal encoding in multidimensional positioning (N = 2 or 3)

In multidimensional positioning, the spatial pattern of morphogen concentrations can be characterized by the relative directions of morphogen gradient vectors at each location (Fig. 5). Thus, infinitely many ways of encoding are possible, which is a major difference from one-dimensional positioning.

Figure 5.

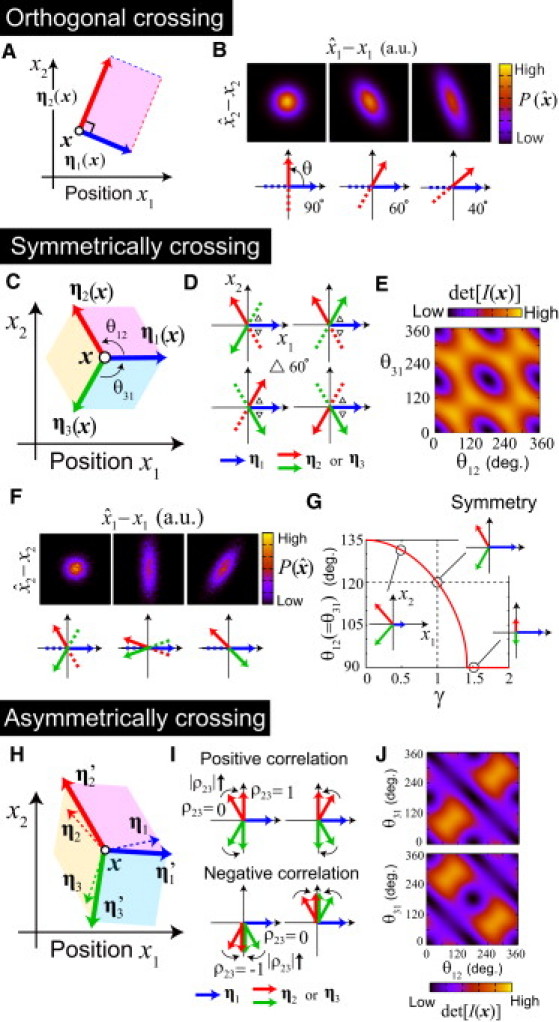
Optimal encoding designs for two-dimensional positioning. (A and B) Orthogonal morphogen gradient vectors is the optimal encoding in the absence of informational redundancy (M = N). In this case, ML decoding (${\hat{\mathit{x}}}_{ML}$) becomes the natural decoding (u⁻¹ (x)). Distribution of $P\left(\hat{\mathit{x}}\right)$ was calculated for the case with grad u₁ (x) = (1,0), grad u₂ (x) = (cos θ, sin θ), σ₁ (x) = σ₂ (x), and ρ₁₂ (x) = 0 at a focal location x. $P\left(\hat{\mathit{x}}\right)$ is the sharpest for the orthogonal crossing. (C–J) Encoding designs in the presence of informational redundancy (M > N). When different morphogens have the same PP and their noises are independent, (C) symmetrically crossing gradient vectors gives the best encoding. (D) Eight possible encoding rules to achieve maximal precision, and (E) dependence of the precision and (F) that of $P\left(\hat{\mathit{x}}\right)$ on the angles between gradient vectors in the case of (N,M) = (2,3). (E) The value det[I(x)] was calculated for the case with η₁ = (1,0), η₂ = (cos θ₁₂, sin θ₁₂), and η₃ = (cos (−θ₃₁), sin (−θ₃₁)). (F) $P\left(\hat{\mathit{x}}\right)$ is shown for the cases with (θ₁₂,θ₃₁) = (120°, 120°) (left), (θ₁₂,θ₃₁) = (160°, 160°) (middle), and (θ₁₂,θ₃₁) = (135°, 45°) (right). When different morphogens have different PP or when their noises are correlated, (H) the best encoding is no longer the symmetrical arrangement. (G) In the case of ‖η₁‖ = γ ‖η₂‖ = γ ‖η₃‖ and ρ₁₂ = ρ₂₃ = ρ₃₁ = 0, for γ >> 1, the maximum precision is achieved when the angle between the gradient vectors of morphogens 1 and 2 (or 3) is 90°; for γ << 1, the best encoding is when the angle of gradient vectors of morphogens 2 and 3 approaches 90°. The relative orientations of gradient vectors are shown for the cases of γ = 0.5, 1.0, 1.5. (I) When ‖η₁‖ = ‖η₂‖ = ‖η₃‖, ρ₁₂ = ρ₃₁ = 0, and ρ₂₃ ≠ 0, the optimal angle between the gradient vectors of morphogens with uncorrelated noises approaches 90° as |ρ₂₃| increases. (J) Dependence of the precision on the angles in the case of ρ₂₃ = ±0.8. In the calculation of det[I(x)], we assume η₁ = (1,0), η₂ = (cos θ₁₂, sin θ₁₂), and η₃ = (cos(−θ₃₁), sin(−θ₃₁)).

Orthogonal morphogen gradient vectors is the best encoding in the absence of informational redundancy

When the number of morphogens (M) is the minimum needed for N-dimensional positioning (i.e., M = N), there is no informational redundancy. In this case, the precision of positional information at each location is proportional to det [E]², i.e., the squared area spanned by two PP vectors in two-dimensional positioning, or the squared volume by three PP vectors in three-dimensional positioning (Fig. 5 A). In both cases, the precision is maximized when the gradient vectors are orthogonal, regardless of the PP values and the noise correlations: $P\left(\hat{\mathit{x}}\right)$ becomes sharper as the angle made by the gradient vectors approaches 90° (Fig. 5 B).

In our previous study, in which the ambiguity of positional information was measured by the information entropy for $P\left(\hat{\mathit{x}}\right)$ (18), we also found orthogonal gradient vectors to be the best encoding. (See subsection SG in the Supporting Material for the relationship between information entropy and the Fisher information matrix.)

Intuitively, it may seem trivial that the orthogonal crossing of the gradient vectors gives the maximum precision at a focal point (i.e., local precision det I[(x)]) in a tissue. In many situations, however, achieving the orthogonal crossing globally (i.e., in a wide region in the tissue) may not be easy. A straight way to achieve it is to adopt linear sources of morphogens crossing orthogonally each other (Fig. 6 A). Then orthogonal crossing of gradient vectors is achieved everywhere. In the wing disk during Drosophila development, this idea appears to be adopted. The morphogen sources of two typical morphogens, Decapenta-plegic (Dpp) and Wingless (Wg), is crossing orthogonally (Fig. 6 A). Because quantitative analysis of spatial profiles of Dpp and Wg is advanced (21, 26), it will be possible in the near future to evaluate the goodness of encoding by examining the spatial dependences of η_i (x) and det I[(x)].

In contrast, when the shapes of morphogen sources and tissue boundaries have large curvature, the contours of morphogen concentrations also become curved. How much and where the orthogonality between morphogen gradient vectors is achieved strongly depends on those shapes and the arrangement of locations of morphogen sources. For example, in the limb development of vertebrates such as chicks and mice, typical information sources—such as the zone of polarizing activity (ZPA) whose molecular substance is Sonic hedgehog (Shh), and the apical ectodermal ridge (AER) from which Fibroblast growth factor (Fgf) and Wnt are released—have curved shapes (Fig. 6 B). We calculated the spatial profiles of ZPA and AER signals by assuming simple diffusion and linear degradation of the diffusive chemicals.

For the arrangement of morphogen sources in the wild-type, the angle between the two gradients is nearly orthogonal in a wide range of tissues, leading to higher precision of positional information globally. On the other hand, when the location of one morphogen source (ZPA) is perturbed from the original position, the orthogonality is lost remarkably in a wide range (bottom panels in Fig. 6 B). Because the anterior-posterior information provided by the ZPA signal during early phases of limb development is critical for the establishment of different digit identities (27), this result implies that better coding design is adopted to realize robust positioning—done by improving the global precision Ψ_Ω in Eq. 10 against the variability of spatial profiles of morphogen concentrations (see also our previous study (18)).

The best encoding in the presence of informational redundancy (M > N)

As with one-dimensional positioning, informational redundancy can improve the precision of positional information if encoding rules appropriate for the given noise are chosen. In this case, the precision of two-dimensional (or three-dimensional) positioning is the sum of squared areas (or volumes) spanned by all possible _MC₂ pairs of {η′_i, η′_j} (i < j) (or _MC₃ triplets of {η′_i, η′_j, η′_k} (i < j < k)), where η′_α is the weighted linear sum of the PP vectors, ${\mathit{\eta }}_{\alpha }^{\prime }={\sum }_k{C}_{\alpha k}^{-1/2}{\mathit{\eta }}_k$, and C^−1/2 is a matrix defined as C^−1/2C^−1/2 = C⁻¹. This is a natural extension of the case without informational redundancy (see Fig. 5, C and H). However, orthogonal gradient vectors may not represent the best encoding to maximize the precision.

We mainly examine two-dimensional positioning in detail because the visual understanding of results is easier. After that, the three-dimensional case is discussed. The two-dimensional results can help us understand intuitively the best encoding rule in three-dimensional positioning.

Symmetrically crossing of gradient vectors is the best encoding when different morphogens have the same PP and their noises are independent of each other

For uncorrelated noises, η′_i = η_i holds. Thus, the precision is the sum of the squared areas spanned by all possible pairs of PP vectors (Fig. 5 C). Further, if different morphogens have the same PP, the precision is maximized when the relative directions of the morphogen gradients are arranged symmetrically. For example, in the case of M = 3, the best encoding is to arrange the gradient vectors so that the angles between each pair of adjacent vectors is 120° (see Fig. 5, D–F, and see subsection SH in the Supporting Material for details). In general, when the best encoding is adopted, the precision is proportional to the square of the number of morphogen species, that is, det[I(x)] ∝ M² (see subsection SE in the Supporting Material).

Asymmetrically crossing gradient vectors

When different morphogens have different PPs or when the noises associated with them are correlated, the best encoding may shift from the symmetric arrangement. Here, we show the two simplest examples with M = 3:

In the first case, the PP of one of the three morphogens is larger or smaller than the PPs of the other two (e.g., ‖η₁‖ = γ ‖η₂‖ = γ ‖η₃‖), and the noises associated with the three morphogens are uncorrelated (Fig. 5 G). When the PP of morphogen 1 is much larger (γ >> 1), the maximum precision is achieved when the angle between the gradient vectors of morphogens 1 and 2 (or 3) is 90°. When the PP of morphogen 1 is much smaller (γ << 1), the best encoding is when the angle of gradient vectors of morphogens 2 and 3 approaches 90°.

In the second case, the three morphogens have the same PP and only ρ₂₃ is nonzero (Fig. 5, I and J). As the magnitude of correlation |ρ₂₃| increases, the optimal angle between the gradient vectors of the morphogens with uncorrelated noises (i.e., 1 and 2 (or 3)) approaches 90°. A typical characteristic of this case is that the preferred relative angle between the gradients of a pair of morphogens with correlated noises (i.e., 2 and 3) depends on the sign of the correlation: when the correlation is positive an obtuse angle (i.e., oppositely directed) is preferred, and when it is negative an acute angle (identically directed) is preferred. This result is consistent with one-dimensional positioning with correlated noises (see the results of one-dimensional case, above). Tendencies similar to these results were also observed for more general situations.

The upper limit of the precision increases as the magnitude of correlation increases, indicating that the precision can be improved by increasing the correlation of noises, as well as by increasing the informational redundancy (see subsection SI in the Supporting Material).

Three-dimensional positioning

Analytical solution of the best encoding rule for three-dimensional positioning is much more complicated than the two-dimensional solution. Therefore, we numerically examined some specific cases, and confirmed that conditions to improve the precision of positional information in three-dimensional positioning are similar to those in the two-dimensional case:

• 1.A symmetric arrangement of morphogen gradients gives the best encoding when the different morphogens have the same PP and their noises are independent of each other, where det[I(x)] ∝ M³ holds (see subsection SE in the Supporting Material).
• 2.Increasing the magnitude of the correlation between noises associated with morphogens and increasing informational redundancy are both possible ways to improve the precision of positional information.

Summary and Discussion

Summary of this study

In this study, we mathematically formulated coding processes of positional information and defined key concepts such as encoding and decoding. The goodness of coding, i.e., the reliability of positioning, is determined by the choice of encoding and decoding rules. According to Cramer-Rao's inequality, the best decoding rule is ML decoding. Then the precision of positional information at a focal location x can be measured by det[I(x)]. We determined mathematically the best encoding rules to maximize det[I(x)] for several different situations. We also discuss the relationship between local (det[I(x)]) and global (Ψ_Ω) precision, and present the biochemical implementation of ML decoding by showing some examples.

Suggestions for data analysis: a possible procedure to validate coding optimality

Deriving the best coding design is useful because it provides a criterion by which to evaluate experimental data. Fig. 7 shows a possible procedure of data analysis to validate coding optimality formulated in this study (see subsection SJ in the Supporting Material for details). Through the procedure, we will be able to quantitatively answer some parts of the following questions: How is good coding adopted in real biological systems, and when, where, and to what extent does each morphogen contribute to positioning?

Figure 7.

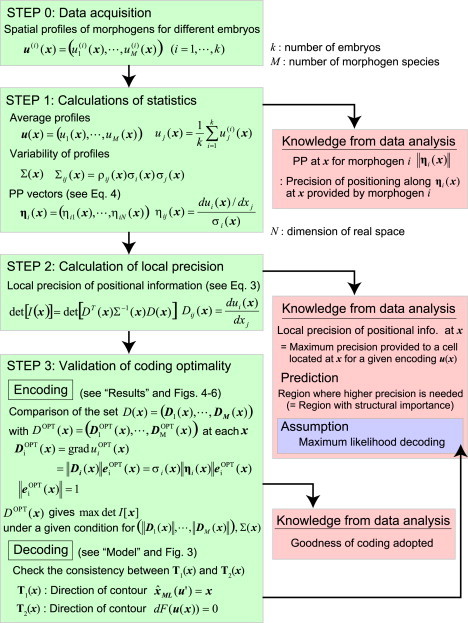
Possible procedure of data analysis to validate coding optimality. This procedure is a possible way to validate coding optimality formulated in this article. Through the procedure, we will be able to quantitatively answer some parts of the questions we proposed in this article. (See subsection SJ in the Supporting Material for details.)

Future works

In our analysis, ML decoding was assumed in discussing the best encoding rules. However, if there are constraints in realizing decoding mechanisms by biochemical reactions, the best encoding may change according to the choice of decoding rule. Considering such constrained situations, and discussing the evolution of a pair of encoding and decoding mechanisms, are interesting and important topics for future work.

Further, in this study, optimal coding rules are derived for static situations, i.e., the tissue growth and the changes of average spatial profiles of morphogen concentrations are neglected. This quasiequilibrium assumption may be a good approximation in some situations. However, to understand more dynamic aspects of organ morphogenesis, we need to extend the mathematical framework developed in this study to a nonsteady version, i.e., a design of space-time and cross-stage information coding. It is, of course, a big challenge but is a very important issue not only for theoretical interest but also for interpreting the large amount of spatiotemporal information about molecules, geometries, and even mechanics that will be available in the near future.

Understanding robust coding of space-time information will also be important in the field of synthetic developmental biology. The main focus of research in current synthetic biology is the construction of genetic circuits within cells (28). However, more-advanced applications will require the regulation of the spatial structures created by multicellular systems. Proposing the design of space-time coding will provide useful insights into this problem.

Editor: Andre Levchenko.