Kinetics of Nanochain Formation in a Simplified Model of Amelogenin Biomacromolecules

Abstract

We show that the kinetics of nanochain formation of amelogenin molecules is well described by a combination of translational and rotational diffusion of a simplified anisotropic bipolar model consisting of hydrophobic spherical colloid particles and a point charge located on each particle surface. The colloid particles interact via a standard depletion attraction whereas the point charges interact through a screened Coulomb repulsion. We study the kinetics via a Brownian dynamics simulation of both translational and rotational motions and show that the anisotropy brought in by the charge dramatically affects the kinetic pathway of cluster formation and our simple model captures the main features of the experimental observations.

Introduction

The self-assembly of colloidal particles and globular proteins with surface heterogeneities into various desired structures is an important area of current research of chemical particle synthesis and biological systems, wherein the inhomogeneity (such as an amphiphilic group and a residual group) plays a crucial role, more specifically in the kinetic pathway of nonequilibrium cluster formation and eventually impacts on the stabilized crystal structures. Examples include Janus particles and DNA-coated colloidal particles that may lead to the next generation of building blocks of new materials and have potential applications in fabricating photonic crystals, targeted drug delivery, and electronic equipment (1, 2, 3, 4).

Another interesting example is amelogenin, the chief hydrophobic protein with a hydrophilic 25-amino-acid C-terminus in nature. Amelogenin is involved in the mineral deposition and has been postulated to fulfill major structural roles during highly organized ribbonlike carbonated apatite crystals formation in enamel development, which is an unusual case in biomineralization (5). Recent experiments show that the self-assembly of amelogenin protein into nanospheres is the key factor in controlling elongated and oriented growth of carbonated apatite crystals, and the organized assembly of nanospheres into collinear arrays (chains) is critical at the initial stage of mineral deposition (6, 7, 8). The experiments also revealed that the hydrophilic C-terminus is essential for this hierarchical self-assembly of amelogenin, and cleaved amelogenin lacking C-terminus fails to conduct such an assembly under the same conditions.

Model and Method

In this article, we present a coarse-grained model of amelogenin and explain how the nanochain forms through self-assembly. The amelogenin molecule is hydrophobic with a charged hydrophilic tail. Our model describes this in a simplified way, representing the monomer as a spherical molecule, with the charged hydrophilic tail replaced by a single tethered point charge located on the surface of the molecule. We make this generic bipolar model specific to the amelogenin case by choosing the parameters for our model based on the experimental study of amelogenin (6). Using Brownian dynamics simulations, we investigate the static and dynamic properties of the self-assembly process. We show that the anisotropy brought by the charge dramatically alters the kinetic pathway of cluster formation, comparing to the isotropic case in which there is no charge (9). Our simple model captures the main features of the experimental observations in chain structure formation.

In these studies of the amelogenin assembly process, one typically adds salt and a precipitant such as polyethylene glycol (PEG). Although PEG-protein interactions are quite complicated (10), we model this as a depletion interaction using the well-known Asakura-Oosawa (AO) potential, plus a repulsive hard-core-like interaction, depending on the center-center distance between spherical particles, U_c(r^c_ij) = U_AO(r^c_ij) + U_hc(r^c_ij), where

$$\frac{U_{AO}\left(r_{ij}^c\right)}{kT}=\{\begin{array}{rr}\hfill {\varphi }_p{\left(\frac{r_c}{\xi }\right)}^3\left[\frac{3r_{ij}^c}{2r_c}-\frac{1}{2}{\left(\frac{r_{ij}^c}{r_c}\right)}^3-1\right],& \hfill r_{ij}^c<r_c\\ \hfill 0,& \hfill r_{ij}^c>r_c.\end{array}$$ (1)

The cutoff range r_c ≡ 1 + ξ, where ξ is the size ratio between a PEG coil and a colloidal amelogenin particle that controls the range of the depletion interaction, and ϕ_p is the value of the PEG volume fraction that controls the strength of the interaction described by the absolute value of the minimum potential depth U_m ≡ |U_min| (11, 12). The hard-core potential is given by

$$\frac{U_{hc}\left(r_{ij}^c\right)}{kT}={\left(r_{ij}^c\right)}^{-\alpha }.$$ (2)

We set α = 36, because the values of α < 36 have been reported to lead to anomalies when a mimic of the hard-core potential is required in the potential (13, 14). The point charges interact with each other through a screened Coulomb potential,

$$U_p\left(r_{ij}^p\right)=\frac{\epsilon }{r_{ij}^p}\text{exp}\left(-\frac{r_{ij}^p}{{\lambda }_D}\right),$$ (3)

in which the magnitude is controlled by ε and the range is controlled by Debye screening length λ_D, and varies in the simulations. We find that the early morphology of the self-assembly is more sensitive to the size of λ_D rather than to the value of ε. These Coulomb charges exert torques on adjacent molecules and hence produce a rotational motion of the molecules that is included in our Brownian equations of motion, which are given as

$$m{\ddot{\overrightarrow{r}}}_i=-\overrightarrow{\nabla }\left(U_i^c+U_i^p\right)-{\Gamma }_t{\dot{\overrightarrow{r}}}_i+{\overrightarrow{W}}_i\left(t\right),$$ (4)

$$I{\dot{\overrightarrow{\omega }}}_i={\overrightarrow{\tau }}_i-{\Gamma }_r{\overrightarrow{\omega }}_i+{\overrightarrow{W}}_i^{\prime }\left(t\right),$$ (5)

where m, I, ${\overrightarrow{r}}_i$, ${\overrightarrow{\omega }}_i$, and ${\overrightarrow{\tau }}_i$ are the mass, moment of inertia, position vector, angular velocity, and torque, respectively, of the i^th colloidal particle. The mass of the point charge is ignored in this model. Γ_t = 6πηr (Γ_t = 8πηr³) is the translational (rotational) friction coefficient, where r is the radius of monomer and η the dynamic viscosity. ${\overrightarrow{W}}_i$and ${\overrightarrow{W}}_i^{\prime }$ are the random forces and torques acting on the i^th colloidal particle, respectively, which satisfy a fluctuation-dissipation relation $\langle {\overrightarrow{W}}_i\left(t\right)·{\overrightarrow{W}}_j\left(t^{\prime }\right)\rangle =6kT{\Gamma }_t{\delta }_{ij}\delta \left(t-t^{\prime }\right)$ and $\langle {\overrightarrow{W}}_i^{\prime }\left(t\right)·{\overrightarrow{W}}_j^{\prime }\left(t^{\prime }\right)\rangle =6kT{\Gamma }_r{\delta }_{ij}\delta \left(t-t^{\prime }\right)$ (15).

In our Brownian dynamics simulations, all length scales are measured in units of the monomer diameter σ and energies are scaled by ε (ε = 1 kT). We choose Γ_t = 0.5, Γ_r = 0.167, and the time step Δt = 0.005 in reduced time units of σ(m/kT)^1/2 with m = 1. For this choice of Γ_t = 0.5, particle motion is purely diffusive for t >> 1/Γ_t, i.e., t >> 2 in our units. We scale the strength and range of interparticle interaction according to the range of values of the experimental data displayed in the article of Du et al. (6). In particular, the results shown here are for the values ξ = 0.1, U_m = 6 kT, and λ_D = 0.4. We consider three-dimensional systems of sizes L = 64 and 128. We pick a small volume fraction of the molecules, typically of the order of f = 0.01 or 0.02, which is in the range of the experimental values (6). Periodic boundary conditions are enforced to minimize wall effects. All simulations start from a random initial monomer conformation and the results for the kinetics are averaged over several (5, 6, 7, 8, 9, 10) runs.

Results and Discussion

We show typical configurations in the nanochain formation in Fig. 1. We see that initially the monomers form oligomers and the oligomers self-assemble into larger aggregates contained (approximately) within nanospheres, then nanospheres associate together into a chain structure, quite similar to the process of amelogenin self-assembly (see Fig. 3 in Du et al. (6)).

Figure 1.

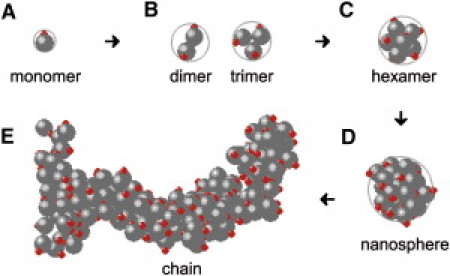
(A) Model of amelogenin molecule consists of a spherical colloid particle and a point charge located on its surface that preserves a bipolar nature. (B and C) Oligomerization of amelogenin molecules occurs by means of hydrophobic interactions and modification due to Coulomb repulsions. (D) Nanosphere structures are formed through aggregation of monomers and oligomers. (E) Further association of nanospheres results in larger assemblies among which chains are formed. (Color online).

The Coulomb forces cause the majority of the charges to point outwards inside the nanospheres, as one would expect; this is shown in Fig. 2. This again is reminiscent of the situation with the hydrophilic tails of amelogenin. To characterize the orientational distribution of point charges within a nanosphere, we introduce a parameter θ, defined as

$$\theta ={\text{cos}}^{-1}\left(\frac{{\overrightarrow{u}}_p\cdot {\overrightarrow{u}}_c}{\left|{\overrightarrow{u}}_p\right|\left|{\overrightarrow{u}}_c\right|}\right),$$

where ${\overrightarrow{u}}_p$ is the position vector of a point charge referenced to the center of its host colloid and ${\overrightarrow{u}}_c$ as the position vector of a colloid referenced to the center of mass of this nanosphere. Therefore, θ < 90° if the charge points outwards and θ > 90° if it points inwards. Due to fluctuations and our choice of short repulsion interaction range, the distribution of θ is spread around a small nonzero peak position, as shown in Fig. 2, for the configuration in the inset. Subsequent aggregation forms via necks between nanospheres, leading to larger structures that eventually form (flexible) nanochains.

Figure 2.

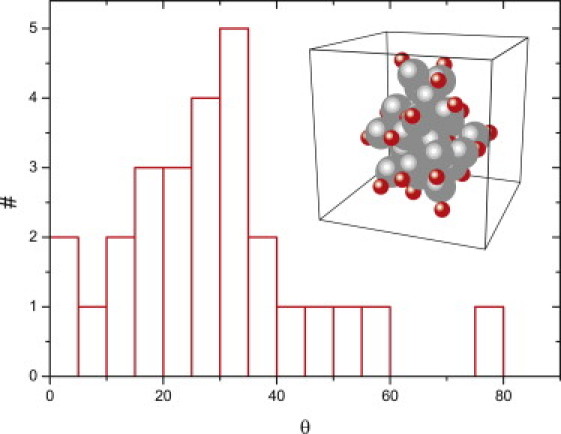
Distribution of θ; θ shows whether the point charge orients outwards (θ < 90°) or inwards (θ > 90°). (Inset) Nanosphere structure, large (gray) spheres indicate amelogenin molecules whereas small (red) ones indicate point charges. (Color online).

We characterize the morphology of the clusters in terms of their fractal dimension D_f. The q-dependence of structure factor S(q,t) shown in Fig. 3 A is given by a slope of –2 on a log-log plot over a reasonable range of wave number q. This value of D_f is larger than the typical diffusion-limited-cluster-cluster aggregation value of 1.8 because the chainlike clusters observed here have significant short-range ordering (16, 17). For this reason, we speculate that the repulsive Coulomb force causes the surface particles to reorganize, which reduces the surface roughness of our model, in contrast to the case without the Coulomb interactions (see Li et al. (9)). We find that a peak develops in the structure factor whose magnitude increases with time. Correspondingly, the peak position decreases as a function of wave number with increasing time; these features typify spinodal decomposition (18). However, we note that for deep quenches that lead to the nonequilibrium cluster growth considered in this model, the system is controlled by two characteristic lengths that evolve differently in time. An apparent scaling for the structure factor can only be observed over some period of time when these two characteristic length scales become comparable to each other (19, 20).

Figure 3.

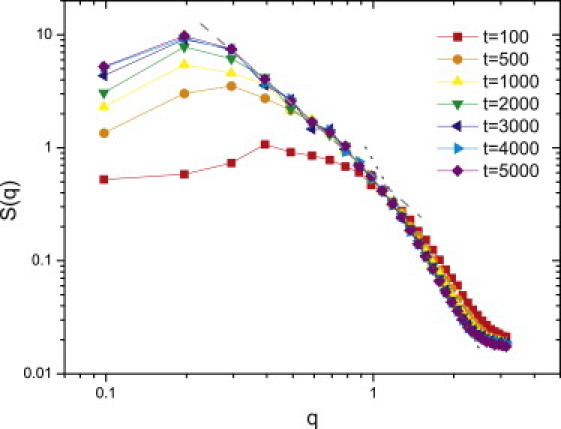
Log-log plot of structure factor at several time steps, q ranges from 2π/L to π in the simulation. (Dashed line) Slope of −2. Fractal clusters with S(q) ∝ q^−Df, where D_f = 2.0. (Dotted line) Slope of −4. Porod regime S(q) ∝ q^−(d+1), d = 3. (Color online).

The kinetics of the cluster growth process in this simple model for amelogenin self-assembly is consistent with a cluster-cluster aggregation mechanism, as shown in Fig. 4. The number of clusters decreases inversely with time (i.e., the kinetic exponent z = 1) and the radius of gyration increases as a power law with an exponent of n = 0.5 (21, 22). The relation between z and n involves the fractal dimension in the following way: n = z/D_f. Thus the kinetic exponents are consistent with a fractal dimension of D_f = 2 as well.

Figure 4.

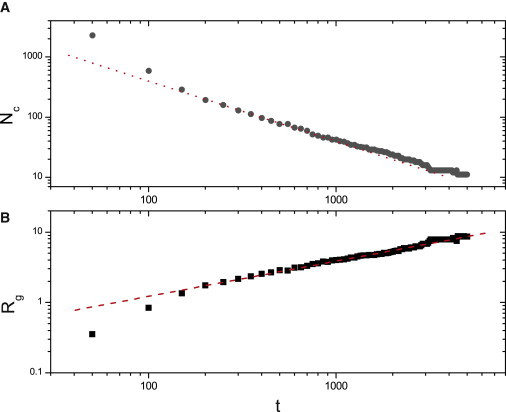
Log-log plot for time evolution of (A) number of clusters, N_c and (B) radius of gyration, R_g. (Dotted line, A) Slope of –1. (Dashed line, B) Slope of 0.50. (Color online).

To check the stability of the clusters produced in straight simulation from a quench (U_m = 6 kT) into the two phase gas-solid region, we “heat” the system formed after 5000 time steps from the initial quench U_m = 6 kT to U_m = 4 kT and run the simulation for another 5000 steps. This heating corresponds to the change in PEG concentration as it is done in the experiment. A typical run (Fig. 5) shows that the nanochains are quite robust under such a change of conditions, as found experimentally for a wide range of conditions (including a change in the PEG concentration). We have also checked the structure factor behavior for the heating process and found that the structure factor curve has the same exponent of –2 as at the cooler temperature (see Fig. 3). This is consistent with the robustness of the major cluster morphology.

Figure 5.

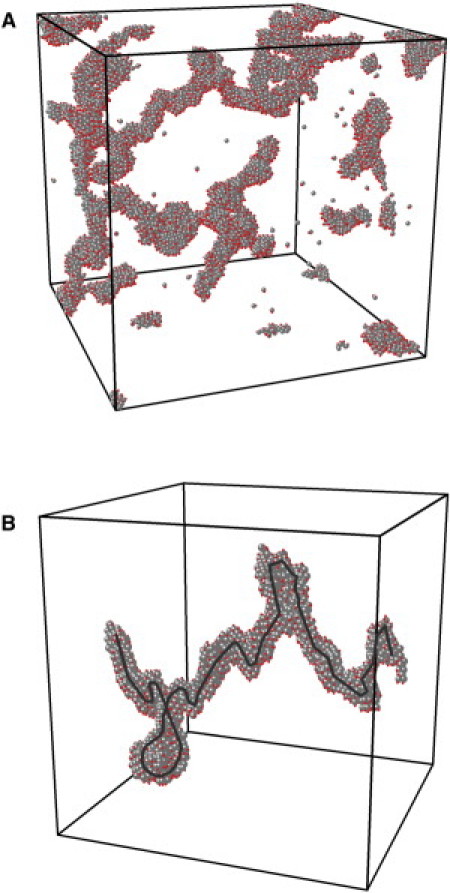
(A) Morphology of entire system (ξ = 0.1, f = 0.02) from another 5000 time steps' shallow quench of U_m = 4 kT after first quench into U_m = 6 kT, 5000 time steps (periodic boundary condition are enforced). (B) One of the clusters inside panel A. (Dark guideline through the cluster) Three-dimensional backbone. Our estimate of this backbone is based on a perspective of the cluster gained from viewing it from several different rotation angles. (Color online).

We characterize these entangled nanochains by computing three eigenvalues of the gyration tensor, denoted as λ₁², λ₂², and λ₃² in descending order (23). We calculate the ratios among these three principal values, which characterize the relative colloid (or charge) particle distribution. A typical result is given in Table 1, for the colloid particles and point charges separately, based on the configuration in Fig. 5 B. These ratios of eigenvalues demonstrate the anisotropy of these clusters, and suggest planar clusters, which might imply that the joining together of chains can eventually lead to the formation of a ribbonlike structure. However, the experimental evidence for this is, at the moment, weak. The difference of the ratios between colloidal particles and point charges may indicate that under electrical repulsion, the rotation of monomers inside the cluster leads to the small reduction of anisotropy in the spatial distribution of the point charges.

Table 1.

Typical ratios of eigenvalues of gyration tensor

	λ12/λ32	λ22/λ32
Colloid particles	9.57	9.03
Point charges	9.25	8.74

From the gyration tensor, we can determine the typical length scales of these clusters by taking square-roots of the eigenvalues. To illustrate this, we use the colloid configuration shown in Fig. 5 B, which gives 18.27, 17.75, and 5.91 for the three length scales. Because the chain structure is the association of several nanospheres (as shown in Fig. 1), the typical diameter of the nanosphere in this configuration is, at the most, 5.91. We can also use this estimate of the diameter to obtain an estimate of the minimum wavenumber that corresponds in Fig. 3 to the crossover to the Porod regime (corresponding to compact clusters on a local scale). This yields a value of q_min ≃ 2π/5.91 = 1.06, which is consistent with the behavior shown in Fig. 3 B. Because the hydrodynamic radius R_H of the amelogenin macromolecule is ∼2.2 nm, the R_H of the nanosphere for the configuration in Fig. 5 B is 2.2 × 5.91 = 13.00 nm; this lies in the range of values of the radii of typical nanospheres, 10 ∼ 25 nm, found in the experiment (compare to Fig. 3, and Du et al. (6)).

Conclusion

We conclude by discussing some issues related to this work:

The first point has to do with the role of the pH in this self-assembly process. The pH could affect the interaction between C-terminal domains of amelogenin monomers, and the monomer's geometric shape, as has been shown in Wiedemann-Bidlack et al. (24) and Delak et al. (25). However, our model is not sufficiently detailed to account for such a change of shape. Rather, the model we have studied here is based on the experimental study of Du et al. (6) for different pH values (4.5, 6.5). In this range, the amelogenin molecule folds into a unique globular form, which we model as a sphere. To extend our model to describe another morphology, such as occurs at pH 3.8 (25) where the monomers are extended and unfolded, would require our choosing such a shape for the monomers. This could be done, but would add considerable complication to the simulations. The main effect of pH in our study is via the Debye-Hückel form for the screened Coulomb potential, in which the Debye screening length and the amplitude of the potential depend on the salt concentration. In this study we chose a value of the prefactor of 1 kT, and a screening length of 0.4, based on the experimental values of parameters in the study of Du et al. (6). However, we have also examined the effects of varying the prefactor from 1 kT to 4 kT and the screening length from 0.4 to 1.2; in all these cases, we found a similar kinetic process and chain formation as reported in this article.

The second point has to do with the possibility of multivalent ions providing another mechanism for amelogenin chain formation. For example, one investigation reported the formation of chains in the presence of calcium ions, in the absence of PEG (26). This relies on the interaction of the ions with the C-terminal sequence of the monomer, leading to a calcium bridging between nanospheres. A theoretical description of this mechanism would require generalizing our model to include the explicit effects of calcium ions interacting with the C-terminal charged sequence, as well as to replace the AO potential model of the depletion interaction due to PEG with some alternative form of the residual hydrophobic interaction. Such a generalization is certainly worth pursuing in future work. Finally, there is some experimental evidence that oligomer subunits can assemble to form chains. From our simulation results we believe that by tuning the interaction strengths and ranges, one could control the size of the stabilized nanospheres, from oligomers to large aggregates. We have found in preliminary simulation work that chains indeed do form from such subunits and we plan to pursue this issue in future work.

In summary, we have developed an anisotropic, bipolar model for the hierarchical self-assembly of amelogenin molecules and have carried out Brownian dynamics simulations of the self-assembly process. Simulations show a hierarchical self-assembly process where the molecules aggregate to form dimers, hexamers to nanospheres, and the assembly of the nanospheres then lead to the formation of nanochains in agreement with experimental findings. The relative strengths of the interaction parameters can lead to a phase diagram where the nanospheres are stable against nanochains formation. Thus a control over the morphology of the clusters can be achieved. Such a study is currently under way.

Editor: R. Dean Astumian.